СПОСОБ ОПРЕДЕЛЕНИЯ ГИДРОДИНАМИЧЕСКИХ ПАРАМЕТРОВ МАТЕМАТИЧЕСКОЙ МОДЕЛИ СУДНА Российский патент 2013 года по МПК B63H25/52 

Изобретение относится к области судовождения и может быть использовано для прогнозирования движения судна при маневрировании.

Известен способ определения гидродинамических параметров математической модели судна (Пат. РФ №2442718, опубл. 20.02.2012), основанный на измерении с помощью приемников спутниковой навигационной системы с дифференциальными поправками в реальном масштабе времени координат двух определенным образом разнесенных в диаметральной плоскости по длине судна точек, условно названных носовой и кормовой, и определении, с использованием данных измерений текущих координат этих точек, текущих значений кинематических параметров движения судна:

- линейных скоростей носовой F (υ_f) и кормовой A (υ_a) точек и их проекций на продольную X (υ_xf, υ_ха) и поперечную Y (υ_yf, υ_ya) координатные оси подвижной системы координат ZXОY, связанной с судном;

- абсциссы центра вращения (х_о) в системе координат ZXОY;

- проекции вектора линейной скорости в центре тяжести на поперечную ось Y (υ_y);

- линейной скорости центра тяжести судна (υ);

- радиуса кривизны траектории ЦТ судна (R);

- угловой скорости судна (ω),

которые используют для вычисления текущих значений гидродинамических параметров математической модели судна, на базе которой выполняют компьютерное моделирование с целью прогнозирования движения судна при маневрировании. Данный способ наиболее близок к предлагаемому и принят за прототип.

Недостатком данного способа является то, что для определения кинематических параметров движения судна приходится прибегать к численному дифференцированию параметров, измеренных с помощью спутниковой навигационной системы, что приводит к снижению точности результатов расчета кинематических параметров движения судна. Указанный недостаток становится более существенным, если точность измерения координат носовой и кормовой точек судна по каким-либо причинам (погодные условия, район плавания и др.) снижается.

Целью предлагаемого способа является исключение отмеченного недостатка при экспериментально-расчетном определении параметров математической модели судна в непрерывном режиме и, как следствие, повышение точности прогнозирования движения судна при выполнении им маневрирования с использованием компьютерного моделирования на базе адекватной математической модели судна.

Технический результат, на достижение которого направлено заявляемое изобретение, состоит в повышении точности прогнозирования движения судна при выполнении им маневрирования.

Для достижения указанного технического результата в способе определения гидродинамических параметров математической модели судна, включающем использование математической модели движения судна, двух разнесенных по длине диаметральной плоскости судна точек носовой F и кормовой A, определение текущих значений кинематических параметров движения судна в подвижной системе координат ZXОY, связанной с судном, и на их основе вычисление текущих гидродинамических параметров математической модели движения судна, компьютерное моделирование движения судна на базе последней, используют датчики ускорений, с их помощью определяют в реальном масштабе времени текущие значения продольных, поперечных и угловых ускорений носовой F (w_fx1, w_fy1, ε) и кормовой A (w_ax1, w_ay1, ε) точек в неподвижной системе координат X₁O₁Y₁, на их основе определяют текущие значения кинематических параметров движения судна.

Предлагаемый способ поясняется чертежом.

Способ заключается в следующем. Математическая модель судна, используемая для компьютерного моделирования при прогнозировании движения судна в процессе маневрирования, представляет собой систему дифференциальных уравнений, общий вид которых, с учетом известных условностей [1], [2], [3], [4], [5], следующий:

$$\begin{array}{l}d{\upsilon }_y/dt=f\left({\upsilon }_x,{\upsilon }_y,\omega ,C_1,C_2,C_3,\dots \right);\\ d\omega /dt=f\left({\upsilon }_x,{\upsilon }_y,\omega ,C_1,C_2,C_3,\dots \right);\left(1\right)\\ d\psi /dt=f\left({\upsilon }_x,{\upsilon }_y,\omega ,C_1,C_2,C_3,\dots \right);\\ d{X}_1/dt=f\left({\upsilon }_x,{\upsilon }_y,\omega ,C_1,C_2,C_3,\dots \right);\\ d{Y}_1/dt=f\left({\upsilon }_x,{\upsilon }_y,\omega ,C_1,C_2,C_3,\dots \right);\end{array}$$

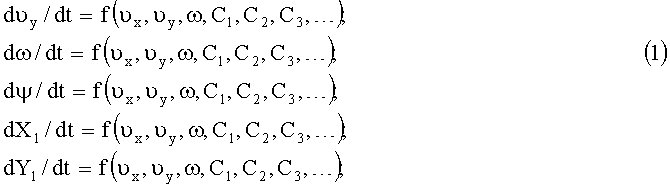
где υ_x, υ_y - проекции вектора линейной скорости в ЦТ судна на продольную ОX и поперечную ОY оси соответственно;

ψ - курс судна;

X₁, Y₁ - координаты ЦТ судна в неподвижной системе координат X₁О₁Y₁;

C₁, С₂, С₃, … - параметры математической модели, численные значения которых определяют в зависимости от геометрических элементов погруженной части корпуса судна, которые постоянны при данном состоянии загрузки последнего [1], [2], [3], [4], [5].

В процессе движения судна с помощью акселерометров определяют продольные, поперечные и угловые ускорения носовой F(w_fx1, w_fy1, ε) и кормовой A (w_ax1, w_ay1, ε) точек судна в неподвижной системе координат X₁О₁Y₁ и рассчитывают продольные и поперечные составляющие линейных скоростей носовой (υ_fx1, υ_fy1) и кормовой (υ_ax1, υ_ay1) точек с использованием известных зависимостей:

$$\begin{array}{l}{\upsilon }_{fx1}={\displaystyle \int w_{fx1}\left(t\right)dt;}\\ {\upsilon }_{fy1}={\displaystyle \int w_{fy1}\left(t\right)dt;}\\ {\upsilon }_{ax1}={\displaystyle \int w_{ax1}\left(t\right)dt;}\left(2\right)\\ {\upsilon }_{ay1}={\displaystyle \int w_{ay1}\left(t\right)dt.}\end{array}$$

Далее рассчитывают продольные и поперечные составляющие линейных скоростей носовой F (υ_fx, υ_fy) и кормовой A (υ_ax, υ_ay) точек судна в подвижной системе координат ZXОY, связанной с судном, с учетом воздействия на судно течения в районе маневрирования:

$$\begin{array}{l}{\upsilon }_{fx}={\upsilon }_{fx1}+{\upsilon }_{st}\cos \left(q_{st}-\psi \right);\\ {\upsilon }_{fy}={\upsilon }_{fx1}-{\upsilon }_{st}\sin \left(q_{st}-\psi \right);\\ {\upsilon }_{ax}={\upsilon }_{ax1}+{\upsilon }_{st}\cos \left(q_{st}-\psi \right);\left(3\right)\\ {\upsilon }_{ay}={\upsilon }_{ay1}-{\upsilon }_{st}\sin \left(q_{st}-\psi \right),\end{array}$$

где υ_st - скорость течения;

q_st - направление течения.

Очевидно, что продольная составляющая линейной скорости судна в любой заданной точке, расположенной на ДП, будет иметь одно значение, следовательно, можно считать, что

$${\upsilon }_{fx}={\upsilon }_{ax}={\upsilon }_x\left(4\right)$$

Используя значения абсциссы носовой точки F в системе координат ZXОY (x_f) и абсциссы кормовой точки A в той же системе координат (x_a), а также поперечные составляющие линейных скоростей в носовой (υ_fy) и кормовой (υ_ay) точках, определенных с использованием зависимостей (3), рассчитывают абсциссу центра вращения судна (см. чертеж) x_o [1], [2], [3], [4], [5] по формуле:

$$x_o=\left({\upsilon }_{ay}{x}_f+{\upsilon }_{fy}{x}_a\right)/\left({\upsilon }_{fy}+{\upsilon }_{ay}\right).\left(5\right)$$

Поперечную составляющую линейной скорости в ЦТ судна определяют по формуле, полученной по чертежу, а именно:

$${\upsilon }_y=\left[{\upsilon }_{fy}\left(x_o-x_G\right)\right]/\left(x_f-x_o\right).\left(6\right)$$

Угловую скорость судна

$$\omega ={\displaystyle \int \epsilon \left(t\right)dt\left(7\right)}$$

Текущие значения коэффициентов C₁, C₂, C₃, … рассчитывают в зависимости от геометрических элементов погруженной части корпуса судна, которые постоянны при данном состоянии загрузки последнего [1], [2], [3], [4], [5].

Таким образом, определяют все гидродинамические параметры математической модели судна, входящие в правые части дифференциальных уравнений (1). Вычислив правые части уравнений (1), можно в любой заданный момент времени рассчитать значения параметров, характеризующих движение судна при выполнении маневрирования, а именно υ_x, υ_y, ω, ψ, X₁, Y₁, что позволяет прогнозировать любой маневр до его выполнения с использованием методов компьютерного моделирования.

Литература

1. Басин A.M. Ходкость и управляемость судов / A.M. Басин. - М.

2. Васильев А.В. Управляемость судов: учеб. пособие / А.В.Васильев. - Л.: Судостроение, 1989. - 328 с.

3. Гофман А.Д. Движительно-рулевой комплекс и маневрирование судна: справочник / А.Д. Гофман. - Л.: Судостроение, 1988. - 360 с.

4. Соболев Г.В. Управляемость корабля и автоматизация судовождения / Г.В. Соболев. - Л.: Судостроение, 1976. - 478 с.

5. Справочник по теории корабля. В 3 т. Т.3: Управляемость водоизмещающих судов. Гидродинамика судов с динамическими принципами поддержания / под ред. Я.И. Войткунского. - Л.: Судостроение, 1985. - 544 с.

Изобретение относится к области судовождения и может быть использовано для прогнозирования движения судна при маневрировании. Способ определения гидродинамических параметров математической модели судна включает использование математической модели движения судна, двух разнесенных по длине диаметральной плоскости судна точек носовой F и кормовой A, определение текущих значений кинематических параметров движения судна в подвижной системе координат ZXОY и на их основе вычисление текущих гидродинамических параметров математической модели движения судна, компьютерное моделирование движения судна на базе последней. Подвижная система координат ZXОY связана с судном. С помощью датчиков ускорений определяют в реальном масштабе времени текущие значения продольных, поперечных и угловых ускорений носовой F (w_fx1, w_fy1, ε) и кормовой A (w_ax1, w_ay1, ε) точек в неподвижной системе координат X₁О₁Y₁. На основе этих значений определяют текущие значения кинематических параметров движения судна. Достигается повышение точности прогнозирования движения судна при выполнении им маневрирования. 1 з.п. ф-лы, 1 ил.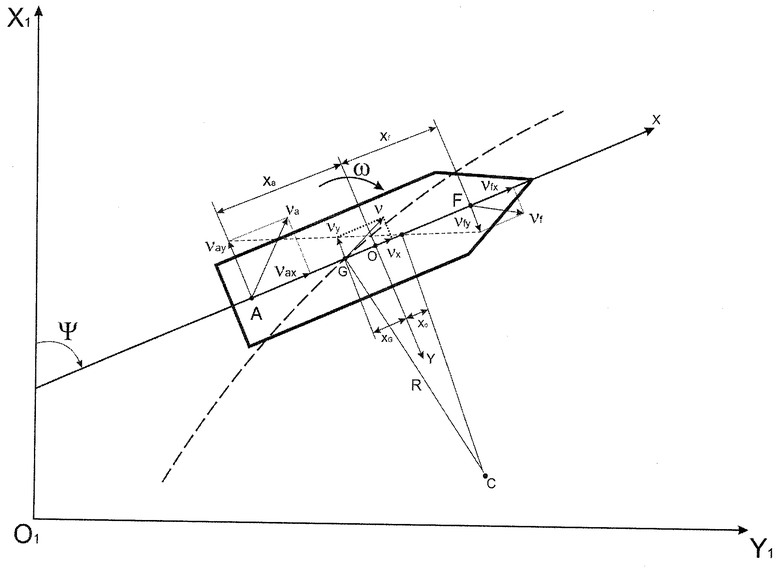

1. Способ определения гидродинамических параметров математической модели судна, включающий использование математической модели движения судна, двух разнесенных по длине диаметральной плоскости судна точек носовой F и кормовой A, определение текущих значений кинематических параметров движения судна в подвижной системе координат ZXОY, связанной с судном, и на их основе вычисление текущих гидродинамических параметров математической модели движения судна, компьютерное моделирование движения судна на базе последней, отличающийся тем, что используют датчики ускорений, с их помощью определяют в реальном масштабе времени текущие значения продольных, поперечных и угловых ускорений носовой F (w_fx1, w_fy1, ε) и кормовой A (w_ax1, w_ay1, ε) точек в неподвижной системе координат X₁О₁Y₁, на их основе определяют текущие значения кинематических параметров движения судна.

2. Способ по п.1, отличающийся тем, что определяют следующие значения кинематических параметров:
- линейные скорости носовой F (υ_f) и кормовой A (υ_a) точек и их проекции на продольную ОX (υ_xf, υ_xa) и поперечную ОY (υ_yf, υ_ya) координатные оси подвижной системы координат ZXОY, связанной с судном;
- абсциссы центра вращения (x_о) в подвижной системе координат ZXОY;
- проекции вектора линейной скорости в центре тяжести на поперечную ось ОY (υ_y);
- угловую скорость судна (ω).