Изобретение относится к способам защиты информации, а более конкретно - к алгоритмам шифрования с публичным ключом, которые применяются для повышения уровня безопасности алгоритмов генерации секретных ключей и шифрования в системах защиты информации на основе идентификационных данных.
Из уровня техники известны способы защиты информации на основе идентификационных данных (СЗИОИД), отличительной чертой которых является возможность использования в качестве публичного ключа уникального идентификатора пользователя (строки произвольной длинны, например, электронного адреса типа someone@somehost.com) [1]. Главным достоинством такой системы является то, что отправителю перед шифрованием не требуется получать публичный ключ получателя и проверять его подлинность. Однако, в системе, реализующей этот способ, необходимо наличие сервера, известного как Генератор Секретных Ключей (ГСК), который генерирует секретные ключи и после аутентификации выдает их пользователям в соответствии с их идентификаторами.
СЗИОИД включает в себя следующий набор этапов:
Этап 1. Начальная инициализация (σ). Алгоритм, который берет на вход параметр безопасности системы σ. На выходе алгоритм выдает (PK, SMK), где РК - публичный ключ системы, SMK - секретный мастер-ключ системы.
Этап 2. Генерация секретного ключа (РК, SMK, ID). Алгоритм, который берет на вход РК, SMK и идентификатор пользователя ID. На выходе алгоритм выдает секретный ключ пользователя SKID.
Этап 3. Шифрование (РК, ID, M). Алгоритм, который берет на вход РК, ID и сообщение M. На выходе алгоритм выдает шифротекст С.
Этап 4. Дешифрование (РК, ID, SKID, С). Алгоритм, который берет на вход РК, ID, SKID и С. На выходе алгоритм выдает М.
Известны несколько реализации СЗИОИД, которые используют разный математический аппарат (см. публикации [2, 3, 4, 5], в которых используют эллиптические кривые; и публикации [6, 7], в которых используют вычеты). Безопасность таких способов и систем базируется на допущении о сложности задачи дискретного логарифмирования или задачи определения квадратичного вычета. Системы защиты информации, основанные на кодах, контролирующих ошибки, базируются на доказано сложной задаче синдромного декодирования случайного линейного кода. Следовательно, применение кодового подхода приводит к обеспечению большей безопасности полученной в результате схемы. Кроме того, кодовые криптосистемы имеют меньшую сложность процедур шифрования и дешифрования по сравнению с криптосистемами на эллиптических кривых, так как требуют только сложения набора двоичных векторов. Однако, криптосистемы, реализованные при помощи эллиптических кривых, имеют высокую вычислительную сложность процедур шифрования и дешифрования, а схемы, базирующиеся на квадратичных вычетах, имеют в основе безопасности допущение о сложности задачи факторизации, что делает их ненадежными в рамках постквантум криптографии.
Наиболее близким к заявляемому способу является техническое решение, предложенное в публикации [8] и описывающее алгоритм цифровой подписи на основе кодов. Ниже приводится краткое описание алгоритма цифровой подписи согласно [8], известного также как «способ Сандрие»:
При начальной инициализации выбирают код Гоппы (n, k), исправляющий t ошибок, и генерируют его проверочную матрицу H размера ((n-k)×n). Секретным мастер-ключом системы является порождающий многочлен Гоппы. Случайным образом выбирают невырожденную матрицу В размера (n-k)×(n-k) и матрицу перестановки Р размера n×n. Вычисляют публичный ключ системы HPK=BHP. Для генерации подписи некоторого сообщения M∈{0,1}* выполняется следующий итерационный алгоритм:
1. Инициализация счетчика рехеширования: counter=0
2. Хеширование исходного сообщения: s=hash(M|counter), через hash() обозначим хэш-функцию, отображающую строку произвольной длины в строку длины (n-k).
3. При помощи известного подписывающему узлу секретного ключа (многочлена Гоппы) выполняют алгоритма декодирования кода Гоппы. В случае успеха возвращают подпись сообщения в виде 
Задача, на решение которой направлено заявляемое изобретение, состоит в создании способа защиты информации на основе идентификационных данных (СЗИОИД) с использованием кодов, контролирующих ошибки, и безопасность которого базируется на доказано сложной задаче. При этом такой способ должен иметь меньшую сложность процедур шифрования и дешифрования, чем существующие аналоги, базирующиеся на эллиптических кривых.
Поставленная задача решается за счет модификации алгоритма цифровой подписи, описанного в прототипе [8] и основанного на кодах.
Основным отличительным признаком заявляемого способа от способа-прототипа является то, что в описанную выше схему цифровой подписи внесены следующие изменения:
- при начальной инициализации
- в зависимости от параметра безопасности σ выбирают двоичный код, имеющий полиномиальный алгоритм декодирования с параметрами (l, k') и корректирующей способностью t' и порождающей матрицей G, а также вероятность р;
- при вычислении секретного ключа пользователя
- применяют процедуру постановки подписи по способу Сандрие;
- при шифровании
- осуществляют предварительное кодирование исходного сообщения в коде, заданном на этапе начальной инициализации (Этап 1), для дальнейшего снятия ошибок на этапе дешифрования (Этап 4);
- закодированное слово шифруют в виде Ci=siAi+Xi, где матрица Ai находится по формуле 
- при дешифровании
- дешифрование осуществляют при помощи секретного ключа по формуле 
- в расшифрованном сообщении производят снятие вектора ошибки SKIDX при помощи декодирования кода, заданного на этапе начальной инициализации (Этап 1) матрицей G, с известной процедурой декодирования.
Далее существо заявляемого изобретения, а именно, СЗИОИД на базе кодов, исправляющих ошибки, поясняется в деталях с привлечением графических материалов, где
Фиг.1. Схема пошагового выполнения этапа начальной инициализации системы.
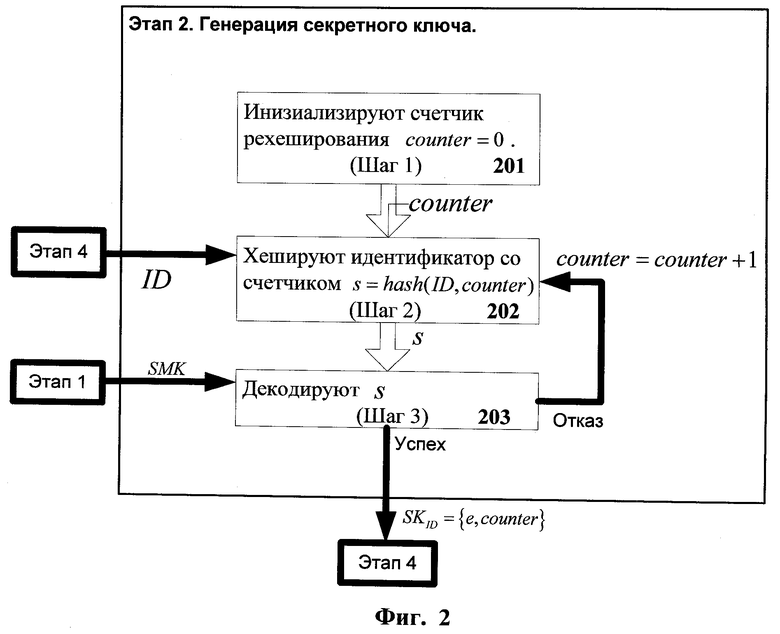
Фиг.2. Схема пошагового выполнения этапа генерации секретного ключа.
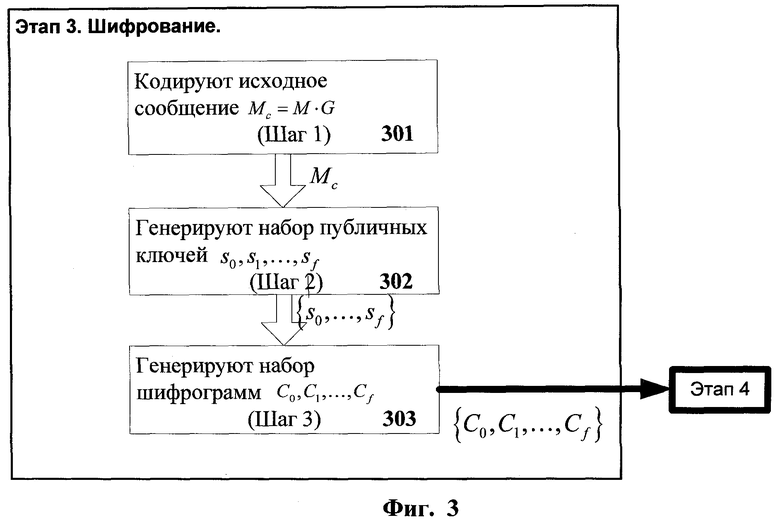
Фиг.3. Схема пошагового выполнения этапа шифрования.
Фиг.4. Схема пошагового выполнения этапа дешифрования.
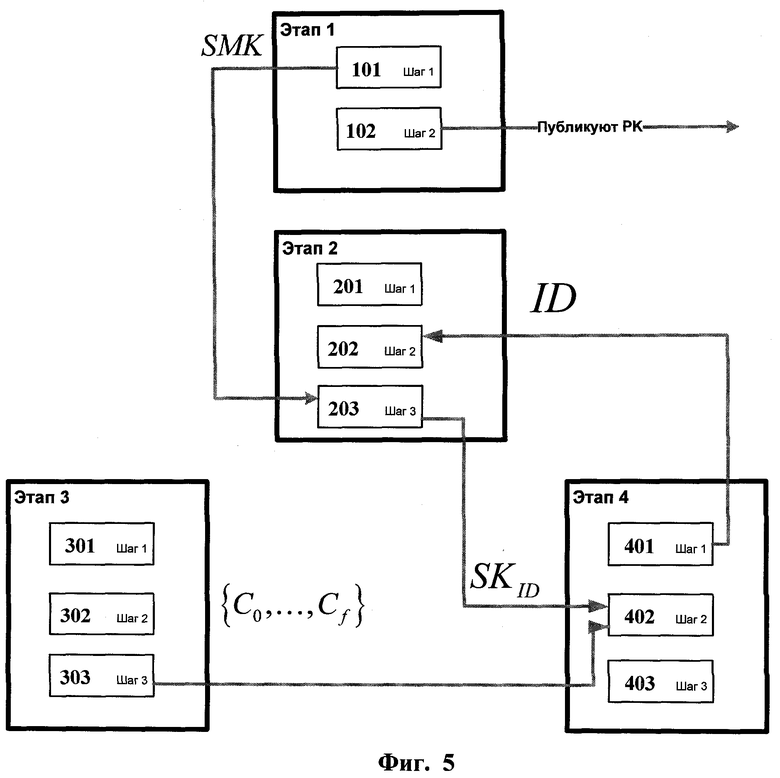
Фиг.5. Схема взаимодействия алгоритмов, реализующих все этапы схемы.
Рассмотрим основные этапы работы СЗИОИД.
Этап 1. Начальная инициализация. Схема данного этапа показана на
Фиг.1. ГСК генерирует публичные параметры системы и секретный мастер-ключ.
Шаг 1 (101). Вычисление секретного мастер-ключа SMK. ГСК выбирает код Гоппы с параметрами (n, k), исправляющий t ошибок и генерирует его проверочную матрицу H размера ((n-k)×n). Секретным мастер-ключом системы является порождающий многочлен Гоппы.
Шаг 2 (102). Вычисление публичного ключа. Случайным образом выбирают невырожденную матрицу B размера (n-k)×(n-k) и матрицу перестановки P размера n×n. Вычисляют HPK=BHP.
В зависимости от параметра безопасности σ выбирают код, имеющий полиномиальный алгоритм декодирования с параметрами (l, k') и корректирующей способностью t' и порождающей матрицей G, а также вероятность р. Итак публичный ключ системы состоит из двух матриц и двух значений: PK=(HRK, G, t, p). Этот ключ публикуют для общего доступа.
Этап 2. Генерация секретного ключа. Схема данного этапа показана на Фиг.2. Эта операция выполняется ГСК в ответ на запрос пользователя о выдаче ключа. Через hash() обозначим хэш-функцию, отображающую строку произвольной длины в строку длины (n-k).
Запрос содержит идентификатор ID пользователя.
Шаг 1 (201). Инициализация счетчика рехеширования: counter=0.
Шаг 2 (202). Хеширование идентификатора: s=hash(ID|counter).
Шаг 3 (202). Попытка декодирования. При помощи известного ГСК мастер-ключа SMK выполняют алгоритма декодирования кода Гоппы. В случае успеха возвращают 
Этап 3. Шифрование. Схема данного этапа показана на Фиг.3.
Шаг 1 (301). Кодирование исходного сообщения, k' бит исходного сообщения кодируют при помощи публичной матрицы G
Mc=MG.
Шаг 2 (302). Генерация набора публичных ключей. При помощи процедуры рехеширования генерируется набор si, i=0, …, f
si=hash(ID/i)
Шаг 3 (303). Генерация набора шифротекстов. Для каждого si, i=0, …, f генерируют матрицу
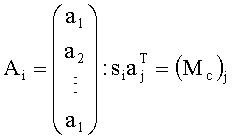
Случайным образом порождают двоичную матрицу 
Этап 4. Дешифрование. Схема данного этапа показана на Фиг.4.
Шаг 1 (401). Дешифрование шифротекст. Получатель сообщения выбирает шифротекст, соответствующий своему секретному ключу Ci:i=counter и вычисляет 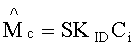
Шаг 2 (402). Декодирование. При помощи известного полиномиального алгоритма декодирования для кода с публичной матрицей G получатель сообщения вычисляет M по 
Взаимодействия алгоритмов, реализующих этапы 1, 2, 3 и 4 описано на Фиг.5. На этапе 1 на шаге 1 (101) генерируют секретный мастер-ключ, который высылают алгоритму этапа 2. На шаге 2 (102) генерируют публичный ключ. который публикуют в общедоступном месте. На этапе 2, получив от алгоритма этапа 4 запрос на выдачу секретного ключа, на шаге 1 (201) инициализирую г счетчик рехеширования. На шаге 2 (202) хешируют пару значений идентификатора и счетчика. На шаге 3 (203) декодируют полученное на шаге 2 (202) значение как синдром и, в случае успеха, отправляют полученный вектор ошибки и значение счетчика алгоритму этапа 4, в случае отказа от декодирования увеличивают счетчик на единицу и возвращаются к шагу 2 (202). На этапе 3, на шаге 1 (301) сначала кодируют информационное сообщение. Затем на шаге 2 (302) генерируют набор публичных ключей. На шаге 3 (303) для каждого публичного ключа генерируют соответствующую шифрограмму и посылают набор шифрограмм алгоритму этапа 4. На этапе 4 на шаге 1 (401) запрашивают секретный ключ у алгоритма этапа 2, потом на шаге 2 (402) дешифруют одну из полученных от алгоритма этапа 3 шифрограмм при помощи секретного ключа, полученного от алгоритма этапа 2. На шаге 3 (403) декодируют полученное на предыдущем шаге сообщение.
Заявляемое изобретение может найти практическое применение в тех случаях, когда требуется обеспечить повышение уровня безопасности алгоритмов генерации секретных ключей и шифрования в системах защиты информации на основе идентификационных данных, например, для поддержки безопасных соединений.
Ссылки:
[1] A. Shamir, Identity-based cryptosystems and signature schemes, Proc. Of Crypto 84, LNCS 196, pp.47-53, 1984
[2] D. Boneh, M. Franklin, Identity Based Encryption from the Weil Pairing, Proc. Crypto 01, LNCS 2139, pp.213-229, 2001
[3] D. Boneh, X. Boyen, Efficient Selective-ID Secure Identity Based Encryption Without Random Oracles, Proc. Eurocrypt 04, LNCS 3027, pp.223-238, 2004
[4] «Systems and methods for identity-based encryption and related cryptographic techniques", US patent application 20030081785, Boneh, Dan (Palo Alto, CA, US), Franklin, Matthew (Davis, CA, US), 2003, May
[5] "Identity-based-encryption system", US patent 7590236, Boneh, Dan (Palo Alto, CA, US). Boyen, Xavier (Palo Alto, CA, US), 2009, September,
[6] С. Cocks, An Identity Based Encryption Scheme based on Quadratic Residues, LNCS 2260, pp.360-363, 2001
[7] D. Boneh, С.Gentry, M. Hamburg, Space-Efficient Identity Based Encryption Without Pairings, Proc. FOCS 07, pp.647-657, 2007
[8] N. Courtois, M. Finiasz, N. Sendrier, How to achieve a MacEliece-based digital signature scheme. Springer-Verlag, 2001
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ПОРОГОВОЙ ГЕНЕРАЦИИ КЛЮЧЕЙ ДЛЯ СИСТЕМЫ ЗАЩИТЫ ИНФОРМАЦИИ НА ОСНОВЕ ИДЕНТИФИКАЦИОННЫХ ДАННЫХ | 2010 |
|
RU2452111C1 |
| СПОСОБ КОДИРОВАНИЯ И ДЕКОДИРОВАНИЯ ЦИФРОВОЙ ИНФОРМАЦИИ В ВИДЕ УЛЬТРАСЖАТОГО НАНОБАР-КОДА (ВАРИАНТЫ) | 2013 |
|
RU2656734C2 |
| СПОСОБ И СИСТЕМА ЗАЩИЩЕННОГО ХРАНЕНИЯ ИНФОРМАЦИИ В ФАЙЛОВЫХ ХРАНИЛИЩАХ ДАННЫХ | 2018 |
|
RU2707398C1 |
| СПОСОБ УПРАВЛЕНИЯ ДЕКОДЕРАМИ ПО МЕНЬШЕЙ МЕРЕ ОДНОЙ ГРУППЫ ДЕКОДЕРОВ, ИМЕЮЩИХ ДОСТУП К АУДИОВИЗУАЛЬНЫМ ДАННЫМ | 2011 |
|
RU2541914C2 |
| СПОСОБ И СИСТЕМА ДЛЯ СЕРИАЛИЗАЦИИ ИЗДЕЛИЙ И ВОССТАНОВЛЕНИЯ ДАННЫХ ИЗ СЕРИАЛИЗОВАННЫХ ИЗДЕЛИЙ | 2021 |
|
RU2829899C1 |
| Способ аутентифицированного шифрования | 2018 |
|
RU2694336C1 |
| СПОСОБ ШИФРОВАНИЯ БЛОКОВ ЦИФРОВЫХ ДАННЫХ | 1997 |
|
RU2124814C1 |
| СИСТЕМА И СПОСОБ УПРОЩЕННОЙ АУТЕНТИФИКАЦИИ ДОСТУПА | 2008 |
|
RU2445740C1 |
| БИОМЕТРИЧЕСКАЯ СИСТЕМА АУТЕНТИФИКАЦИИ | 2004 |
|
RU2316120C2 |
| СПОСОБ ФОРМИРОВАНИЯ КЛЮЧА ШИФРОВАНИЯ/ДЕШИФРОВАНИЯ | 2000 |
|
RU2171012C1 |

Изобретение относится к защите информации, а именно к способам шифрования с открытым (публичным) ключом. Техническим результатом является повышение безопасности. Технический результат достигается тем, что заявлен способ защиты информации на основе идентификационных данных, предусматривающий шифрование исходного сообщения и последующее дешифрование с использованием генератора секретных ключей и с помощью применения вычислительной техники, отличающийся тем, что осуществляют следующие действия: на этапе начальной инициализации вычисляют секретный ключ мастер-ключ и публичный ключ системы, на втором этапе секретный мастер-ключ отправляют на вход алгоритма, реализующего этап вычисления секретного ключа и генерирующего, по запросу алгоритма дешифрования, секретный ключ для нового пользователя системы, на этапе шифрования шифруют исходное сообщение с использованием идентификатора нового пользователя и публичного ключа системы, полученного на этапе начальной инициализации, на этапе дешифрования на вход алгоритма дешифрования подают секретный ключ для нового пользователя и дешифруют сообщение, полученное на этапе шифрования. 4 з.п. ф-лы, 5 ил.
1. Способ защиты информации на основе идентификационных данных, предусматривающий шифрование исходного сообщения и последующее дешифрование с использованием генератора секретных ключей и с помощью применения вычислительной техники, отличающийся тем, что осуществляют следующие действия:
на этапе начальной инициализации вычисляют секретный мастер-ключ в виде порождающего многочлена кода Гоппы и публичный ключ системы, состоящий из двух матриц и двух значений,
на втором этапе секретный мастер-ключ отправляют на вход алгоритма, реализующего этап вычисления секретного ключа при помощи процедуры постановки подписи по способу Сандрие и генерирующего, по запросу алгоритма дешифрования, секретный ключ для нового пользователя системы,
на этапе шифрования предварительно кодируют исходное сообщение, генерируют набор публичных ключей при помощи процедуры рехеширования с использованием идентификатора нового пользователя и публичного ключа системы, полученного на этапе начальной инициализации, а затем шифруют закодированное исходное сообщение, вычисляя набор шифротекстов,
на этапе дешифрования на вход алгоритма дешифрования подают секретный ключ для нового пользователя и дешифруют одно из сообщений, полученных на этапе шифрования и соответствующее секретному ключу, применяя в процессе известный полиномиальный алгоритм декодирования.
2. Способ по п.1, отличающийся тем, что на этапе начальной инициализации в качестве секретного мастер-ключа системы используют двоичный (n, k) код Гоппы, исправляющий t ошибок, а в качестве публичного ключа системы разглашают скрытую проверочную матрицу этого кода HPK, порождающую матрицу G произвольного (l, k') двоичного кода с полиномиальной процедурой декодирования, а также число ошибок, исправляемых кодом Гоппы t и вероятность р для генерации маскирующей матрицы при шифровании.
3. Способ по п.1, отличающийся чем, что на этапе генерации секретного ключа используют итеративную процедуру декодирования случайного синдрома кодом Гоппы, выбранного на этапе инициализации.
4. Способ по п.1, отличающийся тем, что на этапе шифрования осуществляют предварительное кодирование информационного слова М кодом, заданным на этапе начальной инициализации, для дальнейшего исправления ошибок на этапе дешифрования, с последующим шифрованием в виде Ci=siAi+Xi, где матрица 
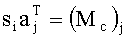

5. Способ по п.1, отличающийся тем, что на этапе дешифрования осуществляют дешифрование при помощи секретного ключа по формуле 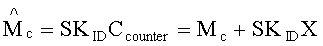
| Приспособление для суммирования отрезков прямых линий | 1923 |
|
SU2010A1 |
| ИСПОЛЬЗОВАНИЕ ИЗОГЕНИЙ ДЛЯ РАЗРАБОТКИ КРИПТОСИСТЕМ | 2004 |
|
RU2376651C2 |
| МНОГООБЪЕМНАЯ БЕЗОПАСНАЯ ПНЕВМАТИЧЕСКАЯ ШИНА | 2013 |
|
RU2526791C2 |
| Приспособление для суммирования отрезков прямых линий | 1923 |
|
SU2010A1 |
| Колосоуборка | 1923 |
|
SU2009A1 |
| N | |||
| Courtois и др., How to achieve a MacEliece-based digital signature scheme, Springer-Verlag, 2001. | |||
Авторы
Даты
2013-09-27—Публикация
2011-05-03—Подача