Изобретение относится к электросвязи и вычислительной технике, в частности к области криптографической защиты электронных данных, передаваемых по телекоммуникационным сетям и сетям ЭВМ, с использованием эллиптических и гиперэллиптических кривых, и может быть использовано в системах передачи данных. Используемые в данном описании специфические термины поясняются в Приложении 1.
Известны системы электронной цифровой подписи (ЭЦП) электронного документа на основе эллиптических кривых [ГОСТ Р 34.10-2001. Криптографическая защита информации. Процессы формирования и проверки электронной цифровой подписи. Госстандарт России, М., 2001]; [ANSI X9.62. Public Key Cryptography for the Financial Services Industry, The Elliptic Curve Digital Signature Algorithm (ECDSA), 2005, http://www.comms.scitech.susx.ac.uk/fft/crypto/ecdsa.pdf], предусматривающие процессы формирования и проверки ЭЦП. Указанные стандарты ЭЦП по сути являются вариантами схем ЭЦП Эль-Гамаля [ElGamal T. A public-key cryptosystem and a signature scheme based on discrete logarithms // IEEE Transactions on Information Theory. 1985. Vol.IT-31. P.469-472.] и Шнорра [Schnorr C.P. Efficient identification and signatures for smart cards // Advances in Cryptology - CRYPTO '89. Lecture Notes in Computer Science. Springer-Verlag. 1990. Vol.435. P.239-252.].
Предусмотренная известными способами ЭЦП эллиптическая кривая состоит из конечного числа точек P=(x, y), удовлетворяющих уравнению y2+a 1xy=x3+a 2x2+a 4x+a 6, допускающих операции сложения и удвоения, см. также Приложение 1. Вычисление точки P+…+P соответствует умножению (называемому также скалярным умножением) точки P на целое число k, обозначаемое kP; умножение точки на число выполняется с использованием сложений и удвоений точек.
Известны способы электронной цифровой подписи на основе гиперэллиптических кривых [FR WO/2004/084485, опубл. 11.03.2004], предусматривающие выполнение действий с битовыми строками (БС), представляющими приведенные дивизоры (см. также Приложение 1).
В известных системах ЭЦП обрабатываемые данные представлены битовой строкой или набором битовых строк. Под битовой строкой (БС) понимается электромагнитный сигнал в цифровой двоичной форме, параметром которого является число битов и порядок следования нулевых и единичных значений. Битовые строки допускают операцию конкатенации, логические и арифметические операции. Формирование и проверка ЭЦП заключается в выполнении действий с БС (преобразованиях БС и выполнении операций с БС) и выполняется с помощью вычислительных устройств, например персональных компьютеров или смарт-карт [доступно с http://www.aloaha.com/press_en/elliptic-curves-and-sha-256-support.php].
В соответствии с Федеральным законом об электронной цифровой подписи юридическая значимость ЭЦП на территории РФ обеспечивается только при реализации ее в соответствии с ГОСТ Р 34.10-2001. Поэтому практически наиболее интересны способы ЭЦП, реализованные в соответствии с действующими стандартами.
Стандарты подписи России [ГОСТ Р 34.10-2001. Криптографическая защита информации. Процессы формирования и проверки электронной цифровой подписи. Госстандарт России, М., 2001], США [ANSI X9.62. Public Key Cryptography for the Financial Services Industry, The Elliptic Curve Digital Signature Algorithm (ECDSA), 2005, доступно с http://www.comms.scitech.susx.ac.uk/fft/crypto/ecdsa.pdf], Германии [Federal Network Agency for Electricity, Gas, Telecommunications, Post and Railway. Notifications in Accordance with the Electronic Signature Act and the Electronic Signature Ordunance (Overview of suitable algorithms) // Federal Gazette, No 19, pp.376, February 5, 2008 (in German)] аналогичны и различаются размером задачи - порядком точки P эллиптической кривой (длиной цикла {P, 2P, 3P, …}), который должен быть большим простым числом q, длина q в ГОСТ Р 34.10-2001 не менее 254 бит, а в ECDSA и стандарте подписи Германии не менее 160 бит.
Стандарты ЭЦП, использующие эллиптические кривые, могут быть легко адаптированы для гиперэллиптических кривых, при этом точка эллиптической кривой заменяется на приведенный дивизор (ПД) гиперэллиптической кривой, сложение точек эллиптической кривой заменяется сложением ПД, а число точек эллиптической кривой заменяется числом ПД гиперэллиптической кривой [Scholten J., Vercauteren F. An introduction to elliptic and hyperelliptic curve cryptography and the NTRU cryptosystem, доступно с http://homes.esat.kuleuven.be/~fvercaut/papers/cc03.pdf], [Ростовцев А.Г. Алгебраические основы криптографии. - СПб.: Мир и Семья, Интерлайн, 2000, главы 6, 7], см. также Приложение. Поэтому для изложения сути заявленного способа достаточно рассмотреть только преобразования БС и операции с БС, предусмотренные в ГОСТ Р 34.10-2001.
Параметрами системы ЭЦП является эллиптическая кривая и точка P простого порядка q>2254 (см. Приложение 1) длиной 254-256 бит. Секретным ключом формирования ЭЦП является натуральное число d, 1≤d≤q-1. Открытым ключом проверки ЭЦП является точка Q=dP, которая задается парой координат длиной по 256 бит каждая. Таким образом, точка эллиптической кривой задается битовой строкой длиной 512 бит.
Для формирования ЭЦП вырабатывают случайную БС, представляющую целое число k, 0<k<q, вычисляют БС, представляющую точку kP, и вычисляют БС, представляющую собственно подпись для электронного документа. В ходе проверки ЭЦП на основе БС, представляющей подпись, и соответствующего электронного документа вычисляют числа z1, z2, 0<z1, z2, <q, и вычисляют БС, представляющие точки z1P, z2Q, с помощью которых судят о подлинности подписи. При умножении точки на число выполняются преобразования БС и логические и арифметические операции с БС.
Скорость формирования и проверки ЭЦП определяется числом выполняемых операций сложения и умножения точек эллиптической кривой. Для повышения скорости процесса формирования и проверки ЭЦП достаточно снизить число операций, выполняемых при умножении фиксированной точки эллиптической кривой на заранее неопределенное число.
Известно устройство, где числа представлены в системе счисления с нецелым основанием [RU 99103806, МПК G06F 7/49, опубл. 27.01.2001]. Однако оно не может быть использовано в системах ЭЦП.
Известен способ [RU 2232476, МПК H04L 9/30, опубл. 7.10.2004]. Недостатком этого способа является то, что он практически не увеличивает скорость формирования и проверки ЭЦП.
Известны способы формирования и проверки ЭЦП [RU 2382505, МПК H04L 9/32, опубл. 20.02.2010], [RU 2380838, МПК H04L 9/32, опубл. 27.01.2010]. Недостатком этих способов является то, что они не совместимы с ГОСТ Р 34.10-2001.
Известны способы формирования и проверки ЭЦП на эллиптической кривой [US 6898284, 7590235 МПК H04L 9/30]. Недостатком данных способов является то, что они не применимы к большинству используемых на практике эллиптических кривых.
Известен способ формирования и проверки ЭЦП на эллиптической кривой [US 20030123655, H04K 1/00, опубл. 29.01.2002], предусматривающий два этапа при умножении точки на число. Недостатком способа является то, что он не применим к подавляющему числу эллиптических кривых, которые могут быть использованы для криптографических целей, и не совместим с ГОСТ Р 34.10-2001.
За прототип принят способ умножения фиксированной точки P простого порядка q на число k, представленное в двоичной системе счисления при формировании и проверке ЭЦП, заключающийся в использовании операций сложения и удвоения точек в соответствии с двоичным представлением числа k, предусматривающий разбиение числа k на цепочки небольшой длины n и использование таблицы предвычислений [US 20090214023, H04L 9/30, опубл. 26.02.2008]. Способ предусматривает два этапа. На первом этапе вычисляются вспомогательные БС, зависящие от P и q и представляющие произведения всевозможных значений цепочек на точку P. При этом каждая из указанных вспомогательных БС состоит из идентификатора, соответствующего значению цепочки, и значения точки эллиптической кривой. На втором этапе точку kP вычисляют рекурсивно, начиная со старших разрядов. При этом вектор двоичных коэффициентов числа k разбивают на цепочки n бит, выбирают вспомогательную БС, полученную на первом этапе, идентификатор которой соответствует старшей цепочке, выбирают из указанной БС координаты точки эллиптической кривой и присваивают их значение точке R. Под присвоением значения точке понимается присвоение ее координатам соответствующих значений. Выполняют рекурсивный переход к предыдущей цепочке. Для этого выполняют n удвоений точки R, значение полученной суммы присваивают точке R, выбирают вспомогательную БС, первая часть которой соответствует указанной предыдущей цепочке, складывают точку R с точкой, заданной второй и третьей частями указанной вспомогательной БС, и значение суммы присваивают точке R. Рекурсию повторяют до тех пор, пока не будет использована цепочка младших коэффициентов.
Например, при длине цепочки 4 бита на первом этапе подготавливают вспомогательные БС вида 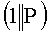 ,
, 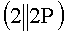 ,
, 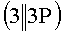 , …
, … 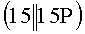 , где
, где 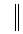 - символ конкатенации битовых строк, левая часть битовой строки - идентификатор, правая часть - координаты точки эллиптической кривой. На втором этапе для
- символ конкатенации битовых строк, левая часть битовой строки - идентификатор, правая часть - координаты точки эллиптической кривой. На втором этапе для 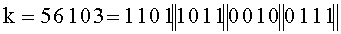 (старшие разряды слева) получают k=13∗163+11∗162+2∗16+7. При вычислении точки kP выбирают вспомогательную БС с идентификатором 13, соответствующим старшему коэффициенту числа k, выбирают из этой битовой строки точку 13P, выполняют 4 удвоения этой точки, полученную точку складывают с точкой 11P, которую выбирают как вторую и третью части БС, первая часть которой имеет код 11 второго коэффициента числа k, выполняют 4 удвоения полученной суммы, полученную точку складывают с точкой 2P, которую выбирают как вторую и третью части БС, первая часть которой имеет код 2 третьего коэффициента числа k, выполняют 4 удвоения, полученную точку складывают с точкой 7P, которую выбирают как вторую и третью части БС, первая часть которой имеет код 7 четвертого коэффициента числа k, и получают окончательный результат. Недостатком этого способа является низкая скорость обработки данных, обусловленная тем, что число удвоений точки равно длине БС, представляющей число k.
(старшие разряды слева) получают k=13∗163+11∗162+2∗16+7. При вычислении точки kP выбирают вспомогательную БС с идентификатором 13, соответствующим старшему коэффициенту числа k, выбирают из этой битовой строки точку 13P, выполняют 4 удвоения этой точки, полученную точку складывают с точкой 11P, которую выбирают как вторую и третью части БС, первая часть которой имеет код 11 второго коэффициента числа k, выполняют 4 удвоения полученной суммы, полученную точку складывают с точкой 2P, которую выбирают как вторую и третью части БС, первая часть которой имеет код 2 третьего коэффициента числа k, выполняют 4 удвоения, полученную точку складывают с точкой 7P, которую выбирают как вторую и третью части БС, первая часть которой имеет код 7 четвертого коэффициента числа k, и получают окончательный результат. Недостатком этого способа является низкая скорость обработки данных, обусловленная тем, что число удвоений точки равно длине БС, представляющей число k.
Существенные признаки прототипа:
1. Способ умножения фиксированной точки P простого порядка q эллиптической кривой на целое число k, причем допускается случайный выбор числа k, который может использоваться при формировании и проверке ЭЦП, обрабатываемые данные представляют собой БС, способ предусматривает преобразование БС и выполнение операций с БС и состоит из двух этапов: на первом этапе подготавливают вспомогательные БС, на втором этапе выполняют умножение P на k путем удвоений и сложений точек эллиптической кривой с помощью вспомогательных БС.
2. Число k представляют в системе счисления с целым основанием.
3. На первом этапе выбирают длину цепочки n и вычисляют БС, представляющие точки miP, где 1≤mi<2n (для целых чисел mi, представленных всеми возможными ненулевыми значениями цепочек), причем каждая БС содержит идентификатор (число mi) и координаты точки miP.
4. На втором этапе вектор коэффициентов двоичного числа k разбивают на цепочки размера n. Умножение точки на число выполняют рекурсивно, начиная со старших разрядов. При этом из вспомогательной БС, идентификатор которой соответствует коду старшей цепочки, выбирают точку эллиптической кривой и значение этой точки присваивают точке R. Рекурсивный переход к предыдущей цепочке состоит из n удвоений точки R и присвоения результата точке R, выбора точки эллиптической кривой из БС, идентификатор которой соответствует значению предыдущей цепочки, сложения этой точки с точкой R и присвоения значения суммы точке R.
Задачей заявляемого технического решения является увеличение скорости формирования и проверки электронной цифровой подписи с использованием эллиптических или гиперэллиптических кривых.
Поставленная цель достигается тем, что число k переводят в систему счисления с основанием 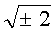 так, что длина БС, представляющей число k, практически не меняется, в результате при использовании четного n число удвоений точек сокращается примерно вдвое. Указанный перевод числа k возможен благодаря тому, что для чисел вида
так, что длина БС, представляющей число k, практически не меняется, в результате при использовании четного n число удвоений точек сокращается примерно вдвое. Указанный перевод числа k возможен благодаря тому, что для чисел вида 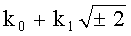 , где k0, k1 - целые числа, существует алгоритм Евклида [Lemmermeyer F. The Euclidean algorithm in algebraic number fields, Expo. Math. 13, No.5 (1995), 385-416]. При этом при формировании ЭЦП случайное число k изначально генерируют в виде
, где k0, k1 - целые числа, существует алгоритм Евклида [Lemmermeyer F. The Euclidean algorithm in algebraic number fields, Expo. Math. 13, No.5 (1995), 385-416]. При этом при формировании ЭЦП случайное число k изначально генерируют в виде 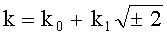 .
.
Ниже перечислены существенные признаки предлагаемого способа. Поскольку способ применим для формирования и проверки ЭЦП на основе как эллиптических, так и гиперэллиптических кривых, то соответствующие существенные признаки для гиперэллиптических кривых указаны в скобках.
1. Способ формирования и проверки электронной цифровой подписи на основе эллиптической или гиперэллиптической кривой, заключающийся в преобразовании БС и выполнении операций с БС, в котором при формировании или при проверке ЭЦП умножают по крайней мере одну заранее определенную точку (ПД) P простого порядка q эллиптической (гиперэллиптической) кривой на целое число k путем сложений и удвоений, при формировании ЭЦП допускается случайный выбор числа k, причем для указанного умножения используют два этапа: на первом этапе выбирают четную длину цепочки n и подготавливают вспомогательные БС, содержащие произведение точки эллиптической кривой (ПД гиперэллиптической кривой) на целые числа, представленные всеми допустимыми значениями цепочек, причем каждая указанная БС содержит хотя бы один идентификатор, на втором этапе рекурсивно выполняют указанное умножение с использованием указанных вспомогательных БС, при этом вектор коэффициентов числа к разбивают на цепочки длины n, выбирают вспомогательную БС, один из идентификаторов которой соответствует старшей цепочке, и значение этой точки (приведенного дивизора) этой БС присваивают точке эллиптической кривой (ПД гиперэллиптической кривой) R, и выполняют рекурсивный переход к предыдущей цепочке, присваивая точке R значения удвоений R и суммы R с точкой эллиптической кривой (ПД гиперэллиптической кривой) БС, один из идентификаторов которой соответствует предыдущей цепочке.
2. На первом этапе выбирают число w=-2 при q≡1, 3 (mod 8) или w=2 при q≡1, 7 (mod 8), вычисляют значение 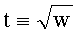 (mod q), а на втором этапе число k преобразовывают в систему счисления с основанием t:
(mod q), а на втором этапе число k преобразовывают в систему счисления с основанием t:
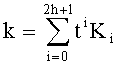 ,
,
где все коэффициенты Ki принимают значения 0, 1 или -1 и 2h≈log2q, а в ходе рекурсивного перехода к предыдущей цепочке коэффициентов выполняют n/2 удвоений точки (приведенного дивизора) R.
3. При формировании подписи случайное число k выбирают в виде пары целых случайных чисел (k0, k1) так, что выполняется условие |k0 2-wk1 2|<q, и полагают k=k0+tk1.
4. Если n≥4 и w=-2, то каждая вспомогательная битовая строка содержит все эквивалентные идентификаторы, обладающие одинаковым значением по модулю q, либо каждая вспомогательная битовая строка содержит идентификатор, значение которого равно абсолютно наименьшему из эквивалентных идентификаторов, а на втором этапе выполняют преобразование цепочек коэффициентов числа k, при котором цепочки вида (…, 1, z, 1, …) заменяются на цепочки вида (…, -1, z, 0, …), а цепочки вида (…, -1, z, -1, …) заменяются на цепочки вида (…, 1, z, 0, …,) причем z означает любую из цифр 0, 1, -1.
5. На первом этапе дополнительно подготавливают БС, представляющие целые числа A и B, такие, что выполняются условия: eq=A2-wB2, e=±1, и целое число А+Bt делится на q.
6. На втором этапе вычисляют ближайшее к дроби (Ak/(eq)) целое число n1 и ближайшее к дроби (Bk/(eq)) целое число n2, вычисляют числа k0=k-An1+wBn2, k1=-Bn1+An2, преобразовывают их в двоичный вид k0=k00+2k01+…+2hk0h, k1=k10+2k11+…+2hk1h и для i=0, 1, …, 2h+1 полагают K2i=±k0i, K2i+1=±k1i для всех i≥0, где знаки определяют с учетом знака w.
В п.1 указаны существенные признаки, общие с прототипом, в п.2 указаны отличительные признаки, общие для данного изобретения. В пп.3-6 указаны признаки для вариантов исполнения.
Способ содержит два этапа. На первом этапе подготавливают вспомогательные битовые строки, зависящие от P, q. Выбирают числа w=-2 при q≡1, 3 (mod 8) или w=2 при q≡±1 (mod 8), вычисляют значение 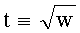 (mod q), выбирают длину цепочки - малое четное число n (на практике обычно n=2 или n=4, так как необходимый объем памяти растет как экспонента от n), и подготавливают следующие вспомогательные БС, зависящие от P и q: вычисляют точки (ПД), представляющие все возможные значения точек (ПД) вида
(mod q), выбирают длину цепочки - малое четное число n (на практике обычно n=2 или n=4, так как необходимый объем памяти растет как экспонента от n), и подготавливают следующие вспомогательные БС, зависящие от P и q: вычисляют точки (ПД), представляющие все возможные значения точек (ПД) вида 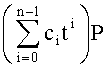 , где ci=0, 1 или -1, при этом для четных i все ci либо неотрицательны либо неположительны и для нечетных i все ci либо неотрицательны либо неположительны. Поскольку по точке (ПД) легко найти противоположную точку (противоположный ПД), достаточно вычислить точки (ПД) вида
, где ci=0, 1 или -1, при этом для четных i все ci либо неотрицательны либо неположительны и для нечетных i все ci либо неотрицательны либо неположительны. Поскольку по точке (ПД) легко найти противоположную точку (противоположный ПД), достаточно вычислить точки (ПД) вида 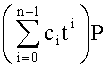 с точностью до знака суммы
с точностью до знака суммы 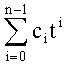 , являющейся идентификатором. Для n=2 возможны следующие значения пар (c0, c1): (0, 0) (соответствует нулевому элементу группы, см. Приложение 1), (1, 0) (соответствует заданной точке (ПД) P), (-1, 0) (соответствует точке (ПД) -P), (0, 1), (0, -1) (противоположна к предыдущей точке (предыдущему ПД)), (1, 1), (-1, -1) (противоположна к предыдущей точке (предыдущему ПД)), (1, -1), (-1, 1) (противоположна к предыдущей точке (предыдущему ПД)). Поэтому кроме P вычисляют 3 точки (ПД) {tP, (1+t)P, (1-t)P)}.
, являющейся идентификатором. Для n=2 возможны следующие значения пар (c0, c1): (0, 0) (соответствует нулевому элементу группы, см. Приложение 1), (1, 0) (соответствует заданной точке (ПД) P), (-1, 0) (соответствует точке (ПД) -P), (0, 1), (0, -1) (противоположна к предыдущей точке (предыдущему ПД)), (1, 1), (-1, -1) (противоположна к предыдущей точке (предыдущему ПД)), (1, -1), (-1, 1) (противоположна к предыдущей точке (предыдущему ПД)). Поэтому кроме P вычисляют 3 точки (ПД) {tP, (1+t)P, (1-t)P)}.
Для n=4 и w=2 вычисляют БС, представляющие 23 точки (ПД), здесь множитель элемента P является идентификатором:
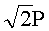 ,
, 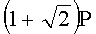 ,
, 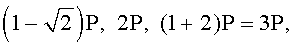
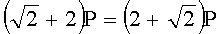 ,
,
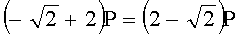 ,
, 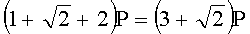 ,
, 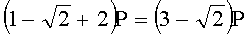 ,
,
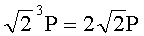 ,
, 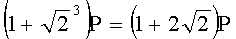 ,
, 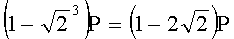 ,
,
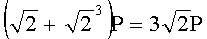 ,
, 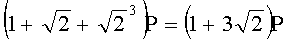 ,
,
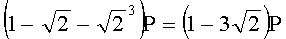 ,
, 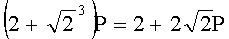 ,
, 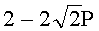 ,
,
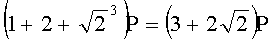 ,
, 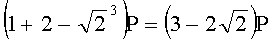 ,
,
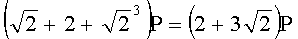 ,
, 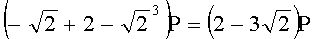 ,
,
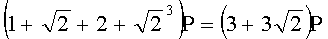 ,
, 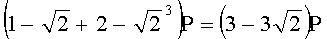 .
.
Для n=4 и w=-2 вычисляют БС, представляющие 11 точек (ПД):
2P, 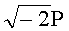 ,
, 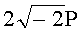 ,
, 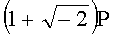 ,
, 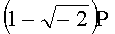 ,
, 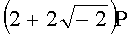 ,
, 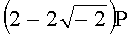 ,
,
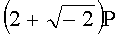 ,
, 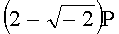 ,
, 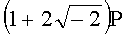 ,
, 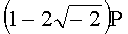 ,
,
поскольку справедливо равенство 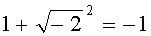 , задающее эквивалентность некоторых сумм
, задающее эквивалентность некоторых сумм 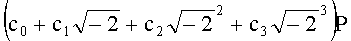 . Например,
. Например, 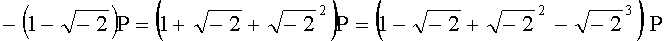 .
.
При формировании ЭЦП по ГОСТ Р 34.10-2001, ECDSA, схемам Эль-Гамаля, Шнорра необходимо выбрать случайное число k и умножить на него точку (ПД) P. В этом случае выбирают пару случайных целых чисел k0, k1, суммарная длина которых близка к длине БС, представляющей число q так, что выполняется условие |k0 2-wk1 2|<q, полагают k=k0+k1t, при этом перевод числа k в систему счисления с основанием t выполняют следующим образом. Находят представление чисел k0, k1 в системе счисления с основанием 2: k0=k00+2k01+22k02+…2hk0h и k1=k10+2k11+22k12+…+2hk1h. Находят число k в системе счисления с основанием t: 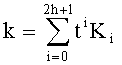 , где K2i=±k0i, K2i+1=±k1i, знак определяется с учетом равенства t2=±2. Вектор коэффициентов (K0, …, K2h+1) при необходимости дополняют нулями справа так, чтобы его длина, равная 2h+2, была кратна n. В остальном процесс формирования ЭЦП аналогичен ГОСТ Р 34.10-2001 (ECDSA, схемам Эль-Гамаля, Шнорра). Сформированная ЭЦП для электронного документа представляется битовой строкой.
, где K2i=±k0i, K2i+1=±k1i, знак определяется с учетом равенства t2=±2. Вектор коэффициентов (K0, …, K2h+1) при необходимости дополняют нулями справа так, чтобы его длина, равная 2h+2, была кратна n. В остальном процесс формирования ЭЦП аналогичен ГОСТ Р 34.10-2001 (ECDSA, схемам Эль-Гамаля, Шнорра). Сформированная ЭЦП для электронного документа представляется битовой строкой.
Для проверки ЭЦП по схемам ГОСТ Р 34.10-2001, ECDSA, а также по схемам Эль-Гамаля, Шнорра необходимо умножить точку (ПД) P на целое число k, зависящее от электронного документа или БС, представляющей ЭЦП. В этом случае выполняют перевод k в систему счисления с основанием t. Для этого на первом этапе находят БС, представляющие числа A, B, такие, что выполняются условия eq=A2-wB2, где e=±1, и A+Bt≡0 (mod q). Числа A, B всегда существуют при w=-2 и q≡1, 3 (mod 8) и при w=2 и q≡1, 7 (mod 8). Их можно найти алгоритмом Полларда и Шнорра [Pollard J.M., Schnorr СР. An efficient solution of the congruence x2+ky2=m (mod n) // IEEE Transactions on Information Theory. 1987. Vol.IT-33. №.5. p.702-709], см. также Приложение 1, при w=-2 числа можно найти с использованием пакета MATHEMATICA командой QuadraticRepresentation[2,q] [http://documents.wolfram.com/v5/Add-[onsLinks/StandardPackages/NumberTheory]./NumberTheoryFunctions. html].
Длина БС, представляющей значение 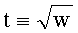 (mod q), не превышает длины строки, представляющей число q, при этом выполняется условие t2-w≡0 (mod q). Для вычисления t можно воспользоваться алгоритмом, описанным в работе [Ростовцев А.Г. Алгебраические основы криптографии. - СПб.: Мир и Семья, Интерлайн, 2000, глава 7], см. также Приложение 1.
(mod q), не превышает длины строки, представляющей число q, при этом выполняется условие t2-w≡0 (mod q). Для вычисления t можно воспользоваться алгоритмом, описанным в работе [Ростовцев А.Г. Алгебраические основы криптографии. - СПб.: Мир и Семья, Интерлайн, 2000, глава 7], см. также Приложение 1.
На втором этапе число k переводят в систему счисления с основанием t с коэффициентами из множества {0, 1, -1}. Для этого находят ближайшее целое число n1 к дроби Ak/(eq) и ближайшее целое число n2 к дроби Bk/(eq), находят целые числа k0=k-An1+wBn2, k1=-Bn1+An2. При этом выполняется условие k≡k0+tk1 (mod q), а длина БС, представляющих числа k0, k1, оказывается минимальной. Число k переводят в систему счисления с основанием t так же, как описано выше: 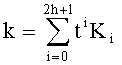 . Вектор коэффициентов (K0, …, K2h+1) при необходимости дополняют нулями справа так, чтобы его длина, равная 2h+2, была кратна n.
. Вектор коэффициентов (K0, …, K2h+1) при необходимости дополняют нулями справа так, чтобы его длина, равная 2h+2, была кратна n.
Для умножения точки (ПД) P на число k вектор коэффициентов (K0, …, K2h+1) разбивают на цепочки из n элементов и вычисляют число k в виде:
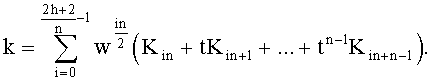
В соответствии со значением цепочки старших коэффициентов:
(K2h-n+2+tK2h-n+3+…+tn-1K2h+1)
выбирают найденную на первом этапе БС с соответствующим идентификатором, из этой БС выбирают точку (ПД) вида:
R=(K2h-n+2+tK2h-n+3+…+tn-1K2h+1)P.
Если вспомогательные БС, представляющие точки (ПД), определены до знака, то может потребоваться смена знака выбранной точки (ПД). Выполняют рекурсивный переход к предыдущей цепочке коэффициентов. Для этого выполняют n/2 последовательных удвоений точки (ПД) R, при каждом удвоении заменяя R на 2R, при этом в случае нечетного n и w=-2 до начала удвоений или после их окончания заменяют R на -R, результат, равный wn/2R, складывают с точкой (ПД), представленной вспомогательной БС, идентификатор которой соответствует предыдущей цепочке коэффициентов, при необходимости заменяя эту точку (ПД) противоположной, и значение суммы присваивают точке (ПД) R. Рекурсивный переход выполняется ((2h+2)/n) - 1 раз.
В случае w=-2 и n≥4 одна точка эллиптической кривой (ПД гиперэллиптической кривой), найденная на первом этапе, может соответствовать нескольким значениям цепочек коэффициентов (Kin+tKin+1+…+tn-1Kin+n-1). Для установления однозначного соответствия между указанными БС и значениями цепочек коэффициентов необходимо либо на втором этапе преобразовать цепочки коэффициентов либо на первом этапе дополнить указанные БС списком соответствующих цепочек коэффициентов.
В остальном процесс проверки ЭЦП аналогичен ГОСТ Р 34.10-2001 (ECDSA, схемам Эль-Гамаля, Шнорра).
Заявленный способ позволяет уменьшить число удвоений точек примерно вдвое и за счет этого повысить скорость формирования и проверки электронной цифровой ЭЦП примерно в 1,5 раза.
Предлагаемый способ может быть применен для формирования и проверки ЭЦП как во вновь проектируемых, так и в существующих системах ЭЦП, использующих эллиптические и гиперэллиптические кривые, в частности в системах ЭЦП, реализованных в соответствии с ГОСТ Р 34.10-2001, ECDSA, стандартом ЭЦП Германии. В одной и той же системе ЭЦП может использоваться указанный выбор случайного числа в виде k=k0+k1t при формировании ЭЦП и перевод целого числа k в систему счисления с основанием t при проверке ЭЦП.
Рассмотрим примеры реализации заявленного способа для небольших чисел p, q. Достаточно проиллюстрировать умножение точки эллиптической кривой или ПД гиперэллиптической кривой на заданное целое число.
Пример 1. Используется система счисления с основанием 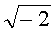 , n=2. Исходные данные. Эллиптическая кривая задана уравнением y2≡x3+x+98 (mod 1049), точка P=(1, 10). Число точек на эллиптической кривой равно q=1033. На первом этапе находят следующие числа:
, n=2. Исходные данные. Эллиптическая кривая задана уравнением y2≡x3+x+98 (mod 1049), точка P=(1, 10). Число точек на эллиптической кривой равно q=1033. На первом этапе находят следующие числа: 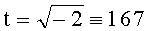 (mod q), A=31, B=6, при этом выполняется условие
(mod q), A=31, B=6, при этом выполняется условие 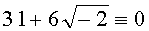 (mod q). Находят вспомогательные БС, содержащие идентификаторы вида {1, t, 1+t, 1-t) и точки P=(1, 10), tP=(441, 731), (1+t)P=(705, 305), (1-t)P=(597, 412), соответствующие этим идентификаторам:
(mod q). Находят вспомогательные БС, содержащие идентификаторы вида {1, t, 1+t, 1-t) и точки P=(1, 10), tP=(441, 731), (1+t)P=(705, 305), (1-t)P=(597, 412), соответствующие этим идентификаторам: 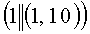 ,
, 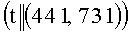 ,
, 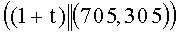 ,
, 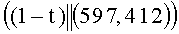 .
.
На втором этапе для формирования (проверки) подписи требуется умножение точки P на число k=527, это число представляют в системе счисления с основанием 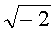 , для чего вычисляют следующие числа:
, для чего вычисляют следующие числа: 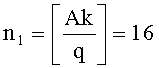 ,
, 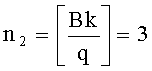 , k0=k-An1-2Bn2=-5, k1=-Bn1+An2=-3, находят представление k≡-1-t+t3-t4 (mod q),
, k0=k-An1-2Bn2=-5, k1=-Bn1+An2=-3, находят представление k≡-1-t+t3-t4 (mod q),
k≡-(1+t)+(-2)·(0+t)+22(-1+0t) (mod q).
Старшая пара коэффициентов в представлении числа k равна -(1+0·t). Выбирают вспомогательную БС с идентификатором 1 и полагают R=-P=(1, 1039). Выполняют удвоение точки R и вычисляют противоположную точку: -2R=(40, 192) и полагают R=(40, 192). Выбирают следующую пару коэффициентов (0+t), соответствующую идентификатору t. Выбирают из вспомогательных БС точку (0+t)P=(441, 731) и вычисляют точку R=(40, 192)+(441, 731)=(416, 56). Вычисляют точку -2R=(335, 62) и полагают R=(335, 62). Последняя пара коэффициентов равна (-1-t)=-(1+1), ей соответствует идентификатор (1+t). Выбирают точку 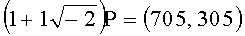 и находят противоположную к ней точку
и находят противоположную к ней точку 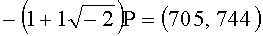 . Вычисляют точку (335, 62)+(705, 744)=(657, 694). Результат: kP=(657, 694). Потребовалось 2 удвоения точек, тогда как известный способ требует 8 удвоений.
. Вычисляют точку (335, 62)+(705, 744)=(657, 694). Результат: kP=(657, 694). Потребовалось 2 удвоения точек, тогда как известный способ требует 8 удвоений.
Пример 2. Использование системы счисления с основанием, 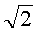 , n=2. Исходные данные. Эллиптическая кривая задана уравнением y2≡x3+x+98 (mod 1049), точка P=(1, 10). Число точек на эллиптической кривой равно q=1033. На первом этапе находят следующие числа:
, n=2. Исходные данные. Эллиптическая кривая задана уравнением y2≡x3+x+98 (mod 1049), точка P=(1, 10). Число точек на эллиптической кривой равно q=1033. На первом этапе находят следующие числа: 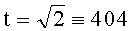 (mod q), A=5, B=23, при этом выполняется условие 5+23t≡0 (mod q). Находят точки (1+0t)P=(1, 10), (0+t)P=(945, 771), (1+t)P=(60,8), (1-t)P=(0,457) и составляют БС вида:
(mod q), A=5, B=23, при этом выполняется условие 5+23t≡0 (mod q). Находят точки (1+0t)P=(1, 10), (0+t)P=(945, 771), (1+t)P=(60,8), (1-t)P=(0,457) и составляют БС вида: 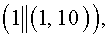
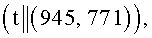
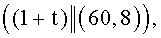
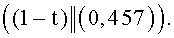
На втором этапе для формирования (проверки) подписи требуется умножение точки P на число k=527, это число представляют в системе счисления с основанием 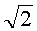 , для чего вычисляют следующие числа:
, для чего вычисляют следующие числа: 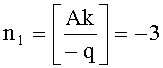 ,
, 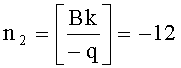 , k0=k-An1+2Bn2=-10, k1=-Bn1+An2=9, находят представление k0=-t2-t6, k1=1+t6, k≡t-t2-t6+t7 (mod q), k≡(0+t)+2(-1+0t)+4(0+0t)+8(-1+t) (mod q).
, k0=k-An1+2Bn2=-10, k1=-Bn1+An2=9, находят представление k0=-t2-t6, k1=1+t6, k≡t-t2-t6+t7 (mod q), k≡(0+t)+2(-1+0t)+4(0+0t)+8(-1+t) (mod q).
Старшая пара коэффициентов числа k соответствует идентификатору (1-t). Полагают R=-(1-t)P=(0, 592). Выполняют удвоение точки R: 2R=(190, 611) и полагают R=(190, 611). Вторая пара коэффициентов нулевая.
Для перехода к третьей паре коэффициентов (-1+0t)=-(1+0t) выполняют удвоение точки R: 2R=(427, 945), полагают R=(427, 945), по идентификатору находят точку -P=(1, 1039), вычисляют сумму R+(-P)=(177, 497) и полагают R=(177, 497). Для перехода к последней паре коэффициентов (0+t) выполняют удвоение точки R: 2R=(783, 537), полагают R=(783, 537), выбирают по идентификатору t точку tP=(945, 771) и находят сумму R+tP=(657, 694). Результат: kP=(657, 694). Потребовалось 3 удвоения точек, тогда как известный способ требует 8 удвоений.
Пример 3. Гиперэллиптическая кривая задана уравнением y2=x5+2x2+x+3 (mod 31), приведенный дивизор Р=(2+5x+x2, 5+x) имеет простой порядок q=1009. Используется система счисления с основанием 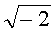 , n=2. На первом этапе находят следующие числа:
, n=2. На первом этапе находят следующие числа: 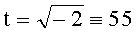 (mod q), A=19, B=18, при этом выполняется условие 19+18t≡0 (mod q). Вычисляют следующие ПД: tP=(20+4x+x2, 11+18x), (1+t)P=(18+22x+x2, 28x), (1-t)P=(18+16x+x2, 14+26x) и составляют соответствующие БС, у которых левые части равенств являются идентификаторами:
(mod q), A=19, B=18, при этом выполняется условие 19+18t≡0 (mod q). Вычисляют следующие ПД: tP=(20+4x+x2, 11+18x), (1+t)P=(18+22x+x2, 28x), (1-t)P=(18+16x+x2, 14+26x) и составляют соответствующие БС, у которых левые части равенств являются идентификаторами: 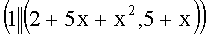 ,
, 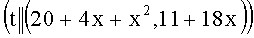 ,
, 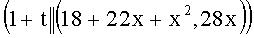 ,
, 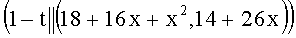 .
.
На втором этапе для формирования (проверки) подписи требуется умножение P на число k=527, это число представляют в системе счисления с основанием t, для чего вычисляют следующие числа:
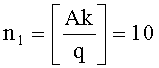 ,
, 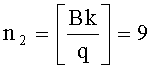 ,
,
k0=k-An1-2Bn2=13, k1=-Bn1+An2=-9, находят представление k≡1-t+t4-t6+t7 (mod q),
k≡(1-t)+2(0-0t)+4(1-0t)+8(1-t) (mod q).
Старшая пара коэффициентов равна (1-t), ей соответствует ПД вида (1-t)P=(18+16x+x2, 14+26x). Это значение присваивают приведенному дивизору R. Выполняют переход ко второй паре коэффициентов (1-0t), соответствующей ПД P, используя одно удвоение: 2R=(9+4x+x2, 12+25x) и присваивают это значение ПД R. Находят сумму ПД: R+P=(8+21x+x2, 15+5x) и присваивают это значение ПД R. Третья пара коэффициентов нулевая, поэтому выполняют два удвоения R:=2R=(27+24x+x2, 21+20x), R:=2R=(17+2x+x2, 19+x). Последняя пара коэффициентов соответствует ПД (1-t)P. Находят сумму R+(1-t)P=(2+18x+x2, 25+3x). Результат: kP=(2+18x+x2, 25+3x). Потребовалось 3 удвоения ПД, тогда как известный способ требует 8 удвоений.
Пример 4. Гиперэллиптическая кривая задана уравнением y2=x5+2x2+x+3 (mod 31), приведенный дивизор P=(2+5x+x2, 5+x) имеет простой порядок q=1009. Используется система счисления с основанием 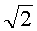 , n=2. На первом этапе находят следующие числа:
, n=2. На первом этапе находят следующие числа: 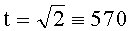 (modq), A=7, B=23, при этом выполняется условие A2-2B2=-q, 7+23t≡0 (mod q). Вычисляют вспомогательные БС, содержащие следующие ПД: tP=(28+28x+x2, 5+9x), (1+t)P=(7+28x+x2, 8+28x), (1-t)P=(29+7x+x2, 6+8x). Левые части равенств являются идентификаторами соответствующих БС:
(modq), A=7, B=23, при этом выполняется условие A2-2B2=-q, 7+23t≡0 (mod q). Вычисляют вспомогательные БС, содержащие следующие ПД: tP=(28+28x+x2, 5+9x), (1+t)P=(7+28x+x2, 8+28x), (1-t)P=(29+7x+x2, 6+8x). Левые части равенств являются идентификаторами соответствующих БС: 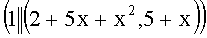 ,
, 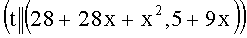 ,
, 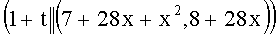 ,
, 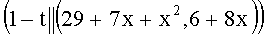 .
.
На втором этапе для формирования (проверки) подписи требуется умножение P на число k=135, это число представляют в системе счисления с основанием t, для чего вычисляют числа
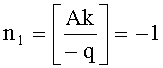 ,
, 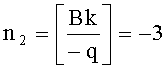 ,
,
k0=k-An1+2Bn2=4, k1=-Bn1+An2=2, находят представление k≡t3+t4 (mod q), k≡(0+0t)+2(0+t)+4(1+0t) (mod q).
Старшая пара коэффициентов равна (1+0t), ей соответствует ПД: R=P=(2+5x+x2, 5+x). Выполняют переход ко второй паре коэффициентов (0+t), соответствующей ПД tP, используя удвоение: 2R=(16+14x+x2, 2+8x) и присваивают это значение ПД R. Находят сумму ПД: R+tP=(26+5x+x2, 2+22x) и присваивают это значение R. Для перехода к последней паре коэффициентов (0+0t) умножают R на 2 и получают ПД вида (27+8x+x2, 26+5x).Результат: kP=(27+8x+x2, 26+5x). Потребовалось 2 удвоения ПД, тогда как известный способ требует 6 удвоений.
Приложение 1
Объяснение специальных терминов и описание заимствованных вычислительных алгоритмов:
Двоичный цифровой электромагнитный сигнал - последовательность битов в виде нулей и единиц.
Параметры двоичного цифрового электромагнитного сигнала: разрядность и порядок следования единичных и нулевых битов.
Разрядность двоичного цифрового электромагнитного сигнала - общее число его единичных и нулевых битов, например сигнал 10011 имеет разрядность 5. Разрядность числа называется также его длиной.
Битовая строка (БС) - двоичный цифровой электромагнитный сигнал конечной разрядности, представляемый в виде конечной последовательности цифр 0 и 1. БС может интерпретироваться как набор независимых нулей и единиц и как целое число. С битовыми строками могут выполняться логические и арифметические операции. Конкатенация БС S=(S1, …, Sn) и T=(T1, …, Tm) представляет собой БС вида 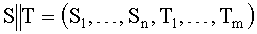 .
.
Электронная цифровая подпись (ЭЦП) - двоичный цифровой электромагнитный сигнал, параметры которого зависят от подписанного электронного документа и от секретного ключа. Проверка подлинности ЭЦП осуществляют с помощью открытого ключа, который зависит от секретного ключа.
Запись а≡b (mod р), где a, b, p - целые числа, означает, что a - b делится на p (сравнимость по модулю простого числа). Запись u≡ν (mod f), где u, ν, f - многочлены, означает, что u - ν делится на f (сравнимость по модулю многочлена).
Поле из простого числа p элементов - множество {0, 1, …, p-1}. Сложение и умножение выполняются по модулю p и обозначается a+b (mod р), ab (modp) (см. [Глухов М.М., Елизаров В.П., Нечаев А.А. Алгебра. - М.: Гелиос-АРВ, 2003]), например, 3+4≡0 (mod 7), 3·4≡5 (mod 7). Поле из pn элементов представляет собой многочлены вида a 0+a 1W+…a n-1Wn-1, где f(W)=0, и многочлен f не раскладывается на множители по модулю p, сложение и умножение в поле выполняется по модулю p и по модулю f(W).
Абелева группа - непустое множество, на котором определена бинарная операция, называемая сложением, где для всех элементов группы выполняются равенства R+S=S+R, R+(S+T)=(R+S)+Т, в группе существует нулевой элемент 0, такой, что R=0=0+R=R для всех элементов группы R, для каждого элемента группы R существует противоположный элемент -R, такой, что R+(-R)=0. Для каждого элемента R группы существуют кратные: 2R=R+R, 3R=2R+R, …. Конечная абелева группа состоит из конечного числа элементов. Наименьшее натуральное число n такое, что nR=0, называется порядком элемента R.
Эллиптическая кривая над полем из pn элементов, n≥1, - подмножество точек P=(x,y) плоскости с координатами из конечного поля, удовлетворяющих уравнению y2+a 1xy=x3+a 2x2+a 4x+a 6 3, дополненное бесконечно удаленной точкой, где ни в одной точке кривой обе частные производные многочлена, задающего кривую, не равны нулю одновременно. Точки эллиптической кривой образуют конечную абелеву группу [Silverman J. The arithmetic of elliptic curves, Springer, 1986]. Нулевым элементом группы является бесконечно удаленная точка. Сложение точек (x1,y1)+(x2,y2)=(x3,y3) задается формулами: x3=λ2+λa 1-a 2-x1-x2, y3=-(λ+a 1)x3-ν,
где 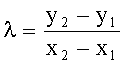 ,
, 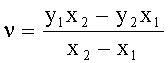 при (x1,y1)≠(x2,y2) и
при (x1,y1)≠(x2,y2) и
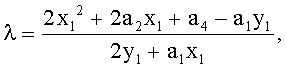
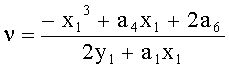 при (x1,y1)=(x2,y2) - случай удвоения точек.
при (x1,y1)=(x2,y2) - случай удвоения точек.
Битовая строка, представляющая точку эллиптической кривой, содержит две координаты этой точки. Бесконечно удаленная точка имеет знаменатель λ.
Гиперэллиптическая кривая над полем из pn элементов, n≥1, - подмножество точек плоскости с координатами из конечного поля, в которых многочлен y2+h(x)y-f(x) обращается в нуль, при этом ни в одной точке кривой обе частные производные многочлена не равны нулю одновременно, степень deg(f) многочлена f(x) равна 2g+1≥5, где g - натуральное число, deg(h)≤g. Пары многочленов (u(x),ν(x)), таких, что u(x) имеет единичный старший коэффициент, f(x)-hν(x)-ν(x)2 делится на u(x), deg(ν)<deg(u)≤g, образуют конечную абелеву группу и называются приведенными дивизорами (ПД) гиперэллиптической кривой. При этом -(u(x),ν(x))=(u(x),-ν(x)). Приведенные дивизоры могут быть представлены битовыми строками, содержащими списки коэффициентов многочленов u(x), ν(x). Сложение приведенных дивизоров (u1,ν1)+(u2,ν2)=(u3, ν3) выполняется следующим алгоритмом [Scholten J., Vercauteren F. An introduction to elliptic and hyperelliptic curve cryptography and the NTRU cryptosystem, доступно с http://homes. esat. Kuleuven. be/~fvercaut/papers/cc03.pdf].
1. Найти расширенным алгоритмом Евклида представление наибольшего общего делителя d1=НОД(u1,u2)=e1u1+e2u2.
2. Найти расширенным алгоритмом Евклида представление наибольшего общего делителя d=НОД(d1,ν1+ν2+h)=c1d1+c2(ν1+ν2+h).
3. Вычислить s1=c1e1, s2=c1e2, s3=c2.
4. Вычислить u=(u1u2)/d2, ν=(s1u1ν2+s2u2ν1+s3(ν1ν2+f)/d(mod u).
5. Вычислить u'=(f-νh-ν2)/u, ν'=(-h-ν)(mod u').
6. Если deg(u')>g, то u=u', ν=ν' и возврат на шаг 5.
7. Поделить коэффициенты многочлена u' на старший коэффициент.
8. Выход: (u', ν').
Квадратный корень 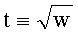 (mod q), w=±2, можно вычислить следующим образом: [Ростовцев А.Г. Алгебраические основы криптографии. - СПб.: Мир и Семья, Интерлайн, 2000, глава 7]. Если q≡3 (mod 4), то
(mod q), w=±2, можно вычислить следующим образом: [Ростовцев А.Г. Алгебраические основы криптографии. - СПб.: Мир и Семья, Интерлайн, 2000, глава 7]. Если q≡3 (mod 4), то 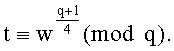 Если q≡1 (mod 4), то можно воспользоваться следующим алгоритмом.
Если q≡1 (mod 4), то можно воспользоваться следующим алгоритмом.
1. Подбором найти элемент b такой, что 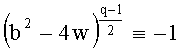 (mod q).
(mod q).
2. Положить f(y)=y2-by+w.
3. Вычислить t=±y(q+1)/2 (mod q, f(y)).
Для вычисления представления q=А2-wB2 можно воспользоваться следующим алгоритмом:
1. Вычислить 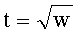 (mod q).
(mod q).
2. Положить i=0, ti=t, mi=q.
3. Вычислить 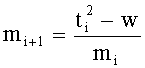 , ti+1=min{ti(mod mi+1), mi+1-ti (mod mi+1)}.
, ti+1=min{ti(mod mi+1), mi+1-ti (mod mi+1)}.
4. Если mi+1=1, то перейти на шаг 5, иначе положить i=i+1 и вернуться на шаг 3.
5. Положить Ai=ti, Bi=1.
6. Если i=0, то положить A=Ai, B=Bi и перейти на шаг 8. Иначе положить 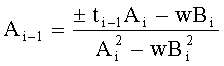 ,
, 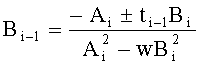 . Знаки подбираются так, чтобы деление было целочисленным.
. Знаки подбираются так, чтобы деление было целочисленным.
7. Положить i=i-1 и вернуться на шаг 6.
8. Результат: A, B.
Для q≡1, 3 (mod 8) представление q=A2+2B2 единственно, а для q≡1, 7 (mod 8) существует бесконечно много представлений ±q=A2-2B2, поэтому существуют числам, В, имеющие минимальную длину.
Способ относится к электросвязи и вычислительной технике и позволяет ускорить формирование и проверку электронной цифровой подписи. Технический результат заявленного изобретения заключается в увеличении скорости формирования и проверки электронной цифровой подписи с использованием эллиптических или гиперэллиптических кривых. Способ, заключающийся в преобразовании битовых строк и выполнении операций с битовыми строками, в котором при формировании или при проверке подписи умножают по крайней мере одну заранее определенную точку (соответственно приведенный дивизор) Р простого порядка q эллиптической (соответственно гиперэллиптической) кривой на целое число k путем сложений и удвоений, при формировании подписи допускается случайный выбор числа k, причем на первом этапе выбирают число w=-2 при q=1,3 (mod 8) или w=2 при q=1,7 (mod 8), вычисляют значение t=√w (mod q), а на втором этапе число k преобразовывают в систему счисления с основанием t: k=K0+K1t+…+K2ht2h+K2h+1t2h+1, где все коэффициенты K0, …, K2h+1 принимают значения 0, 1 или -1, а число 2h близко к log2q, а в ходе рекурсивного перехода к предыдущей цепочке коэффициентов выполняют n/2 удвоений точки (приведенного дивизора) R. 3 з.п. ф-лы.
1. Способ формирования и проверки электронной цифровой подписи на основе эллиптической или гиперэллиптической кривой, заключающийся в преобразовании битовых строк и выполнении операций с битовыми строками, в котором при формировании или при проверке подписи умножают по крайней мере одну заранее определенную точку (соответственно приведенный дивизор) Р простого порядка q эллиптической (соответственно гиперэллиптической) кривой на целое число k путем сложений и удвоений, при формировании подписи допускается случайный выбор числа k, причем для указанного умножения используют два этапа: на первом этапе выбирают четную длину n цепочки и подготавливают вспомогательные битовые строки, содержащие произведение точки эллиптической кривой (соответственно приведенного дивизора гиперэллиптической кривой) на целые числа, представленные всеми допустимыми значениями цепочек, получаемые умножением Р на целые числа, соответствующие всем допустимым значениям цепочек, причем каждая указанная битовая строка содержит хотя бы один идентификатор, на втором этапе выполняют указанное умножение с использованием указанных вспомогательных битовых строк, при этом вектор коэффициентов числа k разбивают на цепочки длины n, выбирают вспомогательную битовую строку, один из идентификаторов которой соответствует старшей цепочке, и значение точки (соответственно приведенного дивизора) этой битовой строки присваивают точке (соответственно приведенному дивизору) R, и выполняют рекурсивный переход к предыдущей цепочке, присваивая R значение удвоений R и суммы R с точкой эллиптической кривой (соответственно с приведенным дивизором гиперэллиптической кривой) битовой строки, один из идентификаторов которой соответствует предыдущей цепочке, отличающийся тем, что на первом этапе выбирают число w=-2 при q=1, 3 (mod 8) или w=2 при q=1, 7 (mod 8), вычисляют значение t=√w (mod q), a на втором этапе число k преобразовывают в систему счисления с основанием t: k=K0+K1t+…+K2ht2h+K2h+1t2h+1, где все коэффициенты K0, …, K2h+1 принимают значения 0, 1 или -1, а число 2h близко к log2q, а в ходе рекурсивного перехода к предыдущей цепочке коэффициентов выполняют n/2 удвоений точки (приведенного дивизора) R.
2. Способ по п.1, отличающийся тем, что при формировании подписи случайное число k выбирают в виде пары целых случайных чисел (k0, k1) так, что выполняется условие 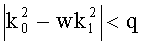 , и полагают k=k0+tk1.
, и полагают k=k0+tk1.
3. Способ по п.1, отличающийся тем, что если w=-2 и n больше или равно 4, то в каждую вспомогательную битовую строку включают все эквивалентные идентификаторы, обладающие одинаковым значением по модулю q, либо каждая вспомогательная битовая строка содержит идентификатор, значение которого равно абсолютно наименьшему из эквивалентных идентификаторов, а на втором этапе выполняют преобразование цепочек коэффициентов числа k, при котором цепочки вида (…, 1, z, 1, …) заменяют на цепочки вида (…, -1, z, 0, …), а цепочки вида (…, -1, z, -1, …), заменяют на цепочки вида (…, 1, z, 0, …), причем z означает любую из цифр 0, 1 или -1.
4. Способ по п.1, отличающийся тем, что в том, что на первом этапе дополнительно подготавливают битовые строки, представляющие целые числа А и В, такие, что выполняются условия: eq=A2-wB2, где е=1 или е=-1, и целое число A+Bt делится на q, а на втором этапе вычисляют ближайшее к дроби (Ak/(eq)) целое число n1 и ближайшее к дроби (Bk/(eq)) целое число n2, вычисляют числа k0=k-An1+wBn2, k1=-Bn1+An2, преобразовывают их в двоичный вид k0=k00+2k01+…+2hk0h, k1=k10+2k11+…+2h*k1h и для i=0, …, 2h+1 присваивают значения K2i=k0i или K2i=-k0i, K2i+1=k1i или K2i+i=-k1i, где знаки определяют с учетом знака w.
| СПОСОБ ФОРМИРОВАНИЯ И ПРОВЕРКИ ПОДЛИННОСТИ ЭЛЕКТРОННОЙ ЦИФРОВОЙ ПОДПИСИ, ЗАВЕРЯЮЩЕЙ ЭЛЕКТРОННЫЙ ДОКУМЕНТ | 2008 |
|
RU2380838C1 |
| ВСЕОБЪЕМЛЮЩАЯ, ОРИЕНТИРОВАННАЯ НА ПОЛЬЗОВАТЕЛЯ СЕТЕВАЯ БЕЗОПАСНОСТЬ, ОБЕСПЕЧИВАЕМАЯ ДИНАМИЧЕСКОЙ КОММУТАЦИЕЙ ДАТАГРАММ И СХЕМОЙ АУТЕНТИФИКАЦИИ И ШИФРОВАНИЯ ПО ТРЕБОВАНИЮ ЧЕРЕЗ ПЕРЕНОСНЫЕ ИНТЕЛЛЕКТУАЛЬНЫЕ НОСИТЕЛИ ИНФОРМАЦИИ | 2004 |
|
RU2308080C2 |
| Колосоуборка | 1923 |
|
SU2009A1 |
| СПОСОБ ФОРМИРОВАНИЯ И ПРОВЕРКИ ПОДЛИННОСТИ ЭЛЕКТРОННОЙ ЦИФРОВОЙ ПОДПИСИ, ЗАВЕРЯЮЩЕЙ ЭЛЕКТРОННЫЙ ДОКУМЕНТ | 2007 |
|
RU2369974C1 |
Авторы
Даты
2012-07-27—Публикация
2010-05-25—Подача