СПОСОБ МАТЕМАТИЧЕСКОГО И КОМПЬЮТЕРНОГО МОДЕЛИРОВАНИЯ Российский патент 2014 года по МПК G06N7/06 G06F17/50 G01M5/00 

Изобретение относится к способам математического и компьютерного моделирования для создания модели поведения конструкций и изделий авиационной техники в условиях неопределенности входных параметров.

Из уровня техники известен способ математического моделирования [1], в котором используются и сравниваются методы конечно-элементного и молекулярно-динамического моделирования. Существенный недостаток предлагаемого способа состоит в том, что в нем рассматривается только ограниченная задача моделирования разрушения и не прогнозируются свойства материалов. Кроме того, этот способ не позволяет рассматривать вопросы моделирования с учетом неопределенности ресурса изделия.

Известен {2] способ иерархического моделирования конструкций, включающий использование основных моделирующих элементов и дополнительных связующих элементов, геометрически подобных моделируемым, при этом разбиение на элементарные элементы используется для упрощения расчетной модели и не связано с неопределенностью параметров конструкции. Недостатком данного способа является невозможность получения неизвестных параметров при моделировании авиационной техники, поскольку элементы разбиения предполагаются заданными и обладающими известными механическими свойствами

Известны компьютерные модели поведения сложных технических систем, реализованные на различных иерархических уровнях [3]. Данный аналог наиболее близкий, т.е. прототип. Согласно этому способу при моделировании активной зоны ядерного реактора вводится ячеистая структура нескольких иерархических уровней, моделируемые параметры рассматриваются на уровне минимальной ячейки и впоследствии осредняются и используются для оценок поведения конструкции на более высоком масштабном уровне. Недостатком этого способа является то, что использование процедуры осреднения ведет к игнорированию существенных, хотя и единичных элементов, например вкраплений инородных веществ в активной зоне. Наличие такого рода единичных включений может нарушить функционирование конструкции, вызвать катастрофические последствия. Кроме того, прототип не позволяет учесть эффекты, связанные с неопределенностью входных параметров.

Сущность проблемы - моделирование авиационной техники - связана с наличием двух типов неопределенностей. Первый тип - недостаточно полная информация по свойствам используемых материалов. Частично эти данные могут быть получены от производителей, но достоверность информации вызывает определенные сомнения, что недопустимо для проектирования ответственных изделий. Эти данные можно получить, проведя стендовые испытания, но это достаточно дорого, а иногда и невозможно. Второй тип неопределенностей связан с реальными нагрузками, возникающими в авиационной технике в процессе эксплуатации. Исследование конкретных режимов нагружения и возникающих силовых факторов в конструкции в целом требует дорогостоящих экспериментов в аэродинамических трубах или в пробных полетах.

Задача, которая решается данным изобретением, - создание способа многоуровневого компьютерного моделирования, позволяющего с большой степенью точности проводить виртуальные испытания механических и эксплуатационных свойств разрабатываемых и восстановленных узлов и деталей на различных масштабных уровнях, позволяющих использовать модели материалов и изделий, максимально соответствующие реальным.

Данная задача решается тем, что способ математического и компьютерного моделирования включает создание иерархической модели. Отличие в том, что моделирование включает создание модели поведения конструкций и изделий авиационной техники в условиях неопределенности входных параметров на двух уровнях: макроскопическом - методом конечно-элементного моделирования и микроскопическом - методами квантовой механики и молекулярной динамики, где сначала рассматриваются микроскопические образцы, представляющие модель геометрически подобную стандартным образцам, используемым для механических испытаний, которые виртуально испытываются методами молекулярной динамики, а полученные механические параметры микроскопических образцов используют, как недостающие макроскопические параметры в моделях материалов для конечно-элементного моделирования, причем при переходе от микроскопического к макроскопическому уровню моделирования и обратно используют масштабную инвариантность механических параметров и законов.

В нашем способе используется не простая иерархия масштабов, но более сложная иерархия законов, это означает, что для получения механических параметров верхнего иерархического уровня используются параметры, полученные на основании иных, нежели механические, закономерностей, подходов (расчеты на базе межатомарного квантово-механического взаимодействия), которые позволяют с большой степенью точности проводить виртуальные испытания. Кроме того, неопределенность параметров в нашем случае обусловлена эмпирическим законом поведения материалов (модели материала) для конечно-элементного анализа.

Изобретение поясняется чертежами, где на

фиг.1 представлен исходный образец для МД-моделирования,

фиг.2 - деформированный образец,

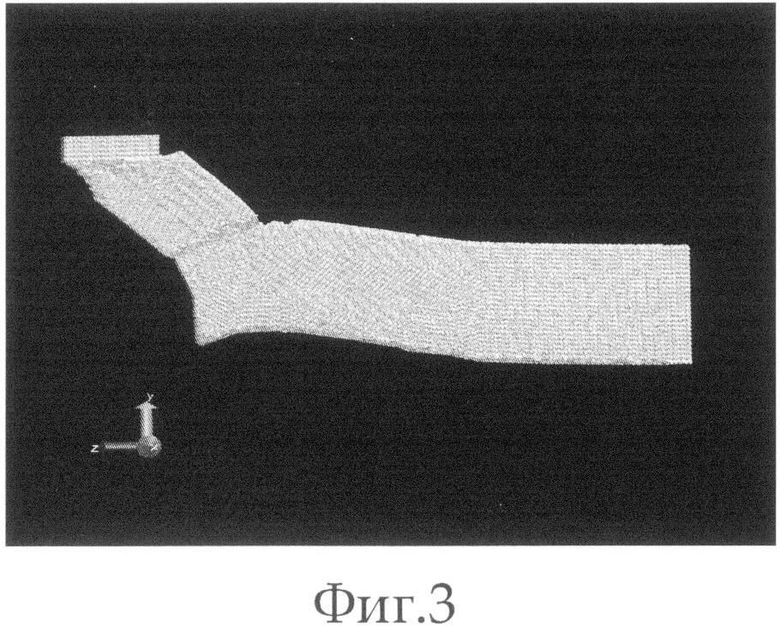
фиг.3 - молекулярно-динамическая модель (образец из титана ВТ1-0) для проведения виртуальных экспериментов,

фиг.4 - конечно-элементная модель для проведения виртуальных экспериментов и сравнения с результатами молекулярно-динамического расчета.

Способ математического и компьютерного моделирования, включающий создание иерархической модели, рассмотрим на примере моделирования элементов авиационных конструкций, изготовленных их α-титана (сплавы ВТ1, ВТ1-0), так как титан является классическим авиационным материалом.

Рассмотрим в качестве примера возможность получения модулей упругости (необходимые параметры при конечно-элементном моделировании) из молекулярно-динамического моделирования, т.е моделирование на микроскопическом уровне - методами квантовой механики и молекулярной динамики, где сначала рассматриваются микроскопические образцы, представляющие модель, геометрически подобную стандартным образцам, используемым для механических испытаний, которые виртуально испытываются методами конечно-элементного моделирования.

Создадим (сгенерируем при помощи компьютера) образец материала в соответствии с заданными экспериментальными величинами параметров решетки, направлением кристаллографических осей, параметрами используемого потенциала межатомного взаимодействия (фиг.1). Эта процедура может быть осуществлена любым стандартным методом известных свободнораспространяемых пакетов молекулярно-динамического моделирования (например, Lampps, NWChem). Затем деформируем образец программным образом согласно заданной программе нагружения (фиг.2). В данном случае проводилось растяжение вдоль оси Z с заданной скоростью. Проведенная процедура соответствует стандартной макроскопической процедуре исследования образца на разрыв, определяемой существующей в машиностроении практикой и стандартами. По результатам компьютерного эксперимента определяем значения а_α - радиуса-вектора, определяющего положение частицы с номером α относительной исходной частицы в отсчетной конфигурации, которые являются параметрами в формуле

$$c_{ijkl}=\frac{1}{2v_{\ast }}{\displaystyle \sum _{\alpha }\left(\frac{1}{a_{\alpha }^2}\frac{d^2\Phi }{d{a}_{\alpha }^2}-\frac{1}{a_{\alpha }^3}\frac{d\Phi }{d{a}_{\alpha }}\right)}{a}_{\alpha }{a}_{\alpha }{a}_{\alpha }{a}_{\alpha }$$

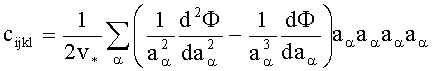
где c_ijkl - модуль жесткости; Φ - используемый в модели потенциал; V_∗ - объем элементарной кристаллической ячейки, решетки; а_α - радиус-вектор, определяющий положение частицы с номером α относительной исходной частицы в отсчетной конфигурации. В формуле расстояние между атомами выражено в виде 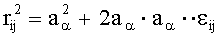$$r_{ij}^2=a_{\alpha }^2+2a_{\alpha }\cdot a_{\alpha }\cdot \cdot {\epsilon }_{ij}$$ и использованы прямые тензорные обозначения для тензорного и диадного умножения, ε_kl - лагранжева деформация объема материала.

Полученные значения используются как входные параметры для конечно-элементного моделирования. Известно, что при конечно-элементном моделировании, например в пакетах LSDYNA, ANSYS, поведение материала определяется набором параметров, из которых тензор модулей упругости (величина, обратная жесткости) является основной механической характеристикой.

Из результатов компьютерного эксперимента (фиг.2) также определяется модуль Пуассона (аналогично стандарту на макроскопическое экспериментальное определение этого модуля).

В основе использования масштабной инвариантности лежит факт, что уравнения механики не меняют своего вида в зависимости от выбранной системы единиц и масштаба длины. Это позволяет распространить параметры и зависимости, полученные для механической системы одних размеров, на систему других размеров.

На микроскопическом уровне создается модельное тело, геометрически подобное стандартным образцам, используемым для макроскопических механических испытаний (фиг.3). Число атомов в микроскопической модели системы слева совпадает с числом узлов в макроскопической системе (фиг.4). Необходимые для микроскопического моделирования параметры (тип и параметры кристаллической решетки, параметры межатомного потенциала) должны совпадать с экспериментально определенными для данного типа вещества параметрами. Микроскопические образцы виртуально испытываются методами молекулярной динамики, например производится воздействие на образец с заданной скоростью до заданного значения деформации. Из полученной компьютерной модели по известным из физики и механики твердого тела зависимостям рассчитываются необходимые параметры, например тензор модулей упругости/жесткости 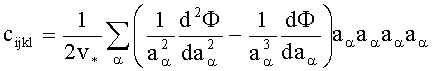$$c_{ijkl}=\frac{1}{2v_{\ast }}{\displaystyle \sum _{\alpha }\left(\frac{1}{a_{\alpha }^2}\frac{d^2\Phi }{d{a}_{\alpha }^2}-\frac{1}{a_{\alpha }^3}\frac{d\Phi }{d{a}_{\alpha }}\right)}{a}_{\alpha }{a}_{\alpha }{a}_{\alpha }{a}_{\alpha }$$ . Поскольку полагается, что принцип масштабной инвариантности выполняется, то эффективные напряжения в материале должны быть идентичными. При этом следует учитывать, что безразмерные параметры (например, коэффициент Пуассона) не нуждаются в дальнейшей перенормировке, а размерные величины необходимо привести к макроскопической шкале исходя из обычной теории размерностей. Например, если L∗ - характерный размер (например, длина) микроскопического образца, L - тот же самый характерный размер макроскопического образца (также длина), то все величины, входящие в расчетные зависимости и имеющие размерность длины, уменьшаются в отношении λ=L∗/L.

Например, если при МД-моделировании используется атомная система единиц (А.Е.М. / Ангстрем / Пикосекунда), то для получения макроскопического значения величины модуля упругости (размерность 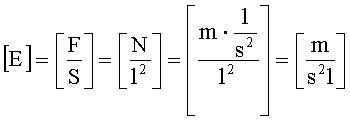$$\left[E\right]=\left[\frac{F}{S}\right]=\left[\frac{N}{l^2}\right]=\left[\frac{m\cdot \frac{l}{s^2}}{l^2}\right]=\left[\frac{m}{s^{2}l}\right]$$ ) следует полученное микроскопическое значение домножить на масштабный коэффициент 1,66∗10⁷,

где [Е] - размерность модуля упругости,

[F] - размерность силы,

[S] - размерность площади.

Кроме нахождения недостающих механических параметров материалов МД-модель позволяет исследовать динамику процессов деформирования и разрушения - приведенные фигуры показывают достаточно хорошее совпадение результатов при прогнозировании распространения трещины, другие процессы.

Источники информации

1. N.V.R. Coffman, J.P.Sethna, G Heber, M.Liu, A.Ingraffea, P.Bailey and E.I.Barker / A comparison of finite element and atomistic modeling of fracture // ModellingSimul. Mater. Sci. Eng. 16 (2008) 065008 (15pp)).

2. Патент России №2376563, опубл. 20.97.2008 г.

3. Патент России №2315375, опубл. 20.01.2008 - прототип.

Изобретение относится к моделированию и может быть использовано для создания модели поведения конструкций и изделий авиационной техники в условиях неопределенности входных параметров. Техническим результатом является повышение точности испытаний механических и эксплуатационных свойств разрабатываемых и восстановленных узлов и деталей. Способ содержит создание модели поведения конструкций и изделий авиационной техники в условиях неопределенности входных параметров на двух уровнях: макроскопическом - методом конечно-элементного моделирования и микроскопическом - методами квантовой механики и молекулярной динамики, сначала рассматриваются микроскопические образцы, представляющие модель, геометрически подобную стандартным образцам, используемым для механических испытаний, которые виртуально испытываются методами молекулярной динамики, а полученные механические параметры микроскопических образцов используют, как недостающие макроскопические параметры в моделях материалов для конечно-элементного моделирования, причем при переходе от микроскопического к макроскопическому уровню моделирования и обратно используют масштабную инвариантность механических параметров и законов. 4 ил.

Способ математического и компьютерного моделирования, включающий создание иерархической модели, отличающийся тем, что моделирование включает создание модели поведения конструкций и изделий авиационной техники в условиях неопределенности входных параметров на двух уровнях: макроскопическом - методом конечно-элементного моделирования и микроскопическом - методами квантовой механики и молекулярной динамики, где сначала рассматриваются микроскопические образцы, представляющие модель, геометрически подобную стандартным образцам, используемым для механических испытаний, которые виртуально испытываются методами молекулярной динамики, а полученные механические параметры микроскопических образцов используют как недостающие макроскопические параметры в моделях материалов для конечно-элементного моделирования, причем при переходе от микроскопического к макроскопическому уровню моделирования и обратно используют масштабную инвариантность механических параметров и законов.