Предлагаемое изобретение относится к области космической техники, и для достижения технического результата использует настройки орбит космических аппаратов (КА) в фазовых плоскостях векторов наклонения и эксцентриситета.
Как правило, коллокацию КА проводят по согласованным схемам. Все схемы-аналоги сводятся к равноудалению точек прицеливания векторов en [en, (Ω+ω)n] (n=1, 2, …) и in [in, Ωn] (n=1, 2, …) в соответствующих фазовых плоскостях КА и поддержанию концов векторов en и in внутри соответствующих областей выбранных радиусов, центрами которых являются соответствующие точки прицеливания. Идеальным вариантом считается для двух КА разнесение долгот восходящих узлов (Ωn) и прямых восхождений перигеев (Ω+ω)n точек прицеливания на 180°, причем аргументы широты перигеев КА должны быть близки нулю. Для трех КА цифру 180 заменяют на 120. Такой принцип коллокации общеизвестен, он следует из уровня техники. Однако за кажущейся простотой схем скрывается сложная и затратная процедура управления векторами коллокации.
Известен способ управления кластером находящихся на геостационарной орбите спутников (RU 2284950 C2, МПК B64G 1/10, B64G 1/24, B64G 1/44), который взят за прототип. Согласно данному способу, включающему измерение параметров орбиты каждого КА, определение по ним текущих значений орбитальных элементов каждого КА, сравнение их с требуемыми и проведение коррекций периода обращения, наклонения и эксцентриситета орбиты, маневры на каждом из КА проводят с помощью двигателей малой тяги, переводя векторы наклонения in КА (n - условный номер КА) в разнесенные относительно друг друга кольцевые области их допустимого изменения так, чтобы угол между линией, соединяющей текущее положение конца каждого вектора с центром соответствующей ему кольцевой области, и направлением на Солнце был равен увеличенной на 180° величине прямого восхождения Солнца, одновременно проводят коррекции векторов эксцентриситета en с целью перевода этих векторов в разнесенные относительно друг друга кольцевые области их допустимого изменения так, чтобы линия, соединяющая текущее положение каждого вектора с центром соответствующей ему кольцевой области, (далее варианты):
1 - отставала от направления на Солнце на половину углового расстояния при движении вектора эксцентриситета по окружности естественного дрейфа в пределах кольцевой области, далее на протяжении всего полета производят изменение относительного расстояния между КА в требуемых пределах за счет компенсации квазивекового приращения вектора наклонения каждого КА в сочетании с коррекцией вектора эксцентриситета, при которой в момент прохождения вектором эксцентриситета середины интервала между точкой входа окружности естественного дрейфа в кольцевую область допустимого изменения вектора эксцентриситета и точкой выхода из этой области линия, соединяющая центр окружности естественного дрейфа и центр соответствующей ему кольцевой области допустимого изменения вектора эксцентриситета, совпадала с направлением на Солнце, приводя тем самым к постоянству относительные векторы наклонения и эксцентриситета между КА;
2 - совпадала с направлением на Солнце, далее на протяжении всего полета производят изменение относительного расстояния между КА в требуемых пределах за счет компенсации квазивекового приращения вектора наклонения каждого КА без коррекции вектора эксцентриситета, приводя тем самым к постоянству относительные векторы наклонения и эксцентриситета между КА.
Здесь «окружность естественного дрейфа» - окружность радиуса устойчивого эксцентриситета (Приложение 1, фиг.1).
Суть данного способа сводится к синхронизации движения концов векторов наклонения и эксцентриситета орбиты КА в соответствующих фазовых плоскостях [ix; iy] и [ex; ey], где ix=i·cosΩ; iy=i·sinΩ; ex=e·cos(Ω+ω); ey=e·sin(Ω+ω); Ω - долгота восходящего узла орбиты КА; ω - аргумент широты перигея; (Ω+ω)=απ - прямое восхождение направления на перигей орбиты КА, причем синхронизации движения КА в обеих плоскостях, синхронизации принудительной, поскольку взаимная ориентация относительных векторов эксцентриситета и наклонения ΔE и ΔI 2-3 КА не сохраняется при годовой цикличности эволюции конца вектора эксцентриситета по окружности естественного дрейфа и существующей при условии компенсации только вековых возмущений вектора наклонения полугодовой цикличности эволюции конца вектора наклонения по окружности естественного дрейфа (Приложение 2). Обе цикличности доминантные и обязаны своим существованием исключительно Солнцу, потому начальная и текущая ориентации векторов наклонения и эксцентриситета относительно Солнца являются необходимым условием достижения технического результата. «Устранение только векового возмущения при совместном управлении спутниками, как правило, не используют, поскольку при несогласованных положениях спутников в части полугодовых возмущающих членов векторов наклонения их различие может составить 0,05°. Однако специальным выбором начальных положений векторов наклонения спутников и при малой периодичности проведения коррекций наклонения (т.е. на спутниках с относительно малой тягой) можно обеспечить, при коррекции только вековой части, синфазную эволюцию положения векторов наклонения спутников по окружностям радиусом 0,025° таким образом, что вектор их разности будет сохранять близкое к постоянному направление» (прототип).
Недостатками прототипа являются:
1 - отсутствие математической формулы «специального выбора начальных положений векторов наклонения»; нет формулы - нет четкого представления совершаемого;
2 - «специальный выбор начальных положений векторов наклонения» предполагает специальный выбор центров кольцевых областей (точек прицеливания) или исходит из него, что тоже требует математического обоснования, но, если говорить просто (об этом никак не сказано в прототипе), прямое восхождение Солнца (сезон) и начальный вектор наклонения (модуль наклонения и восходящий узел орбиты КА) определяют текущее положение годографа кругового движения конца вектора наклонения («солнечного круга») и текущий вектор изменения приращения наклонения, возможные центры кольцевых областей располагаются на окружности радиуса годографа с центром в точке конца начального вектора наклонения (Приложение 2);
3 - если синфазное следование концов векторов наклонения орбит КА в инерциальном пространстве по окружностям естественного дрейфа, либо по границам кольцевых областей их допустимого изменения имеет место: из n точек (начальных условий КА) в фазовой плоскости начинается именно синфазное (с коррекцией вековых возмущений или без) движение по n трассам, то синфазное следование векторов эксцентриситетов орбит КА по своим окружностям естественного дрейфа, либо по границам кольцевых областей их допустимого изменения выбором начальных условий (кроме как совмещением векторов эксцентриситетов всех КА по модулю и направлению) нельзя организовать в принципе, даже если радиус окружности принудительного движения равен устойчивому эксцентриситету. Это очевидно вытекает из рассмотрения формулы (12') Приложения 1. Например, при диаметрально расположенных перигеях движение не только не синфазно, но и направлено навстречу друг к другу; из n точек (начальных условий КА) в фазовой плоскости начинается несинфазное (с коррекцией удержания или без) движение по n трассам, поскольку углы θ в единый момент времени отличаются друг от друга на величину рассогласования направлений на перигеи). В невозможности синфазного движения концов векторов эксцентриситета орбит КА может убедиться каждый на основании собственных расчетов. Только частотой проведения коррекций удержания, влекущей значимые энергозатраты, можно добиться желаемого результата;
4 - это главное - соблюдение, в идеале, постоянства разности векторов (расстояния между концами векторов наклонения, эксцентриситета всех (n) КА и постоянства расстояний между концами векторов наклонения и эксцентриситета каждого КА) не является необходимым и достаточным фактором коллокации, обеспечивающим гарантированное разнесение КА в истинном пространстве и в фазовых плоскостях. Для гарантий качественной коллокации необходимо соблюдать постоянство разнесения векторов наклонения и эксцентриситета по Ω, и απ, поскольку при сближенных и даже пересекающихся областях допустимого изменения концов векторов in и en соответствующие их синхронному движению расхождения по Ω и απ могут достигать порядка 90°. Это происходит потому, что хотя движения концов векторов наклонения при естественном дрейфе с компенсацией вековых возмущений равномерное, центры «солнечных кругов» в общем случае не являются началом координат фазовой плоскости [ix; iy]. Если учесть еще различия в средних скоростях движения вектора наклонения и эксцентриситета, то возможны варианты, когда
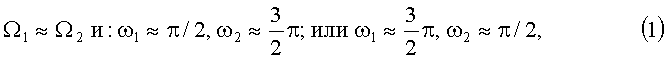
или

или (при i1≈i2≈0)
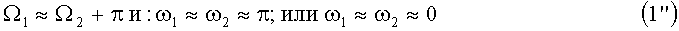
т.е. когда фокальные параметры p орбит КА, зависимость которых от величины эксцентриситета ничтожно мала [p=a(1-e2), где а - большая полуось орбиты], практически совпадают, в результате чего неизбежно критическое сближение в истинном пространстве двух КА вне зависимости от величин разности модулей наклонения и модулей эксцентриситета.
Коллокация в прототипе, как и в аналогах, рассматривается как способ управления движением центров масс, гарантирующий от столкновений КА. Эта задача актуальна, но только в принципе, и удовлетворительно решается для двух КА (даже при нулевых наклонениях) при условиях:

т.е. тогда, когда восходящие узлы орбит равны, для каждой из орбит линия узлов совпадает с линией апсид, направления на восходящий узел и перигей одной из орбит совпадают, другой - взаимно противоположны. Гарантированное минимальное межспутниковое расстояние, при реальном эксцентриситете орбит КА ~ 0,00015, составляет 12,6 км.
Другая задача коллокации - не мешать находящимся рядом КА работать по целевому назначению. Если ориентироваться на условия (2), в районах узлов орбит, при практически одинаковых периодах обращения (отклонение от звездных суток редко когда составляет более 5с), возникают взаимно попеременные помехи связи космических аппаратов с Землей.
И такая задача наилучшим образом для двух КА решается при условиях:
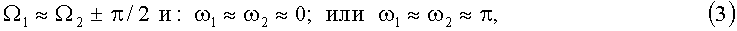
т.е. тогда, когда для каждой из орбит линия узлов перпендикулярна линии апсид, и линии узлов взаимно перпендикулярны. Центры управления всеми КА, находящимися в единой области удержания по широте и долготе, следуют единой стратегии коллокации, обмениваясь баллистической информацией.
Однако для гарантированной коллокации требуется перманентный процесс обмена баллистической информацией между центрами управления КА. Такой процесс может давать сбои, и сбои обязательно будут происходить. Кроме того, нельзя исключать принципиальную невозможность взаимодействия между центрами управления КА. Проще находиться в состоянии автономной коллокации: когда к процессу коллокации не привлекаются другие КА и их центры управления. При постановке такой задачи следует учитывать, что линия узлов и линия апсид орбиты смежного КА (СКА) могут пересекаться под произвольным углом. Далее по тексту под «автономным» КА подразумевается КА, «взявший» на себя всю ответственность по коллокации в заданной области удержания по широте и долготе.
Идея малозатратной автономной коллокации, не накладывающей никаких сколько-нибудь значимых обязательств на центр управления СКА (что означает наличие или отсутствие действий по реализации согласованной стратегии коллокации со стороны такого центра управления), позволяющей за счет настройки векторов наклонения и эксцентриситета обходить в течение суток лучи от всех антенн, включая глобальные, на СКА, не создавая тем самым экранирующих эффектов, представляется актуальной и наиболее эффективной. Идея автономной коллокации (самоколлокации) не имеет аналогов.
Баллистические сведения о СКА и задачу разнесения векторов наклонения и эксцентриситета в режиме самоколлокации возможно получать и решать, например, используя данные - результаты измерения параметров орбиты от международной системы слежения за спутниками NORAD, раскрывающими тактику и стратегию удержания СКА. Эта система работает без ошибок повиткового прогнозирования, главной составляющей которых является реализация удержания КА с помощью двигателей системы коррекции. Ошибки по e, i, ω более чем удовлетворительны.
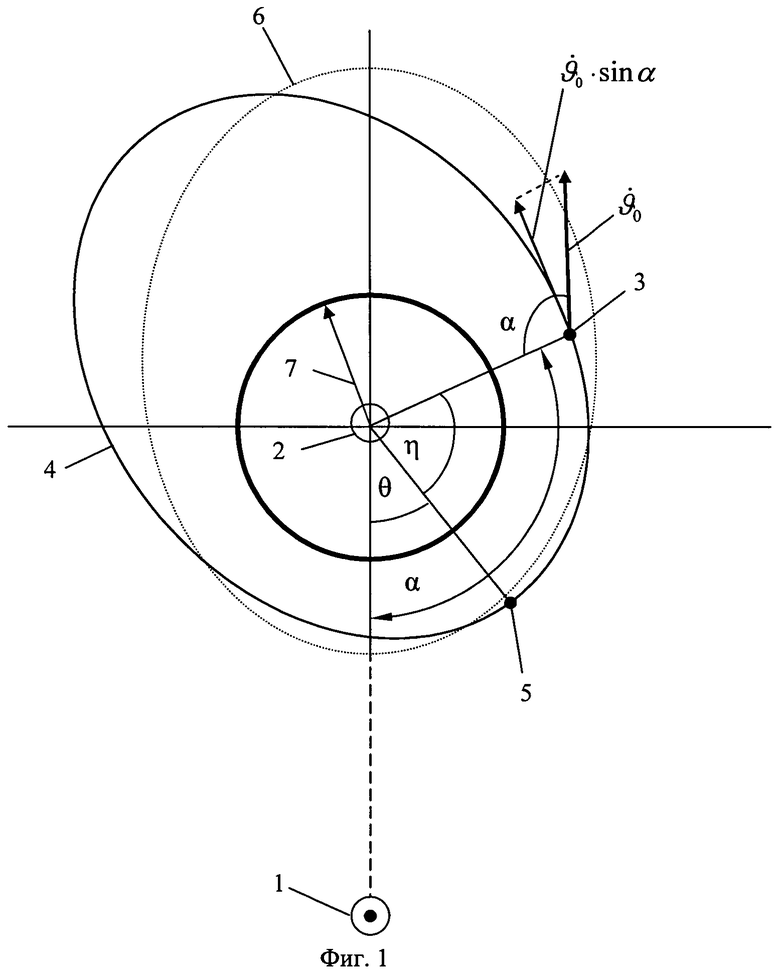
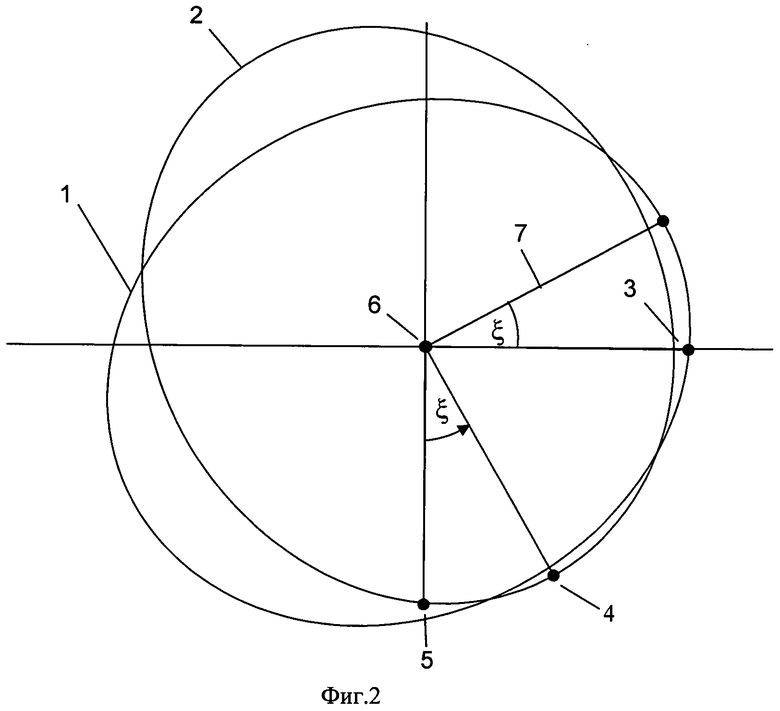
Задача автономной коллокации, как показывают геометрия расположения составляющих элементов векторов наклонения и эксцентриситета в инерциальном пространстве (фиг.2) и расчеты межспутниковых расстояний (фиг.3), оптимальным образом решается при условиях:
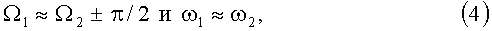
где индекс «1» соответствует «автономному» КА, индекс «2» соответствует СКА, т.е. тогда, когда линии узлов орбит «автономного» и СКА пересекаются под прямым углом, линии апсид орбит «автономного» и СКА пересекаются под прямым углом, угол рассогласования (ξ, фиг.2) между прямым восхождением перигея и восходящим узлом орбиты СКА равен углу рассогласования между прямым восхождением перигея и восходящим узлом орбиты «автономного» КА.
На фиг.2 цифрами обозначено:
1 - орбита «автономного» КА;
2 - орбита СКА;
3 - восходящий узел «автономного» КА;
4 - перигей СКА;
5 - восходящий узел СКА;
6 - Земля;
7 - перигей «автономного» КА.
Сводные результаты расчетов межспутниковых расстояний, при принятых за основу начальных условиях движения КА:
- сидерические периоды обращения - 86164,1 с;
- эксцентриситет орбит - 0,00020;
- наклонение орбит - 1,5 угл.мин,
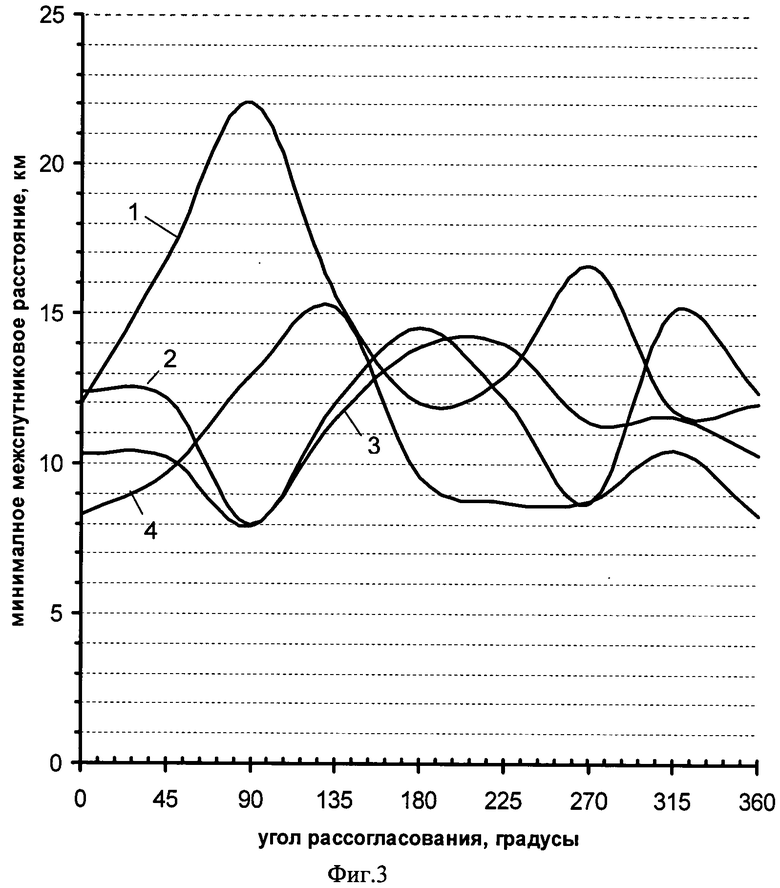
приведены на фиг.3. На фиг.3 цифрами 1-4 обозначены линии минимальных межспутниковых расстояний при условиях (4) и:
1-(i1=1'30''; e1=0,00020; i2=1'30''; e2=0,00020; ξ∈[0-2π]);
2-(i1=1'30''; e1=0,00030; i2=1'30''; e2=0,00010; ξ∈[0-2π]);
3-(i1=1'30''; e1=0,00030; i2=0'10''; e2=0,00010; ξ∈[0-2π]);
4-(i1=0'10''; e1=0,00015; i2=1'30''; e2=0,00015; ξ∈[0-2π]);
индекс «1» соответствует «автономному» КА.
Из фиг.3 следует, что соблюдение условий (4) и допуска на минимальное межспутниковое расстояние в 8 км, технически осуществимо.
Автономная коллокация на принципах (4) позволяет также рассогласование по любому из условий (4) относительно номинала 90° до 25°.
Востребованной является также идея мониторинга одного КА другим КА, предписывающая «автономному» КА находиться на безопасном технологическом и физическом расстоянии от СКА и заниматься непосредственным мониторингом последнего на суточном интервале в течение максимально возможного времени. Непосредственный мониторинг СКА на суточном интервале в течение максимально возможного времени приводит к дополнительным сверх оговоренных затратам по управлению центром масс «автономного» КА. Далее по тексту «автономный» КА, занимающийся мониторингом или (и) управлением другим КА, - мониторинговый КА (МКА).
Баллистические сведения о СКА и задачу коллокации с ним, помимо вышеуказанного варианта определения параметров орбиты с использованием международной системы слежения за спутниками, возможно получать и решать, придавая системе навигации и управления движением МКА комплект приемопередающей радиоаппаратуры по измерению дальности и оптический звездный датчик углового положения.
В принципе, МКА может находиться сбоку намеренным разнесением по долготе относительно СКА, чтобы без хлопот гарантировать межспутниковое расстояние, большее минимально допустимого. Но возникает проблема. Существующим регламентом стояния геостационарных КА предполагается удержание в области, никак не более 0,1° по долготе относительно номинальной рабочей позиции, тогда для уверенного разнесения двух КА по долготе оба КА должны находиться в областях менее ±0,1°, и расстояние между ними должно быть порядка 0,1° (74 км), но на таком отдалении от СКА МКА может попасть в область, где будет находиться сторонний (третий) КА, с которым также надо находиться в состоянии коллокации. Это уже технически неразрешимая задача. Неразрешимой становится и задача коллокации удалением (разнесением) МКА от СКА по долготе в общей с СКА области ±0,05° относительно номинальной рабочей позиции - область слишком узка для маневров относительного движения, особенно, если СКА реализует план маневров, несогласованный с центром управления МКА. С учетом заселенности геостационарной орбиты, возможно изначально - возможно впоследствии, от схемы коллокации только удалением МКА от СКА по долготе придется отказаться. Поскольку следует рассчитывать именно на область ±0,05° по широте и долготе относительно единой для СКА и МКА номинальной орбитальной позиции, надо уметь коллокировать на одном с СКА поле по долготе и широте, выполняя при этом функцию активного слежения за СКА. Значит, параметрами автономной коллокации должны быть и отклонение МКА от СКА по долготе, и эксцентриситет, и наклонение орбиты МКА. Коллокация по эксцентриситету, наклонению и долготе «своими силами» до сих пор не рассматривалась.
Находиться круглосуточно в зоне вещания СКА одному МКА не представляется возможным. Хотя, при наличии необходимого запаса топлива (на порядок больше обычно вырабатываемого на стационарной орбите), это возможно. При разнесении по долготе можно рассчитывать на круглосуточный прием сигналов с СКА «по перпендикуляру». Но из сказанного выше этот вариант нереализуем. Однако находиться эффективно в течение 12 ч/сутки «под СКА» можно.
Стационарная орбита заполнена сигналами с Земли для большого числа аппаратов, находящихся даже не на стационарной орбите, и нахождение МКА рядом с СКА не гарантирует получение информации, предназначенной именно для СКА. Второе - информация для СКА, скорее всего, будет иметь не одну степень защиты, ключи к которым будут меняться по неизвестному (без усилий наземных служб) закону да еще со скоростью, принципиально исключающей адаптацию к потоку информации. Большую часть проблемы можно снять, только снимая часть информации с СКА. Так что способ нахождения МКА «под СКА» актуален, и ему нет качественной альтернативы (вспомним, что стоять в стороне и принимать сигналы «по перпендикуляру» вряд ли удастся). Вообще-то это вполне вероятная и серьезная проблема, которую надо иметь в виду при развертывании системы. Информация с СКА поможет идентифицировать целевую информацию с Земли, и обе суммы информации будут полезно дополнять друг друга и представлять единый суточный файл, не имеющий потерь информации.
Изобретение состоит из двух частей:
1) - баллистическая часть, предлагающая совмещение СКА и МКА по долготе и организацию автономной от СКА коллокации в обеспечение нахождения МКА «под СКА»;
2) - радиотехническая часть, предоставляющая (глобальная антенна - это 8,65°X8,65°) максимальный период времени, когда можно снимать информацию с СКА, находясь под ним, и обосновывающая качество и целесообразность круглосуточного съема информации по линиям «Земля-СКА» и «СКА-Земля».
Целью изобретения является реализация вышеуказанных идей.
Поставленная цель достигается тем, что в способе мониторинговой коллокации на геостационарной орбите, включающем переводы векторов наклонения и эксцентриситета на границы разнесенных относительно друг друга областей прицеливания (областей допустимого изменения векторов наклонения и эксцентриситета), измерения параметров орбиты каждого КА, определение по ним текущих значений орбитальных элементов каждого КА и проведение с помощью двигателей малой тяги коррекций периода обращения, наклонения и эксцентриситета орбиты, введены новые операции, заключающиеся в том, что для организации автономной от СКА коллокации за время до приведения МКА в заданную область удержания по широте (наклонению) и долготе по данным независимых траекторных измерений выявляют стратегию управления движением центра масс СКА, в процессе удержания уточняют положение центра области прицеливания по наклонению СКА, проведением коррекций наклонения вектор наклонения орбиты МКА в фазовой плоскости выставляют так, чтобы линия узлов орбиты МКА стала перпендикулярна линии узлов орбиты СКА и наклонение (imin) орбиты МКА относительно орбиты СКА составляло не менее (14-15) угл.с, проводят коррекции эксцентриситета для удаления направления на перигей от направления на восходящий узел орбиты МКА на величину угла рассогласования между направлениями на перигей и восходящий узел орбиты СКА и поддержания такого положения перигея заданных пределах области прицеливания по эксцентриситету, проводят регулярные комплексные коррекции наклонения орбиты МКА для поддержания прямого угла между линиями узлов орбит КА в заданных пределах области прицеливания по наклонению, для устранения вековой составляющей ухода по наклонению и для превышения imin проводят коррекции долготы (периода) для того, чтобы начало координат [ΔL; ΔR - соответственно отклонение вдоль орбиты и отклонение по радиус-вектору] совпадало в заданных пределах с центром эллипса дистанцирования от СКА, на МКА переопределяют центры областей прицеливания по наклонению и эксцентриситету орбиты МКА при корректировке стратегии управления движением центра масс смежного КА и при нарастании углов рассогласования между линиями апсид и линиями узлов орбит МКА и СКА, в случаях опасного сближения КА проводят коррекции уклонения, представляющие собой одновременные коррекции долготы и эксцентриситета орбиты, после организации автономной коллокации проходом МКА под СКА, когда радиус-вектор МКА меньше радиус-вектора СКА, ежедневно уточняют интервал времени, когда уровень приема на МКА излучения антенн, установленных на СКА удовлетворителен, при снижении уровня приема на МКА переходят в режим приема информации для СКА с наземных антенн, в случае уверенного непрерывного приема на МКА излучения антенн, установленных на СКА, в течение 12 часов непосредственный круглосуточный мониторинг СКА осуществляют двумя МКА, установленными на диаметрально противоположных сторонах эллипса дистанцирования.
Как показывают расчеты (которые может провести каждый) относительное движение двух КА имеет вполне определенные закономерности, а именно:
1 - проекция относительного движения одного КА на плоскость орбиты другого КА - эллипс;
2 - отношение малой полуоси к большой полуоси эллипса дистанцирования составляет 1:2 (фиг.5);
3 - смещение на величину ΔL вдоль орбиты (по долготе в Гринвичской Системе Координат, положительное направление - на восток) одного из КА приводит к смещению с тем же знаком центра прежнего эллипса дистанцирования на величину AL вдоль координатной оси «Отклонение вдоль орбиты».
4 - эллипс дистанцирования всегда ориентирован большой полуосью вдоль координатной оси «Отклонение вдоль орбиты»;
5 - при изменении эксцентриситетов орбит КА большая и малая полуоси эллипса дистанцирования определяются по соотношениям:


где индексы «'» и «''» относятся ко времени соответственно до и после орбитальных маневров;
а', а'' - соответственно большие полуоси до и после орбитальных маневров, км;
b', b'' - соответственно малые полуоси до и после орбитальных маневров, км;
е1, е2 - эксцентриситеты орбит соответственно первого и второго КА.
На фиг.5 приведен эллипс дистанцирования, рассчитанный по программе межспутникового расстояния, для следующего набора начальных условий (линии узлов ортогональны, линии апсид ортогональны).
НУ 1:
- долгота восходящего узла - 0;
- аргумент широты перигея - 0;
- наклонение - (0-1,5) угл. мин.;
- эксцентриситет 
НУ 2:
- долгота восходящего узла - 90°;
- аргумент широты перигея - 0°;
- наклонение - (0-1,5) угл. мин.;
- эксцентриситет 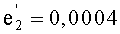
Если в приведенных выше начальных условиях изменить эксцентриситеты на

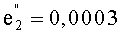
получим:
- максимальные относительные отклонения вдоль орбиты 22,4 км в т.1 (фиг.5) и минус 29,9 км в т.3;
- максимальные относительные отклонения по радиус-вектору 13 км в т.2 и 12,6 км в т.4.
Если в приведенных выше начальных условиях эксцентриситеты будут следующими:

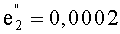
получим:
- максимальные относительные отклонения вдоль орбиты 20,6 км в т.1 (фиг.5) и минус 28,3 км в т.3;
- максимальные относительные отклонения по радиус-вектору 12,5 км в т.2 и 12 км в т.4.
Если МКА отодвинуть по долготе на 0,4 угл. мин (4,9 км для геостационарной орбиты) на запад при е1=е2=0,0002, получим:
- максимальные относительные отклонения вдоль орбиты 20 км в т.1 (фиг.5) и минус 17,5 км в т.3;
- максимальные относительные отклонения по радиус-вектору 9,2 км в т.2 и 9 км в т.4, т.е. при выполнении условий (4) одна из больших полуосей прежнего эллипса дистанцирования изменяется на величину двойного ухода вдоль орбиты, а малая ось эллипса в два раза меньше большой оси.
Основное условие. Линии узлов и линии апсид орбит МКА и СКА должны быть ортогональны и сумма эксцентриситетов орбит должна составлять порядка 0,0004.
Для примера, на фиг.6 приведен эллипс дистанцирования для следующего набора начальных условий (линии узлов ортогональны, перигеи орбит МКА и СКА диаметрально противоположны).
НУ 1:
- долгота восходящего узла - 0;
- аргумент широты перигея - 0;
- наклонение - (0-1,5) угл. мин.;
- эксцентриситет e1=0,0002;
НУ 2:
- долгота восходящего узла - 90°;
- аргумент широты перигея - 90°;
- наклонение - (0-1,5) угл. мин.;
- эксцентриситет e2=0,0004.
Если МКА отодвинуть по долготе на 0,8 угл. мин (9,8 км для геостационарной орбиты) на запад при e1=0,0002, e2=0,0004, получим:
- максимальные относительные отклонения вдоль орбиты 24,2 км в т.1 (фиг.6) и минус 80,8 км в т.3;
- максимальные относительные отклонения по радиус-вектору 26,2 км в т.2 и 25,8 км в т.4,
т.е. при выполнении условий для фиг.6 большая ось прежнего эллипса дистанцирования смещается на величину ухода вдоль орбиты, а малая полуось эллипса (в два раза меньше большой полуоси) остается прежней.
При совмещенных радиус-векторах СКА и МКА (когда МКА, СКА и Земля находятся на одной линии) и реальных эксцентриситетах орбит ~0,0004 и ~0,0002 межспутниковое расстояние составит порядка 19-20 км.
При радиусе r отчуждения (19-20)км и угле 8,65° будем иметь минимальное наклонение орбиты МКА относительно орбиты СКА r·sin(8,65)/42164,1=(14-15) угл.с. Это поддерживается оперативно и «бесплатно», поскольку ровно столько требуется ежесуточно для компенсации вековых уходов по наклонению.
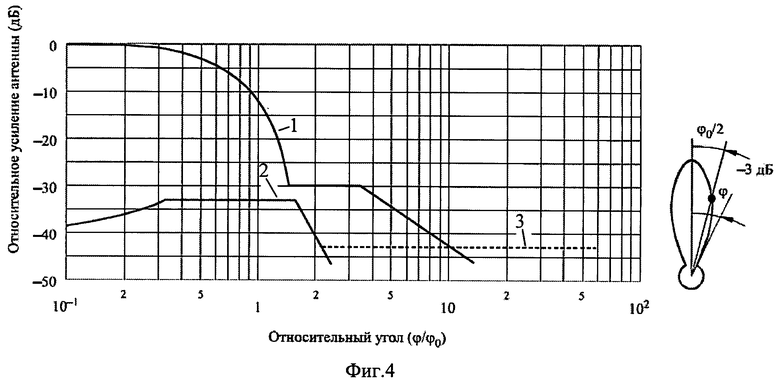
Для оценки реализуемости предлагаемого способа определим относительные уровни излучения, которые может принимать МКА, обращаясь вокруг исследуемого СКА, а также ориентировочные значения угла «Земля-СКА-МКА» (ЗСМ), в пределах которого МКА сможет выполнять возложенную на него задачу. Поскольку на современных спутниках связи и ретрансляции данных используется большая номенклатура бортовых антенн с шириной диаграммы направленности (ДН) в основном от 1° до 18°, рассмотрение начнем с самых узких лучей.
В соответствии с идеей предлагаемого способа МКА должен находиться вне конуса радиовидимости Земли с СКА, вершиной которого является точка нахождения СКА на геостационарной орбите, а образующие конуса являются практически касательными к поверхности Земли, проведенными из вершины данного конуса. Все антенные лучи, используемые для связи с Землей, имеют такую ориентацию в пространстве, что их ДН по уровню половинной мощности (а именно по этому уровню определяется ширина ДН) не выходят за пределы указанного конуса, угол при вершине которого составляет 17,3°. В этом случае, проводя анализ, например, для луча с шириной ДН 1° следует ориентироваться на то, что МКА должен будет принимать излучение от такого луча на уровне боковых лепестков высокого порядка. Целесообразно воспользоваться приведенной в Регламенте радиосвязи, том 2, издание 2008 года, с.578, эталонной диаграммой направленности спутниковых антенн, предназначенной в основном для оценки электромагнитной совместимости с другими спутниками связи (фиг.4). Диаграмма на фиг.4 в форме кривой 1 дает представление об относительном усилении антенны спутника на уровнях от основного лепестка до первых боковых, а прямая 3 соответствует уровню отдаленных боковых лепестков более высокого порядка. (Кривая 2 для нижеследующего анализа не применяется, т.к. характеризует уровень излучения антенны на ортогональной поляризации). Угол φo на данной диаграмме соответствует ширине луча по уровню половинной мощности, а угол φ - углу отклонения от осевого излучения луча (в нашем случае, это угол ЗСМ). Из фиг.4 следует, что для значений относительного угла (φ/φo) от 10 до 60 уровень излучения антенны может быть принят на уровне на 43 дБ ниже (или на уровне минус 43 дБ) относительно уровня излучения вдоль оси луча. Применительно к рассматриваемому в качестве примера лучу с φo=1° можно сказать, что излучение на уровне минус 43 дБ будет наблюдаться в диапазоне углов φ от 10° до 60° относительно оси луча. В дальнейшем будет показано, что имеются потенциальные возможности для увеличения размеров данного диапазона. Очевидно, что для более широких лучей СКА излучение на данном уровне будет наблюдаться в пропорционально более широком секторе углов φ.
Однако необходимо принять во внимание, что для значений φ от 90° до 180° оценить уровень излучения для антенн, установленных на корпусе СКА, крайне затруднительно вследствие затенения этого излучения корпусом спутника и крупными элементами его конструкции. В то же время антенны, расположенные, например, на вынесенных штангах, в этом секторе углов φ способны создать в окружающем пространстве излучение, уровень которого, в первом приближении, также может быть порядка минус 43 дБ.
Теперь необходимо оценить возможность приема на МКА излучений СКА, полученного выше уровня, т.е. на 43 дБ ниже максимального уровня, создаваемого вдоль оси луча. Для этого будем исходить из того, что СКА создает на границе своей зоны обслуживания (на линии пересечения конуса радиовидимости с Землей) плотность потока мощности (ППМ) такой величины, которая требуется для уверенного приема земными станциями сигналов с СКА. При этом ППМ=ЭИИМСКА/4πd2, где ЭИИМСКА - эквивалентная изотропно излучаемая мощность СКА, равная произведению мощности передатчика на коэффициент усиления антенны, a d - протяженность радиолинии. Поскольку указанная ППМ создается для условий связи на расстоянии 35,8 тыс. км, то при сокращении этого расстояния до предполагаемых 20 км (расстояние между МКА и СКА) ППМ для МКА должна была бы возрасти в (35800/20)2=3,2*106 раз или на 65 дБ (т.е. 101g 3,2*106), если бы МКА находился в пределах связного луча антенны СКА. Однако, как было определено выше, коэффициент усиления антенны СКА в направлении МКА будет иметь значение, на 43 дБ ниже, чем для станций на поверхности Земли. Тем не менее, в итоге значение ППМ для МКА оказывается в данном случае на 65-43=22 дБ больше.
Полученный энергетический выигрыш в уровне ППМ может быть использован для повышения вероятности приема сигналов с СКА и расширения сектора приема этих сигналов. Это связано с тем, что форма диаграммы направленности реальных антенн характеризуется как основным лепестком ДН, так и боковыми лепестками, максимальный уровень которых постепенно снижается с увеличением угла φ. Прямая 3 на фиг.4 в некоторой степени олицетворяет как раз максимальный уровень дальних боковых лепестков. Вместе с тем, между максимумами соседних боковых лепестков существуют относительные минимумы ДН с уровнями примерно на 10 дБ ниже уровня предыдущего максимума, поэтому полученный выше энергетический выигрыш может быть использован как для компенсации потерь уровня сигнала в минимумах ДН, так и для компенсации постепенного снижения уровней максимумов дальних боковых лепестков.
В определенной мере энергетический выигрыш может быть при необходимости использован и для варьирования расстояния между МКА и СКА.
Таким образом, проведенная оценка реализуемости предлагаемого способа указывает на возможность осуществления приема на МКА излучений СКА в относительно широком секторе углов ЗСМ даже при использовании на СКА достаточно узких антенных лучей шириной порядка 1°.
Для обеспечения выполнения МКА задач в соответствии с предлагаемым способом на нем потребуется установить два блока приемных антенн, первый из которых обращен в сторону СКА и обеспечивает прием излучаемых СКА сигналов, а другой обращен в сторону Земли и обеспечивает перехват сигналов, предназначенных для СКА. Соответственно, на борту МКА также должна быть установлена передающая антенна для передачи на Землю результатов мониторинга.
Тип и характеристики упомянутых групп приемных антенн выбираются на основе данных о радиотехнических характеристиках СКА (диапазоны частот, уровни передаваемых сигналов) и данных о взаимном расположении МКА и СКА (секторы обзора), что позволит охватить весь спектр контролируемых излучений во всем секторе углов мониторинга СКА. Какие это будут антенны, как они обеспечивают прием сигналов в заданных секторах мониторинга - с помощью ли широкой диаграммы направленности или путем сканирования в этих секторах узким лучом - не так важно, важно, что первый блок имеет механический привод, качающий его в диапазоне ±45° для лучшего приема сигналов с СКА.
Вообще, два МКА решают задачу круглосуточного съема информации с СКА при максимально допустимом угле ЗСМ 90°.
Для сброса данных мониторинга на Землю, по возможности, целесообразно использовать оптический диапазон волн. Тем самым отпадает необходимость в получении радиочастотных присвоений для МКА и, кроме того, оптические радиолинии, благодаря очень узким передающим лучам, обеспечивают практически абсолютную скрытность передачи информации и ее защищенность от перехвата. Оптический диапазон волн может быть использован также для контроля и управления МКА. Необходимая для этого приемопередающая аппаратура в настоящее время уже используется на ряде зарубежных и отечественных КА. Атмосфера Земли не является помехой, если станция приема будет расположена в высокогорье (там, например, сейчас располагается станция приема информации с российских блоков МКС, передаваемых по оптическому каналу). Здесь присутствует четкое разграничение: мониторинг СКА осуществляется МКА в радиодиапазоне, сброс данных на Землю и управление МКА - в оптическом диапазоне. Обе функции (мониторинг и сброс; управление) получают практически идеальную электромагнитную совместимость (развязку).
Если оптический диапазон использовать нецелесообразно, применяют радиодиапазон со штатной схемой электромагнитной совместимости.
ПРИЛОЖЕНИЕ 1
Годограф вектора эксцентриситета
Влияние малого импульса скорости (приращения скорости за секунду) 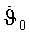
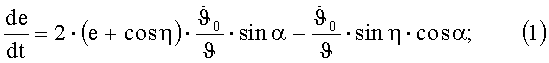
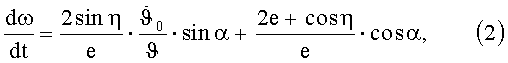
где ϑ - средняя скорость движения КА, 3074 м/с;
η=α-θ - в - истинная аномалия;
θ - угол между направлением на Солнце и на перигей орбиты КА.
Тогда, подставляя выражение η в (3) и используя формулы разности двух углов, получаем:
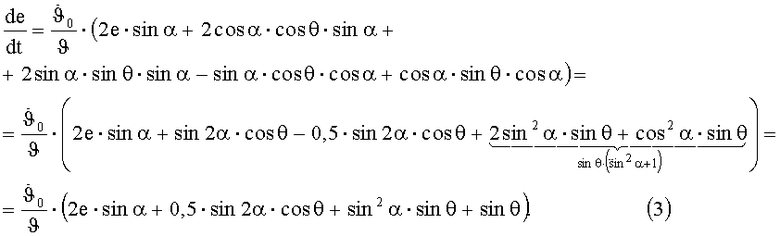
Первое слагаемое, как минимум, на два порядка меньше остальных и не является постоянным членом, тогда
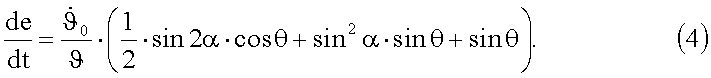
При θ=0
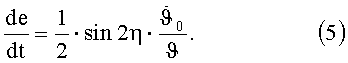
Аналогично рассуждая, будем иметь для скорости движения (аргумента широты) перигея:
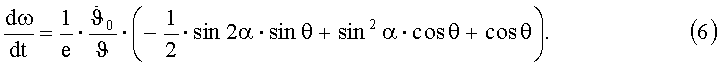
При θ=0

Далее,

где 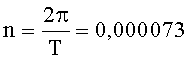
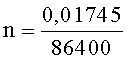
тогда
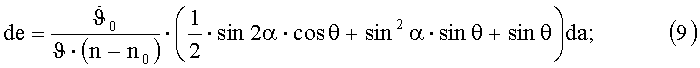

Интегрируем на сутках (на витке):
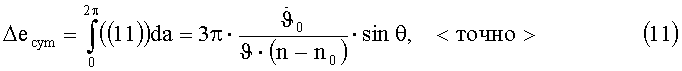
при θ=0 
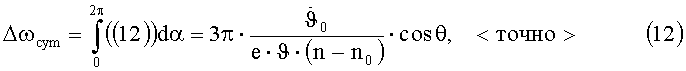
при θ=0 
Дадим оценку 

где S - мощность световой волны, падающей на 1 м2 поверхности тела, вт/м2,
А - коэффициент отражения (А=0 для абсолютно черного тела);
с - скорость света, км/с.
S=1,4·103 вт/м2.
Значение А зависит от отражающей способности деталей конструкции КА и в контексте данного технического решения должно включать (условно) гравитационное воздействие Солнца как «±» относительно положения, когда вектор Лапласа направлен на Солнце. Для реальных КА на высоте стационарной орбиты значения А находятся в пределах [0,28-0,44]. Исходя из А=0,44, будем иметь Р равное 6,72·10-6 н/м2. Поскольку сила светового давления F=S'·P, где S' - площадь миделевого сечения, то

Отношение 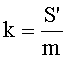
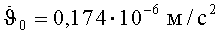
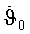
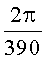
При повитковом анализе можно, к примеру, исходя из того, что

получить формулу:

где 



е0 - значение эксцентриситета на середине цикла удержания;
е - основание натурального логарифма.
На интервале удержания до 20-30 суток можно пользоваться упрощенной формулой:

где 
ПРИЛОЖЕНИЕ 2
Годограф вектора наклонения
Проекции вектора наклонения:


при малом i
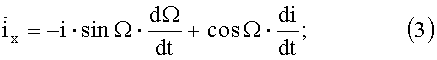
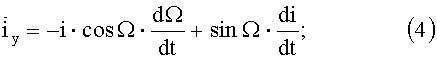
Влияние бокового ускорения 


где Θ - аргумент широты Солнца;
V=3,074 км/с - средняя скорость движения КА на геостационарной орбите.
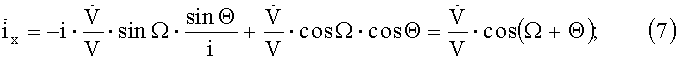
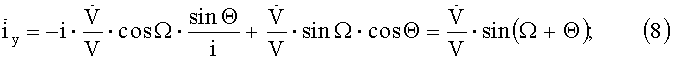
Ω+Θ=αc - прямое восхождение Солнца;
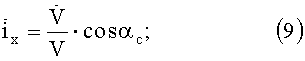

Исходя из общего векторного уравнения возмущений
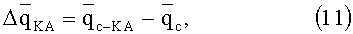
среднее ускорение на витке:
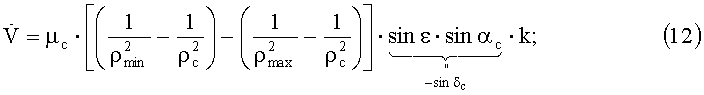
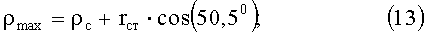
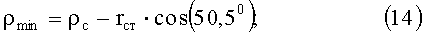
ρc=149600000 км;
cos(50,5°) - средневесовой косинус;
δс - склонение Солнца.
Эффективность любой коррекции оценивается формулой:
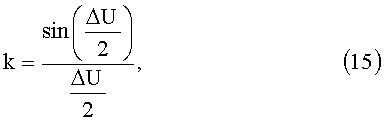
где U - активный участок движения;
на суточном интервале k≈0,6366≈cos(50,5°), при U∈[0-180°].

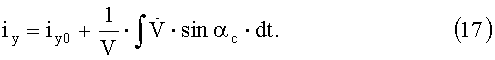
Представим сутки (время) через среднее движение Солнца:

и обозначим постоянную часть уравнений (16), (17) с учетом (18) через А:
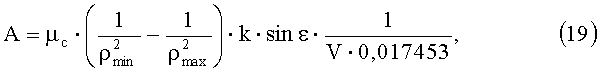
Тогда:
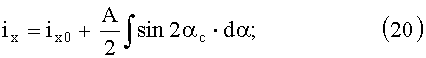
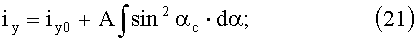

A=0,00175;
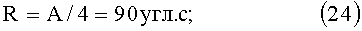
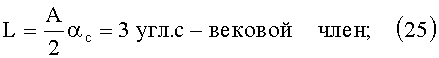
через каждые сутки Δαc≈0,017453.
Система уравнений (22) и (23) без векового члена (25) представляет уравнение окружности («солнечного круга») в параметрической форме, где R - радиус окружности, ix0, iy0 - компоненты конца вектора точки прицеливания по наклонению, рассчитываемые по формулам (1), (2). Зная прямое восхождение Солнца и выбрав координаты точки прицеливания [ix0; iy0], определяют положение конца вектора наклонения на начало очередного цикла удержания сообразно уходу вектора i СКА.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ АВТОНОМНОЙ КОЛЛОКАЦИИ НА ОКОЛОСТАЦИОНАРНОЙ ОРБИТЕ | 2018 |
|
RU2703696C1 |
| СПОСОБ УДЕРЖАНИЯ КОСМИЧЕСКОГО АППАРАТА НА ГЕОСИНХРОННОЙ 24-ЧАСОВОЙ ОРБИТЕ | 2013 |
|
RU2535353C2 |
| СПОСОБ МОНИТОРИНГОВОЙ КОЛЛОКАЦИИ НА ГЕОСТАЦИОНАРНОЙ ОРБИТЕ | 2019 |
|
RU2721812C1 |
| СПОСОБ АВТОНОМНОЙ КОЛЛОКАЦИИ НА ОКОЛОСТАЦИОНАРНОЙ ОРБИТЕ | 2019 |
|
RU2716394C1 |
| СПОСОБ БАЛЛИСТИЧЕСКОГО ОБЕСПЕЧЕНИЯ МОНИТОРИНГА КОСМИЧЕСКОГО АППАРАТА НА ГЕОСТАЦИОНАРНОЙ ОРБИТЕ | 2022 |
|
RU2787796C1 |
| СПОСОБ АВТОНОМНОЙ КОЛЛОКАЦИИ НА ГЕОСТАЦИОНАРНОЙ ОРБИТЕ | 2013 |
|
RU2559371C2 |
| СПОСОБ АВТОНОМНОЙ КОЛЛОКАЦИИ НА ОКОЛОСТАЦИОНАРНОЙ ОРБИТЕ | 2021 |
|
RU2768994C1 |
| СПОСОБ АВТОНОМНОЙ КОЛЛОКАЦИИ НА ГЕОСТАЦИОНАРНОЙ ОРБИТЕ | 2019 |
|
RU2721813C1 |
| СПОСОБ КОЛЛОКАЦИИ ПРИ ПЕРЕВОДЕ ГЕОСТАЦИОНАРНОГО КОСМИЧЕСКОГО АППАРАТА НА ДРУГУЮ ДОЛГОТУ СТОЯНИЯ И УВОДЕ ЕГО НА ОРБИТУ ЗАХОРОНЕНИЯ | 2022 |
|
RU2786680C1 |
| СПОСОБ КОЛЛОКАЦИИ НА ГЕОСТАЦИОНАРНОЙ ОРБИТЕ | 2020 |
|
RU2729347C1 |


Изобретение относится к управлению движением группы (кластера) космических аппаратов (КА), преимущественно геостационарных спутников Земли. Согласно способу линии узлов и линии апсид орбит мониторингового КА (МКА) и смежных КА (СКА) поддерживают ортогональными. Сумма эксцентриситетов орбит должна составлять ~ 0,0004, а наклонение орбиты МКА относительно орбиты СКА - не менее (14-15) угл. с. С этой целью проводят регулярные коррекции для удержания концов (фазовых) векторов наклонения и эксцентриситета в требуемых областях прицеливания. Кроме того, корректируют долготы (периоды обращения) так, чтобы начало осей координат (отклонениий вдоль орбиты и по радиусу-вектору) совпадало в заданных пределах с центром эллипса дистанцирования от СКА. Переопределяют центры областей прицеливания при корректировке стратегии управления движением центра масс СКА. При снижении уровня приема на МКА излучения антенн, установленных на СКА, переходят в режим приема информации для СКА с наземных антенн. В случае уверенного приема на МКА сигналов указанных антенн СКА в течение 12 ч осуществляют непосредственный круглосуточный мониторинг СКА двумя МКА. Данные МКА установлены на диаметрально противоположных сторонах указанного эллипса дистанцирования. Техническим результатом изобретения является удержание КА на рабочей позиции без помех другим КА и мониторингу СКА. 2 з.п. ф-лы, 6 ил.
1. Способ мониторинговой коллокации на геостационарной орбите, включающий переводы векторов наклонения и эксцентриситета на границы разнесенных относительно друг друга областей прицеливания (областей допустимого изменения векторов наклонения и эксцентриситета), измерения параметров орбиты каждого космического аппарата (КА), определение по ним текущих значений орбитальных элементов каждого КА и проведение с помощью двигателей малой тяги коррекций периода обращения, наклонения и эксцентриситета орбиты, отличающийся тем, что для организации автономной от смежного КА (СКА) коллокации за время до приведения мониторингового КА (МКА) в заданную область удержания по широте (наклонению) и долготе по данным независимых траекторных измерений выявляют стратегию управления движением центра масс СКА, в процессе удержания уточняют положение центра области прицеливания по наклонению СКА, проведением коррекций наклонения вектор наклонения орбиты МКА в фазовой плоскости выставляют так, чтобы линия узлов орбиты МКА стала перпендикулярна линии узлов орбиты СКА и наклонение (imin) орбиты МКА относительно орбиты СКА составляло не менее (14-15) угловых секунд, проводят коррекции вектора эксцентриситета:
- для того чтобы сумма эксцентриситетов орбит МКА и СКА составляла порядка 4·10-4,
- для удаления направления на перигей от направления на восходящий узел орбиты МКА на величину угла рассогласования между направлениями на перигей и восходящий узел орбиты СКА,
- для поддержания такого положения перигея в заданных пределах области прицеливания по эксцентриситету,
проводят регулярные комплексные коррекции наклонения орбиты МКА:
- для поддержания прямого угла между линиями узлов орбит КА в заданных пределах области прицеливания по наклонению,
- для устранения вековой составляющей ухода по наклонению,
- для превышения imin указанной величины,
проводят коррекции долготы (периода обращения) для того, чтобы начало координат (ΔL, ΔR - соответственно отклонение вдоль орбиты и отклонение по радиусу-вектору) совпадало в заданных пределах с центром эллипса дистанцирования от СКА, на МКА переопределяют центры областей прицеливания по наклонению и эксцентриситету орбиты МКА при корректировке стратегии управления движением центра масс СКА и при нарастании углов рассогласования между линиями апсид и линиями узлов орбит МКА и СКА в случаях опасного сближения КА проводят коррекции уклонения, представляющие собой одновременные коррекции долготы и эксцентриситета орбиты, после организации автономной коллокации проходом МКА под СКА, когда радиус-вектор МКА меньше радиуса-вектора СКА, ежедневно уточняют интервал времени, когда уровень приема на МКА излучения антенн, установленных на СКА, удовлетворителен, при снижении уровня приема на МКА переходят в режим приема информации для СКА с наземных антенн, в случае уверенного непрерывного приема на МКА излучения антенн, установленных на СКА, в течение 12 часов непосредственный круглосуточный мониторинг СКА осуществляют двумя МКА, установленными на диаметрально противоположных сторонах эллипса дистанцирования.
2. Способ по п.1, отличающийся тем, что блок приемных антенн на МКА, обращенных в сторону СКА, имеет привод, качающий его в диапазоне ±45° для лучшего приема сигналов с СКА.
3. Способ по п.1, отличающийся тем, что передачу данных мониторинга с МКА на Землю, а также контроль и управление МКА, по возможности, осуществляют с использованием оптического диапазона волн.
| СПОСОБ УПРАВЛЕНИЯ КЛАСТЕРОМ НАХОДЯЩИХСЯ НА ГЕОСТАЦИОНАРНОЙ ОРБИТЕ СПУТНИКОВ (ВАРИАНТЫ) | 2004 |
|
RU2284950C2 |
| Г.М.ЧЕРНЯВСКИЙ, В.А.БАРТЕНЕВ, В.А.МАЛЫШЕВ | |||
| Управление орбитой стационарного спутника | |||
| М., Машиностроение, 1984, с.42, 43, 134-136 | |||
| PATTINSON L | |||
| EUTELSAT Satellite Collocation | |||
| Приспособление в пере для письма с целью увеличения на нем запаса чернил и уменьшения скорости их высыхания | 1917 |
|
SU96A1 |
| СПОСОБЫ РАБОТЫ СПУТНИКОВОЙ КОММУНИКАЦИОННОЙ СИСТЕМЫ, СПОСОБ УПРАВЛЕНИЯ ЕЕ РАБОТОЙ И СИСТЕМА УПРАВЛЕНИЯ СПУТНИКОВЫМ АНТЕННЫМ ОХВАТОМ НЕГЕОСТАЦИОНАРНОЙ ОРБИТАЛЬНОЙ МНОГОСПУТНИКОВОЙ СИСТЕМЫ | 1992 |
|
RU2121225C1 |
| US 5120007 A, 09.06.1992 | |||
| US 5506780 A, 09.04.1996 | |||
Авторы
Даты
2015-08-10—Публикация
2013-08-01—Подача