Изобретение относится к вычислительной технике, может быть реализовано на современных быстродействующих ЭВМ и использовано, например, при отборе эффективных вариантов в поисковых, рекомендательных системах, системах поддержки принятия решений, сетях Интернет, системах автоматической классификации пакетов данных, и в других смежных областях. Реализация заявляемого изобретения может включать в себя хранение информации на физических носителях, магнитных дисках, сетевых хранилищах информации, ее обработку на ЭВМ и предоставление полученного набора эффективных вариантов конечному пользователю в любом доступном для него виде.
Перед изложением изобретения для удобства и однозначного понимания целесообразно привести расшифровки и определения используемых далее обозначений и/или терминов.
Поисковая система - компьютерная программа, предназначенная для поиска информации в сети Интернет. Поиск производится на основании сформированного пользователем произвольного текстового запроса. Результаты поиска представляются пользователю отсортированными в соответствии с определенной характеристикой релевантности запросу. Примерами поисковых систем являются Bing, Google, Yahoo, Yandex.
Рекомендательная система - компьютерная программа, выбирающая из всего набора предъявленных альтернатив (вариантов) те, которые могут быть наиболее интересны конкретному пользователю, на основании ряда характеристик, например, введенного пользователем запроса в поисковой системе. Следует отметить, что в большинстве случаев рекомендательные системы представляют результат либо в виде набора рекомендованных вариантов, либо в виде ранжирования всех или части предъявленных вариантов. Таким образом, способы обработки и преобразования информации в рамках рекомендательных систем работают в смежных сферах, таких как, например, задача оценки эффективности деятельности предприятий, и др.
Принцип суперпозиции (в рассматриваемом контексте, в отличие от известного принципа суперпозиции в физике) заключается в последовательном исключении вариантов из исходного множества с использованием процедур, которые на каждом этапе исключения могут быть различными. Пример процедур приведен в приложении 1. На первом этапе исключение производится из всего исходного множества вариантов, на втором этапе входным множеством являются эффективные варианты, выделенные на первом этапе, и т.д.
Эффективными ("хорошими") элементами (вариантами) называют те элементы, которые являются наилучшими, наиболее предпочтительными, наиболее полезными по заданным параметрам для решения конкретных задач, в которых необходимо произвести ранжирование вариантов, и для удовлетворения информационных потребностей пользователей (людей, специалистов, агентов).
Неэффективными ("плохими") элементами (вариантами) называют те элементы, которые заведомо никогда (ни при каких обстоятельствах) не могут быть использованы для решения конкретных задач, так как для их решения существуют более предпочтительные варианты.
Значение эффективности, с помощью которого происходит построение правил отбора и ранжирования вариантов, задается экспертным путем.
Большинство поисковых систем имеют средства хранения и обработки данных, содержащие такие оценки эффективности (релевантности) для больших представительных наборов запросов и результатов поиска по этим запросам. В таких средствах запрос и результаты поиска по нему (варианты) представлены своими наборами критериев и оценкой релевантности результатов поиска, выставленной экспертами.
Существуют различные формальные критерии оценки релевантности поискового элемента поисковому запросу, заданные конструктивно (как, например, частота употребления слова в тексте или критерий TF-IDF, представляющий собой частоту употребления слов запроса в тексте с учетом степени важности каждого слова). Отметим, что такие формальные критерии являются скорее алгоритмами, по которым существующие поисковые системы собственно производят поиск, чем независимыми критериями, оценивающими результаты этого поиска. Оценки, подсчитанные такими формальными критериями, пока еще могут сильно отличаться от оценок релевантности, выставленных экспертами.
На данный момент известны три основных способа, с помощью которых происходит отбор и ранжирование вариантов.
Известен способ выбора и ранжирования вариантов, который заключается в том, что каждому варианту присваивается абсолютная оценка степени "важности", используя значения по нескольким критериям. Наиболее распространенным способом является построение регрессии.
Кроме того, для ранжирования вариантов может быть использован метод классификации McRank, суть которого заключается в вычислении для каждой пары "запрос-документ" так называемой "ожидаемой релевантности" как функции от вероятностей принадлежности к классам релевантности, полученных в результате классификации. В результате вычисления "ожидаемой релевантности" ранжирование пары "запрос-документ" в рамках каждого запроса происходит по убыванию "ожидаемой релевантности" (Л.Пинг, К.Дж.С.Берджес, К.By - McRank: Обучение ранжированию с использованием многофакторного анализа и градиентного ускорения перебора. НИПС. Карран ассошиэйтс.2007 - [Ping L., Burges C.J.С, Wu Q.McRank: Learning to Rank Using Multiple Classification and Gradient Boosting. NIPS. Curran Associates, 2007]).
Известен способ выбора альтернатив, который заключается в попарном сравнении двух вариантов с целью выявления лучшего из них. На основе формирования таких отношений происходит построение порядка, с помощью которого происходит выбор вариантов.
Примером известного способа является метод опорных векторов, который заключается в переводе исходных векторов в пространство более высокой размерности и поиске разделяющих гиперплоскостей с максимальным зазором в этом пространстве (К.Кортес, Вапник В.Н., Метод опорных векторов, Журнал "Machine Learning", 20, 1995 - [С.Cortes, Vapnik V.N.; "Support-Vector Networks", Machine Learning, 20, 1995]), а также другие методы, такие как:
- RankNet (поисковая система Microsoft Bing, К.Дж.С.Берджес, Т.Шейкд и др. "Обучение ранжированию с использованием градиентного спуска", ИСМЛ, 2005: 89-96 - [Christopher J. С.Burges, Tal Shaked, Erin Renshaw, Ari Lazier, Matt Deeds, Nicole Hamilton, Gregory N. Hullender: Learning to rank using gradient descent. ICML 2005: 89-96]), суть которого заключается в использовании «нейронной сети» и вероятностной функции стоимости для ранжирования результатов поиска,
- RankBoost (Й.Фреунд, Р.Иер, Р.Е.Шапаэ и Й.Сингер. Эффективный алгоритм ускорения перебора для комбинированных предпочтений, Журнал "Machine Learning Research", 4:933-969, 2003 - [Y.Freund, R.Iyer, R.E. Schapire, and Y.Singer. An efficient boosting algorithm for combining preferences. J. Mach. Learn. Res., 4:933-969, 2003]), в основе которого лежит процедура последовательного построения композиции алгоритмов машинного обучения для классификации пар документов.
- FRank (М.Тсаи, Т.-Я.Лью и др. Frank: Метод ранжирования с использованием функции потери точности, СИГИР 2007 - [М.Tsai, T.-Y.Liu, et al. FRank: A Ranking Method with Fidelity Loss, SIGIR 2007]), являющийся модификацией метода RankNet, однако в качестве функции стоимости вместо значений энтропии используется функция точности распределений, и другие.
Известен способ выбора альтернатив, который заключается в списочном сравнении вариантов. При этом фильтрация всего множества альтернатив выполняется согласно заданным правилам.
Примерами этого способа могут служить:
1. Метод построения деревьев, минимизация штрафной функции ListNet, в котором вводится вероятностное пространство на множестве перестановок. Функция энтропии на введенном пространстве используется как функция потерь. (Чже Цао, Тао Кин, Тай-Янь Лю, Мин-Фенг Тсаи и Ханг Ли. Обучение ранжированию: От попарного к списочному подходу, 2007 - [Zhe Сао, Тао Qin, Tie-Yan Liu, Ming-Feng Tsai, and Hang Li. Learning to Rank: From Pairwise Approach to Listwise Approach, 2007]),
2. Метод списочного сравнения вариантов RankCosine, который использует функцию потерь, основанной на сходстве косинуса угла между проранжированным списком и исходным списком обучающей выборки, для ранжирования результатов поиска (Т.Кин, Х.-Д.Чжанг, М.-Ф.Тсаи, Д.-С.Ванг, Т.-Я.Лью, X.Ли: Запросо-зависимые функции потерь для информационного поиска. Журнал "Inf. Process. Manage". 44(2): 838-855, 2008 - [Т.Qin, X.-D.Zhang, M.-F.Tsai, D.-S.Wang, T.-Y.Liu, H.Li: Query-level loss functions for information retrieval. Inf. Process. Manage. 44(2): 838-855, 2008)],
3. Метод ранжирования AdaRank, в котором для построения ранжирующей функции используется алгоритм машинного обучения AdaBoost, производящий построение линейной комбинации классификаторов для улучшения работы ранжирующей модели. (Ю.Ху, X.Ли. AdaRank: алгоритм ускоренного перебора для информационного поиска. СИГИР 2007 - [Xu, J., Li, Н.: AdaRank: a boosting algorithm for information retrieval. SIGIR 2007]),
4. Метод ранжирования SoftRank, суть которого заключается в прямой оптимизации негладких метрик ранжирования, (Майке Тэйлор, Джон Гуйвер, Стивен Робертсон, Том Минка. SoftRank: Оптимизация негладких метрик, 2008 - [Michael Taylor, John Guiver, Stephen Robertson, and Tom Minka. SoftRank: Optimising Non-Smooth Rank Metrics, 2008]) и другие.
Все эти методы показывают достаточно высокую точность в своих узкоспециальных областях.
Недостатками известных способов отбора вариантов являются:
- использование сложных процедур отбора в работе с большими объемами данных, что ведет к значительному возрастанию вычислительной сложности;
- невысокая точность при отборе и ранжировании вариантов с использованием большого числа критериев или/и при наличии большого числа вариантов.
Как правило, на больших объемах данных используется способ поиска по деревьям решений. Он заключается в построении последовательности пороговых процедур, с помощью которых осуществляется выбор вариантов.
Недостатком способа поиска по деревьям решений является низкая достоверность результатов, так как выбор пороговых процедур в качестве способа отбора и ранжирования вариантов не всегда обоснован (эффективен). Кроме того, для отбора или ранжирования вариантов может быть одновременно использован не один критерий, а целая группа (их комбинация), что не учитывается в методе поиска по деревьям решений. Зачастую произвести отбор или ранжирование всего списка вариантов по какому-то одному критерию (нескольким критериям) невозможно. В связи с этим для ранжирования вариантов с высокой точностью необходимо выполнить построение большого количества таких деревьев, а результаты их работы необходимо агрегировать.
Известны способы по патенту РФ №2435212 «Сбор данных о пользовательском поведении при веб-поиске для повышения релевантности поиска», патенту РФ №2443015 «Функции ранжирования, использующие модифицированный байесовский классификатор запросов с инкрементным обновлением», по патенту РФ №2367997 «Усовершенствованные системы и способы ранжирования документов на основании структурно взаимосвязанной информации», которые заключаются в сборе дополнительной информации, а именно в использовании байесовского классификатора, сборе информации о поведении пользователей, информации о структурных взаимосвязях документов, с помощью которой осуществляется отбор и ранжирование вариантов. Недостатком известных способов является усложнение существующих методов отбора и ранжирования вариантов за счет добавления новых критериев.
Наиболее близким по технической сущности и достигаемому результату является способ вычисления временного веса для результата поиска, который заключается в том, что идентифицируют пользовательское событие, соответствующее результату поиска, причем пользовательское событие имеет начальное время события, время окончания события и длительность события; определяют текущее время и определяют временной вес для этого результата поиска на основании временной близости текущего времени к пользовательскому событию. В способе предполагается, что временной вес изменяется со временем, увеличивается экспоненциально по мере того, как текущее время приближается к начальному времени события, является постоянным в течение длительности события, достигает пика в момент времени в течение длительности события и уменьшается экспоненциально, когда текущее время удаляется от времени окончания события. Способ предназначен для поиска информации в сети Интернет с использованием временного веса для ранжирования результатов поиска. (Патент РФ №2435213, МПК G06F 17/30, опубл. 27.11.2011 г.).
Недостатком известного способа, как и аналогичных существующих технологий поиска по запросу в сети Интернет, является то, что в них, как правило, применяются "грубые" алгоритмы выбора и ранжирования, т.е. алгоритмы с линейной вычислительной сложностью О(n), где n - число вариантов. Как правило, эта сложность достигается тем, что разработанные правила выбора и ранжирования упрощаются (точнее говоря, огрубляются), чтобы обеспечить приемлемый уровень сложности. При этом результат, достигаемый с помощью таких способов, получается более низкого качества.
Техническая задача, на решение которой направлено заявляемое изобретение, состоит в создании нового способа для более качественного отбора и ранжирования эффективных вариантов, обеспечивающего высокую скорость отбора и высокую точность результатов.
Поставленная техническая задача решается тем, что согласно предложенному изобретению способ отбора и ранжирования эффективных вариантов по первому варианту реализации заключается в том, что предварительно формируют критерии оценки релевантности варианта поисковому запросу и задают конечное число вариантов или набор процедур выбора и ранжирования вариантов и последовательность их выполнения для отбора вариантов, оцениваемых как наиболее эффективные, осуществляют оценку каждого из вариантов по релевантности критериям поискового запроса, на основании которой ранжируют варианты путем присвоения ранга каждому из них из условия соответствия наибольшему числу критериев в порядке их убывания; последовательно осуществляют отбор и ранжирование вариантов по методу суперпозиции по меньшей мере в два этапа, если количество вариантов в оставшейся группе вариантов соответствует предварительно заданному конечному числу вариантов для отбора или использованы все заданные процедуры выбора, отбор вариантов и их ранжирование прекращают и варианты из отобранной группы оценивают как наиболее эффективные, если количество вариантов в оставшейся группе вариантов не соответствует предварительно заданному конечному числу вариантов для отбора, отбор вариантов и их ранжирование продолжают, при этом отбор вариантов, их ранжирование и исключение осуществляют до момента, пока не будет достигнуто заданное число вариантов или пока не будут использованы все заданные процедуры выбора и отобранную группу вариантов оценивают как наиболее эффективную.
Заявляемый способ по первому варианту реализации характеризуется следующими дополнительными существенными признаками:
- на первом этапе осуществляют отбор вариантов при наличии их большого числа по методу суперпозиции с использованием методов выбора и ранжирования, характеризующихся линейной вычислительной сложностью O(n), и исключают группу вариантов, которые имеют самый низкий ранг;
- на втором и последующих этапах формируют критерии оценки поискового запроса, на основании которых ранжируют варианты и осуществляют отбор вариантов из оставшегося обработанного па предыдущем этапе массива по методу суперпозиции с использованием методов, вычислительная сложность которых не ниже квадратичной O(n2) и исключают следующую группу вариантов с меньшим рангом.
Поставленная техническая задача решается тем, что согласно предложенному изобретению способ отбора и ранжирования эффективных вариантов по второму варианту реализации заключается в том, что предварительно формируют критерии оценки релевантности варианта поисковому запросу и задают конечное число вариантов для отбора, оцениваемых как наиболее эффективные, осуществляют оценку каждого из вариантов по релевантности критериям поискового запроса, на основании которой ранжируют варианты путем присвоения ранга каждому из них из условия соответствия наибольшему числу критериев в порядке их убывания; последовательно осуществляют отбор и ранжирование вариантов по методу суперпозиции по меньшей мере в два этапа, если количество вариантов в оставшейся группе вариантов соответствует предварительно заданному конечному числу вариантов для отбора, отбор вариантов и их ранжирование прекращают и варианты из отобранной группы оценивают как наиболее эффективные, если количество вариантов в оставшейся группе вариантов не соответствует предварительно заданному конечному числу вариантов для отбора, отбор вариантов и их ранжирование продолжают, при этом отбор вариантов, их ранжирование и исключение осуществляют до момента, пока не будет достигнуто заданное число вариантов, отобранную группу вариантов оценивают как наиболее эффективную.
Заявляемый способ по второму варианту реализации характеризуется следующими дополнительными существенными признаками:
- на первом этапе осуществляют отбор вариантов при наличии их большого числа по методу суперпозиции с использованием методов выбора и ранжирования, характеризующихся линейной вычислительной сложностью O(n), и исключают группу вариантов, которые имеют самый низкий ранг;
- на втором и последующих этапах формируют критерии оценки поискового запроса, на основании которых ранжируют варианты и осуществляют отбор вариантов из оставшегося обработанного на предыдущем этапе массива по методу суперпозиции с использованием методов, вычислительная сложность которых не ниже квадратичной O(n2) и исключают следующую группу вариантов с меньшим рангом;
в способе дополнительно задают набор процедур выбора и ранжирования вариантов и последовательность их выполнения.
Поставленная техническая задача решается тем, что согласно предложенному изобретению, способ отбора и ранжирования эффективных вариантов по третьему варианту реализации заключается в том, что предварительно формируют критерии оценки релевантности варианта поисковому запросу и задают набор процедур выбора и ранжирования вариантов и последовательность их выполнения для отбора вариантов, оцениваемых как наиболее эффективные, осуществляют оценку каждого из вариантов по релевантности критериям поискового запроса, на основании которой ранжируют варианты путем присвоения ранга каждому из них из условия соответствия наибольшему числу критериев в порядке их убывания; последовательно осуществляют отбор и ранжирование вариантов по методу суперпозиции, по меньшей мере, в два этапа, отбор вариантов, их ранжирование и исключение осуществляют до момента, пока не будут использованы все заданные процедуры выбора и отобранную группу вариантов оценивают как наиболее эффективную.
Заявляемый способ но третьему варианту реализации характеризуется следующими дополнительными существенными признаками:
- на первом этапе осуществляют отбор вариантов при наличии их большого числа по методу суперпозиции с использованием методов выбора и ранжирования, характеризующихся линейной вычислительной сложностью O(n), и исключают группу вариантов, которые имеют самый низкий ранг
- на втором и последующих этапах формируют критерии оценки поискового запроса, на основании которых ранжируют варианты и осуществляют отбор вариантов из оставшегося обработанного на предыдущем этапе массива по методу суперпозиции с использованием методов, вычислительная сложность которых не ниже квадратичной 0(п2) и исключают следующую группу вариантов с меньшим рангом.
- дополнительно задают конечное число вариантов для отбора, оцениваемых как наиболее эффективные;
- для отбора наиболее эффективной группы вариантов задают дополнительные методы выбора и ранжирования и последовательность их выполнения и повторно осуществляют отбор и ранжирование.
Технический результат, достижение которого обеспечивается реализацией всей заявляемой совокупности существенных признаков способа, состоит в повышении скорости и точности (достоверности) отбора эффективных вариантов в поисковых, рекомендательных системах за счет возможности, используя принцип суперпозиции, регулировать сложность процедур выявления эффективных вариантов.
Сущность изобретения поясняется фиг.1, на которой представлена схема последовательности операций при осуществлении заявляемого способа, где:
1 - исходный набор вариантов (множество различных вариантов);
2 - процедура исключения неэффективных объектов на первом этапе с использованием приближенных методов;
3 - набор вариантов, оставшихся после первого этапа отбора;
4 - отсечение неэффективных вариантов с помощью процедур исключения;
5 - последовательное применение процедур исключения неэффективных объектов с использованием приближенных методов;
6 - подмножество вариантов, не содержащее неэффективные варианты;
7 - операция ранжирования полученной на шаге 6 группы вариантов с использованием как приближенных, так и точных методов;
8 - операция присвоения всем неэффективным вариантам самого низкого ранга и добавление этих вариантов в итоговый список после ранжированных вариантов;
9 - предоставление итоговой упорядоченной группы вариантов конечному потребителю;
10 - группы неэффективных вариантов, отсеченных с использованием последовательной суперпозиции процедур исключения.
Предложенный способ основан на методе суперпозиции, который заключается в последовательном исключении предыдущих вариантов с помощью некоторых процедур, которые на каждом этапе исключения могут быть различными.
Заявляемый способ осуществляется следующим образом (фиг.1).
Существует или формируется большой набор вариантов 1, в котором могут находиться неэффективные варианты.
Термин «большой набор вариантов (поисковых элементов)» рассматривается в рамках концепции «Большие данные» (Big Data), появившейся в связи с развитием информационных технологий и включающей в себя подходы к обработке огромных объемов разнородной информации.
Под большим набором вариантов (поисковых элементов) в рамках этой концепции понимается структурированный или неструктурированный набор данных огромного объема и значительного многообразия.
Для того чтобы исключить неэффективные варианты и отобрать наиболее эффективные варианты предварительно формируют критерии оценки релевантности варианта (поискового элемента) поисковому запросу и, при необходимости, задают конечное число вариантов (поисковых элементов) для отбора, оцениваемых как наиболее эффективные (как максимально соответствующие критериям оценки релевантности поисковому запросу). Далее осуществляют оценку каждого из вариантов (поисковых элементов) по релевантности критериям поискового запроса, на основании которой ранжируют варианты (поисковые элементы) путем присвоения ранга каждому из них из условия соответствия наибольшему числу критериев в порядке их убывания. Отбор и ранжирование вариантов (поисковых элементов) осуществляют последовательно по методу суперпозиции по меньшей мере в два этапа.
Способ может быть определен иначе - может быть задан набор используемых методов выбора и ранжирования и последовательность их применения.
На первом этапе осуществляют отбор вариантов из большого числа (поз.2 фиг.1) по методу суперпозиции с использованием методов выбора и ранжирования, характеризующихся линейной вычислительной сложностью O(n).
Для данной операции могут быть использованы известные методы, характеризующиеся линейной вычислительной сложностью O(n), такие как, например, правило относительного большинства, правило Борда, правило надпорогового выбора и другие. Наиболее полный список правил выбора приведен в Приложении 1.
В результате формируют две группы вариантов: группу вариантов 10, имеющих самый низкий ранг, и группу вариантов 3, подлежащих дальнейшему анализу.
Группу вариантов 10, которые имеют самый низкий ранг, исключают (поз.4 фиг.1).
На следующем этапе формируют критерии оценки поискового запроса, на основании которых ранжируют варианты. Отбор вариантов из оставшегося обработанного массива осуществляют по методу суперпозиции (поз.5 фиг.1) с использованием методов, вычислительная сложность которых не ниже квадратичной O(n2).
Для данной операции могут быть использованы известные методы, вычислительная сложность которых не ниже квадратичной O(n2), такие, как, например, минимальное недоминируемое множество, правило Ричелсона или правила, основанные на построении мажоритарной или турнирной матрицы (см. Приложение 1).
Отбор вариантов и их ранжирование прекращают и варианты (поисковые элементы) из отобранной группы оценивают как наиболее эффективные или перспективные, когда будут выполнены все используемые (заданные) методы выбора и ранжирования или если количество вариантов в оставшейся группе вариантов соответствует предварительно заданному конечному числу вариантов (поисковых элементов) для отбора. Отбор вариантов и их ранжирование может быть осуществлено повторно с помощью задания дополнительных способов выбора и ранжирования, а также последовательности их выполнения.
В ином случае отбор и ранжирование продолжают осуществлять, как описано выше (поз.7 и 8 фиг.1). То есть группу вариантов 6 ранжируют с использованием операций ранжирования 7, при необходимости можно добавлять (поз.8 фиг.1) к ней варианты из группы неэффективных вариантов 10. Отбор вариантов (поисковых элементов), их ранжирование и исключение осуществляют (поз.9 фиг.1) до момента, пока не будет достигнуто заданное число вариантов (поисковых элементов) или пока не будут выполнены все используемые (заданные) методы выбора и ранжирования, а отобранную группу вариантов 9 (поисковых элементов) оценивают как наиболее эффективные (перспективные). Таким образом, происходит отбор и ранжирование эффективных вариантов, их ранжирование и предоставление этих вариантов конечному потребителю.
Суперпозиционный подход используется тогда, когда нельзя однозначно определить по одному критерию, какие варианты являются эффективными, а какие нет. Отличительной особенностью способа является возможность выявлять при наличии большого числа критериев из большого числа вариантов те варианты, которые являются эффективными, а также возможность регулировать вычислительную сложность предложенного способа. Заявляемый способ позволяет перейти от сложных механизмов выявления эффективных вариантов к составным, которые представляют собой комбинацию или суперпозицию более простых процедур. Результаты выполнения предыдущих этапов отбора и ранжирования обрабатывают на следующих этапах способа.
Кроме того, в заявляемом способе для ранжирования вариантов может быть одновременно использован не один критерий, а целая группа критериев (их комбинация), что не учитывается, например, в известном методе поиска по деревьям решений, который использует простейшие пороговые процедуры, выбор которых не всегда обоснован.
В отличие от известных методов метод суперпозиции является достаточно гибким и позволяет варьировать число этапов в способе отбора.
В суперпозиционном подходе исключается возможность потерять эффективные варианты в случае использования приближенных методов. После последовательной композиции этапов исключения происходит отбор и ранжирование оставшихся вариантов. Все неэффективные варианты, которые были исключены до процедуры ранжирования, будут иметь низший (наихудший) ранг и будут выбираться (предлагаться) для решения задач в самую последнюю очередь.
Под приближенными методами, которые используются для сокращения числа вариантов с высокой скоростью, понимаются правила выбора и ранжирования с линейной вычислительной сложностью O(n). Такие правила (методы) должны использовать (считывать) значения параметров каждого варианта (альтернативы) только такое число раз к, которое не зависит от числа вариантов (альтернатив) n, и значительно меньше, чем n.В самом быстром (идеальном) случае для правила со сложностью О(n), каждый вариант используется только один раз. Правило имеет возможность определить, эффективен вариант или нет, основываясь только на данных одного этого варианта, не сравнивая его с каждым из остальных вариантов. Например, для правила отбрасывания неэффективных вариантов, со значениями "ниже среднего", по какому- либо параметру (по которому значения чем выше, тем лучше), требуется считать значение каждого варианта только 2 раза: первый раз, чтобы подсчитать среднее, и второй раз, чтобы определить, выше или ниже значение этого варианта, чем среднее. Это правило относится к правилам с линейной вычислительной сложностью O(n).
Таким образом, использование методов выбора и ранжирования, характеризующихся линейной вычислительной сложностью O(n) обеспечивает значительное повышение скорости отбора эффективных вариантов в поисковых, рекомендательных системах.
Однако изначально на всем объеме вариантов достаточно затруднительно использовать тонкие (точные) методы в силу наличия большого количества вариантов. При применении приближенных процедур отсечения неэффективных вариантов количество различных вариантов уменьшается, что, в конце концов, приводит к возможности использовать более тонкие методы для отбора и ранжирования оставшихся вариантов.
Под тонкими (точными) методами, которые используются при наличии небольшого числа вариантов, понимаются правила выбора и ранжирования, вычислительная сложность которых зависит исключительно от количества раз использования каждого варианта. Существует правила, использующие попарные "расстояния" между вариантами (альтернативами), в специальных шкалах. Такие правила должны для каждого варианта перебрать все остальные варианты, т.е. произвести (n умножить на n) действий, вычислительная сложность здесь квадратичная. Существуют также правила, сравнивающие каждый вариант со всевозможными наборами остальных вариантов, чтобы более точно определить позицию данного варианта по отношению к остальным. Вычислительная сложность таких правил еще выше. Можно сказать, что правила со сложностями, начиная с квадратичной O(n2), не могут применяться на полном наборе вариантов (исчисляемых миллионами) при решении задачи поиска и ранжирования в сети Интернет, и в сходных задачах в других сферах деятельности, так как вычислительная сложность этих правил сильно зависит от количества имеющихся в наборе вариантов.
Таким образом, использованием методов, вычислительная сложность которых не ниже квадратичной O(n2) обеспечивает значительное повышение точности (достоверности) отбора эффективных вариантов в поисковых, рекомендательных системах.
Преимуществом способа является также то, что появляется возможность регулировать вычислительную сложность процедуры выявления эффективных вариантов. Это значит, что если на большом объеме данных применение некоторых процедур требовало огромных вычислительных ресурсов, то после последовательного исключения вариантов те же процедуры на оставшемся подмножестве могут работать достаточно быстро. Другими словами, установив некоторый предел по количеству вычислительных ресурсов, используемых на выполнение способа, можно установить количество стадий, с помощью которых можно произвести отсечение заведомо неэффективных вариантов с использованием быстрых приближенных методов, после выполнения которых можно использовать достаточно трудоемкие процедуры, выявляющих эффективные варианты с достаточно высокой точностью. В этом и заключается управление вычислительной сложностью способа.
Заявляемый способ может быть также применен в задаче обучения ранжированию, то есть задаче выбора вариантов с заранее известными оценками их полезности по критериям. Способ позволяет формировать по заранее известной степени полезности (эффективности) одних вариантов правила их отбора и ранжирования (набор применяемых методов выбора и ранжирования, а также последовательность их применения), в соответствии с которым может быть произведен отбор и ранжирование других вариантов, о степени полезности (эффективности) которых ничего не известно.
Заявляемый способ может быть осуществлен с использованием известных аппаратных и программных средств. Реализация заявляемого способа включает:
1. Сбор и хранение данных/
2. Обработка данных, отбор и ранжирование вариантов.
3. Предоставление результатов пользователю.
Сбор и хранение данных. На данной стадии происходит сбор и хранение необходимой информации о существующих вариантах. Информация о вариантах может собираться из существующих источников данных, например, из различных существующих информационных систем, веб-сайтов, веб-сервисов, других серверов данных, файлов на ЭВМ, т.е. из всех источников, хранящих информацию о вариантах в пригодном для дальнейшей обработки формате. Сбор данных может быть произведен с использованием существующих программных средств, производящих извлечение данных из внешних источников (например, ETL-системы или средства сбора содержимого веб-страниц в сети Интернет), или реализован на ЭВМ с использованием любого языка программирования, в частности, языка программирования C, C++, C#, Java, Python, PHP и многих других. Хранение информации может осуществляться как на сервере или группе серверов с использованием существующих платформ, осуществляющих хранение данных, так и на любом носителе информации, с которого возможно производить дальнейшее чтение имеющейся информации. Также хранение информации может осуществляться непосредственно в оперативной памяти ЭВМ в случае, когда нет необходимости производить постоянное хранение информации.
Обработка данных, включающая согласно заявляемому способу отбор и ранжирования вариантов с использованием приближенных и точных методов, реализуется с использованием ЭВМ, которая производит ранжирование вариантов и выявление наиболее эффективных из них. Этап обработки данных может быть произведен как на сервере, так и на самой ЭВМ пользователя.
После выполнения этапа обработки данных полученные результаты предоставляются конечному пользователю в любом пригодном для него формате. Результаты выполнения могут храниться на сервере, других носителях информации, с которых возможно производить ее дальнейшее чтение, либо могут быть предоставлены на экран ЭВМ пользователя напрямую с использованием веб-браузера или любого другого программного средства, с помощью которого осуществляется просмотр информации.
Примеры осуществления способа.
Пример 1
Задача поиска релевантных страниц в сети Интернет с отбором и ранжированием на основе принципа суперпозиции
Задача поиска релевантных страниц в сети Интернет, ранжирование на основе идеи суперпозиции может реализовываться следующим образом. Сначала быстрыми (приближенными) методами исключают заведомо нерелевантные страницы. Этими нерелевантными страницами могут быть, например, те страницы, которые не принадлежат заданной тематике, содержат спам, вирусы, рекламу, нежелательный для пользователя контент, фишинг (интернет-мошенничество) и другое. Затем на оставшемся значительно меньшем наборе страниц применяются более тонкие (точные) методы ранжирования, требующие, однако, больших вычислительных ресурсов (медленные). Упомянутые выше нерелевантные страницы никогда не могут быть релевантными запросу пользователя, а это значит, что их использование в более трудоемких методах избыточно и просто не нужно. В данном примере суперпозиция некоторого набора быстрых, но приближенных методов (применяемых для отсечения только самых нерелевантных страниц) и некоторого набора точных методов (применяемых для окончательного ранжирования не большого числа альтернатив) дает выигрыш в скорости и точности (релевантности) окончательного ранжирования. В частности, для нерелевантных страниц нет необходимости проводить детальное ранжирование, достаточно им всем присвоить один и тот же ранг (последнее место в ранжировании).
В таблице 1 приведен простейший пример использования двух способов выбора вариантов - правила Парето и четырехшагового способа отбора, основанного на идее суперпозиции. В задаче необходимо определить, какие из вариантов являются наиболее релевантными (подходящими) введенному запросу пользователя. Каждый вариант оценивается по трем критериям: количество слов из запроса в заголовке документа, количество слов из запроса во всем документе, булева модель (наличие всех слов запроса в документе). В примере выбор производится из 29 вариантов.
В случае, если использовать обычное правило Парето, то релевантными документами будут являться документы №2, 5, 6. При использовании правила Парето каждый вариант должен быть сопоставлен со всеми остальными вариантами, т.е. каждый из 29 вариантов должен быть сопоставлен друг с другом. Это означает, что чем больше вариантов находится в выборке, тем больше вычислительная сложность этого правила, что ведет к необходимости использования более простых (приближенных) правил выбора.
Однако правило Парето может быть применено, если использовать способ отбора и ранжирования эффективных вариантов, основанный на идее суперпозиции. В таблице 1 приведен способ отбора в четыре этапа, который заключается в последовательном применении трех надпороговых правил, после чего применяется правило Парето.
На первом этапе происходит исключение всех вариантов (документов), в заголовке которых не находится ни одного слова из запроса. Таким образом, число вариантов сокращается с 29 до 8.
На втором этапе происходит исключение тех вариантов, у которых в основной части документа не было найдено ни одного слова из запроса. Тогда число вариантов сокращается с 8 до 6. После этого выбираются только те документы, в которых находятся все слова из запроса. В результате число вариантов сокращается до 4. После этого осуществляют применение правила Парето по оставшимся вариантам, и в итоговый выбор входит только 3 варианта (документа) - №2, 5, 6.
В данном примере результаты обоих способов совпадают. Однако вычислительная сложность правила Парето значительно выше. Поэтому в случае, если число вариантов небольшое, выбор способа отбора и ранжирования не принципиален (не имеет значения). Однако в условиях, когда число вариантов достигает нескольких миллионов, необходимо использовать второй способ, основанный на идее суперпозиции, т.к. он позволяет комбинировать простые и сложные правила выбора, что уменьшает вычислительную сложность способа.
Пример 2
Ведение маркетинговой кампании в социальных сетях
В ряде моделей для представления наиболее интересного и востребованного предложения участникам социальных сетей необходимо сегментировать группы пользователей по их общим интересам или по интенсивности обмена информацией между ними. В этом случае, например, пороговое отсечение по правилу "не более одного контакта за последний год" (для определенного набора товаров и услуг) позволяет сразу сузить число вариантов внутри группы до уровня, приемлемого для более сложных алгоритмов. Разумеется, наличие более одного контакта за год не подразумевает общность интересов пользователей, т.е. отсекаются заведомо неэффективные варианты группировки (сегментации) участников социальных сетей по их интересам, с одновременным и резким снижением объема группы.
Таким образом, представленный способ позволяет с высокой точностью производить отбор и ранжирование вариантов, особенно при наличии большого количества вариантов, характеризуемых большим набором показателей, так как он позволяет производить комбинирование приближенных и точных процедур.
Заявляемый способ может быть использован при отборе эффективных вариантов в поисковых, рекомендательных системах, системах поддержки принятия решений, сетях Интернет, системах автоматической классификации пакетов данных и в других смежных областях.
Кроме того, изобретение может быть использовано при решении задачи обучения ранжированию, то есть задаче выбора вариантов с заранее известными оценками их полезности по критериям, например, при оценке эффективности работы предприятий, торговых точек и других объектов в смежных областях.
Приложение 1. Список правил выбора, приведенных в работе Ф.Т.Алескерова, Э. Курбанова "О степени манипулируемости правил коллективного выбора", Автоматика и телемеханика, 1998, №10, 134-146.
1. Правило относительного большинства (Plurality rule)
В выбор входят альтернативы, которые являются лучшими для наибольшего числа критериев, т.е.
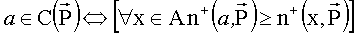 ,
,
где 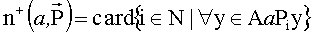 .
.
Данное правило для выбора и ранжирования имеет линейную вычислительную сложность.
2. Одобряющее голосование (Approval voting rule)
Введем
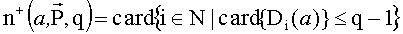 ,
,
т.е. 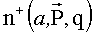 означает число критериев, у которых альтернатива a стоит не ниже q-го места в их упорядочении. Таким образом, если q=1, тогда a - это лучшая альтернатива для критерия i; если q=2, тогда a - либо первая, либо вторая наилучшая альтернатива, и т.д. Число q будем называть уровнем процедуры.
означает число критериев, у которых альтернатива a стоит не ниже q-го места в их упорядочении. Таким образом, если q=1, тогда a - это лучшая альтернатива для критерия i; если q=2, тогда a - либо первая, либо вторая наилучшая альтернатива, и т.д. Число q будем называть уровнем процедуры.
Одобряющее голосование уровня q определяется следующим образом:
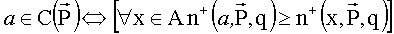 ,
,
т.е. выбираются альтернативы, которые находятся среди q лучших для максимального числа критериев.
Очевидно, что одобряющее голосование - это обобщение правила относительного большинства (случай q=1).
Данное правило для выбора имеет линейную вычислительную сложность, для ранжирования вычислительная сложность правила зависит от значения q. При q<<n вычислительная сложность правила линейная, при q≈ n вычислительная сложность правила квадратичная.
3. Пороговое правило (Threshold rule)
Пусть ν1(x) - число критериев, для которых альтернатива x является наихудшей в их упорядочениях, ν2(x) - число критериев, для которых альтернатива x является второй наихудшей, и так далее, νm(x) - число критериев, для которых альтернатива x является наилучшей. Затем альтернативы упорядочиваются лексикографически. Говорят, что альтернатива x V - доминирует альтернативу y если ν1(x)< ν1(y) или, если существует k≤m такое, что νi(x)= νi(y), i=1, …, k-1, и νk(x)<k(y). Другими словами, в первую очередь сравниваются количества последних мест в упорядочениях для каждой альтернативы, в случае, когда они равны, идет сравнение количества предпоследних мест, и так далее. Выбором являются альтернативы, недоминируемые по V.
Данное правило для выбора и ранжирования имеет линейную вычислительную сложность.
4. Правило Борда (Borda rule)
Каждой альтернативе x∈A ставится в соответствие число 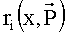
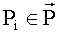
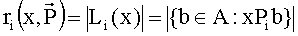
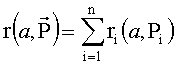
В выбор входят альтернативы с максимальным рангом
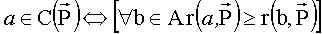 .
.
Данное правило для выбора имеет линейную вычислительную сложность, для ранжирования вычислительная сложность правила сильно зависит от входных данных и в худшем случае является квадратичной.
5. Процедура Блэка
Если существует победитель Кондорсе, то он объявляется коллективным выбором, иначе используется правило Борда.
Данное правило для выбора и ранжирования имеет вычислительную сложность не ниже квадратичной.
6. Процедура Кумбса.
Исключается вариант, который считают худшим максимальное число избирателей. Затем профиль сужается до нового множества X и процедура продолжается до тех пор, пока не останутся только неисключаемые варианты. Отметим здесь разницу между правилом Кумбса и системой передачи голосов. В правиле Кумбса вычеркиваются худшие варианты, в то время как в системе передачи голосов вычеркиваются варианты, лучшие для минимального числа избирателей.
Данное правило для выбора и ранжирования имеет линейную вычислительную сложность.
7. Процедура Хара
Для каждой альтернативы подсчитывается количество первых мест в упорядочениях по критериям. Далее из голосования выбывают альтернативы с наименьшим количеством первых мест.Процедура повторяется, пока выбор остается непустым.
Данное правило для выбора и ранжирования имеет линейную вычислительную сложность.
8. Обратное правило относительного большинства
В выбор входят альтернативы, которые являются худшими для наименьшего числа критериев.
Данное правило для выбора и ранжирования имеет линейную вычислительную сложность.
9. Первое правило Копланда
Для каждой альтернативы считаются два показателя: сумма количеств альтернатив, которые хуже заданной по каждому критерию, и сумма количеств альтернатив, которые лучше заданной по каждому критерию. В коллективный выбор входят альтернативы с наибольшей разностью этих двух показателей.
Данное правило для выбора имеет линейную вычислительную сложность, для ранжирования вычислительная сложность правила сильно зависит от входных данных и в худшем случае является квадратичной.
10. Обратная процедура Борда (с передачей голосов)
Для каждой альтернативы подсчитывается ранг Борда. Далее альтернатива с наименьшим рангом выбывает. Ранги Борда пересчитываются для множества альтернатив без выбывшей альтернативы. Процедура повторяется, пока выбор непустой.
Для выбора вычислительная сложность правила в худшем случае квадратичная. Для ранжирования вычислительная сложность правила не ниже квадратичной.
11. Правило Нансона
Подсчитывается ранг Борда для всех вариантов. Затем подсчитывается средняя оценка Борда и исключаются только те варианты x, для которых оценка Борда ниже средней. Затем строится множество X=A\{x}, и процедура применяется к суженному профилю /X. Процедура продолжается до тех пор, пока не останутся только неисключаемые варианты. Для выбора вычислительная сложность правила в худшем случае квадратичная. Для ранжирования вычислительная сложность правила не ниже квадратичной.
12. Минимальное доминирующее множество
Множество альтернатив Q является доминирующим тогда и только тогда, когда любая альтернатива из Q доминирует любую альтернативу вне Q по мажоритарному отношению.
Доминирующее множество является минимальным, если ни одно из его собственных подмножеств не является доминирующим. Коллективным выбором является минимальное доминирующее множество, если таковое существует одно, или их объединение, если таковых несколько. Данное правило для выбора и ранжирования имеет вычислительную сложность не ниже квадратичной.
13. Минимальное недоминируемое множество
Множество альтернатив Q является недоминируемым тогда и только тогда, когда не существует альтернативы вне Q, которая доминирует какую-либо альтернативу из множества Q.
Недоминируемое множество является минимальным, если ни одно из его собственных подмножеств не является недоминируемым. Коллективным выбором является минимальное недоминируемое множество, если таковое существует одно, или их объединение, если таковых несколько. Данное правило для выбора и ранжирования имеет вычислительную сложность не ниже квадратичной.
14. Минимальное слабоустойчивое множество
Множество альтернатив Q является слабоустойчивым тогда и только тогда, когда из существования альтернативы у вне Q, доминирующей альтернативу x из Q, следует существование альтернативы z из Q такой, что z доминирует У-
Слабоустойчивое множество является минимальным, если ни одно из его собственных подмножеств не является слабоустойчивым. Коллективным выбором является минимальное слабоустойчивое множество, если таковое существует одно, или их объединение, если таковых несколько.
Данное правило для выбора и ранжирования имеет вычислительную сложность не ниже квадратичной.
75. Правило Фишберна
Построим новое бинарное отношение у, в котором х доминирует у тогда и только тогда, когда верхний контур альтернативы х является собственным подмножеством верхнего контура альтернативы у.
Коллективным выбором будет набор альтернатив, недоминируемых по отношению у.
Данное правило для выбора и ранжирования имеет вычислительную сложность не ниже квадратичной.
16. Непокрытое множество I.
Построим новое бинарное отношение 5, в котором x доминирует у тогда и только тогда, когда нижний контур альтернативы у является собственным подмножеством нижнего контура альтернативы x.
Коллективным выбором будет набор альтернатив, недоминируемых по отношению 8.
Данное правило для выбора и ранжирования имеет вычислительную сложность не ниже квадратичной.
17. Непокрытое множество II
Альтернатива x B - доминирует альтернативу y, если x доминирует y по мажоритарному отношению и верхний контур альтернативы x является подмножеством верхнего контура альтернативы y. В коллективный выбор входят альтернативы, недоминируемые по отношению B. Данное правило для выбора и ранжирования имеет вычислительную сложность не ниже квадратичной.
18. Правило Ричелсона
Строится новое бинарное отношение σ, в котором x доминирует y тогда и только тогда, когда
- Нижний контур y является подмножеством нижнего контура x
- Верхний контур x является подмножеством верхнего контура y
- В одном из двух указанных выше случаев вхождение происходит как «собственное подмножество»
В коллективный выбор входят недоминируемые по о альтернативы.
Данное правило для выбора и ранжирования имеет вычислительную сложность не ниже квадратичной.
19. Первое правило Копланда
В коллективный выбор входят альтернативы с максимальной разницей мощностей нижнего контура и верхнего контура.
Данное правило для выбора и ранжирования имеет вычислительную сложность не ниже квадратичной.
20. Второе правило Копланда
В коллективный выбор входят альтернативы с максимальной мощностью нижнего контура.
Данное правило для выбора и ранжирования имеет вычислительную сложность не ниже квадратичной.
21. Третье правило Копланда
В коллективный выбор входят альтернативы с минимальной мощностью верхнего контура.
Данное правило для выбора и ранжирования имеет вычислительную сложность не ниже квадратичной.
22. Двухступенчатое правило относительного большинства
Сначала используется правило простого большинства (т.е. выбирается вариант, получивший больше 50% голосов - первых мест - в упорядочениях избирателей). Если такой вариант найден, то процедура останавливается. Если же такого варианта нет, то выбираются два варианта, набравшие больше голосов, чем другие варианты (если их больше двух, то берутся два с наименьшими номерами). Затем, считая что мнения избирателей относительно этих вариантов (при вычеркивании остальных) не изменяются, вновь применяем правило простого большинства/голосов - уже на двухэлементном множестве.
Поскольку индивидуальные мнения представляются в виде линейных порядков, всегда (при нечетном числе избирателей) существует единственный вариант-победитель.
Данное правило для выбора и ранжирования имеет линейную вычислительную сложность.
23. Система передачи голосов.
Сначала используется правило простого большинства (т.е. выбирается вариант, получивший больше 50% голосов). Если такой вариант найден, то процедура останавливается. Если же такого варианта нет, то из списка вычеркивается вариант x, набравший минимальное количество голосов.
Затем процедура вновь применяется к множеству X=A\{x и профилю /X Данное правило для выбора и ранжирования имеет линейную вычислительную сложность.
24. Процедура Янга
Если для профиля существует победитель Кондорсе, то он выбирается, и процедура на этом останавливается. Если же такого варианта нет, то рассматриваются всевозможные коалиции, на которых существуют частичные победители Кондорсе. Далее определяется функция u(x) как мощность максимальной коалиции, в которой x является победителем Кондорсе.
Тогда выбираются варианты с максимальным значением ux:
Данное правило для выбора и ранжирования имеет вычислительную сложность не ниже квадратичной.
25. Процедура Симпсона (максиминная процедура)
Построим матрицу S+ такую, что ∀a, b∈X, S+=(n(a,b)), где
n(a, b)=card{i∈N|aPib}, n(a,a)=+ ∞.
Коллективный выбор определяется как
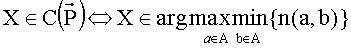
Данное правило для выбора и ранжирования имеет вычислительную сложность не ниже квадратичной.
26. Минимаксная процедура
Построим матрицу S- такую, что ∀a,b∈X, S+=(n(a,b)), n(a,a)=-∞.
Коллективный выбор определяется как
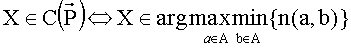
Данное правило для выбора и ранжирования имеет вычислительную сложность не ниже квадратичной.
27. Сильное q-паретовское правило простого большинства
Пусть f(P→;i;q)={X∈A-||card(D↓i(x))≤q} определяет q+1 вариантов от максимального и ниже в линейном порядке Pi. Пусть ℑ={I⊂N-||card(I)=[n/2]) (Где функция [χ] означает минимальное целое число, большее или равное x) есть семейство коалиций простого большинства. Введем функцию выбирающую вариант, который находится среди верхних вариантов для каждого избирателя хотя бы в одной коалиции простого большинства, и начнем с q=0. Если при q=0 такого варианта нет, то заново просматривается выбор по коалициям простого большинства при q, увеличенном на единицу (т.е. гири q=1) и т.д., до тех пор, пока выбор будет не пуст. Из этого непустого множества выбирается вариант с наименьшим номером, который принимается в качестве коллективного выбора.
Данное правило для выбора и ранжирования имеет экспоненциальную вычислительную сложность.
28. Сильное q-паретовское правило относительного большинства
Это правило аналогично правилу 26, с тем дополнением, что если выбраны несколько вариантов, то для каждого из них подсчитывается число выбравших его коалиций. Затем выбираются варианты с максимальным значением этого показателя.
Выбираются варианты с максимальным значением этого показателя. Данное правило для выбора и ранжирования имеет экспоненциальную вычислительную сложность.
29. Сильнейшее q-паретовское правило простого большинства
Введем функцию
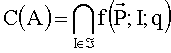
где 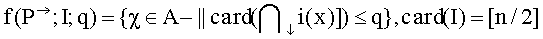
30. Правило надпорогового выбора
Пусть на множестве A задан критерий φ(x), φ:A→R1, а на множестве 2A задана функция порога V: 2А→R1, сопоставляющая каждому набору Хе2А пороговый уровень V(X).
Правило надпорогового выбора представлено в виде следующего выражения:
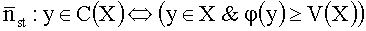
Данное правило для выбора имеет линейную вычислительную сложность, для ранжирования вычислительная сложность зависит входных данных, в худшем случае не выше квадратичной.
Изобретение относится к компьютерной технике. Технический результат - высокая скорость отбора и точность результатов поиска. Способ отбора и ранжирования эффективных вариантов результатов поиска, заключающийся в том, что предварительно формируют критерии оценки релевантности варианта результатов поиска поисковому запросу и задают конечное число вариантов результатов поиска или набор процедур выбора и ранжирования вариантов результатов поиска и последовательность их выполнения для отбора вариантов результатов поиска, оцениваемых как наиболее эффективные, осуществляют оценку каждого из вариантов результатов поиска по релевантности критериям поискового запроса, на основании которой ранжируют варианты результатов поиска путем присвоения ранга каждому из них из условия соответствия наибольшему числу критериев в порядке их убывания; последовательно осуществляют отбор и ранжирование вариантов результатов поиска по методу суперпозиции, по меньшей мере, в два этапа, если количество вариантов результатов поиска в оставшейся группе вариантов результатов поиска соответствует предварительно заданному конечному числу вариантов результатов поиска для отбора или использованы все заданные процедуры выбора, отбор вариантов результатов поиска и их ранжирование прекращают и варианты результатов поиска из отобранной группы оценивают как наиболее эффективные, если количество вариантов результатов поиска в оставшейся группе вариантов результатов поиска не соответствует предварительно заданному конечному числу вариантов результатов поиска для отбора, отбор вариантов результатов поиска и их ранжирование продолжают. 3 н. и 9 з.п. ф-лы, 1 ил.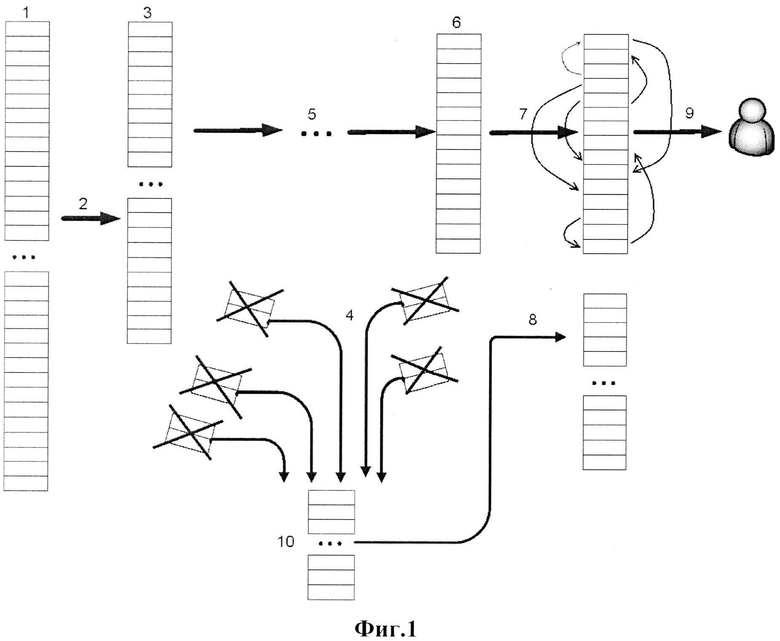
1. Способ отбора и ранжирования эффективных вариантов результатов поиска, заключающийся в том, что предварительно формируют критерии оценки релевантности варианта результатов поиска поисковому запросу и задают конечное число вариантов результатов поиска или набор процедур выбора и ранжирования вариантов результатов поиска и последовательность их выполнения для отбора вариантов результатов поиска, оцениваемых как наиболее эффективные, осуществляют оценку каждого из вариантов результатов поиска по релевантности критериям поискового запроса, на основании которой ранжируют варианты результатов поиска путем присвоения ранга каждому из них из условия соответствия наибольшему числу критериев в порядке их убывания; последовательно осуществляют отбор и ранжирование вариантов результатов поиска по методу суперпозиции по меньшей мере в два этапа, если количество вариантов результатов поиска в оставшейся группе вариантов результатов поиска соответствует предварительно заданному конечному числу вариантов результатов поиска для отбора или использованы все заданные процедуры выбора, отбор вариантов результатов поиска и их ранжирование прекращают и варианты результатов поиска из отобранной группы оценивают как наиболее эффективные, если количество вариантов результатов поиска в оставшейся группе вариантов результатов поиска не соответствует предварительно заданному конечному числу вариантов результатов поиска для отбора, отбор вариантов результатов поиска и их ранжирование продолжают, при этом отбор вариантов результатов поиска, их ранжирование и исключение осуществляют до момента, пока не будет достигнуто заданное число вариантов результатов поиска или пока не будут использованы все заданные процедуры выбора и отобранную группу вариантов оценивают как наиболее эффективную.
2. Способ по п. 1, отличающийся тем, что на первом этапе осуществляют отбор вариантов результатов поиска при наличии их большого числа по методу суперпозиции с использованием методов выбора и ранжирования, характеризующихся линейной вычислительной сложностью О(n), и исключают группу вариантов результатов поиска, которые имеют самый низкий ранг.
3. Способ по п. 1, отличающийся тем, что на втором и последующих этапах формируют критерии оценки поискового запроса, на основании которых ранжируют варианты результатов поиска и осуществляют отбор вариантов результатов поиска из оставшегося обработанного на предыдущем этапе массива по методу суперпозиции с использованием методов, вычислительная сложность которых не ниже квадратичной O(n2) и исключают следующую группу вариантов результатов поиска с меньшим рангом.
4. Способ отбора и ранжирования эффективных вариантов результатов поиска, заключающийся в том, что предварительно формируют критерии оценки релевантности варианта результатов поиска поисковому запросу и задают конечное число вариантов результатов поиска для отбора, оцениваемых как наиболее эффективные, осуществляют оценку каждого из вариантов результатов поиска по релевантности критериям поискового запроса, на основании которой ранжируют варианты результатов поиска путем присвоения ранга каждому из них из условия соответствия наибольшему числу критериев в порядке их убывания; последовательно осуществляют отбор и ранжирование вариантов результатов поиска по методу суперпозиции по меньшей мере в два этапа, если количество вариантов результатов поиска в оставшейся группе вариантов результатов поиска соответствует предварительно заданному конечному числу вариантов результатов поиска для отбора, отбор вариантов результатов поиска и их ранжирование прекращают и варианты результатов поиска из отобранной группы оценивают как наиболее эффективные, если количество вариантов результатов поиска в оставшейся группе вариантов результатов поиска не соответствует предварительно заданному конечному числу вариантов результатов поиска для отбора, отбор вариантов результатов поиска и их ранжирование продолжают, при этом отбор вариантов результатов поиска, их ранжирование и исключение осуществляют до момента, пока не будет достигнуто заданное число вариантов результатов поиска, отобранную группу вариантов результатов поиска оценивают как наиболее эффективную.
5. Способ по п. 4, отличающийся тем, что на первом этапе осуществляют отбор вариантов результатов поиска при наличии их большого числа по методу суперпозиции с использованием методов выбора и ранжирования, характеризующихся линейной вычислительной сложностью О(n), и исключают группу вариантов результатов поиска, которые имеют самый низкий ранг.
6. Способ по п. 4, отличающийся тем, что на втором и последующих этапах формируют критерии оценки поискового запроса, на основании которых ранжируют варианты результатов поиска и осуществляют отбор вариантов результатов поиска из оставшегося обработанного на предыдущем этапе массива по методу суперпозиции с использованием методов, вычислительная сложность которых не ниже квадратичной O(n2) и исключают следующую группу вариантов результатов поиска с меньшим рангом.
7. Способ по п. 4, отличающийся тем, что дополнительно задают набор процедур выбора и ранжирования вариантов результатов поиска и последовательность их выполнения.
8. Способ отбора и ранжирования эффективных вариантов результатов поиска, заключающийся в том, что предварительно формируют критерии оценки релевантности варианта результатов поиска поисковому запросу и задают набор процедур выбора и ранжирования вариантов результатов поиска и последовательность их выполнения для отбора вариантов результатов поиска, оцениваемых как наиболее эффективные, осуществляют оценку каждого из вариантов результатов поиска по релевантности критериям поискового запроса, на основании которой ранжируют варианты результатов поиска путем присвоения ранга каждому из них из условия соответствия наибольшему числу критериев в порядке их убывания; последовательно осуществляют отбор и ранжирование вариантов результатов поиска по методу суперпозиции по меньшей мере в два этапа, отбор вариантов результатов поиска, их ранжирование и исключение осуществляют до момента, пока не будут использованы все заданные процедуры выбора и отобранную группу вариантов результатов поиска оценивают как наиболее эффективную.
9. Способ по п. 8, отличающийся тем, что на первом этапе осуществляют отбор вариантов результатов поиска при наличии их большого числа по методу суперпозиции с использованием методов выбора и ранжирования, характеризующихся линейной вычислительной сложностью О(n), и исключают группу вариантов результатов поиска, которые имеют самый низкий ранг.
10. Способ по п. 8, отличающийся тем, что на втором и последующих этапах формируют критерии оценки поискового запроса, на основании которых ранжируют варианты результатов поиска и осуществляют отбор вариантов результатов поиска из оставшегося обработанного на предыдущем этапе массива по методу суперпозиции с использованием методов, вычислительная сложность которых не ниже квадратичной O(n2) и исключают следующую группу вариантов результатов поиска с меньшим рангом.
11. Способ по п. 8, отличающийся тем, что дополнительно задают конечное число вариантов результатов поиска для отбора, оцениваемых как наиболее эффективные.
12. Способ по п. 8, отличающийся тем, что для отбора наиболее эффективной группы вариантов результатов поиска задают дополнительные методы выбора и ранжирования и последовательность их выполнения и повторно осуществляют отбор и ранжирование.
| Способ приготовления мыла | 1923 |
|
SU2004A1 |
| Приспособление для суммирования отрезков прямых линий | 1923 |
|
SU2010A1 |
| Пресс для выдавливания из деревянных дисков заготовок для ниточных катушек | 1923 |
|
SU2007A1 |
| Многоступенчатая активно-реактивная турбина | 1924 |
|
SU2013A1 |
| Способ определения минимального расхода медного купороса, необходимого для активации цинковой обманки | 1955 |
|
SU105759A1 |
Авторы
Даты
2015-02-27—Публикация
2013-03-22—Подача