Изобретение относится к области цифровых вычислений, а именно к техническим средствам для тестирования чисел большой разрядности на простоту, и предназначено, в частности, для применения в качестве ускорителя вычислений суперкомпьютера, а также в генераторах простых и псевдослучайных чисел, хэшей, устройствах кодирования данных.
Из международной патентной заявки WO 2004/001595 A1 известен способ для тестирования чисел на простоту в криптографии, включающий предварительный тест с малыми простыми числами. Однако известный способ тестирования чисел на простоту оказывается недостаточно эффективным в случае необходимости получения однозначного ответа относительно простоты числа, проходящего простые проверки.
Наиболее близким аналогом настоящего изобретения является способ, известный из патента US 7346637 B2, включающий в себя ряд вычислительных операций и проверок, связанных с тестируемым числом. Однако данный известный способ требует больших вычислительных мощностей, что ограничивает производительность реализующей его вычислительной системы.
Задачей является повышение достоверности алгоритма тестирования чисел на простоту и повышение при этом общей эффективности процесса обработки чисел большой разрядности.
Обеспечиваемый настоящим изобретением технический результат заключается в повышении достоверности и производительности при тестировании чисел на простоту.
Технический результат достигается благодаря тому, что в способе тестирования чисел на простоту делают вывод относительно простоты тестируемого числа исходя из критериев: а) числа Nn=(n2-n)/2, где n - тестируемое число, от тестируемого простого числа и Nn+1 от последующего составного числа всегда нацело делятся на тестируемые числа, если они простые; б) все числа N, получаемые от составных чисел, кроме составных, следующих за простыми, неделимы нацело тестируемыми числами, если они простые; в) число Nn+1, следующее за тестируемым числом, является всегда четным или делящимся на число 5. Для чего подают данные, характеризующие тестируемое число, на вход вычислительной системы, связанный с входом блока вычисления N, и вычисляют Nn. После чего передают данные в блок деления и вычисляют величину Nn/n. Затем подают данные, характеризующие численный результат, на вход блока проверки числа на целость-дробность, причем если число является дробным, то делают вывод, что тестируемое число является составным, и устанавливают выходной логический уровень вычислительной системы в состояние «0», в противном случае в блоке вычисления N вычисляют Nn+1, а в блоке деления вычисляют Nn+1/n и Nn+1/5. После чего проверяют Nn+1/n и Nn+1/5 в блоке проверки числа на целость-дробность, a Nn+1 проверяют в блоке проверки числа на четность-нечетность. Если Nn+1/n является целым числом, а Nn+1 является четным или Nn+1/5 является целым числом, то делают вывод, что тестируемое число является простым, и устанавливают выходной логический уровень вычислительной системы в состояние «1». В противном случае делают вывод, что тестируемое число является составным, и устанавливают выходной логический уровень вычислительной системы в состояние «0».
В частном случае вход вычислительной системы связывают с входом блока проверки числа на четность-нечетность, причем к вычислению Nn переходят, если проверка тестируемого числа показала нечетность данного числа. В противном случае делают вывод, что тестируемое число является составным и устанавливают выходной логический уровень вычислительной системы в состояние «0».
Изобретение поясняется следующими графическими материалами.
Фиг.1 - блок-схема алгоритма тестирования чисел на простоту.
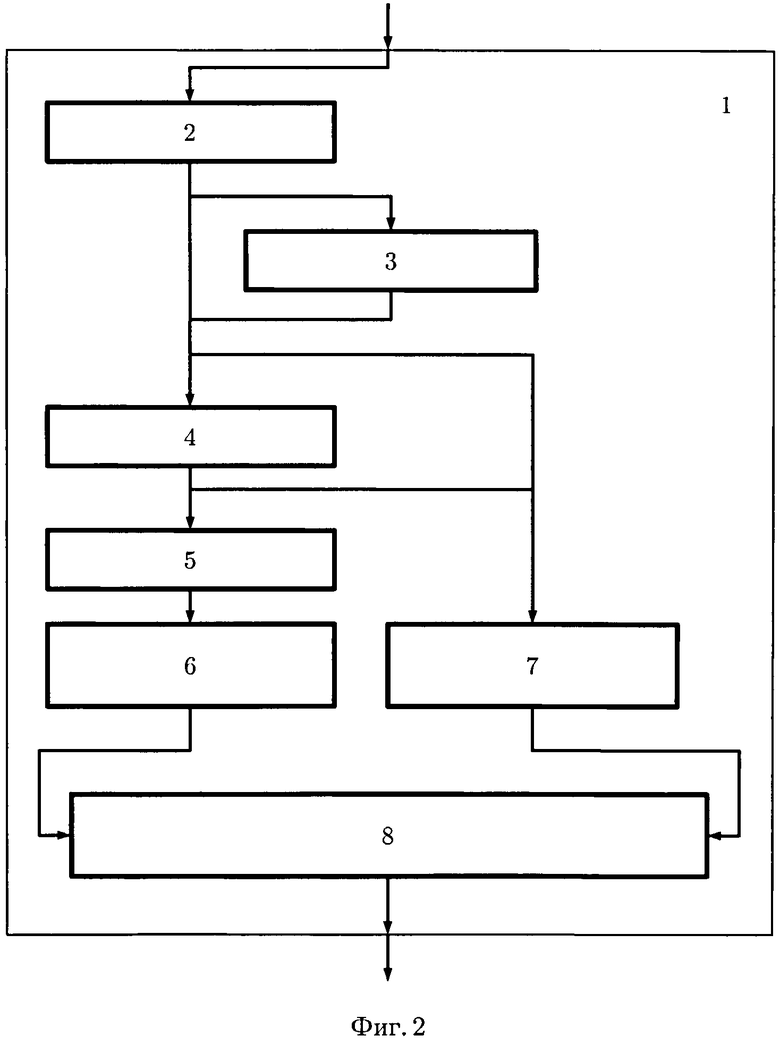
Фиг.2 - структурная схема вычислительной системы.
Способ тестирования чисел на простоту (фиг.1) основан на закономерности Шихаева-Анохина, согласно которой: а) числа, получаемые по формуле Nn=(n2-n)/2, где n - тестируемое число, от тестируемого простого числа (и от составного числа, следующего за ним), всегда нацело делятся на тестируемые числа, если они простые; б) все числа N получаемые от составных чисел, кроме составных, следующих за простыми, неделимы нацело тестируемыми числами, если они простые;
в) число Nn+1, следующее за тестируемым числом, является всегда четным или делящимся без остатка на число 5.
Закономерность Шихаева-Апохина иллюстрируется на примере нескольких малых простых чисел, отмеченных в таблице знаком «*».
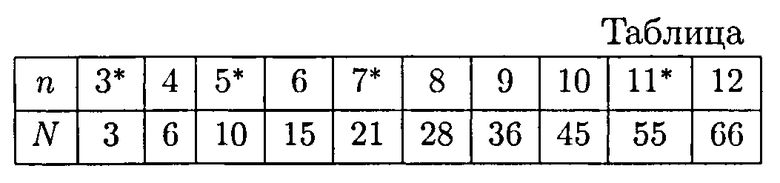
Так, при проверке является ли число 3 простым числом, исходят из следующего: n=3, N3=(32-3)/2=3, N4=(42-4)/2=6. При этом N3/n=3/3=1, a N4/n=6/3=2, то есть производные от тестируемого числа 3 числа N3 и N4 делятся на тестируемое число без остатка. Причем N4 является четным числом. Следовательно, число 3 является простым числом.
Закономерность Шихаева-Анохина справедлива и для больших чисел, что позволяет строить на ее основе производительные технические решения, обеспечивающие высокую достоверность тестирования чисел на простоту.
Тестирование чисел большой разрядности на простоту проводят при помощи вычислительной системы 1, содержащей технические средства для реализации проверки условий закономерности Шихаева-Анохина. На вход вычислительной системы 1 подают тестируемое число в виде цифровых данных. Выход вычислительной системы 1 способен принимать одно из двух возможных состояний в виде логической «1» или «0», соответствующих тому, является ли тестируемое число простым или нет.
Вычислительная система 1 включает в себя запоминающее устройство 2, инкрементор 3, блок 4 вычисления N, блок 5 деления, блок 6 проверки числа на целость-дробность, блок 7 проверки числа на четность-нечетность и устройство управления 8.
Запоминающее устройство 2 выполнено с возможностью хранения тестируемого числа, а блок 4 вычисления N выполнен с возможностью вычисления выражения Nn=(n2-n)/2, где n - тестируемое число. Устройство управления 8 выполнено с возможностью управления работой элементов вычислительной системы 1 для осуществления вычислительного процесса.
Вход вычислительной системы 1 связан с входом запоминающего устройства 2. Выход запоминающего устройства 2 связан с входом инкрементора 3, блока 4 вычисления N и блока 7 проверки числа на четность-нечетность. Выход инкрементора 3 связан с входом блока 4 вычисления N. Выход блока 4 вычисления N связан с входом блока 6 проверки числа на целость-дробность через блок 5 деления и с входом блока 7 проверки числа на четность-нечетность. Выходы блока 6 проверки числа на целость-дробность и блока 7 проверки числа на четность-нечетность связаны с информационным входом устройства управления 8, выполненного с возможностью установки выходного сигнала вычислительной системы 1 в логическое состояние «1» или «0». Управляющие выходы устройства управления 8 связаны с цепями коммутации, задающими поступление данных на вход блока 4 вычисления N и блока 7 проверки числа на четность-нечетность.
Все блоки вычислительной системы 1 являются аппаратными и выполнены на основе элементной базы цифровой микроэлектроники.
Вычислительная система 1 работает следующим образом.
На вход вычислительной системы 1 подают число для тестирования в виде цифровых данных, записываемых в запоминающее устройство 2.
Если в процессе работы допускается возможность поступления на вход вычислительной системы 1 чисел малой разрядности, то сначала производят предварительный отсев путем сравнения тестируемых чисел с рядом известных простых чисел малой разрядности для исключения основных проверок, что дополнительно повышает производительность системы.
Тестирование случайных чисел на простоту предпочтительно начинают с проверки их нечетности, для чего вход вычислительной системы 1 связывают через запоминающее устройство 2 с входом блока 7 проверки числа на четность-нечетность, связанного в свою очередь с устройством управления 8. К вычислению Nn переходят, если проверка тестируемого числа в блоке 7 показала нечетность данного числа, в противном случае делают вывод, что тестируемое число является составным, и устанавливают выходной логический уровень вычислительной системы 1 в состояние «0» при помощи устройства управления 8.
Для проведения проверки условий закономерности Шихаева-Анохина извлекают данные, характеризующие тестируемое число n, из запоминающего устройства 2 и подают их на вход блока вычисления N для вычисления текущего значения Nn, после чего передают данные в блок 5 деления и вычисляют величину Nn/n. Затем подают данные, характеризующие данный промежуточный результат, на вход блока 6 проверки числа на целость-дробность. Если число является дробным, то делают вывод, что тестируемое число n является составным, и устанавливают выходной логический уровень вычислительной системы в состояние «0». В противном случае увеличивают тестируемое число на единицу посредством инкрементора 3 и вычисляют Nn+1 в блоке 4. Затем в блоке 5 деления вычисляют Nn+1/n и Nn+1/5. После чего проверяют Nn+1 и Nn+1/5 в блоке 6 проверки числа на целость-дробность, а Nn+1 проверяют в блоке 7 проверки числа на четность-нечетность. Если Nn+1/n является целым числом, а Nn+1 является четным или Nn+1/5 является целым числом, то делают вывод, что тестируемое число является простым, и устанавливают выходной логический уровень вычислительной системы 1 в состояние «1», в противном случае делают вывод, что тестируемое число является составным, и устанавливают выходной логический уровень вычислительной системы 1 в состояние «0».
По окончании тестирования числа на простоту вычислительный процесс завершается и система 1 переходит в режим ожидания поступления на ее информационный вход следующего числа.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ потокового генерирования последовательности фигурных чисел, используемой при обучении решению уравнения Ферма | 2016 |
|
RU2619527C1 |
| СПОСОБ ШИХАЕВА ОБУЧЕНИЯ РЕШЕНИЮ АЛГЕБРАИЧЕСКИХ И НЕОПРЕДЕЛЕННЫХ УРАВНЕНИЙ ЧИСЛЕННЫМ МОДЕЛИРОВАНИЕМ НА ОСНОВЕ ЕДИНОГО РЕШАТЕЛЯ | 2007 |
|
RU2389082C2 |
| Система надежного облачного хранения с регулируемой избыточностью данных | 2021 |
|
RU2782681C1 |
| Способ определения знака числа в системе остаточных классов | 2021 |
|
RU2767450C1 |
| Устройство для декодирования кода | 1983 |
|
SU1190525A1 |
| Устройство для масштабирования чисел | 1989 |
|
SU1667066A1 |
| Устройство для вычисления симметричных булевых функций | 1980 |
|
SU959064A1 |
| Способ декодирования LDPC-кодов и устройство для его осуществления | 2016 |
|
RU2628459C1 |
| УСТРОЙСТВО ДЛЯ ОПРЕДЕЛЕНИЯ ЗНАКОВ ЧИСЕЛ В СИСТЕМЕ ОСТАТОЧНЫХ КЛАССОВ | 2014 |
|
RU2557446C1 |
| Устройство для кодирования и декодирования цифрового телевизионного сигнала | 1988 |
|
SU1566485A1 |
Изобретение относится к области цифровых вычислений и может быть использовано в криптографии. Техническим результатом является повышение достоверности и производительности. Способ содержит этапы, на которых: подают тестируемое число n на вход вычислительной системы, вычисляют Nn=(n2-n)/2. Передают данные в блок деления и вычисляют величину Nn/n. Затем подают численный результат на вход блока проверки числа на целость-дробность. Если число является дробным, то делают вывод, что тестируемое число является составным. В противном случае вычисляют Nn+1. В блоке деления вычисляют Nn+1/n и Nn+1/5. После чего проверяют Nn+1 и Nn+1/5 в блоке проверки числа на целость-дробность. Nn+1 проверяют в блоке проверки числа на четность-нечетность. Если Nn+1/n является целым числом, а Nn+1 является четным или Nn+1/5 является целым числом, то делают вывод, что тестируемое число является простым. 1 з.п. ф-лы, 2 ил, 1 табл.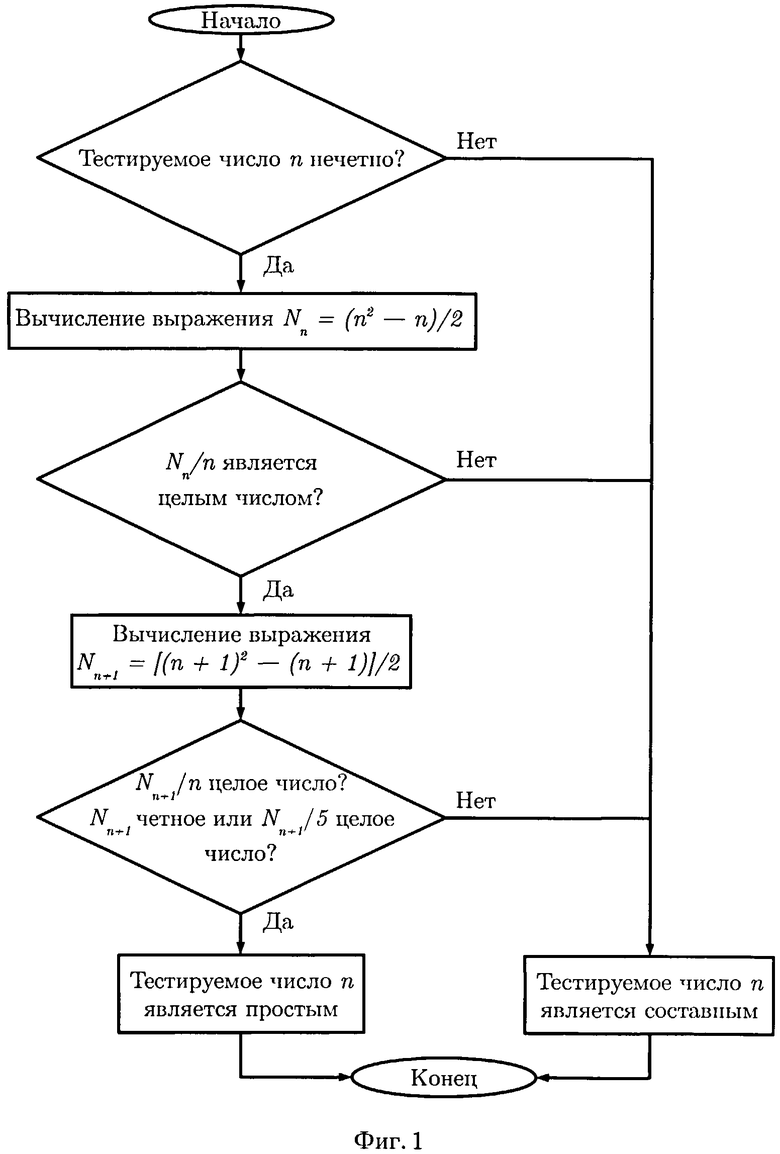
1. Способ тестирования чисел на простоту, характеризующийся тем, что делают вывод относительно простоты тестируемого числа исходя из критериев: а) числа Nn=(n2-n)/2, где n - тестируемое число, от тестируемого простого числа и Nn+1 от последующего составного числа всегда нацело делятся на тестируемые числа, если они простые; б) все числа N, получаемые от составных чисел, кроме составных, следующих за простыми, неделимы нацело тестируемыми числами, если они простые; в) число Nn+1, следующее за тестируемым числом, является всегда четным или делящимся на число 5; для чего подают данные, характеризующие тестируемое число, на вход вычислительной системы, связанный с входом блока вычисления N, и вычисляют Nn, после чего передают данные в блок деления и вычисляют величину Nn/n, затем подают данные, характеризующие численный результат, на вход блока проверки числа на целость-дробность, причем если число является дробным, то делают вывод, что тестируемое число является составным, и устанавливают выходной логический уровень вычислительной системы в состояние «0», в противном случае в блоке вычисления N вычисляют Nn+1, а в блоке деления вычисляют Nn+1/n и Nn+1/5, после чего проверяют данные числа в блоке проверки числа на целость-дробность, a Nn+1 проверяют в блоке проверки числа на четность-нечетность, и если Nn+1/n является целым числом, a Nn+1 является четным или Nn+1/5 является целым числом, то делают вывод, что тестируемое число является простым, и устанавливают выходной логический уровень вычислительной системы в состояние «1», в противном случае делают вывод, что тестируемое число является составным, и устанавливают выходной логический уровень вычислительной системы в состояние «0».
2. Способ по п.1, в котором вход вычислительной системы связывают с входом проверки числа на четность-нечетность, а к вычислению Nn переходят, если проверка тестируемого числа показала нечетность данного числа, в противном случае делают вывод, что тестируемое число является составным, и устанавливают выходной логический уровень вычислительной системы в состояние «0».
| ВАСИЛЕНКО О.Н | |||
| ТЕОРЕТИКО-ЧИСЛОВЫЕ АЛГОРИТМЫ В КРИПТОГРАФИИ | |||
| Москва, МЦНМО, 2003, с | |||
| Способ гальванического снятия позолоты с серебряных изделий без заметного изменения их формы | 1923 |
|
SU12A1 |
| US 7346637 B2, 03.02.2005 | |||
| WO 2004001595 A1, 31.12.2003 | |||
| DE 10326057 A1, 13.01.2005 | |||
| US 7043018 B1, 09.05.2006 | |||
Авторы
Даты
2015-04-20—Публикация
2014-02-21—Подача