Изобретение относится к вычислительной технике и предназначено для определения знака числа, представленного в системе остаточных классов.
Известно устройство для определения знаков чисел в системе остаточных классов (патент РФ 2557446, опубл. 20.07.2015), содержащее группу входных регистров для хранения числа, представленного в коде симметричной системы остаточных классов, энергонезависимые регистры для хранения интервально-позиционной характеристики константы - наибольшего положительного числа в симметричной системе остаточных классов, блок вычисления интервально-позиционной характеристики, блок проверки правильности интервально-позиционной характеристики, блок сравнения интервально-позиционных характеристик, двухвходовой двоичный дешифратор.
Недостатком данного устройства является использование ресурсоемких операций деления с числами с плавающей точкой, что снижает скорость работы и требует округлений.
Известно устройство для определения знака модулярного числа (патент РФ 2503995, опубл. 10.01.2014), содержащее входные регистры для хранения разрядов исходного числа, блоки умножения, выполненные в виде памяти для хранения произведений 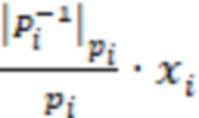 и параллельный сумматор.
и параллельный сумматор.
Недостатком данного устройства является низкая точность, связанная с представлением чисел в формате с плавающей точкой, а именно с ошибками округления.
Наиболее близким к заявляемому изобретению является способ, на котором основано устройство определения знака числа, представленного в системе остаточных классов с модулями 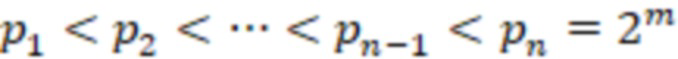 , (заявка на изобретение РФ №2020134778, дата подачи 22.10.2020), содержащее
, (заявка на изобретение РФ №2020134778, дата подачи 22.10.2020), содержащее  входов остатка, где
входов остатка, где  – количество модулей
– количество модулей 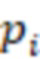 системы остаточных классов,
системы остаточных классов,  регистров для хранения разрядов исходного числа,
регистров для хранения разрядов исходного числа, 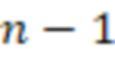 вычислительную ступень, при этом
вычислительную ступень, при этом 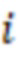 -я вычислительная ступень, где
-я вычислительная ступень, где  , содержит
, содержит 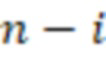 сумматоров по модулю
сумматоров по модулю 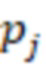 и
и 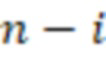 блоков умножения на веса
блоков умножения на веса 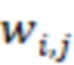 по модулю
по модулю 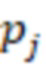 , где
, где 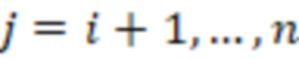 и
и 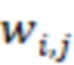 – мультипликативная инверсия модуля
– мультипликативная инверсия модуля 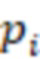 по модулю
по модулю 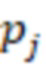 . Старший бит выхода первого блока умножения на веса
. Старший бит выхода первого блока умножения на веса 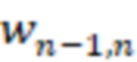 по модулю
по модулю 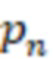 является выходом знака устройства.
является выходом знака устройства.
Работа данного устройства основана на следующем математическом аппарате.
В системе остаточных классов (СОК) любое число 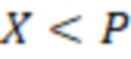 однозначно представляется набором остатков
однозначно представляется набором остатков 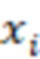 от деления числа
от деления числа 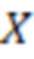 на взаимно простые модули СОК
на взаимно простые модули СОК 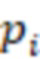 , где
, где 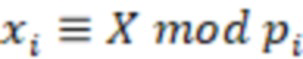 ,
, 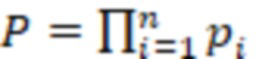 - рабочий диапазон СОК,
- рабочий диапазон СОК, 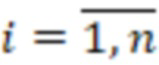 . Возьмем систему остаточных классов с модулями
. Возьмем систему остаточных классов с модулями 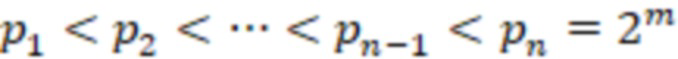 . Знак в системе остаточных классов чаще всего вводится разбиением диапазона на две части, тогда с учетом динамического диапазона
. Знак в системе остаточных классов чаще всего вводится разбиением диапазона на две части, тогда с учетом динамического диапазона 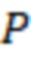 в СОК можно представить числа
в СОК можно представить числа 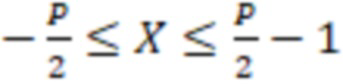 , если
, если 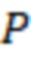 четное.
четное.
Функция определения знака числа, представленного в СОК, определяется следующим образом:

Таким образом 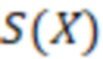 можно представить в виде:
можно представить в виде:
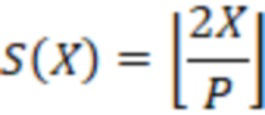 (1)
(1)
Используя свойство 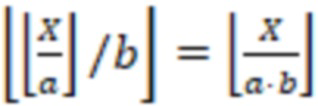 и формулу (1) определение знака сводится двухэтапному алгоритму: первый этап - деление на
и формулу (1) определение знака сводится двухэтапному алгоритму: первый этап - деление на 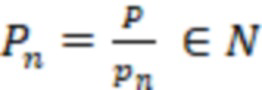 , второй этап - деление на
, второй этап - деление на 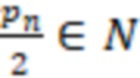 , формально математически определяется следующей формулой
, формально математически определяется следующей формулой
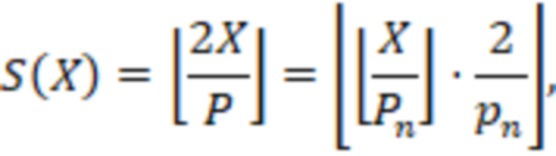
Запишем процесс определения в виде алгоритма:
Алгоритм 1. Определение знака числа
Вход:
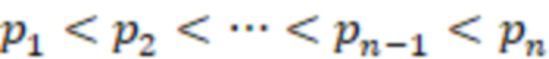 – модули СОК
– модули СОК
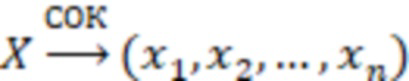 – представление числа
– представление числа 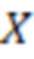 в СОК
в СОК
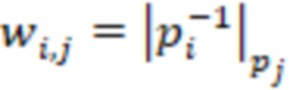 - синоптические веса
- синоптические веса
Выход: 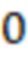 – положительное число,
– положительное число, 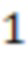 – отрицательное число
– отрицательное число
1. Для 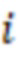 от
от 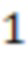 до
до 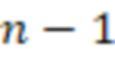 выполнять:
выполнять:
1.1. Для 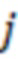 от
от 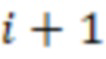 до
до  выполнять: \\ деление на
выполнять: \\ деление на 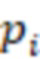
1.1.1. 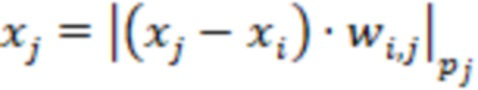
2. Возвратить 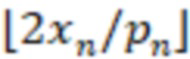
На первом этапе вычисляется 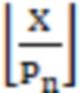 с помощью
с помощью 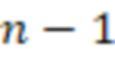 деления на модули СОК
деления на модули СОК  соответственно. На втором этапе вычисляется
соответственно. На втором этапе вычисляется 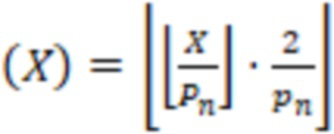 .
.
Недостатком данного способа являются органичные функциональные возможности, связанные с ограничениями, накладываемыми на модули СОК, а именно упорядоченность модулей по возрастанию и представление наибольшего модуля в виде степени 2.
Техническим результатом заявляемого изобретения является расширение функциональности, а именно независимость от порядка модулей.
Данный технический результат достигается тем, что в способе определения знака числа в системе остаточных классов, пригодном для реализации средствами вычислительной техники, включающем для системы остаточных классов с модулями 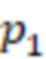 ,
, 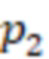 , …,
, …, 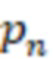 и треугольной матрицы с элементами
и треугольной матрицы с элементами 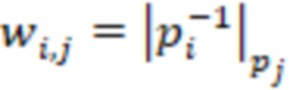 где
где  ,
, 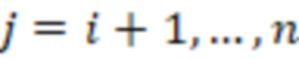 на основе входного значения числа
на основе входного значения числа 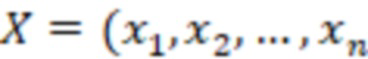 ), где
), где 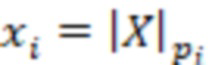 – остаток от деления числа
– остаток от деления числа 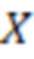 на модуль
на модуль 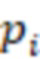 , вычисление промежуточных значений
, вычисление промежуточных значений 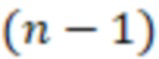 вычислительной ступенью, причем
вычислительной ступенью, причем 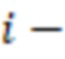 я ступень вычисляет выражение
я ступень вычисляет выражение 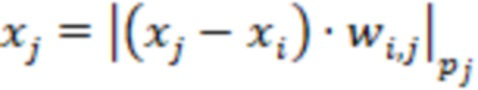 для
для 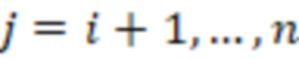 , берут нечетные модули, на основе входного значения
, берут нечетные модули, на основе входного значения 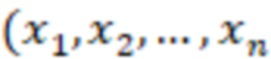 ) вычисляют вспомогательное значение
) вычисляют вспомогательное значение 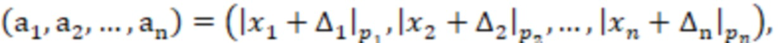 где
где 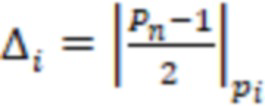 и
и 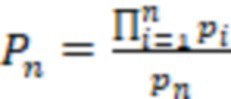 , каждая
, каждая 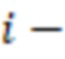 я ступень дополнительно вычисляет выражение
я ступень дополнительно вычисляет выражение 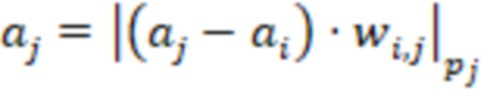 для
для 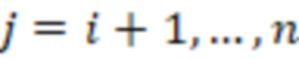 , после вычисления значений
, после вычисления значений 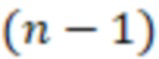 -ой вычислительной ступенью значения
-ой вычислительной ступенью значения 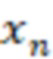 и
и 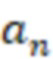 сравнивают соответственно с
сравнивают соответственно с 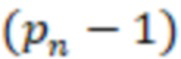 /2 и
/2 и 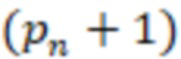 /2 и если
/2 и если 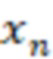 >
>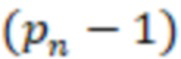 /2 или одновременно
/2 или одновременно 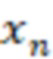 =
=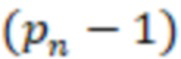 /2 и
/2 и 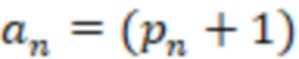 /2, то считают, что исходное число
/2, то считают, что исходное число 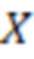 отрицательное, иначе положительное.
отрицательное, иначе положительное.
Сущность способа основана на следующем математическом аппарате. Берется СОК с нечетными модулями  , тогда функция знака имеет вид
, тогда функция знака имеет вид
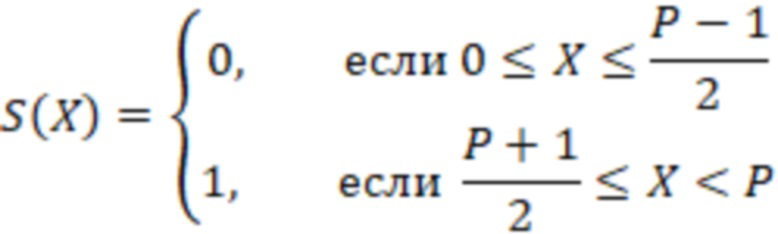
Чтобы определить знак, рассмотрим две функции, 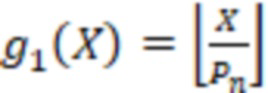 и
и 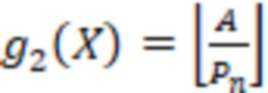 , где
, где 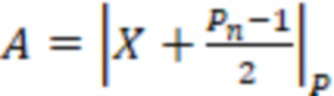 , тогда функцию знака числа
, тогда функцию знака числа 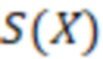 можно получить из выражения
можно получить из выражения
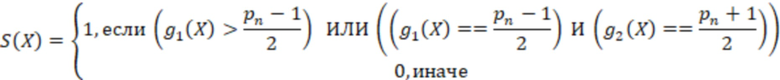
Рассмотрим пример. Возьмем систему остаточных классов с модулями 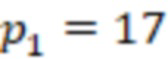 ,
, 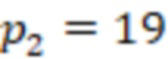 ,
, 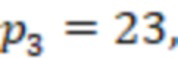
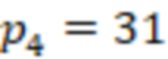 . В данной системе динамический диапазон
. В данной системе динамический диапазон 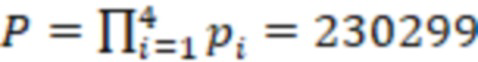 и число
и число 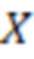 будет положительным, если
будет положительным, если 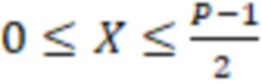 , т.е.
, т.е. 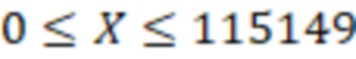 , а отрицательным для
, а отрицательным для 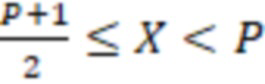 , т.е.
, т.е. 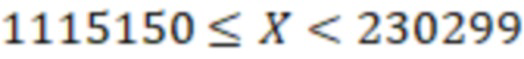 .
.
Рассмотрим значения на границе перехода от отрицательных к положительным числам.
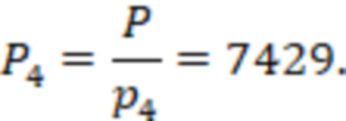
Для числа 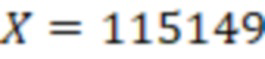 ,
, 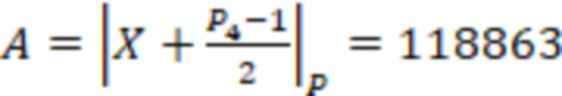 ,тогда
,тогда
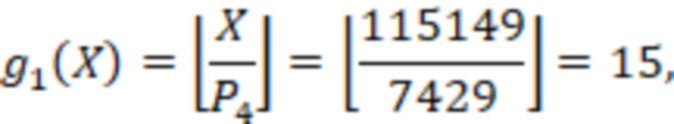
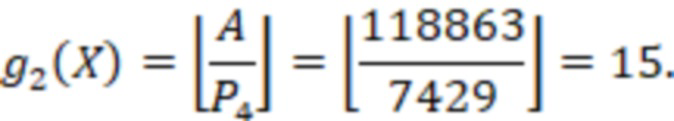
Поскольку 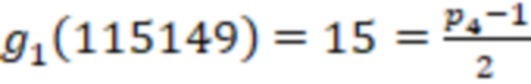 , а
, а 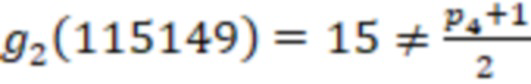 , то
, то 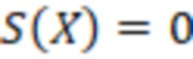 и число положительное.
и число положительное.
Для числа 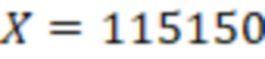 ,
, 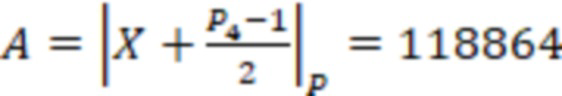 ,тогда
,тогда
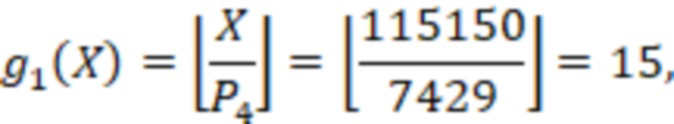
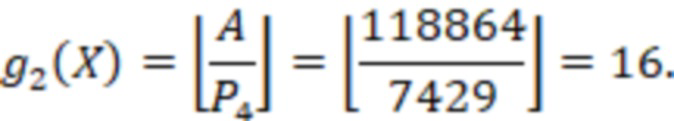
Поскольку 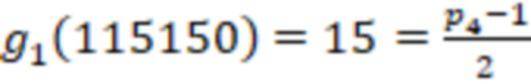 , а
, а 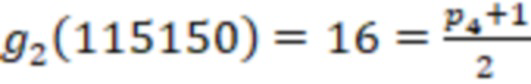 , то
, то 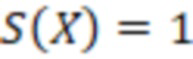 и число отрицательное.
и число отрицательное.
Запишем функцию определения знака 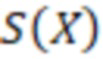 в виде алгоритма для работы с числами, представленными в системе остаточных классов. Данный алгоритм основан на последовательном приближении значения
в виде алгоритма для работы с числами, представленными в системе остаточных классов. Данный алгоритм основан на последовательном приближении значения 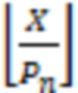 на основе свойства
на основе свойства 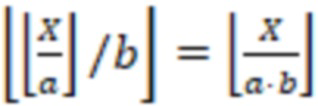 .
.
Алгоритм 2. Определение знака числа
Вход:
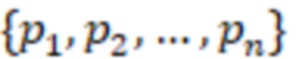 – модули СОК,
– модули СОК, 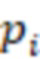 - нечетные числа
- нечетные числа
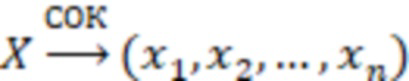 – представление числа
– представление числа 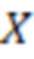 в СОК
в СОК
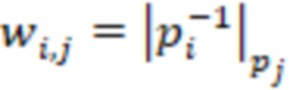 - синоптические веса
- синоптические веса
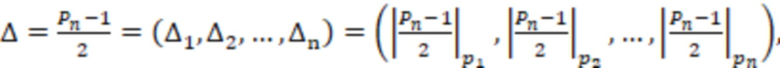 где
где 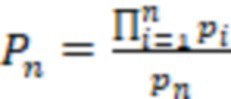
Выход: 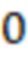 – положительное число,
– положительное число, 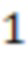 – отрицательное число
– отрицательное число
1. Для  от
от  до
до  выполнять: \\ выполняется параллельно
выполнять: \\ выполняется параллельно
1.1. 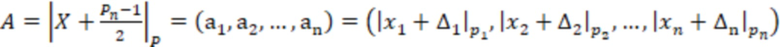
2. Для  от
от 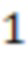 до
до 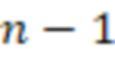 выполнять:
выполнять:
2.1. Для 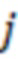 от
от 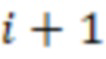 до
до  выполнять:
выполнять:
2.1.1. 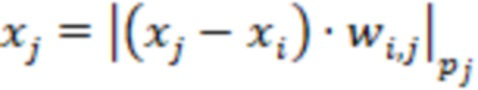
2.1.2. 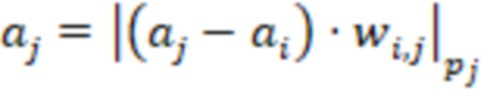
3. Если ((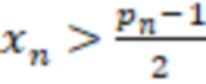 ) ИЛИ ((
) ИЛИ ((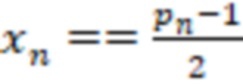 ) И (
) И (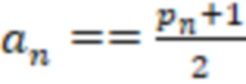 )) то
)) то
3.1. Возвратить 1
4. Иначе
4.1 Возвратить 0
Рассмотрим пример данного способа. Для СОК с нечетными модулями 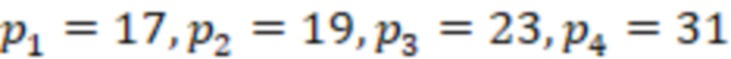 , диапазон СОК
, диапазон СОК 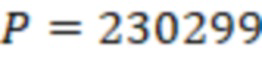 и
и 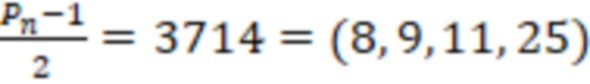 .
.
Синоптические веса 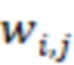 равны:
равны:
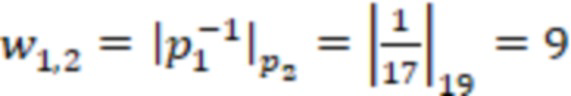 ,
,
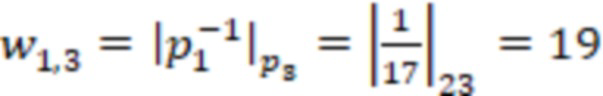 ,
,
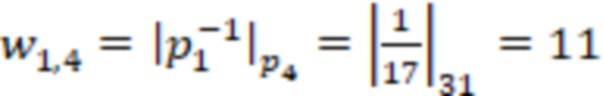
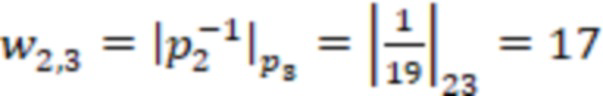 ,
,
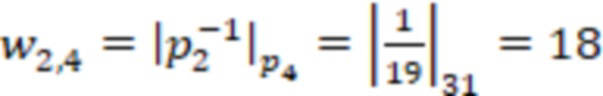
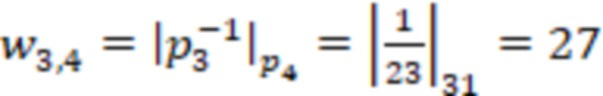 .
.
Определить знак числа 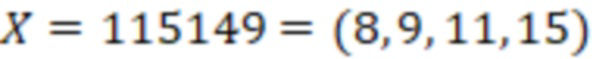 , найдем вспомогательное значение
, найдем вспомогательное значение
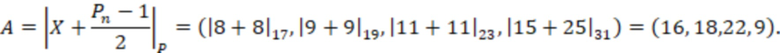
Для удобства запишем вычисления (n-1) вычислительной ступени в виде таблицы, где 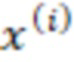 означает, что берется значение
означает, что берется значение 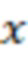 , вычисленное на
, вычисленное на 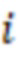 вычислительной ступени.
вычислительной ступени.
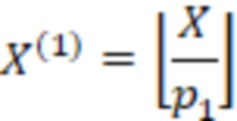

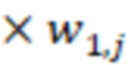
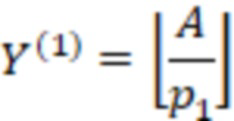
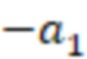
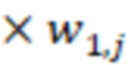
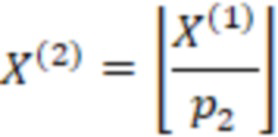
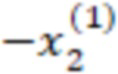
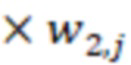
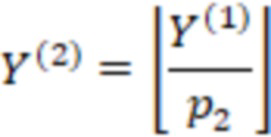
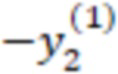
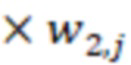
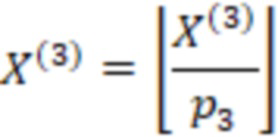
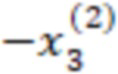
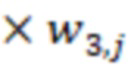
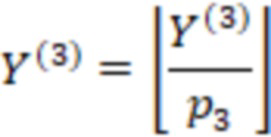
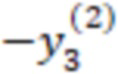
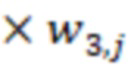
После вычисления трех вычислительных ступеней сравним значения 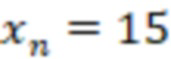 и
и 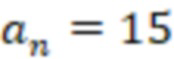 с
с 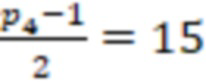 и
и 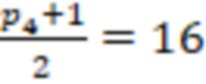 . Поскольку
. Поскольку 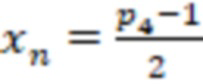 , а
, а 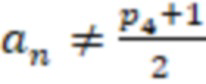 , то число положительное.
, то число положительное.
Определить знак числа 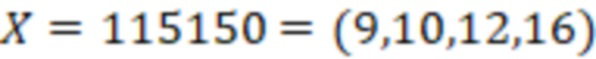 , найдем вспомогательное значение
, найдем вспомогательное значение

Для удобства запишем вычисления (n-1) вычислительной ступени в виде таблицы, где 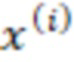 означает, что берется значение
означает, что берется значение 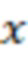 , вычисленное на
, вычисленное на 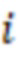 вычислительной ступени.
вычислительной ступени.
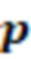
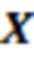
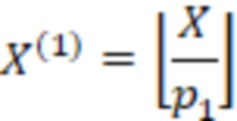

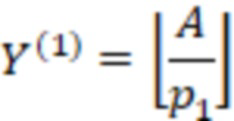
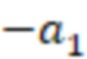
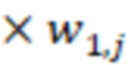
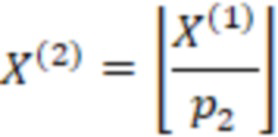
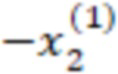
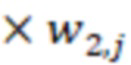
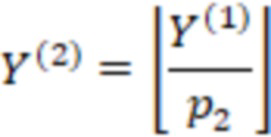
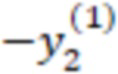
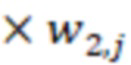
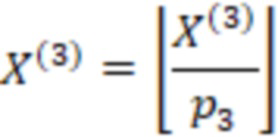
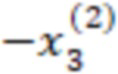
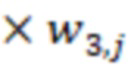
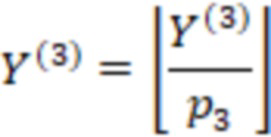
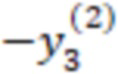
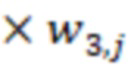
После вычисления трех вычислительных ступеней сравним значения 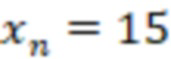 и
и 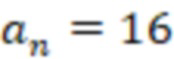 с
с 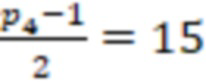 и
и 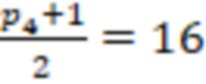 . Поскольку
. Поскольку 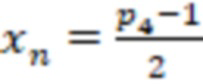 , а
, а 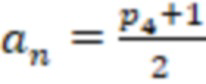 , то число отрицательное.
, то число отрицательное.
Реализация данного способа возможна на программируемых логических интегральных схем (ПЛИС) или с использованием ЭВМ.
| название | год | авторы | номер документа |
|---|---|---|---|
| Устройство определения знака числа, представленного в системе остаточных классов | 2020 |
|
RU2747371C1 |
| Устройство сравнения чисел, представленных в системе остаточных классов | 2020 |
|
RU2751992C1 |
| УСТРОЙСТВО ДЛЯ ОПРЕДЕЛЕНИЯ ЗНАКОВ ЧИСЕЛ В СИСТЕМЕ ОСТАТОЧНЫХ КЛАССОВ | 2014 |
|
RU2557446C1 |
| УСТРОЙСТВО ДЛЯ СРАВНЕНИЯ ЧИСЕЛ В СИСТЕМЕ ОСТАТОЧНЫХ КЛАССОВ НА ОСНОВЕ ИНТЕРВАЛЬНО-ПОЗИЦИОННЫХ ХАРАКТЕРИСТИК | 2014 |
|
RU2557444C1 |
| Устройство для вычисления ранга модулярного числа | 2021 |
|
RU2780400C1 |
| Устройство для сравнения чисел в системе остаточных классов | 2018 |
|
RU2698413C1 |
| НЕЙРОННАЯ СЕТЬ ДЛЯ ДЕЛЕНИЯ ЧИСЕЛ, ПРЕДСТАВЛЕННЫХ В СИСТЕМЕ ОСТАТОЧНЫХ КЛАССОВ | 2005 |
|
RU2305312C2 |
| Способ организации выполнения операции умножения двух чисел в модулярно-логарифмическом формате представления с плавающей точкой на гибридных многоядерных процессорах | 2017 |
|
RU2666285C1 |
| УСТРОЙСТВО ДЛЯ ОПРЕДЕЛЕНИЯ ЗНАКА МОДУЛЯРНОГО ЧИСЛА | 2011 |
|
RU2503995C2 |
| Устройство вычисления модулярного произведения Монтгомери | 2017 |
|
RU2652450C1 |
Изобретение относится к вычислительной технике. Технический результат заключается в расширении функциональности путем независимости от порядка модулей. Способ определения знака числа в системе остаточных классов, пригодный для реализации средствами вычислительной техники, включает для системы остаточных классов с модулями 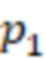 ,
, 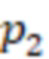 , …,
, …, 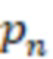 и треугольной матрицы с элементами
и треугольной матрицы с элементами 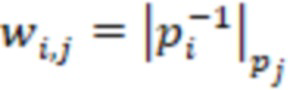 , где
, где  ,
, 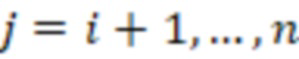 , на основе входного значения числа
, на основе входного значения числа 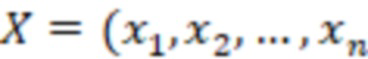 ), где
), где 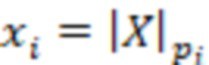 – остаток от деления числа
– остаток от деления числа 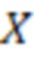 на модуль
на модуль 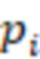 , вычисление промежуточных значений
, вычисление промежуточных значений 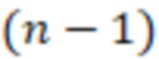 вычислительной ступенью, причем
вычислительной ступенью, причем 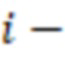 я ступень вычисляет выражение
я ступень вычисляет выражение 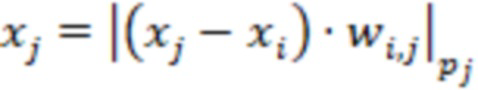 для
для 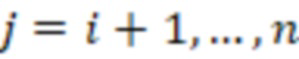 , берут нечетные модули, на основе входного значения
, берут нечетные модули, на основе входного значения 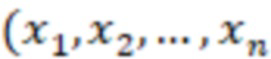 ) вычисляют вспомогательное значение
) вычисляют вспомогательное значение 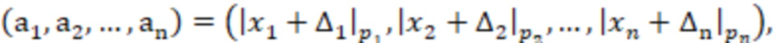 где
где 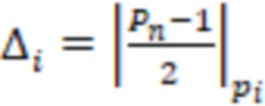 и
и 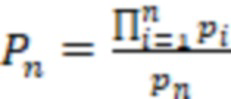 , каждая
, каждая 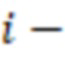 я ступень дополнительно вычисляет выражение
я ступень дополнительно вычисляет выражение 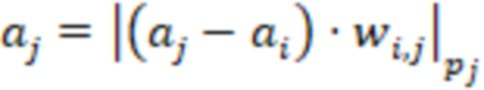 для
для 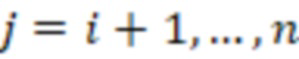 , после вычисления значений
, после вычисления значений 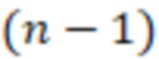 -й вычислительной ступенью значения
-й вычислительной ступенью значения 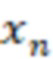 и
и 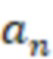 сравнивают соответственно с
сравнивают соответственно с 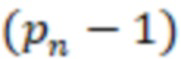 /2 и
/2 и 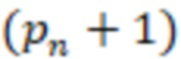 /2 и если
/2 и если 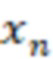 >
>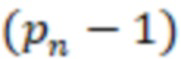 /2 или одновременно
/2 или одновременно 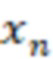 =
=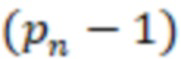 /2 и
/2 и 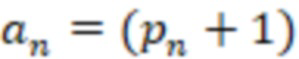 /2, то считают, что исходное число
/2, то считают, что исходное число 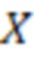 отрицательное, иначе положительное. 2 табл.
отрицательное, иначе положительное. 2 табл.
Способ определения знака числа в системе остаточных классов, пригодный для реализации средствами вычислительной техники, включающий для системы остаточных классов с модулями 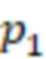 ,
, 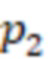 , …,
, …, 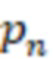 и треугольной матрицы с элементами
и треугольной матрицы с элементами 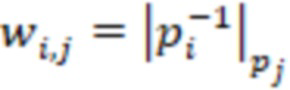 , где
, где  ,
, 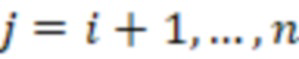 , на основе входного значения числа
, на основе входного значения числа 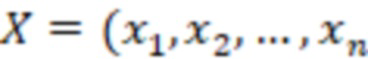 ), где
), где 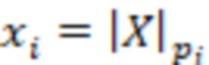 – остаток от деления числа
– остаток от деления числа 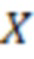 на модуль
на модуль 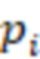 , вычисление промежуточных значений
, вычисление промежуточных значений 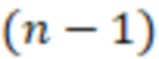 вычислительной ступенью, причем
вычислительной ступенью, причем 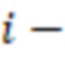 я ступень вычисляет выражение
я ступень вычисляет выражение 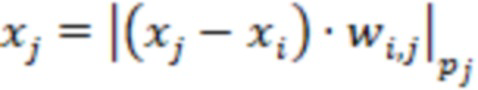 для
для 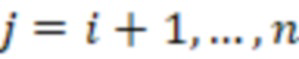 , отличающийся тем, что берут нечетные модули, на основе входного значения
, отличающийся тем, что берут нечетные модули, на основе входного значения 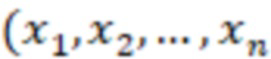 ) вычисляют вспомогательное значение
) вычисляют вспомогательное значение 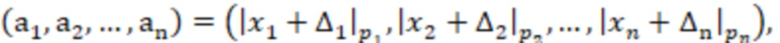 где
где 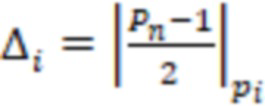 и
и 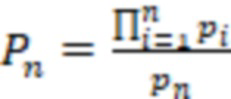 , каждая
, каждая 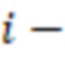 я ступень дополнительно вычисляет выражение
я ступень дополнительно вычисляет выражение 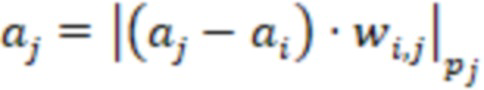 для
для 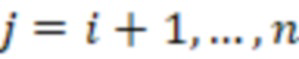 , после вычисления значений
, после вычисления значений 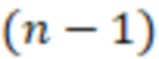 -й вычислительной ступенью значения
-й вычислительной ступенью значения 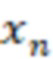 и
и 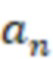 сравнивают соответственно с
сравнивают соответственно с 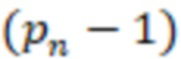 /2 и
/2 и 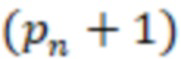 /2 и если
/2 и если 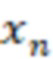 >
>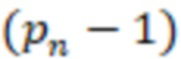 /2 или одновременно
/2 или одновременно 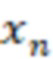 =
=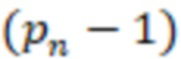 /2 и
/2 и 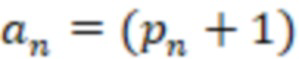 /2, то считают, что исходное число
/2, то считают, что исходное число 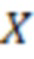 отрицательное, иначе положительное.
отрицательное, иначе положительное.
| УСТРОЙСТВО ДЛЯ ОПРЕДЕЛЕНИЯ ЗНАКА МОДУЛЯРНОГО ЧИСЛА | 2011 |
|
RU2503995C2 |
| УСТРОЙСТВО ДЛЯ СРАВНЕНИЯ ЧИСЕЛ, ПРЕДСТАВЛЕННЫХ В СИСТЕМЕ ОСТАТОЧНЫХ КЛАССОВ | 2011 |
|
RU2503992C2 |
| УСТРОЙСТВО ДЛЯ ОПРЕДЕЛЕНИЯ ЗНАКОВ ЧИСЕЛ В СИСТЕМЕ ОСТАТОЧНЫХ КЛАССОВ | 2014 |
|
RU2557446C1 |
| US 20100030832 A1, 04.02.2010 | |||
| US 20110231465 A1, 22.09.2011. | |||
Авторы
Даты
2022-03-17—Публикация
2021-04-01—Подача