Изобретение относится к вычислительной технике и предназначено для выполнения операции определения знака числа, представленного в системе остаточных классов.
Известно устройство для определения знака числа, представленного в системе остаточных классов (А.С. SU №1552181, БИ №11, 23.03.1990), которое содержит блок 1 определения номера интервала, группу информационных входов 2 устройства, первую 3 и вторую 4 схемы сравнения, первый 5 и второй 6 элементы ИЛИ, первый 7 и второй 8 входы константы устройства, первый 9 и второй 10 выходы устройства. Данное устройство основано на выявлении принадлежности интервала, в котором находится число, представленное в системе остаточных классов (СОК), к группе положительных или отрицательных интервалов по данному основанию СОК pi, на которые разбит полный модулярный диапазон [0, P-1], где P - это произведение всех оснований СОК. Недостаток данного устройства - большая сложность и низкое быстродействие, поскольку для определения знака числа необходимо работать с (P/pi)-разрядными числами.
Наиболее близким к заявленному изобретению является устройство для определения знака модулярного числа, основанное на приближенном методе (А.С. RU №2503995, БИ №1, 10.01.2014), содержащее входные регистры по модулям p1, p2, …, pn для временного хранения разрядов СОК, параллельный сумматор для суммирования 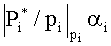

Техническим результатом заявляемого устройства для определения знаков чисел в системе остаточных классов является повышение быстродействия по отношению к устройствам, основанным на точных методах, и обеспечение контроля корректности определения знака. Представленные положения обеспечиваются за счет использования новой интервально-позиционной характеристики модулярной арифметики, которая аппроксимирует с двух сторон относительную величину числа в модулярном представлении.
Описание устройства: в основе функционирования заявляемого устройства для определения знаков чисел в системе остаточных классов лежит новый метод интервальной оценки относительной величины модулярного кода. Рассмотрим его.
Пусть базис СОК задан попарно взаимно простыми нечетными модулями p1, p2, …, pn и 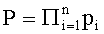
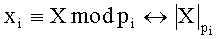

где B1, B2, …, Bn - ортогональные базисы СОК, каждый i-й из которых суть произведение чисел Pi=P/pi и 
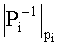
Знак числа в системе остаточных классов может быть введен различными способами. Наиболее распространенным способом является использование симметричной СОК. При этом если P - нечетное число, то весь числовой диапазон [0, P-1] разбивается на два равных интервала [0, (P-1)/2] и [(P+1)/2, P-1], и положительные числа представляются в младшем интервале, а отрицательные - в старшем. Таким образом, задача определения знака числа X, представленного в симметричной СОК, сводится к определению его положения относительно точки разбиения (P-1)/2. Для решения этой задачи требуется оценка позиционной величины числа X. Поскольку вычисление его абсолютной величины (1) трудоемко в силу того, что каждое слагаемое имеет значение порядка произведения модулей P, и его длина может существенно превышать размер машинного слова, заявляемое устройство, также как и известный аналог (А.С. RU №2503995, БИ №1, 10.01.2014), основано на оценке относительной величины.
Относительная величина E(X/P) модулярного числа X - это отношение его позиционного целочисленного значения к произведению всех модулей P, то есть

Так как точное рациональное значение E(X/P), изменяющееся в полуинтервале [0, 1), в общем случае не представимо в ЭВМ с ограниченной разрядной сеткой, возникает задача его аппроксимации. Для решения этой задачи используется новая интервально-позиционная характеристика (ИПХ) 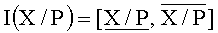

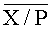
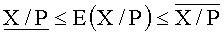
Границы ИПХ представляются в виде двоичных чисел с плавающей точкой, причем при вычислении нижней границы всегда используется округление до разрядности машинного слова с недостатком («вниз»), а при вычислении верхней границы - округление до разрядности машинного слова с избытком («вверх»). За счет этого обеспечивается включение I(X/P)∈E(X/P), то есть точная относительная величина (2) модулярного числа X локализуется его ИПХ. Нижняя граница вычисляется по формуле

а верхняя граница - по формуле
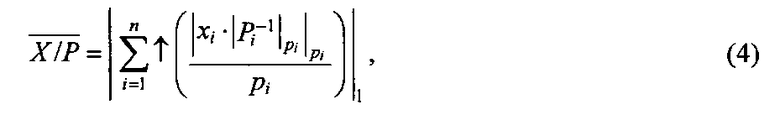
где xi - i-ый остаток числа X, | |1 - дробная часть аргумента, а стрелки соответствуют направленным округлениям до разрядности машинного слова при вычислении и суммировании слагаемых: ↓ - округление с недостатком, ↑ - округление с избытком.
В последовательном случае для вычисления формул (3) и (4) требуется O(n) элементарных операций с плавающей точкой, в параллельном - O(log n). Для сравнения, известные алгоритмы преобразования кода из системы остаточных классов в систему со смешанными основаниями требуют соответственно O(n2) и O(n) операций.
Абсолютную погрешность ИПХ характеризует ее диаметр, равный разности границ

Пусть n - размерность базиса СОК, а k - разрядность мантисс в двоичном представлении границ ИПХ, тогда при вычислении по формулам (3) и (4) диаметр (5) не превышает n2-k. При необходимости более точного вычисления ИПХ вместо формул (3) и (4) может быть использован оригинальный высокоточный алгоритм (Исупов К.С. Алгоритм вычисления интервально-позиционной характеристики для выполнения немодульных операций в системах остаточных классов // Вестник ЮУрГУ. Серия «Компьютерные технологии, управление, радиоэлектроника». - 2014. - Т. 14, №1. - С. 89-97). Этот алгоритм основан на возможности быстрого и безошибочного деления границ ИПХ, представленных нормализованными двоичными числами с плавающей точкой, на натуральные степени двойки и позволяет вычислить ИПХ с относительной ошибкой, определяемой для X≠0 отношением диаметра (5) к точной относительной величине (2), не превышающей априорно заданного предела ε, тем самым получить высокоточную информацию о величине числа в модулярном представлении без использования многоразрядной арифметики и трудоемкого преобразования в позиционную систему.
За счет направленных округлений погрешности, возникающие при вычислении границ ИПХ, приводят лишь к увеличению диаметра (5), не оказывая в общем случае влияния на свойство включения E(X/P)∈I(X/P). Но поскольку область значений границ ограничена полуинтервалом [0, 1), в ряде случаев указанное свойство может нарушаться. Это происходит тогда, когда число X очень мало по отношению к P, либо наоборот, находится в непосредственной близости с точкой P-1. В первом случае неправильно вычисляется нижняя граница ИПХ, а во втором - верхняя. В любом случае diam I(X/P)<0, т.е. нижняя граница больше верхней. Такая ИПХ называется неправильной по Каухеру или просто неправильной. Первое формальное условие корректного определения знака - правильность ИПХ числа X, представленного в симметричной СОК. Если это условие выполняется, то окончательный вывод о корректности знака формулируется на основании проверки второго формального условия, состоящего в отсутствии пересечения (коллизии) ИПХ 


Если диаметр (5) этого интервала меньше нуля, то ИПХ не пересекаются в стандартном теоретико-множественном смысле, т.е. не содержат общих точек. В вырожденном случае может оказаться, что X=(P-1)/2. Поэтому второе формальное условие корректного вычисления знака числа определяется следующим образом:
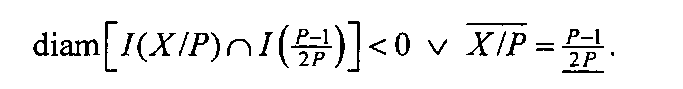
Пусть в симметричной СОК с модулями p1, p2, …, pn дано число X=〈x1, x2, …, xn〉. Алгоритм определения знака sgn(X) числа X на основе использования техники интервально-позиционных характеристик формулируется следующим образом.
АЛГОРИТМ.
Шаг 0. Заранее вычисляется и сохраняется в памяти ЭВМ ИПХ 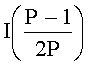
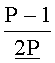
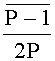

Шаг 1. Для числа X вычисляется 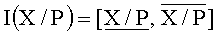
Шаг 2. Проверяется первое формальное условие корректного определения знака: если 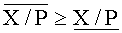
Шаг 3. Если 
Шаг 4. Если 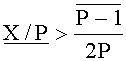
Шаг 5. Если повышение точности вычисления ИПХ на шаге 1 неосуществимо в рамках разрядности используемых форматов представления данных, то необходимо преобразовать число X из СОК в систему счисления со смешанными основаниями и определить его знак на основании сравнения цифр полученного полиадического кода с соответствующими цифрами заранее вычисленного полиадического кода числа (P-1)/2, либо сформировать и выдать сигнал о невозможности определения знака числа X из-за недостаточной точности вычисления его ИПХ. Алгоритм при этом завершается.
ПРИМЕР.
Требуется определить знак модулярного числа X=〈6, 8, 10, 1〉, представленного в симметричной СОК.
1. Вычислим константы:
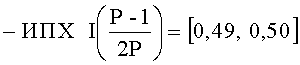
- набор весов ортогональных базисов (7):{6, 5, 9, 10}.
2. Вычисляем ИПХ числа X по формулам (3) и (4) с округлением до двух разрядов


Таким образом, получена ИПХ I(X/P)=[0,52, 0,56], которая является правильной, значит первое формальное условие корректного определения знака числа выполнено.
3. Условие 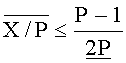
4. Сравниваем противоположные границы ИПХ: 0,52>0,50, следовательно, X - отрицательное число в симметричной СОК и sgn(X)=1.
5. Проверка: P=9009, (P-1)/2=4504, преобразование в десятичную систему дает X=4850. Таким образом, число X лежит во второй половине полного диапазона, поэтому является отрицательным в симметричной системе остаточных классов.
Схема заявляемого устройства для определения знаков чисел в системе остаточных классов, функционирующего в соответствии с представленным алгоритмом, приведена на фиг.2. Устройство содержит группу входных регистров 1 для хранения числа, знак которого необходимо определить, энергонезависимые регистры 2, 3 для хранения соответственно нижней 

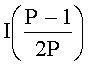
Работа заявляемого устройства для определения знаков чисел в системе остаточных классов осуществляется следующим образом. Заранее и однократно вычислена интервально-позиционная характеристика 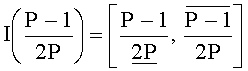

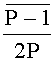
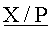

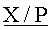
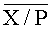

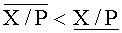
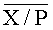

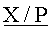

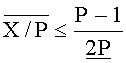

Пример работы заявляемого устройства представлен на фиг.3. В данном примере определялся знак числа X=〈0, 1, 8, 3〉, представленного в симметричной СОК с модулями {7, 9, 11, 13}. Интервально-позиционная характеристика вычислялась в блоке 4 с округлением до двух значащих десятичных цифр после запятой.
Трудоемкость заявляемого устройства оценивается следующим образом. Для вычисления нижней границы ИПХ 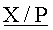

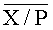
Устройство для определения знаков чисел в системе остаточных классов, содержащее группу из n входных регистров, для хранения числа, представленного в симметричной системе остаточных классов, отличающееся тем, что содержит первый и второй энергонезависимые регистры для хранения соответственно нижней 


блок вычисления интервально-позиционной характеристики, который функционирует по принципу двоичного арифметико-логического устройства с плавающей точкой с возможностью переключения режимов округления и имеет n информационных входов и два выхода,
блок проверки правильности интервально-позиционной характеристики, который имеет два информационных входа и один выход,
блок сравнения интервально-позиционных характеристик, имеющий четыре информационных входа, один управляющий вход и два выхода, двоичный дешифратор, имеющий два входа и четыре выхода,
причем выходы группы входных регистров соединены с информационными входами блока вычисления интервально-позиционной характеристики,
первый и второй выходы блока вычисления интервально-позиционной характеристики соединены соответственно с первым и вторым входами блока проверки правильности интервально-позиционной характеристики, а также с первым и вторым информационными входами блока сравнения интервально-позиционных характеристик,
выходы первого и второго энергонезависимых регистров соединены соответственно с третьим и четвертым информационными входами блока сравнения интервально-позиционных характеристик
выход блока проверки правильности интервально-позиционной характеристики соединен с управляющим входом блока сравнения интервально-позиционных характеристик,
первый и второй выходы блока сравнения интервально-позиционных характеристик соединены соответственно с первым и вторым входами двоичного дешифратора,
выходы двоичного дешифратора являются выходами устройства для определения знака числа в системе остаточных классов: «X≥0», «X<0», «Знак не определен».
| название | год | авторы | номер документа |
|---|---|---|---|
| УСТРОЙСТВО ДЛЯ СРАВНЕНИЯ ЧИСЕЛ В СИСТЕМЕ ОСТАТОЧНЫХ КЛАССОВ НА ОСНОВЕ ИНТЕРВАЛЬНО-ПОЗИЦИОННЫХ ХАРАКТЕРИСТИК | 2014 |
|
RU2557444C1 |
| Устройство для сравнения чисел в системе остаточных классов | 2018 |
|
RU2698413C1 |
| Способ организации выполнения операции умножения двух чисел в модулярно-логарифмическом формате представления с плавающей точкой на гибридных многоядерных процессорах | 2017 |
|
RU2666285C1 |
| Способ определения знака числа в системе остаточных классов | 2021 |
|
RU2767450C1 |
| Система надежного облачного хранения с регулируемой избыточностью данных | 2021 |
|
RU2782681C1 |
| Устройство определения знака числа, представленного в системе остаточных классов | 2020 |
|
RU2747371C1 |
| УСТРОЙСТВО ДЛЯ ОПРЕДЕЛЕНИЯ ЗНАКА МОДУЛЯРНОГО ЧИСЛА | 2011 |
|
RU2503995C2 |
| НЕЙРОННАЯ СЕТЬ ДЛЯ ПРЕОБРАЗОВАНИЯ ОСТАТОЧНОГО КОДА В ДВОИЧНЫЙ ПОЗИЦИОННЫЙ КОД | 2006 |
|
RU2318238C1 |
| НЕЙРОННАЯ СЕТЬ ДЛЯ ВЫЧИСЛЕНИЯ ПОЗИЦИОННЫХ ХАРАКТЕРИСТИК НЕПОЗИЦИОННОГО КОДА | 2003 |
|
RU2257615C2 |
| НЕЙРОННАЯ СЕТЬ ОСНОВНОГО ДЕЛЕНИЯ МОДУЛЯРНЫХ ЧИСЕЛ | 2008 |
|
RU2400813C2 |


Изобретение относится к вычислительной технике и предназначено для выполнения операции определения знака числа, представленного в системе остаточных классов. Техническим результатом является повышение быстродействия и обеспечение контроля корректности определения знака. Устройство содержит группу входных регистров для хранения числа, представленного в коде симметричной системы остаточных классов, энергонезависимые регистры для хранения интервально-позиционной характеристики константы - наибольшего положительного числа в симметричной системе остаточных классов, блок вычисления интервально-позиционной характеристики, блок проверки правильности интервально-позиционной характеристики, блок сравнения интервально-позиционных характеристик, двухвходовой двоичный дешифратор. 3 ил.
Устройство для определения знаков чисел в системе остаточных классов, содержащее группу из n входных регистров, для хранения числа, представленного в симметричной системе остаточных классов, отличающееся тем, что содержит первый и второй энергонезависимые регистры для хранения соответственно нижней 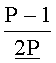 и верхней
и верхней 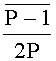 границ интервально-позиционной характеристики
границ интервально-позиционной характеристики 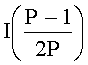 , которые представлены в виде двоичных чисел с плавающей точкой и приближают с двух сторон относительную величину наибольшего положительного числа (P-1)/2 в симметричной системе остаточных классов, где P - произведение всех n модулей системы остаточных классов,
, которые представлены в виде двоичных чисел с плавающей точкой и приближают с двух сторон относительную величину наибольшего положительного числа (P-1)/2 в симметричной системе остаточных классов, где P - произведение всех n модулей системы остаточных классов,
блок вычисления интервально-позиционной характеристики, который функционирует по принципу двоичного арифметико-логического устройства с плавающей точкой с возможностью переключения режимов округления и имеет n информационных входов и два выхода,
блок проверки правильности интервально-позиционной характеристики, который имеет два информационных входа и один выход,
блок сравнения интервально-позиционных характеристик, имеющий четыре информационных входа, один управляющий вход и два выхода, двоичный дешифратор, имеющий два входа и четыре выхода,
причем выходы группы входных регистров соединены с информационными входами блока вычисления интервально-позиционной характеристики,
первый и второй выходы блока вычисления интервально-позиционной характеристики соединены соответственно с первым и вторым входами блока проверки правильности интервально-позиционной характеристики, а также с первым и вторым информационными входами блока сравнения интервально-позиционных характеристик,
выходы первого и второго энергонезависимых регистров соединены соответственно с третьим и четвертым информационными входами блока сравнения интервально-позиционных характеристик,
выход блока проверки правильности интервально-позиционной характеристики соединен с управляющим входом блока сравнения интервально-позиционных характеристик,
первый и второй выходы блока сравнения интервально-позиционных характеристик соединены соответственно с первым и вторым входами двоичного дешифратора,
выходы двоичного дешифратора являются выходами устройства для определения знака числа в системе остаточных классов: «X≥0», «X<0», «Знак не определен».
| УСТРОЙСТВО ДЛЯ ОПРЕДЕЛЕНИЯ ЗНАКА МОДУЛЯРНОГО ЧИСЛА | 2011 |
|
RU2503995C2 |
| Устройство для определения знака числа, представленного в системе остаточных классов | 1988 |
|
SU1552181A1 |
| Устройство для определения знака числа, представленного в системе остаточных классов | 1989 |
|
SU1674121A1 |
| УСТРОЙСТВО ДЛЯ ОПРЕДЕЛЕНИЯ ПОЗИЦИОННЫХ ХАРАКТЕРИСТИК НЕПОЗИЦИОННОГО КОДА | 1991 |
|
RU2020756C1 |
| US 2011231465 A1, 22.09.2011 | |||
| US 2004267858 A1, 30.12.2004 | |||
Авторы
Даты
2015-07-20—Публикация
2014-07-22—Подача