Изобретение относится к радиотехнике, в частности к радиопеленгации, и может быть использовано в быстродействующих системах определения направлений на источники радиоизлучения, работающие на одной частоте.
Пеленгация нескольких источников радиоизлучения (ИРИ), работающих на одной частоте, имеет место в задачах управления радиочастотным спектром и обеспечения электромагнитной совместимости радиоэлектронных средств, в системах радиосвязи, а также в процессе мониторинга радиоэлектронной обстановки при многолучевом распространении радиоволн, воздействии преднамеренных и непреднамеренных помех, отражениях сигнала от различных объектов и слоев атмосферы.
Известные способы пеленгации нескольких источников радиоизлучения на одной частоте опираются на статистические методы проверки гипотез (критерий отношения правдоподобий [1 - Радзиевский В.Т., Уфаев В.А. Алгоритмы обнаружения и пеленгования совокупности частотно неразделимых радиосигналов // Радиотехника, 2005, №9, с.56-69]), на метод максимума правдоподобия [2 - Дзвонковская А.Л., Дмитриенко А.Н., Кузьмин А.В. Эффективность измерения углов прихода сигнала радиопеленгатора на основе метода максимального правдоподобия // Радиотехника и электроника, 2001, т.46, №10, с.1242-1247], на сверхразрешающие методы [3 - Мюнье Ж., Делиль Ж.Ю. Пространственный анализ в пассивных локационных системах с помощью адаптивных методов // ТИИЭР, 1987, т.75, №11, с.21-37], [4 - Manikas A., Ratnarajah Т., Lee Jinsock Evaluation of Super-resolution Array-Techniques as Applied to Coherent Sources // International Journals of Electronic, Jan. 1997, Vol.82, No.1, pp.77-105] и др. Однако задача пеленгации ИРИ, как некорректная задача, не может быть решена надежно [5 - А.А. Грешилов, А.Л. Лебедев, П.А. Плохута Многосигнальная пеленгация источников радиоизлучения на одной частоте как некорректная задача // Успехи современной радиоэлектроники, 2008, №3, с.30-46]: ни статистическими методами, достоверность результата которых определяется точностью полученных оценок параметров сигналов; ни методом наименьших квадратов (МНК) в силу нелинейности и плохой обусловленности решаемой системы уравнений; ни сверхразрешающими методами, которые дают приемлемые результаты лишь при высоких соотношениях сигнал/шум и не обеспечивают разрешение ИРИ, имеющих близкие по значениям пеленги.
В частности, известен способ пеленгации источника сигнала [6 - Патент РФ №2192651, МПК G01S 3/00, G01S 3/14. Способ пеленгования источника сигнала, войсковая часть 11135. Тынянкин С.И., Апульцына И.В., Бурцев С.Ю. Публ. - 10.11.2002 г.], включающий прием пеленгуемого сигнала элементами двух линейных эквидистантных антенных решеток, расположенных взаимно-перпендикулярно, вычисление пространственного спектра Фурье пеленгуемого сигнала, принятого элементами первой линейной эквидистантной антенной решетки и комплексно-сопряженного пространственного спектра Фурье пеленгуемого сигнала, принятого элементами второй линейной эквидистантной антенной решетки, преобразование масштабов обоих вычисленных пространственных спектров пеленгуемого сигнала по логарифмическому закону, корреляционный анализ и измерение относительного сдвига преобразованных пространственных спектров пеленгуемого сигнала и оценку угловых координат.
Недостатком способа является большая вычислительная сложность (за счет вычисления пространственных спектров Фурье пеленгуемых сигналов, корреляционного анализа и измерения относительного сдвига преобразованных пространственных спектров пеленгуемых сигналов), невозможность получения интервальных оценок пеленгов, а также невозможность получения информации об угле наклона фронта волны радиосигнала.
Известен способ пеленгации радиосигналов [7 - Патент РФ №2144200, МПК G01S 3/14. Способ пеленгации радиосигналов и многоканальный пеленгатор. Ашихмин А.В., Виноградов А.Д., Кондращенко В.Н., Рембовский A.M.. Публ. - 10.01.2000 г.], который включает прием радиосигналов антенной решеткой, состоящей из N антенных элементов, выполненных идентичными в количестве не менее трех и расположенных в плоскости пеленгования, измерение в каждом частотном поддиапазоне комплексных амплитуд пар сигналов, характеризующих фазы каждого радиосигнала, принимаемого в соответствующем частотном поддиапазоне одним из антенных элементов пары, выбранным в качестве сигнального, относительно фазы радиосигнала, принимаемом в том же частотном поддиапазоне другим из антенных элементов пары, выбранным в качестве опорного для всех используемых пар антенных элементов, формирование двухмерных угловых спектров каждого принимаемого в соответствующем частотном поддиапазоне радиосигнала по измеренным комплексным амплитудам пар сигналов для различных пар антенных элементов антенной решетки соответственно взаимному расположению этих антенных элементов в плоскости пеленгования, по которым судят об азимутах и углах места принятых радиосигналов.
Недостатком способа является большая временная длительность получения пеленгов (за счет последовательной попарной обработки сигналов, формируемых антенными элементами), низкая точность пеленгования из-за несинхронного подключения (через коммутатор) пары антенных элементов ко входам двухканального приемника, а также невозможность получения интервальных оценок результатов пеленгации.
Рассмотрение решения задач радиопеленгации с учетом их некорректности, например, в [5], [8 - Некорректные задачи цифровой обработки информации и сигналов: монография / А.А. Грешилов. - 2-е изд., доп. - М.: Университетская книга: Логос, 2009.- 360 с], [9 - Патент РФ №2382379, МПК (2006.01) G01S 5/04. Способ многосигнальной пеленгации источников радиоизлучения на одной частоте, ГОУ ВПО "МГТУ им. Н.Э. Баумана". Грешилов А.А., Плохута П.А. Публ. - 20.02.2010 г.], [10 - Патент РФ №2380719, МПК (2006.01) G01S 5/04. Способ пеленгации источников радиоизлучения на одной частоте, ГОУ ВПО "МГТУ им. Н.Э. Баумана". Грешилов А.А. Публ. - 27.01.2010 г.], позволило повысить достоверность получаемых результатов пеленгования, сократить количество необходимых при реализации сложных математических операций, а также получить интервальные оценки результатов пеленгации.
Так, в частности, известен способ пеленгации K ИРИ [10], принятый за прототип, который осуществляют следующим образом.
1. Радиосигналы источников принимают посредством антенной системы (АС), состоящей из M слабонаправленных элементов (вибраторов), расположенных линейно на расстояниях друг от друга, кратных заданной величине d, как правило, не превышающей значения половины длины волны излучения ИРИ.
2. Получают комплексные амплитуды сигналов на выходах вибраторов ym, 
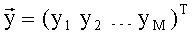

где uk - амплитуда сигнала k-го ИРИ;
φm - фаза сигнала k-го ИРИ на m-м вибраторе, зависящая от азимутального и угломестного пеленгов k-го ИРИ θk и βk соответственно;
nm - шум, имеющий место на m-м вибраторе, включающий в себя шум мирового фона и аппаратуры (с нулевым математическим ожиданием и заданным средним квадратичным отклонением (СКО): σm);
j - мнимая единица.
3. Формируют и решают систему линейных алгебраических уравнений (СЛАУ) вида

запоминают полученный вектор 
где T - знак операции транспонирования.
4. Полагая элементы вектора 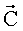

находят и запоминают его корни - экспоненциальные функции, показатели которых содержат информацию об угловом положении ИРИ:
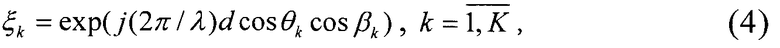
где λ - длина волны сигналов ИРИ.
5. По формуле

находят азимутальные пеленги источников радиоизлучения (если угломестные пеленги равны нулю) или (если угломестные пеленги не равны нулю) по формуле

находят величины произведений косинусов азимутальных и угломестных пеленгов, а затем по тригонометрическим формулам, приведенным, например, в [5] находят значения азимутальных и угломестных пеленгов, запоминают значения пеленгов:
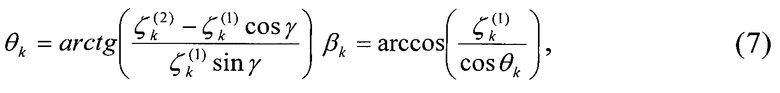
где γ - угол между плоскостью линейной АС и плоскостью, проведенной через смещенный в азимутальной плоскости (дополнительный) вибратор и базовый вибратор линейной АС (фазовый центр);
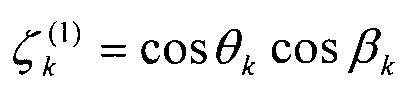 ;
;
 .
.
6. Находят диагональные элементы ковариационной матрицы DC. решения СЛАУ (2) - дисперсии элементов вектора коэффициентов полинома (3) при заданном СКО σy элементов матрицы системы (2)

на основе, например, упрощенной формулы [5], [8]:

7. Находят дисперсии пеленгов по формуле, приведенной в [5], [10] для K=2:
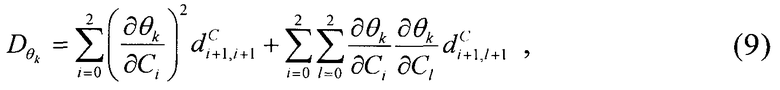
либо как скалярные функции случайных аргументов на основе дисперсий (8) и выражений (3)-(7).
8. На основе дисперсий, полученных в п.7 строят соответствующие доверительные интервалы.
9. Производят визуализацию результатов.
Указанный способ обладает следующими недостатками.
1. Ограниченность применения способа для определения точечных и интервальных оценок результатов пеленгации по рабочему сектору углового положения ИРИ и совокупности полученных реальных измерений:
а. Применение выражений вида (5) обуславливает отсутствие единственности решения, поскольку математическая функция arccos{ϑ} единственному значению (отличному от ϑ=±1) ставит в соответствие два угла в интервале (0°, 360°). Поэтому требуется, например, предложенное в [5], явное задание рабочего сектора пеленгации по каждому из углов - его ширина не должна превышать 180° (что при применении слабонаправленных элементов АС ведет к необходимости введения дополнительных операций в рассматриваемый способ пеленгации).
б. Ограниченность оценки азимутальных углов при использовании формул вида (7) диапазоном от -90° до 90°.
в. Непосредственное применение выражения (5) для оценки азимутального положения ИРИ возможно только в частных случаях получения его действительного значения, когда выполняется условие 
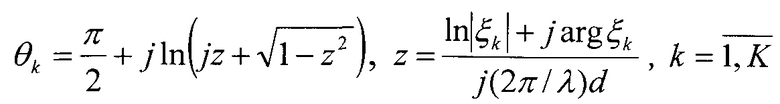
и интерпретация полученных комплекснозначных оценок азимутальных пеленгов требует дополнительного обоснования.
2. Алгоритмические и вычислительные сложности получения интервальных оценок, связанные:
- со сложностями оценки дисперсий азимутальных пеленгов ИРИ при их большом числе (основанные на выражениях вида (9), просто вычислимы только при возможности получения аналитических выражений для частных производных 


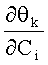


- с получением дисперсий оценок азимутальных и угломестных пеленгов как дисперсий существенно нелинейных скалярных функций от комплекснозначных сигналов ξk, 
3. Получаемые интервальные оценки пространственного углового положения ИРИ, основанные только на дисперсиях, не учитывают факта зависимости случайных величин оценок пространственного углового положения ИРИ (оценки азимутального и угломестного положения ИРИ). При формировании интервальной оценки в виде доверительной области (с заданной доверительной вероятностью) это приводит к тому, что она будет представлять собой прямоугольник, стороны которого определяются границами доверительных интервалов оценок азимутального и угломестного положения ИРИ полученных раздельно: прямоугольник, как форма доверительной области системы двух случайных величин, получается в том случае, когда они являются независимыми. Однако, поскольку каждая из случайных величин (оценки азимутального и угломестного положения ИРИ), входящих в рассматриваемую систему, является по сути функцией одного и того же векторного случайного аргумента (составленного из шумов, имеющих место на вибраторах), то в общем случае они являются зависимыми. В этом случае форма доверительной области представляет собой фигуру, вписанную в прямоугольник. Следовательно, интервальные оценки не адекватны реальным условиям. В практическом плане это приводит к увеличению области неопределенности местоопределения ИРИ. Так, например, если форма сечения пространственной фигуры, образованной точкой положения пеленгатора и областью неопределенности оценки азимутального и угломестного положения ИРИ, плоскостью его возможного положения (поверхность Земли) - эллипс, полуоси (a, b) которого расположены параллельно сторонам описывающего его прямоугольника, то площадь поиска ИРИ будет необоснованно увеличена на 
Предлагаемый способ свободен от указанных недостатков и при этом сохраняет достоинство способа-прототипа - высокую вычислительную эффективность.
Достигаемый технический результат при пеленгации радиосигналов нескольких источников радиоизлучения, работающих на одной частоте, с использованием антенных систем (АС), состоящих из слабонаправленных элементов (вибраторов):
- отсутствие ограничений на применение способа по рабочему сектору углового положения ИРИ и совокупности полученных реальных измерений;
- упрощение процесса получения интервальных оценок углового положения ИРИ;
- повышение адекватности интервальных оценок углового положения ИРИ за счет учета зависимости случайных величин оценок пространственного углового положения ИРИ,
при сохранении повышенного быстродействия (скорости) обработки сигналов.
Указанный технический результат достигают за счет:
1) определенной топологии слабонаправленных элементов АС;
2) организации процессов обработки сигналов с элементов АС для получения оценок углового положения ИРИ на основе интервального анализа и использования отображения областей в комплексных пространствах значений экспоненциальных функций, накрывающих соответствующие им полученные оценки, в пространство дискретных значений угловых координат по азимуту и углу места.
Для достижения указанного технического результа предлагается способ пеленгации источников радиоизлучения на одной частоте, при котором принимают многолучевой сигнал посредством многоэлементной антенной системы, синхронно преобразовывают ансамбль принятых сигналов, зависящих от времени и номера элемента антенной системы, в цифровые сигналы, преобразовывают цифровые сигналы в сигнал амплитудно-фазового распределения, описывающий распределение амплитуд и фаз на элементах антенной системы, формируют из амплитуд комплексных сигналов амплитудно-фазового распределения системы линейных алгебраических уравнений, первая строка которой представляет собой в левой части уравнения сумму произведений коэффициентов полинома экспоненциальных функций и амплитуд сигналов с линейно расположенных антенных элементов, взятых последовательно, начиная с амплитуды, соответствующей антенному элементу, выбранного в качестве фазового центра, число элементов суммирования равно количеству источников радиоизлучения, а правая часть представляет невыбранное еще значение амплитуды сигнала со следующего последовательно расположенного антенного элемента, при этом, каждое последующее уравнение в системе сформированных линейных алгебраических уравнений является сдвигом коэффициентов уравнения (амплитуд сигналов) определяют решения этой системы уравнений(коэффициентов полинома) и определяют корни полинома - экспоненциальных функций, аргументами каждой из которых являются азимутальные и угломестные пеленги только одного из источников радиоизлучения.
Согласно изобретению, до приема сигналов из элементов антенной системы формируют L линейных антенных подсистем (L≥2), расположенных под разными углами относительно друг друга, каждая из которых содержит Ml, 
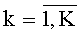
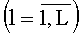
Сочетание отличительных признаков и свойств предлагаемого изобретения из литературы не известны, поэтому оно соответствует критериям новизны и изобретательского уровня
В практическом плане способ осуществляют следующим образом.
Радиосигналы источников принимают посредством антенной системы (АС), состоящей из L линейных подсистем AC - групп вибраторов (L≥2), каждая из которых содержит Ml, 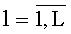
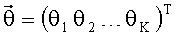
Получают комплексные амплитуды сигналов на выходах вибраторов ym, 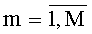
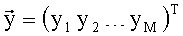
В соответствии с топологией АС из 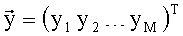



Формируют и решают L СЛАУ вида
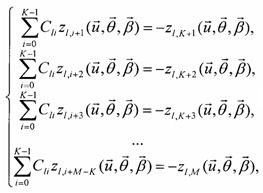 ,
,
запоминают полученные векторы коэффициентов полиномов Cl=(Cl0 Cl1 Cl2 … Cl,K-1)T, 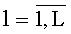
Находят корни полиномов

- оценки 


На основе интервального анализа с заданной точностью (и скоростью) на основе выражений

где (θk,βk)l - множество значений азимутальных углов и углов места, характеризующих положение k-го ИРИ, полученных на основе оценок 
7. Производят визуализацию результатов. - 7
В качестве многоэлементной АС рассматриваем линейную систему, состоящую из нескольких слабонаправленных элементов (вибраторов). В качестве фазового центра (точки, относительно которой происходит измерение фаз сигналов, приходящих на элементы антенной системы) выбираем один из вибраторов.
Необходимо определение азимутального и угломестного положения ИРИ, присутствующих в эфире:
В качестве практически оправданного допущения для предлагаемого способа (как и в способе-прототипе) сигналы, оценки параметров которых подлежат определению, рассматривают как детерминированные, подверженные аддитивной помехе.
Поскольку на результаты измерений неизбежно накладывается помеха, а также имеют место ошибки измерений, обусловленные используемой аппаратурой, необходимо получить интервальные оценки искомых параметров. Кроме того, интервальная оценка пространственного углового положения ИРИ должна учитывать зависимость случайных величин оценок пеленгов по азимуту и углу места.
Полагаем, что излучение на одной частоте осуществляет K ИРИ. Требуется по сигналу комплексного амплитудно-фазового распределения 

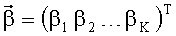

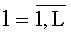
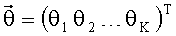
Таким образом, из элементов вектора 
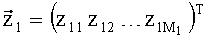



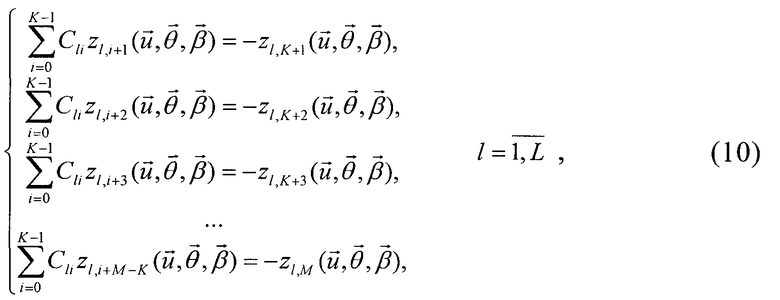
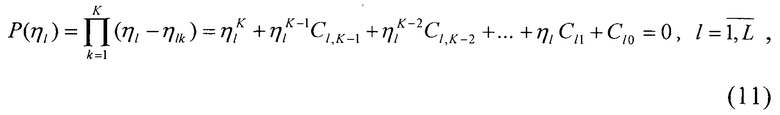

а СКО σm, 

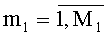
В соответствии с прототипом решение (10), (11) позволяет найти в общем случае комплекснозначные оценки 
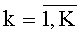



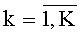



Согласно предлагаемому способу (θk,βk)инт ((θk,βk)инт - обозначение интервальной оценки углового положения k-го ИРИ) формируют на основе сравнения оценок 
Пусть Ωlk(θk,βk) - событие, заключающееся в одновременном выполнении для некоторой точки (θk,βk) пространства угловых координат θ, β следующих условий:
 ,
,
где 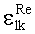



Значения 

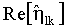



Тогда событие, заключающееся в одновременном появлении всех событий Ωlk(θk,βk), 

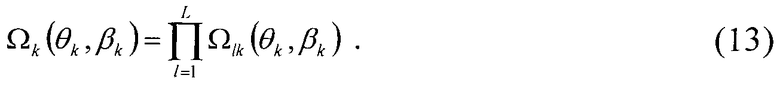
При этом каждому событию Ωlk(θk,βk) соответствует точка в пространстве угловых координат θ, β, принадлежащая интервальной оценке

где (θk,βk)l - множество значений азимутальных углов и углов места, характеризующих положение k-го ИРИ, полученных на основе оценок 
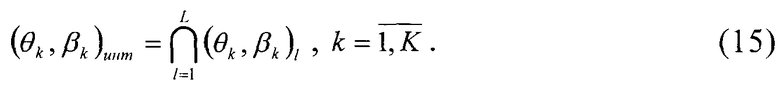
Практическую реализацию приближенного поиска (θk,βk)инт можно представить в виде процедуры формирования сети точек (θk,βk) в пространстве угловых координат θ, β, проверки их принадлежности допустимому множеству по выражениям:

с последующим определением (θk,βk)инт как оболочки множества допустимых точек.
Таким образом, интервальная оценка (θk,βk)инт углового положения k-го ИРИ есть двумерная область в пространстве азимутальных углов и углов места, являющаяся пересечением L областей, полученных для каждой l-й 

Способ и порядок построения сети рассматриваемых точек в пространстве угловых координат θ, β определяется требуемой точностью и скоростью решения задачи пеленгации. Отметим, что она, в общем случае, не зависит от числа ИРИ и, таким образом, увеличение числа ИРИ не влияет существенно на вычислительные затраты реализации интервального анализа.
Критерий определения количества сигналов, принимаемых АС, относительно способа-прототипа модифицируется следующим образом: их количество равно обобщенному (по одному из возможных правил) числу «больших» собственных чисел матриц 
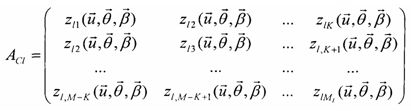 .
.
Таким образом, предлагаемый способ, так же как и прототип, обладает повышенным быстродействием за счет отсутствия математических операций, требующих больших вычислительных затрат, таких как, например, преобразование Фурье. Кроме того, он имеет следующие преимущества:
- отсутствуют ограничения по рабочему сектору углового положения ИРИ и совокупности полученных реальных измерений;
- упрощен процесс получения интервальных оценок углового положения ИРИ, в частности, формирование интервальных оценок углового положения ИРИ реализуется без необходимости, в общем случае, многократного нахождения корней полинома высокой степени, и решения задачи получения дисперсий оценок азимутальных и угломестных пеленгов как дисперсий существенно нелинейных скалярных функций от комплекснозначных сигналов, являющихся в свою очередь функциями случайных величин - оценок решений СЛАУ;
- повышена адекватность интервальных оценок углового положения ИРИ за счет учета зависимости случайных величин оценок пеленгов по азимуту и углу места.
Таким образом, предлагаемый способ имеет следующие отличительные признаки в последовательности его реализации от способа-прототипа, которые сведены в таблице 1.

(вектор АФР -

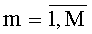
(вектор АФР -

уравнений вида (2), запоминают полученное решение - вектор

уравнений вида (10), запоминают полученные решения - Clk,









антенной подсистемы. При этом каждая из этих L областей формируется как отображение областей в комплексных пространствах значений ηlk, накрывающих соответствующие им оценки 
результатов формируют интервальные оценки в виде соответствующих доверительных интервалов, не учитывающих зависимость случайных величин - точечных оценок азимутальных и угломестных пеленгов.
точечные оценки углового положения источников радиоизлучения как середины соответствующих интервальных оценок.
Таким образом, из представленной таблицы сравнения последовательностей реализации способа-прототипа и предлагаемого способа видно, что в предлагаемом способе относительно способа прототипа изменена последовательность действий с радиосигналами по получению результатов пеленгации (в отличие от способа-прототипа сначала формируются интервальные оценки азимутальных и угломестных пеленгов, а затем их точечные аналоги) и введена новая совокупность операций по определению интервальных оценок углового положения ИРИ, приводящие к положительному эффекту: отсутствию ограничений на применение способа по рабочему сектору углового положения ИРИ и совокупности полученных реальных измерений; упрощению процесса получения интервальных оценок углового положения ИРИ; повышению адекватности интервальных оценок углового положения ИРИ за счет учета зависимости случайных величин оценок пространственного углового положения ИРИ.
Порядок выполнения интервального анализа рассмотрим на примере пеленгации двух ИРИ, работающих на частоте 1000 МГц. Характеристики углового положения ИРИ: θ1=35°, β1=20°, θ2=195°, β2=40°; амплитудные характеристики ИРИ: u1=10 мВ, u2=8 мВ.
Помеха имеет математическое ожидание, равное нулю, и СКО σm=0,1 мВ. Пеленгацию будем осуществлять посредством АС, состоящей из двух линейных подсистем по 7 вибраторов в каждой, отстоящих друг от друга на расстоянии, равном 0,15 м. Угол между подсистемами в азимутальной плоскости: γ2=90°.
В результате выполнения последовательности операций над принятыми сигналами, содержание которых определяется приемом радиосигналов источников посредством АС, получением вектора АФР, формированием и решением СЛАУ вида (10), нахождением и запоминанием корней полиномов вида (11) получим оценки экспоненциальных функций, показатели которых содержат информацию об угловом положении ИРИ.
С целью сравнения результатов зафиксируем реализацию шумового воздействия. В таблице 2 представлены значения шумов в сигналах 

Для представленной реализации шумов значения оценок экспоненциальных функций принимают вид: 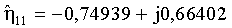
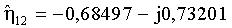
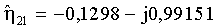
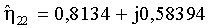
Реализация интервального анализа в пространстве угловых координат θ ∈ [0°, 360°], β ∈ [0°, 90°] с шагом в один градус для εlk=ε (

Результаты интервальной оценки при ε=0,05
Результаты интервальной оценки при ε=0,04
Результаты интервальной оценки при ε=0,03
Результаты интервальной оценки при ε=0,02
Результаты интервальной оценки при ε=0,01
Оценки, полученные на основе способа-прототипа:
θ1=35,03°, β1=18,29°, θ2=15,00°, β2=139,91°.
Из результатов сравнения видно, что предлагаемый способ устойчиво дает результат в виде интервальных оценок, середины интервалов совпадают с точным угловым положением ИРИ, а при уменьшении порога сравнения частей комплексных чисел до значения ε=0,01 интервальная оценка вырождается в точечную, совпадающую с точным угловым положением ИРИ.
Более того, результат получен в виде поля в пространстве азимутальных углов и углов места, что актуально для последующей обработки полученных оценок в системах принятия решений с нечеткой логикой.
Отметим, что при отсутствии шумов значения оценок экспоненциальных функций принимают вид: η11=-0,7507+j0,66064, η12=-0,68559-j0,72799, η21=-0,12333-j0,99237, η22=0,81195+j0,58372, т.е. абсолютные погрешности определения их действительных и мнимых частей, соответственно равны (таблица 8).
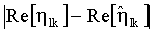

и их максимальные значения не превышают значений 0,00402 и 0,00338, соответственно, для первого и второго ИРИ. Таким образом, для получения оценки углового положения соответствующих ИРИ в соответствии с предлагаемым способом величина е должна быть не меньше этих значений.
При этом оценки, полученные на основе способа-прототипа, существенно не улучшаются: θ1=35,00°, β1=13,09°, θ2=15,00°, β2=148,41°. Результаты по предлагаемому способу для этого случая представлены в таблицах 9-13.
Результаты интервальной оценки при ε=0,05
Результаты интервальной оценки при ε=0,04
Результаты интервальной оценки при ε=0,03
Результаты интервальной оценки при ε=0,02
результата при сравнении
Результаты интервальной оценки при ε=0,01
Таким образом, предлагаемый способ обладает устойчивостью к действию рассматриваемого класса помех. Кроме того, приведенные результаты показывают, что способ-прототип даже при отсутствии помех дает существенную погрешность в определении углов места и азимутальных углов, больших 180°.
Изобретение относится к радиотехнике, в частности к радиопеленгации. Достигаемый технический результат - отсутствие ограничений на применение способа по рабочему сектору углового положения источников радиоизлучений (ИРИ) и совокупности полученных реальных измерений; упрощение процесса получения интервальных оценок углового положения ИРИ; повышение адекватности интервальных оценок углового положения ИРИ при сохранении повышенного быстродействия (скорости) обработки сигналов при пеленгации радиосигналов нескольких ИРИ, работающих на одной частоте, с использованием антенных систем (АС), состоящих из слабонаправленных элементов (вибраторов). Указанный технический результат достигается за счет формирования определенной топологии слабонаправленных элементов АС; организации процессов обработки сигналов с элементов АС для получения оценок углового положения ИРИ на основе интервального анализа и использования отображения областей в комплексных пространствах значений экспоненциальных функций, накрывающих соответствующие им полученные оценки, формируемых в пространство дискретных значений угловых координат по азимуту и углу места. 13 табл.
Способ пеленгации источников радиоизлучения на одной частоте, при котором принимают многолучевой сигнал посредством многоэлементной антенной системы, синхронно преобразовывают ансамбль принятых сигналов, зависящих от времени и номера элемента антенной системы, в цифровые сигналы, преобразовывают цифровые сигналы в сигнал амплитудно-фазового распределения, описывающий распределение амплитуд и фаз на элементах антенной системы, формируют из амплитуд комплексных сигналов амплитудно-фазового распределения системы линейных алгебраических уравнений, первая строка которой представляет собой в левой части уравнения сумму произведений коэффициентов полинома экспоненциальных функций и амплитуд сигналов с линейно расположенных антенных элементов, взятых последовательно, начиная с амплитуды, соответствующей антенному элементу, выбранного в качестве фазового центра, число элементов суммирования равно количеству источников радиоизлучения, а правая часть представляет невыбранное еще значение амплитуды сигнала со следующего последовательно расположенного антенного элемента, при этом каждое последующее уравнение в системе сформированных линейных алгебраических уравнений является сдвигом коэффициентов уравнения вправо на одну позицию по отношению к предыдущему уравнению, определяют решения этой системы уравнений и определяют корни полинома - экспоненциальные функции, аргументами каждой из которых являются азимутальные и угломестные пеленги только одного из источников радиоизлучения, отличающийся тем, что до приема сигналов из элементов антенной системы формируют L линейных антенных подсистем, L≥2, расположенных под разными углами относительно друг друга, каждая из которых содержит Ml, 
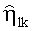
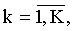
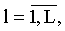
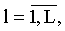
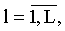
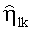
| СПОСОБ ПЕЛЕНГАЦИИ ИСТОЧНИКОВ РАДИОИЗЛУЧЕНИЯ НА ОДНОЙ ЧАСТОТЕ | 2008 |
|
RU2380719C2 |
| СПОСОБ МНОГОСИГНАЛЬНОЙ ПЕЛЕНГАЦИИ ИСТОЧНИКОВ РАДИОИЗЛУЧЕНИЯ НА ОДНОЙ ЧАСТОТЕ | 2008 |
|
RU2382379C2 |
| СПОСОБ ОБНАРУЖЕНИЯ И ПЕЛЕНГОВАНИЯ РАДИОСИГНАЛОВ | 2005 |
|
RU2289146C9 |
| СПОСОБ ПЕЛЕНГАЦИИ МНОЖЕСТВА ИСТОЧНИКОВ РАДИОИЗЛУЧЕНИЯ, ОДНОВРЕМЕННО ПОПАДАЮЩИХ В ПОЛОСУ ПРИЕМА | 2001 |
|
RU2207583C1 |
| Способ изготовления ферритовыхСЕРдЕчНиКОВ МАгНиТНыХ гОлОВОК | 1979 |
|
SU834748A1 |
| US 5361073 A, 01.11.1994 | |||
| US 4339755 A, 13.07.1982 | |||
| WO 2006114426 A1, 02.11.2006 | |||
| WO 2005073749 A1, 11.08.2005 | |||
Авторы
Даты
2015-07-20—Публикация
2014-04-02—Подача