СПОСОБ ОПРЕДЕЛЕНИЯ НАИБОЛЕЕ ВЕРОЯТНЫХ ЗНАЧЕНИЙ ПЕЛЕНГОВ ИСТОЧНИКОВ РАДИОИЗЛУЧЕНИЯ НА ОДНОЙ ЧАСТОТЕ Российский патент 2014 года по МПК G01S5/04 

Многосигнальная пеленгация источников радиоизлучения (ИРИ) имеет место в процессе мониторинга радиоэлектронной обстановки при многолучевом распространении радиоволн, воздействии преднамеренных и непреднамеренных помех, отражениях сигнала от различных объектов и слоев атмосферы. Повышение точности определения пеленгов источников ИРИ имеет принципиальное значение.

Известны способы пеленгации с повышенной разрешающей способностью [1, 2], но неизвестны работы, в которых бы при определении пеленгов ИРИ учитывались погрешности всех величин, участвующих в определении значений пеленгов.

В патенте [2] задача решается с помощью l_P - регуляризации. Этот способ требует достаточно много времени для обработки сигнала, что не позволяет его применить в оперативной обстановке, и квалифицированных операторов, т.к. в методе необходимо для каждого измерения задавать значения параметра регуляризации и показатель степени регуляризирующего функционала. Однозначных подходов для их выбора не существует.

В качестве прототипа принят способ, описанный в патенте [1]. Способ многосигнальной пеленгации источников радиоизлучения на одной частоте включает в себя прием многолучевого сигнала посредством многоэлементной антенной системы (АС), синхронное преобразование ансамбля принятых сигналов, зависящих от времени и номера элемента АС, в цифровые сигналы, преобразование цифровых сигналов в сигнал-вектор амплитудно-фазового распределения (АФР) y (u, θ, β), описывающий распределение амплитуд и фаз на элементах АС.

Способ-прототип обладает следующими недостатками. В изобретении не учитываются погрешности значений координат материальных элементов и параметров АС, а измеренные с погрешностью значения принимаются в качестве истинных. В действительности каждая координата и параметр АС имеют свою погрешность измерения и истинное значение принадлежит некоторому интервалу. Электромагнитная волна учитывает именно истинные значения. Известно, что при определении оценок параметров функции будут получены смещенные оценки параметров, если не учтены погрешности всех входящих в расчет величин (конфлюэнтный анализ) [3]. Таким образом, если не учитывать погрешности всех участвующих в расчете величин, будут получены неверные значения пеленгов и их погрешностей.

Раскрытие изобретения

Достигаемый технический результат - повышение точности пеленгации при приеме радиосигналов одного или нескольких источников радиоизлучения, работающих на одной частоте, за счет учета неопределенностей значений координат материальных элементов и параметров АС, состоящих из слабонаправленных элементов (вибраторов), а также получение интервальных оценок значений пеленгов.

В общем случае математическая модель задачи определения пеленгов имеет следующий вид:

$$A(\theta ,\beta \text{, t})u+n(t)=y(t),\text{ t}=\left\{{\text{t}}_{\text{1}};{\text{ t}}_{\text{2}};\dots {\text{; t}}_{\text{T}}\right\},\text{ (1)}$$

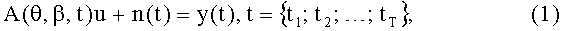
где матрица A(θ, β, t} формируется с учетом вида сигналов пеленгуемых ИРИ и пространственной конфигурации AC, n(t) - вектор аддитивной помехи с нулевым математическим ожиданием и ковариационной матрицей вида σ²I, I - единичная матрица, σ - среднеквадратическое отклонение (СКО). Система (1) - система нелинейных уравнений относительно неизвестных θ, β и u, где θ, β - векторы азимутальных и угломестных пеленгов ИРИ соответственно; u - вектор амплитуд (мощностей) сигналов, излучаемых ИРИ.

Для линейной АС с фазовым центром, расположенным на крайнем вибраторе, элементы матрицы А(θ, β, t) имеют вид

$$a_m({\theta }_k,{\beta }_k,t)=\exp \left\{j\left[2\pi f_{0}t+{\varphi }_k+(m-1)(2\pi /\lambda )d\cos {\theta }_k\cos {\beta }_k\right]\right\},\text{ (2)}$$

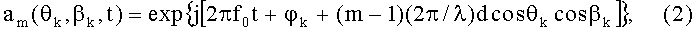
m=1,2,…,М; k=1,2, …,K,

где j - мнимая единица, 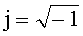$$j=\sqrt{-1}$$ ,

t - аргумент времени,

f₀ - частота сигналов, излучаемых пеленгуемыми ИРИ,

φ_k - начальная фаза k-гo сигнала,

λ - длина волны сигналов ИРИ,

d - расстояние между соседними элементами АС,

γ₁, i=1; 2;…; М - угол между линией отсчета пеленгов и линией, проведенной через центр окружности и i-й элемент АС (для круговой АС),

М - количество элементов в АС.

Выход y_m m-го элемента круговой АС имеет вид

$$y_m(u,\theta ,\beta )={\displaystyle \sum _{i=1}^k{u}_i}\exp (j2\pi f_{0}t+(2\pi R/\lambda )\cos ({\theta }_i-{\gamma }_m)\cos {\beta }_i+{\alpha }_i),\text{ (3)}$$

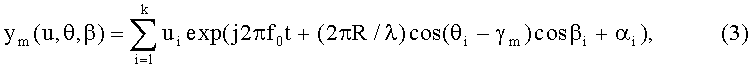
где u - вектор амплитуд (мощностей) сигналов, излучаемых ИРИ;

θ, β - векторы азимутальных и угломестных пеленгов ИРИ соответственно;

R - радиус круговой АС;

λ - длина волны сигнала, излучаемого ИРИ;

a_i - начальная фаза i-го сигнала;

γ_m - угол между линией, проведенной через центр АС и ее m-й элемент, и линией нулевого отсчета азимутальных пеленгов.

В предлагаемой заявке требуется определить для каждого одновременно поступившего на АС сигнала амплитуду (мощность) u_i, азимутальный пеленг θ_i и угломестный пеленг β_i. При этом надо учесть не только погрешность сигнала выхода y_m m-го элемента АС, но и погрешности: f₀ - частоты сигналов, излучаемых пеленгуемыми ИРИ, φ_k - начальной фазы каждого сигнала, R - радиуса окружности, вдоль которой расположены элементы круговой АС, γ_i, i=1; 2;…; М - углов между линией отсчета пеленгов и линией, проведенной через центр окружности и i-й элемент круговой АС, λ - длины волны сигналов ИРИ, d - расстояния между соседними элементами линейной АС. Все они дают свой вклад в погрешности определения пеленгов. При необходимости получения точности пеленга, равной долям градуса, необходим учет всех источников погрешности.

Способ многосигнальной пеленгации источников радиоизлучения на одной частоте включает в себя прием многолучевого сигнала посредством многоэлементной АС, синхронное преобразование ансамбля принятых сигналов, зависящих от времени и номера элемента АС, в цифровые сигналы, преобразование цифровых сигналов в сигнал-вектор АФР у, описывающий распределение амплитуд и фаз на элементах АС, вычисление сигнала фазирующей функции и определение пеленгов сигналов при заданных с погрешностью параметрах АС. При этом получение истинных значений пеленгов осуществляется посредством идентификации наиболее вероятных оценок параметров АС, участвующих в расчете с помощью итерационного процесса конфлюэнтного анализа сигналов, который позволяет учесть неопределенности всех величин, участвующих в расчете, для уточнения значений элементов АС и сигнала АФР, входящих в определение пеленгов. После завершения итерационного процесса определяют интервальную оценку найденных пеленгов на основе вычисленной корреляционной (ковариационной) матрицы ошибок найденных значений пеленгов - для определения погрешностей полученных значений пеленгов как элементов обратной матрицы вторых производных функционала (12) при найденных значениях пеленгов.

Перечень фигур

Фиг.1 - схема итерационного способа уточнения оценок пеленгов ИРИ.

Осуществление изобретения

Рассмотрим конфлюэнтный анализ сигналов, который позволит учесть неопределенности всех величин, участвующих в расчете.

Наиболее часто применяется пассивная схема конфлюэнтного анализа при обработке экспериментальных сигналов (фиг.1). Для упрощения формул будем считать, что требуется найти интервальную оценку параметра θ функции выхода y_m m-го элемента AC η=f(ξ,θ}, когда точные (истинные) значения функции η и аргумента ξ, определить нельзя, а вместо них измеряются случайные величины y и х, связанные с η и ξ, следующим образом:

$$x_i={\xi }_i+{\delta }_i;y_i={\eta }_i+{\epsilon }_i,i=\overline{\mathrm{1,}n},\text{ (4)}$$

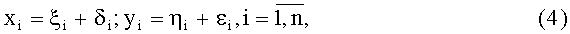
где δ_i и ε_i - соответственно ошибки значений переменных и функции, т.е. случайные величины.

Для рассматриваемого случая: х - измеренные значения параметров АС, входящие в расчет пеленгов, ξ, - неизвестные истинные значения параметров АС, входящие в расчет пеленгов (фиг.1), y - измеренный выход y_m m-го элемента AC, η - неизвестное точное значение выхода y_m m-го элемента АС.

Пусть имеем ряд экспериментальных значений Х={x_i}∈Х и соответствующий им ряд значений функции Y={y_i}∈Y, i=1, 2, …, n; n≥m, где m - число оцениваемых параметров θ. Будем считать, что переменные x_i и y_i не являются детерминированными, но являются выборками из генеральных совокупностей Х и Y с известными функциями распределений. Переменные х_i=ξ_i+δ_i и y_i=η_i+ε_i могут быть статистически зависимы или независимы, коррелированными или не коррелированными.

В основном будем иметь дело с выборками из n независимых наблюдений из одного и того же распределения. Пусть f₁(x_i/θ) и f₂(y_i/θ) - соответственно плотности распределения случайных величин x_i и y_i, если x_i и y_i непрерывны, либо соответственно вероятности значений x_i и y_i, если распределения x_i и y_i дискретны; y_i, x_i и соответственно распределения f₁(x_i/θ) и f₂(y_i/θ) могут быть как одномерными, так и многомерными.

Найдем выражение для совместной плотности вероятности экспериментальных данных при условии, что ξ_i и η_i связаны функциональной зависимостью, но их погрешности δ_i и ε_i являются независимьми при переходе от одной точки (x_i, y_i) к другой. Тогда совместная плотность вероятности получить одновременно значения x_i и y_i будет определяться формулой:

P_i=f₁(x_i/θ)f₂(y_i/θ).

А совместная плотность вероятности получить n статистически независимых точек (x_i, y_i) будет определяться формулой:

$$L={\displaystyle \prod _{i=1}^n{P}_i}={\displaystyle \prod _{i=1}^n{f}_1(x_i/\theta )f_2(y_i/\theta )}$$ .

Аналогично можно получить формулы совместной плотности вероятности для зависимых или коррелированных экспериментальных точек.

В выражения для совместной плотности вероятности входят математические ожидания экспериментальных данных, экспериментальные значения и оцениваемые параметры, так как f₁(x_i/θ) - функция математического ожидания ξ_i, экспериментальных значений x_i и параметров θ; f₂(y_i/θ) - функция математического ожидания η_i, экспериментальных значений y_i, x_i и параметров θ. Кроме того, нам известно функциональное соотношение

η=f(ξ_i,θ),

которое порождает структурные соотношения между наблюдаемыми случайными величинами x_i и y_i:

y_i=ψ(x_i,θ, δ_i, ε_i) или y_i=f(x_i-δ_i, θ)+ε_i

при аддитивных помехах из формулы (4).

Таким образом, в поставленной задаче следует отметить две проблемы: первая - каким образом ввести в рассмотрение погрешность аргумента х, погрешность всех участвующих в расчете величин у; вторая состоит в том, что функционалы, которые требуется минимизировать при отыскании оценок пеленгов, имеют сложную форму, и соответствующие системы уравнений для определения этих же оценок нелинейны.

Наиболее часто в практике встречается нормальное распределение Гаусса. Найдем вид функционала, из которого затем могут быть получены оценки искомых параметров (пеленгов и наиболее вероятных значений всех параметров, участвующих в расчете).

Пусть экспериментальные значения x_i, y_i - случайные величины, каждая из которых имеет функцию плотности вероятности, описываемую функцией Гаусса соответственно с математическими ожиданиями ξ_i и η_i, дисперсиями σ²(x_i) и σ²(y_i) и коэффициентом корреляции p(x_i, y_i)=p_i. Тогда плотность вероятности получить точку с координатами (x_i, y_i) описывается формулой:

$$P_i=\frac{1}{2\sigma (x_i)\sigma (y_i)\sqrt{1-p_i^2}}\exp \left[\frac{u_{1i}^2-2p_i{u}_{1i}{u}_{2i}+u_{2i}^2}{2(1-p_i^2)}\right]$$ ,

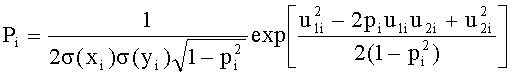
где 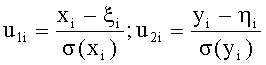$$u_{1i}=\frac{x_i-{\xi }_i}{\sigma (x_i)};u_{2i}=\frac{y_i-{\eta }_i}{\sigma (y_i)}$$ .

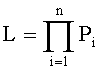
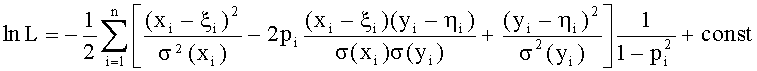
Совместная плотность вероятности получить n независимых таких точек $$L={\displaystyle \prod _{i=1}^n{P}_i}$$ описывается формулой с логарифмированием:

$$\ln L=-\frac{1}{2}{\displaystyle \sum _{i=1}^n\left[\frac{{(x_i-{\xi }_i)}^2}{{\sigma }^{{}_2}(x_i)}-2p_i\frac{(x_i-{\xi }_i)(y_i-{\eta }_i)}{\sigma (x_i)\sigma (y_i)}+\frac{{(y_i-{\eta }_i)}^2}{{\sigma }^2(y_i)}\right]}\frac{1}{1-p_i^2}+const$$ .

Оценки искомых параметров θ находят из условия минимума функционала

$$F=\frac{1}{2}{\displaystyle \sum _{i=1}^n\frac{1}{1-p_i^2}\left[\frac{{(x_i-{\xi }_i)}^2}{{\sigma }^{{}_2}(x_i)}-2p_i\frac{(x_i-{\xi }_i)(y_i-{\eta }_i)}{\sigma (x_i)\sigma (y_i)}+\frac{{(y_i-{\eta }_i)}^2}{{\sigma }^2(y_i)}\right].}\text{ (5)}$$

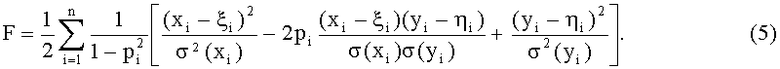
Для важного в практике частного случая, когда погрешности δ_i и ε_i некоррелированны, выражение (5) примет вид

$$F_1=\frac{1}{2}{\displaystyle \sum _{i=1}^n\left[\frac{{(x_i-{\xi }_i)}^2}{{\sigma }^{{}_2}(x_i)}+\frac{{(y_i-{\eta }_i)}^2}{{\sigma }^2(y_i)}\right]}\text{. (6)}$$

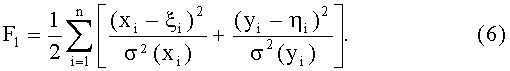
Аналогичны подобные функционалы для любого другого закона распределения. Теперь рассмотрим задачу отыскания минимума функционалов типа (5)-(6) по параметрам вектора θ (прим.: обозначение θ повторяет сходное по написанию обозначение Θ (оба этих обозначения считаем одинаковыми)).

Нам неизвестны истинные значения абсцисс экспериментальных точек, а известны только их доверительные области. Перед тем как приступить к определению точки минимума функционалов (5), (6) по θ, требуется каким-то образом определить ξ_i и только затем, подставив выражения для ξ_i и η_i в функционал, приступать к отысканию минимума получившейся функции нескольких переменных.

Искомые значения ξ_i определяются из условий:

$$\frac{\partial F}{\partial {\xi }_i}=\mathrm{0,}i=\overline{\mathrm{1,}n};\text{ (7)}$$

а оценки параметров в

$$\frac{\partial F}{\partial \eta }\frac{\partial \eta }{\partial {\Theta }_j}=\mathrm{0,}j=\overline{\mathrm{1,}m}.\text{ (8)}$$

Получаемые оценки ξ_i должны принадлежать области неопределенности интервальных оценок D_i измеренных значений x_i, т.е. ξ_i∈D_i. В условиях, когда известен закон распределения погрешности измерения x_i, это условие может быть выражено в более конкретной форме: при нормальном законе распределения случайной величины x_i можно взять 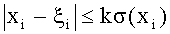$$\left|x_i-{\xi }_i\right|\le k\sigma (x_i)$$ , где коэффициент k(=1,2,3) определяется выбранным уровнем доверия.

Таким образом, например, задача минимизации функционала (6) при условии (7) эквивалентна решению системы уравнений

$${\displaystyle \sum _{i=1}^n\frac{(y_i-{\eta }_i)}{{\sigma }^2(y_i)}\frac{\partial f}{\partial {\Theta }_j}=\mathrm{0,}j=\overline{\mathrm{1,}m};i=\overline{\mathrm{1,}n};n\ge m,\text{ (9)}}$$

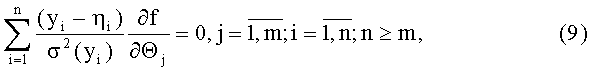
при условии

$$\frac{x_i-{\xi }_i}{{\sigma }^2(x_i)}+\frac{y_i-{\eta }_i}{{\sigma }^2(y_i)}\frac{\partial f}{\partial {\xi }_i}=0.\text{ (10)}$$

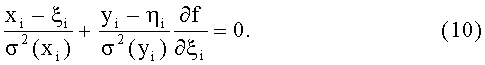
Эти два уравнения формируют итерационный процесс. Выражение (9) позволяет нам определить значения пеленгов при известных ξ_i∈D_i; уравнение (10) позволяет выбрать наиболее вероятные значения ξ_i∈D_i

Таким образом, переходя к практике, сначала любым известным способом решают задачу нахождения оценок θ при фиксированном ξ=x (как обычно все и поступают и считают, что задача решена), затем определяют оценки ξ, по формуле (10) и возвращаются к уравнениям (9) до тех пор, пока не будет получено в итерационном процессе наиболее вероятное решение.

Рассмотрим применение изложенного подхода к задаче определения оценок параметров для случая, когда на одной частоте поступили несколько сигналов, т.е.

$$\eta \text{=f( }{\xi }_{\text{1}}\text{,}\dots \text{,}{\xi }_{\text{m}}\text{,}{\theta }_{\text{1}}\text{,}\dots \text{,}{\theta }_{\text{n}}\text{) (11)}$$

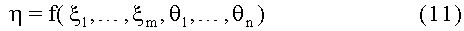
с погрешностями в системе уравнений (9, 10) и в правой части при условии, что все ошибки измерений - суть независимые нормально распределенные случайные величины с нулевыми средними (это справедливо для ошибок измерений) и известными дисперсиями σ²(x_ij) и σ²(y_i). В этом случае функционал (6) будет иметь вид

$$F_1=\frac{1}{2}{\displaystyle \sum _{j=1}^m\left\{{\displaystyle \sum _{i=1}^n\frac{{(x_{ij}-{\xi }_{ij})}^2}{{\sigma }^{{}_2}(x_{ij})}+\frac{{(y_j-f({\xi }_j,\Theta ))}^2}{{\sigma }^2(y_j)}}\right\},}\text{. (12)}$$

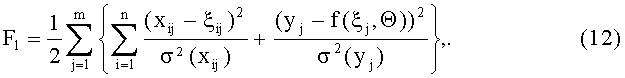
а ограничение ξ_i∈D_i можно записать следующим образом:

$$\left|x_{ij}-{\xi }_{ij}\right|\le 3\sigma (x_{ij})\text{ (13)}$$

В рассматриваемом случае ошибки измерений считаются статистически независимыми для упрощения вида функционала (12).

Элементы ковариационной матрицы ошибок (матрицы рассеивания) для интервальных оценок искомых параметров подсчитываются как элементы матрицы, обратной матрице М:

$$M_{ij}={-\frac{{\partial }^{2}F}{\partial {\Theta }_i\partial {\Theta }_j}|}_{\theta =\widehat{\theta }}$$ ,

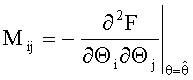
где 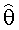$$\stackrel{⌢}{\theta }$$ - полученные оценки параметров θ (прим.: θ одинаково, что и Θ).

Таким образом, в результате производят следующие шаги согласно схеме итерационного способа уточнения оценок пеленгов ИРИ на фиг.1.

1. Находят значения пеленгов любым известным пользователю способом при заданных значениях характеристик АС (используют измеренные значения, т.е. с погрешностями).

2. При найденных значениях пеленгов вычисляют наиболее вероятные значения параметров AC ξ по формулам (10).

3. Подставляют найденные значения ξ в (9) и находят уточненные значения пеленгов как в п.1/

4. Пункты 2 и 3 повторяют до тех пор, пока итерационный процесс не сойдется: пока не будут удовлетворены условия

$${\displaystyle \sum _{i=1}^n\left|\frac{{\theta }_i^v-{\theta }_i^{v+1}}{{\theta }_i^v}\right|\le E_1;}{\displaystyle \sum _{i=1}^n\left|\frac{{\xi }_i^v-{\xi }_i^{v+1}}{{\xi }_i^v}\right|\le E_2}$$

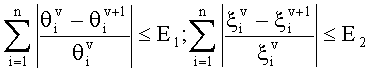
или не будет исчерпан лимит итераций. Здесь v - номер итерации, а E₁, Е₂ - точности, задаваемые пользователем.

5. После завершения итерационного процесса вычисляется корреляционная матрица ошибок искомых значений пеленгов как обратная матрица вторых производных функционала (12) при найденных значениях пеленгов.

Полученные новые значения ξ_ij, рассчитанные в п.2, должны удовлетворять условию (13). Если это не так, то те ξ_ij, которые выходят за указанные границы, заменяются на значения ближайшей граничной точки; после пересчета ξ, те наборы ξ_ij, при которых произошло увеличение соответствующих слагаемых функционала

$$F_j={\displaystyle \sum _{i=1}^n\frac{{(x_{ij}-{\xi }_{ij})}^2}{{\sigma }^{{}_2}(x_{ij})}+\frac{[y_j-f({\xi }_j,\Theta )]}{{\sigma }^2(y_j)}}$$

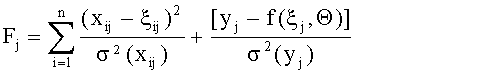
по сравнению с предыдущей итерацией, заменяются значениями с предыдущего шага.

Изложенный способ обладает высоким быстродействием, т.к. не содержит в себе операций, требующих больших вычислительных затрат.

Пример реализации способа

Продемонстрируем процедуру определения истинного значения угла γ в формуле (3) для круговой АС; измеренное значение угла обозначим 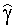$$\stackrel{⌢}{\gamma }$$ . Значения средних квадратических отклонений положим для простоты равными единице.

Функционал (6) имеет вид

$$\begin{array}{l}\frac{1}{2}{\displaystyle \sum _{m=1}^k[{(u\exp (j[2\pi f_{0}t+(2\pi R/\lambda )\cos (\theta -{\gamma }_m)\cos \beta +\alpha ])-{\stackrel{⌢}{\gamma }}_m(u,\theta ,\beta ))}^2+}\\ +{(}^{{\gamma }_m}]\to \min \end{array}$$

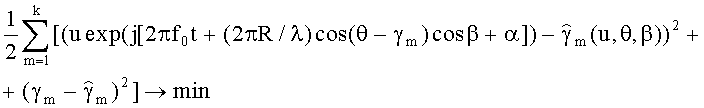
выражение (7; 10)-

$$\begin{array}{l}(u\exp (j[2\pi f_{0}t+(2\pi R/\lambda )\cos (\theta -{\gamma }_m)\cos \beta +\alpha ])-\\ -{\stackrel{⌢}{\gamma }}_m(u,\theta ,\beta ))u\exp (j[2\pi f_{0}t+(2\pi R/\lambda )\cos (\theta -{\gamma }_m)\cos \beta +\alpha ])\\ j\frac{2\pi R}{\lambda }\sin (\theta -{\gamma }_m)\cos \beta +{\gamma }_m-{\stackrel{⌢}{\gamma }}_m=0\end{array}$$

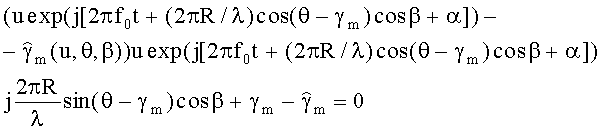
Здесь неизвестно только γ_m, т.е. имеем выражение вида

$$\begin{array}{l}(u\exp (j[C_1+C_2\cos (\theta -{\gamma }_m)+\alpha ])-\\ -{\stackrel{⌢}{\gamma }}_{m}u\exp (j[C_3+C_4\cos (\theta -{\gamma }_m)+\alpha ])\\ j{C}_5\sin (\theta -{\gamma }_m)+{\gamma }_m-{\stackrel{⌢}{\gamma }}_m=0\end{array}$$ ,

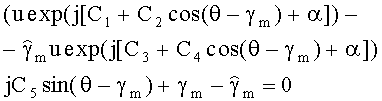
из которого надо определить оценку γ_m. Причем 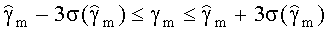$${\stackrel{⌢}{\gamma }}_m-3\sigma ({\stackrel{⌢}{\gamma }}_m)\le {\gamma }_m\le {\stackrel{⌢}{\gamma }}_m+3\sigma ({\stackrel{⌢}{\gamma }}_m)$$ . Константы С - известны.

Чтобы определить оценку γ_m надо раздельно приравнять нулю действительные и мнимые части данного уравнения. Истинное значение γ_m достаточно точно можно определить путем деления отрезка 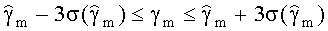$${\stackrel{⌢}{\gamma }}_m-3\sigma ({\stackrel{⌢}{\gamma }}_m)\le {\gamma }_m\le {\stackrel{⌢}{\gamma }}_m+3\sigma ({\stackrel{⌢}{\gamma }}_m)$$ пополам.

Приведем результаты модельного расчета пеленга на компьютере с процессором с тактовой частотой 2 ГГц. Рассматривалась пеленгация двух ИРИ, работающих на частоте 20 МГц. Азимутальные пеленги 30 и 50 градусов, угломестные пеленги не вводились. Учитывалось влияние только погрешностей координат вибраторов. Без учета погрешностей координат вибраторов получены азимутальные пеленги 28,30 и 51,89 градусов, с учетом погрешностей координат вибраторов получены азимутальные пеленги 30 и 50 градусов. При этом устранено смещение (это не стохастическая погрешность).

Источники информации

1. Патент RU 23 80719, опубликовано 27.01.2010, МПК G01S 5/04.

2. Патент RU 2382379, опубликовано 20.02.2010, МПК G01S 5/04.

3. Грешилов А.А. Математические методы принятия решений: Учебное пособие для вузов. - М.: Изд-во МГТУ им. Н.Э.Баумана, 2006. - 584 с.

Изобретение относится к радиопеленгации. Достигаемый технический результат - повышение точности пеленгации при приеме радиосигналов одного или нескольких источников радиоизлучения, работающих на одной частоте, а также получение интервальных оценок значений пеленгов. Указанный результат достигается за счет того, что способ включает в себя прием многолучевого сигнала посредством многоэлементной антенной системы (АС), синхронное преобразование ансамбля принятых сигналов, зависящих от времени и номера элемента АС, в цифровые сигналы, преобразование цифровых сигналов в сигнал-вектор амплитудно-фазового распределения (АФР), описывающий распределение амплитуд и фаз на элементах АС, вычисление сигнала фазирующей функции и определение пеленгов сигналов при заданных с погрешностью параметрах АС. При этом получение истинных значений пеленгов осуществляют посредством идентификации наиболее вероятных оценок параметров АС, участвующих в расчете с помощью итерационного процесса конфлюэнтного анализа сигналов, который позволяет учесть неопределенности всех величин, участвующих в расчете, для уточнения значений элементов АС и сигнала АФР, входящих в определение пеленгов. После окончания итерационного процесса определяют интервальную оценку найденных пеленгов на основе вычисленной корреляционной матрицы ошибок найденных значений пеленгов. 1 ил.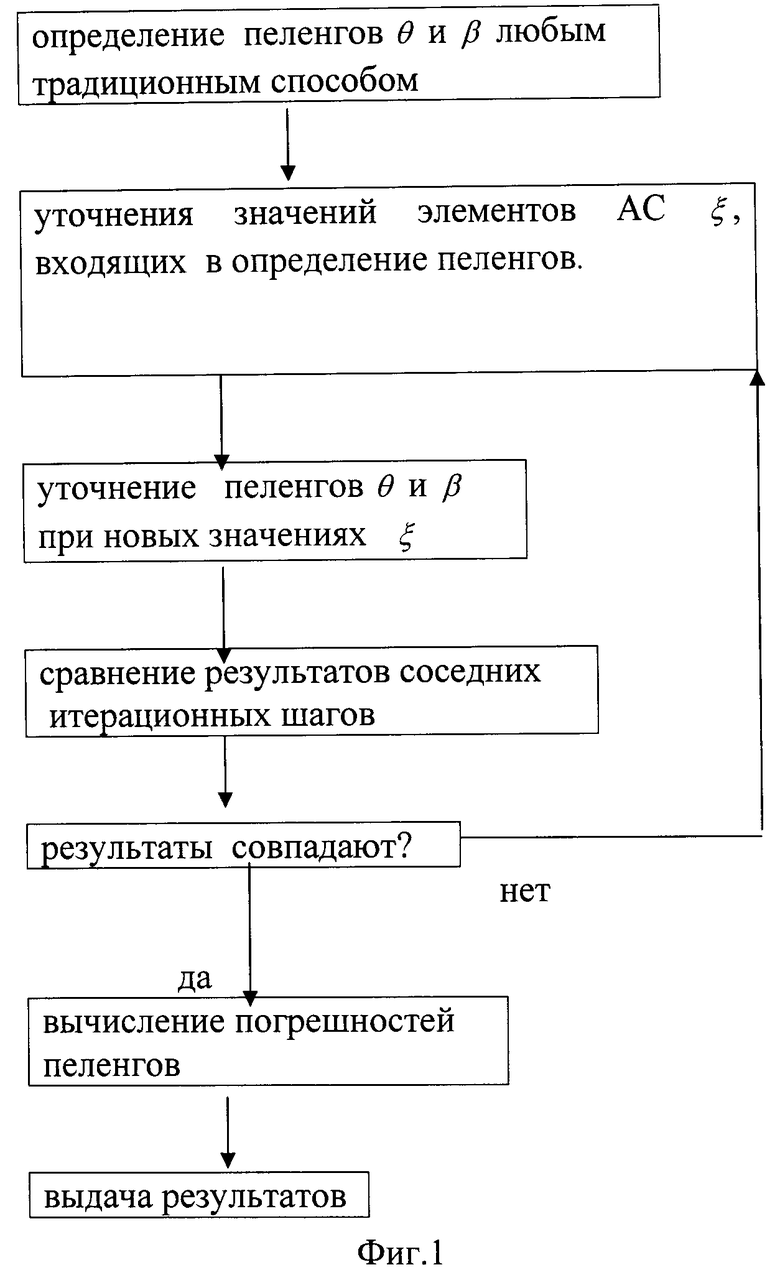

Способ многосигнальной пеленгации источников радиоизлучения на одной частоте, включающий в себя прием многолучевого сигнала посредством многоэлементной антенной системы (АС), синхронное преобразование ансамбля принятых сигналов, зависящих от времени и номера элемента АС, в цифровые сигналы, преобразование цифровых сигналов в сигнал-вектор амплитудно-фазового распределения (АФР), описывающий распределение амплитуд и фаз на элементах АС, вычисление сигнала фазирующей функции и определение пеленгов сигналов, отличающийся тем, что при заданных с погрешностью параметрах антенной системы получение значений пеленгов с минимальной погрешностью осуществляют посредством определения наиболее вероятных оценок параметров АС, участвующих в определении пеленгов, с помощью итерационного процесса, в котором одновременно уточняются значения параметров элементов АС, входящих в определение пеленгов, в пределах их неопределенности и пеленгов в сравнении с сигналом АФР, путем нахождения значения пеленгов на первом шаге любым способом, используемым пеленгатором, при заданных значениях характеристик АС, при этом используют измеренные значения сигналов с погрешностями, далее найденные пеленги поступают в блок уточнения значений параметров элементов АС, необходимых для определения пеленгов, вычисляют при известных на тот момент значениях пеленгов значения параметров элементов АС по формуле
$$\frac{x_i-{\xi }_i}{{\sigma }^2(x_i)}+\frac{y_i-{\eta }_i}{{\sigma }^2(y_i)}\frac{\partial f}{\partial {\xi }_i}=\mathrm{0,}$$
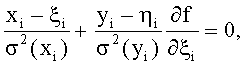
где x_i - измеренные значения и ξ_i - истинные неизвестные значения параметров АС;
y_i - измеренные значения и η_i - истинные неизвестные значения сигнала;
σ²(x_i); σ²(y_i) - дисперсии измеренных значений x_i и y_i;
$$\frac{\partial f}{\partial {\xi }_i}$$ - скорость изменения разности (y_i-η_i) за счет изменения ξ_i,
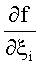
уточненные значения параметров элементов АС поступают в пеленгатор для уточнения угломестных и азимутальных пеленгов на последующем шаге итерации по формуле
$${\displaystyle \sum _{i=1}^n\frac{(y_i-{\eta }_i)}{{\sigma }^2(y_i)}\frac{\partial f}{\partial {\Theta }_j}=\mathrm{0,}j=\overline{\mathrm{1,}m};i=\overline{\mathrm{1,}n};n\ge m,}$$
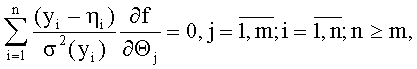
где $$\frac{\partial f}{\partial {\Theta }_j}$$ - скорость изменения разности (y_i-η_i) за счет изменения θ_j,
значения сигналов пеленгов и параметров элементов АС подают в блок сравнения результатов, итерационный процесс продолжают до заданных малых ошибок сходимости значений сигналов пеленгов и параметров элементов АС на соседних шагах итераций.