Изобретение относиться к вычислительной технике и, в частности к непозиционным компьютерным системам, и предназначено для обеспечения требуемой точности при вычислении с использованием модулярного кода
Одним из основных достоинств полиномиального модулярного кода (ПМК) является параллельная обработка данных по основаниям ПМК p1(z), p2(z), …, pn(z), где pi(z) - неприводимый полином поля GF(2). Данное свойство полиномиального модулярного кода позволяет не только повысить скорость обработки данных за счет использования малоразрядных остатков, но и обеспечить построение отказоустойчивых вычислительных систем.
Так как информация обрабатывается в параллельно функционирующих вычислительных каналах по числу оснований ПМК, то при возникновении отказов несправный канал можно отключить. Это приводит к деградации структуры вычислительного устройства и уменьшению точности вычисления. Поэтому для обеспечения требуемой точности осуществляется процедура расширения оснований.
При расширении набора оснований полиномиального модулярного кода на основании pn+1(z) диапазон представления чисел

Расширяется до значения

Задача расширения системы оснований заключается в нахождении остатка αn+1(z) по модулю pn+1(z), удовлетворяющего
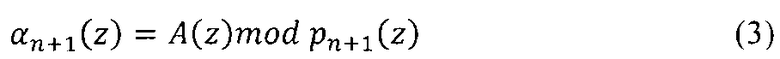
где A(z)=(α1(z), α2(z), …, αn(z)) - результат вычислений в модулярном коде, представленный в системе оснований p1(z), p2(z), …, pn(z)
В работе [1] (Червяков Н.И., Сахнюк П.А., Шапошников А.В., Макоха А.Н. Нейрокомпьютеры в остаточных классах. Кн.11. - М.: Радиотехника, 2003, 272 с. - С.138-139) представлен алгоритм реализации процедуры расширения системы оснований.
В основу данного алгоритма положена китайская теорема об остатках (КТО), с помощью которой осуществляется перевод из модулярного кода в позиционный код
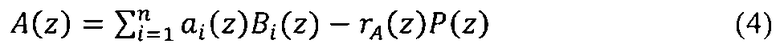
где Bi - ортогональный базис i-го основания; rA(z) - ранг A(z) в модулярном коде.
Тогда для вычисления остатка αn+1(z) справедливо выражение ([1 с.138])
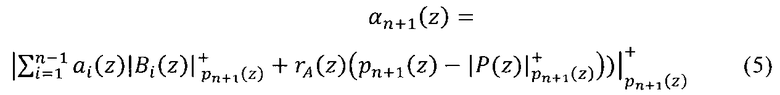
Таким образом, для расширения системы оснований необходимо:
1. Вычислить значение ранга rA(z)

где  ; mi(z) - вес ортогонального базиса;
; mi(z) - вес ортогонального базиса;

2. Найти остаток αn+1(z) по формуле (5).
Основным недостатком представленного алгоритма расширения оснований являются значительные аппаратные затраты.
Целью изобретения является уменьшение аппаратных затрат на вычисление остатка αn+1(z). Цель достигается за счет применения нового алгоритма расширения системы оснований.
Техническим результатом, достигнутым при осуществлении заявленного изобретения, является снижение аппаратурных затрат на расширение системы основания.
Рассмотрим алгоритм перевода из полиномиального модулярного кода в позиционный код согласно китайской теореме об остатках (КТО), имеем
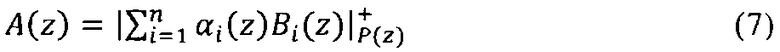
где 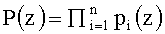
Воспользуемся определением ортогональных базисов Bi(z), тогда выражение (7) можно представить в виде
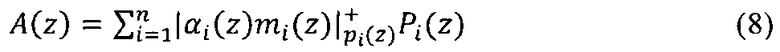
где  ; mi(z) - вес ортогонального базиса.
; mi(z) - вес ортогонального базиса.
Умножение остатка αi(z) на вес ортогонального базиса mi(z) по модулю pi(z) с учетом, что суммирование в ПКМ выполняется по модулю два, позволяют отказаться от вычисления ранга rA(z) при использовании китайской теоремы об остатках при переводе к позиционному коду.
Тогда для вычисления нового остатка αn+1(z) по основанию pn+1(z) воспользуемся следующим выражением:
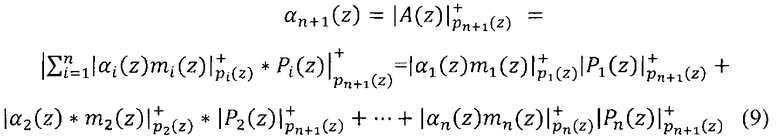
Пример. Пусть задана упорядоченная система оснований p1(z)=z+1, p2(z)=z2+z+1, p3(z)=z4+z3+z2+z+1.
В этом случае диапазон составляет

Вычислим значения Pi(z) и mi(z). Имеем
P1(z)=p2(z)*p3(z)=(z2+z+1)*(z4+z3+z2+z+1)=z6+z4+z3+z2+1
P2(z)=p1(z)*p3(z)=(z+1)*(z4+z3+z2+z+1)=z5+1
P3(z)=p1(z)*p2(z)=(z+1)*(z2+z+1)=z3+1
Вычислим значение веса ортогонального базиса mi(z) из условия

Тогда имеем
m1(z)=1;
m2(z)=z+1;
m3(z)=z2+z+1.
Следовательно, ортогональные базисы такой системы оснований равны
B1(z)=m1(z)*P1(z)=z6+z4+z3+z2+1;
B2(z)=m2(z)*P2(z)=z6+z5+z+1;
B3(z)=m3(z)*P3(z)=z5+z4+z3+z2+z+1.
Пусть задан полином A(z)=z6. Данный полином в модулярном коде представляется A(z)=(1, 1, z).
В качестве основания расширения выбираем
pn+1(z)=p4(z)=z4+z+1
Вычислим значения Pi(z)modp4(z)
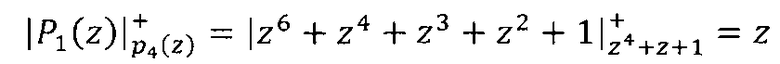
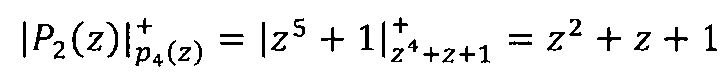

Определим произведение 



Подставим полученные значения в выражение (9)
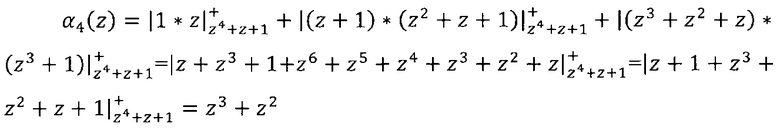
Определим остаток

Структура устройства расширения оснований модулярного кода представлена на фиг.1.
Устройство содержит вход устройства 1, первый блок умножителей 2, который содержит n умножителей по модулю pi(z), где i=1, 2, …, n, первый блок памяти 3, для хранения ортогональных весов mi(z); второй блок умножителей 4, который содержит n умножителей по модулю pn+1(z), второй блок памяти 5 для хранения 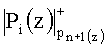
Причем вход устройства 1 подключен к первому входу каждого из умножителей pi(z), i=1, …, n, (обозначение диапазона) первого блока умножителей 2, вторые входы умножителей этого блока подключены к выходу первого блока памяти 3. Выход умножителя 2.i, выполняющего операцию умножения по модулю pi(z) первого блока умножителей 2, подключен к первому входу умножителя 4.i, выполняющего операцию умножения по модулю pn+1(z), второго блока умножителей 4. Второй вход умножителя 4.i второго блока умножителей 4 подключен к входу второго блока памяти 5. Выход умножителя 4.i подается на вход сумматора 6 по модулю 2, выход которого является выходом устройства 7.
Устройство работает следующим образом. На вход устройства 1 поступает модулярный код (α1(z), α2(z), …, αn(z)). Остаток αi(z) подается на вход умножителя 2.i первого блока умножителей 2. На второй вход умножителя 2.i подается вес ортогонального базиса mi(z) с выхода первого блока памяти 3. С выхода умножителя 2.i первого блока 2 умножителей снимаются значения 
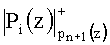

Вычисленные значения произведения подаются на входы сумматора 6 по модулю 2. На входе сумматора 6 по модулю два появляется значение остатка αn+1(z) в расширенной системе оснований. Вычисленное значение остатка αn+1(z)поступает на выход устройства 7.
| название | год | авторы | номер документа |
|---|---|---|---|
| Устройство коррекции ошибок в модулярном коде на основе расширения системы оснований | 2017 |
|
RU2652446C1 |
| УСТРОЙСТВО ДЛЯ ПРЕОБРАЗОВАНИЯ ИЗ ПОЛИНОМИАЛЬНОЙ СИСТЕМЫ КЛАССОВ ВЫЧЕТОВ В ПОЗИЦИОННЫЙ КОД С ПЕРЕСЧЕТОМ ОРТОГОНАЛЬНЫХ БАЗИСОВ | 2005 |
|
RU2298873C1 |
| УСТРОЙСТВО ДЛЯ ПРЕОБРАЗОВАНИЯ ИЗ ПОЛИНОМИАЛЬНОЙ СИСТЕМЫ КЛАССОВ ВЫЧЕТОВ В ПОЗИЦИОННЫЙ КОД | 2008 |
|
RU2409840C2 |
| УСТРОЙСТВО ДЛЯ ПРЕОБРАЗОВАНИЯ ИЗ ПОЛИНОМИАЛЬНОЙ СИСТЕМЫ КЛАССОВ ВЫЧЕТОВ В ПОЗИЦИОННЫЙ КОД | 2013 |
|
RU2513915C1 |
| УСТРОЙСТВО ОБНАРУЖЕНИЯ И КОРРЕКЦИИ ОШИБОК В КОДАХ ПОЛИНОМИАЛЬНОЙ СИСТЕМЫ КЛАССОВ ВЫЧЕТОВ НА ОСНОВЕ НУЛЕВИЗАЦИИ | 2005 |
|
RU2300801C2 |
| УСТРОЙСТВО ДЛЯ ВЫЧИСЛЕНИЯ СУММ ПАРНЫХ ПРОИЗВЕДЕНИЙ В ПОЛИНОМИАЛЬНОЙ СИСТЕМЕ КЛАССОВ ВЫЧЕТОВ | 2004 |
|
RU2270475C2 |
| УСТРОЙСТВО ДЛЯ КОРРЕКЦИИ ОШИБОК В ПОЛИНОМИАЛЬНОЙ СИСТЕМЕ КЛАССОВ ВЫЧЕТОВ С ИСПОЛЬЗОВАНИЕМ ПСЕВДООРТОГОНАЛЬНЫХ ПОЛИНОМОВ | 2005 |
|
RU2294529C2 |
| УСТРОЙСТВО СПЕКТРАЛЬНОГО ОБНАРУЖЕНИЯ И КОРРЕКЦИИ ОШИБОК В КОДАХ ПОЛИНОМИАЛЬНОЙ СИСТЕМЫ КЛАССОВ ВЫЧЕТОВ | 2005 |
|
RU2301441C2 |
| Устройство для вычисления сумм парных произведений в полиномиальной системе классов вычетов | 2016 |
|
RU2622881C1 |
| УСТРОЙСТВО ДЛЯ ОБНАРУЖЕНИЯ И ИСПРАВЛЕНИЯ ОШИБОК В ПОЛИНОМИАЛЬНОЙ СИСТЕМЕ КЛАССА ВЫЧЕТОВ | 2004 |
|
RU2267808C2 |
Изобретение относится к вычислительной технике и, в частности, к непозиционным компьютерным системам, и предназначено для обеспечения требуемой точности при вычислении с использованием модулярного кода. Техническим результатом является снижение аппаратных затрат на выполнение операции расширения оснований в полиномиальном модулярном коде. Устройство расширения оснований модулярного кода характеризуется тем, что вход устройства, на который подается модулярный полиномиальный код A(z)=(α1(z), α2(z), …, αn(z)), где αi(z) - остатки по основанию pi(z), i=1, …, n, используемому в полиномиальном модулярном коде, подключается к первым входам умножителей по модулю pi(z) первого блока умножителей соответственно, а вторые входы этих умножителей соединены с выходами первого блока памяти, выход 2.i-го умножителя по модулю pi(z), первого блока умножителей подсоединен к первому входу 4.i-го умножителя по модулю pn+1(z) второго блока умножителей, при этом второй вход умножителя по модулю pn+1(z) подключен к выходу второго блока памяти, выходы умножителей второго блока умножителей подсоединены к входам сумматора по модулю два, выход которого является выходом устройства. 1 ил. 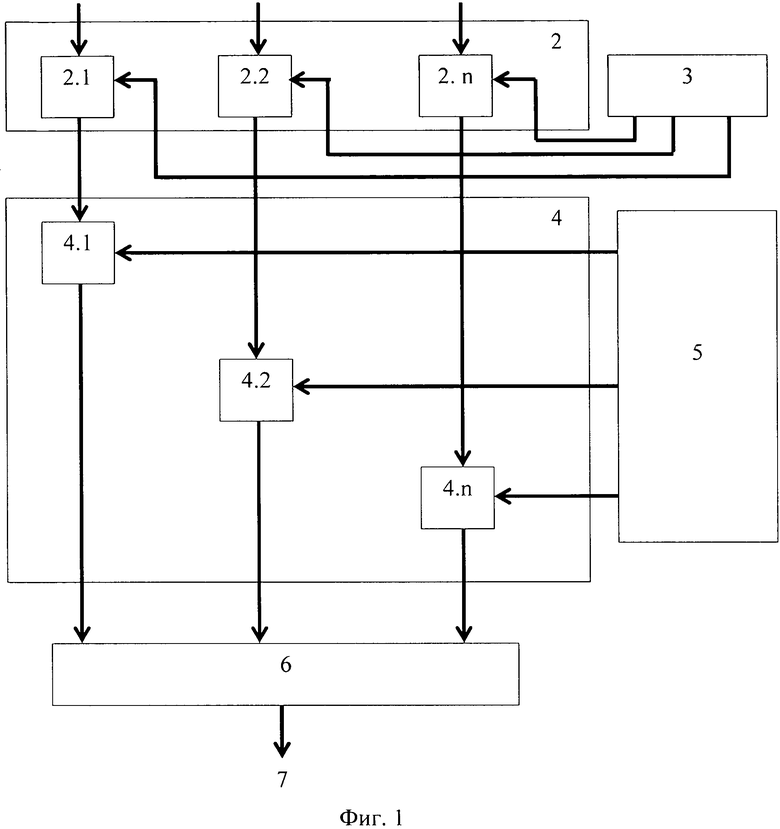
Устройство расширения оснований модулярного кода отличается тем, что вход устройства, на который подается модулярный полиномиальный код A(z)=(α1(z), α2(z), …, αn(z)), где αi(z) - остатки по основанию pi(z), i=1, …, n, используемому в полиномиальном модулярном коде, подключается к первым входам умножителей по модулю pi(z) первого блока умножителей соответственно, а вторые входы этих умножителей соединены с выходами первого блока памяти, выход 2.i-го умножителя по модулю pi(z) первого блока умножителей подсоединен к первому входу 4.i-го умножителя по модулю pn+1(z) второго блока умножителей, при этом второй вход умножителя по модулю pn+1(z) подключен к выходу второго блока памяти, выходы умножителей второго блока умножителей подсоединены к входам сумматора по модулю два, выход которого является выходом устройства.
| Устройство для расширения системы оснований модулярного кода | 1985 |
|
SU1282134A1 |
| НЕЙРОННАЯ СЕТЬ ДЛЯ РАСШИРЕНИЯ КОРТЕЖА ЧИСЛОВОЙ СИСТЕМЫ ВЫЧЕТОВ | 2003 |
|
RU2256226C2 |
| УСТРОЙСТВО ДЛЯ КОРРЕКЦИИ ОШИБОК В ПОЛИНОМИАЛЬНОЙ СИСТЕМЕ КЛАССОВ ВЫЧЕТОВ С ИСПОЛЬЗОВАНИЕМ ПСЕВДООРТОГОНАЛЬНЫХ ПОЛИНОМОВ | 2005 |
|
RU2294529C2 |
| УСТРОЙСТВО ДЛЯ УМНОЖЕНИЯ ПОЛИНОМОВ ПО МОДУЛЮ | 2006 |
|
RU2321883C1 |
| Колосоуборка | 1923 |
|
SU2009A1 |
Авторы
Даты
2015-09-10—Публикация
2014-03-12—Подача