Настоящее изобретение относится к искусственным нейронным сетям и может быть использовано для обучения нейронной сети при моделировании физических явлений технологических процессов.
На существующем уровне развития техники известен способ обучения искусственной нейронной сети с учителем, широко применяемый для решения различных задач (Хайкин С. Нейронные сети: полный курс, 2-е изд.: Пер. с англ. - М.: Издательский дом «Вильяме», 2006. - 1104 с.; Галушкин А.И. Теория нейронных сетей. Кн. 1: Учебное пособие для вузов / Общая ред. А.И. Галушкина. - М.: ИПРЖР, 2000. - 416 с.). Обучение с учителем предполагает, что для каждого входного вектора существует целевой вектор, представляющий собой требуемый выход. Вместе они называются обучающей парой. Сеть обучается на некотором числе таких обучающих пар. Задается входной вектор, вычисляется выход сети и сравнивается с соответствующим целевым вектором, разность (градиент ошибки) с помощью обратной связи подается в сеть и весовые коэффициенты изменяются в направлении антиградиента, минимизирую ошибку. Векторы обучающего множества предъявляются последовательно и многократно, вычисляются ошибки и весовые коэффициенты подстраиваются для каждого вектора до тех пор, пока ошибка по всему обучающему массиву не достигнет приемлемо низкого уровня. Недостатком этого способа является отсутствие гарантии сходимости процесса обучения.
Известен способ моделирования нейрона (патент RU 2402813 C1; МПК G06N 3/06, опубл. 10.01.2014). Это способ основан на том, что в весовых блоках вычисляют квадраты евклидова расстояния от вектора входа до каждой из 2n вершин единичного n-мерного куба, затем величины, обратные этим расстояниям, перемножают соответственно с компонентами целевого вектора, после чего суммируют в сумматоре и преобразуют в активационном блоке функцией активации. Способ моделирования нейрона принимается для обеспечения возможности реализации любой заданной булевой логической функции неравнозначности из полного их набора от n переменных. Необходимо отметить, что в данном способе рассматриваются булевы (переменные и значения функции - двоичные, 0 и 1) логические функции, а их аппроксимации с помощью нейронной сети представляют собой непрерывные функции. Области их определения (входы нейронной сети) и значения (выходы нейронной сети) представляют непрерывный отрезок. Булевы функции являются частным случаем соответствующих нейросетевых функций. Сложность алгоритма обучения данного способа определяется достаточно большим числом вычислительных операций в процессе обучения. Таким образом, данный способ имеет недостатки: узкая область применения, ограниченная количеством рассматриваемых булевых функций; процесс обучения может занимать длительные времени и не гарантирует сходимости, особенно при большом числе входов (n≥3).
Известен также способ обучения искусственной нейронной сети (патент РФ 2504006; МПК G06N 3/08, опубл. 27.10.2010). Данный способ предназначен для решения задач классификации объектов при отсутствии статистически достаточного ряда наблюдений исследуемых объектов. Сущность этого способа заключается в том, что обучающие векторы формируют на основе знаний экспертов в рассматриваемой области. Эксперты последовательно определяют классы исследуемых объектов, к которым относятся сгенерированные с помощью генератора псевдослучайных чисел обучающие векторы входных сигналов искусственной нейронной сети. Созданные компьютером их визуальные образы, наглядно описывают объекты, задаваемые сгенерированными обучающими векторами. Недостатком данного способа является узкая область применения, ограниченная решением задач классификации объектов.
Наиболее близким к заявленному изобретению является способ оптимизации весов скрытого и выходного слоев нейронной сети, предназначенный для обучения многослойной искусственной нейронной сети персептрона (Hung-Han Chen, Michael Т. Manry And Hema Chandrasekaran, A neural network training algorithm utilizing multiple set of linear equations. Neurocomputing, vol. 40, No. 1, January 1992, pp. 202-210). Это способ заключается в том, что в ходе процедуры обучения после последовательной передачи многомерного входного вектора Χ=[x1, x2, … xN] в многослойную нейронную сеть (со структурой: N синапсов во входном слое, один скрытый слой с Nh синапсами и Nc синапсов в выходном слое, вычисляют соответствующие кросскорреляционные и автокорреляционные функции, и далее определяют веса скрытого и выходного слоев на основе решения системы уравнений для антиградиента для минимизации средней квадратичной ошибки между выходными значениями нейронной сети и их желаемыми значениями. Сущность данного способа заключается в выполнении следующих действий:
1. Ввести структуру нейронной сети и параметры обучения, то есть: значения размерности входного Ν, скрытого Nh и выходного слоев Nc; количество примеров обучающих данных Nv, число опытов Nit и допустимое значение ошибки Емин.
2. Для начального значения опыта, инициализировать все веса у всех слоев с помощью функции генерации случайных чисел в диапазоне от 0 до 1. Пусть it=0, где it - счет опыта.
3, 4. Увеличить значение опыта it на 1. При условии it>Nit или значении средней квадратичной ошибки, меньшем допустимой ошибки 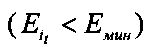 , где Nit - число опытов, перейти на шаг 16.
, где Nit - число опытов, перейти на шаг 16.
5, 6. Передать данные для обучения нейронной сети. Для каждого входного вектора рассчитать выходные значения каждого j-го синапса скрытого слоя нейронной сети Op(j), а также значения кросскорреляционной RTO(m) и автокорреляционной ROO(k, m) функций выходного слоя следующим образом:
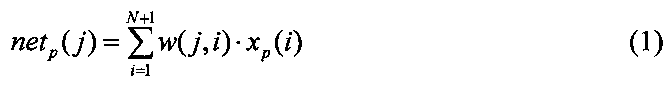


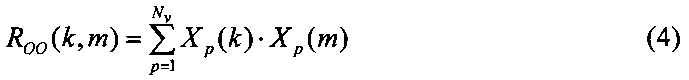
1≤p≤Nv, 1≤i≤N, 1≤j≤Nh
где netp(j) - входное значение j-го синапса скрытого слоя; w(j, i) - вес от i-го синапса входного слоя в j-м синапсе скрытого слоя; f1 - функция активации скрытого слоя; xp(i) - входное значение i-го синапса входного слоя; N, Nh, Nv - размерность входного слоя, скрытого слоя и обучающих данных соответственно; ytp - желаемое выходное значение нейронной сети; Xp(k) - входное значение k-го синапса выходного слоя; p - индекс примера обучающих данных; k - индекс входного значения в выходном слое; m - текущий индекс входного значения в выходном слое, 1≤k, m≤Nu, Nu=1+N+Nh.
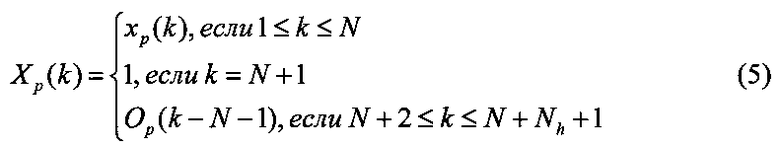
7. Решить систему линейных уравнений для определения весов выходного слоя
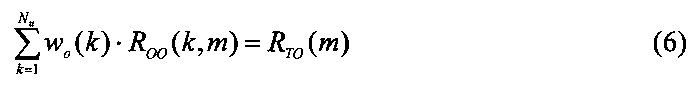
где wo(k) - вес синапса выходного слоя от k-го из Nu суммарных синапсов входного и скрытого слоев.
8. Рассчитать значение выходной величины и среднюю квадратичную ошибку Е:


где yop - выходное значение нейронной сети.
9, 10. При i≥2, сравнивать текущее значение 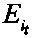 с значением
с значением 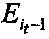 предыдущего опыта, если ошибка увеличивается, то перейти на шаг 15. В противном случае перейти на шаг 11.
предыдущего опыта, если ошибка увеличивается, то перейти на шаг 15. В противном случае перейти на шаг 11.
11. Определить значения кросскорреляционной и автокорреляционной (RδO(j, k) и ROO(j, m)) функций для скрытого слоя следующим образом:


где δpo и δp(j) - дельта-функции выходного и скрытого слоев соответственно.
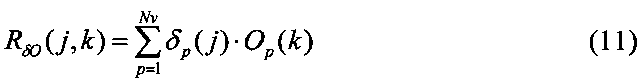
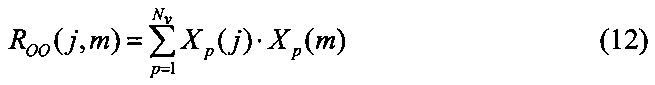
где k - индекс входного значения в скрытом слое; m - случайный индекс входного значения в скрытом слое, 1≤j, k, m≤Nh.
12. Решить систему линейных уравнений для определения изменения весов скрытого слоя следующим образом:
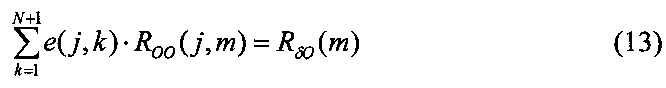
где e(j, k) - изменение веса скрытого слоя, соответствующее весу w(j, k).
13. Рассчитать шаг обучения Z по следующей формуле:
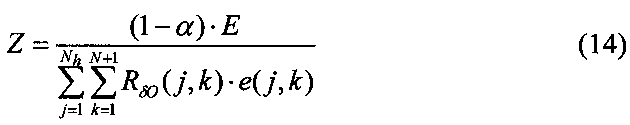
где 0<α<0,1.
14. Обновить веса скрытого слоя по следующей формуле и перейти на шаг 3 (новый опыт):
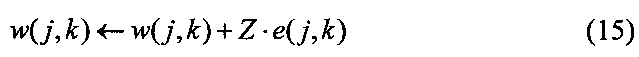
15. Уменьшить шаг обучения на 2 раза и перейти на шаг 14.
16. Вывести все веса всех слоев нейронной сети и остановить процесс обучения.
Недостаток этого способа - отсутствие гарантии того, что ошибка будет уменьшаться с каждым шагом обучения. Данный способ изменяет веса скрытого слоя в направлении их уменьшения в случае увеличения ошибки. Это приводит к возрастанию времени процесса обучения.
Задачей, на решение которой направлено заявляемое изобретение, является обеспечение гарантии сходимости и ускорения процесса обучения искусственной нейронной сети.
Данная задача решается за счет того, что в заявленном изобретении оптимизация весов скрытого и выходного слоев производится с учетом направления изменения весов скрытого слоя в случае увеличения ошибки.
Способ обучения искусственной нейронной сети, характеризующийся тем, что: передают многомерный входной вектор Х=[х1, х2, … ,xN] в многослойную нейронную сеть со структурой: N синапсов в входном слое, один скрытый слой с Nh синапсами и Nc синапсов в выходном слое; вычисляют соответствующие кросскорреляционные и автокорреляционные функции; далее определяют веса скрытого и выходного слоев на основе решения системы уравнений антиградиента, причем дополнительно производят выбор направления изменения весов скрытого слоя путем последовательного назначения пары ближайших значений текущего веса скрытого слоя w1(j, k)=w(j, k)-ξ и w2(j, k)=w(j, k)+ξ, где 0<ξ≤0,001, и сравнивают соответствующие им изменения средней квадратичной ошибки 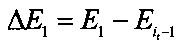 и
и 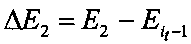 , где Е1, Е2 - значения средней квадратичной ошибки, соответствующей весам скрытого слоя w1(j, k) и w2(j, k),
, где Е1, Е2 - значения средней квадратичной ошибки, соответствующей весам скрытого слоя w1(j, k) и w2(j, k), 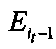 - значение средней квадратичной ошибки предыдущего опыта, если ΔЕ1<ΔE2, то изменяют веса скрытого слоя в направлении уменьшения, если ΔЕ1≥ΔЕ2, то изменяют веса скрытого слоя в направлении увеличения.
- значение средней квадратичной ошибки предыдущего опыта, если ΔЕ1<ΔE2, то изменяют веса скрытого слоя в направлении уменьшения, если ΔЕ1≥ΔЕ2, то изменяют веса скрытого слоя в направлении увеличения.
Структурная схема для способа обучения искусственной нейронной сети (фиг. 1) содержит: блок питания 1, на который поступает многомерный входной вектор. Выход блока питания 1 соединен с входом блока вычислители 2, на котором вычисляют кросскорреляционные и автокорреляционные функции. Выход блока вычислители 2 является входом блока весов 3, выход которого соединен с входом блока выхода 4. В весовом блоке 3 определяют веса скрытого и выходного слоев нейронной сети. Выходные значения и их соответствующие ошибки определяют в блоке 4. Выход блока 4 соединен с входом блока корректировки 5 с обратной связью. На основе оценки средней квадратичной ошибки, которые определяются в блоке 4, производят выбор направления изменения весов скрытого слоя нейронной сети. Выход блока 5 соединен со вторым входом блока 3. Выход блока 4 является выходом нейронной сети в условии достижения допустимой минимальной средней квадратичной ошибки.
Техническим результатом, обеспечиваемым приведенной совокупностью признаков, является уменьшение времени обучения, средней квадратичной ошибки (Е), и объема выборки при гарантии сходимости процесса обучения.
Сущность изобретения поясняется чертежами, на которых изображено:
На фиг. 1 - структурная схема для способа обучения искусственной нейронной сети;
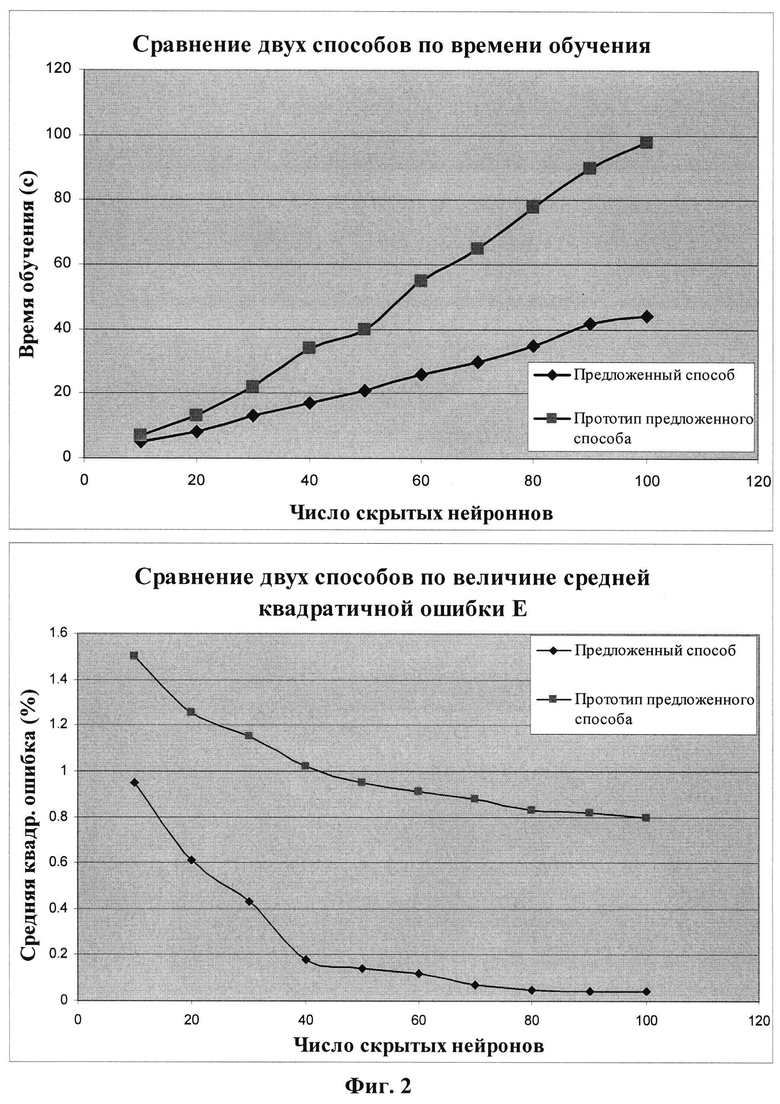
На фиг. 2 - сравнение эффективности использования двух способов обучения искусственной нейронной сети (предложенный способ и его прототип) на примере обучения теплового процесса в зоне резания.
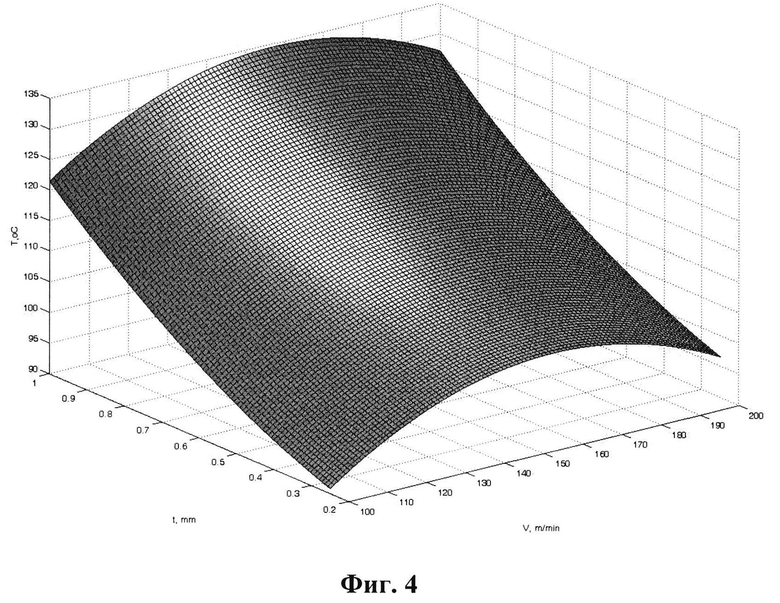
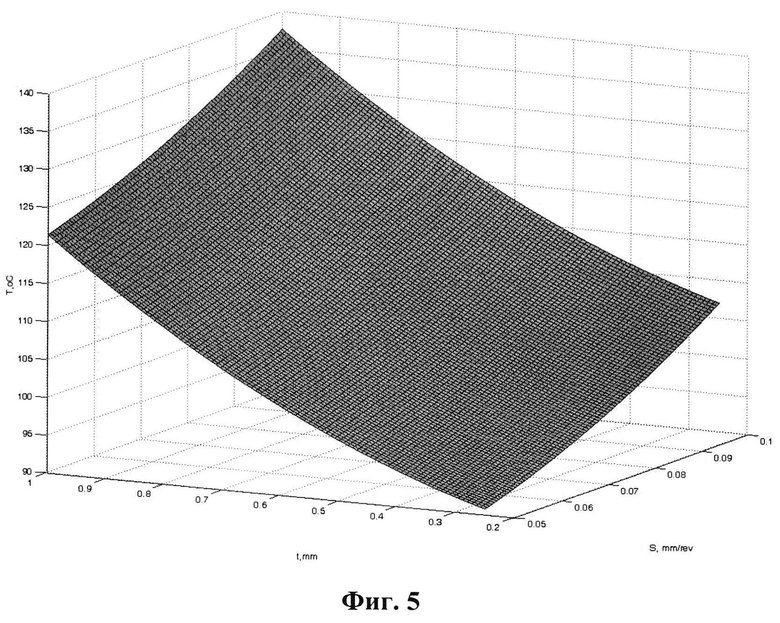
На фиг. 3- 5 - результаты обучения теплового процесса в зоне резания.
Способ обучения искусственной нейронной сети осуществляется следующим образом:
1. Вводим структуру нейронной сети и параметры обучения.
2. Для начального значения опыта, инициализируем все веса у всех слоев с помощью функции генерации случайных чисел в диапазоне от 0 до 1. Пусть it=0.
3. 4. Увеличиваем значение опыта it на 1. При условии it>Nit или значении средней квадратичной ошибки, меньшем допустимой ошибки 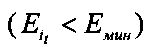 , переходим на шаг 18.
, переходим на шаг 18.
5, 6. Передаем данные для обучения нейронной сети. Для каждого входного вектора рассчитаем выходные значения каждого j-го синапса скрытого слоя нейронной сети Op(j), а также значения кросскорреляционной RTO(m) и автокорреляционной ROO(k, m) функций выходного слоя по формулам (1)-(5).
7. Решаем систему линейных уравнений (6) для определения весов выходного слоя.
8. Рассчитаем значение выходной величины и среднюю квадратичную ошибку Е по формулам (7)-(8).
9, 10. При i≥2, сравниваем текущее значение 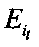 со значением
со значением 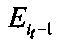 предыдущего опыта, если ошибка увеличивается, то переходим на шаг 15. В противном случае переходим на шаг 11.
предыдущего опыта, если ошибка увеличивается, то переходим на шаг 15. В противном случае переходим на шаг 11.
11. Определяем значения кросскорреляционной и автокорреляционной (RδO(j, k) и ROO(j, m)) функций для скрытого слоя по формулам (9)-(12).
12. Решаем систему линейных уравнений (13) для определения изменения весов скрытого слоя.
13. Рассчитаем шаг обучения по формуле (14).
14. Обновляем веса скрытого слоя по формуле (15) и переходим на шаг 3 (новый опыт).
15, 16. Проверяем условие «выбрано ли направление изменения весов?». Если «да», то переходим на шаг 17, если «нет» то выполняем выбор направления.
Выбираем направления изменения весов скрытого слоя путем последовательного назначения пары ближайших значений текущего веса скрытого слоя (w1(j, k)=w(j, k)-ξ и w2(j, k)=w(j, k)+ξ, где 0<ξ≤0,001) и сравнения соответствующих им изменений средней квадратичной ошибки ΔЕ1 и ΔЕ2

где Е1, Е2 - значения средней квадратичной ошибки, соответствующей весам скрытого слоя w1(j, k) и w2(j, k), вычисляются путем выполнения шагов 5-8.
Если ΔЕ1<ΔE2, то изменяем веса скрытого слоя в направлении уменьшения. Если ΔΕ1≥ΔE2, то изменяем веса скрытого слоя в направлении увеличения.
17. Изменяем скрытые веса в выбранном на 16-м шаге направлении и переодим на шаг 5.
18. Выводим все веса всех слоев нейронной сети и остановим процесс обучения.
Рассмотрим пример реализации способа обучения искусственной нейронной сети для теплового процесса в зоне резания. Используем нейронную сеть, которая имеет 6 входов (скорость - V, подача - S, глубина резания - t, теплопроводность обрабатываемого материала - λ∂, главный угол в плане - φ и радиус закругления вершины резца - r) и 1 выход (температура резания). Данные для обучения нейронной сети взяты из экспериментальных данных, которые получены при проведении 64 опытов. Условие проведенных опытов: точения вала диаметра 40 мм из Ал 6061 на токарном станке Kirloska Turnmaster-35 (мощность 2,2 кВт) проходным резцом быстрорежущей стали Р9 (главный угол в плане φ=45°, передний угол γ=0°, задний угол α=12°, радиус закругления 3 мм) со следующими режимами: V=100…200 м/мин; S=0,05…0,1 мм/об; t=0,25…0,1 мм.
Из фиг. 2 видно, что значение средней квадратичной ошибки достигается допустимых значений при числе нейронов в скрытом слое Nh≥60. В этом случае оно в два раза меньше и время обучения в пять раз меньше по предложенному способу по сравнению с прототипом.
Результаты обучения теплового процесса в зоне резания с помощью нейронной сети соответствуют результатом исследования, приведенным в литературных источниках (Макаров А.Д. Оптимизация процессов резания. - М.: Машиностроение, 1976. - 278 с.; Резников А.Н., Резников Л.А. Тепловые процессы в технологических системах. - М.: Машиностроение, 1990. - 288 с.).
Предложенное техническое решение позволяет ускорить процесс обучения искусственной нейронной сети в два раза и уменьшить ошибку в пять раз по сравнению с его прототипом.

Изобретение относится к искусственным нейронным сетям и может быть использовано для обучения нейронной сети при моделировании физических явлений технологических процессов. Техническим результатом является обеспечение гарантии сходимости и ускорения процесса обучения искусственной нейронной сети. Способ состоит в том, что передают многомерный входной вектор X=[x1, x2, … xN] в многослойную нейронную сеть со структурой: N синапсов в входном слое, один скрытый слой с Nh синапсами и Nc синапсов в выходном слое, вычисляют соответствующие кросскорреляционные и автокорреляционные функции, определяют веса скрытого и выходного слоев на основе решения системы уравнений антиградиента, причем в случае увеличения ошибки производят выбор направления изменения весов скрытого слоя путем последовательного назначения пары ближайших значений текущего веса скрытого слоя w1(j,k)=w(j,k)-ξ и w2(j,k)=w(j,k)+ξ, где 0<ξ≤0,001, и сравнивают соответствующие им изменения средней квадратичной ошибки 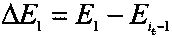 и
и 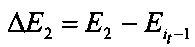 , где Е1, Е2 - значения средней квадратичной ошибки, соответствующей весам скрытого слоя w1(j,k) и w2(j,k);
, где Е1, Е2 - значения средней квадратичной ошибки, соответствующей весам скрытого слоя w1(j,k) и w2(j,k); 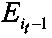 - значение средней квадратичной ошибки предыдущего опыта, если ΔЕ1<ΔE2, то изменяют веса скрытого слоя в направлении уменьшения, если ΔЕ1≥ΔЕ2, то изменяют веса скрытого слоя в направлении увеличения. 5 ил.
- значение средней квадратичной ошибки предыдущего опыта, если ΔЕ1<ΔE2, то изменяют веса скрытого слоя в направлении уменьшения, если ΔЕ1≥ΔЕ2, то изменяют веса скрытого слоя в направлении увеличения. 5 ил.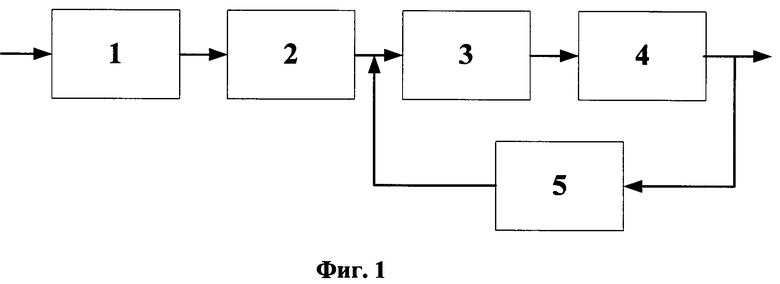
Способ обучения искусственной нейронной сети, характеризующийся тем, что передают многомерный входной вектор X=[x1, x2,…,xN] в многослойную нейронную сеть со структурой: N синапсов в входном слое, один скрытый слой с Nh синапсами и Nc синапсов в выходном слое, вычисляют соответствующие кросскорреляционные и автокорреляционные функции, определяют веса скрытого и выходного слоев на основе решения системы уравнений антиградиента, отличающийся тем, что дополнительно производят выбор направления изменения весов скрытого слоя путем последовательного назначения пары ближайших значений текущего веса скрытого слоя w1(j, k) = w(j, k) - ξ и w2(j, k) = w(j, k) + ξ, где 0<ξ≤0,001, и сравнивают соответствующие им изменения средней квадратичной ошибки 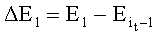
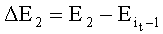
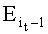
| Hung-Han Chen, Michael Т | |||
| Manry And Hema Chandrasekaran, A neural network training algorithm utilizing multiple set of linear equations | |||
| Neurocomputing, vol | |||
| Приспособление с иглой для прочистки кухонь типа "Примус" | 1923 |
|
SU40A1 |
| Печь для непрерывного получения сернистого натрия | 1921 |
|
SU1A1 |
| Приспособление к тростильной машине для прекращения намотки шпули | 1923 |
|
SU202A1 |
| СПОСОБ КОМПЬЮТЕРИЗОВАННОГО ОБУЧЕНИЯ ОДНОЙ ИЛИ БОЛЕЕ НЕЙРОННЫХ СЕТЕЙ | 2007 |
|
RU2459254C2 |
| СПОСОБ ОБУЧЕНИЯ ИСКУССТВЕННОЙ НЕЙРОННОЙ СЕТИ | 2012 |
|
RU2504006C1 |
| JP 5159086 A, 25.06.1993 | |||
| JP 6314267 A, 08.11.1994 | |||
| JP 9265463 A, 07.10.1997 | |||
| JP 9138786 A, 27.05.1997 | |||
Авторы
Даты
2015-10-27—Публикация
2014-12-15—Подача