СПОСОБ ПРОВЕДЕНИЯ СПЕКТРАЛЬНЫХ ТЕСТОВ МУЛЬТИПЛИКАТИВНОГО КОНГРУЭНТНОГО ГЕНЕРАТОРА СЛУЧАЙНЫХ ЧИСЕЛ Российский патент 2016 года по МПК G06F7/58 

Область изобретения

[0001] Изобретение относится к вычислительной технике, а именно к новым способам проведения спектральных тестов, и может быть использовано в устройствах, моделирующих случайные процессы. Целью является их инновационное усовершенствование при отборе и создании эффективных мультипликативных конгруэнтных генераторов, технический результат - получение на компьютерах однородных и независимых случайных чисел. В частности, изобретение представляет новые спектральные тесты степени L для L≥3, а также создает способы получения более достоверных оценок, что позволяет признать годными эффективные генераторы, которыми до сих пор пренебрегали, а также создать более точные критерии для исключения неподходящих генераторов. Обозначим как (d,z,n) мультипликативный конгруэнтный генератор случайных чисел, с натуральным числом d>0 в качестве модуля, целым взаимно-простым числом z в качестве множителя и целым числом n, также являющимся взаимно-простым с d, для задания начального случайного числа. Генератор (d,z,n) или (d,z), выражаясь кратко, производит последовательность целых чисел {n_k≡nz^k-1 mod(d)| 0<n_k<d, k=1,2,^...} в виде решения отношений рекурсивной эквивалентности

n₁≡n mod(d), n_k+1:≡zn_k mod(d), 0<n_k<d, k=1,2, ^….

На компьютерах выход генератора (d,z,n) представляет собой действительные числа v_k:=n_k/d с 0<v_k<1, последовательно выдаваемые для k=1,2,^... как последовательность однородных и независимых случайных чисел.

Описание материалов, использованных при экспертизе заявки

[0002]

Прежде всего, проанализируем структуры существующих спектральных тестов. Спектральные тесты L-й степени для генератора (d,z) стремятся оценивать, в частности, степень независимости L последовательных случайных чисел. При указанном способе, берутся L-последовательности целых чисел {Q_k:=(n_k,n_k+1,^...,n_k+L-1)| k=1,2,^...}, выданных генератором (d,z), и рассматриваются в качестве точек в L-мерном евклидовом пространстве E_L. Основополагающим фактом является то, что эти точки {Q₁,Q₂,^…} находятся в решетке G_L(d,z), определяемой d и z. Точнее говоря, точки, соответствующие L-последовательностям случайных чисел, занимают свои места в узлах решетки, которая определяется d и z и обозначается как G_L(d,z). При этом способе, почти не уделяется внимание вышеупомянутым процессам занятия мест выходами (d,z). Здесь внимание сосредоточено на оценке распределения мест, подготавливаемого решеткой G_L(d,z) в E_L, на предмет пригодности полученной конфигурации в качестве мест для однородных и независимых случайных чисел. Значение этого утверждения становится очевидным из наглядных примеров решеток G₂(d,z) в евклидовой плоскости Е₂, заданных последовательными 2-ками случайных чисел (d,z). На Фиг. 1 показаны графики расположения точек одного периода {Q_k:=(n_k,n_k+1)|k=1,2,^…}, выдаваемых генератором (d,z) с нечетным простым d и его первообразным корнем z. Чтобы отдельные точки были различимы для глаз наблюдателя, значения (d,z) выбраны малыми. Точки находятся в квадрате C_d с длиной стороны d, одна из вершин которого совпадает с началом координат О, при этом проведенная наружная рамка представляет собой квадрат несколько больших размеров. На верхних графиках показаны ровные массивы выдаваемых точек, близкие к так называемой треугольной решетке, образованной правильными треугольниками. Если последовательные 2-ки случайных чисел занимают места в этих ровно распределенных положениях некоторым образом, который, надо надеяться, выглядит случайным, нет оснований отрицать статистическую гипотезу, что последовательные 2-ки случайных чисел оказываются однородными и независимыми друг от друга. В противоположность этому, в конце Фиг. 1 мы видим такие распределения узлов решетки, которые представляются сосредоточенными на нескольких отчетливо выраженных линиях, между которыми находится очевидное разделительное пространство. Если точки 2-к оказываются на местах такого типа, мы обнаруживаем устойчивую зависимость их распределения от направления, что указывает на то, что последовательные случайные числа или их пары выглядят коррелированными и их независимость представляется весьма сомнительной. Спектральные тесты дают число ρ₂(d,z)>1 в качестве количественной оценки этих впечатлений для генератора (d,z); см. Фиг. 1 со значениями ρ=ρ₂(d,z), указанными для решеток G₂(d,z); при этом следует иметь в виду, что лучшим является ρ, которое ближе к 1 сверху.

КРАТКОЕ ИЗЛОЖЕНИЕ СУЩНОСТИ ИЗОБРЕТЕНИЯ

[0003]

Нами описываются составляющие настоящее изобретение новые идеи. Вернемся к математическим основам решетчатых структур, возникающих в последовательных L-ках случайных чисел (d,z), начиная с простейшего случая, где L=2. Последовательную 2-ку Q_k можно для удобства рассматривать в качестве радиус-вектора типа «строка», Q_k:=(nz^k-1,nz^k)=nz^k-1e₁, e₁:=(1,z). Целочисленные координаты Q_k принимаются без эквивалентности по модулю d. Вектор положения любой точки в евклидовой плоскости Е₂, вторая координата которого равна остатку от деления второй координаты Q_k на d, можно получить прибавлением целочисленного вектора, кратного e₂:=(0,d). 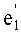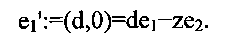Подобным же образом, точка, первая координата которой равна остатку от деления первой координаты Q_k на d, получается прибавлением целочисленного вектора, кратного $$e_1^{\text{'}}$$ :

Таким образом, точки 2-к, сгенерированные (d,z), вместе с их эквивалентами по модулю d, содержатся в множестве S всех целочисленных линейных комбинаций векторов {е₁,е₂}, S:={c₁e₁+c₂e₂|, где c₁,c₂ - целые числа}. Это S определяет решетку, образованную базисными векторами {е₁,е₂}. Так как S определяется d и z, обозначим решетку как S=G₂(d,z). Прежде всего, отметим, что G₂(d,z) содержит точки с координатами, которые не являются взаимно-простыми с d. Таким образом, 2-ки, выдаваемые генератором (d,z), занимают только часть узлов решетки G₂(d,z). Поэтому на всех графиках Фиг. 1, соответствующих нечетным простым модулям и первообразным корням, среди отмеченных точек неизменно отсутствует начало координат О.

[0004]

Следует отметить две общие особенности G₂(d,z). Одна из них заключается в том, что базисные векторы {е₁,е₂} охватывают параллелограмм площади d, равной определителю матрицы, составленной из этих векторов. Эта площадь независима от множителя z. Другая особенность состоит в том, что в квадрате C_d со сторонами длиной d имеется ровно d узлов решетки. На это указывает тот факт, что площадь C_d составляет d². Можно также привести более содержательный количественно довод о том, что узел решетки c₁e₁+c₂e₂=(c₁, zc₁+dc₂) имеет d возможных значений {0,1, ^… ,d-1} для первой целочисленной координаты c₁ в C_d, в то время как вторая координата zc₁+dc₂ в C_d фиксирует с₂ без выбора. Параллелограмм, ограниченный {е₁,е₂}, точно заполняет C_d, рассматриваемый в качестве 2-мерного тора с периодом d в обоих направлениях. Теперь, когда мы знаем, что G₂(d,z) - это решетка, обладающая двумя названными особенностями, геометрия Е₂ дает нам значимые структуры, для чего не требуется информация о z. Прежде всего, отметим общий способ построения любого множества базисных векторов. Определим линию решетки как линию, включающую два отдельных узла решетки. Фактически, на линии решетки в Е₂ существует бесконечно много узлов решетки. Рассмотрим пару параллельных и соседних линий решетки и еще одну пару параллельных линий решетки, которые не параллельны предыдущей паре. 4 рассматриваемых линии решетки пересекаются в 4 узлах решетки; при этом каждая линия решетки имеет 2 точки пересечения, находящиеся в соседних узлах решетки. Выберем одну из вершин параллелограмма, обозначив ее как $$Q_0^{\text{'}}$$ , и определим векторы $$\left\{e_1^{\text{'}},e_2^{\text{'}}\right\}$$ как направленные стороны параллелограмма, исходящего из точки $$Q_0^{\text{'}}$$ . Если мы предоставим параллелограмму смещаться всеми возможными способами вдоль принятых нами линий решетки, $$Q_0^{\text{'}}$$ пройдет через все d точек решетки, а параллелограмм заполнит тор C_d площадью d² без пересечений. Так, векторы $$\left\{e_1^{\text{'}},e_2^{\text{'}}\right\}$$ образуют множество базисных векторов решетки G₂(d,z). Придерживаясь терминологии, принятой в физике, назовем описываемый параллелограмм площади d элементарной ячейкой. Таким образом, две пары соседних линий решетки определяют множество базисных векторов $$\left\{e_1^{\text{'}},e_2^{\text{'}}\right\}$$ решетки и элементарную ячейку. И наоборот: любое множество $$\left\{e_1^{\text{'}\text{'}},e_2^{\text{'}\text{'}}\right\}$$ базисных векторов решетки, очевидно, дает две пары параллельных и соседних линий решетки, образующих параллелограмм, а заданная ими элементарная ячейка имеет такую же площадь d. Указанное соответствие является взаимно-однозначным. Теперь рассмотрим расстояние h между любой парой параллельных и соседних линий решетки. Из отмеченного выше соответствия, приходим к заключению о том, что h - высота, опущенная из вершины параллелограмма элементарной ячейки на противоположное ей основание. И наоборот: любая высота, опущенная из любой вершины параллелограмма элементарной ячейки на противоположное ей основание, определенно соответствует расстоянию между парой параллельных и соседних линий решетки. Это становится более очевидно, если рассмотреть треугольник площади d/2, образованный базисными векторами $$\left\{e_1^{\text{'}},e_2^{\text{'}}\right\}$$ : расстояние h между любым множеством параллельных и соседних линий решетки - это высота такого треугольника, и наоборот.

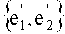
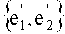
[0005]

Теперь перефразируем это общее описание применительно к большим размерностям. Предположим, что дана решетка. Операционное определение множества базисных векторов решетки выглядит следующим образом. (1) Возьмем линию решетки, (2) выберем на ней узел решетки $$Q_0^{\text{'}}$$ , (3) зададим вектор $$e_1^{\text{'}}$$ , исходящий из $$Q_0^{\text{'}}$$ и направленный на L-1=1 соседнего к нему узла решетки на линии решетки, (4) возьмем параллельную и соседнюю линию решетки к первой, (5) возьмем любой узел решетки на ней (6) и наконец зададим вектор $$e_2^{\text{'}}$$ из $$Q_0^{\text{'}}$$ до этой точки. Множество $$\left\{e_1^{\text{'}},e_2^{\text{'}}\right\}$$ - это, в силу рассмотренных выше аргументов, множество линейно независимых базисных векторов решетки. Очевидно, что указанным образом может быть построено любое множество базисных векторов. Назовем треугольник, образованный любыми двумя базисными векторами $$\left\{e_1^{\text{'}},e_2^{\text{'}}\right\}$$ , 2-симплексом, пользуясь терминологией, принятой в геометрии. Если имеет место решетка G₂(d,z), то любой 2-симплекс, образованный базисными векторами, имеет постоянную площадь d/2. При этом расстояние между любыми параллельными соседними линиями решетки - это высота, проведенная из некоторой вершины 2-симплекса, образованного некоторым множеством базисных векторов. И наоборот: высота, проведенная из любой вершины любого 2-симплекса, образованного любым множеством базисных векторов, является расстоянием между некоторыми параллельными линиями решетки.

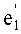
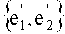
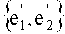
[0006]

Теперь, располагая более четким представлением, вновь рассмотрим графики, приведенные на Фиг. 1. Из них видно, что 2-симплексы на этих участках принимают различные формы в соответствии с выбором (d,z) и выбором базисных векторов. Верхние графики на Фиг. 1 демонстрируют решетки, которые легко можно воспринять как построенные из почти правильных треугольников. Так как точки фактически дискретны, наблюдения нужно проводить с некоторым размыванием небольшими зонами или полосами малой ширины. Исходя из этого допущения, можно сказать, что верхние графики на Фиг. 1 дают 2-ки случайных чисел (d,z), расположенные на плоскости почти эквидистантно. Такие решетки практически не оставляют возможностей для возражений против статистической гипотезы о том, что случайные числа выдаются однородным и независимым образом. В противоположность этому, на графиках, расположенных ближе к концу Фиг. 1, мы видим разреженные распределения нескольких плотно сосредоточенных линий решетки, которые располагаются параллельно на очевидно большом расстоянии друг от друга. Будет трудно настаивать на том, что на этих графиках показано появление последовательных случайных чисел со статистической независимостью. Если нам нужно будет выбрать для наших компьютеров генератор случайных чисел, мы вряд ли возьмем такие (d,z) для генерации 2-ек, как показаны на этих графиках.

[0007]

В соответствии с нашим наблюдением, спектральные тесты 2 степени дают количественные оценки при использовании наибольшего расстояния λ₂(d,z) между параллельными соседними линиями решетки на G₂(d,z).

(Заключение 1) Среди всех треугольников с заданной площадью, правильный треугольник реализует наименьшее значение для наибольшей из высот, опущенных из вершин на противоположные им основания. В условиях, когда площадь составляет d/2, правильный треугольник или правильный 2-симплекс реализует это наименьшее значение наибольшей высоты как Λ₂(d)=2^-1/23^1/4d^1/2 ≈0.93060d^1/2.

(Доказательство) Воспользуемся доказательством от противного, предполагая его дальнейшее обобщение на случай большей размерности. Допустим, что наименьшая длина наибольшей высоты реализуется в треугольнике, который не является правильным. Тогда дихотомия заключается в существовании двух или одной кратчайших сторон. Если существуют две кратчайшие стороны, примем одну из них в качестве основания и позволим противоположной ему вершине перемещаться параллельно основанию, без изменения площади треугольника и высоты вершины. Существует направление, в котором удлиняется другая кратчайшая сторона таким образом, что небольшое перемещение вершины реализует треугольник такой же площади только с одной кратчайшей стороной, где высота, опущенная на нее из противоположной вершины сохраняет наименьшее значение наибольшей высоты среди всех возможных форм. Таким образом, нам нужно рассмотреть только случай, когда k=1. Тогда мы можем взять за основание другую сторону и позволить противоположной ей вершине перемещаться параллельно этому новому основанию. Тогда кратчайшая сторона может незначительно удлиниться, но не переставая быть кратчайшей в силу непрерывности действительных чисел. Из сказанного следует, что наименьшая длина наибольшей высоты может быть уменьшена, что противоречит допущению о том, что первоначальная длина является наименьшим из реализуемых значений среди треугольников всех форм. Полученное противоречие доказывает, что форма треугольника должна быть правильной. Построив правильный треугольник с площадью d/2, мы легко получим вышеупомянутое наименьшее значение Λ₂(d).

[0008]

Как указывалось выше, решетка в Е₂ с базисными векторами {е₁,е₂}, образующими правильный треугольник или правильный 2-симплекс, именуется треугольной решеткой. Правильный 2-симплекс образуется двумя линейно независимыми векторами и характеризуется тем, что все 3 вершины - скажем, исходная точка и две точки с указанными радиус-векторами, дают 3 пары, в каждой из которых точки находятся на одинаковом расстоянии друг от друга. В некотором смысле, это представляет собой идеальную геометрическую конфигурацию узлов решетки, в которой занимают свои места последовательные 2-ки точек, образуемых однородными и независимыми случайными числами. Предположим снова, что λ₂(d,z) - наибольшее расстояние между параллельными соседними линиями решетки в решетке G₂(d,z). Заключение 1 доказывает строгое неравенство λ₂(d,z)>Λ₂(d). Здесь равенство никогда не может быть выполнено, так как базисные векторы {е₁,е₂} решетки G₂(d,z) обязательно имеют целочисленные координаты и никогда не могут реализовать глобальные минимумы, обеспечиваемые правильными треугольниками, для чего требуются иррациональные координаты. Близость отношения

к 1 является хорошим показателем того, насколько близка решетка G₂(d,z) к идеальной треугольной решетке и до какой степени генератор (d,z) выдает последовательные 2-ки с наименьшими основаниями отрицать статистическую гипотезу об однородности и независимости. Использование этого факта является основополагающей идеей спектральных тестов второй степени. Вычислим ρ2(d,z)>1 для каждого возможного множителя z с модулем d и выберем z, который реализует 1<ρ₂(d,z)<R₂ для заданного критерия R₂>1. Первыми выполнившие это Fishman и Moore (1986) выбрали R₂=1.25, и этот критерий оказался универсальным и полезным для всех последующих приложений. На Фиг. 1 показано ρ=ρ₂(d,z) для каждого изображенного генератора (d,z). Беглого взгляда на графики достаточно для того, чтобы убедиться, что критерий ρ<1.25 является вполне разумным. К сожалению, не столь однозначна ситуация с последовательными L-ками случайных чисел для L≥3.

Fishman and Moore (1986)/ G.S. Fishman and L.R. Moore: An exhaustive analysis of multiplicative congruential random number generator with modulus 2³¹-1, SIAM Journal on Scientific and Statistical Computing Vol.7 (1986), pp. 24-45.

(Fishman и Moore (1986)/ G.S. Fishman и L.R. Moore: Исчерпывающий анализ мультипликативного конгруэнтного генератора случайных чисел с модулем 2³¹-1, SIAM Journal on Scientific and Statistical Computing: Том 7 (1986), стр. 24-45).

[0009]

Примем L≥2 и рассмотрим, в целом, последовательные L-ки случайных чисел, выдаваемые генератором (d,z,n). Вновь введем обозначение C_d - для гиперкуба с гранями длиной d, исходящего из начала координат О L-мерного евклидова пространства E_L. Точки

в E_L представляют собой последовательные L-ки, выдаваемые генератором (d,z,n), и все их эквиваленты по модулю d с очевидностью выражаются подходящими целочисленными линейными комбинациями следующих векторов:

Эти векторы линейно независимы и ограничивают параллелепипед объема d^L-1, равного определителю матрицы, составленной из этих векторов. Обозначим как G_L(d,z) решетку в E_L, ограничиваемую этими L базисными векторами. Объем d^L гиперкуба C_d непосредственно указывает, что эта решетка имеет d узлов решетки в C_d. Этот факт может быть подтвержден следующим образом. Вектор c₁e₁+c₂e₂+^…+c_Le_L с целочисленными коэффициентами c₁,c₂, ^…, c_l имеет первую координату с₁, которая может иметь d различных значений {0,1, ^…, d-1} в C_d. Когда в качестве одного из них фиксируется с₁, вторая координата c₁z+c₂d выбирает уникальное целое число с₂ в C_d; этот вопрос аналогично решается с c₃, ^…, c_L. Следовательно, в C_d имеется d узлов решетки G_L(d,z).

[0010]

Так же как в случае с треугольником или 2-симплексом, образованным линейно независимыми 2 базисными векторами в размерности L=2, вышеупомянутые линейно независимые L базисных векторов {е₁,е₂, ^…, e_L} G_L(d,z) образуют L-мерный симплекс или L-симплекс. По аналогии с 2-мерным случаем, представим себе общее множество $$\left\{e_1^{\text{'}},e_2^{\text{'}},\cdots ,e_L^{\text{'}}\right\}$$ базисных векторов для этой заданной G_L(d,z) и назовем образованный ими параллелепипед элементарной ячейкой. Линии решетки теперь соответствует гиперплоскости решетки с размерностью L-1, которая содержит L-1 узлов решетки {Р₁,Р₂, ^…, P_L-1}, радиус-векторы которых, проведенные, скажем, из узла решетки Р₀, являются линейно независимыми. Выражаясь в понятиях геометрии, можно сказать, что эта гиперплоскость решетки определяется включением L аффинно независимых точек {Р₀,Р₁,Р₂, ^…, P_L-1}. Не составит труда задать операционное определение общего множества базисных векторов $$\left\{e_1^{\text{'}},e_2^{\text{'}},\cdots ,e_L^{\text{'}}\right\}$$ . Возьмем (1) пару параллельных и соседних гиперплоскостей, возьмем (2) любое множество аффинно независимых узлов решетки $$\left\{P_0^{\text{'}},P_1^{\text{'}},\cdots ,P_{L-1}^{\text{'}}\right\}$$ на одной из гиперплоскостей решетки, с тем ограничением, что $$\left\{P_1^{\text{'}},\cdots ,P_{L-1}^{\text{'}}\right\}$$ - это ближайшие к $$P_0^{\text{'}}$$ узлы решетки на соединяющих их линиях, возьмем (3) любой узел решетки $$P_L^{\text{'}}$$ на другой параллельной гиперплоскости решетки и зададим (4) векторы $$\left\{e_1^{\text{'}},e_2^{\text{'}},\cdots ,e_L^{\text{'}}\right\}$$ как радиус-векторы $$\left\{P_1^{\text{'}},P_2^{\text{'}},\cdots ,P_L^{\text{'}}\right\}$$ , проведенные из начальной точки $$P_0^{\text{'}}$$ . При переносах вдоль каждого из этих векторов параллелепипед или элементарная ячейка, образованная $$\left\{e_1^{\text{'}},e_2^{\text{'}},\cdots ,e_L^{\text{'}}\right\}$$ , заполняет гиперкуб C_d гиперобъема d^L, который принимается в виде тора с периодом d в координатах, и начальная точка решетки $$P_0^{\text{'}}$$ проходит через все d узлов решетки в C_d. Элементарная ячейка имеет гиперобъем d^L-1, который является определителем матрицы векторов $$\left\{e_1^{\text{'}},e_2^{\text{'}},\cdots ,e_L^{\text{'}}\right\}$$ . Последние представляют собой базисные векторы решетки G_L(d,z). Они образуют L-симплекс с L вершинами $$\left\{P_0^{\text{'}},P_1^{\text{'}},\cdots ,P_{L-1}^{\text{'}}\right\}$$ . В этом симплексе каждая вершина обращена к (L-1)-мерной гиперплоскости решетки, которая определяется включением других L-1 вершин. Хорошо известно, что любой L-симплекс, образованный L линейно независимыми векторами $$\left\{e_1^{\text{'}},e_2^{\text{'}},\cdots ,e_L^{\text{'}}\right\}$$ с детерминантным объемом d^L-1 имеет гиперобъем V=d^L-1/L!. Это объясняется тем, что V линеен относительно этих векторов, так как радиус-вектор $$e_j^{\text{'}}+e_j^{\text{'}\text{'}}$$ вершины дает высоту, которая представляет собой сумму высот соответствующих векторов от гиперплоскости, противоположной вершине; а L-симплексы, образованные единичными векторами, направленными вдоль осей координат, имеют гиперобъем 1/L!. Так, в L-симплексе, образованном $$\left\{e_1^{\text{'}},e_2^{\text{'}},\cdots ,e_L^{\text{'}}\right\}$$ , длина h перпендикуляра, опущенного из вершины на противоположную гиперплоскость с гиперплощадью S, определяет гиперобъем hS/L=d^L-1/L! в виде конуса. Важным здесь является то, что гиперобъем L-симплекса одинаков для любого выбора базисных векторов, и в любом таком L-симплексе его произвольная вершина с высотой h, опущенной на противоположную гиперплоскость площади S, дает постоянное произведение hS. Таким образом, наибольшее расстояние между соседними параллельными гиперплоскостями решетки с размерностью L-1 задается высотой вершины относительно противолежащей гиперплоскости решетки с наименьшей гиперплощадью в некотором L-симплексе. Все постановки для описываемой L-размерности - такие же, как для размерности L=2. Вместе с тем, суть вопроса получает дополнительную особенность, в общих чертах описываемую ниже.

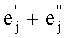
(Заключение 2) Зададим размерность L≥3 и рассмотрим L-симплексы, которые исходят из начала координат О пространства E_L и определяются точкой О и L точками с L линейно-независимыми радиус-векторами, проведенными из О. Определим правильный симплекс в E_L таким условием, что его (L+1)L/2 пар вершин имеют одно и то же расстояние между вершинами. При условии что L-симплексы имеют один и тот же гиперобъем приблизительно правильной формы, правильный L-симплекс дает локальный минимум наибольшей высоты вершины относительно гиперплоскости противоположного ей основания.

(Доказательство) Вновь воспользуемся доказательством от противного. Рассмотрим окрестность конфигурации L-симплексов постоянного гиперобъема приблизительно правильной формы, а именно такой, где каждое из всех (L+1)L/2 ребер имеет такую длину, что можно говорить о значительной близости к их полному равенству. Отметим, что высоты каждой вершины относительно гиперплоскости противолежащего основания постоянно изменяются, так же как и площади гиперплоскостей основания. Предположим, что L-симплекс не имеет правильной формы, но его k вершин обращены к гиперплоскостям основания с наименьшей гиперплощадью и имеют одинаковую высоту h, которая является наименьшей среди всех возможных конфигураций L-симплекса в этом локальном диапазоне, близком к правильной форме. Если гиперплоскость основания с наименьшей площадью единственна (т.е. k=1), то при незначительной деформации L-симплекса (например, осуществляемой незначительным перемещением вершины, обращенной к другой гиперплоскости основания, в направлении, параллельном ее гиперплоскости основания) гиперплоскость основания будет по-прежнему иметь наименьшую площадь, хотя само значение площади незначительно увеличится, а высота h обращенной к ней вершины незначительно уменьшится. Это противоречит допущению о том, что h является локально наименьшей среди всех возможных форм L-симплекса с единственной гиперплоскостью основания наименьшей площади. Таким образом, случай k=1 не реализуется. Остается возможность того, что k гиперплоскостей основания с 2≤k≤L-l являются наименьшими. Но в этом случае мы можем взять любую из них в качестве гиперплоскости основания и переместить противоположную вершину параллельно гиперплоскости основания. Тогда площадь такой гиперплоскости и высота h противоположной вершины останутся одинаковыми, но площадь некоторой другой гиперплоскости основания (которая обязательно должна быть непараллельной неподвижной гиперплоскости основания) может быть увеличена выбором подходящего перемещения вершины. Это уменьшает число k гиперплоскостей основания с наименьшей площадью. Эту процедуру можно повторять для сведения k к k=1, что, как доказано, содержит противоречие. Таким образом, исходная гипотеза является ложной, а доказуемое утверждение - истинным.

[0011]

Пусть точки {P₁,P₂, ^…, P_l} в евклидовом пространстве E_L имеют линейно независимые радиус-векторы относительно начальной точки Р₀, или, иначе говоря, {Р₀,Р₁,Р₂, ^…, P_L} являются аффинно независимыми. Правильный L-симплекс с вершинами {Р₀,Р₁,Р₂, ^…,P_L} определяется тем условием, что любая пара вершин, общее количество которых равно (L+1)L/2, имеет одно и то же евклидово расстояние между вершинами. В рассматриваемой нами задаче L линейно независимых базисных векторов {е₁,е₂, ^…, e_L} решетки могут использоваться для задания правильного L-симплекса согласно вышеуказанному определению - скажем, с точкой Р₀, помещенной в начало координат О. С точки зрения спектральных тестов, правильный L-симплекс, очевидно, является идеальной конфигурацией для структурных элементов решетки G_L(d,z). Забыв о том, что решетка составлена L-ками выходов генератора (d,z), мы начинаем с того, что допускаем, что правильный L-симплекс образовывается базовыми векторами следующей формы:

Константы а и b определяются согласно следующим двум ограничениям:

(1) Эти векторы охватывают своим определителем объем d^L-1.

(2) Они образуют правильный L-симплекс.

В силу их формы векторы имеют одну и ту же евклидову длину 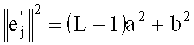$${\Vert e_j^{\text{'}}\Vert }^2=\left(L-1\right)a^2+b^2$$ для любого j. Кроме того, скалярное произведение для i≠j, $$\left(e_i^{\text{'}},e_j^{\text{'}}\right)=\left(L-2\right)a^2+2ab$$ , не зависит от i и j, поэтому векторы, составляющие любую пару, образуют между собой один и тот же угол. Единичный вектор

дает скалярное произведение $$\left(e_0^{\text{'}},e_j^{\text{'}}\right)=\left\{\left(L-1\right)a+b\right\}/L^{1/2}=:h$$ для любого 1≤j≤L; здесь h - это расстояние от начала координат О до центроида гиперплоскости основания, содержащего точки с радиус-векторами $$\left\{e_1^{\text{'}},e_2^{\text{'}},\cdots ,e_L^{\text{'}}\right\}$$ . Таким образом, высота M_L(d) любой вершины относительно гиперплоскости противоположного ей основания в правильном L-симплексе, образованном этими базисными векторами, где определитель задает элементарной ячейке объем d^L-1, задается M_L(d)=h={(L-1)a+b}/L^1/2=s/L^1/2, s:=(L-1)a+b, что можно получить, определив предварительно а и b по (1) и (2). Прежде всего, вычислим объем, задаваемый определителем:

Вычитая 1-й столбец из всех остальных столбцов, получаем d^L-1=s(b-a)^L-1. Далее рассмотрим ограничение (2). Используя 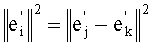$${\Vert e_i^{\text{'}}\Vert }^2={\Vert e_j^{\text{'}}-e_k^{\text{'}}\Vert }^2$$ для 1≤i,j,k≤L при j≠k, получаем

Представив b=ξа, получаем, что ξ соответствует ξ²+(L-1)=2(ξ-1)², или ξ=2±(L+1)^1/2. Произведя некоторые алгебраические выкладки для любого из этих решений, получим один и тот же результат для правильного L-симплекса любой размерности L≥2,

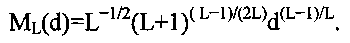
Таким образом, задача оказывается решенной. Ниже приведены конкретные выражения для M^L(d) в случае 2≤L≤6:

Fishman and Moore (1986) сослались на геометрию чисел для поиска минимума Λ_L(d) наибольшего расстояния λ_L(d,z) между параллельными и соседними гиперплоскостями решетки в L-мерной решетке G_L(d,z) и провели свои революционные исчерпывающие спектральные тесты на первообразных корнях простого модуля d=2³¹-1. Значения {Λ_L(d)|2≤L≤6} в их Ур. (15) выглядят следующим образом:

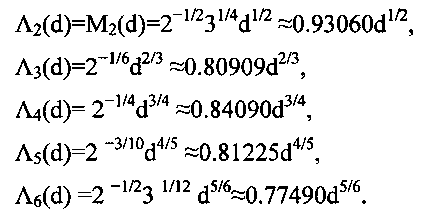
Они меньше, чем M_L(d) для L≥3. Короче говоря, Fishman и Moore выполнили спектральные тесты, приняв глобальные минимумы наибольших расстояний для соседних параллельных гиперплоскостей решетки в качестве значений, реализуемых генераторами (d,z). Авторы настоящего изобретения склонны полагать, что форма правильного L-симплекса является идеальной для реализации решеткой G_L(d,z) и спектральные тесты должны в предпочтительном случае использовать локальные минимумы {M_L(d)|2≤L≤6} в качестве контрольных значений. Это приводит к необходимости ввести новое множество оценок, отличных от предложенного Fishman и Moore (1986) {ρ_L(d,z)|L≥3}:

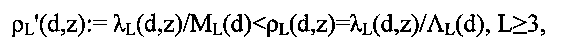
в качестве подходящих показателей эффективности генератора (d,z). Так как M_L(d) не является глобальным минимумом, некоторые решетки могут иметь значения $${\rho }_L^{\text{'}}\left(d,z\right)\le 1$$ . Если имеет место $${\rho }_L^{\text{'}}\left(d,z\right)\le 1$$ , это предполагает, что решетка G_L(d,z) имеет конфигурацию, не вписывающуюся в так называемую локальную область притяжения минимума или ее геометрическая конфигурация не близка к правильному L-симплексу. Таким образом, будет правомерным полагать, что (d,z) является подходящим только в том случае, если $$1<{\rho }_L^{\text{'}}\left(d,z\right)<R_L$$ выполняется для заданного R_L. При этом следует отклонять такие (d,z), при которых $${\rho }_L^{\text{'}}\left(d,z\right)\le 1$$ , даже если $${\rho }_L^{\text{'}}\left(d,z\right)$$ близко к единице снизу.

ПОДРОБНОЕ ОПИСАНИЕ ИЗОБРЕТЕНИЯ

[0012]

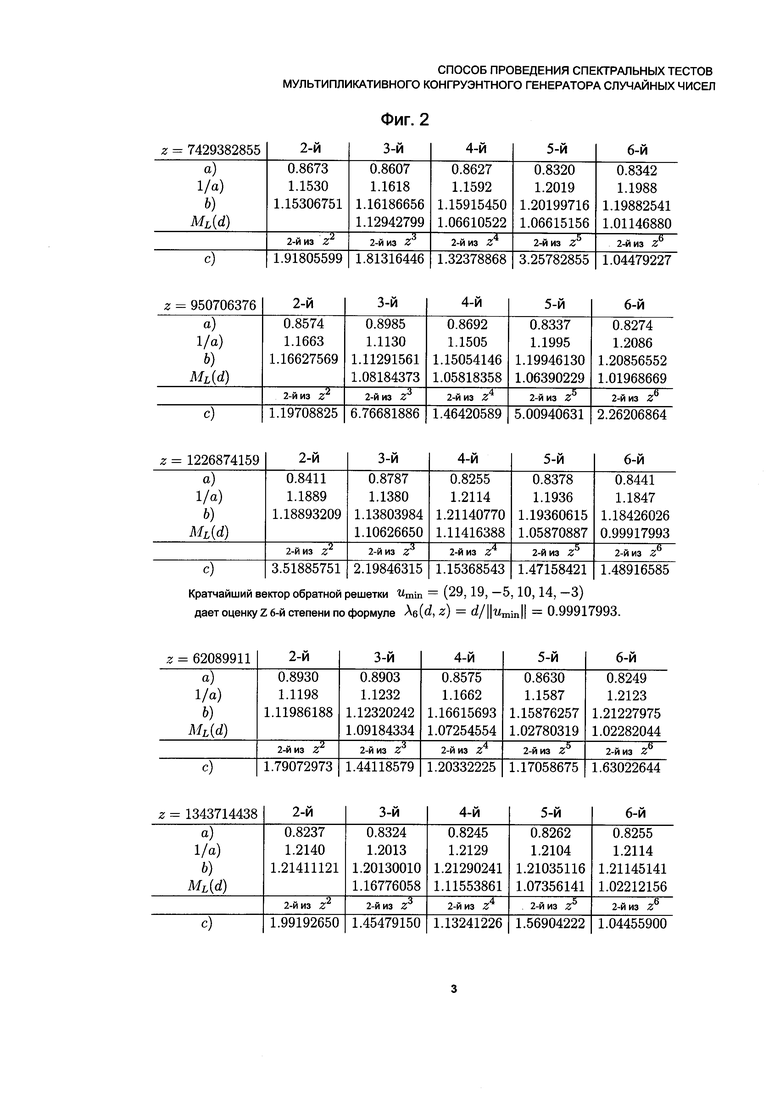
Мы обсудили, что {M_L(d)|2≤L≤6} - это стандартные контрольные значения, которые подлежат использованию в спектральных тестах более высокой степени. Технологически, задача заключается в том, чтобы определить процедуры, необходимые для непосредственной реализации тестов. Это будет ясно показано на примерах. Fishman и Moore (1986) дали 5 превосходных множителей в своей Таблице 2 для простого модуля d=2³¹-1. Мы цитируем их в Перечнях 2А-2Е в представленной здесь Фиг. 2. Аналогичная иллюстрация была дана в наших предыдущих патентных заявках I27665HIR, OUS27668HIR, OEP27669HIR и ORU27670HIR, где упоминались тесты второй степени (d,z²), (d,z³), ^…, (d,z⁶). Строка, обозначенная как а), воспроизводит строку S₁ в работе Fishman и Moore. Строка, обозначенная как 1/а), представляет собой обратные величины чисел в строке а) и соответствует представленному ρ_L(d,z):=λ_L(d,z)/Λ_L(d). Эти же значения заново пересчитываются авторами в строке b). Числа в строке, обозначенной как M_L(d), показывают $${\rho }_L^{\text{'}}\left(d,z\right):={\lambda }_L\left(d,z\right)/M_L\left(d\right)$$ для L≥3. Они также могут быть подтверждены преобразованием из строки с). Необходимо особо упомянуть Перечень 2С для множителя первообразных корней z=1226874159. Как уже отмечалось, оценка (d,z²) в строке с) является неудовлетворительной: этот множитель не подходит. Строка M_L(d) также содержит $${\rho }_6^{\text{'}}\left(d,z\right)=0.999179993<1$$ , что означает, что решетка G₆(d,z) не вписывается в локальную область притяжения правильного 6-симплекса. Хотя само число очень близко к 1 снизу, этот множитель первообразных корней следует исключить как неподходящий и в этом тесте 6 степени, что подкрепляет заключение в отношении спектрального теста второй степени (d,z²).

[0013]

Таким образом, мы приходим к выводу о том, что в качестве более точного способа для правильного отбора эффективных генераторов (d,z) следует использовать новые спектральные тесты, основанные на {M_L(d)|L≥3}. Последние также нужны для признания подходящими множителей, которые прежде отклонялись в отношении {Λ_L(d))|L≥3} как не прошедшие проверку, хотя они фактически могли быть подходящими применительно к большим {M_L(d)|L≥3}. Вместе с тем, новые тесты на основе {M_L(d))|L≥3} следует проводить с определенной осторожностью. Для прояснения этого вопроса, вернемся к способу вычисления наибольшего расстояния λ_L(d,z) между параллельными соседними гиперплоскостями решеток (d,z). Этот способ основан на использовании векторов решетки G_L*(d,z), являющейся обратной по отношению к решетке G_L(d,z). Эта обратная решетка G_L*(d,z) задается множеством {f₁,f₂, ^…, f_L} базисных векторов:

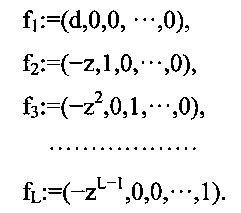
Последние с очевидностью являются линейно независимыми и имеют скалярные произведения

Пусть матрицы Е и F задаются векторами-строками {е₁,е₂, ^…, e_L} и {f₁,f₂, ^…, f_L}, соответственно. Указанные скалярные произведения имеют отношение к матричному произведению E^tF=dI, где ^tF - транспонированная матрица F, a I - единичная матрица размерности L×L. Таким образом, ^tF однозначно определяется как ^tF=dE^-1. Можно утверждать следующее.

(Заключение 3) Базисные векторы обратной решетки {f₁,f₂, ^…, f_L} имеют целочисленные координаты, и кратчайший ненулевой вектор имеет евклидову длину не меньше 1. Пусть u_min - кратчайший ненулевой вектор обратной решетки. Тогда для наибольшего расстояния λ_L(d,z) между L-1-мерными параллельными и соседними гиперплоскостями решетки G_L(d,z) справедливо:

где ||u_min|| - евклидова длина вектора u_min. (Конец Заключения 3)

Доказательство этого утверждения является простым, но несколько длинным. Полное изложение этого доказательства см. в работе Nakazawa и Nakazawa (2012). Данное заключение позволяет нам конвертировать спектральные тесты L-й степени в поиск кратчайших векторов в G_L*(d,z). Этот поиск удобнее всего выполнять в декартовой системе координат.

(Заключение 4) Пусть u - вектор с целочисленными декартовыми координатами (u₁,u₂, ^…, u_L). Необходимым и достаточным условием нахождения u в обратной решетке G_L*(d,z) является следующее:

(Доказательство) Если вектор и находится в G_L*(d,z), то он представляет собой линейную комбинацию базисных векторов {f₁,f₂, ^…, f_L} с целыми коэффициентами c₁,c₂, ^…, c_L, и имеет декартовы координаты

Это доказывает, что u₁+zu₂+z²u₃+^…+z^L-1u_L=c₁d=0 mod(d). Таким образом, условие является необходимым. И наоборот: если u₁+zu₂+z²u₃+^…+z^L-1u_L=0 mod(d) верно, то существует целое число с, которое дает u₁+zu₂+z²u₃+^…+z^L-1u_L=cd. Мы имеем u₁=cd-u₂z-u₃z²-^…-u_Lz^L-1 и

Следовательно, вектор и находится в G_L*(d,z), то есть условие является также достаточным.

Важно уяснить то, что глобальные минимумы {Λ_L(d)|L≥2}, используемые в работе Fishman и Moore (1986), сохраняют свои важные роли в поиске кратчайшего вектора u_min решетки G_L*(d,z), так как они определяют справедливость λ_L(d,z)=d/||u_min||>Λ_L(d) или ||u_min||<d/Λ_L(d). Таким образом, мы можем в общем виде представить процедуры спектральных тестов L-й степени следующим образом.

(Заключение 5) Пусть задано L≥2. Оценка 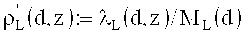$${\rho }_L^{\text{'}}\left(d,z\right):={\lambda }_L\left(d,z\right)/M_L\left(d\right)$$ спектрального теста L-й степени для генератора (d,z) достигается выполнением следующих шагов.

(1) Получим вектор u_min обратной решетки G_L*(d,z), для чего проверяется каждый вектор и с декартовыми координатами u=(u₁,u₂, ^…, u_L), удовлетворяющий условию и находится такой из них, который имеет наименьшую метрику ||u||.

(2) Вычислим λ_L(d,z)=d/||u_min||.

(3) Вычислим оценку $${\rho }_L^{\text{'}}\left(d,z\right):={\lambda }_L\left(d,z\right)/M_L\left(d\right)$$ .

(4) Если $$1<{\rho }_L^{\text{'}}\left(d,z\right)<R_L$$ выполняется для заданного уровня R_L>1, то генератор (d,z) принимается как прошедший тест.

Nakazawa and Nakazawa (2012)/ N. Nakazawa and H. Nakazawa: Multiplicative congruential generators with moduluses formed by two odd-prime factors for uniform and independent random numbers II. Structures of spectral tests, uploaded (October, 13, 2012) in the URL http://www10.plala.or.jp/h-nkzw/. (Nakazawa и Nakazawa (2012)/ N. Nakazawa и H. Nakazawa: Мультипликативные конгруэнтные генераторы с модулями, формируемыми двумя множителями в виде нечетных простых чисел для однородных и независимых случайных чисел II. Структуры спектральных тестов, загружено (13 октября 2012 года) по адресу URL http://www10.plala.or.ip/h-nkzw/).

[0014]

После подачи авторами настоящего изобретения предыдущей патентной заявки наиболее актуальным в том, что касается спектральных тестов, является включение вторых тестов (d,z²), (d,z³), ^…. Нахождение идеальных значений {M_L(d)=L^-1/2(L+1)^(L-1)/(2L)d^(L-1)/L|L≥3} в виде расстояний от вершин правильных L-симплексов до противоположных им L-1-мерных гиперплоскостей решетки позволяет заслуженно выбрать эти новые идеальные значения в качестве контрольных уровней в спектральных тестах более высокой степени вместе с использовавшимся до сих пор уровнем M₂(d)=Λ₂(d). По мнению авторов, {R_L=1.25|2≤L≤6} может быть целесообразным выбором при принятии решения о прохождении теста множителем z, но это может зависеть от количества прошедших тест значений. Можно ли сделать спектральные тесты еще лучше? Пока этот вопрос остается открытым для дальнейших исследований. Но один вывод из вышеизложенного можно сделать со всей определенностью: имея дело с задачами со случайными числами, никогда нельзя полагаться на интуицию или догадки. Прежде чем что-либо применять, это необходимо подвергнуть испытаниям. В настоящее время мы полагаем, что находимся на правильном пути, но для дополнительного подкрепления или подтверждения этого утверждения могут потребоваться дополнительные проверки. Авторы будут признательны всем, кто сочтет возможным прислать свои отзывы и комментарии.

КРАТКИЕ ПОЯСНЕНИЯ К ЧЕРТЕЖАМ

[0015]

(Фиг. 1A и 1B) Геометрия 2-к случайных чисел и оценка ρ=ρ₂(d,z)

Типичные графики точек, образуемые последовательными 2-ками случайных чисел, выдаваемых мультипликативным конгруэнтным генератором (d,z); изображенные распределения соответствуют оценке ρ:=ρ₂(d,z) около 1.05, 1.10, ^…; изображенные квадраты несколько больше, чем квадрат C_d; значения (d,z) могут быть считаны из подписей к рисункам.

[0016]

(Фиг. 2) Множитель z (работа Fishman и Moore (1986)) для модуля d=2³¹-1: Показатели эффективности 5 лучших множителей из работы Fishman и Moore (1986), представленные у них на стр. 37 в виде Таблицы 2; строка а) соответствует значениям, показанным в их работе как S₁, строка 1/а) представляет обратные величины значений из а) и согласуется с представленными здесь p_L(d,z), строка b) представляет собой расчет p_L(d,z), выполненный авторами настоящего изобретения, в строке M_L(d) показана оценка $${\rho }_L^{\text{'}}\left(d,z\right)$$ на основе значений для правильного L-симплекса, и наконец в строке с) показаны ρ₂(d,z^j) для j=2,3, ^…, 6.

Изобретение относится к вычислительной технике и может быть использовано в устройствах, моделирующих случайные процессы. Техническим результатом является получение на компьютерах однородных и независимых случайных чисел. Способ проведения спектральных тестов мультипликативного конгруэнтного генератора (d,z,n) или (d,z), содержащего нечетное целое число d в качестве модуля, а также целое число z, взаимно-простое с d, в качестве множителя, и целое число n, взаимно-простое с d, в качестве начального случайного числа, генерирующего последовательность целых чисел {n_k:≡nz^k-1 mod(d)| 1≤n_k≤d, k=1,2,^...} последовательным образом и выдающего на выходе последовательность случайных чисел за счет реализации арифметики {v_k:=n_k/d| 0≤v_k≤1, k=1,2,^...}, основан на оценке геометрической формы решетки G_L(d,z), в которой занимают свои места L последовательных целых чисел {Q_k:=(n_k,n_k+1,^…,n_k+L-1)| k=1,2,^...}, выданных генератором (d,z,n), посредством вычисления наибольшего расстояния λ_L(d,z) между параллельными и соседними гиперплоскостями решетки G_L(d,z) и оценки ρ_L′(d,z):=λ_L(d,z)/M_L(d) генератора (d,z) на основе новых контрольных значений M_L(d):=L^-1/2(L+1)^(L-1)/(2L)d^(L-1)/L, L≥3, а также принятия решения о прохождении теста (d,z), если условия 1<ρ_L′(d,z)<R_L, 3≤L≤6 выполняются для заданных уровней {R_L>1| 3≤L≤6}. 3 ил.

Способ проведения спектральных тестов мультипликативного конгруэнтного генератора (d,z,n) или (d,z), содержащего нечетное целое число d в качестве модуля, а также целое число z, взаимно-простое с d, в качестве множителя, и целое число n, взаимно-простое с d, в качестве начального случайного числа, генерирующего последовательность целых чисел {n_k:≡nz^k-1 mod(d)| 1≤n_k≤d, k=1,2,^...} последовательным образом и выдающего на выходе последовательность случайных чисел за счет реализации арифметики {v_k:=n_k/d| 0≤v_k≤1, k=1,2,^...}, характеризующийся тем, что названный способ основан на оценке геометрической формы решетки G_L(d,z), в которой занимают свои места L последовательных целых чисел {Q_k:=(n_k,n_k+1,^…,n_k+L-1)| k=1,2,^...}, выданных генератором (d,z,n), посредством вычисления наибольшего расстояния λ_L(d,z) между параллельными и соседними гиперплоскостями решетки G_L(d,z) и оценки ρ_L′(d,z):=λ_L(d,z)/M_L(d) генератора (d,z) на основе новых контрольных значений
M_L(d):=L^-1/2(L+1)^(L-1)/(2L)d^(L-1)/L, L≥3,
а также принятия решения о прохождении теста (d,z), если условия
1<ρ_L′(d,z)<R_L, 3≤L≤6
выполняются для заданных уровней {R_L>1| 3≤L≤6}.