ОБЛАСТЬ ТЕХНИКИ, К КОТОРОЙ ОТНОСИТСЯ ИЗОБРЕТЕНИЕ
Настоящее изобретение относится к области техники, связанной с измерением фазоров, в частности к разновидности способа синхрофазорного измерения, применяемого к устройству измерения фазоров (PMU) Р-класса.
УРОВЕНЬ ТЕХНИКИ
В настоящее время применение устройства измерения фазоров (PMU) открывает принципиально новые возможности в технологии измерений энергетических систем; при этом, помимо обеспечения синхрофазора, преимущество, связанное с высокой точностью частотой загрузки высокой скорости, расширяет применение PMU в качестве источника данных фазора при динамическом контроле безопасности. В соответствии с требованием стандарта IEEE С37.118.1, PMU Р-класса может быстро и точно отслеживать процесс динамического отклика энергетической системы, при этом отсутствует какие-либо требования на сглаживание и подавление помех наложения спектров фазора. Таким образом, точность измерения фазора и скорость измерения крайне важны, прежде всего, в динамических условиях. Неточная или медленная ответная реакция измерения фазора может привести к неправильным решениям управления и даже к аварии.
Для расчета фазора в устройствах PMU широко используют дискретное преобразование Фурье (DFT) по причине невысоких вычислительных требований этого способа, а также потому, что он позволяет извлекать компонент номинальной частоты из волнового сигнала, который часто искажается другими гармониками. Однако DFT основывается на предположении, что параметры сигнала не изменяются, а номинальное значение частоты сохраняется в пределах некоторого окна времени. Однако в течение процесса динамической реакции энергетической системы это предположение оказывается недействительным, и все параметры изменяются с течением времени. Поэтому использование DFT имеет недостатки, обуславливающие две проблемы измерения. Во-первых, утечка спектра происходит не только из-за отклонения частоты, но и вследствие модуляции входных сигналов. Во-вторых, использование модели статического фазора приводит, в результате, к усредняющему эффекту DFT, что вносит существенные ошибки в динамических условиях.
С выпуском и постепенным усовершенствованием стандартов IEEE и Китая для PMU точность измерений PMU в динамических условиях получает признание все большего количества исследовательских организаций, при этом в способе измерения применяют много новых технологий. Например, в некоторых литературных источниках предлагается моделировать трехфазный фазор способом смещаемого окна времени, чтобы устранить утечку спектра DFT в условиях отклонения частоты. Однако этот способ подходит только для статического входного сигнала и не может решать задачу утечки спектра, которая вызвана динамическими входными сигналами. Таким образом, в существующем техническом решении отсутствует единый алгоритм оценки, основанный на модели динамического фазора. Кроме того, существующие алгоритмы не могут решить проблемы утечки спектра и усредняющего эффекта, которые вызваны динамическими входными сигналами.
РАСКРЫТИЕ ИЗОБРЕТЕНИЯ
Задача данного изобретения заключается в создании способа синхрофазорного измерения для использования в устройстве измерения фазоров (PMU) Р-класса. Этот способ измерения обеспечивает возможность точного и быстрого измерения фазора как в статических, так и в динамических условиях. Точность способа не только удовлетворяет техническим требованиям соответствующих стандартов, но и на порядок выше требований стандартов.
Способ синхрофазорного измерения для использования в устройстве измерения фазоров (PMU) Р-класса выполняют на основе математической модели динамического фазора, при этом конструируют цифровой фильтр низких частот для коэффициентов фазора, объединенный с DFT и устраняющий утечку спектра, вызванную входными сигналами динамического фазора, причем после устранения утечки спектра могут проводить измерения исходного фазора.
Динамический фазор аппроксимируют с использованием ряда Тейлора второго порядка. Исследуют линейную зависимость между ошибками измерения, вызванными усредняющим эффектом DFT, и коэффициентами ряда Тейлора второго порядка. Затем используют упомянутую линейную зависимость для компенсации исходных ошибок измерения в динамических условиях. Наконец, выполняют точные измерения динамического фазора.
Исследование линейной зависимости между ошибками измерения, вызванными усредняющим эффектом DFT, и коэффициентами ряда Тейлора второго порядка, использование упомянутой линейной зависимости для коррекции исходных ошибок измерения в динамических условиях и выполнение точных измерений динамического фазора включают в себя:
вычисление по способу наименьших квадратов коэффициентов ряда Тейлора второго порядка динамического входного сигнала фазора и получение исходной частоты, скорости изменения частоты (ROCOF) и связанных с ними коэффициентов ряда Тейлора второго порядка, при этом все параметры входного сигнала динамического фазора повторно вычисляют в соответствии с упомянутыми коэффициентами ряда Тейлора второго порядка;
проведение динамической коррекции параметров исходных измерений фазора и статическую коррекцию амплитуды, причем точные измерения динамического фазора получают путем динамической калибровки;
и калибровку исходных параметров динамического фазора и статическую коррекцию амплитуды исходного динамического фазора, при этом точные измерения динамического фазора получают путем динамической калибровки.
Упомянутый способ измерения после выполнения точных измерений динамического фазора дополнительно включает в себя:
введение второго цифрового фильтра низких частот для устранения эффекта от гармоник и белого шума для получения измерений фазора с более высокой точностью.
Частота среза цифрового фильтра низких частот, объединенного с дискретным преобразованием Фурье (DFT), составляет 2,5 Гц, при этом окно времени составляет два номинальных периода динамического входного сигнала и расчетная частота исходного фазора составляет 400 Гц.
Частота среза второго цифрового фильтра низких частот составляет 2,5 Гц, при этом окно времени составляет 27,5 миллисекунд.
Как можно заметить, в вышеупомянутом техническом решении в соответствии с настоящим изобретением предложен способ измерения, обеспечивающий возможность точного и быстрого измерения фазора как в статических, так и в динамических условиях. Кроме того, точность упомянутого способа измерения может на порядок превышать ту точность, которая требуется в соответствии с упомянутым стандартом.
КРАТКОЕ ОПИСАНИЕ ЧЕРТЕЖЕЙ
Для ясного понимания упомянутого технического решения при описании вариантов осуществления настоящего изобретения дается краткое представление необходимых чертежей. Очевидно, что нижеупомянутые чертежи предназначены для описания лишь некоторых вариантов осуществления настоящего изобретения. Специалисту в данной области техники понятно, что могут быть получены также другие чертежи, в соответствии с приведенными, без затрат какой-либо творческой работы.
На фиг. 1 показана блок-схема способа синхрофазорного измерения для использования в устройстве измерения фазоров (PMU) Р-класса, который выполняют в соответствии с вариантом осуществления изобретения.
На фиг. 2 показано соответствие ошибок измерения амплитуды и частот, которое получено в соответствии с вариантом осуществления изобретения.
На фиг. 3 показана максимальная суммарная векторная ошибка (TVE) для различных основных частот при моделировании теста частотного сканирования, которая получена в соответствии с вариантом осуществления изобретения.
На фиг. 4 показаны максимальные ошибки частоты и скорости изменения частоты (ROCOF) для различных основных частот при моделировании теста частотного сканирования, полученные в соответствии с вариантом осуществления изобретения.
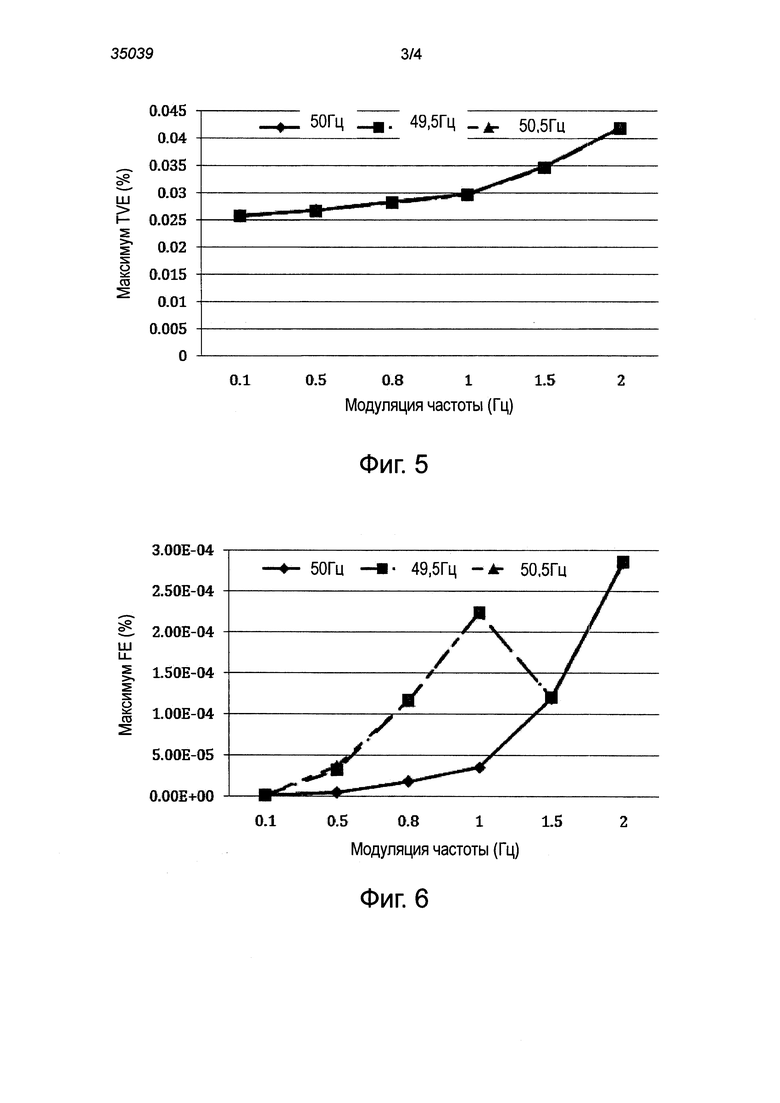
На фиг. 5 показана максимальная TVE для различных частот модуляции при моделировании теста модуляции, полученная в соответствии с вариантом осуществления изобретения.
На фиг. 6 показаны максимальные ошибки частоты для различных частот модуляции при моделировании теста модуляции, полученные в соответствии с вариантом осуществления изобретения.
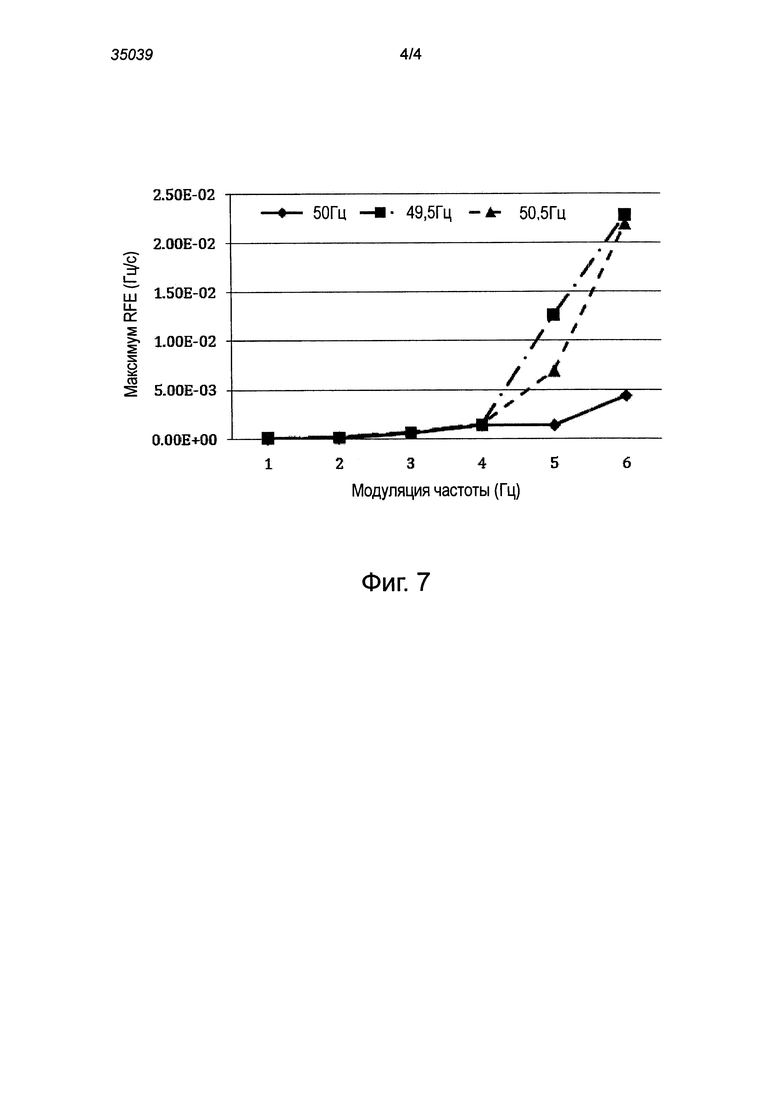
На фиг. 7 показаны максимальные ошибки ROCOF для различных частот модуляции при моделировании теста модуляции, полученные в соответствии с вариантом осуществления изобретения.
ОСУЩЕСТВЛЕНИЕ ИЗОБРЕТЕНИЯ
Техническое решение варианта осуществления изобретения описано ясно и исчерпывающе ниже со ссылками на вышеупомянутые чертежи. Очевидно, что описанные конструктивные решения не исчерпывают всех конструктивных решений, а составляют лишь часть упомянутого варианта осуществления изобретения. Все другие конструктивные решения, основанные на этом варианте осуществления изобретения и полученные специалистами в данной области без затрат творческого труда, входят в объем правовой охраны настоящего изобретения.
Упомянутый вариант осуществления настоящего изобретения подробно описан ниже с привлечением чертежей. На фиг. 1 изображена блок-схема способа синхрофазорного измерения для использования в устройстве измерения фазоров (PMU) Р-класса, который выполняют в соответствии с вариантом осуществления изобретения. Упомянутый способ включает в себя:
этап 11, на котором конструируют цифровой фильтр низких частот для коэффициентов фазора на основе математической модели динамического фазора, который объединяют с DFT. Этот фильтр устраняет утечку спектра, вызванную входными сигналами динамического фазора. Затем, после устранения утечки спектра, могут быть выполнены измерения исходного фазора.
На этом этапе формулируют математическую модель динамического фазора. Для выполнения вычислений предложена математическая модель динамического фазора, основанная на ряде Тейлора второго порядка. В этой модели все параметры фазора, включая амплитуду, угол сдвига фаз, частоту и ROCOF, изменяются с течением времени в расчетном окне времени.
Например, в этом случае прежде всего выражают динамический сигнал основной частоты в виде:
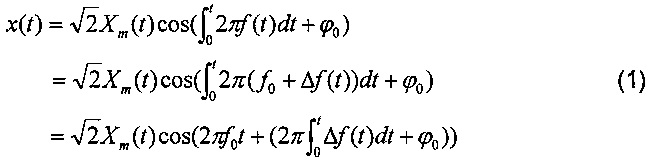
где x(t) - текущее значение сигнала, Xm(t) - амплитуда, f(t) - частота сигнала, ϕ0 - исходный угол сдвига фаз, f0 - номинальная частота, Δf(t) - отклонение частоты. Амплитуда и частота сигнала являются функцией времени.
Выражение (1) можно перезаписать следующим образом:
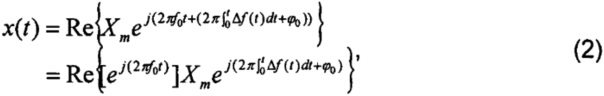
где Re - вещественная часть формулы. В этом случае в вышеприведенном выражении обычно можно пренебречь величиной 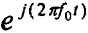 , учитывая при этом, что базовая система координат синхронно вращается с угловой частотой 2πf0. Тогда формула (1) выражается величиной
, учитывая при этом, что базовая система координат синхронно вращается с угловой частотой 2πf0. Тогда формула (1) выражается величиной 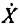 и формула математической модели динамического фазора представляет собой:
и формула математической модели динамического фазора представляет собой:
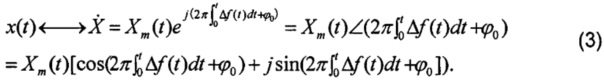
ROCOF имеет вид
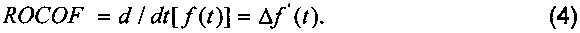
Таким образом, все параметры динамического фазора являются функцией времени. Для аппроксимации динамического входного сигнала в пределах одного окна времени применяют ряд Тейлора второго порядка ко всем параметрам фазора, чтобы смоделировать изменяющийся нелинейным образом волновой сигнал, как показано в выражениях (5-8):
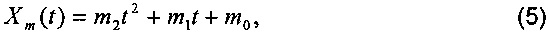


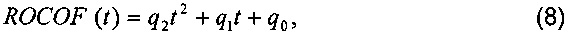
где m2=d2Xm(t)/dt2|t=0, m1=dXm(t)/dt|t=0, m0=Xm(0); n2=d2ϕ(t)/dt2|t=0, n1=dϕ(t)/dt|t=0, n0=ϕ(0); p2=d2f(t)/dt2|t=0, p1=df(t)/dt|t=0, p0=f(0); q2=d2ROCOF(t)/dr2|t=0, q1=dROCOF(t)/dt|t=0, q0=ROCOF(0).
Затем, на основе математической модели динамического фазора, анализируют явление утечки спектра, вызванное DFT в случае динамического фазора, и его влияние на измерения фазора. Предложено DFT с цифровым фильтром низких частот для устранения утечки спектра и получения исходного фазора (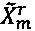 и
и 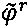 ). Частота среза цифрового фильтра низких частот, объединенного с DFT, составляет 2,5 Гц, при этом окно времени составляет 2 номинальных периода входного сигнала динамического фазора и расчетная частота исходного фазора составляет 400 Гц.
). Частота среза цифрового фильтра низких частот, объединенного с DFT, составляет 2,5 Гц, при этом окно времени составляет 2 номинальных периода входного сигнала динамического фазора и расчетная частота исходного фазора составляет 400 Гц.
Например, формула стандартного алгоритма DFT в отношении сигнала электрического тока выглядит как

где 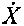 - измеренный фазор, N - объем выборки, x(k) - k-е значение выборки, f0 - номинальная частота и Δt- интервал выборки.
- измеренный фазор, N - объем выборки, x(k) - k-е значение выборки, f0 - номинальная частота и Δt- интервал выборки.
Можно считать, что вычислительный процесс DFT должен обеспечивать измерение фазора путем усреднения произведений выборок сигнала и ортогональных коэффициентов в окне времени. Тогда γ полагают равным
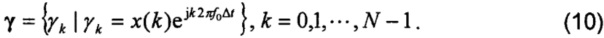
Вещественную и мнимую части γ следующим образом при этом выделяют:


где x={diag[x(k); n=0, 1, …, N-1]}, CT=[cos[2πf0(0)Δt], cos[2πf0(1)Δt], …, cos[2nf0(N-1)Δt]], ST=[sin[2πf0(0)Δt], sin[2πf0(1)Δt], …, sin[2πf0(N-1)Δt]]. Здесь Cx и Sx относятся к коэффициентам фазора, которые существенны для характеристики измерения DFT. При этом формула (1) может быть перезаписана с коэффициентами фазора следующим образом:
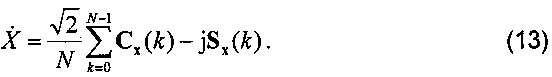
Если входной сигнал статичен и имеет номинальную частоту
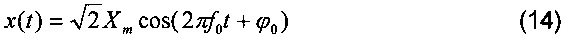
то Cx и Sx
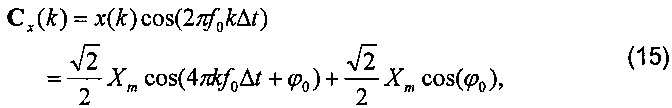
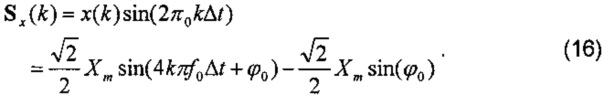
В соответствии с выражениями (15) и (16) при увеличении k коэффициенты фазора состоят из компоненты 2f0 и компоненты постоянного тока. Путем усреднения коэффициентов фазора в одном цикле сигнала компонента 2f0 может быть исключена и затем может быть получен действительный фазор, как показано в формуле (17). Это алгоритм DFT с одним циклом.
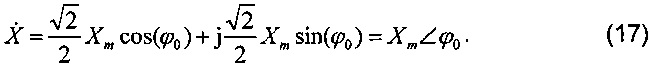
Алгоритм DFT широко используют из-за того, что он позволяет исключать гармоники и извлекать основную волну. Однако если частота смещается от номинального значения, то будет происходить утечка спектра. В частности, если частота изменяется в зависимости от времени, то трудно устранить утечку спектра. Кроме того, при поступлении динамического сигнала также будет происходить утечка спектра.
Прежде всего, используют формулу (1) в качестве входного сигнала, тогда Cx и Sx будут
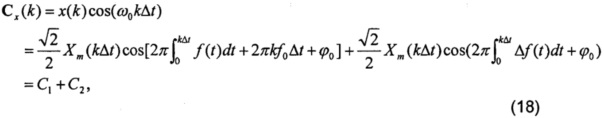
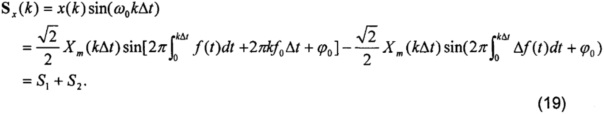
Реальный фазор должен походить на формулу (3), которая составлена из C2 и S2 согласно формуле (18) и формуле (19). Однако C1 и S1 не могут быть устранены, так как их частоты больше не являются кратными f0. Поэтому происходит утечка спектра.
Как показано в формулах (18) и (19), все частоты частотных компонент, приводящих к утечке спектра, находятся вблизи 2f0, в то время как частоты частотных компонент, составляющих реальный фазор, относительно низки. Согласно требованиям для PMU Р-класса, содержащимся в IEEE стандарте С37.118.1, все значения Δf и f1 составляют менее 2 Гц, и для сохранения низкочастотных компонент может быть осуществлен фильтр низких частот, в то время как высокочастотные компоненты фильтруются в коэффициентах фазора. По этой причине в варианте осуществления настоящего изобретения предложен усовершенствованный алгоритм DFT с цифровым фильтром низких частот для устранения утечки спектра и получения исходного фазора (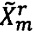 и
и 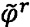 ). Формула выглядит следующим образом:
). Формула выглядит следующим образом:
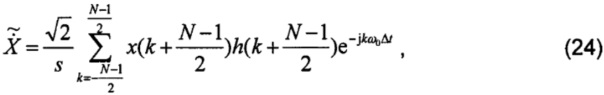
где 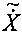 - рассчитываемый фазор,
- рассчитываемый фазор, 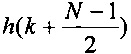 - коэффициенты фильтра нижних частот и
- коэффициенты фильтра нижних частот и 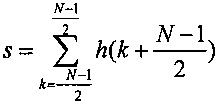 . Следует отметить, что k начинается с -(N-1)/2, потому что положение метки времени установлено в середине окна времени.
. Следует отметить, что k начинается с -(N-1)/2, потому что положение метки времени установлено в середине окна времени.
Переписав формулу (24) с коэффициентом фазора, получают:
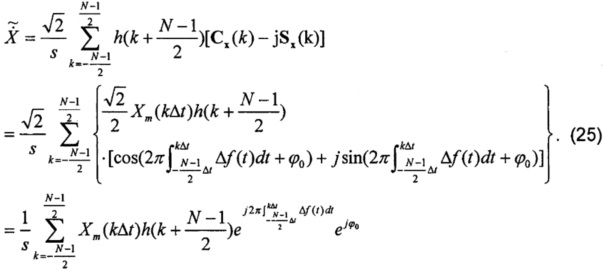
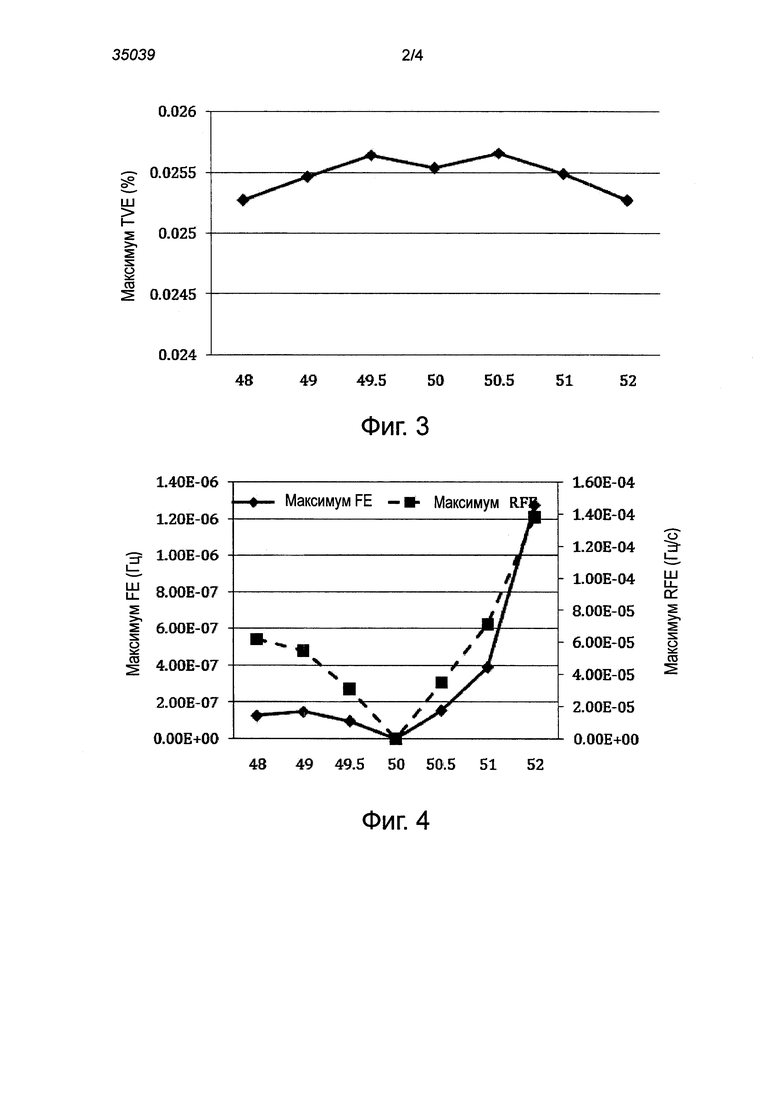
Можно заметить, что, несмотря на то, что утечка спектра устранена, амплитуда 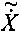 зависит от Xm(t), Δf(t) и коэффициентов фильтра. Точный фазор, который выражается как
зависит от Xm(t), Δf(t) и коэффициентов фильтра. Точный фазор, который выражается как 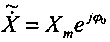 , может быть получен, только если Xm(t) является константой и Δf(t)=0. Иначе существует ошибка измерения амплитуды. Тем не менее, коэффициенты фильтра считают величинами, фиксированными для выполняемого алгоритма. Ошибка вычисления амплитуды связана только с Δf(t). Зависимость между ними может быть принята и аппроксимирована в виде квадратичной функции путем подбора кривой для результатов моделирования, как показано на фиг.2, где
, может быть получен, только если Xm(t) является константой и Δf(t)=0. Иначе существует ошибка измерения амплитуды. Тем не менее, коэффициенты фильтра считают величинами, фиксированными для выполняемого алгоритма. Ошибка вычисления амплитуды связана только с Δf(t). Зависимость между ними может быть принята и аппроксимирована в виде квадратичной функции путем подбора кривой для результатов моделирования, как показано на фиг.2, где 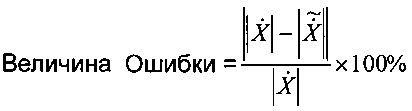
Этап 12: Входной сигнал динамического фазора аппроксимируют с использованием ряда Тейлора второго порядка. Находят линейную зависимость между ошибками измерения, вызванными усредняющим эффектом DFT, и коэффициентами второго порядка ряда Тейлора. Затем используют упомянутую линейную зависимость для калибровки исходных ошибок измерения. Наконец, могут выполнять точные измерения динамического фазора.
На этом этапе, прежде всего, аппроксимируют входной сигнал динамического фазора с использованием ряда Тейлора второго порядка. Находят линейную зависимость между ошибками измерения, вызванными усредняющим эффектом DFT, и коэффициентами второго порядка ряда Тейлора. Затем используют упомянутую линейную зависимость для калибровки исходных ошибок измерения. Наконец, выполняют точные измерения динамического фазора.
В частности, во-первых, вычисляют по способу наименьших квадратов коэффициенты ряда Тейлора второго порядка для входного сигнала динамического фазора и получают исходную частоту, ROCOF (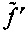 и
и  ), и их коэффициенты ряда Тейлора второго порядка. Повторно вычисляют все параметры динамического фазора в соответствии с коэффициентами ряда Тейлора второго порядка.
), и их коэффициенты ряда Тейлора второго порядка. Повторно вычисляют все параметры динамического фазора в соответствии с коэффициентами ряда Тейлора второго порядка.
Во-вторых, уточняют параметры исходного динамического фазора для получения 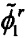 ,
, 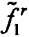 и
и 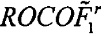 .
.
Затем выполняют статическую коррекцию амплитуды исходного динамического фазора для получения 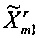 в соответствии с
в соответствии с 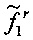 и выполняют динамическое измерение фазора
и выполняют динамическое измерение фазора 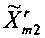 путем динамической калибровки.
путем динамической калибровки.
Например, путем выполнения DFT с фильтром низких частот, как указано в этапе 11, вычисляют исходный фазор, который устойчив к утечке спектра. Однако из-за предположения, что фазор находится в равновесном состоянии, измерение исходного фазора все еще является недостаточно точным для динамических входных сигналов, что не отвечает требованиям упомянутого стандарта.
В течение колебаний энергетической системы амплитуда, угол сдвига фаз, частота и ROCOF изменяются нелинейно.
Заменяя Xm(t) в формуле (25) выражением (5) и предполагая для упрощения процесса получения производной Δf(t)=0, формулу (25) можно перезаписать в следующем виде:
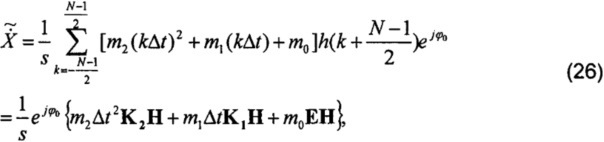
где 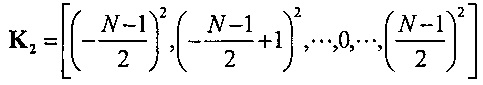 ,
, 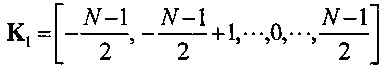 ,
, 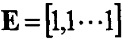 и
и 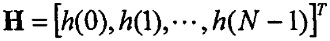
Поскольку коэффициенты фильтра являются симметричными, H может быть выражен как
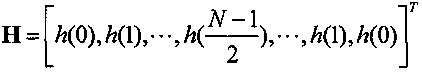 .
.
Таким образом,
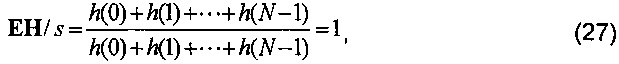
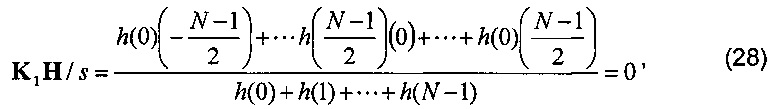
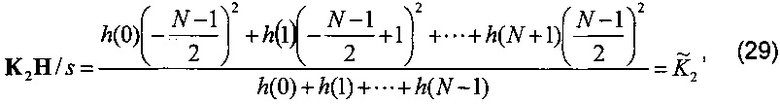
где 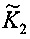 - средневзвешенное значение K2. Заменив относительные переменные в формуле (26) выражениями (27), (28), (29), получим
- средневзвешенное значение K2. Заменив относительные переменные в формуле (26) выражениями (27), (28), (29), получим

Поскольку метка времени установлена в середине окна времени, действительный фазор будет 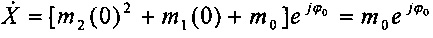 . Таким образом, ошибка измерения амплитуды фазора
. Таким образом, ошибка измерения амплитуды фазора
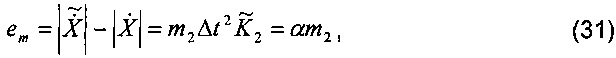
где em - ошибка измерения амплитуды, 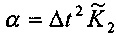 . Для алгоритма, выполняемого в устройстве, интервал выборки и коэффициенты фильтра являются фиксированными, то есть Δt и
. Для алгоритма, выполняемого в устройстве, интервал выборки и коэффициенты фильтра являются фиксированными, то есть Δt и 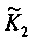 постоянны. Следовательно, ошибка измерения амплитуды фазора имеет линейную зависимость от m2. Кроме того, коэффициент наклона линейной зависимости зависит от фильтра низких частот.
постоянны. Следовательно, ошибка измерения амплитуды фазора имеет линейную зависимость от m2. Кроме того, коэффициент наклона линейной зависимости зависит от фильтра низких частот.
Для компенсации ошибки измерения сначала необходимо вычислить m2. В предположении, что фазор “М” измерений амплитуды, вычисленный по формуле (20), имеет вид
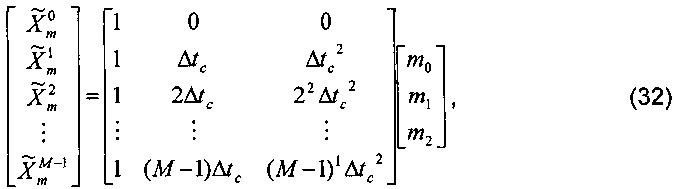
где  - r-е измерение амплитуды фазора, Δtc - интервал расчета фазора. Вышеупомянутая формула может быть записана в матричном представлении как
- r-е измерение амплитуды фазора, Δtc - интервал расчета фазора. Вышеупомянутая формула может быть записана в матричном представлении как

где Т - матрица коэффициентов. Неизвестную матрицу Cm вычисляют по способу взвешенных наименьших квадратов (WLS):

Опять же, поскольку метка времени установлена в середине, повторно вычисляют 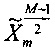 для получения аппроксимированной кривой:
для получения аппроксимированной кривой:
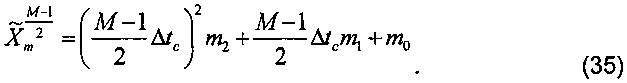
Затем вычисленный m2 используют для калибровки 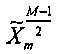 . Компенсирующий коэффициент α может быть определен модельными экспериментами.
. Компенсирующий коэффициент α может быть определен модельными экспериментами.
Аналогично, этим способом с использованием измеренного фазора ( ) может быть вычислен также n2. Затем выполняют измерения первоначальной частоты и ROCOF:
) может быть вычислен также n2. Затем выполняют измерения первоначальной частоты и ROCOF:
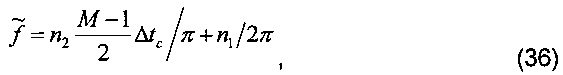

В течение времени изменения ϕ(t), f(t) и ROCOF(t) ошибки их измерения также линейно связаны с коэффициентами ряда Тейлора второго порядка для каждой из этих величин. Эти ошибки могут быть проверены результатами моделирования.
Кроме того, в варианте осуществления изобретения для рассматриваемого конкретного случая в стандартное DFT вводят цифровой фильтр низких частот для устранения утечки спектра и явления искажения частоты, которые вызваны динамическими входными сигналами. Однако цифровой фильтр низких частот нарушает характеристики стандартного DFT, что может устранить гармоники, кратные целому числу. Поэтому после получения точных измерений динамического фазора применяют второй цифровой фильтр низких частот, чтобы избавиться от влияния гармоник и белых шумов. Затем могут быть выполнены с более высокой точностью измерения фазора, то есть 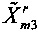 ,
, 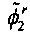 ,
, 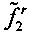 и
и  . N′ является длиной окна времени второго цифрового фильтра низких частот. Поскольку для устройства PMU Р-класса требуется более высокая скорость реакции для ступенчатых сигналов, порядок второго цифрового фильтра оказывается ниже. Однако он все еще достаточен для создания эффекта устранения гармонических помех.
. N′ является длиной окна времени второго цифрового фильтра низких частот. Поскольку для устройства PMU Р-класса требуется более высокая скорость реакции для ступенчатых сигналов, порядок второго цифрового фильтра оказывается ниже. Однако он все еще достаточен для создания эффекта устранения гармонических помех.
Для рассматриваемого конкретного случая частота среза второго цифрового фильтра низких частот составляет 2,5 Гц. Для обеспечения высокой скорости динамической реакции окно времени устанавливают величиной 27,5 миллисекунд.
Для проведения испытания способом моделирования для вышеупомянутого способа измерения использованы конкретные варианты осуществления настоящего изобретения. В частности:
В стандарте IEEE С37.118.1 четко определены максимальные ошибки при измерении фазора, а также статические и динамические тесты для имитирования статических и динамических процессов в энергетической системе. Предложенный вариант выполнения способа синхрофазорного измерения в соответствии с настоящим изобретением был подвергнут имитационному тесту в условиях отклонения частоты, гармонических искажений, колебаний, рассинхронизации и замыканий. Показано сравнение с предельными ошибками согласно стандарту, чтобы продемонстрировать преимущество предложенного способа. Для выполнения алгоритма номинальная частота составляет 50 Гц, скорость выдачи отчетов составляет 50 Гц и частота выборки составляет 1200 Гц. N=48, M=7, N'=10. Матрица Cm в формуле (34) может быть вычислена предварительно, при этом при оценке фазора может использоваться способ таблиц подстановки. Полная вычислительная нагрузка при расчете фазора, частоты и ROCOF составляет приблизительно 296 операций умножения и 237 операций суммирования.
1) Тест частотного сканирования
Различные режимы работы энергетической системы могут вызывать дрейф частоты относительно ее номинального значения. Кроме того, замыкания могут приводить к большим отклонениям частоты. В этой секции исследована точность измерения предложенного алгоритма в отношении сигналов с отклонением частоты. Диапазон изменения частоты входного сигнала составляет 48-52 Гц и остается неизменным во время каждого состояния. В тесте частотного сканирования, в соответствии с IEEE С37.118.1а, максимальная суммарная векторная ошибка (TVE) ограничена в пределах 1%, максимальная ошибка частоты (FE) составляет 0,005 Гц и максимальная ошибка ROCOF (RFE) равна 0,1 Гц/с. Соответствующие измерения показаны на фиг. 3 и 4. На фиг. 3 изображена максимальная TVE для различных основных частот при моделировании теста частотного сканирования, выполненного в соответствии с этим вариантом осуществления изобретения. На фиг. 4 изображены максимальные ошибки частоты и ROCOF для различных основных частот при моделировании теста частотного сканирования, выполненного в соответствии с этим вариантом осуществления изобретения. Можно заметить, что предложенный алгоритм достигает намного лучшей точности, чем это определено требованиями IEEE С37.118.1а.
2) Тест влияния гармоник
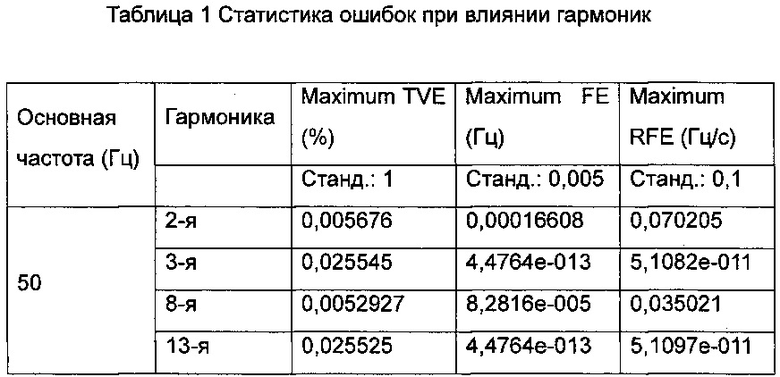
В этой секции для исследования характеристики восприимчивости предложенного алгоритма к гармоникам использован сигнал энергетической системы с частотой 50 Гц, содержащий 2-ю, 3-ю, 8-ю и 13-ю гармоники в количестве 1%. В Таблице 1 также показаны допустимые ошибки согласно стандарту (станд.).
Результаты измерения для каждого случая гармонического искажения представлены в Таблице 1. Можно заметить, что для гармоник четного порядка ошибки больше, чем для гармоник нечетного порядка. Однако ошибки значительно ниже требуемых предельных значений, что демонстрирует устойчивость предложенного способа к гармоническим искажениям.
3) Тест модуляции
Тест модуляции выполняют для отражения изменений амплитуды и угла сдвига фаз сигнала напряжения, когда энергетическая система генерирует колебания. Как правило, в узле электрической сети амплитуда и угол сдвига фаз напряжений прямой последовательности должны колебаться одновременно, при этом эти две модуляции находятся в противофазе. Во время теста амплитуда и угол сдвига фаз сигнала изменяются как синусоидальная функция. Ошибка может иметь максимум там, где нелинейные участки являются самыми резкими (пик или впадина колебания и т.д.).
В этом тесте считается, что глубина модуляции амплитуды составляет 10%, глубина модуляции угла сдвига фаз составляет 0,1 рад, частота модуляции изменяется от 0,1 до 2 Гц. В тесте модуляции, согласно IEEE С37.118.1а, максимальная TVE ограничена величиной 3%, максимальная ошибка частоты (FE) составляет 3 Гц. Ошибки измерения показаны на фиг. 5, 6 и 7. На фиг. 5 показана максимальная TVE для различных частот модуляции при моделировании теста модуляции, выполненного в соответствии с этим вариантом осуществления изобретения. На фиг. 6 показана максимальная ошибка частоты для различных частот модуляции при моделировании теста модуляции, выполненного в соответствии с этим вариантом осуществления настоящего изобретения. На фиг. 7 показана максимальная ошибка ROCOF для различных частот модуляции при моделировании теста модуляции, выполненного в соответствии с этим вариантом осуществления настоящего изобретения. Можно заметить, что все показанные на фиг.5-7 ошибки измерений непрерывно увеличиваются при увеличении частоты модуляции, потому что в пределах одного окна времени сигнал изменяется все быстрее. Тем не менее, предложенный алгоритм показывает возможность точного динамического отслеживания по сравнению с предельными ошибками, указанными в IEEE С37.118.1а.
4) Тест линейного изменения частоты
Тест линейного изменения частоты имитирует рассинхронизацию энергетической системы, что отличается от теста частотного сканирования, в котором основная частота сигнала изменяется от 48 до 52 Гц со скоростью 1 Гц/с. Из этого теста можно заметить, что способ измерения, предложенный в настоящем изобретении, обеспечивает возможность точного измерения фазора, частоты и скорости изменения частоты при непрерывном изменении частоты, как показано в Таблице 2. 
5) Тест ступенчатого изменения
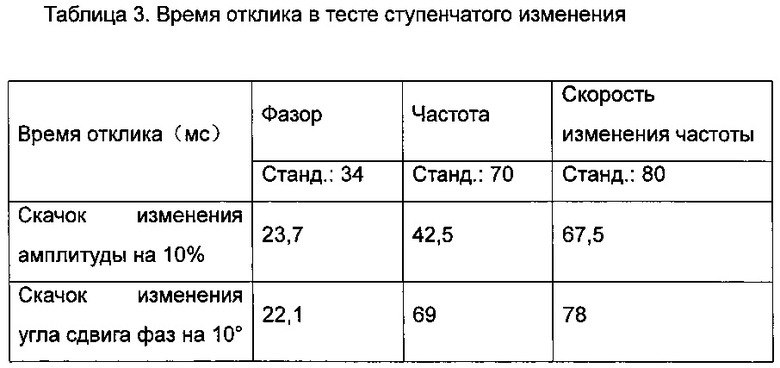
Внезапные изменения амплитуды и угла сдвига фаз сигналов напряжения и тока могут произойти при возникновении замыканий или операций переключения в энергетических системах. Для устройств PMU Р-класса скорость реакции крайне важна для динамического мониторинга безопасности энергетической системы.
В этом тесте входной сигнал изменяли путем скачкообразного изменения амплитуды на 10% и путем скачкообразного изменения угла сдвига фаз на 10°. Время реакции в каждом случае показано в Таблице 3. Можно видеть, что время реакции фазора удовлетворяет требованиям стандартов.
Таким образом, способ измерения в соответствии с рассмотренным вариантом осуществления настоящего изобретения обеспечивает возможность точных расчетных измерений фазора в условиях отклонения частоты, колебания мощности и рассинхронизации. Кроме того, способ имеет высокую скорость реакции и устойчив в отношении целочисленной гармоники и нецелочисленных гармоник.
Вышеприведенное описание раскрывает только предпочтительный вариант частного случая осуществления данного изобретения. Однако объем правовой охраны настоящего изобретения не ограничен указанным частным случаем осуществления. Подразумевается, что любые изменения или замены в пределах сущности изобретения, которые могут быть сделаны любым специалистом в области техники, к которой относится настоящее изобретение, включены в объем правовой охраны изобретения. Таким образом, при определении объема правовой охраны изобретения следует руководствоваться формулой изобретения.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ и устройство для выполнения синхронизированных векторных измерений | 2019 |
|
RU2788340C2 |
| СПОСОБ ИЗМЕРЕНИЯ ЧАСТОТНОГО СДВИГА МЕЖДУ РАДИОСИГНАЛАМИ | 2017 |
|
RU2668342C2 |
| УСТРОЙСТВО, СПОСОБ И КОМПЬЮТЕРНАЯ ПРОГРАММА ДЛЯ СВОБОДНО ВЫБИРАЕМЫХ СДВИГОВ ЧАСТОТЫ В ОБЛАСТИ ПОДДИАПАЗОНОВ | 2013 |
|
RU2595889C1 |
| ИЗМЕРЕНИЕ ВЛАЖНОГО ГАЗА | 2007 |
|
RU2453816C2 |
| СПОСОБ ИЗМЕРЕНИЯ УХОДА ЧАСТОТЫ НЕСУЩЕЙ В СИГНАЛЕ ДАЛЬНЕГО ЭХА В КОММУТИРУЕМОМ ДВУХПРОВОДНОМ КАНАЛЕ ТЕЛЕФОННОЙ СЕТИ ОБЩЕГО ПОЛЬЗОВАНИЯ | 2007 |
|
RU2345373C1 |
| ОЦЕНКА ПАРАМЕТРОВ ТЕПЛОВОЙ МОДЕЛИ ЛИНИИ ЭЛЕКТРОПИТАНИЯ | 2007 |
|
RU2430457C2 |
| Способ обработки сигналов с дискретным преобразованием Фурье половины цикла | 2024 |
|
RU2829331C1 |
| СПОСОБ ИЗМЕРЕНИЯ ДАЛЬНОСТИ И РАДИАЛЬНОЙ СКОРОСТИ В РЛС С ЗОНДИРУЮЩИМ СОСТАВНЫМ ПСЕВДОСЛУЧАЙНЫМ ЛЧМ ИМПУЛЬСОМ | 2014 |
|
RU2553272C1 |
| ПРЕЦИЗИОННОЕ ИЗМЕРЕНИЕ ФОРМЫ КОЛЕБАНИЙ | 2009 |
|
RU2526889C2 |
| ДЕМПФИРОВАНИЕ ЭЛЕКТРОМАГНИТНЫХ КОЛЕБАНИЙ В СИСТЕМАХ ЭНЕРГОСНАБЖЕНИЯ | 2008 |
|
RU2461944C2 |
Изобретение относится к способу синхрофазорного измерения для использования в устройстве измерения фазоров (PMU) Р-класса. Упомянутый способ измерения основывают на математической модели динамического фазора. Конструируют цифровой фильтр низких частот для коэффициентов фазора, объединенный с DFT. Этот фильтр устраняет утечку спектра, вызванную входными сигналами динамического фазора, причем после устранения утечки спектра могут провести измерения исходного фазора. Динамический фазор аппроксимируют с использованием ряда Тейлора второго порядка. Исследуют линейную зависимость между ошибками измерения, вызванными усредняющим эффектом DFT, и коэффициентами ряда Тейлора второго порядка. Затем используют упомянутую линейную зависимость для компенсации исходных ошибок измерения в динамических условиях. Техническим результатом при реализации заявленного способа измерения является возможность точного и быстрого измерения фазора как в статических, так и в динамических условиях. Точность упомянутого способа измерения не только удовлетворяет техническим требованиям соответствующих стандартов, но и на порядок превышает требования этих стандартов. 4 з.п. ф-лы, 3 табл., 7 ил.
1. Способ синхрофазорного измерения для использования в устройстве измерения фазоров (PMU) Р-класса со следующими характеристиками:
упомянутый способ измерения основывают на математической модели динамического фазора, конструируют цифровой фильтр низких частот для коэффициентов фазора, объединенный с дискретным преобразованием Фурье (DFT) и устраняющий утечку спектра, вызванную входными сигналами динамического фазора, при этом после устранения утечки спектра могут проводить измерения исходного фазора;
причем динамический фазор аппроксимируют с использованием ряда Тейлора второго порядка, исследуют линейную зависимость между ошибками измерения, вызванными усредняющим эффектом DFT, и коэффициентами ряда Тейлора второго порядка и используют линейную зависимость для компенсации исходных ошибок измерения в динамических условиях, при этом могут получить точные измерения динамического фазора.
2. Способ по п. 1, в котором исследование линейной зависимости между ошибками измерения, вызванными усредняющим эффектом DFT, и коэффициентами ряда Тейлора второго порядка, использование упомянутой линейной зависимости для коррекции исходных ошибок измерения в динамических условиях и возможное выполнение точных измерений динамического фазора включают в себя:
вычисление по способу наименьших квадратов коэффициентов ряда Тейлора второго порядка входного сигнала динамического фазора и получение исходной частоты, скорости изменения частоты (ROCOF) и их коэффициентов ряда Тейлора второго порядка, при этом все параметры входного сигнала динамического фазора повторно вычисляют в соответствии с упомянутыми коэффициентами ряда Тейлора второго порядка;
калибровку исходных параметров динамического фазора и статическую коррекцию амплитуды исходного динамического фазора, проведение точных измерений динамического фазора путем динамической калибровки.
3. Способ по п. 1, который, после выполнения точных измерений динамического фазора, дополнительно включает в себя:
введение второго цифрового фильтра низких частот для уменьшения эффекта от гармоник и белого шума и дополнительно для получения измерений фазора с более высокой точностью.
4. Способ по п. 1, в котором частота среза цифрового фильтра низких частот, объединенного с дискретным преобразованием Фурье (DFT), составляет 2,5 Гц, окно времени составляет два номинальных периода динамического входного сигнала и расчетная частота исходного фазора составляет 400 Гц.
5. Способ по п. 3, в котором частота среза второго цифрового фильтра низких частот составляет 2,5 Гц и окно времени составляет 27,5 мс.
| "New Standards for Test and Calibration of Phasor Measurement Units", 2012 NCSL International Workshop and Symposium | |||
| US 20140028116 A1, 30.01.2014 | |||
| US 7444248 B2, 28.10.2008 | |||
| " Model Estimation of Electric Power Systems by Phasor Measurement Units Data", January 2012. |
Авторы
Даты
2017-04-04—Публикация
2014-04-18—Подача