Изобретение относится к области информационно-вычислительной техники и может найти применение в испытательных системах, спектральных анализаторах и системах автоматизации научных исследований.
Известен цифровой вычислитель синуса и косинуса [АС 419896 СССР, 1974], содержащий счетчик аргумента, вход которого соединен со входом устройства и первым входом блока управления, генератор тактовых импульсов, выход которого соединен с вторым входом блока управления, первый, второй, третий и четвертый выходы которого подключены к первому и второму входам соответственно сумматора приращений синуса и сумматора приращений косинуса, формирователь знаков квадрата. Его выход соединен с первыми входами реверсивных счетчиков синуса и косинуса, вход - с первым выходом счетчика аргумента.
Его недостатком является техническая сложность.
Наиболее близким техническим решением к заявляемому является цифровой вычислитель синуса и косинуса по [АС 682905 СССР, 1979], содержащий дешифратор, вход которого подключен ко второму выходу счетчика аргумента, выход - к третьему входу блока управления. Выходы сумматоров синуса и косинуса подсоединены ко вторым входам реверсивных счетчиков синуса и косинуса, а третьи входы - к их выходам соответственно.
Его недостатком является низкая точность функционального преобразования по закону синуса и косинуса.
Задачей настоящего изобретения является повышение точности функционирования.
Технический результат - точное воспроизведение цифровых отсчетов гармонических сигналов при последовательном увеличении аргумента.
Технический результат достигается предложенным цифровым генератором, содержащим дешифратор, счетчик аргумента, вход которого соединен с входом устройства и первым входом блока управления, генератор тактовых импульсов, выход которого подключен к второму входу блока управления, первый, второй, третий и четвертый выходы которого подсоединены к первому и второму входам соответственно сумматора приращений синуса и сумматора приращений косинуса, формирователь знаков квадранта, выходы которого соединены с первыми и третьими входами реверсивных счетчиков синуса и косинуса, а вход - с выходом счетчика аргумента, причем выходы сумматоров приращений синуса и косинуса подключены к вторым входам реверсивных счетчиков синуса и косинуса, а третьи входы сумматоров приращений синуса и косинуса - к выходам соответственно реверсивных счетчиков косинуса и синуса.
В сумматоры приращений синуса и косинуса добавлены в качестве младших, (s+1)-х разрядов одноразрядные сумматоры, управляемые старшими разрядами реверсивных счетчиков синуса и косинуса, соответственно. Это позволит обеспечить точное воспроизведение цифровых отсчетов синуса и косинуса.
Это является новым техническим решением в технике цифровых вычислительных устройств, поскольку результаты проведенного заявителем анализа аналогов и прототипа не позволили выявить признаки, тождественные всем существенным признакам данного изобретения.
Предложенный цифровой генератор имеет изобретательский уровень, так как из опубликованных научных данных и существующих технических решений явным образом не следует, что заявляемая совокупность блоков, узлов и связей между ними позволяет повысить точность функционирования.
Предложенный цифровой генератор промышленно применим, поскольку его техническая реализация возможна с использованием типовых элементов микроэлектронной техники (интегральных логических элементов).
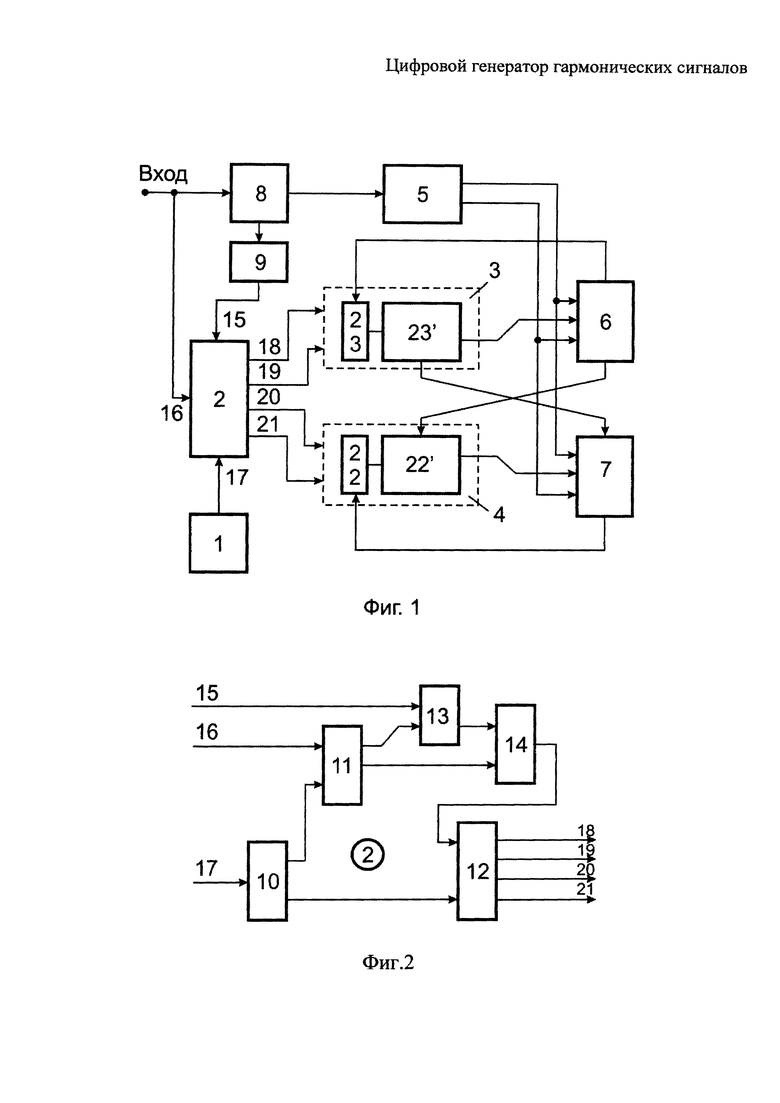
На фиг. 1 изображена структурная схема цифрового генератора гармонических сигналов, на фиг. 2 - то же для его блока управления.
Цифровой генератор гармонических сигналов содержит генератор тактовых импульсов 1, блок 2 управления, сумматоры приращений синуса 3 и косинуса 4, формирователь 5 знаков квадрантов, реверсивные счетчики синуса 6 и косинуса 7, счетчик 8 аргумента, дешифратор 9, одноразрядные сумматоры 22 и 23, находящиеся в составе каждого из сумматоров 3 и 4 в качестве их младшего, (s+1)-го разряда. Остальные s разрядов каждого из сумматоров приращений 3 и 4 составляют сумматоры 22' и 23' соответственно.
Блок 2 управления содержит делитель 10 частоты, первый 11 и второй 12 распределители импульсов, логические элементы И 13 и ИЛИ 14, входы блока управления 15, 16, 17, выходы - 18, 19, 20, 21.
В основу принципа действия предлагаемого генератора положены формулы, обеспечивающие повышение точности за счет численного интегрирования дифуравнений по методу трапеций [Булатникова И.Н. Целочисленные алгоритмы генерации гармонических сигналов // Изв. вузов, Северо-Кавказский регион, Техн. науки, 2005, №3, с. 13-17].
Их сущность заключается в следующем. Обозначим 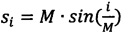 и
и 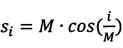 , М - масштабный коэффициент
, М - масштабный коэффициент 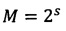 (s - разрядность результата), i - номер итерации и одновременно величина аргумента в масштабе 1:М.
(s - разрядность результата), i - номер итерации и одновременно величина аргумента в масштабе 1:М.
Тогда приращения величин Si и Ci на единичном интервале (i, i+1) будут следующими:


Формулы (1) и (2) получены на основе усреднения производных в начале и конце единичного интервала между соседними итерациями. При этом учтено, что производная от синуса равна косинусу, а производная от косинуса равна минус синус.
Упрощая, имеем систему уравнений


Решая ее относительно ΔSi и ΔCi, получаем


Упростим знаменатель (4М2>>1), и, разделив на 4М2, имеем
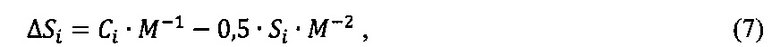
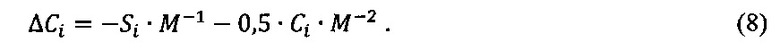
Окончательно, учтя, что 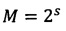 , имеем
, имеем
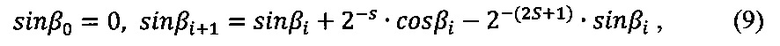
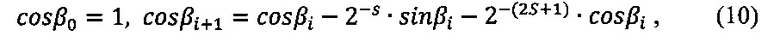
где S - разрядность выходных результатов; i - номер итерации и цена одного импульса аргумента в масштабе 1:2S.
Алгоритмы (9) и (10) позволяют формировать отчеты с помощью сумматоров приращений синуса 3 и косинуса 4, а также реверсивных счетчиков синуса 6 и косинуса 7.
Приращения для этих счетчиков (+1, -1 младшего разряда) формируются как сигналы переполнения сумматоров. Реверсивные счетчики синуса и косинуса подсчитывают значение функции, прибавляя или вычитая приращения из текущего значения функции в зависимости от квадранта. Так, для функции синуса в первом и третьем квадрантах реверсивный счетчик должен быть включен на сложение, а во втором и четвертом - на вычитание, для функции косинуса во втором и четвертом квадрантах - на сложение и в первом и в третьем - на вычитание. Устройство работает следующим образом.
При поступлении импульса на вход вычислителя запускается первый распределитель 11 импульсов в блоке 2 управления. Первый импульс с распределителя 11 импульсов поступает на первый вход логического элемента 13 И, на второй вход которого подается разрешение с дешифратора 9, соответствующее ряду значений аргумента, при которых происходит дополнительный цикл расчета. Дешифратор 9 служит корректирующей цепью для обеспечения соответствия значений синуса и косинуса аргумента.
Импульс с логического элемента 13 И через логический элемент 14 ИЛИ запускает второй распределитель 12 импульсов, при каждом запуске которого формируются четыре сдвинутых во времени импульса, обеспечивающих один цикл расчета функций синуса и косинуса.
Второй импульс с первого распределителя 11 импульсов через логический элемент 14 ИЛИ запускает второй распределитель 12 импульсов, при каждом запуске которого формируются четыре сдвинутых во времени импульса, обеспечивающих один цикл расчета функций синуса и косинуса.
Второй импульс с первого распределителя 11 импульсов через элемент 14 ИЛИ обеспечивает второй цикл расчета. Формирование значений функций синуса и косинуса осуществляется по тактам второго распределителя 12 импульсов. По первому и второму импульсам второго распределителя 12 производится управление суммированием числа, поступающим из реверсивного счетчика 7 косинуса.
Импульс переноса старшего разряда сумматора приращения 3 синуса, возникающий при переполнении сумматора, поступает в реверсивный счетчик 6 синуса.
Управление переключением осуществляется формирователем 5 знаков квадрантов. Третьим и четвертым тактами со второго распределителя 12 импульсов осуществляется управление суммированием числа, содержащего в сумматоре приращений 4 косинуса с числом, поступающим из реверсивного счетчика 6 синуса. Импульс переноса старшего разряда сумматора приращений 4 косинуса, возникающий при переполнении сумматора, поступает в реверсивный счетчик 7 косинуса, который включается на вычитание на углах 0, π и на сложение 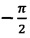 ,
, 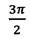 .
.
Третьим импульсом с первого распределителя 11 импульсов обеспечивается установ начальных значений функций в реверсивных счетчиках 6, 7 и сумматорах приращений 3, 4 синуса и косинуса в момент смены квадранта. Одновременно, в реверсивных счетчиках синуса 6 и косинуса 7 сигналы переполнения подаются в младшие, (s+1)-ые разряды одноименных сумматоров приращений 3 и 4, т.е. на одноразрядные сумматоры 22 и 23, соответственно, состыкованные с s-разрядными сумматорами 22/ и 23/.
Сумматоры приращений 3,4 приращений синуса и косинуса являются типовыми и для своей работы требуют два такта сдвинутых во времени, для суммирования и записи результата суммирования в регистр хранения, чем обеспечивается режим накопления.
Блок 2 управления содержит делитель 10 частоты импульсов от генератора 1 тактовых импульсов. Деление частоты необходимо для осуществления вычислительного процесса. Так, частота импульсов с делителя 10 частоты на второй распределитель 12 импульсов может быть выбрана, например, в четыре раза большей, чем на первый распределитель 11 импульсов.
Использование дополнительных одноразрядных сумматоров позволило в два раза снизить максимальную абсолютную погрешность цифрового генерирования гармонических сигналов.
| название | год | авторы | номер документа |
|---|---|---|---|
| Цифровой вычислитель синуса и косинуса | 1977 |
|
SU682905A1 |
| Цифровой вычислитель функций синуса и косинуса | 1976 |
|
SU781817A1 |
| Обратимый преобразователь координат | 1982 |
|
SU1035617A1 |
| Синусно-косинусный функциональный преобразователь | 2016 |
|
RU2631978C1 |
| Преобразователь угловых перемещений в код | 1985 |
|
SU1311024A1 |
| Цифровой генератор гармоническихфуНКций | 1979 |
|
SU840858A1 |
| Цифровой генератор гармонических функций | 1983 |
|
SU1164686A1 |
| Цифровой генератор гармонических функций | 1981 |
|
SU1001069A1 |
| Синусно-косинусный цифровой преобразователь | 2016 |
|
RU2625609C1 |
| Цифровой генератор гармонических колебаний | 1981 |
|
SU972487A1 |
Изобретение относится к области информационно-вычислительной техники и может найти применение в испытательных системах, спектральных анализаторах. Технический результат - повышение точности воспроизведения цифровых отсчетов гармонических сигналов при последовательном увеличении аргумента. Цифровой генератор гармонических сигналов содержит генератор тактовых импульсов, блок управления, сумматор приращений синуса, сумматор приращений косинуса, формирователь знаков квадрантов, реверсивные счетчики синуса и косинуса, счетчик аргумента, дешифратор, а также содержит в качестве младших разрядов одноразрядные сумматоры, размещенные в сумматорах приращений синуса и косинуса, связанные по входу со старшим разрядом одноименных реверсивных счетчиков синуса и косинуса. 2 ил.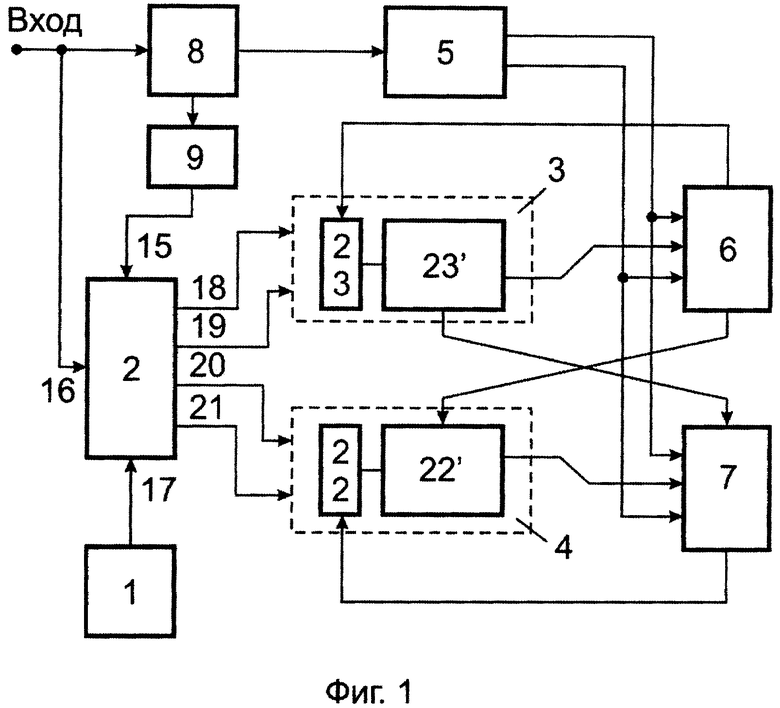
Цифровой генератор гармонических сигналов, содержащий дешифратор, счетчик аргумента, вход которого соединен с входом устройства и первым входом блока управления, генератор тактовых импульсов, выход которого подключен к второму входу блока управления, первый и второй, третий и четвертый выходы которого подсоединены к первому и второму входам соответственно сумматора приращений синуса и сумматора приращений косинуса, формирователь знаков квадрантов, выходы которого соединены с первыми и третьими входами реверсивных счетчиков синуса и косинуса, а вход - с выходом счетчика аргумента, причем выходы сумматоров приращений синуса и косинуса подключены к вторым входам реверсивных счетчиков синуса и косинуса, а третьи входы сумматоров приращений синуса и косинуса - к выходам соответственно реверсивных счетчиков косинуса и синуса, отличающийся тем, что дополнительно содержит в качестве младших разрядов одноразрядные сумматоры, размещенные в сумматорах приращений синуса и косинуса, связанные по входу со старшим разрядом одноименных реверсивных счетчиков синуса и косинуса, соответственно.
| Цифровой вычислитель синуса и косинуса | 1977 |
|
SU682905A1 |
| ЦИФРОВОЙ СИНТЕЗАТОР ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ | 2003 |
|
RU2239281C2 |
| СПОСОБ ИНТЕГРИРУЮЩЕГО АНАЛОГО-ЦИФРОВОГО ПРЕОБРАЗОВАНИЯ | 2014 |
|
RU2571549C1 |
| US 5070310 A, 03.12.1991. | |||
Авторы
Даты
2017-04-18—Публикация
2015-12-07—Подача