1. ОБЛАСТЬ ПРИМЕНЕНИЯ
Изобретение относится к области разработки, производства, эксплуатации и модернизации средств криптографической защиты информации в системах обработки информации различного назначения. Изобретение рекомендуется использовать при построении средств обработки и защиты информации, в том числе для обеспечения конфиденциальности, аутентичности и целостности информации при ее передаче, обработке и хранении в автоматизированных системах.
Понятие ортоморфизма было впервые введено в работах [21, 22], детально изучено в работах [24, 25], получило развитие после доклада [23]. Ортоморфизмы находят широкое применение во многих криптографических конструкциях [16, 17]. Их изучение тесно связано с задачами построения кодов аутентификации [7, 12], систем ортогональных латинских квадратов [10, 11, 14] и квазигрупп [3, 4]. В основе проекта американского стандарта хеш-функции, участника конкурса SHA-3, Edon-R [20] лежит использование квазигрупп и двух ортогональных латинских квадратов 8-го порядка. А некоторые атаки на блочные шифрсистемы существенно используют свойство неравномерности распределения суммы входных и выходных значений подстановки [13, 15, 18, 26].
2. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ И ОБОЗНАЧЕНИЯ
В настоящем описании используются следующие обозначения:
Vn - векторное пространство размерности n над полем GF(2), 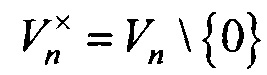 ;
;
S(Vn) - симметрическая группа;
Fn,m - множество всех отображений из Vn в Vm;
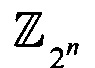 _ кольцо вычетов по модулю 2n;
_ кольцо вычетов по модулю 2n;
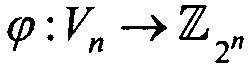 - биективное отображение, сопоставляющее элементу u=(un-1, …, u0) векторного пространства Vn элемент u=u0+u1⋅2+u2⋅22+…+un-1⋅2n-1 кольца
- биективное отображение, сопоставляющее элементу u=(un-1, …, u0) векторного пространства Vn элемент u=u0+u1⋅2+u2⋅22+…+un-1⋅2n-1 кольца 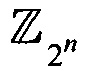 ;
;
 - отображение, обратное к отображению ϕ;
- отображение, обратное к отображению ϕ;
 - бинарная операция на Vn,, заданная правилом: для u, ν∈Vn справедливо равенство
- бинарная операция на Vn,, заданная правилом: для u, ν∈Vn справедливо равенство  ;
;
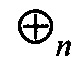 - бинарная операция покомпонентного сложения по модулю 2 элементов векторного пространства Vn;
- бинарная операция покомпонентного сложения по модулю 2 элементов векторного пространства Vn;
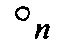 - бинарная операция умножения двух элементов Vn, заданная правилом: для u=(un-1, …, u0), ν=(νn-1, …, ν0)∈Vn справедливо равенство
- бинарная операция умножения двух элементов Vn, заданная правилом: для u=(un-1, …, u0), ν=(νn-1, …, ν0)∈Vn справедливо равенство 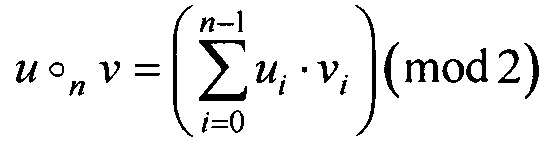 ;
;
В настоящем описании используются следующие термины с соответствующими определениями.
Определение 1. Подстановка g∈S(G) называется ортоморфизмом группы G, если отображение p: G→G, определяемое условием p(x)=x-1g(x), ∀x∈G, является подстановкой из S(G).
Упорядоченное множество значений отображения p будем называть строкой разностей подстановки g.
Определение 2. Разностной характеристикой 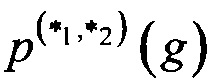 подстановки g∈S(Vn) относительно операций
подстановки g∈S(Vn) относительно операций  называется величина
называется величина 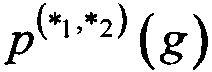 ,
,
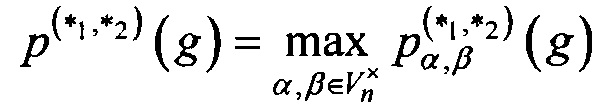 ,
,
где 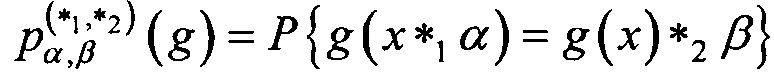 , а вероятность
, а вероятность 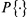 вычисляется при случайном равновероятном выборе x∈Vn. Матрицу размеров (2n-1)×(2n-1), составленную из коэффициентов
вычисляется при случайном равновероятном выборе x∈Vn. Матрицу размеров (2n-1)×(2n-1), составленную из коэффициентов 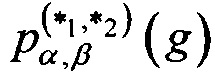 , будем называть разностной матрицей отображения g относительно операций
, будем называть разностной матрицей отображения g относительно операций 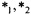 .
.
Повышение стойкости средств криптографической защиты относительно разностного метода криптографического анализа требует минимизации значения 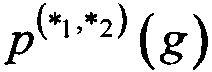 .
.
Определение 3. Линейной характеристикой δ(g) подстановки g∈S(Vn) называется величина δ(g),
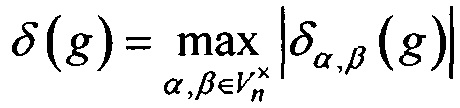 ,
,
где δα,β(g) - спектральный коэффициент подстановки g (преобладание линейного статистического аналога), который задается парой функций  . Величина преобладания вычисляется по формуле
. Величина преобладания вычисляется по формуле 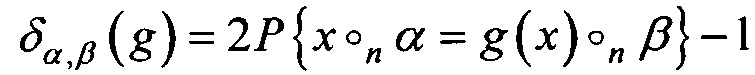 при x∈Vn, выбираемом случайно равновероятно. Матрицу размеров (2n-1)×(2n-1), составленную из коэффициентов |δα,β(g)|, будем называть матрицей модулей спектральных коэффициентов отображения g.
при x∈Vn, выбираемом случайно равновероятно. Матрицу размеров (2n-1)×(2n-1), составленную из коэффициентов |δα,β(g)|, будем называть матрицей модулей спектральных коэффициентов отображения g.
Повышение стойкости средств криптографической защиты относительно линейного метода криптографического анализа требует минимизации значения δ(g).
Определение 4. Обобщенной степенью нелинейности  подстановки g∈S(Vn) называется величина
подстановки g∈S(Vn) называется величина  ,
,
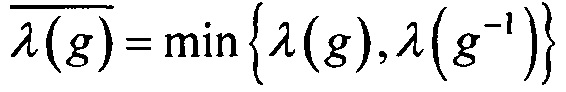 ,
,
где 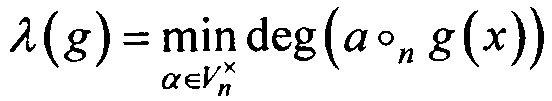 , a deg обозначает степень нелинейности многочлена Жегалкина булевой функции.
, a deg обозначает степень нелинейности многочлена Жегалкина булевой функции.
Определение 5. Размерностью пространства полиномиальных соотношений степени не выше i>0 подстановки g∈S(Vn) называется число r(i)(g),
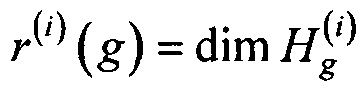 ,
,
где
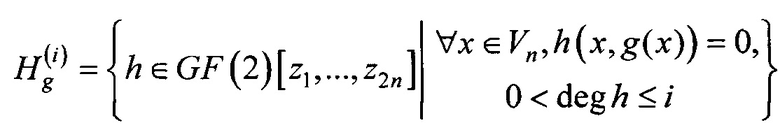 .
.
Определение 6. Минимальной степенью полиномиального соотношения подстановки g∈S(Vn) назовем число r(g),
r(g)=min{i|r(i)(g)>0}.
Замечание 7. Для подстановок g∈S(V8) в силу неравенства 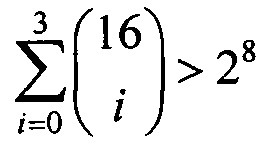 имеет место неравенство r(g)≤3.
имеет место неравенство r(g)≤3.
Повышение стойкости средств криптографической защиты относительно методов линеаризации требует минимизации величин r(i)(g), i=r(g), …, n и максимизации величин 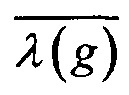 и r(g).
и r(g).
3. УРОВЕНЬ ТЕХНИКИ
Среди известных подходов к синтезу ортоморфизмов, действующих на векторном пространстве Vn достаточно большой размерности n(n≥6), можно выделить следующие.
Первый подход заключается в случайном поиске ортоморфизма g∈S(Vn) среди представителей некоторого известного класса (например, класса кусочно-линейных подстановок [2, 9]), содержащего существенно большую, относительно всей симметрической группы, долю подстановок, обладающих этим свойством. Подход удобен тем, что в некоторых известных классах подстановок сравнительно просто найти представителя с высокими значениями криптографических параметров. Недостатком подхода является наличие алгебраической структуры подстановок.
Второй подход состоит в использовании известных конструкций (например, двухраундовой схемы Фейстеля [19]), для которых доказано, что получаемые подстановки являются ортоморфизмами. Недостатком такого подхода являются низкие значения основных криптографических параметров и аналитического строения получаемых подстановок.
Третий подход состоит в случайном выборе линейного ортоморфизма g∈S(Vn). Подход заключается в генерации случайной двоичной матрицы An×n, вычислении матрицы  , где En×n - единичная матрица, проверки обратимости матриц An×n и Bn×n. Линейность построенных подстановок g резко ограничивает возможность их использования в криптографических приложениях.
, где En×n - единичная матрица, проверки обратимости матриц An×n и Bn×n. Линейность построенных подстановок g резко ограничивает возможность их использования в криптографических приложениях.
Общим недостатком представленных подходов является низкая степень полиномиальных соотношений получаемых подстановок (низкое значение параметра rg).
4. УСТРОЙСТВО ДЛЯ ПОСТРОЕНИЯ ОРТОМОРФИЗМОВ, ИСПОЛЬЗУЮЩЕЕ ПАРНЫЕ РАЗНОСТИ
Целью предлагаемого изобретения является построение из некоторого случайного или известного ортоморфизма большого числа новых аффинно неэквивалентных ортоморфизмов, имеющих высокие значения основных криптографических параметров и не имеющих полиномиальных соотношений низкой степени.
Для достижения цели предложено устройство, использующее парные разности.
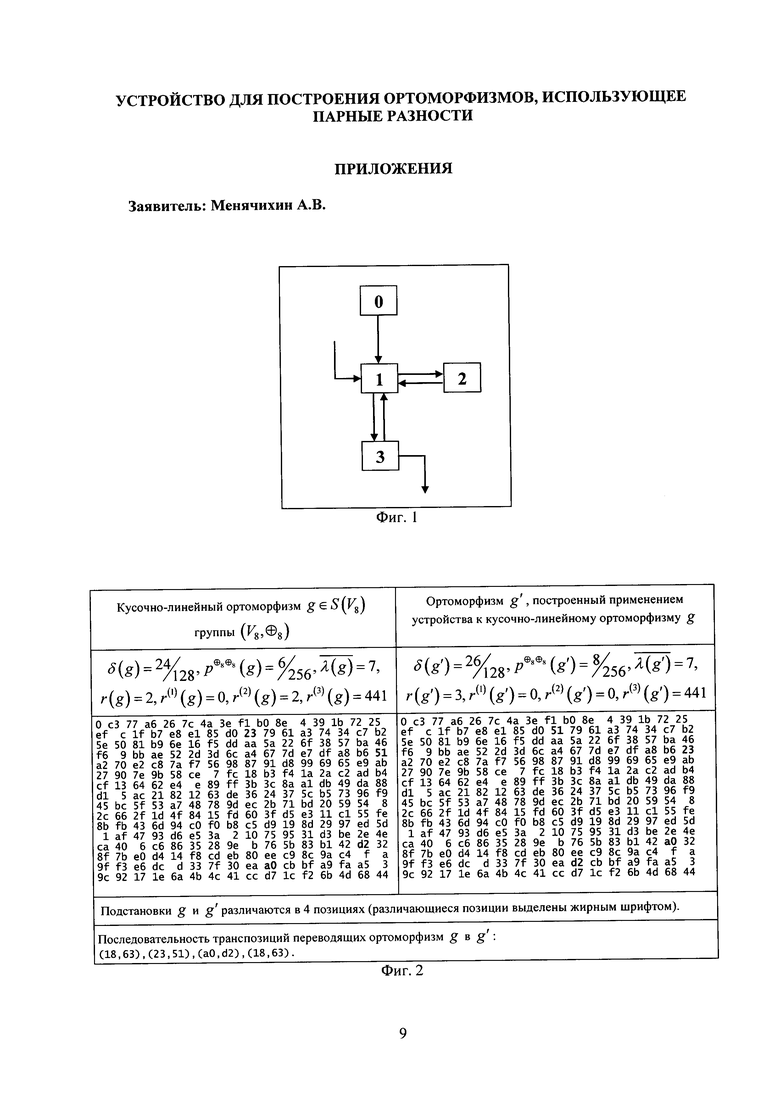
Устройство для построения ортоморфизмов, использующее парные разности (фиг. 1 приложений), содержит:
- блок выбора режима - 0;
- управляющий блок - 1;
- блок умножения подстановки на транспозицию - 2;
- оперативное запоминающее устройство (ОЗУ) - 3.
Блок выбора режима 0 состоит из переключателя и позволяет пользователю определить используемую группу 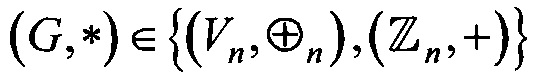 .
.
Управляющий блок 1 производит выборку, сравнение, изменение содержимого оперативного запоминающего устройства, принимает решение об остановке работы устройства или продолжении его работы.
Блок умножения подстановки на транспозицию 2 реализует стандартное произведение преобразований путем последовательного их выполнения.
Оперативное запоминающее устройство 3 выполняет сохранение текущей подстановки.
Устройство для построения ортоморфизмов, использующее парные разности, работает следующим образом.
На вход устройства поступает некоторый начальный ортоморфизм g0∈S(G), с вычисленной строкой разностей p, и произвольная транспозиция (x,y), x,y∈G, x<y.
1. Управляющий блок 1 выполняет последовательность действий:
1.1. вычисляет значения p0=x-1*g0(x), p1=y-1*g0(y) и записывает эти значения в оперативное запоминающее устройство 3;
1.2. передает ортоморфизм g0 и транспозицию (x,y) в блок умножения подстановки на транспозицию 2, который реализует стандартное произведение преобразований путем последовательного их выполнения:
g=(x,y)⋅g0;
1.3. полученная подстановка g записывается в ОЗУ 3.
2. Управляющий блок 1 выполняет последовательность действий:
2.1. осуществляет поиск в ОЗУ 3 элементов x',y'∈G, x'≠x, y'≠y со свойством
p(x')=(x')-1*g(x')=x-1*g(x)=p(x),
p(y')=(y')-1*g(y')=y-1*g(y)=p(y);
2.2. передает подстановку g и транспозицию (x',y') из ОЗУ 3 в блок умножения подстановки на транспозицию 2;
2.3. вычисляет значения p[x']=(y')-1*g(x') и p[y']=(x')-1*g(y');
3. Управляющий блок 1 записывает g в ОЗУ 3 и сравнивает полученные значения p[x'], p[y'] со значениями p0, p1,
- если p[x']=p0 или p[x']=p1, устройство заканчивает свою работу, на выход подается подстановка g;
- в противном случае, положить x=x', y=y' и устройство повторяет цикл операций, начиная с шага 2.
Работу устройства иллюстрирует следующий пример.
Пример. Переключатель блока 0 выставлен в позицию  .
.
Вход: ортоморфизм g0∈S(V4):
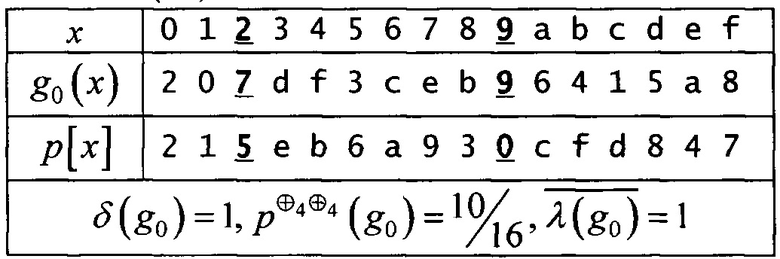
транспозиция (2,9).




Выход: ортоморфизм g∈S(V4):
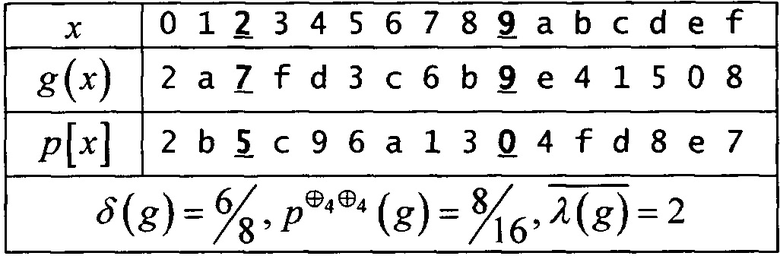
Реализация устройства может быть аппаратной, программной или аппаратно-программной.
5. ДОСТИГНУТЫЕ ТЕХНИЧЕСКИЕ РЕЗУЛЬТАТЫ
Устройство для построения ортоморфизмов, использующее парные разности, было использовано для построения новых ортоморфизмов, имеющих высокие значения основных криптографических параметров и не имеющих полиномиальных соотношений низкой степени. Некоторые из полученных результатов представлены далее.
Фиг. 2 приложений содержит ортоморфизм g'∈S(V8), построенный применением описанного устройства к ортоморфизму g∈S(V8) представителю класса кусочно-линейных подстановок [2, 9]. Из таблицы следует, что g' имеет актуальные (как в государственном стандарте Республики Беларусь «BelT» [1, 8]) значения основных криптографических параметров  ,
, 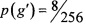 ,
,  , r(g')=3, r(3)(g')=441 и в отличие от исходного ортоморфизма не имеет квадратичных соотношений.
, r(g')=3, r(3)(g')=441 и в отличие от исходного ортоморфизма не имеет квадратичных соотношений.
Фиг. 3 приложений содержит ортоморфизм g'∈S(V8), построенный применением описанного устройства к некоторому, случайно выбранному, линейному ортоморфизму g∈S(V8). Из таблицы следует, что g' имеет актуальные (как в национальных стандартах РФ ГОСТ Р 34.11-2015 [5] и ГОСТ P 34.12-2012 [6]) значения основных криптографических параметров 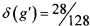 ,
, 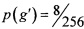 ,
, 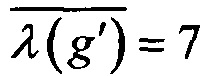 , r(g')=3, r(3)(g')=441.
, r(g')=3, r(3)(g')=441.
Устройство для построения ортоморфизмов было также применено более чем к сотне случайно выработанных линейных ортоморфизмов g∈S(V8). Каждый случай применения устройства позволил построить большое число новых аффинно неэквивалентных ортоморфизмов g∈S(V8) со следующими значениями криптографических параметров
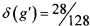 ,
, 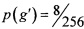 ,
, 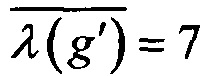 , r(g')=3, r(3)(g')=441.
, r(g')=3, r(3)(g')=441.
Достигаемым техническим результатом предложенного устройства является построение из некоторого случайного или известного ортоморфизма большого числа новых аффинно неэквивалентных ортоморфизмов, имеющих высокие значения основных криптографических параметров и не имеющих полиномиальных соотношений низкой степени.
ЛИТЕРАТУРА
[1] Агиевич С.В., Галинский В.А., Микулич Н.Д., Харин Ю.С. Алгоритм блочного шифрования BelT.
[2] Бугров А.Д. Кусочно-аффинные подстановки конечных полей. Прикладная дискретная математика, 2015, №4(30), сс. 5-23.
[3] Глухов М.М. О методах построения систем ортогональных квазигрупп с использованием групп. Математические вопросы криптографии, 2011, т. 2, №4, сс. 5-24.
[4] Глухов М.М. О применениях квазигрупп в криптографии. Прикладная дискретная математика, 2008, №2(2), сс. 28-32.
[5] ГОСТ Р 34.12-2015 Информационная технология. Криптографическая защита информации. Блочные шифры. - Москва: Стандартинформ, 2015.
[6] ГОСТ Р 34.11-2012 Информационная технология. Криптографическая защита информации. Функция хэширования. - Москва: Стандартинформ, 2012.
[7] Зубов А.Ю. Математика кодов аутентификации. М.: Гелиос АРВ, 2007, 480 с.
[8] СТБ 34.101.31-2011 Информационные технологии. Защита информации. Криптографические алгоритмы шифрования и контроля целостности. - Минск: Госстандарт, 2011.
[9] Тришин А.Е. О показателе нелинейности кусочно-линейных подстановок аддитивной группы поля 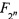 . Прикладная дискретная математика, 2015, №4(30), сс. 32-42.
. Прикладная дискретная математика, 2015, №4(30), сс. 32-42.
[10] Тришин А.Е. Способ построения ортогональных латинских квадратов на основе подстановочных двучленов конечных полей. Тезисы доклада Научный журнал «Обозрение прикладной и промышленной математики». М.: ТВП, 2008, Т. 15, №4.
[11] Тужилин М.Э. Латинские квадраты и их применение в криптографии. Прикладная дискретная математика. Приложение, 2012, №3(17), сс. 47-52.
[12] Черемушкин А.В. Криптографические протоколы. Основные свойства и уязвимости. М.: Изд. Центр «Академия», 2009, 272 с.
[13] Daemen J. Limitations of the Even-Mansour construction. ASIACRYPT, LNCS, vol. 739, pp. 495-498. Springer, 1991.
[14] Denes J., Keedwell A.D. Latin squares and their applications. London: English Univ. Press, 1975.
[15] Dinur I., Dunkelman O., Keller N., Shamir A. Key recovery attacks on 3-round Even-Mansour, 8-step LED-128, and full AES. http://eprint.iacr.org/2013/391, 2013.
[16] Evans A. Orthomorphisms graphs and groups, Springer-Verlag, Berlin, 1992.
[17] Evans A. Applications of complete mappings and orthomorphisms of finite groups.
[18] Even E. Mansour Y.A construction of a cipher from a single pseudorandom permutation. ASIACRYPT 1991. LNCS, vol. 739, pp. 210-224. Springer, Heidelberg (2013).
[19] Gilboa S., Gueron S. Balanced permutations Even-Mansour ciphers. arXiv preprint arXiv: 1409.0421, 2014.
[20] Gligoroski D., Odegard R.S., Mihova M., et al. Cryptographic Hash Function Edon-R // Proc. IWSCN. Trondheim, 2009, pp. 1-9.
[21] Johnson D.M., Dulmage A.L. and Mendelsohn N.S. Orthomorphisms of groups and orthogonal latin squares, I. Canad. J. Math. 13, 1961, pp. 356-372.
[22] Mann H.B. On orthogonal latin squares, Bull. Amer. Math. Soc. 50, 1944, pp. 249-257.
[23] Menyachikhin A. Spectral-linear and spectral-differential methods for generating cryptographicaly strong S-boxes. In: Pre-proceedings of CTCrypt'16-Yaroslavl, Russia, 2016. p. 232-252.
[24] Niederreiter H., Robinson K. Bol loops of order pq, Math. Proc. Cambridge Philos. Soc, 1981, pp. 241-256.
[25] Niederreiter H., Robinson K. Complete mappings of finite fields. J. Austral. Math. Soc. Ser., 1982, pp. 197-212.
[26] Nikolic I., Wang L., Wu S. Cryptoanalysis of Round-Reduce LED. In Fast Software Encryption, 2013. LNCS, vol. 8424, pp. 112-130. Springer, Heidelberg (2014).
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ построения узлов замены, использующий значения линейного и разностных спектров, и устройство его реализующее | 2016 |
|
RU2633132C1 |
| СПОСОБ КРИПТОГРАФИЧЕСКОГО ПРЕОБРАЗОВАНИЯ БЛОКОВ ЦИФРОВЫХ ДАННЫХ | 1997 |
|
RU2140709C1 |
| СПОСОБ КРИПТОГРАФИЧЕСКОГО ПРЕОБРАЗОВАНИЯ L-БИТОВЫХ ВХОДНЫХ БЛОКОВ ЦИФРОВЫХ ДАННЫХ В L-БИТОВЫЕ ВЫХОДНЫЕ БЛОКИ | 1997 |
|
RU2188513C2 |
| СПОСОБ КРИПТОГРАФИЧЕСКОГО ПРЕОБРАЗОВАНИЯ ЦИФРОВЫХ ДАННЫХ | 2003 |
|
RU2309549C2 |
| СПОСОБ КРИПТОГРАФИЧЕСКОГО ПРЕОБРАЗОВАНИЯ | 2014 |
|
RU2564243C1 |
| КРИПТОГРАФИЧЕСКИЙ ПРЕОБРАЗОВАТЕЛЬ ДВОИЧНЫХ ДАННЫХ | 2003 |
|
RU2239955C1 |
| СПОСОБ ИТЕРАТИВНОГО ШИФРОВАНИЯ БЛОКОВ ДАННЫХ | 1999 |
|
RU2140714C1 |
| СПОСОБ БЛОЧНОГО ШИФРОВАНИЯ ДВОИЧНОЙ ИНФОРМАЦИИ | 1998 |
|
RU2140712C1 |
| СПОСОБ ИТЕРАТИВНОГО ШИФРОВАНИЯ БЛОКОВ ДВОИЧНЫХ ДАННЫХ | 1999 |
|
RU2144268C1 |
| ИТЕРАТИВНЫЙ СПОСОБ БЛОЧНОГО ШИФРОВАНИЯ | 1999 |
|
RU2172075C1 |

Изобретение относится к области разработки, производства, эксплуатации и модернизации средств криптографической защиты информации в системах обработки информации различного назначения. Технический результат заключается в обеспечении построения из некоторого случайного или известного ортоморфизма большого числа новых аффинно неэквивалентных ортоморфизмов, имеющих высокие значения основных криптографических параметров и не имеющих полиномиальных соотношений низкой степени. Технический результат достигается за счет устройства для построения ортоморфизмов, состоящего из блока выбора режима, управляющего блока, блока умножения подстановки на транспозицию и оперативного запоминающего устройства. 3 ил.
Устройство для построения ортоморфизмов, состоящее из блока выбора режима, управляющего блока, блока умножения подстановки на транспозицию, оперативного запоминающего устройства, при этом блок выбора режима имеет выход, который соединен с управляющим блоком и предназначен для передачи в управляющий блок информации о групповой операции, выбранной пользователем в качестве режима работы устройства, управляющий блок имеет 4 входа, первый из которых является входом для начального ортоморфизма, поступающего на вход устройства, второй предназначен для получения информации о режиме работы устройства, третий предназначен для получения результатов умножения подстановки на транспозицию, четвертый предназначен для получения текущего содержимого оперативного запоминающего устройства, и два выхода, первый из которых соединен с блоком умножения подстановки на транспозицию и предназначен для передачи в этот блок подстановки и транспозиции, а второй соединен с оперативным запоминающим устройством и предназначен для обновления его содержимого, блок умножения подстановки на транспозицию имеет вход для получения от управляющего блока подстановки и транспозиции, и один выход, который соединен с управляющим блоком и предназначен для передачи в управляющий блок результатов умножения, оперативное запоминающее устройство имеет вход, для получения подстановки, определяемой в оперативное запоминающее устройство управляющим блоком, и два выхода, первый из которых соединен с управляющим блоком и предназначен для передачи содержимого в управляющий блок, а второй предназначен для передачи на выход устройства ортоморфизма, являющегося результатом работы устройства.
| СПОСОБ ФОРМИРОВАНИЯ И ПРОВЕРКИ ПОДЛИННОСТИ ЭЛЕКТРОННОЙ ЦИФРОВОЙ ПОДПИСИ, ЗАВЕРЯЮЩЕЙ ЭЛЕКТРОННЫЙ ДОКУМЕНТ | 2008 |
|
RU2401513C2 |
| СПОСОБ ГЕНЕРАЦИИ И ПРОВЕРКИ ПОДЛИННОСТИ ЭЛЕКТРОННОЙ ЦИФРОВОЙ ПОДПИСИ, ЗАВЕРЯЮЩЕЙ ЭЛЕКТРОННЫЙ ДОКУМЕНТ | 2008 |
|
RU2392736C1 |
| US 7499542 B2, 03.03.2009 | |||
| Способ обработки целлюлозных материалов, с целью тонкого измельчения или переведения в коллоидальный раствор | 1923 |
|
SU2005A1 |
| WO 00/10285 A1, 24.02.2000 | |||
| US 6035042 A, 07.03.2000. | |||
Авторы
Даты
2017-10-02—Публикация
2016-06-02—Подача