1. ОБЛАСТЬ ПРИМЕНЕНИЯ
Изобретение относится к области разработки, производства, эксплуатации и модернизации средств криптографической защиты информации в системах обработки информации различного назначения. Изобретение рекомендуется использовать при построении средств обработки и защиты информации, в том числе для обеспечения конфиденциальности, аутентичности и целостности информации при ее передаче, обработке и хранении в автоматизированных системах.
Нелинейное перемешивающее преобразование в современных шифр-системах реализуется, чаще всего, параллельным действием криптографических примитивов, получивших название узлов замены. Узлы замены действуют на двоичных векторах небольшой размерности n, как правило, n≤16.
От значений криптографических параметров нелинейных преобразований существенно зависит возможность применения многих методов анализа. А обоснованность и прозрачность выбора узлов замены часто определяет выбор того или иного средства криптографической защиты конечным пользователем. К числу основных криптографических параметров узлов замены относятся, прежде всего, линейная и разностные характеристики, степень нелинейности, минимальная степень полиномиальных соотношений между компонентами входного и выходного векторов.
2. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ И ОБОЗНАЧЕНИЯ
В настоящем описании используются следующие обозначения.
Vn - векторное пространство размерности n над полем GF(2), 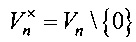 ;
;
S(Vn) - симметрическая группа;
Fn,m - множество всех отображений из Vn в Vm;
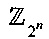 - кольцо вычетов по модулю 2n;
- кольцо вычетов по модулю 2n;
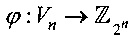 - биективное отображение, сопоставляющее элементу u=(un-1, …, u0) векторного пространства Vn элемент u=u0+u1⋅2+u2⋅22+…+un-1⋅2n-1 кольца
- биективное отображение, сопоставляющее элементу u=(un-1, …, u0) векторного пространства Vn элемент u=u0+u1⋅2+u2⋅22+…+un-1⋅2n-1 кольца 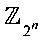 ;
;
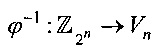 - отображение, обратное к отображению ϕ;
- отображение, обратное к отображению ϕ;
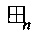 - бинарная операция на Vn заданная правилом:
- бинарная операция на Vn заданная правилом:
для u, v∈Vn справедливо равенство 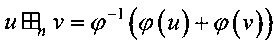 ;
;
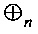 - бинарная операция покомпонентного сложения по модулю двух элементов векторного пространства Vn;
- бинарная операция покомпонентного сложения по модулю двух элементов векторного пространства Vn;
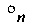 - бинарная операция умножения двух элементов Vn заданная правилом: для u=(un-1, …, u0), v=(vn-1, …, v0)∈Vn справедливо равенство
- бинарная операция умножения двух элементов Vn заданная правилом: для u=(un-1, …, u0), v=(vn-1, …, v0)∈Vn справедливо равенство 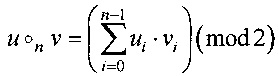 .
.
В настоящем описании используются следующие термины с соответствующими определениями.
Определение 1. Разностной характеристикой 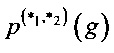 отображения g:Vn→Vm относительно операций
отображения g:Vn→Vm относительно операций 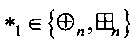 ,
, 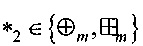 называется величина
называется величина 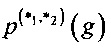 ,
, 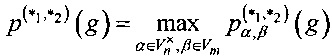 ,
,
где 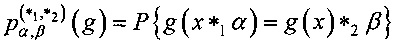 , а вероятность Р{⋅} вычисляется при случайном равновероятном выборе х∈Vn. Матрицу размеров (2n-1)×2m, составленную из коэффициентов
, а вероятность Р{⋅} вычисляется при случайном равновероятном выборе х∈Vn. Матрицу размеров (2n-1)×2m, составленную из коэффициентов 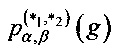 , будем называть разностной матрицей отображения g относительно операций *1, *2.
, будем называть разностной матрицей отображения g относительно операций *1, *2.
Повышение стойкости средств криптографической защиты относительно разностного метода криптографического анализа требует минимизации значения 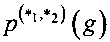 .
.
Определение 2. Линейной характеристикой δ(g) отображения g:Vn→Vm называется величина δ(g),
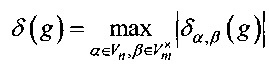 ,
,
где δα,β(g) - спектральный коэффициент отображения g (преобладание линейного статистического аналога), который задается парой функций 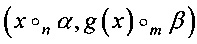 . Величина преобладания вычисляется по формуле
. Величина преобладания вычисляется по формуле 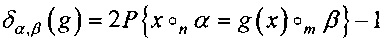 при x∈Vn, выбираемом случайно равновероятно. Матрицу размеров 2n×(2m-1), составленную из коэффициентов
при x∈Vn, выбираемом случайно равновероятно. Матрицу размеров 2n×(2m-1), составленную из коэффициентов 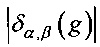 , будем называть матрицей модулей спектральных коэффициентов отображения g.
, будем называть матрицей модулей спектральных коэффициентов отображения g.
Повышение стойкости средств криптографической защиты относительно линейного метода криптографического анализа требует минимизации значения δ(g).
Определение 3. Степенью нелинейности λ(g) отображения g:Vn→Vm называется величина λ(g),
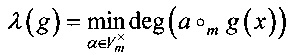 ,
,
где deg обозначает степень нелинейности многочлена Жегалкина булевой функции.
Замечание 4. В случае, когда g - биективное отображение, рассматривают обобщенную степень нелинейности 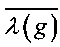 ,
,
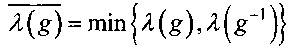 .
.
Определение 5. Размерностью пространства полиномиальных соотношений степени не выше i>0 отображения g:Vn→Vm называется число r(i)(g),
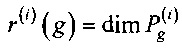 ,
,
где 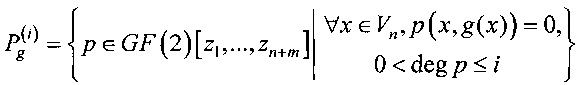 .
.
Определение 6. Минимальной степенью полиномиального соотношения отображения g:Vn→Vm назовем число r(g),
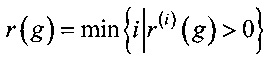
Замечание 7. Для биективных отображений g∈S(V8) в силу неравенства 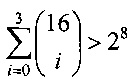 имеет место неравенство r(g)≤3.
имеет место неравенство r(g)≤3.
Повышение стойкости шифр-системы относительно методов линеаризации требует минимизации величин r(i)(g), i=r(g), …, n и максимизации величин 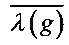 и r(g).
и r(g).
Разностные характеристики 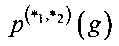 отображения g относительно операций
отображения g относительно операций 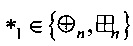 ,
, 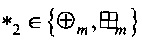 и линейная характеристика δ(g) есть максимальные значения, содержащиеся соответственно в разностных матрицах отображения g относительно операций *1, *2 и матрице модулей спектральных коэффициентов отображения g. Количество максимальных значений в разностных матрицах и количество максимальных значений в матрице модулей спектральных коэффициентов являются важнейшими параметрами заявляемого способа. В этой связи, следуя работе [38], определим разностный и линейный спектры отображения g.
и линейная характеристика δ(g) есть максимальные значения, содержащиеся соответственно в разностных матрицах отображения g относительно операций *1, *2 и матрице модулей спектральных коэффициентов отображения g. Количество максимальных значений в разностных матрицах и количество максимальных значений в матрице модулей спектральных коэффициентов являются важнейшими параметрами заявляемого способа. В этой связи, следуя работе [38], определим разностный и линейный спектры отображения g.
Для отображения g:Vn→Vm и чисел р∈Рn и δ∈Рn-2,
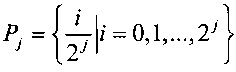 ,
, 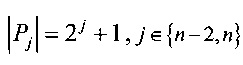 ;
;
определим множества
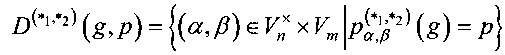 ;
;
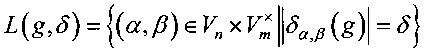 .
.
Определение 8. Разностным спектром отображения g:Vn→Vm относительно операций 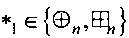 ,
, 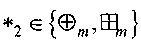 называется упорядоченное множество
называется упорядоченное множество
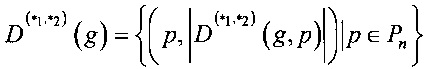 ,
, 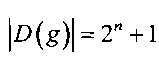 .
.
Определение 9. Линейным спектром отображения g:Vn→Vm называется упорядоченное множество
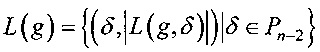 ,
, 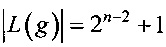 .
.
Под задачей комбинаторной оптимизации в настоящем описании понимается задача нахождения глобального оптимума (минимума) некоторой функции ƒ, т.е. такого аргумента iopt, что 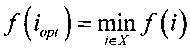 , где X - область определения функции.
, где X - область определения функции.
Функция ƒ носит название целевой функции.
Определение 10. Подстановка g g∈S(Vn) называется инволютивной (инволюцией), если для каждого х∈Vn справедливо равенство g(g(х))=х.
Определение 11. Элемент x∈Vn называется неподвижной точкой подстановки g∈S(Vn), если g(x)=x.
Множество всех инволютивных подстановок степени 2n без неподвижных точек обозначим через In,
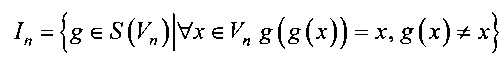 .
.
3. УРОВЕНЬ ТЕХНИКИ
Вопросы построения узлов замены с оптимальными и близкими к оптимальным значениями криптографических параметров активно изучаются как в отечественной специальной (например, [3-16, 18-22]), так и зарубежной литературе (например, [1, 2, 17, 27-29, 32, 34, 36, 38, 40-47]).
Среди известных способов построения узлов замены можно выделить три наиболее близких по своей сущности к заявляемому изобретению.
Первый способ заключается в выборе узла замены g0 среди представителей некоторого известного класса отображений (например, из класса экспоненциальных отображений [1, 35, 45], класса подстановочных двучленов [21], класса логарифмических [22] или кусочно-линейных подстановок [3, 20]) с последующим умножением g0 слева и справа на аффинные подстановки. Способ удобен тем, что в некоторых известных классах сравнительно просто найти подстановки с высокими значениями основных криптографических параметров. Умножение на невырожденные аффинные преобразования не меняет значения этих параметров. Недостатком подхода является ограниченность выбора и аналитическое строение получаемых узлов замены.
Второй способ состоит в применении к некоторому узлу замены g0 различных вариантов генетических алгоритмов, алгоритмов имитации отжига и градиентного спуска [33, 34, 36, 40]. Этот способ лишен недостатков первого, но имеет высокую трудоемкость и низкую вероятность получения за приемлемое время узлов g∈S(Vn) со значениями линейной δ(g) и разностных 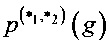 характеристик, близкими к оптимальным.
характеристик, близкими к оптимальным.
Третьим способом к построению узлов замены является способ случайного поиска [37] с заданным ограничением на значения криптографических параметров. Способ заключается в выработке узлов замены g с помощью генераторов псевдослучайных последовательностей (например, [39]) и вычислении значений криптографических параметров g. Алгоритм, реализующий указанный способ, заканчивает свою работу, когда значения криптографических параметров выработанного узла окажутся в необходимых пределах. Достоинством способа является отсутствие ярко выраженных закономерностей в строении получаемых узлов, в частности высокая вероятность отсутствия криптографических «закладок» и потенциальных слабостей. Главным недостатком - низкая вероятность получения за приемлемое время преобразования g со значениями линейной δ(g) и разностных 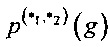 характеристик, близкими к минимально возможным.
характеристик, близкими к минимально возможным.
Существуют и другие, не столь универсальные, способы построения узлов замены, например, на основе рекуррентных последовательностей [2], АВ и APN - отображений [29, 44], и другие.
4. СПОСОБ ПОСТРОЕНИЯ УЗЛОВ ЗАМЕНЫ, ИСПОЛЬЗУЮЩИЙ ЗНАЧЕНИЯ ЛИНЕЙНОГО И РАЗНОСТНЫХ СПЕКТРОВ
Целью предлагаемого изобретения является построение с приемлемой трудоемкостью большого числа аффинно-неэквивалентных узлов замены с высокими значениями основных криптографических параметров из случайных отображений или известных узлов.
Для достижения цели предложен способ построения узлов замены, заключающийся в последовательном умножении некоторого начального узла на преобразования, выбор которых производится с помощью целевой функции, отличающийся тем, что в качестве параметров целевой функции используются значения линейного и разностных спектров. В конечном счете, как правило, это приводит к построению узлов замены, превосходящих по значениям основных криптографических параметров результаты применения других известных способов.
Пусть g0:Vn→Vm - некоторый начальный узел замены,
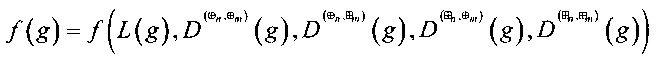 - целевая вектор-функция, определенная на множестве значений линейного и разностных спектров. На множестве значений целевой вектор-функции ƒ вводится отношение порядка.
- целевая вектор-функция, определенная на множестве значений линейного и разностных спектров. На множестве значений целевой вектор-функции ƒ вводится отношение порядка.
Обозначим через w1∈N - параметр способа, ограничивающий объем списка I
Вход: Узел замены g0:Vn→Vm, параметр w1∈N.
1. Для узла замены g0 вычислить значения:
- линейного спектра L(g0);
- разностных спектров 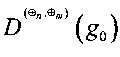 ,
, 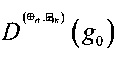 ,
, 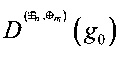 ,
, 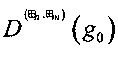 ;
;
- целевой функции
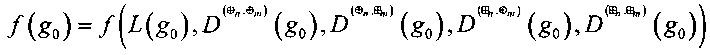
Инициализировать список I
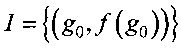 ,
,  .
.
2. По списку
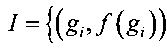 ,
, 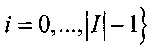
построить новый список I',
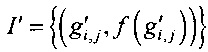 ,
, 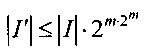 .
.
В список I' отбираются узлы 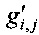 , полученные умножением узла gi на специальным образом выбираемые преобразования h1:Vn→Vn и h2:Vm→Vm:
, полученные умножением узла gi на специальным образом выбираемые преобразования h1:Vn→Vn и h2:Vm→Vm:
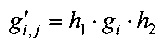 ,
, 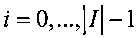 , j=j(h1,h2) - инъективное отображение;
, j=j(h1,h2) - инъективное отображение;
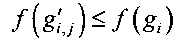 .
.
3.
3.1. Удалить из списка I' повторы.
3.2. Вычислить мощность полученного списка 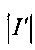 .
.
3.3. Список I' упорядочить по возрастанию значений 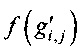 .
.
3.4. Элементы упорядоченного списка занумеровать индексами 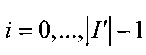 .
.
3.5. Вычислить числа
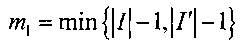 и
и 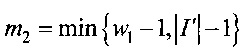 .
.
4. Элементы списка I' с индексами i=0, …, m1 сравнить с элементами списка I:
- если 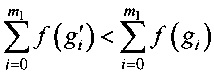 , то
, то
4.1. Очистить список I.
4.2. Инициализировать список I элементами списка I' с индексами i=0, …, m2.
4.3. Положить 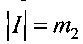 .
.
4.4. Перейти на шаг 2.
- в противном случае, содержимое списка I' с индексами 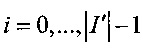 является результатом применения способа.
является результатом применения способа.
Выход: список,  ,
, 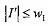 .
.
5. УСТРОЙСТВО, РЕАЛИЗУЮЩЕЕ СПОСОБ ПОСТРОЕНИЯ УЗЛОВ ЗАМЕНЫ
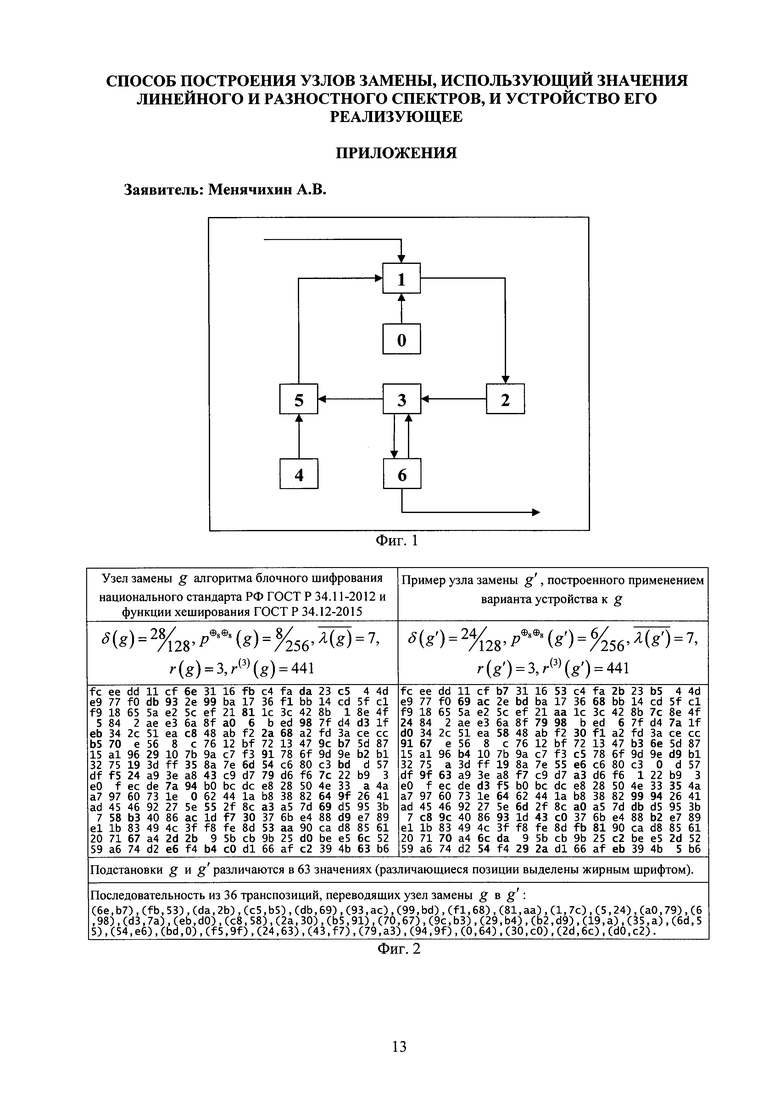
Устройство, реализующее способ построения узлов замены, использующий значения линейного и разностного спектров (фиг. 1 приложений), содержит:
- блок выбора режима - 0;
- блок вычисления криптографических параметров - 1;
- блок вычисления значений целевой функции - 2;
- управляющий блок - 3;
- блок выработки преобразований - 4;
- блок умножения узла замены на преобразование - 5;
- оперативное запоминающее устройство (ОЗУ) - 6.
Блок выбора режима 0 состоит из переключателя и позволяет пользователю определить режим работы устройства. Блок определяет спектр, вычисляемый блоком вычисления криптографических параметров,
Блок вычисления криптографических параметров 1 вычисляет значения линейной характеристики и разностных характеристик, линейного спектра и разностных спектров узла замены.
Блок вычисления значений целевой функции 2 вычисляет значение целевой вектор-функции, используя в качестве параметров значения линейного и разностного спектров узла замены.
Управляющий блок 3 производит выборку, сравнение, сортировку, изменение содержимого списков I и I' оперативного запоминающего устройства, на основании которого принимается решение об остановке работы устройства или продолжении его работы.
Блок выработки преобразований 4 реализует выработку транспозиций на множестве значений узла замены.
Блок умножения узла замены на преобразование 5 реализует стандартное произведение преобразований путем последовательного их выполнения.
Оперативное запоминающее устройство 6 выполняет сохранение текущих и вновь построенных узлов замены, с вычисленными параметрами, в списках I и I' соответственно.
Целевую вектор-функцию 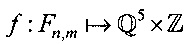 определим следующим образом
определим следующим образом
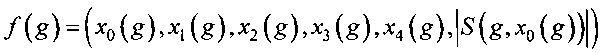 ,
,
где 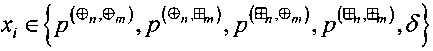 , i=0, … 4, xi≠xj, i≠j;
, i=0, … 4, xi≠xj, i≠j;
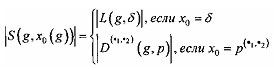 .
.
На множестве значений целевой вектор-функции ƒ введем отношение порядка:
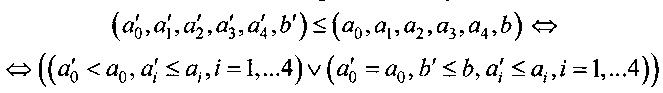 .
.
Устройство работает в режиме оптимизации исходного узла замены по одной из 5 криптографических характеристик. При необходимости оптимизации по нескольким характеристикам, устройство последовательно запускается в требуемых режимах, получая на вход результаты работы устройства в предшествующем режиме.
Устройство, реализующее способ, работает следующим образом.
На вход устройства поступает некоторый начальный узел замены g0.
1. Для узла замены g0 блоком 1 вычисляются значения:
- линейной характеристики δ(g0);
- линейного спектра L(g0);
- разностных характеристик 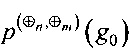 ,
, 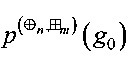 ,
, 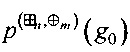 ,
, 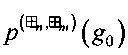 ;
;
- разностных спектров 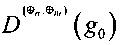 ,
, 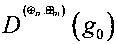 ,
, 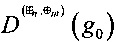 ,
, 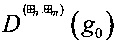 .
.
2. Узел замены g0 с криптографическими параметрами, вычисленными блоком 1, поступает на вход блока вычисления значений целевой вектор-функции 2. Блок 2, используя в качестве параметров значения линейного и разностного спектров узла замены, вычисляет значение целевой вектор-функции ƒ(g0).
3. Узел замены g0 со значением целевой вектор-функции ƒ(g0) вычисленным блоком 2, инициализирует список I оперативного запоминающего устройства 6.
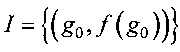 ,
, 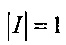 .
.
4. По списку I в ОЗУ 6 формируется новый список I'.
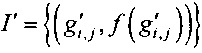 ,
, 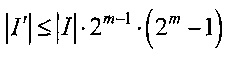
4.1. В список I' отбираются узлы 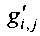 , полученные умножением узла gi на специальным образом выбираемые транспозиции, вырабатываемые блоком 4.
, полученные умножением узла gi на специальным образом выбираемые транспозиции, вырабатываемые блоком 4.
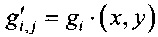 ,
,
где х, у∈Vm, х≤у, 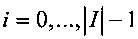 , j=j(x,y) - инъективное отображение.
, j=j(x,y) - инъективное отображение.
4.2. Узел замены 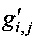 проходит через блок 1 и блок 2.
проходит через блок 1 и блок 2.
4.3. Если 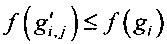 , то управляющий блок 3 записывает узел замены
, то управляющий блок 3 записывает узел замены 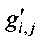 в список I' ОЗУ 6.
в список I' ОЗУ 6.
5. Управляющим блоком 3 выполняются следующие операции.
5.1. Список I' ОЗУ 6 очищается от повторов.
5.2. Вычисляется мощность полученного списка 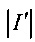 .
.
5.3. Список I' ОЗУ 6 упорядочивается по возрастанию значений 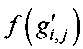 .
.
5.4. Элементы упорядоченного списка нумеруются индексами 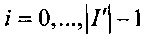 .
.
5.5. Вычисляются числа
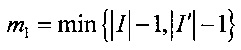 и
и 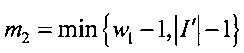 .
.
6. Элементы списка I' с индексами i=0, …, m1 сравниваются управляющим блоком 3 с элементами списка I:
- если 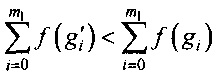 , то
, то
6.1. Очищается список I.
6.2. Список I инициализируется элементами списка I' с индексами i=0, …, m2.
6.3. Полагается 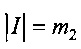 .
.
6.4. Устройство повторяет цикл операций, начиная с шага 4.
- в противном случае, устройство заканчивает свою работу, содержимое списка I' с индексами 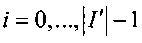 подается на выход устройства.
подается на выход устройства.
Результатом работы устройства являются узлы замены, содержащиеся в списке I'.
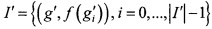 ,
, 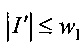 .
.
Реализация устройства, реализующего способ, может быть аппаратной, программной или аппаратно-программной.
Описанное устройство может быть модифицировано для построения инволютивных узлов замены без неподвижных точек. На вход устройства, в этом случае, поступает некоторая инволюция g∈In, а блок выработки преобразований 4 устройства реализует выработку пар транспозиций следующего вида
(x,y)(g(x), g(y)), где x, y∈Vm, x≤y, g(x)≠y.
6. ДОСТИГНУТЫЕ ТЕХНИЧЕСКИЕ РЕЗУЛЬТАТЫ
Варианты устройств, реализующих способ построения узлов замены, использующего значения линейного и разностных спектров, были применены к узлам замены, используемым в современных блочных шифр-системах. Некоторые из полученных результатов представлены далее.
Фиг. 2 приложений содержит пример узла замены g'∈S(V8), построенного применением описанного способа к узлу замены g∈S(V8) национальных стандартов РФ ГОСТ Р 34.11-2015 [6] и ГОСТ Р 34.12-2012 [7]. Из таблицы следует, что g' превосходит g по значениям двух основных криптографических параметров δ, 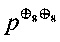 , сохранив оптимальными для данной размерности значения параметров
, сохранив оптимальными для данной размерности значения параметров 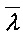 , r, r(3).
, r, r(3).
Фиг. 3 приложений содержит пример узла замены g'∈S(V8), построенного применением описанного способа к узлу замены g∈S(V8) государственного стандарта Республики Беларусь «BelT» [2, 17]. Из таблицы следует, что g' превосходит g по значениям трех основных криптографических параметров δ, 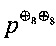 ,
, 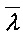 , сохранив оптимальными для данной размерности значения параметров r, r(3).
, сохранив оптимальными для данной размерности значения параметров r, r(3).
Фиг. 4 приложений содержит пример узла замены g'∈S(V8), построенного применением описанного способа к узлу замены g∈S(V8) алгоритма шифрования, разработанного АНБ США «Skipjack» [25, 47]. Из таблицы следует, что g' превосходит g по значениям трех основных криптографических параметров δ, 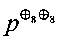 ,
, 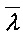 ,, сохранив оптимальными для данной размерности значения параметров r, r(3).
,, сохранив оптимальными для данной размерности значения параметров r, r(3).
Фиг. 5 приложений содержит пример инволютивного узла замены g'∈S(V8), построенного применением описанного способа к узлу замены g∈S(V8) алгоритма шифрования, участника конкурса NESSIE, «Khazad-0» [46]. Из таблицы следует, что g' превосходит g по значениям двух основных криптографических параметров δ, 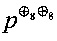 , сохранив оптимальными для данной размерности значения параметров
, сохранив оптимальными для данной размерности значения параметров 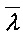 , r, r(3).
, r, r(3).
Способ построения узлов замены, использующий значения линейного и разностного спектров, был также применен более чем к сотне случайно выработанным биективным узлам g∈S(V8). Каждый случай их применения позволил за 50-65 транспозиций получать узлы замены g'∈S(V8) со следующими значениями криптографических параметров:
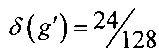 ,
, 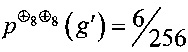 ,
, 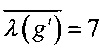 , r(g')=3, r(3)(g')=441.
, r(g')=3, r(3)(g')=441.
Достигаемым техническим результатом предложенного способа является построение с приемлемой трудоемкостью большого числа аффинно-неэквивалентных узлов замены с высокими значениями основных криптографических параметров из случайных отображений или известных узлов.
ЛИТЕРАТУРА
[1] Агиевич С.В., Афоненко А.А. О свойствах экспоненциальных подстановок. Вести НАН Беларуси, 2005, №1, сс. 106-112.
[2] Агиевич С.В., Галинский В.А., Микулич Н.Д., Харин Ю.С. Алгоритм блочного шифрования BelT.
[3] Бугров А.Д. Кусочно-аффинные подстановки конечных полей. Прикладная дискретная математика, 2015, №4 (30), сс. 5-23.
[4] Глухов М.М. О матрицах переходов разностей при использовании некоторых модулярных групп. Математические вопросы криптографии, 2013, том 4, выпуск 4, сс. 27-47.
[5] Глухов М.М. О методах построения систем ортогональных квазигрупп с использованием групп. Математические вопросы криптографии, 2011, том 2, выпуск 4, сс. 5-24.
[6] ГОСТ Р 34.12-2015 Информационная технология. Криптографическая защита информации. Блочные шифры. - Москва: Стандартинформ, 2015.
[7] ГОСТ Р 34.11-2012 Информационная технология. Криптографическая защита информации. Функция хэширования. - Москва: Стандартинформ, 2012.
[8] Дыгин Д.М., Лавриков И.В., Маршалко Г.Б., Рудской В.И., Трифонов Д.И., Шишкин В.А. О новом российском стандарте шифрования. Математические вопросы криптографии, 2015, том 6, выпуск 2, сс. 29-34.
[9] Малышев Ф.М. Дважды транзитивные XSL-семейства подстановок. Математические вопросы криптографии, 2010, том 1, выпуск 2, сс. 93-103.
[10] Малышев Ф.М. Двойственность разностного и линейного методов в криптографии. Математические вопросы криптографии, 2014, том 5, выпуск 3, сс. 35-47.
[11] Пичкур А.Б. Описание класса подстановок, представимых в виде произведения двух подстановок с фиксированным числом мобильных точек. Математические вопросы криптографии, 2012, том 3, выпуск 2, сс. 79-95.
[12] Пичкур А.Б. Описание класса подстановок, представимых в виде произведения двух подстановок с фиксированным числом мобильных точек II. Математические вопросы криптографии, 2013, том 4, выпуск 1, сс. 87-109.
[13] Погорелое Б.А. Группы подстановок. Часть 1 (обзор за 1981-95 гг.). Труды по дискретной математике, 1998, том 2, сс. 237-281.
[14] Погорелов Б.А. Пудовкина М.А. О расстояниях от подстановок до импримитивных групп при фиксированной системе импримитивности. Дискретная математика, 2013, том 25, выпуск 3, сс. 78-95.
[15] Сачков В.Н. Комбинаторные свойства дифференциально 2-равномерных подстановок, Математические вопросы криптографии, 2011, том 2, выпуск 2, сс. 95-118.
[16] Сачков В.Н. Случайные отображения с неподвижными элементами. Математические вопросы криптографии, 2015, том 6, выпуск 1, сс. 159-179.
[17] СТБ 34.101.31-2011 Информационные технологии. Защита информации. Криптографические алгоритмы шифрования и контроля целостности. - Минск: Госстандарт, 2011.
[18] Токарева Н.Н. Квадратичные аппроксимации специального вида для четырехразрядных подстановок в S-блоках. Прикладная дискретная математика, 2008, Т. 1., №1, сс. 50-54.
[19] Токарева Н.Н. О квадратичных аппроксимациях в блочных шифрах. Проблемы передачи информации, 2008, том 44, выпуск 3, сс. 105-127.
[20] Тришин А.Е. О показателе нелинейности кусочно-линейных подстановок аддитивной группы поля 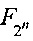 . Прикладная дискретная математика, 2015, №4(30), сс. 32-42.
. Прикладная дискретная математика, 2015, №4(30), сс. 32-42.
[21] Тришин А.Е. Способ построения ортогональных латинских квадратов на основе подстановочных двучленов конечных полей. Тезисы доклада Научный журнал «Обозрение прикладной и промышленной математики». М.: ТВП, 2008, Т. 15., №4.
[22] Шемякина О.В. Об оценке характеристик разбиений различных алгебраических структур. Сб. трудов конф. ИБРР-2011, СПб.: СПОИСУ, 2011, с. 137.
[23] Alekseychuk A., Kovalchuk L., Pal'chenko S. Cryptographic parameters of s-boxes that characterize the security of GOST-like block ciphers against linear and differential cryptanalysis. Zakhist Inform, 2007, 2, pp. 12-23.
[24] Alekseychuk A., Kovalchuk L. Upper bounds of maximum values of average differential and linear characteristic probabilities of Fiestel cipher with adder modulo 2m. Theory of Stochastic Processes, 2006, 12(28), pp. 20-32.
[25] Biham E., Biryukov A., Shamir A, Cryptanalysis of Skipjack Reduced to 31 Rounds Using Impossible Differentials, Advances in Cryptology, Proceedings of EUROCRYPT'99, Lecture Notes in Computer Science 1592, 1999, pp. 12-23.
[26] Blondeau C., Gerard B. Links between theoretical and effective differential probabilities: experiments on PRESENT. In: Ecrypt II Workshop on Tools for Cryptanalysis, 2010.
[27] Bogdanov A., Knudsen L.R., Leander G., Paar C., Poschmann A., Robshaw M.J.В., Seurin Y., and Vikkelsoe C. PRESENT: An ultra-lightweight block cipher. Lecture Notes in Computer Science, 2007, 4727: 450.
[28] Carlet C., Ding C. Nonlinearities of S-boxes. Finite fields and its applications, 2007, 13(1), pp. 121-135.
[29] Chabaud F., Vaudenay S. Links between differential and linear cryptoanalysis. EUROCRYPT, 1994, pp. 356-365.
[30] Daemen J, Rijmen V. Probability distributions of correlations and differentials in block ciphers. Journal on Mathematical Cryptology, 2007, 1(3), pp. 221-242.
[31] Daemen J., Rijmen V. The Design of Rinjdael: AES - The Advanced Encryption Standard / Springer, 2002.
[32] Evans A. Orthomorphisms graphs and groups, Springer-Verlag, Berlin, 1992.
[33] Goldberg D. Genetic Algorithms in search, optimization and machine learning // Addsion-Wesley, Reading, 1985.
[34] Izbenko Y., Kovtun V., Kuznetsov A. The Design of Boolean Functions by Modified Hill Climbing Method. In TNG'09: Proceeding of the 2009 Sixth International Conference on Information Technology: New Generations, pages 356-361, Washington, DC, USA, 2009. IEEE Computer Society.
[35] Jacobson Jr. M., Huber K. The MAGENTA Block Cipher Algorithm. NIST AES Proposol, 1998.
[36] Kazymyrov О.V., Kazymyrova V.N., Oliynykov R.V. A method for generation of high-nonlinear S-boxes based on gradient descent, Mat. Vopr. Kriptogr., 2014, Volume 5, Issue 2, pp. 71-78.
[37] Knuth D. The art of computer programming, vol. 2 (3rd ed.): seminumerical algorithms, Addison-Wesley Longman Publishing Co., Inc., Boston, 1997.
[38] Leander G, Poscmann A. On the classification of 4 bit s-boxes. Lecture Notes in Computer Science, 2007, vol. 4547, pp. 159-176.
[39] Matsumoto M., Nishimura T. Mersenne Twister: A 623-Dimensionally Equidistributed Uniform Pseudo-Random Generator. ACM Transactions On Modeling and Computer Simulation, 1998, Vol. 8, No. 1.
[40] Millan W., Clark A., Dawson E. Smart Hill Climbing Finds Better Boolean Functions, In Proceedings of the Workshop on Selected Areas on Cryptography, SAC'97, 1997, pp. 50-63.
[41] Millan W. How to Improve the Nonlinearity of Bijective S-boxes. Lect. Notes in Comp. Sci., 1998.
[42] Nyberg K. On the construction of Hihgly Nonlinear Permutations. Advances in Cryptology - EUROCRYPT'92. Proceeding, 1992.
[43] Nyberg K. Perfect nonlinear S-boxes. Advances in Cryptology - EUROCRYPT'91. Proceedings, 1991.
[44] Nyberg K., Knudsen L. Provable security against differential cryptanalysis. CRYPTO, 1992, pp. 566-574.
[45] Pieprzyk J. Non-linearity of Exponent Permutations. Advances in Cryptology - EUROCRYPT'89. Proceedings, 1990.
[46] Rijmen V., Barreto P. "The KHAZAD legacy-level block cipher," NESSIE submission, 2000.
[47] Skipjack and KEA Algorithm Specifications, Version 2.0. Available at the National Institute of Standards and Technology's web page, http://csrc.nist.gov/encryption/skipjack-kea/htm, 1998.


Изобретение относится к области разработки, производства, эксплуатации и модернизации средств криптографической защиты информации в системах обработки информации различного назначения. Технический результат – построение с приемлемой трудоемкостью большого числа аффинно-неэквивалентных узлов замены с высокими значениями основных криптографических параметров из случайных отображений или известных узлов. Устройство для построения узлов замены, состоящее из блока выбора режима, блока вычисления криптографических параметров, блока вычисления значений целевой вектор-функции, управляющего блока, блока выработки преобразований, блока умножения узла замены на преобразование, оперативного запоминающего устройства. 2 н. и 1 з.п. ф-лы, 5 ил.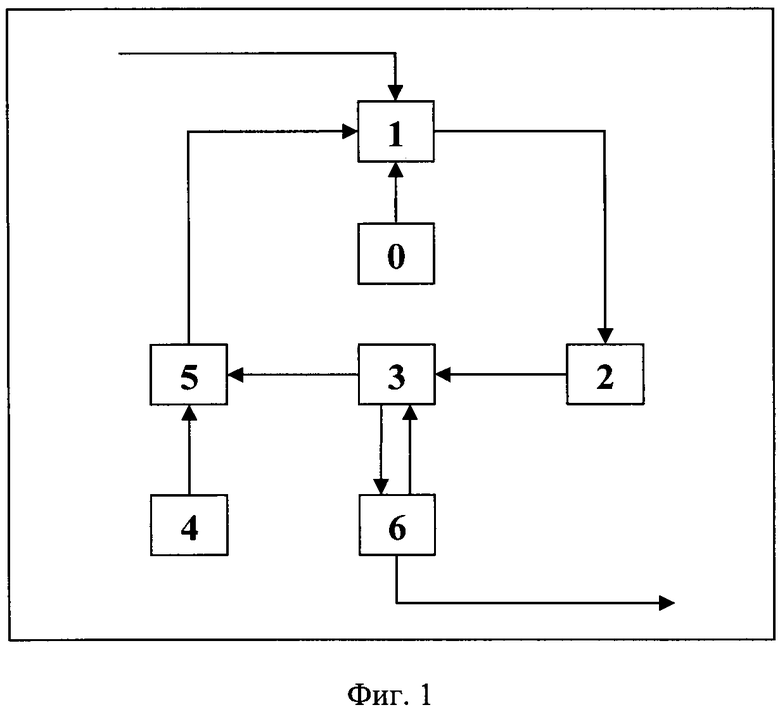
1. Способ построения узлов замены, заключающийся в последовательном умножении некоторого начального узла замены на преобразования, выбор которых производится с помощью целевой вектор-функции, отличающийся тем, что в качестве параметров целевой вектор-функции используются значения линейного и разностных спектров отображения, выраженных в виде упорядоченных множеств вида
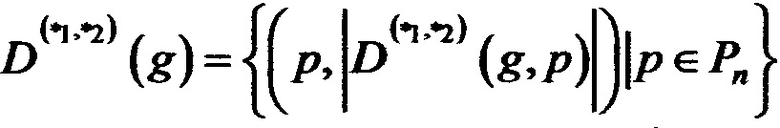 ,
,
|D(g)|=2n+1, 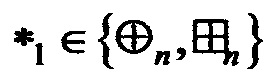 ,
, 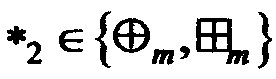 для разностных спектров отображения и упорядоченного множества вида
для разностных спектров отображения и упорядоченного множества вида 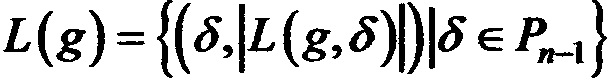 ,
, 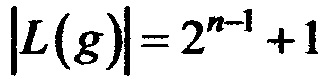 для линейного спектра отображения.
для линейного спектра отображения.
2. Устройство для построения узлов замены, состоящее из блока выбора режима, блока вычисления криптографических параметров, блока вычисления значений целевой вектор-функции, управляющего блока, блока выработки преобразований, блока умножения узла замены на преобразование, оперативного запоминающего устройства, при этом блок выбора режима имеет один выход, который соединен с блоком вычисления криптографических параметров и предназначен для передачи в этот блок информации о режиме работы устройства, блок вычисления криптографических параметров имеет три входа, первый из которых является входом для начальных узлов замены, поступающих на вход устройства, второй - для узлов, поступающих с блока умножения узла замены на преобразование, третий - для получения информации о режиме работы устройства и выход, который соединен с блоком вычисления значений целевой функции и предназначен для передачи в этот блок текущего узла замены с вычисленными криптографическими параметрами, блок вычисления значений целевой вектор-функции имеет вход для узла замены с вычисленными криптографическими параметрами, и выход, который соединен с управляющим блоком, управляющий блок имеет два входа, первый из которых является входом для узла замены с вычисленным значением целевой вектор-функции, а второй является входом для получения содержимого оперативного запоминающего устройства, и два выхода, первый из которых соединен с оперативным запоминающим устройством и служит для обновления его содержимого, а второй выход соединен с блоком умножения узла замены на преобразование и служит для передачи в этот блок узла замены, выбранного управляющим блоком из оперативного запоминающего устройства, блок выработки преобразований имеет выход, который соединен с блоком умножения узла замены на преобразование и предназначен для передачи в этот блок очередной выработанной транспозиции, блок умножения узла замены на преобразование имеет два входа, первый из которых является входом для узла замены, поступающего с управляющего блока, а второй для транспозиции, поступающей с блока выработки преобразований, и выход, который соединен с блоком вычисления криптографических параметров и предназначен для передачи в этот блок полученного узла замены, оперативное запоминающее устройство имеет вход для получения узлов замены, определяемых в оперативное запоминающее устройство управляющим блоком, и два выхода, первый из которых соединен с управляющим блоком и предназначен для передачи содержимого в управляющий блок, а второй предназначен для передачи на выход устройства конечных узлов замены.
3. Устройство по п. 2 для построения инволютивных узлов замены без неподвижных точек, отличающееся тем, что на вход устройства поступает инволютивная подстановка без неподвижных точек, а блок выработки преобразований устройства реализует выработку пар транспозиций, сохраняющих свойство инволютивности.
| RU 2012130652 A, 27.02.2014 | |||
| EA 201200672 A1, 30.10.2013 | |||
| УСТРОЙСТВО ШИФРОВАНИЯ ДАННЫХ ПО СТАНДАРТУ ГОСТ 28147-89 | 2012 |
|
RU2498416C1 |
| СПОСОБ ИТЕРАТИВНОГО КРИПТОГРАФИЧЕСКОГО ПРЕОБРАЗОВАНИЯ ДАННЫХ | 2012 |
|
RU2504911C1 |
Авторы
Даты
2017-10-11—Публикация
2016-06-02—Подача