УСТРОЙСТВО ДЛЯ КОРРЕКЦИИ ОШИБОК В ПОЛИНОМИАЛЬНОЙ СИСТЕМЕ КЛАССОВ Российский патент 2015 года по МПК G06F11/08 

Изобретение относится к области вычислительной техники и может быть использовано для обнаружения и коррекции ошибок при передаче информации.

Известно устройство для коррекции ошибок в полиномиальной системе классов вычетов (ПСКВ) (патент RU 2453902, авторы: Калмыков И.А., Щелкунова Ю.О., Дагаева О.И., Барильская А.В., Кихтенко О.А., опубл. 20.06.2012), содержащее регистр, модуль вычисления синдрома ошибки, блок памяти, сумматор, при этом модуль вычисления синдрома ошибки содержит два блока вычисления синдрома ошибки, каждый из которых содержит четыре многовходовых сумматоров по модулю два.

Недостатком данного устройства является низкие функциональные возможности, которые заключаются в том, что устройство корректирует только однократные ошибки.

Основной задачей является расширение функциональных возможностей, которые позволят устройству корректировать двухкратные ошибки.

Техническим результатом, достигнутым при осуществлении заявленного изобретения, является расширение функциональных возможностей, позволяющих исправлять двухкратные ошибки в комбинации ПСКВ.

Указанный технический результат достигается за счет введения блока управления, блока памяти, блока устранения коллизии.

В полиномиальной системе классов вычетов в качестве оснований системы используются неприводимые полиномы p_i(z), где i=1, 2, …, n. В этом случае любой полином A(z), удовлетворяющий условию

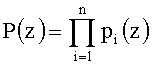
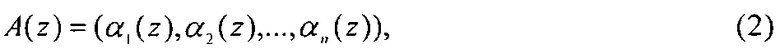
где $$P\left(z\right)={\displaystyle \prod _{i=1}^n{p}_i\left(z\right)}$$ - рабочий диапазон системы, degP(z) - степень полинома, можно однозначно представить в виде набора остатков

где α_i(z)≡A(z)modp_i(z); i=1, 2, …, n.

Применение ПСКВ позволяет свести операции умножения, сложения и вычитания к соответствующим операциям над остатками.

Для реализации процесса обнаружения и исправления ошибок в модулярном коде полинома A(z)=(α₁(z),α₂(z), …, α_n(z)) вводят избыточность. С этой целью выбирается одно контрольное основание p_n+1(z), удовлетворяющее условию

В прототипе доказано, что, используя данное контрольное основание для вычисления двух проверочных остатков

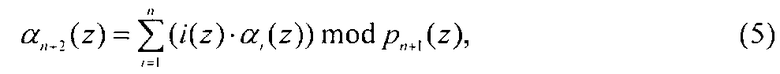
где i(z) - полиномиальная форма i-го порядкового номера, ∑ - суммирование по модулю два, можно однозначно исправить однократную ошибку.

Под однократной ошибкой понимается искажение одного разряда в кодовой комбинации, представленной (2).

При работе данное устройство обрабатывает n информационных остатков α₁(z)÷α_n(z) и два контрольных остатка α_n+1(z) и α_n+2(z).

Для обнаружения ошибки в переданной кодовой комбинации вычисляются значения

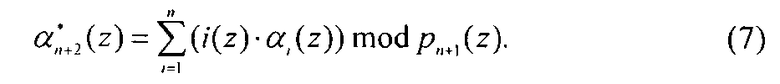
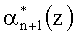
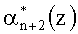
Полученные значения $${\alpha }_{n+1}^{\ast }\left(z\right)$$ и $${\alpha }_{n+2}^{\ast }\left(z\right)$$ используются для вычисления синдрома ошибки согласно

где ⊕ - суммирование по модулю два.

Если синдром ошибки δ₁(z)=0 и δ₂(z)=0, то данная комбинация не содержит ошибки. В противном случае, когда δ₁(z)≠0 и δ₂(z)≠0, принятая комбинация является запрещенной, т.е. ошибочной. По величине δ₁(z) и δ₂(z) можно провести коррекцию однократной ошибки, т.е. определить местоположение ошибочного разряда и исправить его значение.

В таблице 1 приведены значения синдромов δ₁(z) и δ₂(z) и соответствующие им константы ошибки для рабочих оснований p₁(z)=z+1, p₂(z)=z²+z+1, p₃(z)=z⁴+z³+z²+z+1 и контрольного основания p₄(z)=z⁴+z+1.

Однако, используя два контрольных остатка α_n+1(z) и α_n+2(z), можно исправить и двухкратные ошибки, т.е. ошибки, произошедшие в двух разрядах комбинации A(z)=(α₁(z),α₂(z), …, α_n+1(z), α_n+2(z)) одновременно.

В таблице 2 приведены значения синдромов ошибки δ₁(z) и δ₂(z) при всех возможных двухкратных ошибках по рабочим основаниям p₁(z)=z+1, p₂(z)=z²+z+1, p₃(z)=z⁴+z³+z²+z+1.

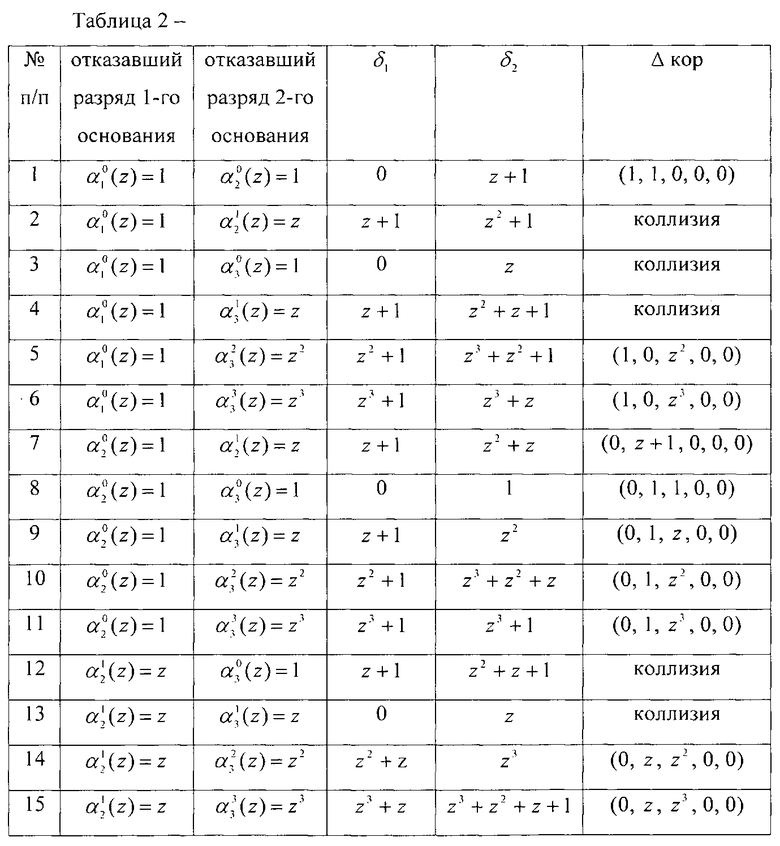
При этом одной из ошибок является изменения разряда первого основания p₁(z)=z+1.

Проведенный анализ таблицы 2 показывает, что совпадение пар значений δ₁(z) и δ₂(z) не произошло, за исключением строк 2 и 16, 3 и 13, 4 и 12. Это означает, что устройство способно корректировать двухкратные ошибки за исключением отмеченных совпадающих строк.

Чтобы обеспечить процедуру коррекции результата в условиях коллизии (совпадение синдрома δ₁(z) и δ₂(z)), в устройство введены блок управления, второй блок памяти, блок устранения коллизии.

Функциональная схема устройства представлена на фигуре 1. Она включает: регистр 1, вход 2, блок устранения коллизии 3, модуль вычисления синдрома ошибки 4, содержащий первый блок вычисления синдрома ошибки 5, второй блок вычисления синдрома ошибки 6, блок управления 7, первый блок памяти 8, второй блок памяти 9, сумматор 10, выход устройства 11.

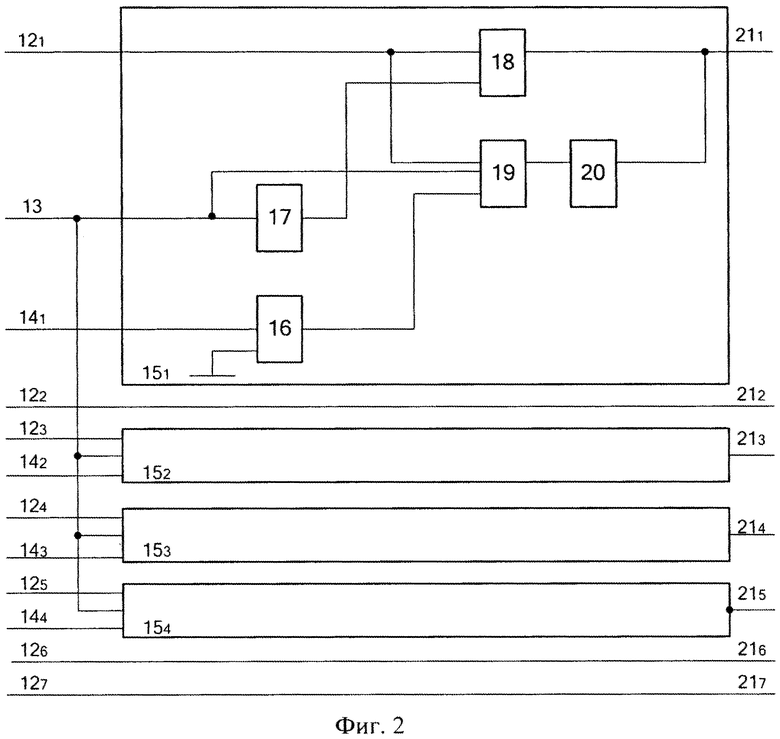
Функциональная схема блока устранения коллизии 3 показана на фигуре 2. Блок содержит первый вход 12, второй вход 13, третий вход 14, четыре блока 15 коррекции разряда, каждый из которых содержит RS-триггер 16, два элемента НЕ 17 и 20, двухвходовой элемент И 18, трехвходовой элемент И 19, выход блока 21.

При этом вход регистра 1 подключен ко входу устройства 2. Первый выход регистра 1 подключен к первому входу блока устранения коллизии 3, выход которого соединен с первым входом первого 5 и второго 6 блоков вычисления синдрома ошибки, входящих в состав модуля вычисления синдрома ошибки 4, а также с первым входом сумматора 10. Второй выход регистра 1 подключен ко второму входу первого блока 5 вычисления синдрома ошибки и третьему входу сумматора 10. Третий выход регистра 1 подсоединен ко второму входу второго блока 6 вычисления синдрома ошибки и четвертому входу сумматора 10. Выход первого блока 5 вычисления синдрома ошибки подключен к первому входу первого блока 8 памяти, второго блока 9 памяти и блока управления 7. Выход второго блока 6 вычисления синдрома ошибки подключен ко второму входу первого блока 8 памяти второго блока 9 памяти и блока управления 7. Выход блока управления 7 подключен ко второму входу блока 3 устранения коллизии, третий вход которого соединен с выходом второго блока 9 памяти. Выход первого блока 8 памяти соединен со вторым входом сумматора 10, выход которого является выходом 11 устройства.

Устройство работает следующим образом: на вход 2 устройства поступает модулярный код полинома A(z)=(α₁(z),α₂(z), …, α_n+1(z), α_n+2(z)). Контролируемая комбинация записывается в регистр 1. На первый вход блока 3 устранения коллизии с первого выхода регистра 1 поступает значение (α₁(z),α₂(z), …, α_n(z)). Если коллизия не обнаружена блоком управления 7, то на второй вход блока 3 поступает управляющая комбинация y=0. Одновременно с выхода второго блока 9 памяти на третий вход блока 3 устранения коллизии поступает четырехразрядная комбинация x=0000. Благодаря этому входная комбинация не изменяется и с выхода блока 3 устранения коллизии подается на первый вход первого блока 5 и второго блока 6 вычисления синдрома ошибки, входящих в состав модуля 4 вычисления синдрома ошибки, а также на первый вход сумматора 10.

На второй вход первого блока 5 вычисления синдрома ошибки подается с второго выхода регистра 1 значение первого контрольного остатка α_n+1(z). Блок 5 реализует выражение (8).

На второй вход второго блока 6 вычисления синдрома ошибки подается с третьего выхода регистра 1 значение второго контрольного остатка α_n+2(z). Данный блок 6 реализует выражение (9).

Величины δ₁(z) и δ₂(z) в двоичном коде поступают на соответствующие входы первого 8 и второго 9 блоков памяти и блок управления 7.

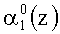
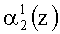
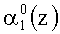
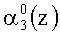
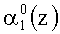
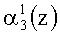
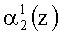
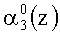
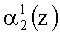
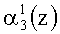
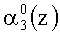
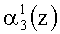
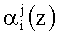
Если коллизия отсутствует, а это соответствует условию, когда контролируемая комбинация A(z)=(α₁(z), α₂(z), …, α_n+1(z), α_n+2(z)) не содержит ошибки или имеет однократную ошибку или двухкратную, за исключением когда ошибка одновременно произошла в комбинациях $${\alpha }_1^0\left(z\right)$$ и $${\alpha }_2^1\left(z\right)$$ ; $${\alpha }_1^0\left(z\right)$$ и $${\alpha }_3^0\left(z\right)$$ ; $${\alpha }_1^0\left(z\right)$$ и $${\alpha }_3^1\left(z\right)$$ ; $${\alpha }_2^1\left(z\right)$$ и $${\alpha }_3^0\left(z\right)$$ ; $${\alpha }_2^1\left(z\right)$$ и $${\alpha }_3^1\left(z\right)$$ ; $${\alpha }_3^0\left(z\right)$$ и $${\alpha }_3^1\left(z\right)$$ , где $${\alpha }_i^j\left(z\right)$$ - j-й разряд i-го канала, то с выхода блока управления 7 поступает управляющий сигнал y=0 на второй вход блока 3 устранения коллизии.

Если однократная ошибка произошла в нулевом разряде первого основания 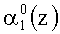$${\alpha }_1^0\left(z\right)$$ , т.е. когда значение синдрома ошибки δ₁(z)=1 и δ₂(z)=1, то с выхода второго блока 9 памяти снимается комбинация x=1000, которая подается на третий вход блока 3 устранения коллизии.

Если однократная ошибка произошла в первом разряде второго основания 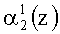$${\alpha }_2^1\left(z\right)$$ , т.е. когда значение синдрома ошибки δ₁(z)=z и δ₂(z)=z², то с выхода второго блока 9 памяти подается на третий вход блока 3 устранения коллизии комбинация x=0100.

Если однократная ошибка произошла в нулевом разряде третьего основания 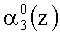$${\alpha }_3^0\left(z\right)$$ , т.е. когда значение синдрома ошибки δ₁(z)=1 и δ₂(z)=z+1, то с выхода второго блока 9 памяти подается на третий вход блока 3 устранения коллизии комбинация x=0010.

Если однократная ошибка произошла в первом разряде третьего основания 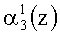$${\alpha }_3^1\left(z\right)$$ , т.е. когда значение синдрома ошибки δ₁(z)=z и δ₂(z)=z²+z, то с выхода второго блока 9 памяти подается на третий вход блока 3 устранения коллизии комбинация x=0001.

В зависимости от величины δ₁(z) и δ₂(z) с выхода первого блока 8 памяти выдается соответствующая константа ошибки Δконс. Это значение поступает в сумматор 10, где суммируется с контролируемым значением комбинации A(z)=(α₁(z), α₂(z), …, α_n+1(z), α_n+2(z)), которая подается в параллельном коде на первый, третий и четвертый входы сумматора 10. Исправленное значение A(z) с выхода сумматора 10 подается на выход 11 устройства.

При возникновении коллизии это соответствует ситуации, когда с выходов блоков 5 и 6 вычисления синдрома ошибки подаются значения δ₁(z)=z+1 и δ₂(z)=z²+1, δ₁(z)=0 и δ₂(z)=z, δ₁(z)=z+1 и δ₂(z)=z²+z+1, то с выхода блока управления 7 на второй вход блока 3 поступает управляющий сигнал y=1.

Рассмотрим работу блока 3 устранения коллизии.

Входная комбинация A(z)=(α₁(z), …, α_n(z)) по рабочим основаниям в параллельном коде поступает на входы 12₁-12₇. При этом входы 12₁, 12₆, 12₇ напрямую подаются на соответствующие выходы блока устранения коллизии 21₂, 21₆, 21₇. Остальные разряды первого входа 12₁, 12₃, 12₄ и 12₅ подсоединены к первым входам блоков 15 коррекции разряда. Второй вход 13 блока устранения коллизии подключен ко вторым входам блоков 15 коррекции разрядов. Первый разряд третьего входа 14 блока устранения коллизии подключен к третьему входу первого блока 15 коррекции разряда. Второй разряд третьего входа 14 блока устранения коллизии подключен к третьему входу второго блока 15 коррекции разряда. Третий разряд третьего входа 14 блока устранения коллизии подключен к третьему входу третьего блока 15 коррекции разряда. Четвертый разряд третьего входа 14 блока устранения коллизии подключен к третьему входу четвертого блока 15 коррекции разряда.

Первый вход 12 блока 15 коррекции разряда подключен к первым входам элементов И 18 и 19. Второй вход 13 блока 15 коррекции разряда подсоединен к второму входу второго элемента И 19, а также ко входу первого элемента НЕ 17, выход которого подключен ко второму входу первого элемента И 18, выход последнего соединен с выходом блока 21.

Третий вход 14 блока 15 коррекции разряда подключен ко входу «S» RS-триггера 16, на вход R которого подается нулевой сигнал. Прямой выход RS-триггера 16 подключен к третьему входу второго элемента И 19, выход которого подсоединен ко входу второго элемента НЕ 20. Выход последнего подключен к выходу 21 блока.

При подаче управляющего сигнала y=0 на второй вход 13 блока 15 коррекции разряда он закрывает второй элемент И 19 и через элемент НЕ 17 открывает первый элемент И 18. Тогда сигнал, поступивший на первый вход 12 блока 15, без изменения подается на выход 21 блока. При подаче на третий вход 14 блока 15 коррекции разряда сигнала «1» со второго блока 9 памяти на прямом выходе RS-триггера 16 появится единичный сигнал.

При возникновении коллизии с выхода блока 7 управления на второй вход 13 блока 15 коррекции подается управляющий сигнал y=1, который поступает на вход первого элемента НЕ 17 и закрывает первый элемент И 18, и открывает второй элемент И 19. Входная последовательность со входа 12 подается через открытый элемент И 19, на вход второго элемента НЕ 20, где инвертируется и поступает на выход 21 блока. Таким образом, происходит исправление ошибочного разряда.

В результате контролируемая комбинация модулярного кода A(z)=(α₁(z), α₂(z), …, α_n+1(z), α_n+2(z)) будет содержать только однократную ошибку. Эта ошибка будет обнаружена в модуле 4 вычисления синдрома по значениям δ₁(z) и δ₂(z). Эти значения подаются на входы первого блока 8 памяти, с выхода которого выдается Δкор, что позволяет исправить вторую ошибку в контролируемой комбинации.

Рассмотрим пример. Пусть в качестве информационных оснований ПСКВ выбраны следующие n=3 неприводимых полинома p₁(z)=z+1; p₂(z)=z²+z+1; p₃(z)=z⁴+z³+z²+z+1.

Данные основания образуют рабочий диапазон

.

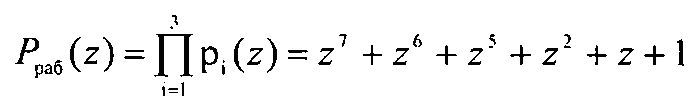В качестве контрольного основания выбирается неприводимый полином p₄(z)=z⁴+z+1.

Пусть контролируемый полином A(z)=z⁵=(1, z+1, 1), который удовлетворяет (1). Вычислим значения α_n+1(z) и α_n+2(z), используя выражения (6) и (7). Имеем

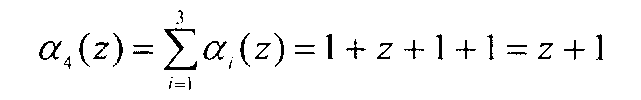
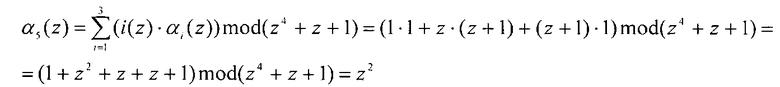
Тогда на вход устройства подается кодовая комбинация A(z)=(1, z+1, 1, z+1, z²). Так как данная комбинация не содержит ошибку, то δ₁(z)=0 и δ₂(z)=0.

Пусть ошибка произошла в первом основании Δα₁(z)=1. Тогда 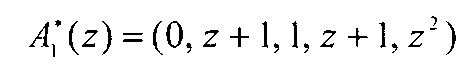поступает на вход устройства, записывается в регистр 1, а затем на соответствующие входы первого 5 и второго 6 блоков вычисления синдрома, а также сумматора 10. При этом остатки α₁(z)-α₃(z) по рабочим основаниям проходят через блок 3 устранения коллизии без изменения.

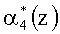
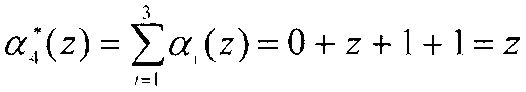Первый блок вычисления синдрома ошибки 5 определяет значение $${\alpha }_4^{\ast }\left(z\right)$$ согласно (6). Имеем .

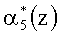
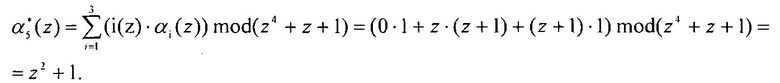
Второй блок вычисления синдрома ошибки 6 определяет значение $${\alpha }_5^{\ast }\left(z\right)$$ согласно (7). Имеем

Тогда значения синдрома равно

.

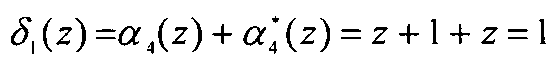
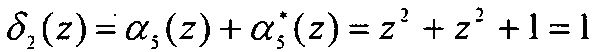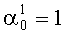
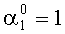
Согласно таблице 1 ошибка произошла в первом основании и ее глубина $${\alpha }_0^1=1$$ . Одновременно с этим из второго блока 9 памяти в блок 3 устранения коллизии поступает сигнал X=1000. В первом блоке 15 коррекции разряда, который соответствует разряду $${\alpha }_1^0=1$$ первого основания p₁(z)=z+1, RS-триггер 16 перебрасывается в состояние «1».

Пусть вторая ошибка произошла по второму основанию и ее глубина Δα₂=z. Для примера возьмем ту же полиномиальную комбинацию. Тогда ошибочный полином имеет вид 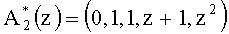$$A_2^{\ast }\left(z\right)=\left(\mathrm{0,}\mathrm{1,}\mathrm{1,}z+\mathrm{1,}{z}^2\right)$$ . С выхода регистра 1 данная комбинация поступает на соответствующие входы первого 5 и второго 6 блоков вычисления синдрома ошибки, а также сумматора 7.

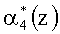
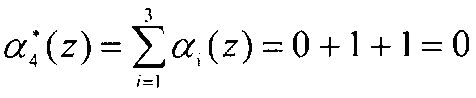Первый блок вычисления синдрома ошибки 5 определяет значение $${\alpha }_4^{\ast }\left(z\right)$$ согласно (6). Имеем .

Тогда значения .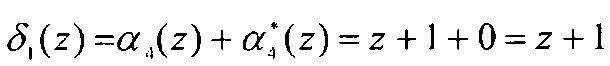

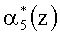
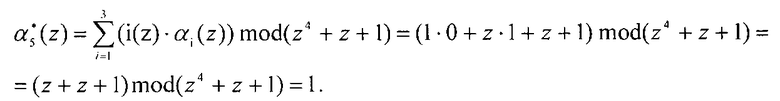
Второй блок вычисления синдрома ошибки 6 определяет значение $${\alpha }_5^{\ast }\left(z\right)$$ согласно (7). Имеем

Тогда значение .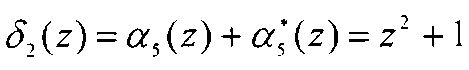

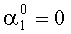
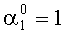
Эти значения соответствуют коллизии, поэтому с выхода блока 7 управления на второй вход блока 3 устранения коллизии поступает управляющий сигнал y=1. Данный сигнал поступает на второй вход 13 каждого блока 15 коррекции разряда. При этом в первом блоке 15 коррекции разряда происходит закрытие первого элемента И 18 и открытие второго элемента И 19. Тогда ошибочное значение первого основания $${\alpha }_1^0=0$$ , поступившее на первый вход 12₁, инвертируется благодаря второму элементу НЕ 20, и в виде $${\alpha }_1^0=1$$ подается на выход 21₁.

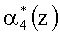
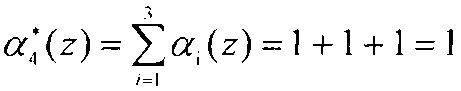Таким образом, с выхода блока 3 устранения коллизии выдается комбинация A^*(z)=(1, 1, 1), которая содержит одну ошибку по второму основанию. Тогда первый блок вычисления синдрома 5 определяет значение $${\alpha }_4^{\ast }\left(z\right)$$ , согласно (6). Имеем .

Следовательно, значение .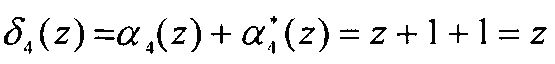

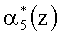
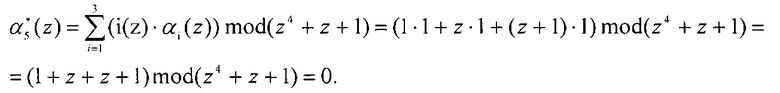
Второй блок вычисления синдрома 6 определяет значение $${\alpha }_5^{\ast }\left(z\right)$$ согласно (7). Имеем

Следовательно, значение .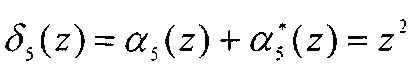

Согласно таблице 1 ошибка произошла по второму основанию p₂(z)=z²+z+1, а ее глубина Δα₂=z. Следовательно, с выхода сумматора 11 будет снят результат коррекции

А_испр(z)=A^*(z)+Δ_кор=(1, 1, 1, z+1, z²)+(0, z, 0, 0, 0)=(1, z+1, 1, z+1, z²).

Таким образом, устройство произвело коррекцию двухкратной ошибки при возникновении коллизии.

Во всех остальных случаях возникновения двухкратных ошибок устройство работает аналогично прототипу при исправлении однократных ошибок.

Изобретение относится к области вычислительной техники и может быть использовано для обнаружения и коррекции ошибок при передаче информации. Техническим результатом является обеспечение возможности исправлять двухкратные ошибки в комбинациях модулярного кода. Устройство для коррекции ошибок в полиномиальной системе классов вычетов содержит регистр, вход которого является входом устройства, модуль вычисления синдрома, содержащий первый и второй блоки вычисления синдрома, первый блок памяти, сумматор выход которого является выходом устройства, причем выход первого и второго блоков вычисления синдрома подсоединены к соответствующим входам первого блока памяти, выход которого соединен со вторым входом сумматора, третий и четвертый вход которого подключены ко второму и третьему выходам регистра, кроме того, третий и четвертый выходы регистра соединены соответственно со вторыми входами первого и второго блока вычисления синдрома, входящих в состав модуля вычисления синдрома, отличающееся тем, что в него введены блок управления, второй блок памяти и блок устранения коллизии, первый вход последнего подключен к первому выходу регистра, второй вход этого блока соединен с выходом блока управления, третий вход блока устранения коллизии подключен к выходу второго блока памяти, выход блока устранения коллизии подключен к первому входу первого и второго блока вычисления синдрома, а также к первому входу сумматора, выходы первого и второго блоков вычисления синдрома ошибки соединены с соответствующими входами блока управления и второго сумматора. 1 з.п. ф-лы, 2 ил., 2 табл.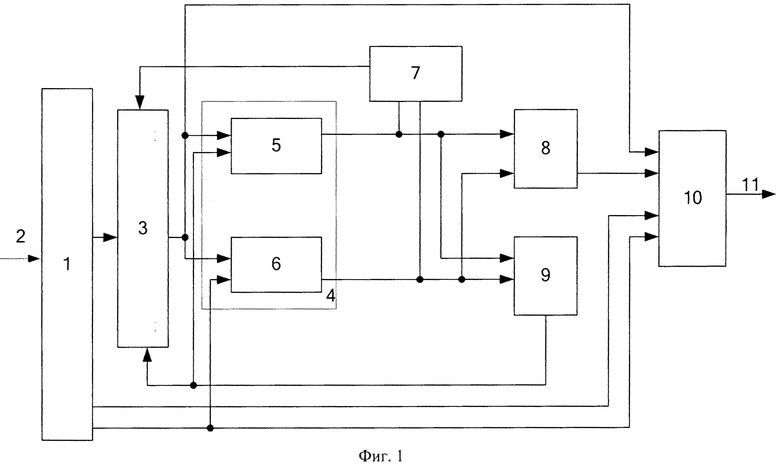

1. Устройство для коррекции ошибок в полиномиальной системе классов вычетов, содержащее регистр, вход которого является входом устройства, модуль вычисления синдрома, содержащий первый и второй блоки вычисления синдрома, первый блок памяти, сумматор, выход которого является выходом устройства, причем выход первого и второго блоков вычисления синдрома подсоединены к соответствующим входам первого блока памяти, выход которого соединен со вторым входом сумматора, третий и четвертый вход которого подключены ко второму и третьему выходам регистра, кроме того, третий и четвертый выходы регистра соединены соответственно со вторыми входами первого и второго блока вычисления синдрома, входящих в состав модуля вычисления синдрома, отличающееся тем, что в него введены блок управления, второй блок памяти и блок устранения коллизии, первый вход последнего подключен к первому выходу регистра, второй вход этого блока соединен с выходом блока управления, третий вход блока устранения коллизии подключен к выходу второго блока памяти, выход блока устранения коллизии подключен к первому входу первого и второго блока вычисления синдрома, а также к первому входу сумматора, выходы первого и второго блоков вычисления синдрома ошибки соединены с соответствующими входами блока управления и второго сумматора.

2. Устройство по п.1, отличающееся тем, что блок устранения коллизии содержит три входа, выход, четыре блока коррекции разряда, каждый из которых имеет три входа, RS-триггер, два элемента НЕ и два элемента И, причем первый, третий и четвертый разряды первого входа подключены соответственно к первым входам блоков коррекции разрядов, а второй, шестой и седьмой разряды первого входа блока устранения коллизии соединены с соответствующими разрядами выхода этого блока, второй вход блока устранения коллизии подключен ко вторым входам блоков коррекции разряда, а третий четырехразрядный вход блока устранения коллизии поразрядно подключен к третьим входам соответствующих блоков коррекции разряда, первый вход блока коррекции разряда соединен с первыми входами первого и второго элемента И, второй вход блока коррекции разряда подсоединен ко второму входу второго элемента И, а также ко входу первого элемента НЕ, выход которого соединен со вторым входом первого элемента И, выход последнего подключен к выходу блока, третий вход блока коррекции разряда подключен к «S»-входу RS-триггера, на вход R которого подается нуль, а выход RS-триггера соединен с третьим входом второго элемента И, выход которого соединен со входом второго элемента НЕ, выход последнего подключен к соответствующему выходу блока устранения коллизии.