Область техники, к которой относится изобретение
Изобретение относится к вычислительной технике и может быть использовано для параллельной реализации систем многозначных функций алгебры логики (МФАЛ) в средствах криптографической защиты информации.
Уровень техники
а) Описание аналогов
Известно устройство получения псевдослучайных последовательностей (псевдошумовых, регистровых последовательностей максимальной длины, М-последовательностей), элементы которых принадлежат алфавиту из q символов (q - простое число или степень простого числа), основанные на применении переключательных схем специального вида, называемых линейными рекуррентными регистрами сдвига с обратной связью (ЛРРС) [MacWilliams F., Sloane N. Pseudo-random sequences and arrays, Proc. IEEE, 64, pp. 1715-1729, 1976; Lidl R., Niederreiter H. Introduction to finite fields and their applications, Cambridge: Cambridge Univ. Press, 1987]. Построение ЛРРС над GF(q) (далее q-ЛРРС) осуществляется по заданному примитивному, неприводимому (характеристическому) многочлену:
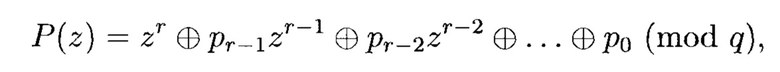
где pi ∈ GF(q), r - степень полинома P(z), r G N, GF(q) - поле Галуа из q элементов и построенному в соответствии с ним однородному рекуррентному уравнению:
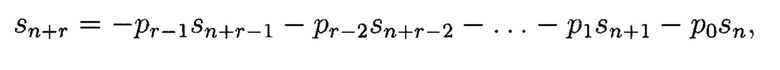
или
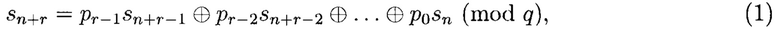
где n=0, 1, 2, …; pj ∈ GF(q), 0 ≤ j ≤ r - 1; ⊕ - символ сложения по mod q.
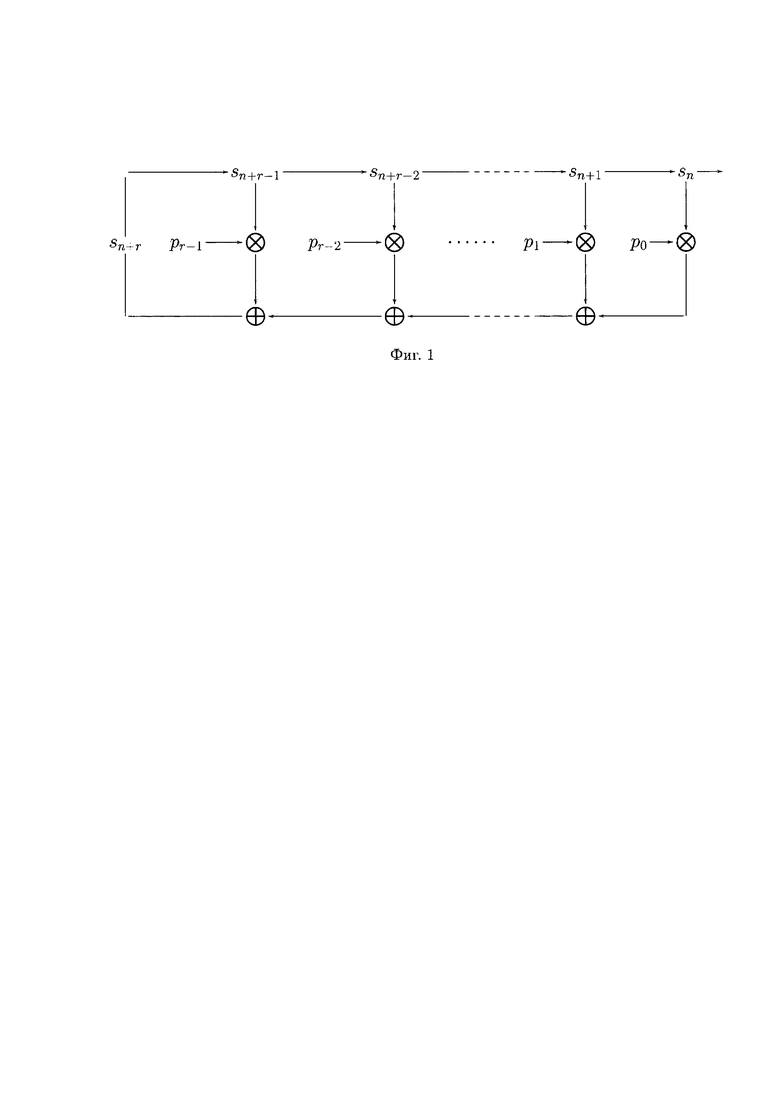
В общем случае q-ЛРРС состоит из конструктивных элементов: ячеек Dj (j=0, 1, …, r-1), сумматоров по mod q, усилителей mod q и имеет начальное заполнение (элементы поля GF(q)): s0, s1, …, sr-1. Под «ячейкой» понимается параллельный [log2q] - разрядный регистр (⎡х⎤ - наименьшее целое число равное или превышающее х). После первого такта работы q-ЛРРС содержит заполнение: s1, s2, …, sr. В целом q-ЛРРС (фиг. 1) генерирует бесконечную выходную q-значную последовательность s0, s1, s2, …, sr-1, … с периодом qr - 1 (при ненулевом исходном состоянии), причем каждое ненулевое состояние появляется один раз за период. Сформированный сегмент выходной последовательности длины qr - 1 является псевдослучайной последовательностью (ПСП) над GF(q).
В терминах линейной алгебры очередной элемент ПСП sn+r, получаемый с помощью (1) вычисляется в соответствии с выражением:
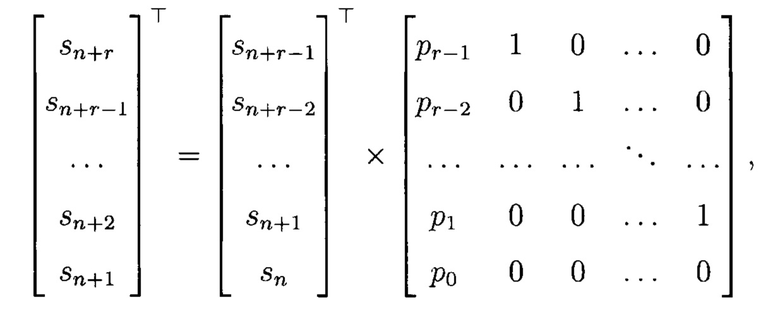
Где 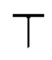 - символ транспонирования.
- символ транспонирования.
К недостатку устройства следует отнести последовательную организацию вычислений, при которых осуществляется формирование сегмента выходной ПСП. б) Описание ближайшего аналога (прототипа)
Наиболее близким по своей технической сущности к заявленному техническому решению и принятым за прототип является устройство, описанное в [Патент РФ №2579991 С1 опубл. 10.04.2016].
Рассматриваемое устройство содержащит шину подачи т булевых переменных, блок памяти, предназначенный для хранения коэффициентов линейного числового полинома (ЛЧП), к входу которого подключена шина подачи коэффициентов ЛЧП; дополнительно введены регистр памяти, входы которого являются входами устройства, к которым подключена шина подачи τ булевых переменных; блок памяти, предназначенный для хранения оснований системы, к входу которого подключена шина подачи оснований системы, выходы которого вместе с выходами блока памяти хранения коэффициентов ЛЧП подключены к входам блоков вычисления наименьших неотрицательных вычетов числа (коэффициентов ЛЧП) по основаниям системы, выходы которых вместе с выходами регистра памяти подключены к входам множителей, выходы которых подключены к входам многоместных сумматоров, выходы которых подключены к входам блока решения системы сравнений с одним неизвестным, выход которого подключен к входам блока сравнения и блока оператора маскирования, выход блока сравнения подключен ко второму входу блока оператора маскирования, выходы которого являются выходами устройства выдачи значений τ булевых функций.
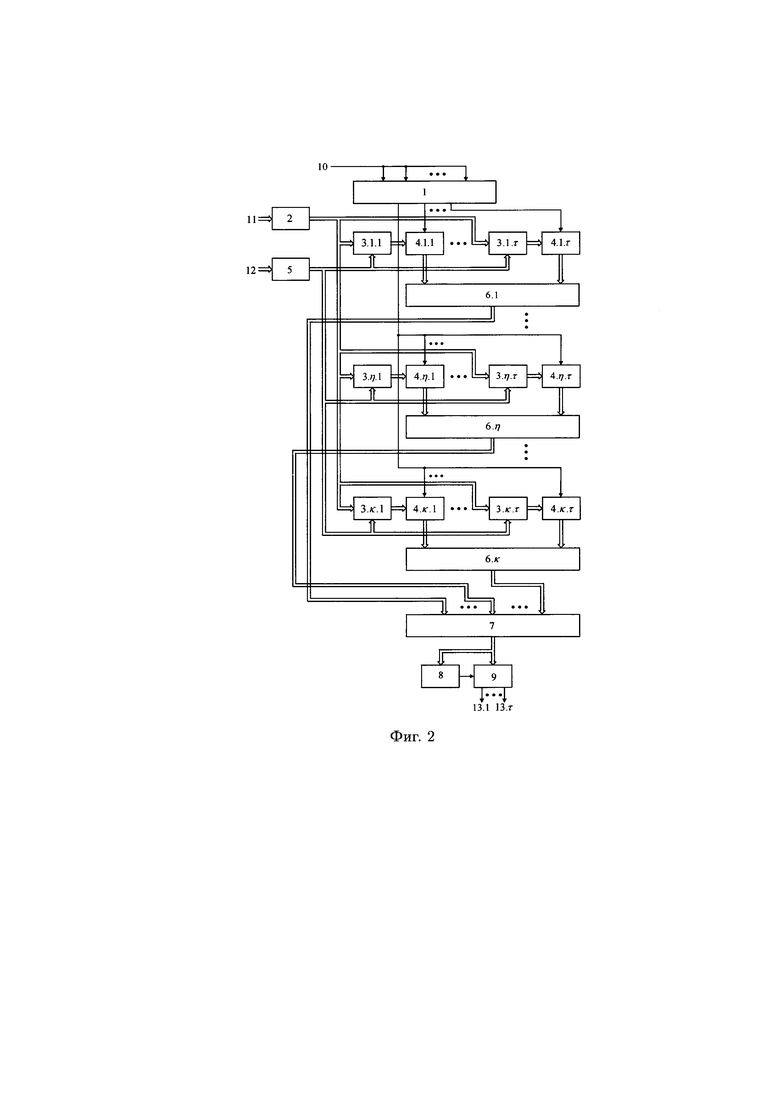
Структурная схема устройства-прототипа представлена на фиг. 2.
Рассматриваемое в качестве прототипа устройство предназначено для вычисления двоичных ПСП, идентичных ПСП, получаемым посредством классических генераторов на ЛРРС, с функцией осуществления контроля ошибок вычислений. Работа устройства основана на представлении систем рекурсивных характеристических уравнений ЛЧП.
Недостаток известного устройства - отсутствие функциональных возможностей получения многозначных ПСП.
Раскрытие изобретения
а) Технический результат, на достижение которого направлено изобретение Целью заявляемого технического решения является обеспечение параллельного вычисления многозначных ПСП, идентичных ПСП над GF(q) (q>2), получаемым посредством классических генераторов на q-ЛРРС.
б) Совокупность существенных признаков Технический результат изобретения достигается тем, что:
Поставленная цель достигается тем, что в устройство параллельного формирования q-значных псевдослучайных последовательностей на арифметических полиномах, содержащее блок памяти, предназначенный для хранения коэффициентов полиномов, к входу которого подключена шина подачи коэффициентов; множители, выходы которых подключены к входам многоместных сумматоров; блок оператора маскирования, выходы которого являются выходами устройства, дополнительно введены регистр памяти, входы которого являются входами устройства, к которым подключена шина подачи r переменных многозначных функций алгебры логики; умножители, к входам которых подключена шина подачи r переменных многозначных функций алгебры логики, выходы которого подключены к первых входам множителей, ко вторым входам которых подключены выход блока памяти коэффициентов арифметического полинома; умножитель на весовые коэффициенты qi-1, к первым входам которого подключены выходы многоместных сумматоров, ко вторым входам которого подключен блок памяти весовых коэффициентов, к выходу которого подключена шина подачи весовых коэффициентов; многоместный сумматор по модулю qr, выход которого подключен к оператору маскирования, выходы которого являются выходами устройства выдачи значений r многозначных функций алгебры логики.
в) Причинно-следственная связь между признаками и техническим результатом
Благодаря введению в известный объект совокупности существенных отличительных признаков, устройство параллельного формирования q-значных ПСП на арифметических полиномах позволяет реализовать алгоритм параллельного формирования q-значных ПСП для реализации перспективных высокопроизводительных средств криптографической защиты информации.
Доказательства соответствия заявленного изобретения условиям патентноспособности «новизна» и «изобретательский уровень»
Проведенный анализ уровня техники позволил установить, что аналоги, характеризующие совокупности признаков, тождественных всем признакам заявленного технического технического решения, отсутствуют, что указывает на соответствие заявленного способа условию патентноспособности «новизна».
Результаты поиска известных решений в данной и смежных областях техники с целью выявления признаков, совпадающих с отличительными от прототипа признаками заявленного объекта показали, что они не следуют явными из уровня техники. Из уровня техники также не выявлена известность отличительных существенных признаков, обуславливающих тот же технический результат, который достигнут в заявленном способе. Следовательно, заявленное изобретение соответствует уровню патентноспособности «изобретательский уровень».
Краткое описание чертежей
Заявленное устройство поясняется чертежами, на которых показано:
- на фиг. 1 - структурная схема q-ЛРРС, функционирующего в соответствии с однородным рекуррентным уравнением (1);
- на фиг. 2 - схема устройства-прототипа;
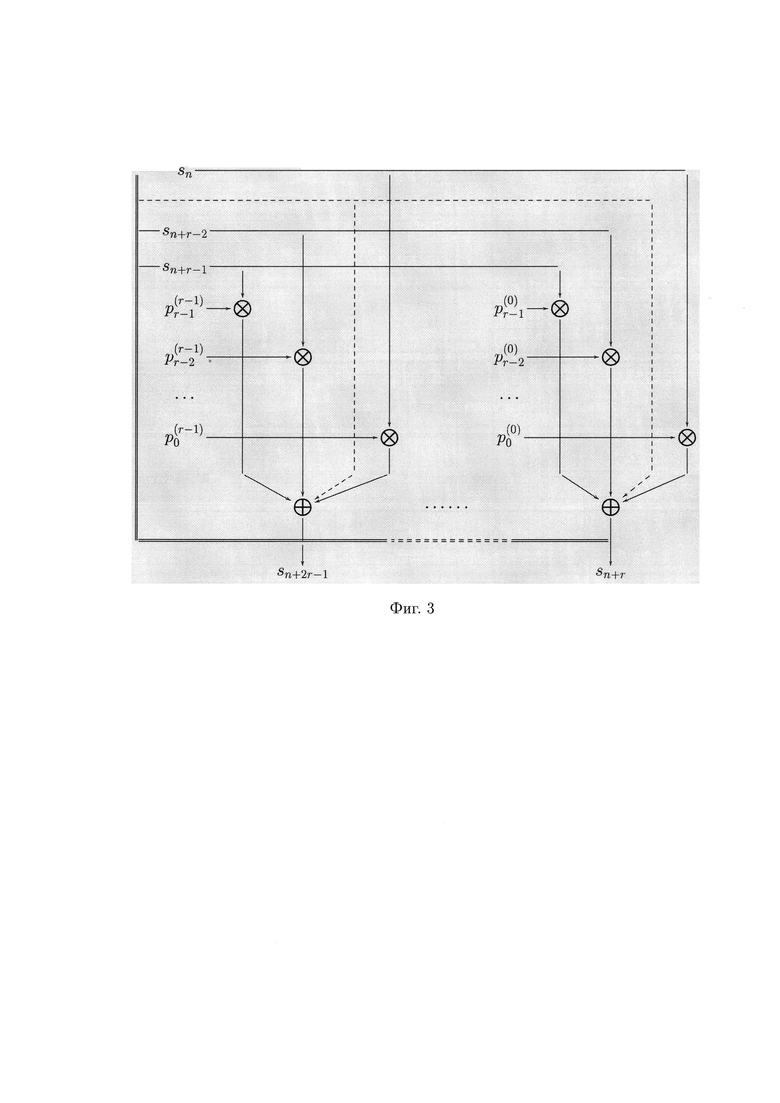
- на фиг. 3 - структурная схема параллельного q-ЛРРС, функционирующего в соответствии с выражением (4);
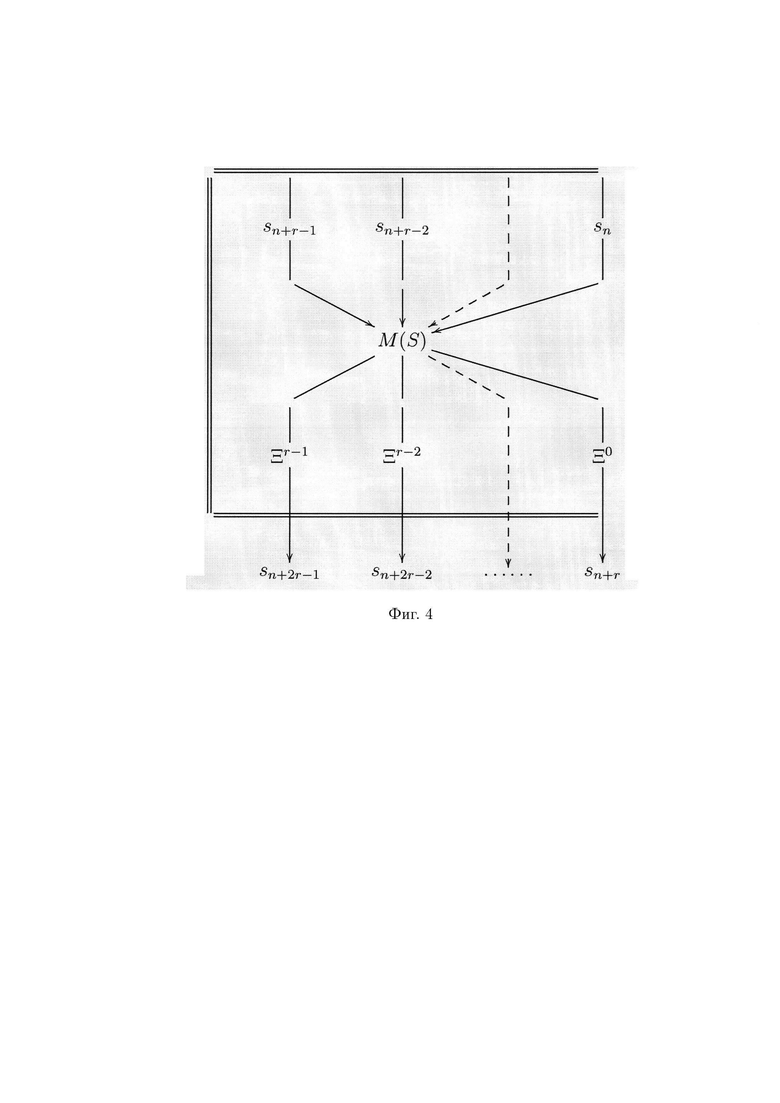
- на фиг. 4 - схема параллельных вычислений генератора, соответствующая выражению (7);
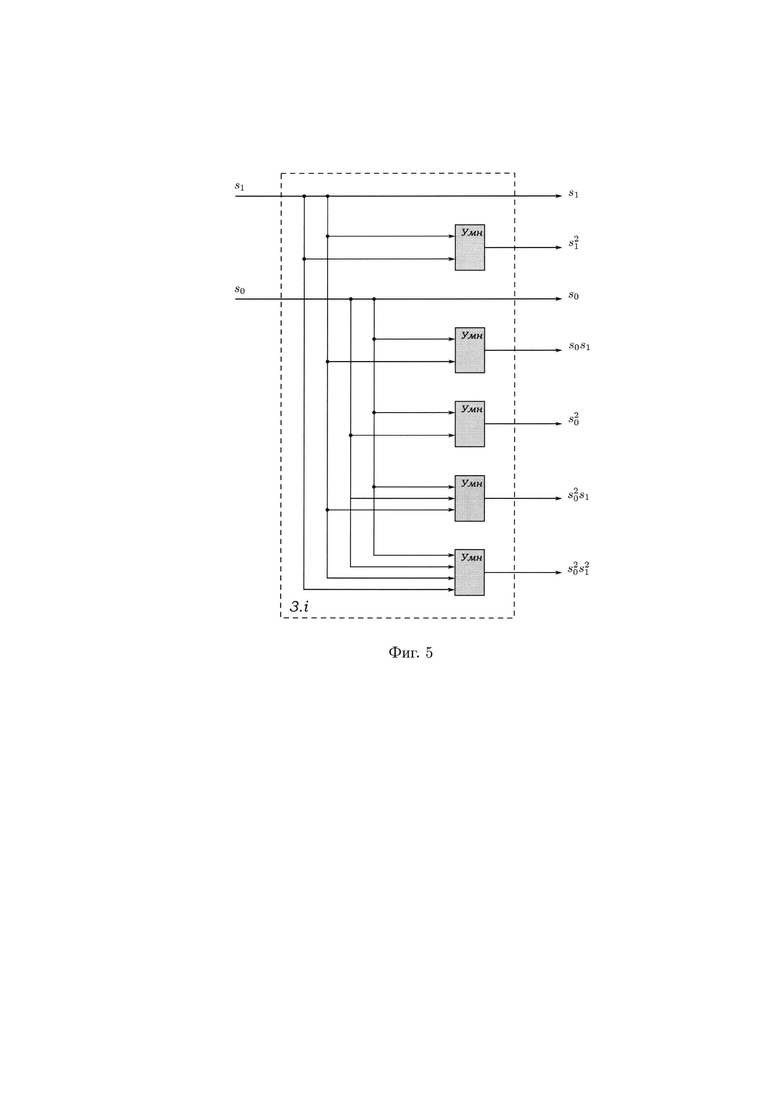
- на фиг. 5 - схема, поясняющая принцип работы умножителей 3.r;
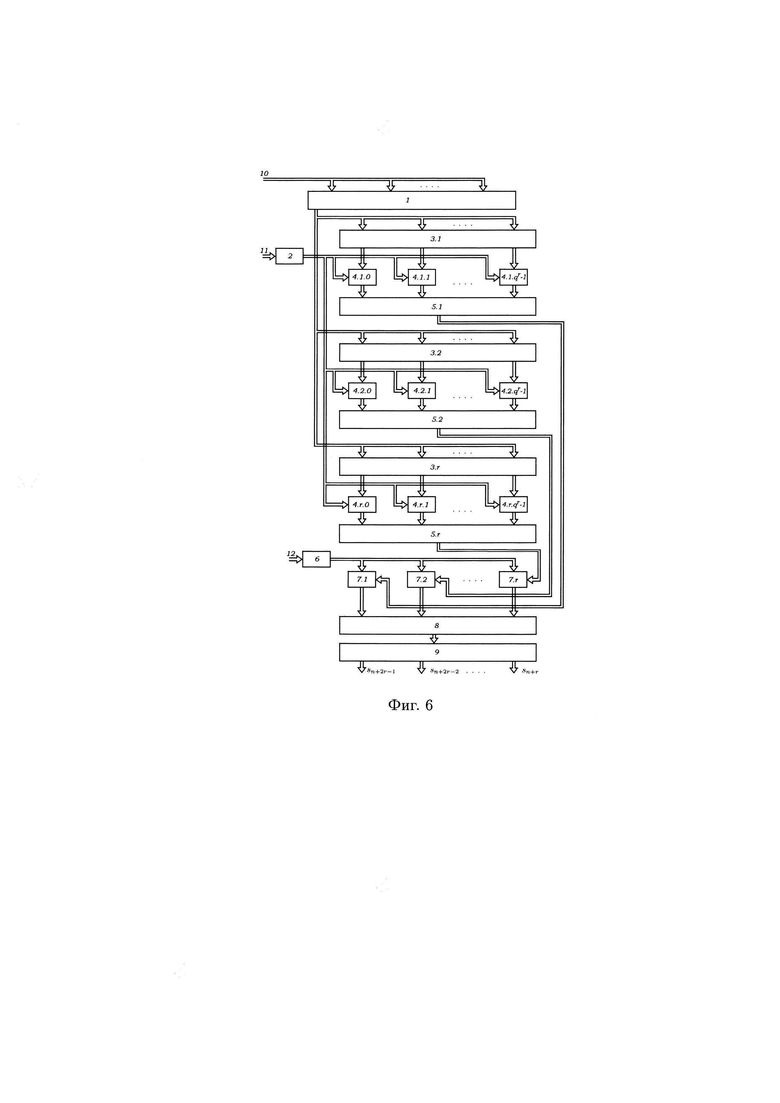
- на фиг. 6 - устройство параллельного формирования q-значных псевдослучайных последовательностей на арифметических полиномах.
Осуществление изобретения
Рассмотрим алгоритм работы устройства.
Пусть s0, s1, s2, …, sr-1, … - элементы ПСП, удовлетворяющие многозначному рекуррентному уравнению (1). Ввиду того, что произвольный элемент sn (n ≥ r) последовательности s0, s1, s2, …, sr-1, … определяется по предшествующим r элементам, представим элементы участка ПСП длинной r sn+r, sn+r+1, …, sn+2r-1 в виде системы рекуррентных уравнений:

где [sn+r sn+r+1 … sn+2r-1] - вектор r-того состояния ПСП (или внутреннее состояние q-ЛРРС на r-м такте работы).
Выразим правые части системы (2) через заданные начальные условия:

Упростив выражение (3), запишем полученную систему рекуррентных уравнений как систему r многозначных функций алгебры логики (МФАЛ) от r переменных:
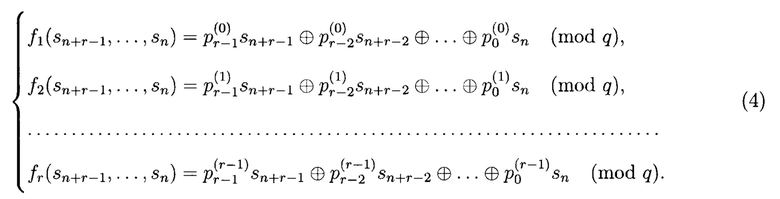
Коэффициенты 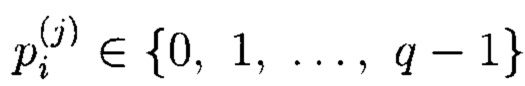 формируются после сокращения выражения (3). На фигуре 3 в соответствии с выражением (4) представлена структурная схема параллельных вычислений генератора.
формируются после сокращения выражения (3). На фигуре 3 в соответствии с выражением (4) представлена структурная схема параллельных вычислений генератора.
Произвольную МФАЛ представим в виде арифметического полинома:
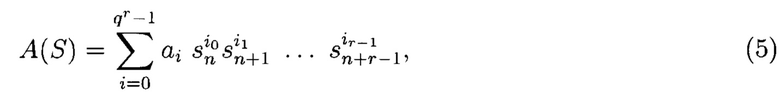
где ai - i-й коэффициент арифметического полинома; s=sn, sn+1, …, sn+r-1 - аргументы МФАЛ su ∈ {0, 1, …, q - 1} (u=0, 1, …, r - 1); (i0 i1 … ir-1)q - представление параметра i в q-ичной системе счисления:
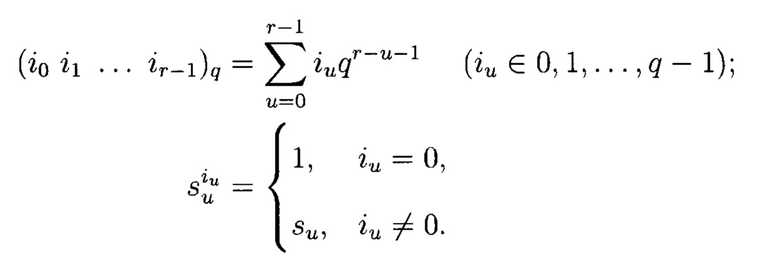
Для МФАЛ известны алгебраический и матричный методы построения арифметического полинома [Кухарев Г.А., Шмерко В.П., Зайцева Е.Н. Алгоритмы и систолические процессоры для обработки многозначных данных. - Минск: Наука и техника, 1990. - 296 с.]. Прямое и обратное матричное преобразование определяется выражениями

где Nk - нормализирующий множитель; 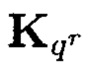 и
и 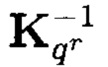 - матрицы прямого и инверсного арифметического преобразования размерности qr × qr (базис преобразования); S - вектор истинности МФАЛ:
- матрицы прямого и инверсного арифметического преобразования размерности qr × qr (базис преобразования); S - вектор истинности МФАЛ:
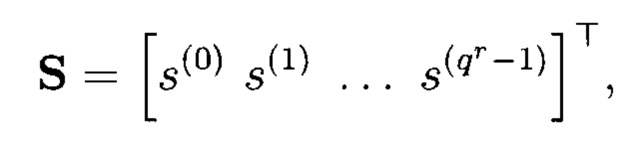
где s(i) - числовое значение, принимаемое МФАЛ на i-м наборе переменных; вектор коэффициентов (спектр) арифметического полинома (5):
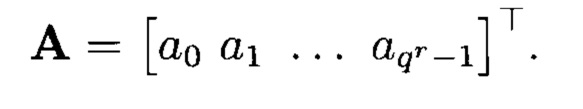
Матрицы 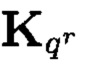 и
и 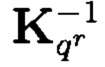 определяется кронекеровским возведением в степень:
определяется кронекеровским возведением в степень:
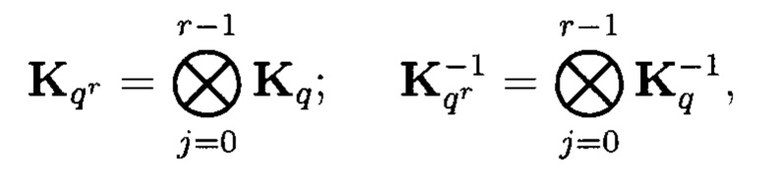
Где 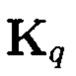 и
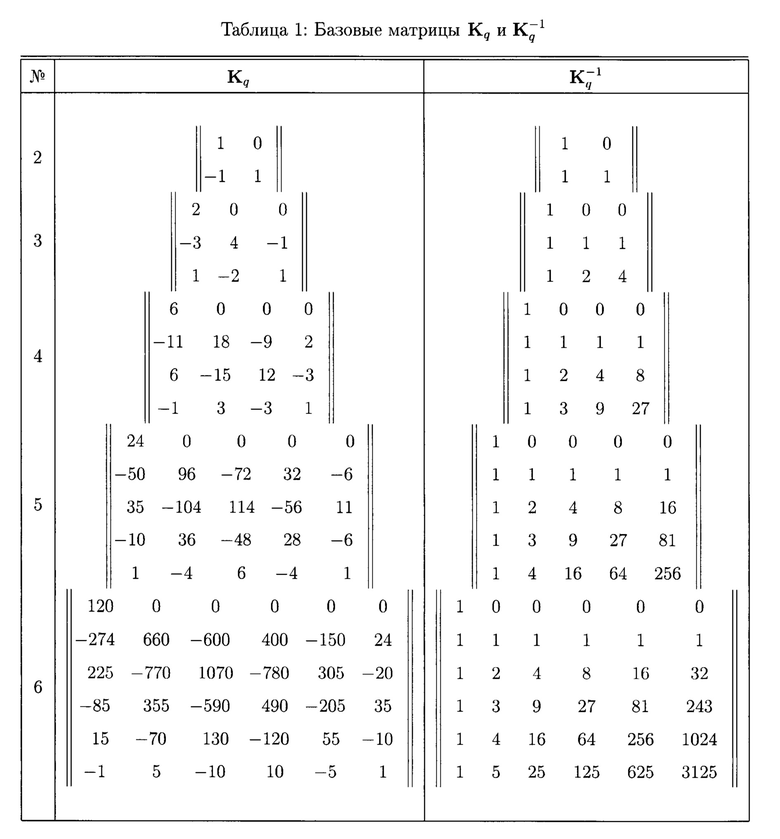
и 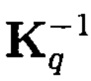 - базовые матрицы прямого и обратного преобразования (таблица 1 - для q=2, 3, …, 6).
- базовые матрицы прямого и обратного преобразования (таблица 1 - для q=2, 3, …, 6).
Для МФАЛ f(S)=2s0 ⊕ 2s1 (mod 3) вектор принимаемых значений МФАЛ имеет вид S=[0 2 1 2 1 0 1 0 2]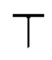 .
.
Соответственно, прямое преобразование (6) может быть представлено в следующем виде:
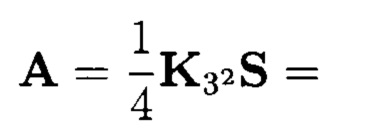

Тогда в соответствии с выражением (5) алгебраическая форма МФАЛ примет вид
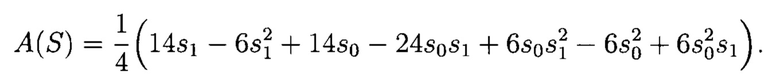
Например, при s0=2 и s1=2 МФАЛ соответствует значение:
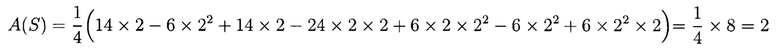
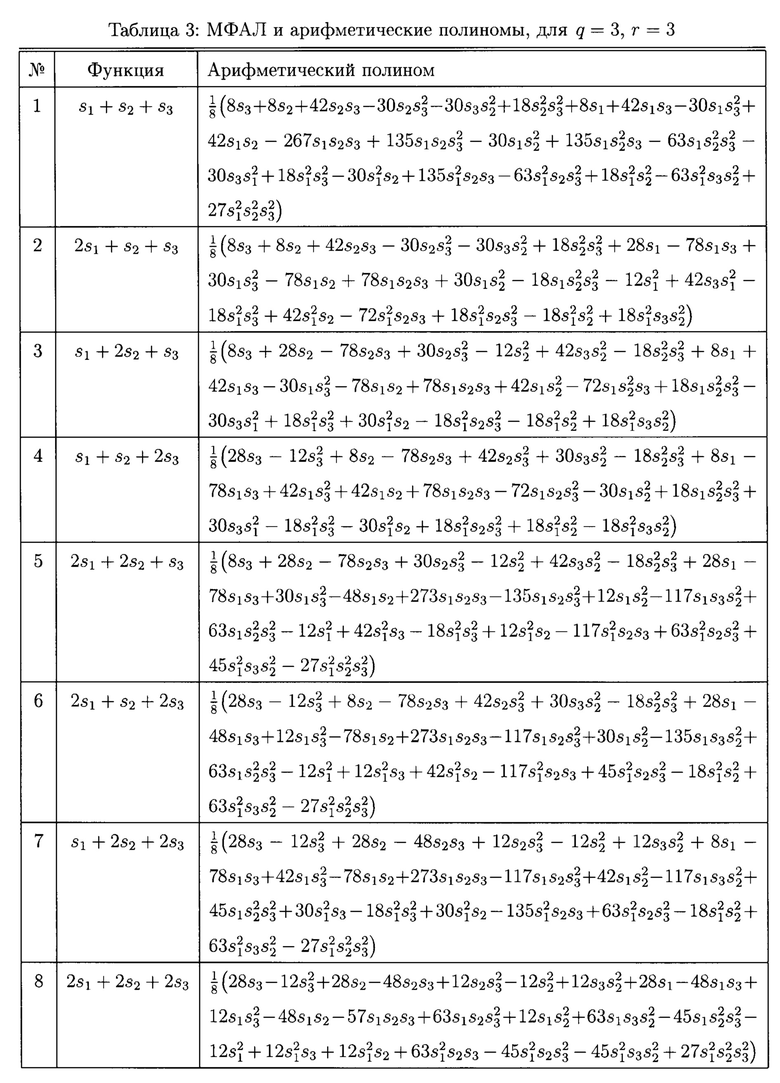
Для 3-значной функции алгебры логики, зависящей от 2 переменных в таблице 2, представлены соответствующие арифметические полиномы. В таблице 3 в качестве примера представлены рассчитанные арифметические полиномы для 3-значной функции алгебры логики, зависящей от 3 переменных.
Реализуем систему МФАЛ (4) посредством вычисления некоторого арифметического полинома. Для этого поставим в соответствие системе МФАЛ (4) систему арифметических полиномов вида (5). Получим:
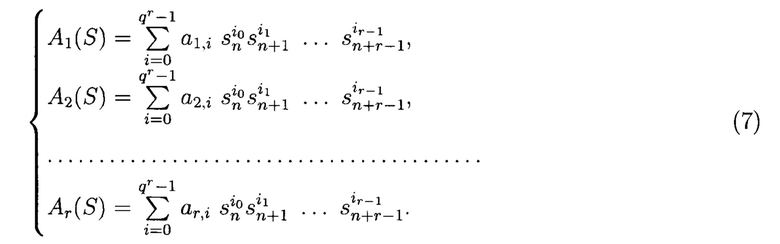
Умножим полиномы системы (7) на веса ql-1 (l=1, 2, …, r):
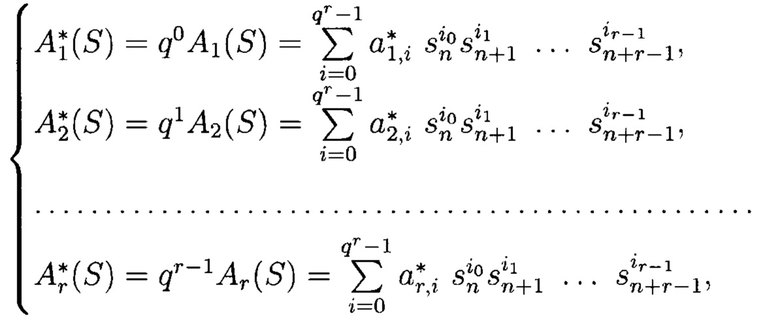
где 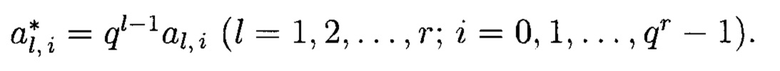
Тогда, получим:
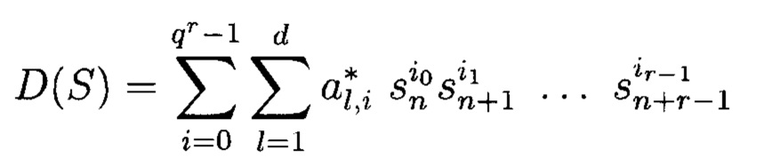
или с использованием положений обобщения модулярных форм на МФАЛ [Финько О.А. Модулярная арифметика параллельных логических вычислений. - Краснодар: Краснодарский военный институт, 2003. - 224 с.]:

где 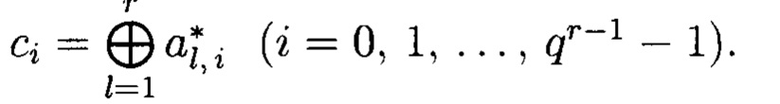
Вычислим значения искомых МФАЛ. Для этого результат вычисления M(S) представим в q-ичной системе счисления и применим оператор маскирования Ξt{M(S)}:
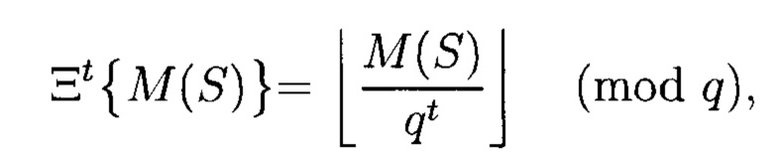
где t - искомый q-ичный разряд представления M(S). На фигуре 3 представлена схема, поясняющая сущность параллельных вычислений генератора в соответствии с выражением (8).
Предлагаемое устройство содержит шину 10 подачи значений r переменных МФАЛ sn+r-1, sn+r-2, …, sn, шину 11 подачи коэффициентов ar,i арифметических полиномов, шину 12 подачи весовых коэффициентов ql-1, регистр памяти 1, блок 2 памяти коэффициентов аr,i арифметических полиномов, блок 6 памяти весовых коэффициентов ql-1, блоки 3.1, 3.2, …., 3.r умножителей, множители 4.1.0, 4.1.1, …, 4.1.qr - 1, 4.2.0, 4.2.1, …, 4.2.qr - 1, 4.r.0, 4.r.1,…, 4.r.qr - 1, многоместные сумматоры 5.1, 5.2, …, 5.r, множители 7.1, 7.2, …, 7.r, многоместный сумматор по модулю qr 8, блок 9 оператора маскирования, выходы 13.1, 13.2, …, 13.r значений r многозначных функций алгебры логики f1(sn+r-1, sn+r-2, …, sn), f2(sn+r-1, sn+r-2, …, sn) …, fr(sn+r-1, sn+r-2, …, sn).
Шина 10 подачи значений r переменных МФАЛ sn+r-1, sn+r-2, …, sn, является входом регистра памяти 1, выход которого подключен к входам умножителей 3.1, 3.2, …, 3.r, выходы которых подключены к первым входам множителей 4.1.0, 4.1.1, …, 4.1.qr - 1, 4.2.0, 4.2.1, …, 4.2.qr - 1, 4.r.0,4.r.1, …, 4.r.qr - 1, ко вторым входам которых подключен выход блока 2 памяти, к входу которого подключена шина 11 подачи коэффициентов ar,i арифметических полиномов; выходы множителей 4.1.0, 4.1.1, …, 4.1.qr - 1, 4.2.0, 4.2.1, …, 4.2.qr - 1, 4.r.0, 4.r.1, …, 4.r.qr - 1 подключены к входам многоместных сумматоров 5.1, 5.2, …, 5.r, соответствующие выходы которых подключены к первым входам множителей 7.1, 7.2, …, 7.r на весовые коэффициенты ql-1, ко вторым входам которых подключен блок 6 памяти, к входу которого подключена шина 12 подачи весовых коэффицентов ql-1; выходы множителей 7.1, 7.2, …, 7.r подключены к входу многоместного сумматора 8 по модулю qr, выход которого подключен к входу блока 9 оператора маскирования, выходы которого являются выходами устройства выдачи значений r многозначных функций алгебры логики f1 (sn+г-1, sn+r-2, …, sn), f2(sn+r-1, sn+r-2, …, sn), …, fr (sn+-1, sn+r-2, …,sn).
Предлагаемое устройство работает следующим образом.
В исходном состоянии в блоки 2 и 6 памяти занесены по шинам 11 и 12 коэффициенты ar,i арифметических полиномов и весовые коэффициенты ql-1 соответственно. С выхода блока 2 памяти на вход множителей 4.1.0, 4.1.1, …, 4.1.qr - 1, 4.2.0, 4.2.1, …, 4.2. qr - 1, 4.r.0,4.r.1, …, 4.r.qr - 1 поступают коэффициенты ar,i арифметических полиномов. В момент времени, соответствующему началу преобразований, на входы регистра памяти 1 из шины 10 поступают значения r переменных МФАЛ sn+r-1, sn+r-2, …, sn. С выхода регистра памяти 1 значения r переменных МФАЛ sn+r-1, sn+r-2, …, sn поступают на входы блоков 3.1, 3.2, …, 3.r умножителей, с выхода которых аргументы  поступают на входы множителей 4.1.0, 4.1.1, …, 4.1.qr - 1, 4.2.0, 4.2.1, …, 4.2.qr - 1, 4.r.0, 4.r.1, …, 4.r.qr - 1. С выходов множителей 4.1.0, 4.1.1, …, 4.1.qr - 1, 4.2.0, 4.2.1, …, 4.2.qr - 1, 4.r.0, 4.r.1, …, 4.r.qг - 1. на входы многоместных сумматоров 5.1,5.2, …, 5.r поступают произведения
поступают на входы множителей 4.1.0, 4.1.1, …, 4.1.qr - 1, 4.2.0, 4.2.1, …, 4.2.qr - 1, 4.r.0, 4.r.1, …, 4.r.qr - 1. С выходов множителей 4.1.0, 4.1.1, …, 4.1.qr - 1, 4.2.0, 4.2.1, …, 4.2.qr - 1, 4.r.0, 4.r.1, …, 4.r.qг - 1. на входы многоместных сумматоров 5.1,5.2, …, 5.r поступают произведения 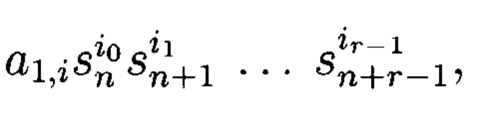
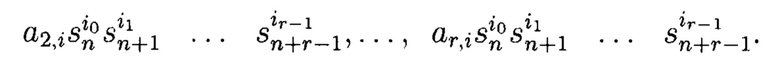 С выходов многоместных сумматоров 5.1,5.2, …, 5.r на соответствующие входы множителей 7.1, 7.2, …, 7.r поступают результаты вычисления арифметических полиномов A±(S), A2(S), …, Ar(S), также на вход множителей 7.1, 7.2, …, 7.r из блока памяти 6 поступают весовые коэффициенты ql-1. Далее с выходов множителей 7.1, 7.2, …, 7.r результаты вычислений q0A1(S), q1 A2(S), …, qr-lAr(S) поступают на вход многоместного сумматора 8 по модулю qr. С выхода многоместного сумматора 8 по модулю qr на вход блока 9 оператора маскирования поступает числовой результат вычисления (8). Далее выхода блока 9 оператора маскирования получим значения МФАЛ f1(sn+r-1, sn+r-2, …, sn), f2(sn+r-1, sn+r-2, …, sn), …, fr(sn+r-1, sn+r-2, …, sn), которые соответствуют элементам r-го блока ПСП sn+2r-1, sn+2r-2, …,sn+r.
С выходов многоместных сумматоров 5.1,5.2, …, 5.r на соответствующие входы множителей 7.1, 7.2, …, 7.r поступают результаты вычисления арифметических полиномов A±(S), A2(S), …, Ar(S), также на вход множителей 7.1, 7.2, …, 7.r из блока памяти 6 поступают весовые коэффициенты ql-1. Далее с выходов множителей 7.1, 7.2, …, 7.r результаты вычислений q0A1(S), q1 A2(S), …, qr-lAr(S) поступают на вход многоместного сумматора 8 по модулю qr. С выхода многоместного сумматора 8 по модулю qr на вход блока 9 оператора маскирования поступает числовой результат вычисления (8). Далее выхода блока 9 оператора маскирования получим значения МФАЛ f1(sn+r-1, sn+r-2, …, sn), f2(sn+r-1, sn+r-2, …, sn), …, fr(sn+r-1, sn+r-2, …, sn), которые соответствуют элементам r-го блока ПСП sn+2r-1, sn+2r-2, …,sn+r.
Заявленное изобретение может быть осуществлено с помощью средств и методов, описанных в доступных источниках информации. Это позволяет сделать вывод о соответствии заявленного изобретения признакам «промышленной применимости».

Пример. Рассмотрим построение q=3 ЛРРС, генерирующего 3-значную ПСП, задаваемую рекуррентным уравнением: sk+3=2sk+2 ⊕ sk (mod 3) и начальным заполнением: s0=0, s1=1, s2=2. Соответствующий характеристический многочлен имеет вид: P(z)=z3+2z2+1.
Тогда система рекуррентных уравнений для участка ПСП длинной три элемента примет вид:
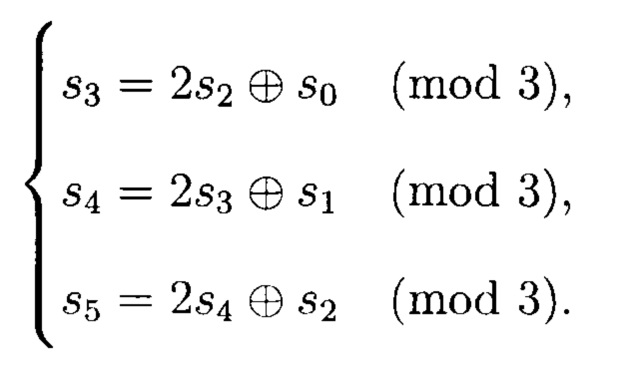
Далее запишем систему рекуррентных уравнений как систему МФАЛ с правыми частями равенств, выраженными через заданные начальные условия:
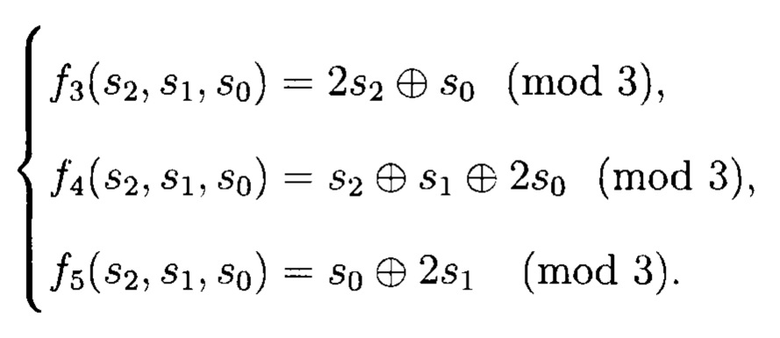
В соответствии с (7) получим систему арифметических полиномов следующего вида:
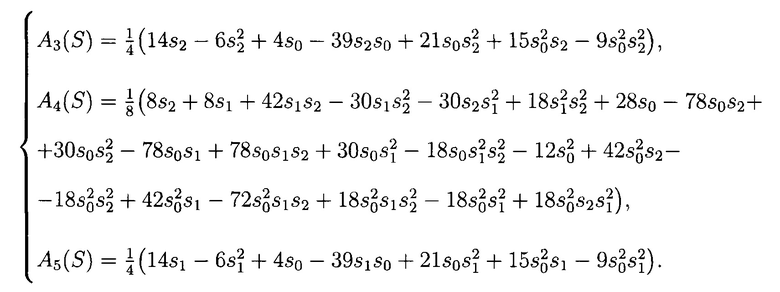
Реализуем систему арифметических выражений в виде арифметического полинома:
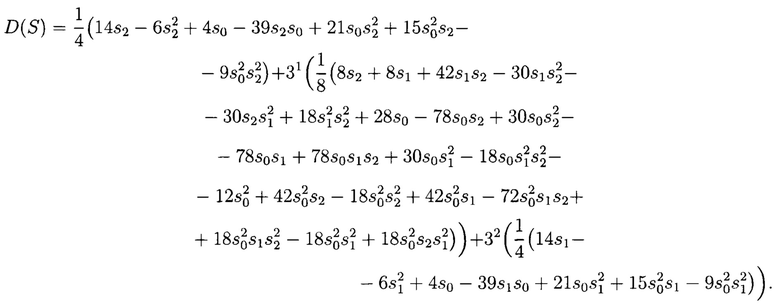
Модулярная полиномиальная форма примет вид:

В соответствии с заданными начальными условиями можно получить следующий фрагмент 3-значной ПСП:
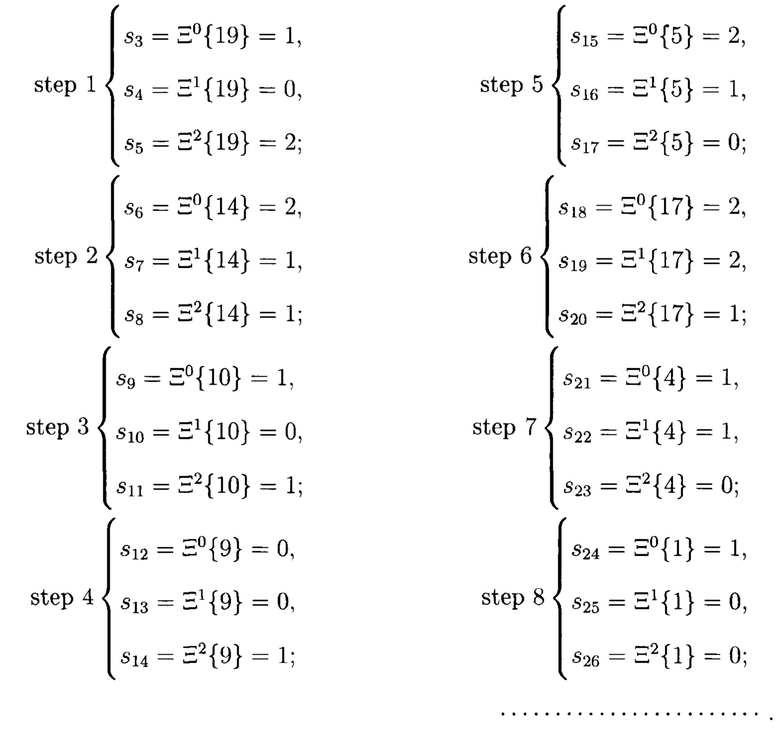
Приведенный пример показал, что заявляемое устройство параллельного формирования q-значных ПСП на арифметических полиномах функционирует корректно, технически реализуемо и позволяет решить поставленную задачу.
| название | год | авторы | номер документа |
|---|---|---|---|
| САМОПРОВЕРЯЕМЫЙ СПЕЦИАЛИЗИРОВАННЫЙ ВЫЧИСЛИТЕЛЬ СИСТЕМ БУЛЕВЫХ ФУНКЦИЙ | 2015 |
|
RU2579991C1 |
| ОТКАЗОУСТОЙЧИВЫЙ СПЕЦИАЛИЗИРОВАННЫЙ ВЫЧИСЛИТЕЛЬ СИСТЕМ БУЛЕВЫХ ФУНКЦИЙ | 2018 |
|
RU2680035C1 |
| Устройство генерации псевдослучайных чисел | 2023 |
|
RU2812094C1 |
| Генератор псевдослучайных чисел | 2023 |
|
RU2815827C1 |
| Устройство генерации псевдослучайных чисел | 2023 |
|
RU2815828C1 |
| УСТРОЙСТВО ФОРМИРОВАНИЯ ТРИПЛЕКСНЫХ ЧИСЕЛ | 2023 |
|
RU2812412C1 |
| УСТРОЙСТВО ФОРМИРОВАНИЯ ПСЕВДОСЛУЧАЙНЫХ КОМПЛЕКСНЫХ ЧИСЕЛ | 2022 |
|
RU2800190C1 |
| АРИФМЕТИЧЕСКИЙ ВЫЧИСЛИТЕЛЬ СИСТЕМ БУЛЕВЫХ ФУНКЦИЙ | 2011 |
|
RU2461868C1 |
| САМОПРОВЕРЯЕМЫЙ СПЕЦИАЛИЗИРОВАННЫЙ ВЫЧИСЛИТЕЛЬ СИСТЕМ БУЛЕВЫХ ФУНКЦИЙ | 2012 |
|
RU2485575C1 |
| Устройство для вычисления полинома | 1983 |
|
SU1179323A1 |
Изобретение относится к устройству параллельного формирования q-значных псевдослучайных последовательностей на арифметических полиномах. Технический результат заключается в обеспечении параллельного вычисления многозначных псевдослучайных последовательностей. Устройство содержит блок памяти, предназначенный для хранения коэффициентов полиномов, к входу которого подключена шина подачи коэффициентов; множители, выходы которых подключены к входам многоместных сумматоров; блок оператора маскирования, выходы которого являются выходами устройства, регистр памяти, входы которого являются входами устройства, к которым подключена шина подачи r переменных многозначных функций алгебры логики; умножители, к входам которых подключена шина подачи r переменных многозначных функций алгебры логики, выходы которого подключены к первым входам множителей, ко вторым входам которых подключен выход блока памяти коэффициентов арифметического полинома; умножитель на весовые коэффициенты qj-1, к первым входам которого подключены выходы многоместных сумматоров, ко вторым входам которого подключен блок памяти весовых коэффициентов, к выходу которого подключена шина подачи весовых коэффициентов; многоместный сумматор по модулю qr, выход которого подключен к оператору маскирования, выходы которого являются выходами устройства выдачи значений r многозначных функций алгебры логики. 6 ил., 3 табл.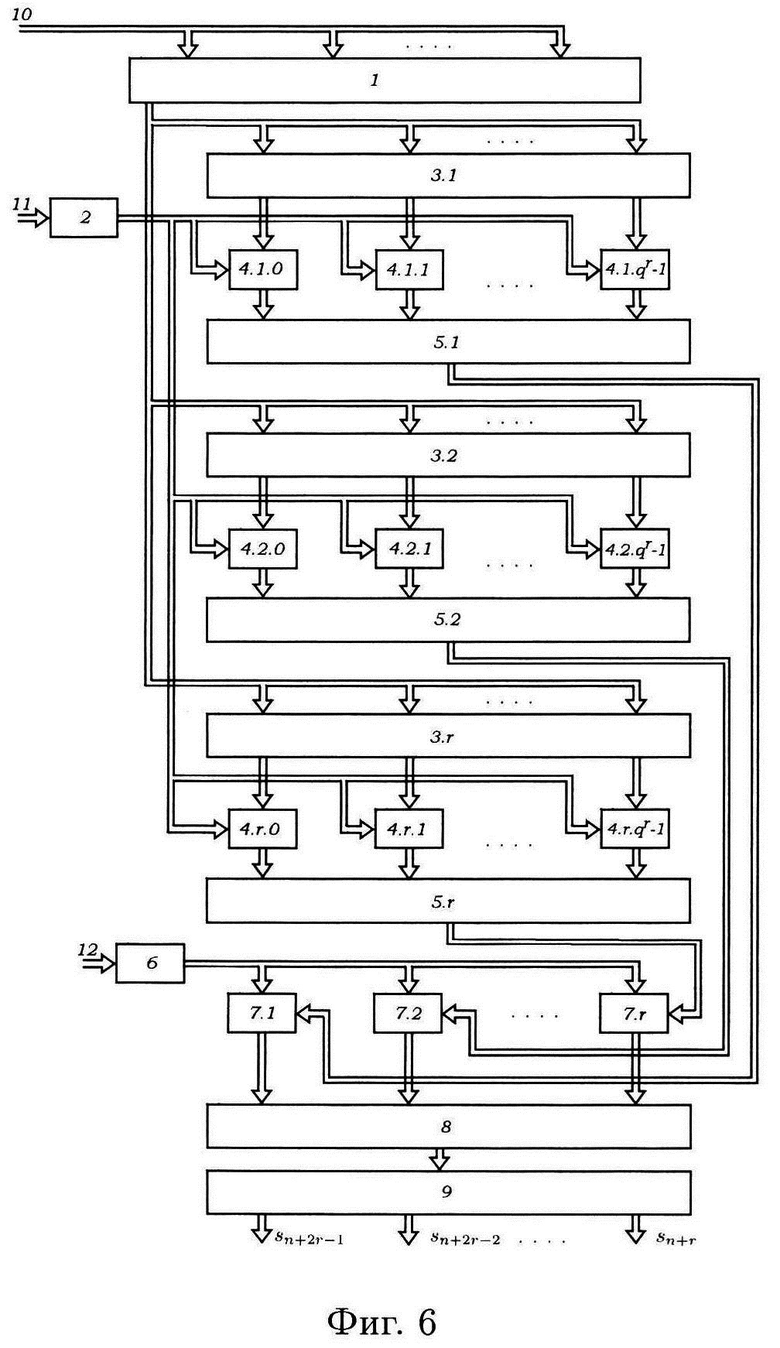
Устройство параллельного формирования q-значных псевдослучайных последовательностей на арифметических полиномах, содержащее блок памяти, предназначенный для хранения коэффициентов полиномов, к входу которого подключена шина подачи коэффициентов; множители, выходы которых подключены к входам многоместных сумматоров; блок оператора маскирования, выходы которого являются выходами устройства, отличающееся тем, что введены регистр памяти, входы которого являются входами устройства, к которым подключена шина подачи r переменных многозначных функций алгебры логики; умножители, к входам которых подключена шина подачи r переменных многозначных функций алгебры логики, выходы которого подключены к первым входам множителей, ко вторым входам которых подключен выход блока памяти коэффициентов арифметического полинома; умножитель на весовые коэффициенты qj-1, к первым входам которого подключены выходы многоместных сумматоров, ко вторым входам которого подключен блок памяти весовых коэффициентов, к выходу которого подключена шина подачи весовых коэффициентов; многоместный сумматор по модулю qr, выход которого подключен к оператору маскирования, выходы которого являются выходами устройства выдачи значений r многозначных функций алгебры логики.
| ПОЛИНОМИАЛЬНЫЙ МОДУЛЯРНЫЙ ВЫЧИСЛИТЕЛЬ СИСТЕМ БУЛЕВЫХ ФУНКЦИЙ С ОБНАРУЖЕНИЕМ ОШИБОК | 2015 |
|
RU2586574C1 |
| МОДУЛЯРНЫЙ ПОЛИНОМИАЛЬНЫЙ ВЫЧИСЛИТЕЛЬ СИСТЕМ БУЛЕВЫХ ФУНКЦИЙ | 2015 |
|
RU2586575C1 |
| Вальцевый макаронный агрегат | 1949 |
|
SU92270A1 |
| ГЕНЕРАТОР ПСЕВДОСЛУЧАЙНЫХ БИНАРНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ | 2009 |
|
RU2427886C2 |
| Полуавтомат для фрезерования уреза подошвы для обуви | 1962 |
|
SU151948A1 |
| US 9563403 B2, 07.02.2017 | |||
| Металлический водоудерживающий щит висячей системы | 1922 |
|
SU1999A1 |
| Колосоуборка | 1923 |
|
SU2009A1 |
Авторы
Даты
2021-12-16—Публикация
2021-03-23—Подача