Изобретение относится к области радиолокационной техники и может быть использовано при построении различных радиолокационных или аналогичных систем, предназначенных для определения местоположения летательных аппаратов.
При обеспечении навигации летательных аппаратов (ЛА) их местоположение определяют путем измерения текущих координат.
Известен способ спутниковой радионавигации ГЛОНАСС, обеспечивающий непрерывность навигационно-временного обеспечения [1]. Это означает, что существует возможность определения координат местоположения, например, ЛА в любое время суток на базе спутниковых радионавигационных систем, включающих навигационные спутники с бортовой радиопередающей аппаратурой (НС), наземный комплекс (НК), в составе наземной станции траекторных измерений (НИ) и наземного вычислительного центра (НЦ).
Реализация способа [1] заключается в следующем.
Используют несколько навигационных спутников (НС).
Формируют каждым НС сложный радиосигнал, который представляет собой гармоническое колебание с цифровой фазовой модуляцией.
Излучают сформированные НС сложные радиосигналы.
Принимают излученные сложные радиосигналы.
Измеряют дальность до ЛА с помощью принятых излученных сложных сигналов и доплеровское смещение частоты излученного сложного сигнала, используя НИ.
Определяют (вычисляют) составляющие вектора скорости, три пространственные координаты ЛА и текущее время с помощью НЦ.
Передают вычисленную информацию с НК на борт НС.
Принимают переданную вычисленную информацию на борту НС.
Запоминают принятую информацию от НК на борту НС.
Передают запомненную принятую информацию с борта НС о навигационном сообщении.
Принимают на ЛА навигационное сообщение с борта НС и используют полученную информацию для вычисления местоположения ЛА и последующего управления движением ЛА (коррекции движения ЛА).
Недостатками способа [1] являются низкая помехоустойчивость навигации ЛА при реализации способа при воздействии искусственных (преднамеренных) помех, которые делают способ [1] неработоспособным и отсутствие автономности работы способа, поскольку необходим информационный контакт с несколькими НС. В результате во время действия помех информация о местоположении ЛА не поступает на борт ЛА, что не позволяет управлять движением ЛА путем коррекции его местоположения.
Известен способ навигации летательных аппаратов [2], выбранный за прототип.
Способ [2] заключается в следующем.
Используют картосличительные корреляционно-экстремальные способы навигации (КЭСН), обеспечивающие поиск и слежение за оптимальным режимом движения ЛА [3]. КЭСН основаны на сравнении текущих карт местности, полученных с использованием радиоволн, с эталонными картами той же местности, априори находящимися на ЛА, в основе которых лежит определение местоположения ЛА с последующим управлением движением ЛА путем коррекции их местоположения. Эталонные карты устанавливают на ЛА до момента начала движения над заданной поверхностью местности, а текущие карты получают во время движения ЛА. По отклонениям эталонных карт местности от текущих в заданной точке траектории движения ЛА определяют отклонение фактической траектории от заданной. В результате сравнения эталонных и текущих карт местности вырабатывают поправки в координаты ЛА для управления движением путем коррекции местоположения ЛА.
Сравнение эталонной и текущей карт осуществляется на основе вычисления функционалов, достигающих глобального экстремума при полном совмещении изображений указанных карт. Для обработки полученной при движении ЛА информации используют разностные алгоритмы, основанные на вычислении разностей измеренных высот текущей карты.
Способ [2] реализуется следующим образом.
Выбирают участок местности (мерный участок), размер которого в плановых координатах должен быть достаточен для определения местоположения ЛА.
Для мерного участка составляют эталонную карту местности в виде цифровой матрицы, размеры которой определяются размерами мерного участка.
Поскольку задачей корреляционно-экстремальной навигации является уточнение местоположения ЛА, определенного иными средствами навигации, то определение поправок к координатам ЛА (уточнение координат) производится в пределах области, определяемой погрешностью этих средств навигации (инерциальные средства навигации). Эта область имеет форму квадрата, сторона которого равна удвоенной погрешности иных средств навигации, находится внутри мерного участка и называется квадратом неопределенности.
Эталонная карта местности до начала движения находится на ЛА.
Реализацию способа навигации ЛА рассмотрим на примере составления текущей карты с помощью трех лучей радиоволн, расположенных в одной плоскости, которая находится перпендикулярно направлению движения ЛА.
Составляют первую текущую карту мерного участка в пределах первого квадрата неопределенности, представляющего собой массив данных М1, путем измерения параметров мерного участка с помощью радиоволн. Лучи радиоволн излучают циклически следующим образом. Первым излучают луч, направление распространения которого расположено в плоскости, ортогональной плоскости горизонта мерного участка или в плоскости, которая находится под углом к плоскости горизонта мерного участка (первый луч). Далее излучают лучи, направления распространения которых не совпадают с направлением распространения первого луча, причем направления распространения одной части лучей находятся слева (по направлению движения ЛА) от первого луча, а другой части - справа (по направлению движения ЛА) от первого луча. Количество лучей справа и слева от первого луча одинаковое. Далее цикл излучения повторяется.
По полученным данным о наклонных дальностях, а также об углах эволюций вычисляют координаты точек измерений в системе координат, связанной с ЛА.
Вычисляют местные координаты проекции точки траектории ЛА на плоскость плановых координат.
Для каждой гипотезы, то есть для всех возможных положений ЛА внутри первого квадрата неопределенности, по полученным данным о наклонных дальностях вычисляют одно слагаемое показателя близости.
Вычисляют для всех гипотез внутри первого квадрата неопределенности слагаемые показателя близости.
Проводят по завершении всех измерений поиск глобального экстремума показателя близости.
Определяют поправки к координатам местоположения ЛА в плановых координатах мерного участка на основе анализа взаимных смещений эталонной и первой текущей карт местности мерного участка.
После определения местоположения ЛА в плановых координатах мерного участка, вычисляют высоту ЛА над поверхностью мерного участка в координатах мерного участка (в точке определения местоположения ЛА в плановых координатах мерного участка).
Перед вычислением сигнала коррекции через равные интервалы времени Δt после получения первой текущей карты мерного участка последовательно получают вторую текущую карту и третью текущую карту мерного участка.
Определяют по выше приведенному алгоритму второе и третье местоположения ЛА в плановых координатах эталонной карты путем сравнения второй текущей и эталонной карт мерного участка в пределах второго квадрата неопределенности, и третьей текущей и эталонной карт мерного участка в пределах второго квадрата неопределенности. Размеры второго квадрата неопределенности значительно меньше размеров первого квадрата неопределенности.
Определяют направление движения, скорость и ускорение ЛА путем сравнения координат первого, второго и третьего местоположения ЛА.
Вычисляют сигнал коррекции траектории движения.
Управляют движением ЛА путем коррекции его местоположения, используя полученные значения координат (плановые координаты и высота) и трехмерного вектора движения ЛА (направление, скорость и ускорение движения по трем координатам).
Недостатком способа [2] является низкая точность вычисления сигнала коррекции траектории движения ЛА, связанная с дискретностью получения трехмерного вектора движения ЛА, определение которого производится всего лишь по трем точкам координат (плановые координаты и высота): первого, второго и третьего местоположений ЛА.
Для повторного определения местоположения ЛА необходимо заново повторить полный цикл вычислений по определению местоположения, включая составление новой текущей карты местности. То есть повторное определение местоположения ЛА возможно только через большой временной интервал, длительность которого определяется полным циклом вычислений. Данное время определяет минимальный дискрет времени между моментами определения местоположения ЛА, не позволяет с меньшим дискретом времени получать значения трехмерного вектора движения ЛА, а также ограничивает количество точек, в которых может быть определено местоположение ЛА (из за ограниченных размеров эталонной карты), что и не позволяет более точно получать трехмерный вектор движения ЛА и снижает точность вычисления сигнала коррекции траектории движения ЛА.
Техническим результатом предлагаемого изобретения является повышение точности навигации ЛА.
Технический результат достигается тем, что в способе навигации летательных аппаратов, заключающемся в использовании эталонной карты местности, выборе участка местности (мерный участок), находящегося в пределах эталонной карты, составлении первой текущей карты мерного участка путем циклических измерений наклонных дальностей с помощью многолучевого режима измерения при помощи радиоволн, излучаемых в виде лучей, определении разности результатов многолучевых измерений по первой текущей карте, циклическом сравнении первой текущей и эталонной карт для определения значений слагаемых показателя близости в пределах первого квадрата неопределенности, поиска глобального экстремума показателя близости и определения первого местоположения летательного аппарата в координатах эталонной карты, составлении второй текущей карты мерного участка и определении второго местоположения летательного аппарата путем сравнения второй текущей и эталонной карт мерного участка в пределах второго квадрата неопределенности, составлении третьей текущей карты мерного участка и определении третьего местоположения летательного аппарата путем сравнения третьей текущей и эталонной карт мерного участка в пределах второго квадрата неопределенности, причем размеры второго квадрата неопределенности значительно меньше размеров первого квадрата неопределенности, определении направления движения, скорости и ускорения летательного аппарата путем сравнения координат первого, второго и третьего местоположения летательного аппарата в координатах эталонной карты, вычислении сигнала коррекции траектории движения и управлении движением летательного аппарата путем коррекции его местоположения с использованием полученных значений координат и трехмерного вектора движения летательного аппарата: направления, скорости и ускорения движения по трем координатам, при поиске глобального экстремума показателя близости для определения первого местоположения летательного аппарата запоминают значения слагаемых показателя близости при каждом цикле сравнений первой текущей и эталонной карт и номер цикла сравнения первой текущей и эталонной карт, после определения первого местоположения летательного аппарата в координатах эталонной карты производят дальнейший поиск глобальных экстремумов показателя близости для определения последующих (N-1) местоположений летательного аппарата, для чего определение второго и последующих местоположений летательного аппарата производят при помощи метода скользящего окна: при каждом последующем цикле сравнения текущей и эталонной карт запоминают новые значения слагаемых показателя близости и номер цикла сравнения, исключая при этом из памяти значения слагаемых показателя близости, соответствующие наиболее раннему номеру цикла сравнения текущей и эталонной карт, и циклически производят поиск (N-1) глобальных экстремумов показателя близости, определение второго и последующих местоположений летательного аппарата производят путем сравнения текущей и эталонной карт мерного участка в пределах второго квадрата неопределенности.
В результате в предложенном способе навигации определение слагаемых показателя близости, при которых достигается глобальный экстремум, после первого определения аргументов показателя близости, при которых достигается первый глобальный экстремум, производят при помощи метода скользящего окна, что сокращает временной дискрет между моментами определения местоположения ЛА до цикла измерений наклонных дальностей и снимает ограничение на количество определяемых местоположений. Что позволяет повысить точность навигации ЛА за счет использования полной информации о параметрах траектории движения ЛА - о координатах местоположения ЛА и трехмерном векторе движения ЛА (направлении, скорости и ускорении движения) с меньшим временным дискретом и в большем объеме.
Способ навигации ЛА поясняют следующие чертежи:
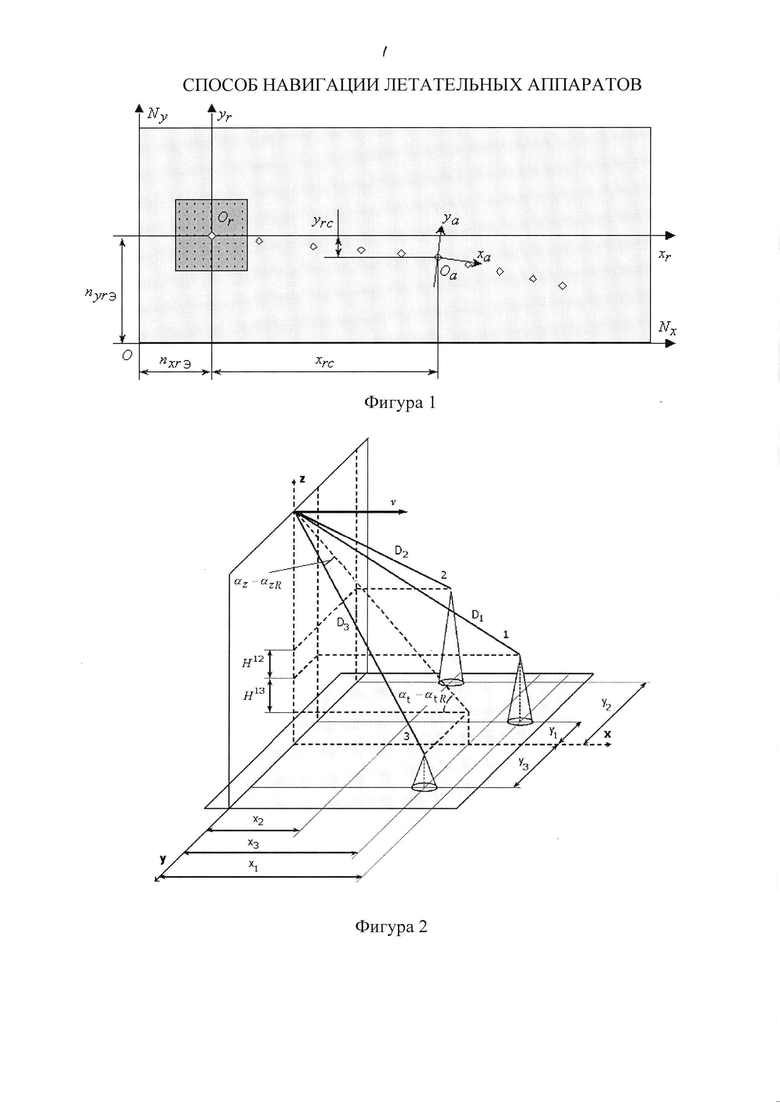
- на фигуре 1 представлено взаимное расположение систем координат при движении ЛА;
- на фигуре 2 показано измерение наклонной дальности по отдельным лучам радиоволн;
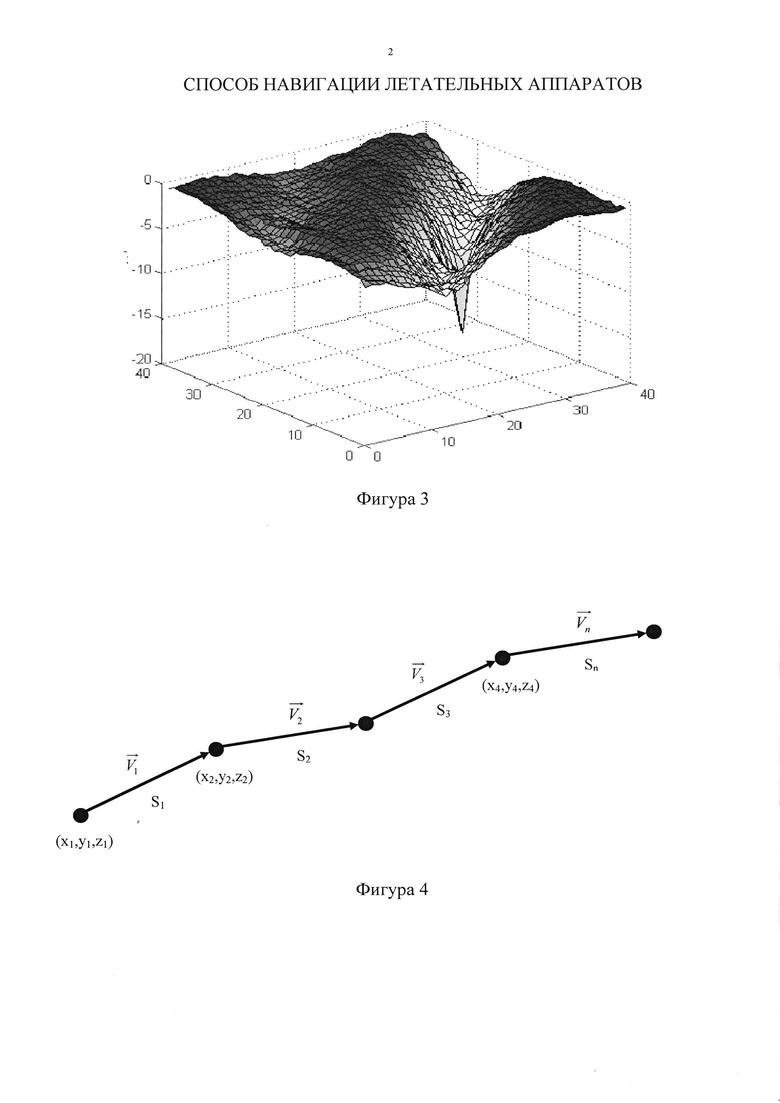
- на фигуре 3 представлен пример показателя близости данных;
- на фигуре 4 показан вектор движения ЛА, причем координаты ЛА (x1, y1, z1), где (x1, y1) - плановые координаты и z1 - высота, получены без применения метода скользящего окна, координаты ЛА (x2, y2, z2)…(xn, yn, zn) получены при помощи метода скользящего окна, стрелка - вектор движения ЛА, указывающий направление движения, 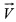 - вектор скорости движения ЛА, представленный в виде векторов скоростей
- вектор скорости движения ЛА, представленный в виде векторов скоростей 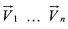 , S - расстояние между местоположениями ЛА, представленное в виде расстояний S1…Sn.
, S - расстояние между местоположениями ЛА, представленное в виде расстояний S1…Sn.
Способ навигации ЛА осуществляется следующим образом.
За время движения над мерным участком определяют текущую карту местности, для составления которой используют данные об измеренных значениях наклонной дальности с помощью лучей радиоволн, а также значениях скорости и углах эволюций ЛА (тангаж, крен и курс).
Применяют следующие системы координат, показанные на фиг. 1, для:
- эталонной карты рельефа местности (большой прямоугольник на фиг. 1);
- квадрата неопределенности (квадрат на фиг. 1);
- возможных положений ЛА внутри квадрата неопределенности в момент начала измерений (точки на фиг. 1), и точек траектории ЛА, в которых производят измерения (ромбы на фиг. 1).
Местная система координат является левой прямоугольной декартовой системой координат Orxryrzr с началом Оr. При этом оси Orхr и Oryr лежат в плоскости местного горизонта, то есть xr и yr являются плановыми координатами ЛА. Относительно плоскости Orxryr определяют высоты рельефа местности и ЛА. Таким образом, указанные высоты являются соответствующими значениями координаты zr. Начало координат Or выбрано так, что ось Orxr направлена в расчетную точку появления ЛА над участком местности, соответствующим эталонной карте. Ось Orxr считается коллинеарной по отношению к горизонтальной составляющей расчетного вектора скорости ЛА (фиг. 1). Плановая система координат неподвижна и связана с эталонной картой.
Для того, чтобы привязать плановые координаты к эталонной карте, используют дискретную систему координат. При этом оси Nx и Ny сонаправлены с осями местной системы Orxryr (фиг. 1). Нулевым индексам в дискретной системе координат соответствует левый нижний угол эталонной карты. Предполагаемое значение дискретных координат ЛА в момент начала сбора данных Or обозначим как (nxrЭ, nyrЭ).
Связь между координатами дискретной и местной систем координат определяется выражениями вида

где ΔЭ - размер ячейки сетки эталонной карты.
При определении координат точек измерений в виде точек пересечения подстилающей поверхности и лучей радиоволн используют систему координат, связанную с текущим положением ЛА. Начало координат этой системы (точка Оа) поместим в текущую точку проекции траектории ЛА на плоскость плановых координат. Ось Оаха по направлению совпадает с текущим направлением вектора скорости ЛА.
Связь между координатами системы, связанной с ЛА, и местной системы координат определяется выражениями
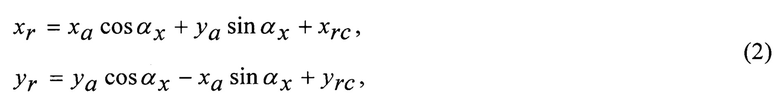
где хrc и yrc - координаты проекции текущего положения ЛА на плоскость плановых координат;
α х - курс ЛА в текущей точке измерений (угол между вектором скорости ЛА и осью Orxr, на фиг. 1 это угол между осями хr и ха).
Исходными данными для вычислений в КЭСН являются:
- эталонная карта, представляющая собой массив данных о рельефе местности, элементы которого представляют собой высоты рельефа в узлах координатной сетки эталонной карты на плоскости Orxryr (фиг. 1);
- данные, определяемые углом между лучами αR радиоволн;
- данные измерений, отличных от полученных с помощью лучей радиоволн, поступающие с каждым результатом измерений: значения угла αz крена, угла αх курса, угла αt тангажа, скорости ν ЛА (фиг. 2);
- первая текущая карта, представляющая собой массив данных M1 в виде набора значений наклонных дальностей по всем трем лучам, полученных в каждом измерении.
Первая текущая карта местности определяется матрицей Н(nх, ny) размером Nx×Ny, а эталонная карта - матрицей НЭ(nх, nу) размером NxЭ×NyЭ. Дискретные значения nsx и nsy соответствуют горизонтальному и вертикальному смещению текущей карты относительно эталонной и отсчитываются от левого нижнего угла эталонной карты, для которого nsx=nsy=0.
В предлагаемом способе используют дифференциально-разностный алгоритм обработки многолучевых измерений, который рассмотрим на примере трехлучевого КЭСН. Лучи радиоволн излучают последовательно в следующем порядке: первым - центральный луч (по направлению движения ЛА), вторым - левый луч и третьим - правый луч относительно центрального луча.
Используемый алгоритм одного цикла измерений наклонных дальностей состоит в определении разности измерений левого и центрального лучей, правого и центрального лучей текущего измерения, а также в вычислении разности измерений центрального луча в текущем измерении и в предыдущем.
Обработку данных каждого измерения производят следующим образом.
По измеренным значениям наклонных дальностей до элементов подстилающей поверхности Dj (j∈[1, 3] - номер луча радиоволн) определяют координаты точек измерений в системе координат, связанной с ЛА, а также измеряемые значения высоты рельефа Нj.
Согласно фиг. 2, получим систему уравнений для каждого луча j в следующем виде
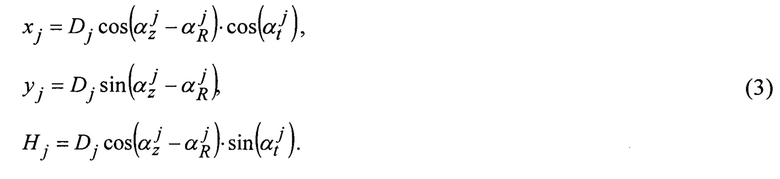
По полученным данным о скорости и углах эволюции определяют координаты проекции точки траектории ЛА на плоскость плановых координат.
Для первого измерения эти координаты считаются нулевыми (то есть положение ЛА во время первого измерения совпадает с началом координат системы Orxryr - фиг. 1)

Местные координаты ЛА во время выполнения следующих измерений вычисляют по рекуррентным соотношениям

где Тс - период поступления измеренных данных, i=1, 2,… - номер текущего измерения.
Зная координаты точек измерений в системе координат, связанной с ЛА (Оахауa) и местные координаты начала Оа, определяют координаты точек измерений в местной системе координат

Циклически сравнивают первую текущую и эталонную карты (цикл сравнения карт соответствует циклу измерения наклонных дальностей). В каждом цикле сравнения первой текущей и эталонной карт выполняют перебор гипотез.
Перебор гипотез заключается в следующем. Для каждого из возможных положений ЛА в пределах квадрата неопределенности (размеры первого квадрата неопределенности М1) вычисляют координаты (в дискретной системе координат) точек измерений, определенных ранее в местной системе координат. Для этого точку Or помещают поочередно в узлы координатной сетки внутри квадрата неопределенности и выполняют вычисление показателя близости данных. Координаты точек измерений в дискретной системе координат определяют как

где nhx и nhy - смещения точки Оr для различных гипотез, определенные в количестве узлов сетки эталонной карты.
Показатель близости данных Р(nhx, nhy) для данного случая имеет вид
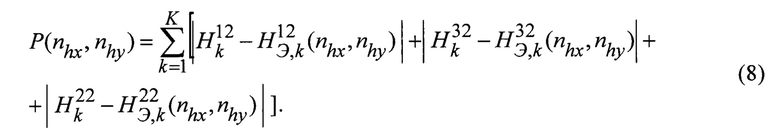
Здесь nhx и nhy - смещения точки Or для различных гипотез; K - количество циклов измерений наклонных дальностей; 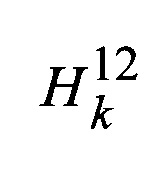 - разность значений высоты по первому и левому лучам, измеренных в k-м цикле измерений;
- разность значений высоты по первому и левому лучам, измеренных в k-м цикле измерений; 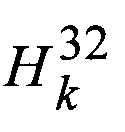 - разность значений высоты по первому и правому лучам, измеренных в k-м измерении;
- разность значений высоты по первому и правому лучам, измеренных в k-м измерении; 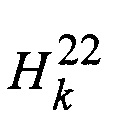 - разность значений высоты измеренных в k-м и (k-1)-м циклах измерений наклонных дальностей;
- разность значений высоты измеренных в k-м и (k-1)-м циклах измерений наклонных дальностей; 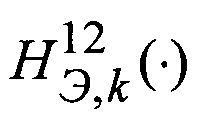 - разность определенных для некоторой гипотезы (для определенного значения nhx и nhy) значений высоты по данным эталонной карты на k-м цикле измерений по первому и левому лучам;
- разность определенных для некоторой гипотезы (для определенного значения nhx и nhy) значений высоты по данным эталонной карты на k-м цикле измерений по первому и левому лучам; 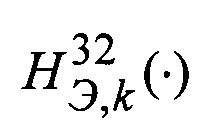 - разность определенных для некоторой гипотезы значений высоты по данным трехмерной эталонной карты на k-м цикле измерений по первому и правому лучам;
- разность определенных для некоторой гипотезы значений высоты по данным трехмерной эталонной карты на k-м цикле измерений по первому и правому лучам; 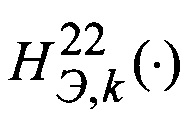 - разность определенных для некоторой гипотезы значений высоты по данным эталонной карты на k-м и (k-1)-м циклах измерений по первому лучу.
- разность определенных для некоторой гипотезы значений высоты по данным эталонной карты на k-м и (k-1)-м циклах измерений по первому лучу.
Для каждой гипотезы, то есть для всех возможных положений ЛА внутри квадрата неопределенности, по полученным данным о наклонных дальностях вычисляют слагаемые показателя близости.
Запоминают значения слагаемых показателя близости при каждом цикле сравнений первой текущей и эталонной карт и номер сравнения первой текущей и эталонной карт.
По завершении всех измерений производят поиск первого глобального экстремума показателя близости данных P(nhx, nhy) и определяют поправки к координатам местоположения ЛА по плановым координатам (фиг. 3).
Определяют первое местоположение ЛА и поправки к координатам местоположения ЛА по высоте в момент определения поправок местоположения ЛА в плановых координатах мерного участка.
После определения первого местоположения ЛА продолжают составление первой текущей карты мерного участка.
Определение второго и последующих местоположений ЛА производят при помощи метода скользящего окна путем сравнения первой текущей и эталонной карт мерного участка в пределах второго квадрата неопределенности, представляющего собой массив данных М2.
Для определения второго местоположения ЛА выполняют очередной цикл сравнения первой текущей и эталонной карт, запоминают новые значения слагаемых показателя близости и номер цикла сравнения, исключая при этом из памяти значения слагаемых показателя близости, соответствующие первому циклу сравнения первой текущей и эталонной карт.
Производят поиск второго глобального экстремума показателя близости данных P(nhx, nhy) и определяют второе местоположение ЛА (плановые координаты и высота).
Описанную выше последовательность операций применяют для определения последующих местоположений ЛА:
- при каждом последующем цикле сравнения первой текущей и эталонной карт запоминают новые значения слагаемых показателя близости и номер цикла сравнения, исключая при этом из памяти значения слагаемых показателя близости, соответствующие наиболее раннему номеру цикла сравнения первой текущей и эталонной карт;
- производят поиск очередного глобального экстремума показателя близости данных (цикл поиска второго и последующих глобальных экстремумов соответствует циклу сравнения карт) путем сравнения первой текущей и эталонной карт мерного участка в пределах второго квадрата неопределенности, представляющего собой массив данных М2;
- определяют очередное местоположение ЛА.
Размеры первого квадрата неопределенности М1 при определении первого местоположения ЛА в плановых координатах эталонной карты определяются величиной допустимых отклонений фактической траектории ЛА от заданной.
При определении первого местоположения ЛА с использованием первого квадрата неопределенности происходит перебор максимального количества гипотез (зона поиска максимальна). При втором и последующих определениях местоположения ЛА, общее число которых (N-1), количество гипотез при переборе значительно сокращается, т.к. размеры второго квадрата неопределенности будут определяться величиной удвоенной погрешности определения первого местоположения ЛА. Это позволяет использовать второй квадрат неопределенности значительно меньших размеров, по сравнению с размерами первого квадрата неопределенности: М2<<М1. При этом не происходит снижения точности измерений, поскольку при переборе гипотез уменьшилось количество переборов за счет исключения гипотез, не влияющих на определение местоположения ЛА.
Таким образом, вычисляют координаты первого (x1, y1, z1), второго (x2, y2, z2)…N-го (xn, yn, zn) местоположений ЛА.
Определяют по координатам местоположений ЛА вектор направления движения ЛА (фиг. 4) - скорость движения, направление движения и ускорение ЛА.
Скорость V1 движения ЛА определим в виде

где S1 - расстояние между точкой с координатами (x1, у1, z1) на эталонной карте (первое местоположение ЛА) и точкой с координатами (х2, y2, z2) на эталонной карте (второе местоположение ЛА) (фиг. 4);
Δt1 - временной интервал между моментом времени t1, в который было определено первое местоположение ЛА, и моментом времени t2, в который было определено второе местоположение ЛА.
Направление движения ЛА определим как направление вектора скорости 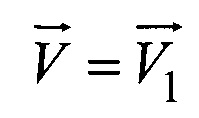 из точки с координатами (х1, y1, z1) в точку с координатами (x2, y2, x2) (ФИГ. 4).
из точки с координатами (х1, y1, z1) в точку с координатами (x2, y2, x2) (ФИГ. 4).
Скорость V2 движения ЛА определим в виде

где S2 - расстояние между точкой с координатами (х2, y2, z2) на эталонной карте (второе местоположение ЛА) и точкой с координатами (x3, y3, z3) на эталонной карте (третье местоположение ЛА) (фиг. 4);
Δt2 - временной интервал между моментом времени t2, в который было определено второе местоположение ЛА, и моментом времени, в который было определено третье местоположение ЛА.
Направление движения ЛА определим как направление вектора скорости 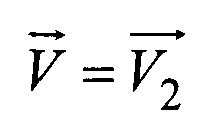 из точки с координатами (х2, y2, z2) в точку с координатами (x3, y3, z3) (фиг. 4).
из точки с координатами (х2, y2, z2) в точку с координатами (x3, y3, z3) (фиг. 4).
Ускорение W1 движения ЛА определим как

где ΔV1=V2-V1 - изменение скорости движения ЛА за время Δt2.
Скорость Vn движения ЛА определим в виде

где ΔSn - расстояние между точкой с координатами (хn-1, yn-1, zn-1) на эталонной карте ((n-1)-ое местоположение ЛА) и точкой с координатами (хn, yn, zn) на эталонной карте (n-ое местоположение ЛА) (фиг. 4);
Δtn - временной интервал между моментом времени tn-1, в который было определено первое местоположение ЛА, и моментом времени tn, в который было определено второе местоположение ЛА.
Направление движения ЛА определим как направление вектора скорости 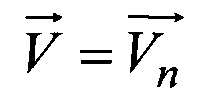 из точки с координатами (хn-1, yn-1, zn-1) в точку с координатами (xn, yn, zn) (фиг. 4).
из точки с координатами (хn-1, yn-1, zn-1) в точку с координатами (xn, yn, zn) (фиг. 4).
Ускорение Wn-1 движения ЛА определим как

где ΔVn-1=Vn-Vn-1 - изменение скорости движения ЛА за время Δtn.
Уточненную (среднюю) Vcр скорость движения ЛА определим как

Уточненное (среднее) направление движения ЛА определим как направление вектора скорости 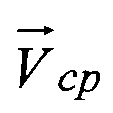 из точки с координатами (x1, y1, z1) в точку с координатами (хn, yn, zn).
из точки с координатами (x1, y1, z1) в точку с координатами (хn, yn, zn).
Уточненное (среднее) ускорение движения ЛА определим как
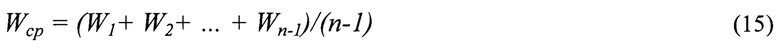
Вычисляют сигналы коррекции траектории движения и управляют движением ЛА путем коррекции его местоположения с использованием полученных значений координат (плановые координаты и высота) и трехмерного вектора движения ЛА (направление, скорость и ускорение движения по трем координатам).
Таким образом, данный способ навигации ЛА имеет существенные отличия от известных способов навигации, т.к. за счет использования информации о параметрах траектории движения ЛА - о координатах местоположения ЛА и трехмерном векторе движения ЛА (направлении, скорости и ускорении движения) с малым временным дискретом между точками, в которых производится определение местоположения, реализуется повышенная точность управления движением ЛА.
Данный способ навигации ЛА имеет существенные отличия от известного способа навигации, взятого за прототип, за счет того, что определение слагаемых показателя близости, при которых достигается глобальный экстремум, после первого определения аргументов показателя близости, при которых достигается первый глобальный экстремум, производят при помощи метода скользящего окна, что сокращает временной дискрет между моментами определения местоположения ЛА до цикла измерений наклонных дальностей и снимает ограничение на количество определяемых местоположений.
Важно отметить, что рассмотренный способ навигации ЛА с предложенным алгоритмом сохраняет свои положительные свойства при различном количестве лучей радиоволн и обеспечивает работоспособность и для трех, и для большего количества лучей радиоволн. Число используемых лучей радиоволн определяется только временем, в течение которого обеспечивается измерение местоположения ЛА при движении над мерным участком поверхности.
ЛИТЕРАТУРА
1. ГЛОНАСС. Принципы построения и функционирования / Под ред. А.И. Перова, В.Н. Харисова. - М.: Радиотехника, 2005. - 688С. (С. 12-15).
2. Патент №2515469 РФ, МПК G01S 5/02 (2010.01). Способ навигации летательных аппаратов / Хрусталев А.А., Кольцов Ю.В. // Изобретения. Полезные модели. - 2014. - Опубл. 10.05.2014. - Бюл. №13. (прототип).
3. Белоглазов И.Н., Джанджгава Г.И., Чигин Г.П. Основы навигации по геофизическим полям. - М.: Наука, 1985. – 328 С. (С. 10-11, 19-22, 25-34).
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ навигации летательных аппаратов | 2016 |
|
RU2611564C1 |
| СПОСОБ НАВИГАЦИИ ЛЕТАТЕЛЬНЫХ АППАРАТОВ | 2012 |
|
RU2515469C1 |
| СПОСОБ НАВИГАЦИИ ЛЕТАТЕЛЬНЫХ АППАРАТОВ | 2007 |
|
RU2338158C1 |
| СПОСОБ НАВИГАЦИИ ЛЕТАТЕЛЬНЫХ АППАРАТОВ | 2007 |
|
RU2340874C1 |
| СПОСОБ НАВИГАЦИИ ЛЕТАТЕЛЬНЫХ АППАРАТОВ | 2005 |
|
RU2284544C1 |
| СПОСОБ НАВИГАЦИИ ДВИЖУЩИХСЯ ОБЪЕКТОВ | 2014 |
|
RU2559820C1 |
| СПОСОБ НАВИГАЦИИ ЛЕТАТЕЛЬНЫХ АППАРАТОВ | 2020 |
|
RU2739872C1 |
| СПОСОБ НАВИГАЦИИ ЛЕТАТЕЛЬНЫХ АППАРАТОВ | 2011 |
|
RU2471152C1 |
| СПОСОБ НАВИГАЦИИ ДВИЖУЩИХСЯ ОБЪЕКТОВ | 2008 |
|
RU2385468C1 |
| СПОСОБ НАВИГАЦИИ ДВИЖУЩИХСЯ ОБЪЕКТОВ | 2010 |
|
RU2426073C1 |
Изобретение относится к области радиолокационной техники и может быть использовано при построении различных радиолокационных или аналогичных систем, предназначенных для навигации летательных аппаратов (ЛА) с использованием радиоволн путем определения местоположения и управления движением ЛА. Технический результат изобретения - повышение точности навигации летательных аппаратов. Способ навигации ЛА заключается в использовании эталонной карты местности, выборе мерного участка местности, находящегося в пределах эталонной карты, составлении текущей карты мерного участка путем циклических измерений наклонных дальностей с помощью многолучевого режима измерения при помощи радиоволн, определении разности результатов многолучевых измерений по текущей карте, циклическом сравнении текущей и эталонных карт для определения слагаемых показателя близости, поиске глобального экстремума показателя близости, определении координат (плановые координаты и высота) местоположений ЛА в плановых координатах эталонной карты, сравнении координат местоположений ЛА, определении направления, скорости и ускорения движения ЛА, вычислении сигнала коррекции траектории движения и управлении движением ЛА путем коррекции его местоположения, используя то, что определение слагаемых показателя близости, при которых достигается глобальный экстремум, после первого определения аргументов показателя близости, при которых достигается первый глобальный экстремум, производят при помощи метода скользящего окна. 4 ил.
Способ навигации летательных аппаратов, заключающийся в использовании эталонной карты местности, выборе участка местности (мерный участок), находящегося в пределах эталонной карты, составлении первой текущей карты мерного участка путем циклических измерений наклонных дальностей с помощью многолучевого режима измерения при помощи радиоволн, излучаемых в виде лучей, определении разности результатов многолучевых измерений по первой текущей карте, циклическом сравнении первой текущей и эталонной карт для определения значений слагаемых показателя близости в пределах первого квадрата неопределенности, поиске глобального экстремума показателя близости и определении первого местоположения летательного аппарата в координатах эталонной карты, составлении второй текущей карты мерного участка и определении второго местоположения летательного аппарата путем сравнения второй текущей и эталонной карт мерного участка в пределах второго квадрата неопределенности, составлении третьей текущей карты мерного участка и определении третьего местоположения летательного аппарата путем сравнения третьей текущей и эталонной карт мерного участка в пределах второго квадрата неопределенности, причем размеры второго квадрата неопределенности значительно меньше размеров первого квадрата неопределенности, определении направления движения, скорости и ускорения летательного аппарата путем сравнения координат первого, второго и третьего местоположения летательного аппарата в координатах эталонной карты, вычислении сигнала коррекции траектории движения и управлении движением летательного аппарата путем коррекции его местоположения с использованием полученных значений координат и трехмерного вектора движения летательного аппарата: направления, скорости и ускорения движения по трем координатам, отличающийся тем, что при поиске глобального экстремума показателя близости для определения первого местоположения летательного аппарата запоминают значения слагаемых показателя близости при каждом цикле сравнений первой текущей и эталонной карт и номер цикла сравнения первой текущей и эталонной карт, после определения первого местоположения летательного аппарата в координатах эталонной карты производят дальнейший поиск глобальных экстремумов показателя близости для определения последующих (N-1) местоположений летательного аппарата, для чего определение второго и последующих местоположений летательного аппарата производят при помощи метода скользящего окна: при каждом последующем цикле сравнения текущей и эталонной карт запоминают новые значения слагаемых показателя близости и номер цикла сравнения, исключая при этом из памяти значения слагаемых показателя близости, соответствующие наиболее раннему номеру цикла сравнения текущей и эталонной карт, и циклически производят поиск (N-1) глобальных экстремумов показателя близости, определение второго и последующих местоположений летательного аппарата производят путем сравнения текущей и эталонной карт мерного участка в пределах второго квадрата неопределенности.
| СПОСОБ НАВИГАЦИИ ЛЕТАТЕЛЬНЫХ АППАРАТОВ | 2012 |
|
RU2515469C1 |
| Способ навигации летательных аппаратов | 2016 |
|
RU2611564C1 |
| СПОСОБ НАВИГАЦИИ ЛЕТАТЕЛЬНОГО АППАРАТА ПО РАДИОЛОКАЦИОННЫМ ИЗОБРАЖЕНИЯМ ЗЕМНОЙ ПОВЕРХНОСТИ | 2011 |
|
RU2483324C1 |
| US 5087916 A,11.02.1992 | |||
| WO 2005033631 A1, 14.04.2005 | |||
| JP 2014157093 A, 28.08.2014 | |||
| Этажная литьевая форма | 1990 |
|
SU1742084A1 |
Авторы
Даты
2019-03-01—Публикация
2018-04-02—Подача