Перекрестная ссылка на связанные изобретения
Изобретение представляется впервые. Наиболее близкими являются изобретения: US 2016/0261466 A1 - SIEMENS AKTIENGESELLSCHAFT (München, DE), RU 2 435 201 C2 - МЮРЕКС С.А.С. (FR).
Техническая область
Изобретение представляет собой способ и программную систему, и относится к области программной инженерии специализированных вычислительных систем и систем инженерного анализа. Изобретение включает программную технологию автоматизации разработки сопровождаемого и масштабируемого программного обеспечения, ориентированного для решения ресурсоёмких прикладных задач инженерного анализа в сложных технических системах и процессах.
Уровень техники
В области программных систем, применяемых для разработки программных реализаций вычислительных методов существуют запатентованные аналоги [US 2016/0261466 A1 - SIEMENS AKTIENGESELLSCHAFT (München, DE), METHOD AND DIGITAL TOOL FOR ENGINEERING SOFTWARE ARCHITECTURES OF COMPLEX CYBER-PHYSICAL SYSTEMS OF DIFFERENT TECHNICAL DOMAINS (2016), RU 2 435 201 C2 - МЮРЕКС С.А.С. (FR) - ПАРАЛЛЕЛИЗАЦИЯ И ИНСТРУМЕНТАЛЬНЫЕ СРЕДСТВА В ИНФРАСТРУКТУРЕ ГРАФООРИЕНТИРОВАННОГО ПРОГРАММИРОВАНИЯ НА ОСНОВЕ ПРОИЗВОДИТЕЛЕЙ (2011)], а также ряд известных программных систем представлен в литературе [MatLab [Патент 8], LabView [Патенты 4, 5], LUSTRE [41], FEniCS [8]].
Стоит отметить, что большинство представленных разработок узкоспециализированы и основной целью их создания была автоматизация разработки специализированного программного обеспечения в определенных направлениях.
Например, известная система LabView [Патенты 4, 5] предлагает пользователям платформу для выполнения программ, созданных с использованием графического языка программирования «G» фирмы National Instruments (США). Первая версия LabVIEW была выпущена в 1986 году для Apple Macintosh, в настоящее время существуют версии для Microsoft Windows, UNIX, Linux, Mac OS и пр.
LabView используется в системах сбора и обработки данных, а также для управления техническими объектами и технологическими процессами по аналогии с системами класса SCADA, но помимо решения задач в области АСУ ТП в большей степени ориентирована на решение задач в области автоматизации научных исследований. Основное назначение LabView – построение моделей технических систем и устройств, для этой цели LabView включает в состав множество специализированных библиотек реализованных компонентов, на базе которых возможно построение новых систем из конкретных технических областей.
LabView - это продукт с закрытым исходным кодом. Новые версии для Windows требуют активации, при этом версии для Linux и MAC имеют ограниченную поддержку.
Еще одной известной системой является пакет Simulink, входящий в поставку программной системы MatLab. Simulink - это графическая среда имитационного моделирования, позволяющая при помощи блок-диаграмм в виде направленных графов, строить динамические модели, включая дискретные, непрерывные и гибридные, нелинейные и разрывные системы. Simulink также ориентирован на решение задач моделирования сложных технических систем и представляет собой модельно-ориентированную систему проектирования. В первую очередь Simulink позволяет создавать графическую модель системы, собрав ее на основе стандартных базовых элементов (интегратор, звено задержки, сумматор, произведение, справочная таблица, мультиплексор, переключатель, селектор шины и пр.), которой будет соответствовать конкретная математическая модель системы на основе систем обыкновенных дифференциальных уравнений или уравнений в частных производных.
Еще одной близкой к представляемой разработке системой, ориентированной на графическое моделирование систем является система FEniCS. В первую очередь система ориентирована на задачи, которые могут быть решены при помощи метода конечных элементов.
FEniCS позволяет пользователям быстро преобразовывать математические модели процессов моделирования в удобный и просто сопровождаемый конечно-элементный код. FEniCS является кроссплатформенной системой с открытым кодом и предоставляет удобные интерфейсы для доступа к функциям с использованием языков программирования Python и C++. Ряд реализованных алгоритмов FEniCS могут задействовать высокопроизводительные многопроцессорные вычислительные ресурсы.
Одна из важнейших особенностей FEniCS – реализация гибкого механизма ввода математических моделей буквально в исходной интегро-дифференциальной форме. В рамках FEniCS реализованы удобные механизмы работы с конечно-элементными расчетными сетками, функциями решения систем линейных алгебраических уравнений и пр.[8].
Также следует отметить систему TensorFlow (https://www.tensorflow.org). TensorFlow представляет собой библиотеку с отрытым исходным кодом, для построения программных реализации численных методов. В основе TensorFlow также лежат понятия теории графов, а также понятие граф потоков данных. Принципиальным отличием TensorFlow от представляемого способа является различные определений узлов и ребер. Для TensorFlow узлы представляют математические операции, а ребра - многомерные массивы данных (тензоры), тогда как для представляемого способа узлы определяют фиксированные состояния общих данных (которые, в том числе, могут включать массивы данных), а ребра определяют функции преобразования данных.
В том числе представлены источники, описывающие и другие системы, созданные ранее, но которые не нашли столь широкого распространения: GRIDS, FUNSOFT.
Следует отметить также и другие узкоспециализированные системы и языки программирования:
PTOLEMY II (http://ptolemy.eecs.berkeley.edu/ptolemyII/),
ProGraph (http://www.andescotia.com),
Apache Storm (http://storm.apache.org),
IBM InfoSphere Streams (https://www.ibm.com/software/products/ru/ibm-streams),
Erlang (https://www.erlang.org/),
PROGRES (https://en.wikipedia.org/wiki/OpenEdge_Advanced_Business_Language),
Cantata, LUSTRE, KLIEG, DOME, GME, Atom3, Moses, DRACO, GenVoca, Datadvance (pSeven)
Современный мировой уровень исследований в рассматриваемом направлении определяют представленные публикации, патенты и программные разработки.
Краткое описание изобретения
Изобретение включает в свой состав программный каркас и систему выполнения специальных программ (G06F 9/44), построение которых формализовано и автоматизировано. Изобретение предназначено для упрощения процессов создания программных реализаций сложных вычислительных методов (СВМ). Способ получил название графоориентированная программная инженерия (ГПИ) или графоориентированный подход.
Изобретение обеспечивает возможности формализации процедуры разработки программного обеспечения инженерного анализа в сложных технических системах и процессах за счет формализации понятия алгоритм реализации СВМ в форме ориентированного графа - графовой модели (ГМ).
Изобретение включает систему (программный каркас) интерпретации графовых моделей (ГМ), сохраняя обработанную ГМ в памяти вычислительной машины (G06F 9/06, G06F 9/445) с последующим автоматическим построением масштабируемой (однопоточной или многопоточной) программы и ее выполнения (G06F 9/445). Графовыми моделями описывают алгоритмы решения конкретных математических задач инженерного анализа (МЗИА) в сложных технических системах и процессах, что после интерпретации обеспечивает проведение численных расчетов и обработку данных (G06F 17/10).
Изобретение позволят автоматизировать процессы проведения инженерных расчетов при проектировании (G06F 17/50) конкретных технических изделий.
Используя предлагаемый способ, построенная графовая модель конкретного алгоритма может быть легко встроена в ранее созданную графовую модель другого алгоритма и так далее. Тем самым реализуется возможность создания программ на различных уровнях абстракции, что способствует минимальному дублированию исходного кода при разработке и обеспечивает возможности создания легко модифицируемых и одновременно автоматически формируемых программных реализаций СВМ.
Возможности программирования на различных уровнях абстракции обеспечивают возможности создания универсальных программных систем тестирования, валидации, эмуляции и имитирования уже созданного программного обеспечения, построенного на основе тех же принципов (G06F 9/455).
Краткое описание иллюстраций
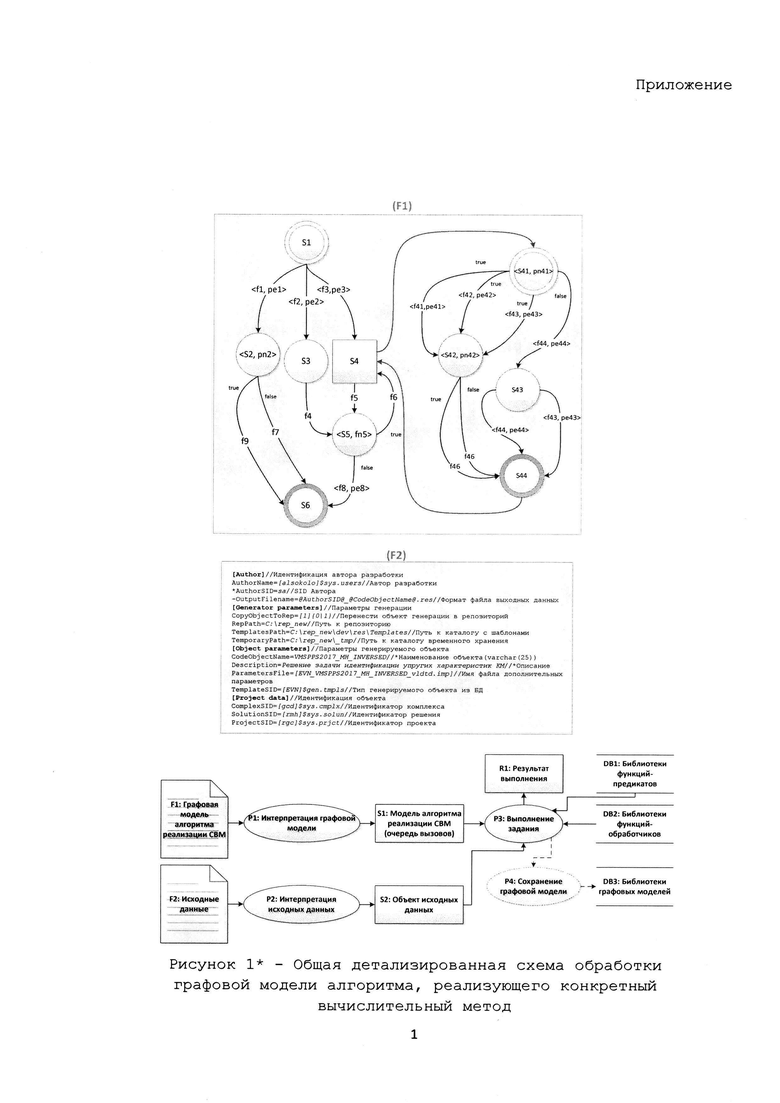
Рис.1* – Общая детализированная схема обработки графовой модели алгоритма, реализующего конкретный вычислительный метод.
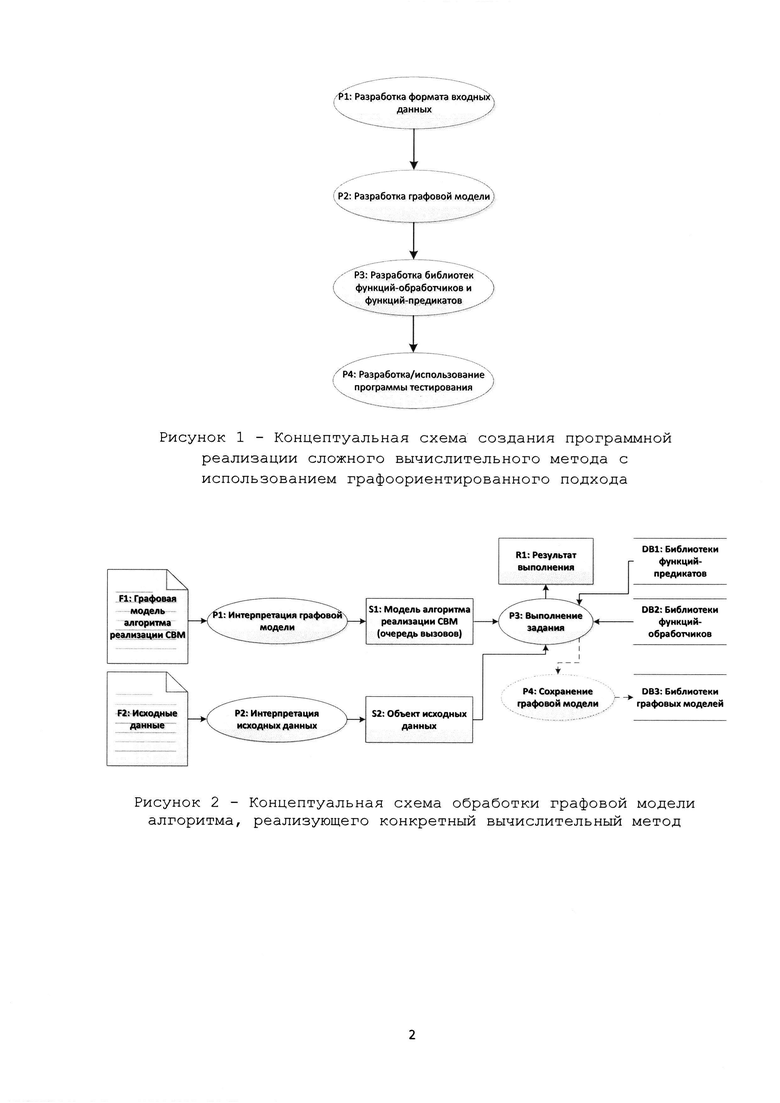
Рис.1 – Концептуальная схема создания программной реализации сложного вычислительного метода с использованием графоориентированного подхода.
Рис.2 – Концептуальная схема обработки графовой модели алгоритма, реализующего конкретный вычислительный метод.
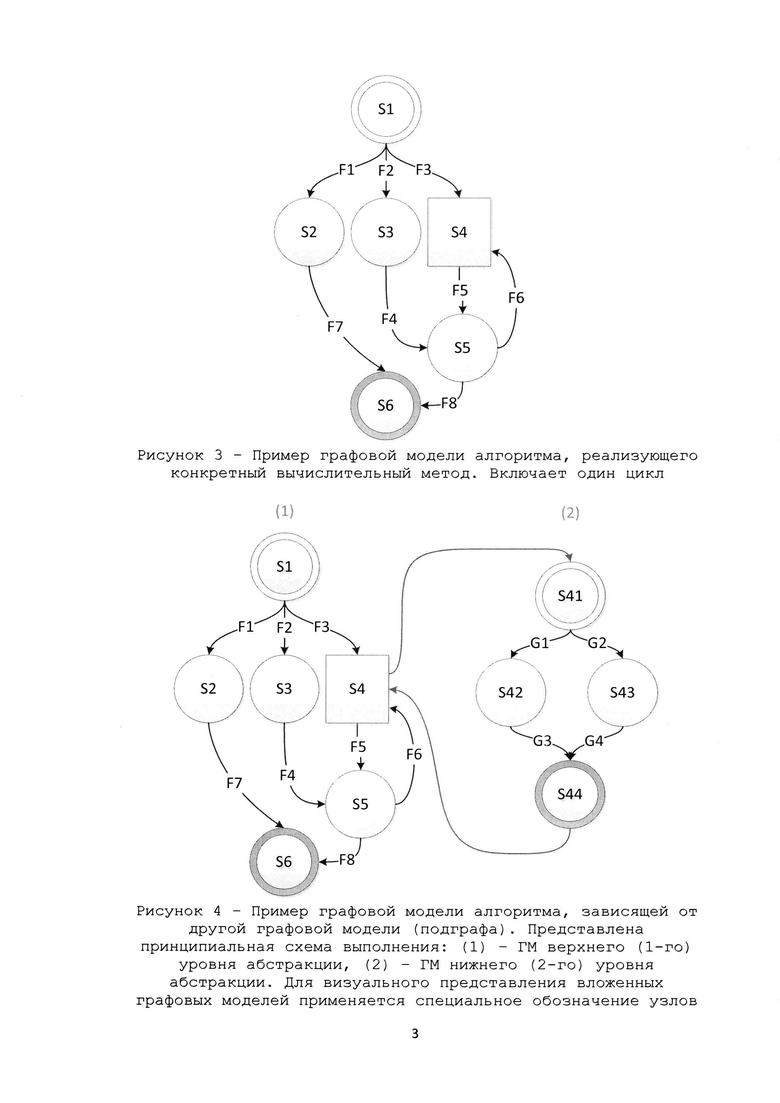
Рис.3 – Пример графовой модели алгоритма, реализующего конкретный вычислительный метод. Включает один цикл.
Рис.4 – Пример графовой модели алгоритма, зависящей от другой графовой модели (подграфа). Представлена принципиальная схема выполнения: (1) – ГМ верхнего (1-го) уровня абстракции, (2) – ГМ нижнего (2-го) уровня абстракции. Для визуального представления вложенных графовых моделей применяется специальное обозначение узлов.
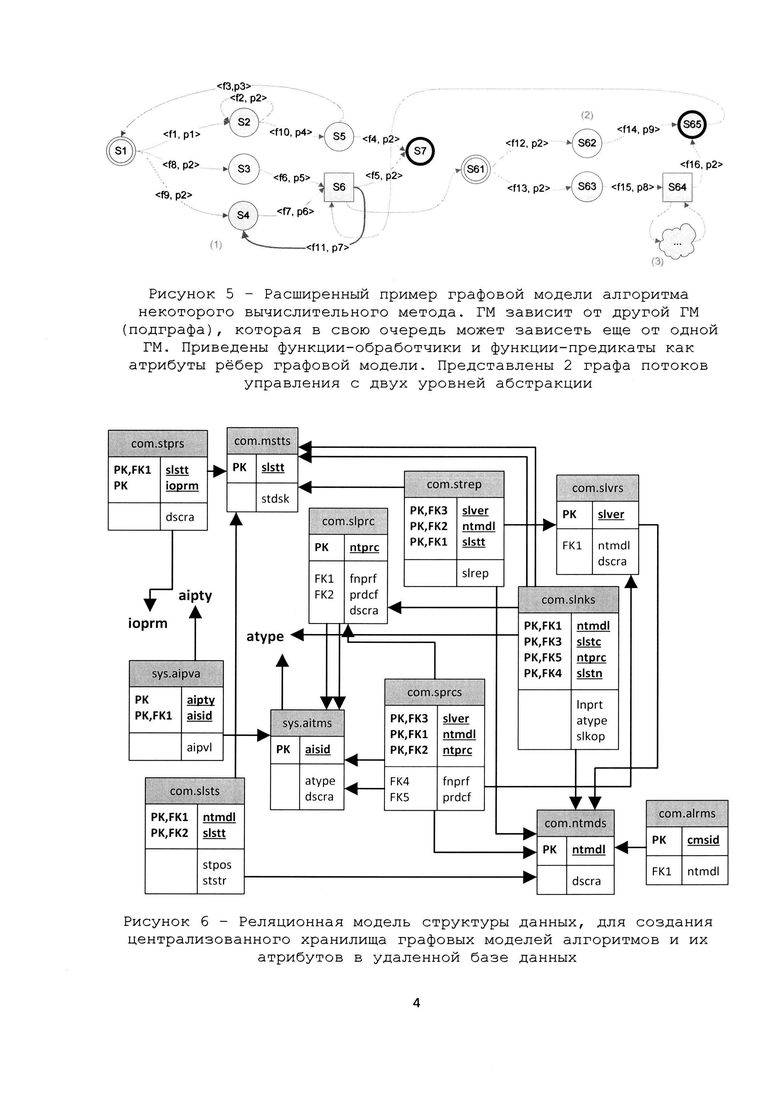
Рис.5 – Расширенный пример графовой модели алгоритма некоторого вычислительного метода. ГМ зависит от другой ГМ (подграфа), которая в свою очередь может зависеть еще от одной ГМ. Приведены функции-обработчики и функции-предикаты как атрибуты рёбер графовой модели. Представлены 2 графа потоков управления с двух уровней абстракции.
Рис.6 – Реляционная модель структуры данных, для создания централизованного хранилища графовых моделей алгоритмов и их атрибутов в удаленной базе данных.
Рис.7 - Множество возможных различных и эквивалентных очередей вызовов функций обработки при однопоточном режиме выполнения, по каждой из которых может быть построена различная, но эквивалентная, программа выполнения. Все очереди соответствуют одной фиксированной графовой модели. Число возможных очередей определяется цикломатическим числом графа.
Рис.8 – Очереди вызовов при многопоточном режиме выполнения графовой модели.
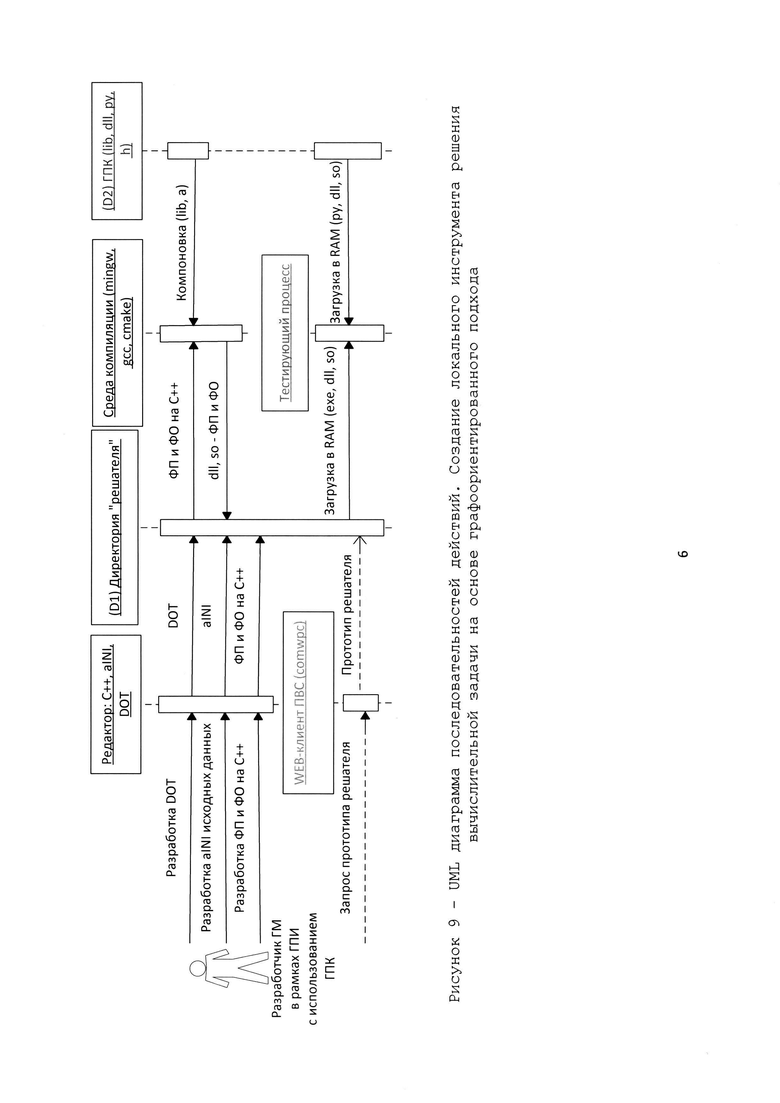
Рис.9 – UML диаграмма последовательностей действий. Создание локального инструмента решения вычислительной задачи на основе графоориентированного подхода.
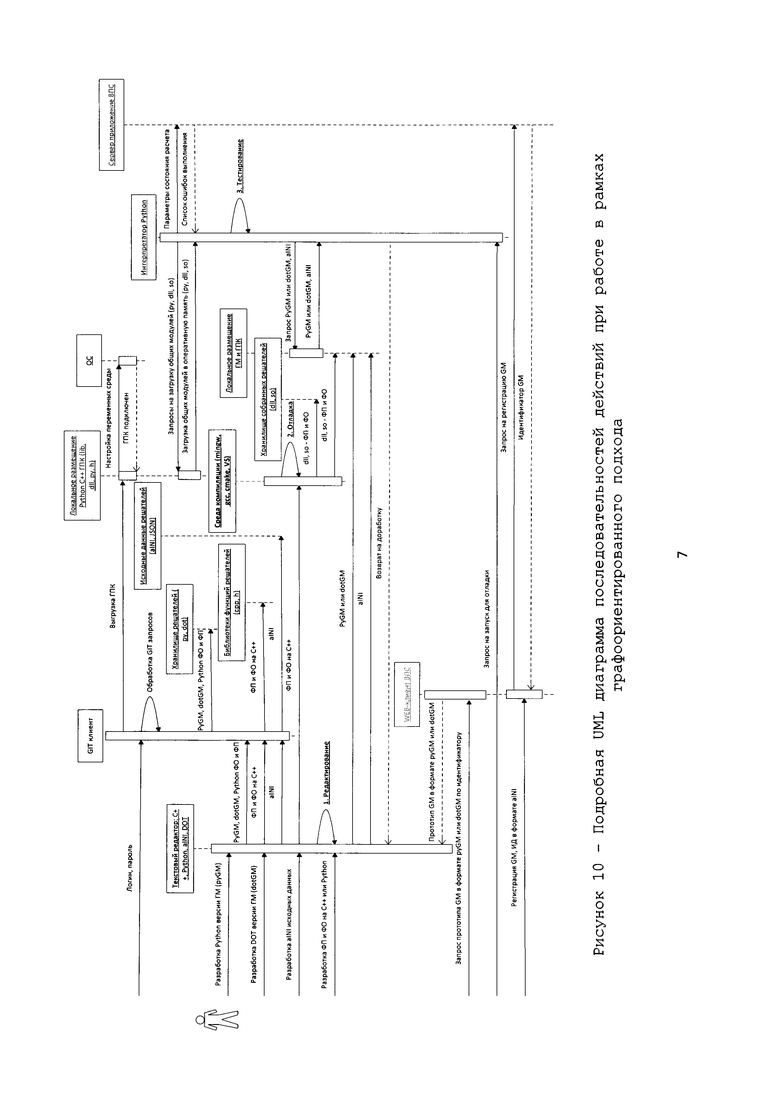
Рис.10 – Подробная UML диаграмма последовательностей действий при работе в рамках графоориентированного подхода.
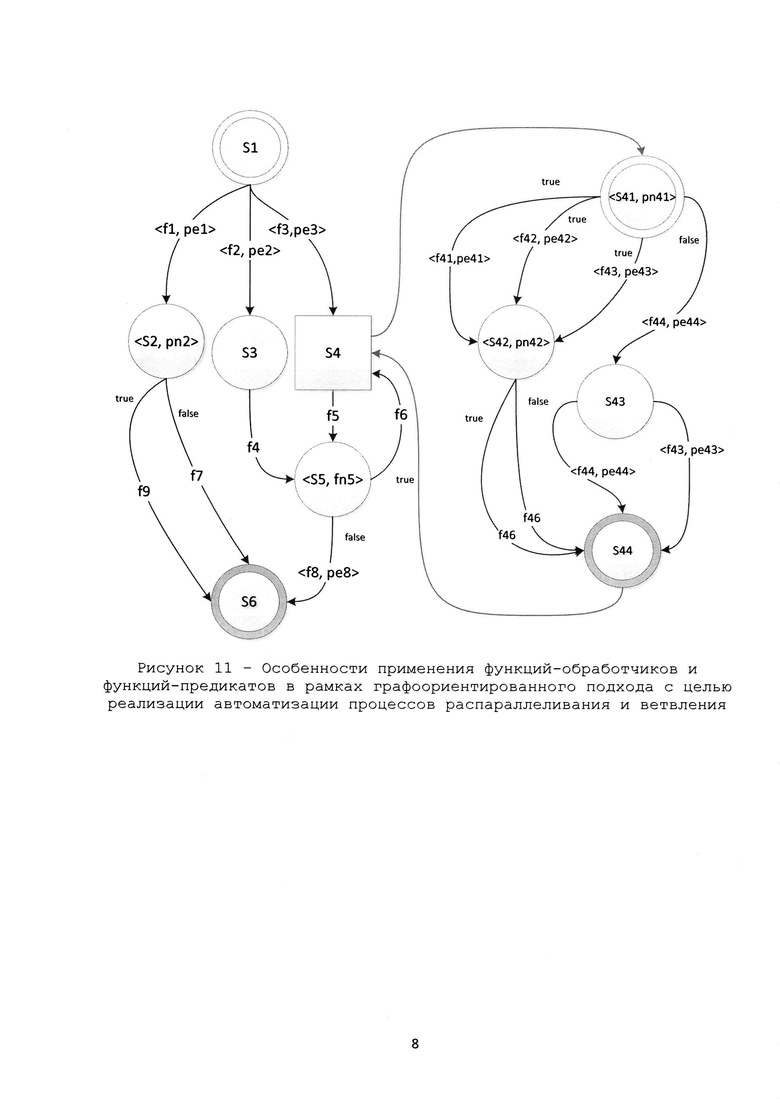
Рис.11 – Особенности применения функций-обработчиков и функций-предикатов в рамках графоориентированного подхода с целью реализации автоматизации процессов распараллеливания и ветвления.
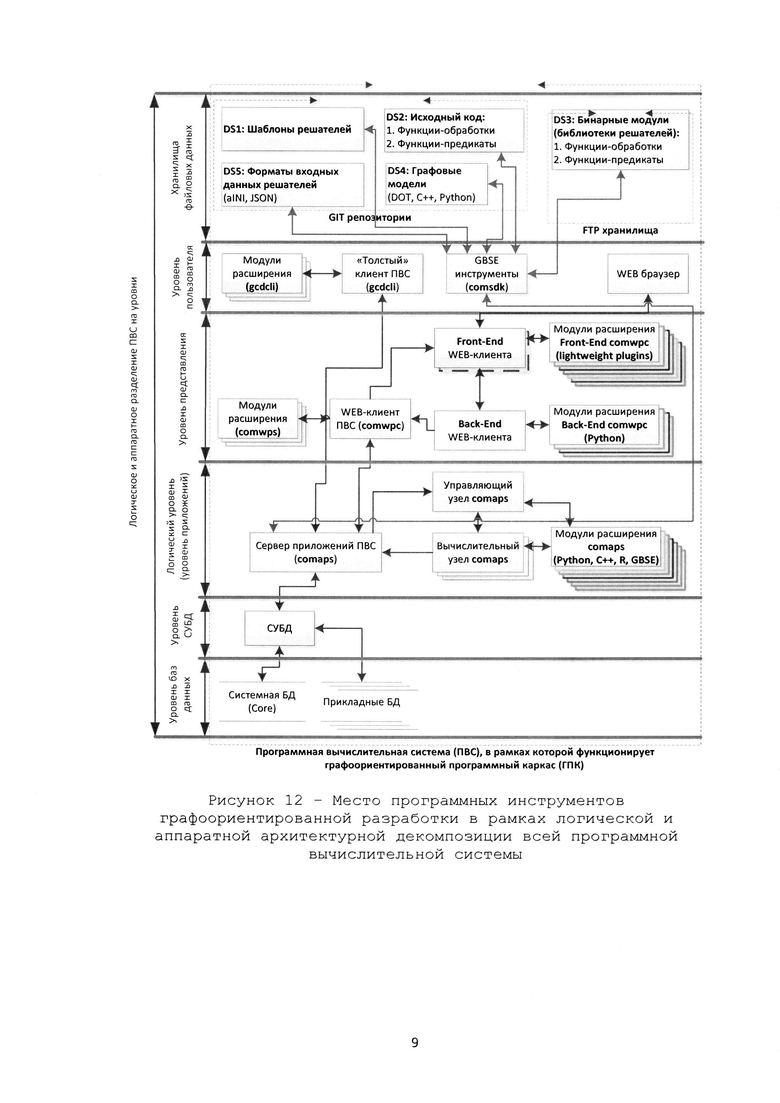
Рис.12 – Место программных инструментов графооринетированной разработки в рамках логической и аппаратной архитектурной декомпозиции всей программной вычислительной системы.
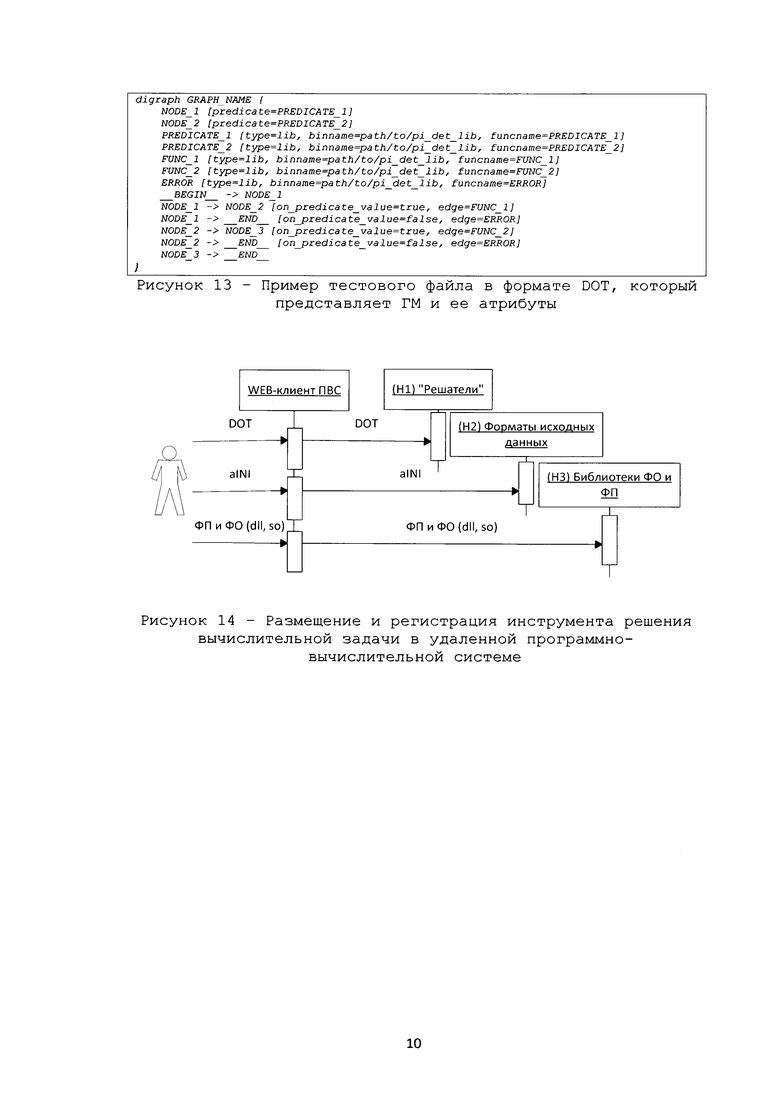
Рис.13 – Пример тестового файла в формате DOT, который представляет ГМ и ее атрибуты.
Рис.14 – Размещение и регистрация инструмента решения вычислительной задачи в удаленной программно-вычислительной системе.
Рис.15 – Пример файла исходных данных в формате aINI.
Рис.16 – Выполнение конкретной программной реализации сложного вычислительного метода, построенного на основе графоориентированного подхода, на базе удаленного вычислительного ресурса (в том числе многопроцессорного).
Рис.17 – Пример простой графовой модели, реализующей ПР некоторого СВМ.
Рис.18 – Пример DOT файла, представляющего простую графовую модель, представленную на рисунке 17.
Рис.19 – Пример файла исходных данных в формате aINI, который может быть подан на вход ПР СВМ, реализуемой графовой моделью, представленной на рисунке 17.
Рис.20 – Примеры возможных последовательных состояний общих данных СВМ D, при использовании графовой модели, представленной на рисунке 17 и подаче ей на вход файла исходных данных в формате aINI, представленного на рисунке 19.
Подробное описание
Представлен оригинальный способ разработки программных реализаций сложных вычислительных методов (СВМ). Принципиальная схема использования предлагаемого способа представлена на Рисунке 1 и определяет стандартную рекомендуемую последовательность действий для создания программных реализаций в рамках предлагаемого подхода.
Основное назначение способа – разработка программных реализаций сложных вычислительных методов для решения задач инженерного анализа в технических системах, а также для решения задач научных исследований.
Способ получил название «Графоориентированная технология разработки программных реализаций сложных вычислительных методов» или графоориентированная программная инженерия (ГПИ).
Используя ГПИ (рисунок 1), в первую очередь (рисунок 1 позиция P1) создают формат файлов входных данных. Для разработки формата файла входных данных следует использовать формат aINI, который позволяет создавать форматы исходных данных для широкого класса вычислительных задач.
Следующей операцией (рисунок 1 позиция P2) непосредственно создают графовую модель (ГМ) алгоритма решения поставленной задачи. ГМ может быть разработана с помощью применения различных подходов: а) на основе использования специализированного языка описания графов DOT, а) на основе использования специализированного программного интерфейса ГПК путем непосредственного создания ГМ, б) на основе непосредственного создания ГМ и ее атрибутов в реляционных моделях данных в удаленной базе данных (рисунок 6).
После построения ГМ разрабатывают функции-обработчики и функции-предикаты (рисунок 1 позиция P3), определенные графовой моделью. Функции-обработчики и функции-предикаты могут быть разработаны с использованием различных языков программирования: а) язык программирования С++, б) язык программирования Python и прочие, - в зависимости от соответствующей поддержки программного инструментария, реализующего ГПИ (далее графоориентированный программный каркас (ГПК)).
Для проведения отладки и тестирования (рисунок 1 позиция P4) создаваемой программной реализации (ПР) сложного вычислительного метода используют стандартную программу тестирования, включенную в состав ГПК или разрабатывают новую программу тестирования на одном из поддерживаемых ГПК языков программирования: С++ или Python.
Основы ГПИ
В основе способа:
1)понятия теории графов;
2)технологии хранения информации в реляционных базах данных;
3)технологии применения библиотек динамической компоновки;
4)технологии применения специализированных структур данных (ассоциативных массивов, деревьев, графов).
Прикладная область применения
Прикладная область апробации способа – создание программных реализаций численных методов в следующих прикладных областях инженерного анализа: прикладные задачи математической физики в целом, задачи механики сплошной среды, построение ПР конечно-элементных методов, методов гомогенизации, методов решения прямых и обратных задач в области микромеханики композиционных материалов и другие.
Предлагаемый способ обеспечивает возможности внедрения создаваемых с его помощью программных реализаций сложных вычислительных методов в прикладные программные пакеты инженерного анализа и в более общем случае в CAE системы.
Приложения и системы, в рамках которых актуально применение ГПИ:
1) системы инженерного анализа (CAE);
2) оптимизационные системы;
3) программное обеспечение, требующее определение понятия бизнес-процесс (ERP, CRM, веб-приложения с встроенной бизнес логикой).
Предпосылки к созданию ГПИ. Проблемная ситуация.
Особые условия, отличающие разработку программной реализации СВМ (ПР СВМ), ориентированной для решения прикладных задач инженерного анализа сложных технических систем и процессов от программной реализации вычислительного алгоритма решения конкретной узкоспециализированной задачи:
T1) существенный объем работ по написанию исходных кодов ПР СВМ, ограничивающий возможности создания качественной ПР СВМ одним исследователем;
T2) существенный объем исходных данных (скалярных и/или векторных), задаваемых точно и/или неточно;
T3) существенное количество особых условий функционирования и согласованности выбранных численных методов выбранным алгоритмам;
T4) требование обеспечения масштабируемости создаваемой ПР: учет возможности задействовать доступные вычислительные ресурсы (использование многопроцессорной техники) при большой вычислительной сложности задачи, что в особенности актуально для прикладных инженерных расчетов и для коммерческого промышленного программного обеспечения инженерного анализа;
T5) требование возможности запуска созданных ПР на различных платформах;
T7) необходимость обеспечения универсальности форматов представления постановок задач и отправки их на расчет;
T8) при решении прикладных задач в т.ч. требуется обеспечить возможность гибкого сопровождения, трудозатраты на которое не должно зависеть от объема исходного кода создаваемой ПР СВМ.
Основная цель создания способа ГПИ - обеспечить технологичность (стандартизацию, унификацию, преемственность каждого из вновь создаваемых программных модулей СВМ) процесса проектирования и разработки ПР СВМ на протяжении этапов жизненного цикла программного обеспечения в области систем инженерного анализа и научных исследований.
Основные задачи использования способа ГПИ.
1) Обеспечить возможность создания программных реализаций СВМ коллективом инженеров-исследователей и программистов одновременно.
2) Обеспечить возможность быстрой перестройки ПР СВМ при изменении требований как на этапе разработки и отладки так и на этапе сопровождения.
3) Обеспечить удовлетворение требования масштабируемости создаваемых ПР СВМ: имеется в виду возможность частичной автоматизации процесса задействования доступных ресурсов многопроцессорной техники.
4) Обеспечить удовлетворение требований T1-T8, описанных выше.
Формальные базовые понятия ГПИ
Определение 1 (вычислительная операция): Вычислительной операцией будем называть отдельную функцию F алгоритма, обеспечивающего реализацию некоторого численного метода.
Определение 2 (сложный вычислительный метод): Сложным вычислительным методом будем называть комплекс взаимосвязанных вычислительных операций, основанных на применении численных методов (возможно различных), по преобразованию входных данных, заданных численно, с целью получения численного результата.
Определение 3 (данные сложного вычислительного метода): Данными СВМ будем называть множество D пар «параметр-значение», где D – ассоциативный многомерный контейнер, каждый элемент D содержит уникальный идентификатор элемента и ему соответствующее значение произвольного типа.
В рамках применяемого графоориентированного программного каркаса был разработан специализированный класс, реализующий указанную функциональность. Класса получил название AnyMap.
Определение 4 (состояние СВМ): Состоянием СВМ будем называть именованное подмножество S множества имен элементов D.
Для фиксированного алгоритма, реализующего СВМ, состояния СВМ могут модифицироваться со временем.
Определение 5 (данные СВМ в состоянии S): Данными СВМ D в состоянии S будем называть подмножество G множества D, индуцированное S. Такие подмножества будем обозначать DS.
Определение 6 (функция-обработчик): Функцией-обработчиком будем называть отображение f: D → D.
Сигнатура функции-обработчика (на языке программирования С++): int f(AnyMap& D);
Определение 7 (функция-предикат): Функцией-предикатом будем называть одно из возможных отображений: а) p: D → {1,0}; б) p: D → N*, где N* счетное конечное подмножество из множества N (натуральных чисел); в) p: D → R*, где R* конечное множество действительных чисел.
Возможные сигнатуры функции-предиката (на языке программирования С++):
bool f(const AnyMap& D);
double f(const AnyMap& D);
int f(const AnyMap& D);
Определение 8 (функция преобразования или перехода): Функцией преобразования или перехода СВМ F, определенной на множестве данных СВМ D, из состояния S1 в состояние S2 будем называть отображение F: D → D, для которого: F(DS1)=< f(DS1),p(DS1) >, где <f(DS),p(DS)> = ((p(DS))?f(DS1):Error(DS1)), - тернарный оператор языка С/С++, f – функция-обработчик данных DS1 и преобразующая их к DS2, p – функция-предикат, определяет возможность перехода данных D из состояния S1 при помощи функции-обработчика f в состояние S2 (например, рисунки 5, 11), Error(DS1) – некоторая стандартная функция-обработчик исключительной ситуации.
Определение 9 (графовая модель): Сетевой моделью (ГМ) (графовой моделью) M алгоритма ПР СВМ будем называть ориентированный граф, при обходе которого реализуется алгоритм решения конкретной вычислительной задачи. С каждым узлом графа может быть соотнесена функция-предикат, а с каждым ребром графа должны быть соотнесены функция-предикат и функция-обработчик, обе вместе определяющие понятие функции перехода.
Понятие ГМ расширяет понятие граф потока управления [Майерс Г. Искусство тестирования программ. М.: Финансы и статистика, 1982. 176 с]. Сетевая модель алгоритма определяет модель передачи управления в процессе решения вычислительной задачи, имеет иерархический принцип построения и описывает алгоритм на различных уровнях абстракции (п.3 формулы изобретения).
Число используемых для конкретной ПР СВМ состояний определяется числом узлов соответствующей графовой модели M.
Определение 10 (программная реализация (ПР) СВМ): Программной реализацией (ПР) СВМ на основе ГПИ (или просто ПР СВМ) или «решателем» СВМ будем называть тройку: графовая модель M, данные СВМ D и множество функций преобразования F, обеспечивающих переходы данных D из одних состояний в другие.
Разработка ПР СВМ с использованием способа ГПИ (п.2 формулы изобретения)
1. Определение особенностей вычислительных ресурсов (ОВР)
В первую очередь определяют ОВР, на которые должна быть ориентирована ПР СВМ: архитектура (многопроцессорная система с общей или распределенной памятью), количество доступных вычислителей (процессоров), доступная оперативная память каждому вычислителю (процессору), доступная общая оперативная память.
2. Разработка формата входных данных (рисунок 1 позиция P1)
Разрабатывают формат файла исходных данных (ФФ ИД) для проектируемой ПР СВМ. Формат должен быть совместим с используемым программным каркасом ГПК, реализующим ГПИ.
ФФ ИД должен обеспечить возможность формирования на его основе файлов входных данных для конкретных расчетных задач, решение которых будет базироваться на использовании созданной ПР СВМ.
ФФ ИД должен исключить необходимость разработки графических пользовательских интерфейсов для создаваемой ПР СВМ для удобного ввода данных. ФФ ИД должен обеспечить гибкую возможность внесения изменений уже после разработки ПР СВМ на базе ГПИ. В качестве базового формата для построения ФФ ИД для проектируемой ПР СВМ используют формат aINI или JSON (пример в формате aINI представлен на рисунке 15).
3. Разработка графовой модели (рисунок 1 позиция P2)
Разработка графовой модели включает определение топологии ГМ (рисунок 3), множества состояний данных (узлы ГМ) и множества переходов данных (рёбра ГМ).
ГМ СВМ разрабатывают с применением языка описания графов DOT (рисунок 13) или используют программный интерфейс ГПК или ГМ СВМ сохраняют непосредственно в базе данных (реляционная модель данных представлена на рисунке 6) общей программной вычислительной системы (ПВС)(рисунок 12).
Созданная ГМ СВМ может быть зарегистрирована в ручную (рисунок 14) и автоматически в фоновом режиме при непосредственном выполнении (рисунок 2 позиция P4) в базе данных (БД), входящей в состав общей ПВС (рисунок 12). БД включает записи о реализованных ГМ конкретных СВМ, их топологиях и соответствующих им ФП и ФО, включая их классификацию и типизацию. Регистрация ГМ в единой базе данных позволяет осуществлять предварительный поиск готовых типовых ГМ, осуществлять их доработку, позволяет реализовывать механизмы комбинирования ГМ, включать одну ГМ в другую и снижает негативные последствия дублирования. При регистрации ГМ СВМ определяются права доступа к этой ГМ других пользователей ПВС.
4. Разработка библиотек, реализующих функции-обработки и функции-проедикаты (рисунок 1 позиция P3)
Функция-обработчик (ФО) – функция преобразования общих данных СВМ в целом (Определение 6).
Функция-предикат (ФП) – функция проверки корректности данных в конкретном состоянии данных СВМ (Определение 7).
Функции-обработчики (ФО) могут быть привязаны только к рёбрам. Если ФО не привязана к ребру, то будет запускаться стандартная ФО, которая не реализует никаких специальных действий: такая стратегия полезна для создания функций-заглушек, фактическую реализацию которых можно отложить на неопределенный срок.
Функции-предикаты (ФП) могут привязываться к узлам и/или к рёбрам. В случае привязки ФП к узлу для ГМ реализуется ветвление (рисунок 11). ФП, привязываемая к ребру, определяет возможность запуска соответствующей ФО (рисунки 5, 11) и т.о. реализуется механизм распараллеливания потока управления алгоритма (рисунок 11). Если ФП не привязана к узлу, то специально не осуществляется запуск каких-либо стандартных ФП с помощью используемой ГПК, однако, если ФП не привязана к ребру, то в рамках используемого ГПК будет вызвана стандартная ФП, которая осуществит проверку корректности данных для возможности последующего вызова ФО. Т.о. ФП могут и не быть привязаны как к узлам так и к рёбрам ГМ, разрабатываемой ПР СВМ. Такая стратегия позволяет снижать требования к специалистам, занятым при разработке ПР СВМ с применением ГПИ в целом.
Разработка ФО и ФП осуществляется в два этапа. Первым этапом всем ФО и ФП дают имена при разработке ГМ создаваемой ПР СВМ. Вторым этапом осуществляют непосредственную разработку ФО и ФП с использованием выбранных языков программирования.
При разработке исходного кода каждой ФО и ФП входные и выходные данные функций размещаются в объекте D (данные СВМ) в формате, определяемом классом AnyMap (ассоциативный многомерный массив). Согласно определенным и зафиксированным заголовкам ФО и ФП (определения 6,7) объект D передаётся в ФО по ссылке (с возможностью внесения изменений), а в ФП по константной ссылке (без возможности внесения изменений).
Для хранения значений конкретных параметров (входных и выходных) для каждой ФО и ФП в рамках используемой структуры AnyMap общих данных СВМ D был определен специальный принцип именования. Предложенный принцип именования заключается в том, что каждый параметр данных СВМ D должен получать имя, понятное разработчику соответствующей функции с одной стороны и очевидный способ поиска этого параметра среди накопленных параметров D – с другой стороны. В рамках ГПИ бы определен принцип именования, включивший следующие позиции (пример на рисунке 20).
1. Параметр, имя которого, и лишь оно, определяется в ФО, должен получать уникальное полное имя в формате (для текущей ГМ):
[<Имя узла назначения>][<Имя параметра>].
Для случая вложенной ГМ представленный выше формат должен быть дополнен информацией об узле, который замещается, и информацией о вложенном решателе, т.е. формат примет вид:
[<Имя замещаемого узла>][<Имя вложенного решателя>][<Имя узла назначения>][<Имя параметра>]
2. [<Имя узла назначения>], очевидно, должно быть уникальным среди всех узлов данной ГМ. При этом имена узлов не обязаны быть уникальными для всех ГМ, реализующих разрабатываемую ПР СВМ, включая все вложенные ГМ.
3. Первая часть имени [<Имя узла назначения>] и/или [<Имя замещаемого узла>][<Имя вложенного решателя>][<Имя узла назначения>] не может быть определена на уровне разработчика ФО ПР СВМ, так как в этом случае ограничивается возможность использования данной ФО в другой части ГМ или в другой ГМ вовсе.
4. Так как запуск конкретной ФО инициируется в ГПК, то и [<Имя узла назначения>] и/или [<Имя замещаемого узла>][<Имя вложенного решателя>][<Имя узла назначения>] в момент запуска для построенной модели алгоритма ПР СВМ (рисунки 7, 8) будут известны.
5. Процесс чтения данных из общих данных СВМ D и процесс записи данных в данные СВМ D должны осуществляться по-разному (рисунок 20).
6. Для осуществления непосредственной записи значения параметра в объект данных СВМ D следует использовать функцию push_data программного каркаса ГПК, принимающую на вход объект AnyMap, имя записываемого параметра [<Имя параметра>] и его значение.
7. Чтение должно осуществляться с использованием оператора [] рекурсивно, который должен быть перегружен для класса AnyMap.
Такой формат обеспечивает разработчику следующей ФО возможность очевидного механизма идентификации любого параметра в ГМ любой сложности. Пример представлен для графовой модели (рисунок 17), далее представлен ей соответствующих файл DOT (рисунок 18), далее представлен пример файла входных данных в формате aINI (рисунок 19) и, наконец, на рисунке 20 представлены примеры возможных последовательных состояний общих данных СВМ D.
Используя представленный формат упрощается механизм использования существующих ПР СВМ в целом, включая сопровождение и доработку: для определения полного имени нужного параметра необходима информация о ГМ конкретного СВМ, ее атрибутах, имени узла, определяющего начальное состояние данных СВМ D, из которого осуществляется переход разрабатываемой ФО, и имени нужного параметра для чтения.
Такая стратегия именования приводит к упрощению кода для чтения нужных параметров в соответствующих ФО, систематизируя этот процесс.
Касательно ФП – запись в данные СВМ D в ФП невозможна, поэтому метод push не может быть вызван относительно ФП, тогда как чтение параметров в ФП осуществляется аналогично как и для ФО.
После разработки исходного кода множеств ФО и ФП для разрабатываемой ПР СВМ в рамках ГПИ в зависимости от выбранного языка программирования может потребоваться осуществить компиляцию и сборку созданных ФО и ФП в библиотеки динамической компоновки (для случая, если был выбран компилируемый язык программирования ФО и/или ФП).
После сборки ФО и ФП в библиотеки динамической компоновки созданные библиотеки размещают в специализированных каталогах файловых систем (рекомендуется сразу осуществлять сборку библиотек в корректные каталоги для их последующего использования). Указанные каталоги должны быть доступны операционной системе для использования этих библиотек при локальном запуске процедур отладки и тестирования созданной ПР СВМ. В случае разработки отдельных ФО и ФП с использованием интерпретируемых языков программирования в процессе отладки и тестирования к созданным библиотекам ФО и ФП обеспечивают доступ соответствующих программных интерпретаторов (например, языка Python) (рисунок 10).
Созданные и отлаженные ФО и ФП могут быть зарегистрированы в базе данных (БД), входящей в состав общей ПВС (рисунок 10). БД включает записи о реализованных ГМ конкретных СВМ и соответствующих им ФП и ФО, включая их классификацию и типизацию. Регистрация ФО, ФП и ГМ в единой базе данных позволяет осуществлять предварительный поиск готовых ФО, ФП и ГМ, их доработку, а также снижает негативные последствия дублирования кода. Воспользоваться существующей в системе ФО и ФП возможно на основе использования доступного исходного кода либо в бинарном виде в форме доступной динамической библиотеки. Доступ предоставляется в случае, если автор данных исходных кодов и им соответствующих бинарных модулей ФО и/или ФП предоставил такие возможности при регистрации. Предоставление возможного доступа к функции и тип доступа определяется при регистрации ФО и ФП в рамки ПВС (рисунки 10, 14).
Непосредственная загрузка исходного кода или собранных бинарных модулей ФО и/или ФП, а также ГМ в формате DOT и прочих форматах, возможна посредством WEB-ориентированных приложений, предоставленных ПВС (рисунок 14).
Разработка в целом ГМ, ФО и ФП, формата файла исходных данных, а также включая процессы отладки и тестирования может быть осуществлена локально без доступа к каким-либо внешним системам посредством применения ГПК, распространяемого в форме архива (рисунок 9).
Итого определен состав ГПК.
1. Формализованные понятия: сетевая модель, состояние данных, функция преобразования, функция-предикат, функция-обработчик.
2. Универсальный интерпретатор ГМ. Программа реализует обход произвольной ГМ с учетом вложенных ГМ (рисунок 5).
3. Специализированная структура данных, обеспечивающая хранение общих данных (определение 3).
4. Фиксированный метод определения сигнатур произвольных функций-предикатов и функций-обработчиков (определения 6, 7).
5. Фиксированные универсальные методы хранения ГМ и их атрибутов, включая названия каждой ФО и ФП. В свою очередь ГПК обеспечивает возможности преобразования ГМ и ее атрибутов из одного формата в другой.
5. Разработка/использование программы тестирования (рисунок 1 позиция P4)
Принципиальная схема процесса разработки и проведения тестирования созданной программной реализации на основе ГПИ представлена на рисунке 9 (формат файла ГМ - DOT). Непосредственный процесс исполнения ПР СВМ представлен на рисунке 2.
Процесс отладки и тестирования созданных ПР СВМ осуществляется путем динамического построения очереди вызовов с учетом используемой в настоящий момент вычислительной аппаратной системы (рисунок 12). ГПК осуществляет анализ доступных вычислительных ресурсов и автоматически формирует однопоточный (рисунок 7) или многопоточный (рисунок 8) план исполнения созданной ГМ, реализующей конкретный СВМ. План исполнения представляется в форме одной или нескольких очередей вызовов. После формирования плана исполнения осуществляется непосредственное выполнение задания, - тем самым осуществляется динамическая сборка алгоритма, реализующего интересующий СВМ во время выполнения (рисунок 2).
Особенности ГПИ
Иерархический принцип построения ГМ ПР СВМ (п.3 формулы изобретения)
По аналогии с диаграммами потоков данных (ДПД или Data Flow Diagram (DFD)), графовые модели позволяют обеспечить абстрагирование деталей реализации путём вложения одной ГМ в другую (рисунки 4,5). Следует отметить, что программа интерпретатор (рисунок 2), осуществляющая обход такого графа, остается прежней!
Хранение ГМ и ее атрибутов
Хранение ГМ может быть реализовано в едином файле в стандартном текстовом формате DOT(пример представлен на рисунке 13), который позволяет сохранить и топологию ГМ, а также определить типы узлов, их имена и осуществить привязку имен ФО и ФП.
Хранение ГМ может быть реализовано в базе данных. Реляционная модель данных для хранения приведена на рисунке 6. Представлен фрагмент реляционной модели данных для хранения атрибутов ПР СВМ, реализуемой с помощью ГПИ.
Размещение и регистрация нового инструмента решения вычислительной задачи
Размещение и регистрация инструмента решения вычислительной задачи в удаленной программно-вычислительной системе осуществляется согласно алгоритму, представленному на рисунке 14 посредством последовательной выгрузки элементов ГМ конкретной ПР СВМ в соответствующие удаленные хранилища данных: отдельно исходные данные (пример на рисунке 15), графовые модели СВМ и им соответствующие бинарные модули ФО и ФП. Выгрузка осуществляется за счет использования специализированного WEB приложения ПВС (рисунке 12) согласно алгоритму, представленному на рисунке 14.
Масштабирование в рамках ГПИ (п.4 и п.5 формулы изобретения)
В процессе обхода ГМ может быть сформировано множество различных эквивалентных очередей вызовов функций преобразования данных (рисунок 7). При классическом подходе к разработке ПО, исследователь разрабатывает программу, которой соответствует лишь одна из представленных очередей вызовов (однопоточная программа), т.о. исследователь изначально «не видит» ее принципиальную структуру (топологию), что затрудняет возможность создания ее параллельной версии в будущем. В случае существенного объема исходных кодов возможность создания параллельной версии ПР СВМ вовсе сводится к нулю.
Созданная ГМ позволяет обеспечить многопоточное выполнение ПР СВМ автоматически (п.5 формулы изобретения) за счет наличия данных об исходной топологии алгоритма, реализующего СВМ (рисунки 3,4,5). Очевидно, что использование ГМ и запуск в многопоточном режиме, при прочих равных, обеспечивает повышение производительности ПР СВМ (рисунок 8). Т.о. использование ГПИ обеспечивает автоматическое масштабирование выполняемой ПР СВМ.
Независимость от коммерческих программных пакетов (п.6 формулы изобретения)
Графоориентированный подход позволяет создавать программные реализации сложных вычислительных методов независимо от коммерческого стороннего программного обеспечения. Созданные локально ПР СВМ могут работать локально и одновременно, при согласии авторов, могут быть интегрированы в рамки стороннего программного обеспечения, в коммерческую CAE систему, а также в рамки общей программной вычислительной системы. Такая интеграция обеспечит возможность использования многопроцессорных вычислительных ресурсов, доступных соответствующим программным системам.
Коллективная разработка одной ПР СВМ (п.7 формулы изобретения)
Временные затраты T(N,Mс) на создание ПР СВМ не должны расти более чем линейно (желательно) с увеличением числа программных функций N, требуемых для разработки, при фиксированной команде разработки, определяемой числом разработчиков Mс.
С увеличением числа функций N конкретной ПР СВМ увеличение разработчиков Mс должно эффективно компенсировать возрастающий объем работы без усложнения процесса разработки.
За счет стандартизации формата для представления графовых моделей алгоритмов реализуемых СВМ (определение 9), заголовков функций-обработчиков и функций-предикатов (определения 6, 7), применения универсальной структуры данных AnyMap для хранения данных СВМ в процессе проведения расчета (определение 3), а также за счет использования принятого соглашения о стандартном принципе именования () сохраняемых в данных СВМ D параметрах, исходный код функций-обработчиков и функций-предикатов может разрабатываться независимо.
Независимость реализуемого вычислительного метода от формата представления исходных данных (п.8 формулы изобретения)
Указанное свойство ГПИ основано на применении: а) универсального формата представления исходных данных aINI (рисунок 14), который позволяет сохранить произвольное количество исходных данных разных типов в одном файле и не ограниченно добавлять в этот файл произвольное количество новых параметров в перспективе при изменяющихся требованиях к ПР СВМ; б) универсальной структуры данных AnyMap, реализующей общие данные СВМ D (определение 3), обеспечивающей сохранение произвольных исходных данных различных типов и их количества. Использование указанных технологий позволило создать универсальный алгоритм чтения исходных данных, реализованный в рамках ГПК.
Независимость процедур формирования постановки задачи, отправки постановки на расчет и проведения расчета (п.9 формулы изобретения)
Указанное свойство ГПИ реализовано за счет реализации автоматических программных механизмов: а) преобразования текстовых данных в формате aINI в объект типа AnyMap (реализация общих данных СВМ D), б) сериализации и десериализации объектов типа AnyMap.
Реализация указанных программных механизмов обеспечивает независимость процедур постановки задачи от процедуры проведения расчета и тем самым обеспечивает реализацию отправки постановки задачи на удаленный вычислительный узел с целью проведения расчета (рисунок 16).
Формализация процедуры локальной корректировки созданной ПР СВМ при независимом изменении типов и количества исходных данных (п.10 формулы изобретения)
Процедура локальной корректировки созданной ПР СВМ при независимом изменении типов и количества исходных данных обеспечивается за счет применения: а) стандартизованных фиксированных заголовков используемых для определения ФО и ФП (определения 6, 7); б) универсального формата представления исходных данных aINI (рисунок 14), который позволяет сохранить произвольное количество исходных данных разных типов в одном файле и не ограниченно добавлять в этот файл произвольное количество новых параметров в перспективе при изменяющихся требованиях к ПР СВМ; в) универсальной структуры данных AnyMap, реализующей общие данные СВМ D (определение 3).
Реализация возможностей учета изменяющихся условий функционирования и согласованности работы выбранных численных методов выбранным алгоритмам в течение жизненного цикла создаваемой ПР СВМ (п.11 формулы изобретения)
При изменении условий функционирования и согласованности работы выбранных численных методов выбранным алгоритмам ГПИ позволяет гибко заменить используемые в данный момент ФО и ФП: а) либо непосредственно в файле, описывающем ГМ ПР СВМ (рисунок 13), б) либо используя специальные реляционные структуры данных при хранении ГМ в удаленной базе данных (рисунок 6), реализующие механизмы перегрузки функций.
Также, используя ГПИ, возможен учет изменяющихся условий функционирования и согласованности выбранных численных методов выбранным алгоритмам за счет непосредственного использования функций-предикатов, определяемых в узлах, реализующих ветвление.
Независимость от аппаратной и программной платформ функционирования (п.12 формулы изобретения)
Независимость обеспечивается за счет изначальной распределенной архитектуры программной вычислительной системы и кроссплатформенной реализации графоориентированного программного каркаса (рисунок 12).
Ближайшие аналоги (в порядке наибольшего соответствия)
Ссылки
1. US 2016/0261466 A1 - SIEMENS AKTIENGESELLSCHAFT (München, DE), METHOD AND DIGITAL TOOL FOR ENGINEERING SOFTWARE ARCHITECTURES OF COMPLEX CYBER-PHYSICAL SYSTEMS OF DIFFERENT TECHNICAL DOMAINS (2016).
2. RU 2 435 201 C2 - МЮРЕКС С.А.С. (FR) - ПАРАЛЛЕЛИЗАЦИЯ И ИНСТРУМЕНТАЛЬНЫЕ СРЕДСТВА В ИНФРАСТРУКТУРЕ ГРАФООРИЕНТИРОВАННОГО ПРОГРАММИРОВАНИЯ НА ОСНОВЕ ПРОИЗВОДИТЕЛЕЙ (2011).
3. KR 20060134087 (A) - BEPTECH INC. (US), METHOD OF PROGRAMMING A PROCESSING SYSTEM (2006).
4. US 4,901,221 - National Instruments Corporation (Austin, Texas, US) - GRAPHICAL SYSTEM FOR MODELLING A PROCESS AND ASSOCIATED METHOD (1990) – LabView.
5. US 5,610,828 - National Instruments Corporation (Austin, Texas, US) - GRAPHICAL SYSTEM FOR MODELLING A PROCESS AND ASSOCIATED METHOD (1997) – LabView.
6. US 8,949,772 Bl - Amazon Technologies, Inc., (Reno, NV, US) - DYNAMIC MODEL BASED SOFTWARE APPLICATION DEVELOPMENT (2015) - стандартизация процесса построения приложений на базе диаграмм без привязки к предметной области.
7. US 2004/0056908 Al - Turbo Worx, Inc. (New Haven, CT, US) - METHOD AND SYSTEM FOR DATAFLOW CREATION AND EXECUTION (2004) - построение приложений на базе диаграмм.
8. EP 3,098,736 A1 - The MathWorks, Inc. (Natick, MA 01760, US) - GRAPHICAL MODELING FOR ACCESSING DYNAMIC SYSTEM STATES ACROSS DIFFERENT COMPONENTS (2016) – MatLab.
9. US 2012/0030646 A1 - Ravindran et al. - DEVELOPING PROGRAMS IN A GRAPHICAL SPECIFICATION AND CONSTRAINT LANGUAGE (2012).
Прочие публикации (отсортировано по году):
1. Марков А.В. Автоматизация проектирования и анализа программного обеспечения с использованием языка UML и сетей Петри. Диссертация на соискание уч. степ. канд.тех.наук, Нобосибирск, 2015.
2. Samuel M. Smith. Flow-based programming: Why you should care even if you never plan to use it. In Proceedings of OpenWest (report), page 42 p., 2015.
3. Мараховский В.Б., Розенблюм Л.Я., Яковлев А.В. Моделирование параллельных процессов. Сети Петри. Курс для системных архитекторов, программистов, системных аналитиков, проектировщиков сложных систем управления. Профессиональная литература, АйТи-Подготовка, Санкт-Петербург, 2014.
4. Carkci M. Dataflow and Reactive Programming Systems. Create Space Independent Publishing Platform, 2014.
5. Torsten Meyer, Michael Goedicke, and Gabriele Taentzer. Viewpoint-oriented software development by distributed graph. 2013. 21-st IEEE International Requirements Engineering Conference (RE), 00(1):92.
6. Patrick K. Notz, Roger P. Pawlowski, and James C. Sutherland. Graph-based software design for managing complexity and enabling concurrency in multiphysics PDE software. ACM Trans. Math. Softw., 39(1):1–21, November 2012.
7. Pamela Bhattacharya, Marios Iliofotou, Iulian Neamtiu and Michalis Faloutsos. Graph-based analysis and prediction for software evolution. In Proceedings of the 34th International Conference on Software Engineering, pages 419–429, Piscataway, NJ, USA, 2012. IEEE Press.
8. Mikael Mortensen, Hans Petter Langtangen, Garth N. Wells. A FEniCS-based programming framework for modeling turbulent flow by the Reynolds-averaged Navier-Stokes equations. Computational Engineering, Finance, and Science, 2011.
9. Tiago Boldt Sousa. Dataflow programming concept, languages and applications. Page 12, 2010.
10. Ищенко М.А. Разработка моделей и методов синтеза модульной структуры автоматизированных информационных систем с использованием сетей Петри. Диссертация кандидата технических наук: 05.25.05, Российский государственный гуманитарных университет (РГГУ), Москва, 2009.
11. Morrison J. Paul. Flow-based programming. Unpublished, 2009.
12. Nam H. Pham, Hoan Anh Nguyen, Tung Thanh Nguyen, Jafar M. Al-Kofahi and Tien N. Nguyen. Complete and accurate clone detection in graph-based models. In Proceedings of the 31-st International Conference on Software Engineering, pages 276–286, Washington, DC, USA, 2009. IEEE Computer Society.
13. Roberto Bruni, Antonio Bucchiarone, Stefania Gnesi, Dan Hirsch, and Alberto Lluch Lafuente Graph-Based Design and Analysis of Dynamic Software Architectures, pages 37–56. 2008.
14. Wilke Havinga, Istvan Nagy, Lodewijk Bergmans and Mehmet Aksit. A graph-based approach to modeling and detecting composition conflicts related to introductions. In Proceedings of the 6-th International Conference on Aspect-oriented Software Development, pages 85–95, New York, NY, USA, 2007. ACM.
15. Christian S. Collberg, Clark Thomborson, Gregg M. Townsend. Dynamic graph-based software fingerprinting. ACM Transactions on Programming Languages and Systems, 29(6):35:1–53:67, 2007.
16. Ji Zhang and Betty H. C. Cheng. Model-based development of dynamically adaptive software. In Proceedings of the 28th International Conference on Software Engineering, pages 371–380, New York, NY, USA, 2006. ACM.
17. S. Kounev. Performance modeling and evaluation of distributed component-based systems using queueing Petri-nets. IEEE Transactions on Software Engineering, 32(7):486–502, July 2006.
18. Andy Schurr. Specification of graph translators with triple graph grammars, pages 151–163. June 2005.
19. Manfred Nagl. A software development environment based on graph technology. Pages 458–478, June 2005.
20. Aditya Agrawal. Model based software engineering, graph grammars and graph transformations. Area Paper, page p. 48, 2004.
21. Гуров В.С., Мазин М.А., Нарвский А.С., Шалыто А.А. UML Switch-технология. Eclipse. Информационно-управляющие системы, 1(6), 2004.
22. Bernd Bruegge. Graph-based programming (presentation). Lecture course, Technische Universitaet, Muenchen, 2004.
23. Wesley M. Johnston, J.R. Paul Hanna, Richard J. Millar. Advances in dataflow programming languages. ACM Computing Surveys, 36(1):1–34, 2004.
24. Christian Collberg, Stephen Kobourov, Jasvir Nagra, Jacob Pitts, and Kevin Wampler. A system for graph-based visualization of the evolution of software. In Proceedings of the 2003 ACM Symposium on Software Visualization, pages 77–99, New York, NY, USA, 2003. ACM.
25. Jack Greenfield and Keith Short. Software factories: Assembling applications with patterns, models, frameworks and tools. In Companion of the 18th Annual ACM SIGPLAN Conference on Object-oriented Programming, Systems, Languages, and Applications, pages 16–27, New York, NY, USA, 2003. ACM.
26. Mary Jean, Harrold Gregg, Rothermel Alex Orso. Representation and analysis of software. CiteSeerX, page 19, 2002.
27. Dorina C. Petriu and Hui Shen. Applying the UML Performance Profile: Graph Grammar-Based Derivation of LQN Models from UML Specifications, pages 159–177. April 2002.
28. Tom Mensa and Michele Lanzab. A graph-based metamodel for object-oriented software metrics. Electronic Notes in Theoretical Computer Science, 72(2):57–68, November 2002.
29. B. Bohlen, D. Jager, A. Schleicher and B. Westfechtel. Upgrade: A framework for building graph-based interactive tools. Electronic Notes in Theoretical Computer Science, 72(2):91–101, November 2002.
30. Stephen J. Garland, Nancy Lynch. Using I/O automata for developing distributed systems. Pages 277–303, 2000.
31. Walter J. Gutjahr. A graph-based ant system and its convergence. Future Generation Computer Systems, 16(8):873–888, June 2000.
32. Peter Heimann, Carl-Arndt Krapp, Bernhard Westfechtel. Graph-based software process management. International Journal of Software Engineering and Knowledge Engineering, 7(1), 1997.
33. Jeff Magee and Jeff Kramer. Dynamic structure in software architectures. SIGSOFT Software Engineering Notes, 21(6):3–14, October 1996.
34. G. Heidenreich, M. Minas, and D. Kips. A new approach to consistency control in software engineering. In Proceedings of the 18th International Conference on Software Engineering, pages 289-297, Berlin, Mar. 1996. IEEE Computer Society Press.
35. Zamperoni. GRIDS-graph-based, integrated development of software: integrating different perspectives of software engineering. In Proceedings of IEEE 18th International Conference on Software Engineering, pages 48–59, Mar 1996.
36. W. Deiters and V. Gruhn. The FUNSOFT net approach to software process management. International Journal of Software Engineering and Know ledge Engineering, 4(2):229-256, 1994.
37. Guido Wirtz. Graph-based software construction for parallel message-passing programs. Information and Software Technology, 36(7):405–411, July 1994.
38. Allen S Parrishand, Richard B. Borie and David W. Cordes. Automated flow graph-based testing of object-oriented software modules. Journal of Systems and Software, 23(2):95–109, November 1993.
39. Chris Jones. An integrated modeling environment based on attributed graphs and graph grammars. Decision Support Systems, 10(3):255–275, October 1993.
40. Isa S. Qamber. Flow graph development method. Microelectron Reliab., 33(9):1387–1395, 1992.
41. Nicholas Halbwachs, Paul Caspi, Pascal Raymond, Daniel Pilaud. The synchronous data flow programming language LUSTRE. Proceedings of the, 79(9), 1991.
42. B. Korel and J. Laski. Dynamic program slicing. Information Processing Letters, 29(3):155–63, October 1988.
43. Karl J. Ottenstein and Linda M. Ottenstein. The program dependence graph in a software development environment. SIGSOFT Software Engineering Notes, 9(3):177–184, April 1984.
44. Питерсон Дж. Теория сетей Петри и моделирование систем. Мир, Москва, 1984.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ и система поддержки принятия врачебных решений с использованием математических моделей представления пациентов | 2017 |
|
RU2703679C2 |
| Способ формирования математических моделей пациента с использованием технологий искусственного интеллекта | 2017 |
|
RU2720363C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ РИСКА РАЗВИТИЯ ЗАБОЛЕВАНИЙ ИНДИВИДА ПО ЕГО ГОЛОСУ И АППАРАТНО-ПРОГРАММНЫЙ КОМПЛЕКС ДЛЯ РЕАЛИЗАЦИИ СПОСОБА | 2013 |
|
RU2559689C2 |
| СПОСОБ И СИСТЕМА МОДИФИКАЦИИ ПРОГРАММНОГО КОДА | 2023 |
|
RU2824522C1 |
| СПОСОБ И СИСТЕМА ЦИКЛИЧЕСКОГО РАСПРЕДЕЛЕННОГО АСИНХРОННОГО ОБМЕНА СООБЩЕНИЯМИ СО СЛАБОЙ СИНХРОНИЗАЦИЕЙ ДЛЯ РАБОТЫ С БОЛЬШИМИ ГРАФАМИ | 2021 |
|
RU2761136C1 |
| СПОСОБ ГРАФОВОЙ НЕЙРОСЕТЕВОЙ КЛАССИФИКАЦИИ НА ОТСУТСТВИЕ ИЛИ НАЛИЧИЕ БОЛЬШОГО ДЕПРЕССИВНОГО РАССТРОЙСТВА ПО ДАННЫМ ФМРТ | 2023 |
|
RU2819348C1 |
| СИСТЕМА И СПОСОБ ПОИСКА ДАННЫХ В БАЗЕ ДАННЫХ ГРАФОВ | 2015 |
|
RU2707708C2 |
| СПОСОБ И СИСТЕМА ДЛЯ ГЛОБАЛЬНОЙ ИДЕНТИФИКАЦИИ В КОЛЛЕКЦИИ ДОКУМЕНТОВ | 2015 |
|
RU2591175C1 |
| СИСТЕМА И СПОСОБ ОБРАБОТКИ ДАННЫХ ГРАФОВ | 2015 |
|
RU2708939C2 |
| СПОСОБ НЕПРЕРЫВНОГО МОНИТОРИНГА КРИТИЧЕСКИ ВАЖНЫХ ОБЪЕКТОВ ГРУППОЙ БЕСПИЛОТНЫХ ЛЕТАТЕЛЬНЫХ АППАРАТОВ ПО ЗАМКНУТОМУ МАРШРУТУ | 2024 |
|
RU2837602C1 |




Изобретение относится к области компьютерной техники. Техническим результатом является упрощение процессов проектирования, разработки, тестирования и сопровождения программных реализаций сложных вычислительных методов. Способ графо-ориентированного создания программных реализаций сложных вычислительных методов включает построение и последующую автоматическую интерпретацию графического представления алгоритма в форме ориентированного графа, реализующего рассматриваемый сложный вычислительный метод, и заключается в выполнении последовательности действий: а) создание формата файлов входных данных для создаваемой программной реализации сложного вычислительного метода; б) создание графовой модели алгоритма, реализующего сложный вычислительный метод, в форме ориентированного графа, для которого каждый узел имеет уникальное имя и определяет фиксированное состояние общих данных, а с каждым ребром связана функция, называемая функцией перехода, которая определяет преобразование общих данных из одного состояния в другое; в) разработка программных реализаций функций перехода, определяемых графовой моделью, причем каждая функция перехода определяется парой функций с унифицированными сигнатурами: функцией-предикатом и функцией-обработчиком; г) отладка и тестирование разработанной программной реализации сложного вычислительного метода, включающие автоматическую интерпретацию графовой модели, которая заключается в загрузке входных данных, в оперативную память вычислительной машины в объект общих данных, и последующем обходе графа модели с запуском всех функций перехода с передачей им на вход модифицируемого объекта общих данных. 11 з.п. ф-лы, 20 ил.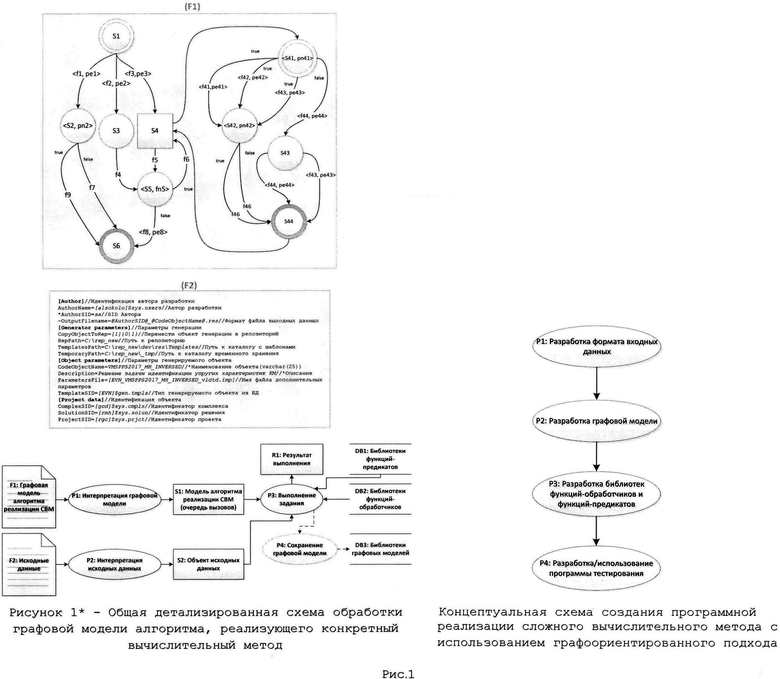
1. Способ графо-ориентированного создания программных реализаций сложных вычислительных методов, включающий построение и последующую автоматическую интерпретацию графического представления алгоритма в форме ориентированного графа, реализующего рассматриваемый сложный вычислительный метод, и заключающийся в выполнении следующей последовательности действий:
а) создание формата файлов входных данных для создаваемой программной реализации сложного вычислительного метода, в основе которого следует применять форматы, отличающиеся возможностями определения списков исходных параметров и их значений;
б) создание графовой модели алгоритма, реализующего сложный вычислительный метод, в форме ориентированного графа, для которого каждый узел имеет уникальное имя и определяет фиксированное состояние общих данных, а с каждым ребром связана функция, называемая функцией перехода, которая определяет преобразование общих данных из одного состояния в другое;
в) разработка программных реализаций функций перехода, определяемых графовой моделью, описанной по п. 1б, и отличающихся тем, что каждая функция перехода определяется парой функций с унифицированными сигнатурами: функцией-предикатом и функцией-обработчиком;
г) отладка и тестирование разработанной программной реализации сложного вычислительного метода, включающие автоматическую интерпретацию графовой модели, которая заключается в загрузке входных данных, имеющих формат, определенный по п. 1а, в оперативную память вычислительной машины в объект общих данных, и последующем обходе графа модели с запуском всех функций перехода с передачей им на вход модифицируемого объекта общих данных.
2. Способ по п. 1, отличающийся применением обобщенного формата структурированных текстовых данных (например, aINI, JSON, XML), который должен обеспечивать определение текстовых форматов исходных данных для широкого класса вычислительных задач.
3. Способ по п. 2, отличающийся возможностью создания универсальной программной реализации функции загрузки исходных данных, описываемых указанным образом, в оперативную память вычислительной машины с помощью программной реализации предлагаемого способа (далее, графо-ориентированного программного каркаса) в форму объекта многомерного ассоциативного контейнера при произвольном изменении количества, типов и значений загружаемых исходных параметров.
4. Способ по п. 1, отличающийся тем, что каждая функция перехода, связанная с конкретным ребром графовой модели, получает данные в формате объекта многомерного ассоциативного контейнера в состоянии, определяемом первым узлом, и преобразующей эти данные в новое состояние, определяемое вторым узлом.
5. Способ по п. 1, отличающийся тем, что графовая модель алгоритма, реализующего сложный вычислительный метод, может быть представлена различным образом:
а) в форме описания на известном языке графов (например, DOT);
б) в форме программы на компилируемом языке программирования (например, С++), создающей модель во время выполнения с использованием возможностей графо-ориентированного программного каркаса.
в) в форме сценария, включающего массив запросов, обеспечивающего создание, сохранение и регистрацию модели в хранилище, которое определяется используемым графо-ориентированным программным каркасом (например, в виде набора записей в базе данных с заранее фиксированной структурой).
6. Способ по п. 1, отличающийся тем, что функции-обработчики и функции-предикаты могут быть разработаны с использованием произвольных языков программирования, что определяется и обеспечивается поддержкой применяемого графо-ориентированного программного каркаса.
7. Способ по п. 1, отличающийся тем, что функции-обработчики и функции-предикаты взаимозаменяемы с точностью до учета внутренней структуры обрабатываемых данных в форме объекта многомерного ассоциативного контейнера.
8. Способ по п. 1, отличающийся использованием стандартной исполняемой тестирующей программы, входящей в состав применяемого графо-ориентированного программного каркаса, обеспечивающей интерпретацию любой графовой модели и локальный запуск создаваемой программной реализации сложного вычислительного метода.
9. Способ по п. 1, отличающийся возможностью иерархического вложения в графовые модели одних вычислительных методов графовых моделей, реализующих другие вычислительные методы.
10. Способ по п. 1, отличающийся независимостью реализуемого вычислительного метода от формата представления исходных данных.
11. Способ по п. 1, отличающийся обеспечением независимости процедур: формирования постановки задачи; загрузки постановки и ее отправки на расчет; проведения расчета.
12. Способ по п. 1, отличающийся обеспечением автоматического распараллеливания исполнения созданной программной реализации сложного вычислительного метода за счет заранее известной топологии графовой модели.
| Токарный резец | 1924 |
|
SU2016A1 |
| Пресс для выдавливания из деревянных дисков заготовок для ниточных катушек | 1923 |
|
SU2007A1 |
| US 4901221 A1, 13.02.1990 | |||
| ГРАФООРИЕНТИРОВАННОЕ ПРОГРАММИРОВАНИЕ И ВЫПОЛНЕНИЕ НА ОСНОВЕ ПРОИЗВОДИТЕЛЕЙ | 2007 |
|
RU2445682C2 |
| ИНТЕРФЕЙС ПРОГРАММИРОВАНИЯ ДЛЯ КОМПЬЮТЕРНОЙ ПЛАТФОРМЫ | 2004 |
|
RU2371758C2 |
Авторы
Даты
2019-03-06—Публикация
2017-08-22—Подача