Изобретение относится к области контрольно- измерительной техники, в частности к измерению структурных свойств многофазных сильно рассеивающих и слабо поглощающих сред оптическими методами, может быть использовано для исследования размеров пор и прочих включений в керамике, стекле и других дисперсных системах. Изобретение может найти применение в медицине, коллоидной химии, для контроля загрязнений окружающей среды и других отраслях, где необходимо вести быстрый контроль размеров или содержания включений дисперсных систем.
Известны способы определения размеров включений, основанные на рассеянии излучения, где в качестве экспериментальных данных используются спектры направленного пропускания при небольших концентрациях рассеивающих примесей [1-6].
Возможности этих методов ограничены плотной керамикой с небольшой объемной долей включений или сильно разбавленными растворами.
Наиболее близким техническим решением (прототипом) является способ, который основан на расчете коэффициентов экстинкции при помощи теории Ми и решении обратной задачи переноса излучения в трехпотоковом приближении для непоглощающего материала [7]. При решении обратной задачи определяется эффективная оптическая толщина, зависящая как от показателей рассеяния, так и от индикатрисы рассеяния, а в качестве экспериментальных данных используются спектры диффузного пропускания.
Недостатком прототипа является возможность анализировать только непоглощающие материалы и двухфазные системы.
Задачей, на решение которой направлено предлагаемое изобретение, является повышение достоверности получаемых данных и расширение области применимости оптических методов анализа структуры частично прозрачных рассеивающих материалов.
Техническим результатом изобретения является повышение информативности и точности исследований структурных свойств дисперсных систем в области их частичной прозрачности, возможность получения данных о структурных свойствах (распределение пор и включений по размерам) на натурном изделии.
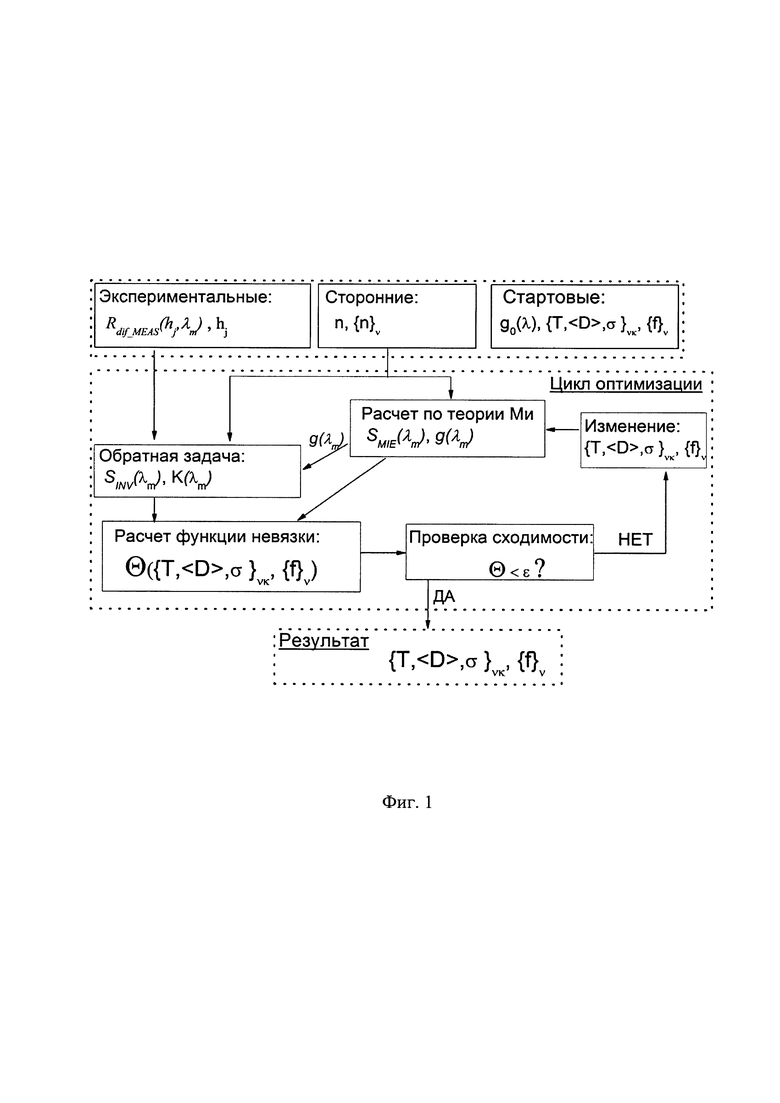
Технический результат изобретения достигается путем оптимизации параметров распределения пор или включений по размерам и их объемной доли таким образом, чтобы спектральный показатель рассеяния, определяемый расчетом по теории Ми, совпал с результатом решения обратной задачи переноса излучения.
Входными данным для процесса оптимизации служат: стартовые параметры распределений по размерам, стартовое значение объемных долей включений для каждой из фаз, действительная и мнимая часть показателей преломления материала включений для каждой из фаз и материала среды, спектральные коэффициенты диффузного отражения или пропускания слоев различных толщин, измеренные в диапазоне длин волн частичной прозрачности материала.
Способ определения распределения по размерам и концентрации включений в частично прозрачных сильно рассеивающих материалах, отличающийся тем, что в качестве экспериментальных данных используют спектральные коэффициенты диффузного отражения или пропускания слоев материала известных толщин, распределение включений по размерам задаются в параметрической форме, а параметры распределений рассчитываются минимизацией функции невязки между спектральным показателем рассеяния 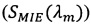 , рассчитываемым по теории Ми и спектральным показателем рассеяния
, рассчитываемым по теории Ми и спектральным показателем рассеяния 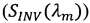 , определяемым путем решения обратной задачи переноса излучения:
, определяемым путем решения обратной задачи переноса излучения:
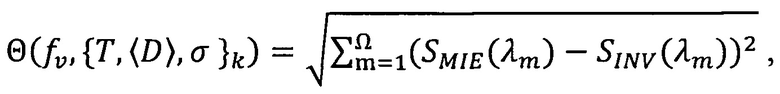
Спектральный показатель рассеяния по теории Ми, рассчитывается:
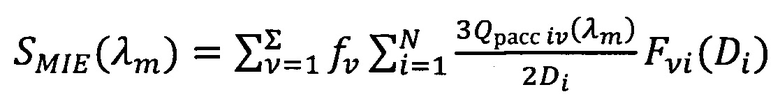
Результат решения обратной задачи получается путем минимизации функции невязки:
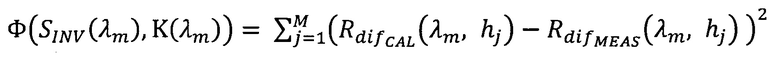
между экспериментально измеренным коэффициентом диффузного отражения или пропускания 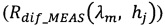 , и рассчитанным по асимптотическим формулам при помощи теории переноса излучения для коэффициента отражения:
, и рассчитанным по асимптотическим формулам при помощи теории переноса излучения для коэффициента отражения:
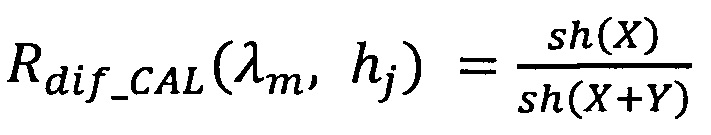
или пропускания:
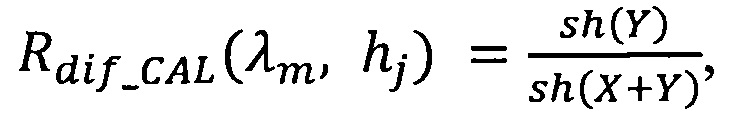
где
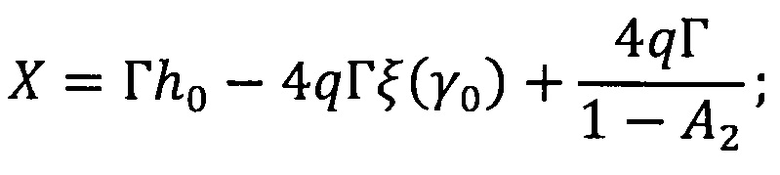
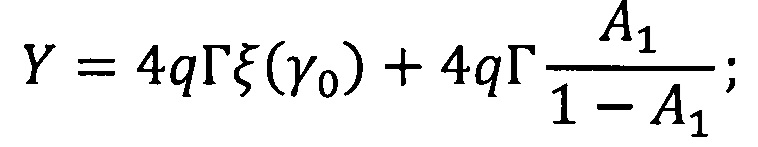
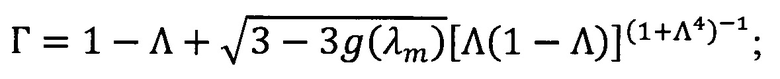
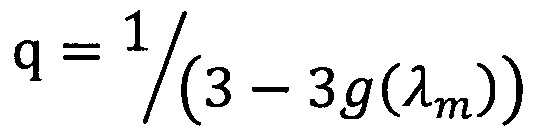 - параметр, связанный с формой индикатрисы рассеяния;
- параметр, связанный с формой индикатрисы рассеяния;
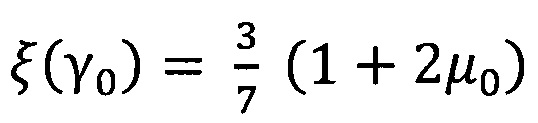 - параметр, учитывающий направление падения излучения;
- параметр, учитывающий направление падения излучения;
μ0 - косинус угла падения параллельного пучка на поверхность рассеивающего слоя при измерении коэффициента отражения;
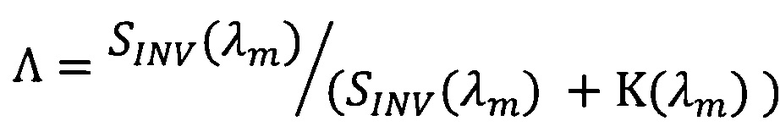 - альбедо однократного рассеяния;
- альбедо однократного рассеяния;
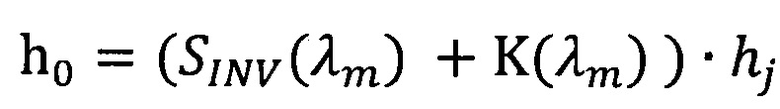 - оптическая толщина слоя;
- оптическая толщина слоя;
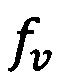 - объемная доля включений ν-й фазы;
- объемная доля включений ν-й фазы;
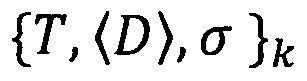 - набор параметров, определяющих распределение включений по размерам;
- набор параметров, определяющих распределение включений по размерам;
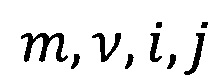 - индексы суммирования по длинам волн, фазам, диаметрам и толщинам, соответственно;
- индексы суммирования по длинам волн, фазам, диаметрам и толщинам, соответственно;
Ω, Е, N, М - общее число точек длин волн, фаз включений, дискретов по диаметру и геометрических толщин, соответственно;
 - длина волны;
- длина волны;
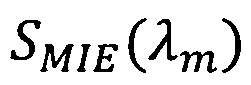 - спектральный показатель рассеяния, рассчитываемый по теории Ми;
- спектральный показатель рассеяния, рассчитываемый по теории Ми;
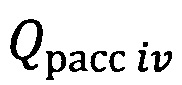 - эффективность рассеяния шаром диаметром Di из материала ν-й фазы;
- эффективность рассеяния шаром диаметром Di из материала ν-й фазы;
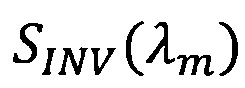 - спектральный показатель рассеяния, определяемый путем решения обратной задачи переноса излучения;
- спектральный показатель рассеяния, определяемый путем решения обратной задачи переноса излучения;
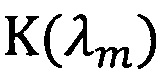 - показатель поглощения;
- показатель поглощения;
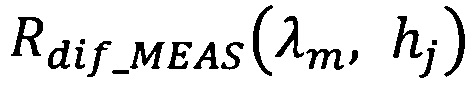 - измеренный спектральный коэффициент диффузного отражения или пропускания для слоя толщиной hj;
- измеренный спектральный коэффициент диффузного отражения или пропускания для слоя толщиной hj;
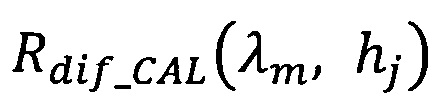 - коэффициент диффузного отражения или пропускания для слоя толщиной hj, рассчитанный по теории переноса излучения;
- коэффициент диффузного отражения или пропускания для слоя толщиной hj, рассчитанный по теории переноса излучения;
hj - геометрическая толщина j-го слоя;
А1 и А2 - коэффициенты отражения освещаемой внешним источником (верхней) и тыльной (нижней) границ слоя при диффузном падении излучения изнутри слоя;
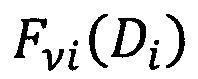 - объемное распределение частиц ν-й фазы диаметром Di (нормированное на единицу для каждой из фаз).
- объемное распределение частиц ν-й фазы диаметром Di (нормированное на единицу для каждой из фаз).
На фиг. 1 представлена иллюстрация принципов, лежащих в основе предлагаемого способа.
Расчет спектрального показателя рассеяния 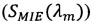 производится по формуле:
производится по формуле:
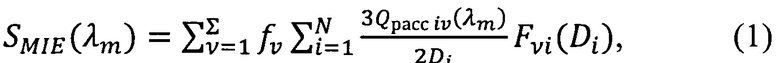 --L
--L
где 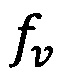 - объемная доля включений ν-й фазы;
- объемная доля включений ν-й фазы;
 - спектральная эффективность рассеяния для шара диаметром Di с оптическими свойствами ν-й фазы, рассчитываемая по теории Ми;
- спектральная эффективность рассеяния для шара диаметром Di с оптическими свойствами ν-й фазы, рассчитываемая по теории Ми;
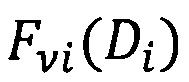 - относительная объемная доля включений ν-й фазы диаметром Di среди суммарного объема включений ν-й фазы;
- относительная объемная доля включений ν-й фазы диаметром Di среди суммарного объема включений ν-й фазы;
N - число дискретов по диаметрам рассеивателей;
Σ - число фаз.
Для расчета среднего косинуса угла рассеяния шаром диаметром Di используется известное выражение теории Ми:
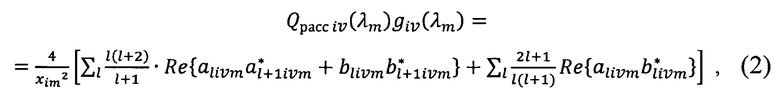
где 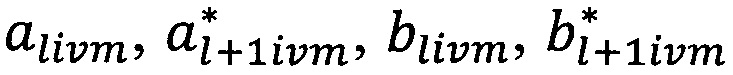 - коэффициенты, рассчитываемые по теории Ми и зависящие от относительного комплексного показателя преломления
- коэффициенты, рассчитываемые по теории Ми и зависящие от относительного комплексного показателя преломления 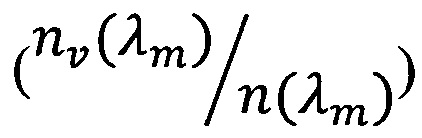 материала включений ν-й фазы и среды, и дифракционного параметра xim, равного
материала включений ν-й фазы и среды, и дифракционного параметра xim, равного 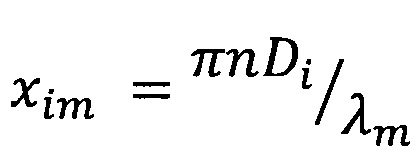 ;
; 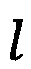 - целые числа.
- целые числа.
Средний косинус угла рассеяния совокупности включений рассчитывается по формуле:
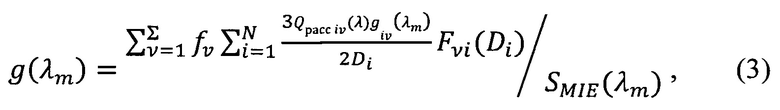
Распределение включений по размерам задается в параметрической форме в виде суммы пиков, нормированных на единицу:
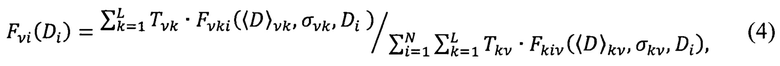
где L - число пиков распределения включений по размерам;
k - индекс, задающий номер пика;
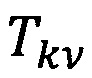 - постоянные коэффициенты;
- постоянные коэффициенты;
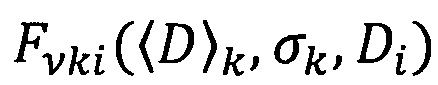 - любое распределение, задаваемое парамерами
- любое распределение, задаваемое парамерами 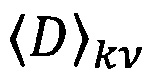 и
и 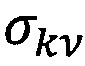 , например, логнормальное или гауссово.
, например, логнормальное или гауссово.
Распределение включений всех фаз по размерам полностью определяется совокупностью параметров: 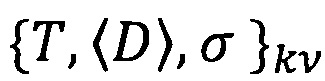 .
.
Обратная задача для определения спектрального показателя рассеяния 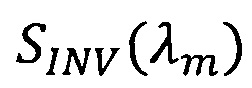 строится на основе асимптотических формул для спектрального коэффициента отражения:
строится на основе асимптотических формул для спектрального коэффициента отражения:
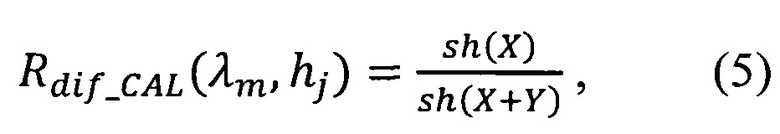
или пропускания
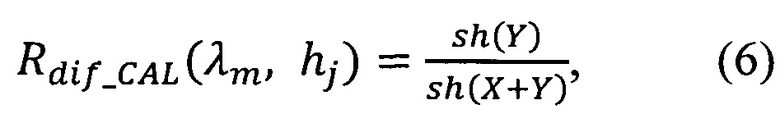
где
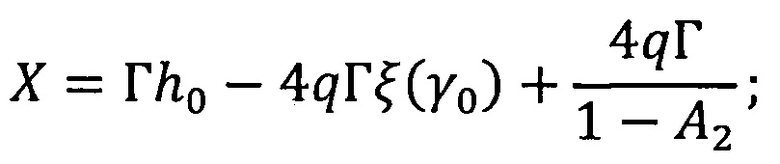
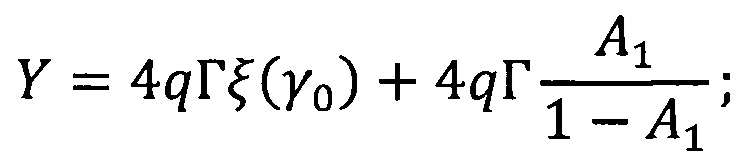
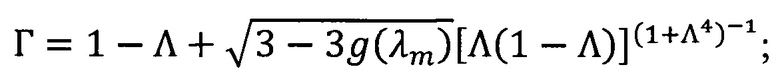
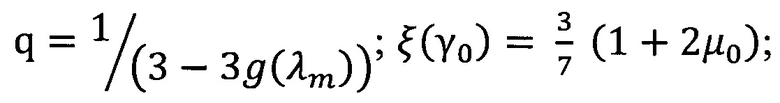
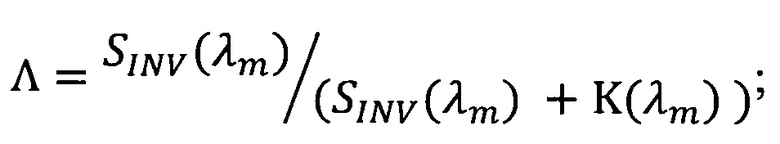
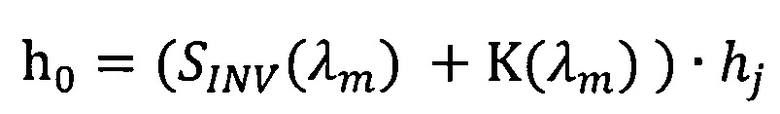
где 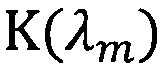 - показатель поглощения;
- показатель поглощения;
hj - геометрическая толщина j-го слоя;
μ0 - косинус угла падения параллельного пучка на поверхность рассеивающего слоя;
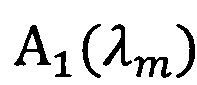 и
и 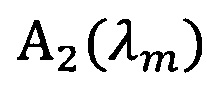 - коэффициенты отражения освещаемой внешним источником (верхней) и тыльной (нижней) границ слоя при диффузном падении излучения изнутри слоя, рассчитываемые путем усреднения формул Френеля для угловой зависимости коэффициента зеркального отражения [8].
- коэффициенты отражения освещаемой внешним источником (верхней) и тыльной (нижней) границ слоя при диффузном падении излучения изнутри слоя, рассчитываемые путем усреднения формул Френеля для угловой зависимости коэффициента зеркального отражения [8].
Обратная задача решается путем минимизации функции невязки между измеренными 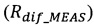 и рассчитанными
и рассчитанными 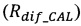 коэффициентами диффузного отражения или пропускания для слоев материала нескольких толщин по параметрам
коэффициентами диффузного отражения или пропускания для слоев материала нескольких толщин по параметрам 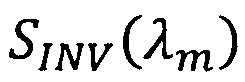 и
и 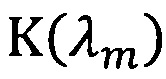 :
:
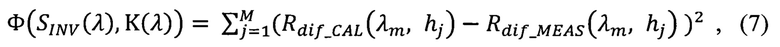
где М - число слоев различной толщины.
При известной зависимости показателя поглощения материала среды от длины волны минимизация функции невязки  может производиться только по параметру
может производиться только по параметру 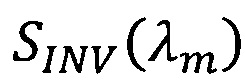 . В этом случае для решения обратной задачи будет достаточно измерить спектральный коэффициент отражения или пропускания слоя одной толщины (М=1).
. В этом случае для решения обратной задачи будет достаточно измерить спектральный коэффициент отражения или пропускания слоя одной толщины (М=1).
Следующим шагом является построение функции невязки показателей рассеяния и ее минимизация:
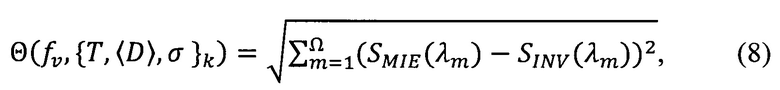
где Ω - число точек в спектре.
Минимизация производится в пространстве параметров, задающих распределение по размерам 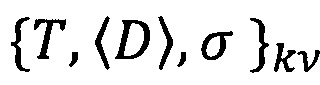 , или их объемную долю
, или их объемную долю 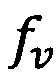 .
.
На каждом шаге цикла оптимизации производится пересчет 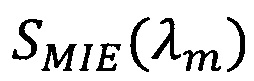 и
и 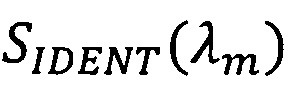 в соответствии с приведенными формулами.
в соответствии с приведенными формулами.
Минимизация функции  может производиться, как по нескольким или одному из параметров распределения, так и по всей совокупности.
может производиться, как по нескольким или одному из параметров распределения, так и по всей совокупности.
Предложенный способ отличается быстротой получения результата, так как он не требует сложной подготовки и специального оборудования.
Решение обратной задачи строится на аналитических выражениях для коэффициентов отражения или пропускания, метод отличается быстротой численной обработки.
Изобретение поясняется конкретным примером выполнения способа определения распределения пор по размерам в кварцевой керамике. Кварцевая керамика является двухфазной дисперсной системой. Одной фазой в ней является кварцевое стекло, второй - поры, заполненные воздухом.
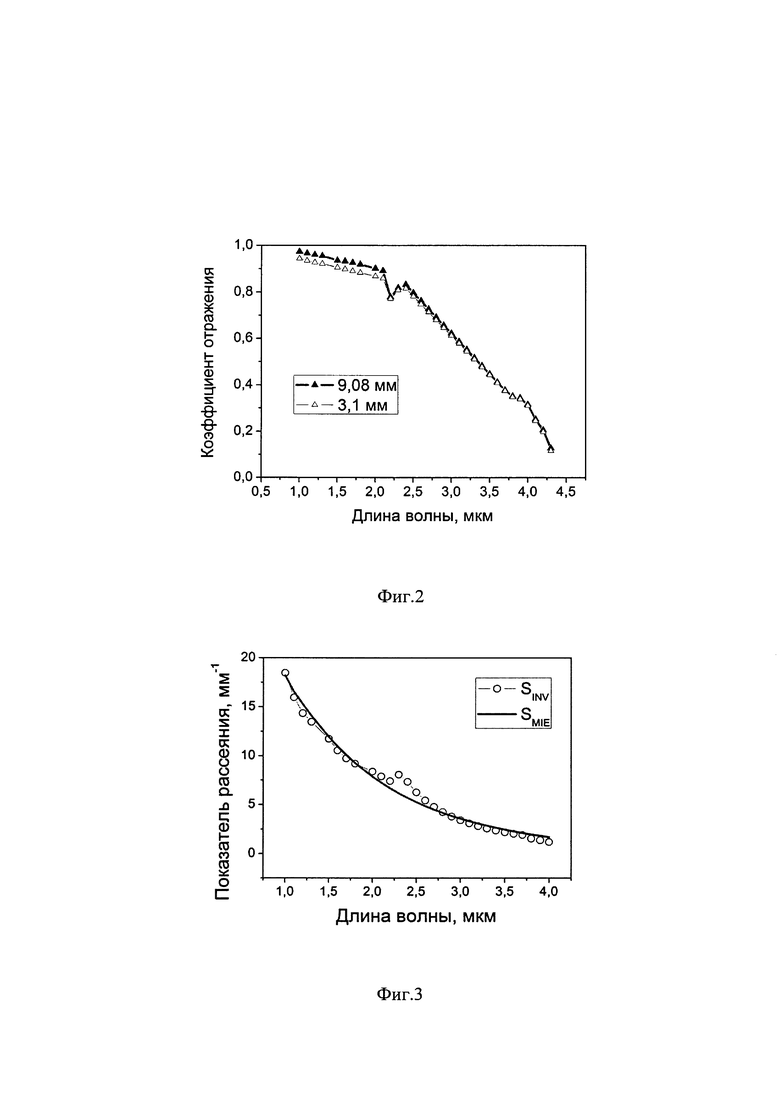
На фиг. 2 показаны результаты измерения спектров коэффициента диффузного отражения при помощи ИК-Фурье спектрометра is50 с интегрирующей сферой IntegratIR. По спектрам коэффициента отражения проводилось решение обратной задачи и оптимизация в соответствии с описанным способом.
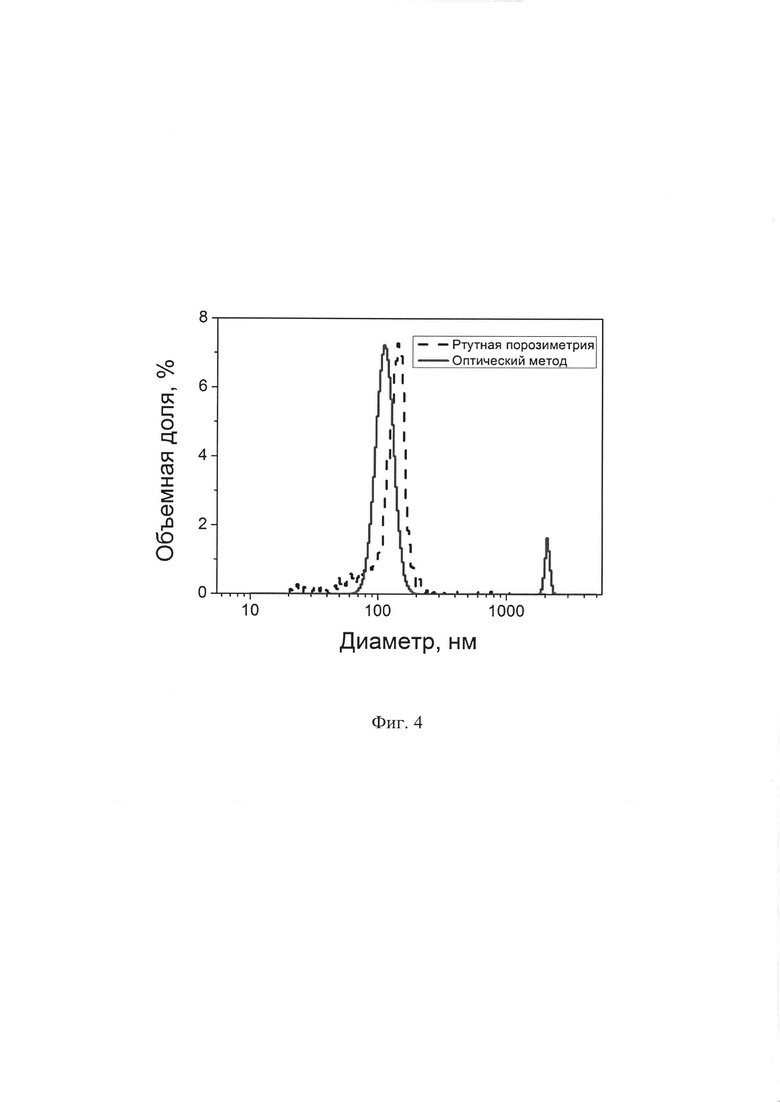
На фиг. 3 приведены спектры показателя рассеяния, определенного путем решения обратной задачи и расчетом по теории Ми после окончания процесса оптимизации. Оптимизация позволила определить параметры распределения пор по размерам. Форма распределения задавалась логнормальной зависимостью.
На фиг. 4 приведено распределение пор по размерам, определенное предлагаемым оптическим способом в сравнении с измеренным методом ртутной порозиметрии.
Приведенные результаты показывают, что оптический способ позволяет определить распределение включений по размерам (в данном случае пор) и демонстрирует согласие с альтернативным методом ртутной порозиметрии.
Оптический способ имеет ряд преимуществ по сравнению с ртутной порозиметрией, способ позволяет анализировать закрытые поры, анализ занимает не более 1 минуты при нескольких часах для ртутной порозиметрии и позволяет анализировать больший объем материала.
Предлагаемый способ позволяет расширить допустимую область концентраций до 10-15 объемных процентов за счет учета многократного рассеяния при помощи теории переноса излучения и анализировать многокомпонентные дисперсные системы.
Способ строится на одновременном определении спектрального показателя рассеяния дисперсной системы путем решения обратной задачи переноса излучения и расчетом по теории Ми. Для решения обратной задачи переноса излучения используются формулы, описанные в [9]. Основы теории Ми описаны в литературе [10]. Теоретические основы способа описаны в работе [8].
Отличительной особенностью предлагаемого способа является то, что для решения используются асимптотические формулы, которые позволяют анализировать материалы с поглощением. Рассчитываемая по теории Ми индикатриса рассеяния является изменяемым в процессе оптимизации параметром, что повышает точность получаемых данных.
ЛИТЕРАТУРА
1 Jones A.R. Light scattering for particle characterization // Progress in Energy and Combustion Science. 1999. V. 25. P. 1-53.
2. Peelen J.G.J., Metselaar R. Light scattering by pores in polycrystalline materials: Transmission properties of alumina // J. Appl. Phys. 1974. V. 45. N 1. P. 216-220.
3. Chen, W.W., B. Dunn. Characterization of Pore Size Distribution by Infrared Scattering in Highly Dense ZnS // Journal of the American Ceramic Society. 1993. V 76/ N 8. P. 2086-2092.
4. Mei L., Somesfalean G., Svanberg S. Light propagation in porous ceramics: porosity and optical property studies using tunable diode laser spectroscopy. // Appl. Phys. A. 2014. V. 114. N 2. P. 393-400.
5. V.I. Bredikhin, E.M. Gavrishchuk, V.B. Ikonnikov, E.V. Karaksina, L.A. Ketkova, S.P. Kuznetsov, and O.A. Mal'shakova. Optical losses in polycrystalline CVD ZnS // Inorganic Materials. 2009. V. 45. N 3. P. 235-241.
6. Патент РФ №2441218, МПК G01N 15/02 Способ определения дисперсности и концентрации частиц в аэрозольном облаке / В.А. Архипов, А.А. Павленко, С.С. Титов, О.Б. Кудряшова, С.С. Бондарчук. №2010143653/28; заявл. 25.10.2010; опубл. 27.01.2012, Бюл. №3 - 12 с.
7. Manara J., Caps R., Raether F., Fricke J. Characterization of the pore structure of alumina ceramics by diffuse radiation propagation in the near infrared // Optics Communications. 1999. V.168. P. 237-250.
8. Э.П. Зеге и И.Л. Кацев. Определение оптических характеристик рассеивающей среды по отражению от полубесконечного слоя // Журнал прикладной спектроскопии. - 1980. - Т. 33. - №3. - С. 550-556.
9. Борен К., Хафмен Д. Поглощение и рассеяние света малыми частицами. М.: Мир, 1986. - 664 с.
10. Миронов Р.А., Забежайлов М.О., Георгиу И.Ф., Черепанов В.В., Русин М.Ю. Определение размеров пор в частично прозрачной керамике по спектрам коэффициента полного отражения // Оптика и спектроскопия. - 2018. - Т. 124. - №3. - С. 295-302.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ОПРЕДЕЛЕНИЯ СОДЕРЖАНИЯ ПРОИЗВОДНЫХ ГЕМОГЛОБИНА В КРОВИ | 2013 |
|
RU2536217C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ КОНЦЕНТРАЦИЙ ХРОМОФОРОВ БИОЛОГИЧЕСКОЙ ТКАНИ | 2012 |
|
RU2506567C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ФИЗИКО-БИОЛОГИЧЕСКИХ ПАРАМЕТРОВ КОЖИ И КОНЦЕНТРАЦИЙ ПРОИЗВОДНЫХ ГЕМОГЛОБИНА В КРОВИ | 2013 |
|
RU2545814C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ГЛУБИНЫ ПРОНИКНОВЕНИЯ СВЕТА В КОЖУ И УСТРОЙСТВО ДЛЯ ЕГО РЕАЛИЗАЦИИ | 2012 |
|
RU2521838C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ОПТИЧЕСКИХ И БИОФИЗИЧЕСКИХ ПАРАМЕТРОВ БИОТКАНИ | 2012 |
|
RU2510506C2 |
| Нестационарный способ определения истинного коэффициента теплопроводности сильнорассеивающих материалов | 1991 |
|
SU1784890A1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ОПТИЧЕСКИХ СВОЙСТВ НАНОЧАСТИЦ | 2014 |
|
RU2586938C1 |
| СПОСОБ ФОТОДИНАМИЧЕСКОЙ ТЕРАПИИ ОНКОЛОГИЧЕСКИХ ЗАБОЛЕВАНИЙ | 2013 |
|
RU2539367C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ КОНЦЕНТРАЦИЙ ПРОИЗВОДНЫХ ГЕМОГЛОБИНА В БИОЛОГИЧЕСКИХ ТКАНЯХ | 2013 |
|
RU2517155C1 |
| УСТРОЙСТВО ДЛЯ ОПРЕДЕЛЕНИЯ КОНЦЕНТРАЦИИ ГЕМОГЛОБИНА И СТЕПЕНИ ОКСИГЕНАЦИИ КРОВИ В СЛИЗИСТЫХ ОБОЛОЧКАХ | 2013 |
|
RU2528087C1 |
Изобретение относится к области контрольно-измерительной техники и касается способа определения распределения по размерам и концентрации включений в частично прозрачных сильно рассеивающих материалах. Способ включает в себя получение в качестве экспериментальных данных спектральных коэффициентов диффузного отражения или пропускания слоев материала известных толщин. Распределение включений по размерам задается в параметрической форме, а параметры распределений рассчитываются минимизацией функции невязки между спектральным показателем рассеяния, рассчитываемым по теории Ми, и спектральным показателем рассеяния, определяемым путем решения обратной задачи переноса излучения. Результат решения обратной задачи получается путем минимизации функции невязки между экспериментально измеренным коэффициентом диффузного отражения или пропускания и рассчитанным по асимптотическим формулам при помощи теории переноса излучения для коэффициента отражения или пропускания. Технический результат заключается в повышении информативности и точности исследований. 4 ил.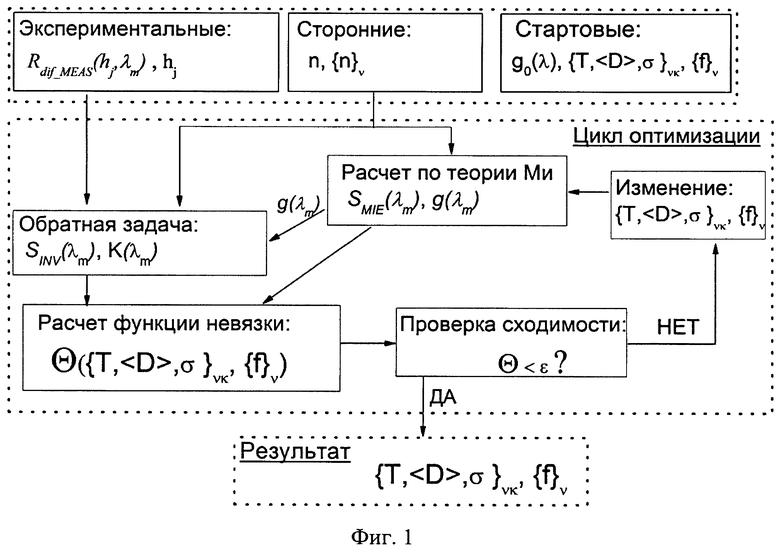
Способ определения распределения по размерам и концентрации включений в частично прозрачных сильно рассеивающих материалах, отличающийся тем, что в качестве экспериментальных данных используют спектральные коэффициенты диффузного отражения или пропускания слоев материала известных толщин, распределение включений по размерам задается в параметрической форме, а параметры распределений рассчитываются минимизацией функции невязки между спектральным показателем рассеяния (SMIE(λm)), рассчитываемым по теории Ми, и спектральным показателем рассеяния (SINV(λm)), определяемым путем решения обратной задачи переноса излучения:
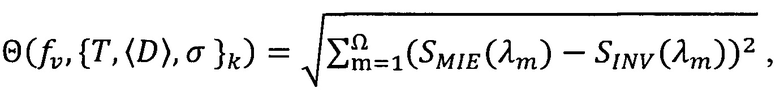
спектральный показатель рассеяния по теории Ми, рассчитывается:
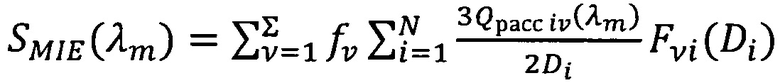 ,
,
результат решения обратной задачи получается путем минимизации функции невязки:
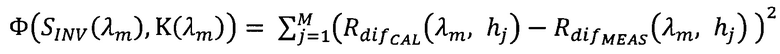
между экспериментально измеренным коэффициентом диффузного отражения или пропускания (Rdiƒ_MEAS(λm, hj)) и рассчитанным по асимптотическим формулам при помощи теории переноса излучения для коэффициента отражения:
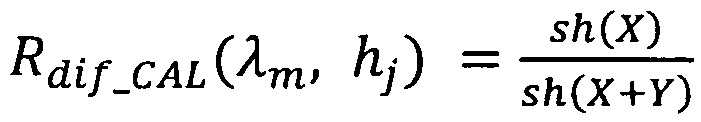
или пропускания:
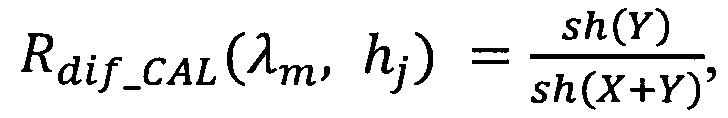
где

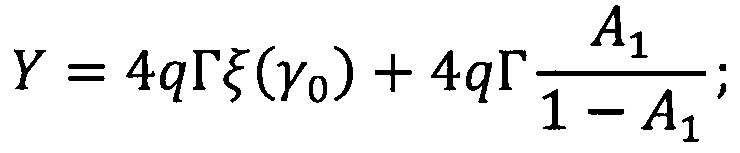
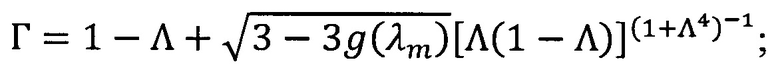
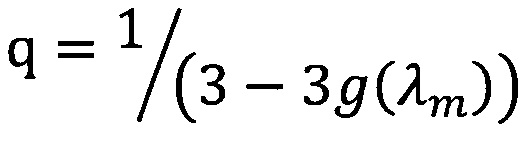 - параметр, связанный с формой индикатрисы рассеяния;
- параметр, связанный с формой индикатрисы рассеяния;
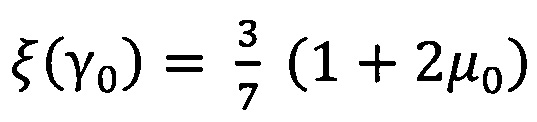 - параметр, учитывающий направление падения излучения;
- параметр, учитывающий направление падения излучения;
μ0 - косинус угла падения параллельного пучка на поверхность рассеивающего слоя при измерении коэффициента отражения;
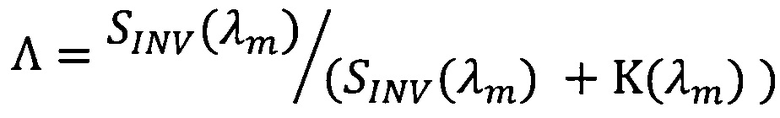 - альбедо однократного рассеяния;
- альбедо однократного рассеяния;
h0=(SINV(λm)+K(λm)) ⋅ hj - оптическая толщина слоя;
ƒν - объемная доля включений ν-й фазы;
{T, 〈D〉, σ}k - набор параметров, определяющих распределение включений по размерам;
m, ν, i, j - индексы суммирования по длинам волн, фазам, диаметрам и толщинам, соответственно;
Ω, Σ, N, М - общее число точек длин волн, фаз включений, дискретов по диаметру и геометрических толщин, соответственно;
λm - длина волны;
SМIЕ(λm) - спектральный показатель рассеяния, рассчитываемый по теории Ми;
Qpacc iν - эффективность рассеяния шаром диаметром Di из материала ν-й фазы;
SINV(λm) - спектральный показатель рассеяния, определяемый путем решения обратной задачи переноса излучения;
K(λm) - показатель поглощения;
Rdiƒ_MEAS(λm, hj) - измеренный спектральный коэффициент диффузного отражения или пропускания для слоя толщиной hj;
Rdiƒ_CAL(λm, hj) - коэффициент диффузного отражения или пропускания для слоя толщиной hj, рассчитанный по теории переноса излучения;
hj - геометрическая толщина j-го слоя;
А1 и А2 - коэффициенты отражения освещаемой внешним источником (верхней) и тыльной (нижней) границ слоя при диффузном падении излучения изнутри слоя;
Fνi(Di) - объемное распределение частиц ν-й фазы диаметром Di (нормированное на единицу для каждой из фаз).
| Manara J | |||
| и др | |||
| "Characterization of the pore structure of alumina ceramics by diffuse radiation propagation in the near infrared" OPTICS COMMUNICATIONS | |||
| т | |||
| Приспособление, заменяющее сигнальную веревку | 1921 |
|
SU168A1 |
| Прибор для корчевания пней | 1921 |
|
SU237A1 |
| Р | |||
| А | |||
| Миронов и др | |||
| "Расчетно-экспериментальное определение температурной зависимости спектральных и интегральных коэффициентов излучения кварцевой керамики различной пористости", ТЕПЛОФИЗИКА ВЫСОКИХ ТЕМПЕРАТУР, т | |||
| Видоизменение прибора для получения стереоскопических впечатлений от двух изображений различного масштаба | 1919 |
|
SU54A1 |
| СПОСОБ ИЗГОТОВЛЕНИЯ НА ТКАЦКИХ СТАНКАХ ГОТОВЫХ ПРЕДМЕТОВ БЕЛЬЯ И ОДЕЖДЫ | 1920 |
|
SU724A1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ОПТИЧЕСКИХ СВОЙСТВ НАНОЧАСТИЦ | 2014 |
|
RU2586938C1 |
| WO 1998020323 A1, 14.05.1998. | |||
Авторы
Даты
2019-05-21—Публикация
2018-07-09—Подача