Способ помехоустойчивого градиентного выделения контуров объектов на цифровых полутоновых изображениях Российский патент 2019 года по МПК G06K9/48 

Изобретение относится к области цифровой обработки изображений и может быть использовано в фото, видео, оптико-локационной и оптико-электронной технике при решении задач распознавания образов по их контурам на цифровых изображениях.

Необходимыми условиями того, что через некоторую точку цифрового полутонового изображения проходит контур, являются следующие:

- резкое изменение яркости в данной точке по сравнению хотя бы с одной из соседних точек;

- наличие хотя бы двух соседних точек, сопоставимых по яркости с рассматриваемой точкой.

В связи с этим большинство известных способов выделения контуров на цифровых полутоновых изображениях основаны на вычислении модуля градиента на всей площади цифрового изображения по приближениям первой производной - локальным конечным разностям яркости. При этом приближенные компоненты градиента вычисляют с использованием скользящего окна (маски), перемещающегося по всему изображению. При этом яркости пикселей изображения, попадающих в скользящее окно, перемножают на коэффициенты маски, а затем суммируют [1 – Гонсалес Р., Вудс Р. Цифровая обработка изображений. -М.: Техносфера, 2005, 1072с.; 2 - Гонсалес Р., Вудс Р., Эддинс С. Цифровая обработка изображений в среде MATLAB.-М.: Техносфера,2006, 616с.; 3 – Прэтт У. Цифровая обработка изображений: Пер.с англ. - М.: Мир, 1982. Кн.2. 480с.; 4 - Гданский Н.И., Марченко Ю.А. Градиентный способ выделения контуров объектов на матрице полутонового растрового изображения. // Патент РФ №2325044 на изобретение. МПК H04N1/409, G06K9/46. Заявит. Гданский Н.И., Марченко Ю.А. Патентообл. МГУИЭ. - № 2007106412/09; заявл. 21.02.2007; опубл. 20.05.2008.].

В настоящее время известно несколько типов масок: Робертса, Превитта, Собеля, Щарра и др. Маска Робертса является наиболее простой, поскольку имеет размер 2х2 пикселя. Маски Превитта, Собеля и Щарра имеют размерность 3х3 пикселя и отличаются значениями коэффициентов. Следует отметить, что подобные маски вычисления компонент градиента яркости при помощи конечных разностей используются в составе более сложных алгоритмов выделения контуров. Одним из лучших подобных алгоритмов является детектор границ «Canny», использующий, в частности, маску Собеля. Недостатками способов выделения контуров изображений на основе применения скользящих окон и определения компонент градиента яркости при помощи конечных разностей является их достаточно сильная чувствительность к помехам, относящимся к классу импульсных, возникающих вследствие многих явлений при цифровом преобразовании и передаче изображений (пораженные пиксели).

К другим способам выделения контуров объектов на изображениях относятся способы, основанные на вычислении приближений вторых производных – операторы типа «лапласиан» «гауссиан», или операторы, использующие разновидности масок Лапласа. Известна также корреляционная маска, коэффициенты которой пропорциональны соответствующим коэффициентам корреляции элементов изображения. В случае, когда корреляция между элементами изображения отсутствует, маска не оказывает влияния на изображение, в противоположном случае коэффициент корреляции равен единице, данная маска сводится к маске Лапласа [Прэтт У.Цифровая обработка изображений: Пер. с англ. - М.: Мир, 1982. Кн.2, 480с., C.500-508.]. Данные способы благодаря пересечению нулевого уровня прямой, соединяющей разнозначные вторые производные, позволяют получить более точное положение контура, но являются более чувствительными к различным помехам, в том числе и импульсным, чем градиентные, а также имеют недостаток, связанный с обнаружением многочисленных ложных замкнутых кривых.

Также известны способы выделения контуров объектов на изображениях, более далекие от заявляемого способа, которые основаны на аппроксимации перепадов яркости и статистические способы, например, способ на основе локально-полиномиальной аппроксимации [5 - Sherstobitov A. I., Marchuk V. I., Timofeev D. V., Voronin V. V., Egiazarian K. O.  Local feature descriptor based on 2D local polynomial approximation kernel indices. Image Processing: Algorithms and Systems XII, edited by Karen O. Egiazarian, Sos S. Agaian, Atanas P. Gotchev, Proceedings of SPIE Vol. 9019 (SPIE, San Francisco, WA 2014) 901908, DOI: 10.1117/12.2041610.]. Однако недостатком способов, основанных на аппроксимации перепадов яркости, является чувствительность к наличию на матрице цифрового изображения импульсных помех.

Следует отметить, что повышение устойчивости известных способов выделения контуров изображения возможно за счет предварительной коррекции изображения, связанной со сглаживанием яркости изображения. Однако такой подход может привести не только к устранению импульсных помех, но и к потере части полезной информации о контуре изображения.

Наиболее близким по технической сущности к заявляемому способу является способ помехоустойчивого градиентного выделения контуров объектов на цифровых полутоновых изображениях [6 - Безуглов Д.А., Мищенко С.Е., Кузин А.П. Способ помехоустойчивого градиентного выделения контуров объектов на цифровых полутоновых изображениях //Патент РФ № 2648954, МПК G06K 9/48. Заявит. и патентообл. Ростовский филиал РТА - № 2016104498/08; заявл. 10.02.2016; опубл. 15.08.2017 Бюл. № 23], взятый за прототип, заключающийся в том, что сначала вычисляют прямое вейвлет-преобразование строк и столбцов цифрового полутонового изображения, а затем формируют две матрицы 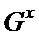и компонент градиента яркости в каждой точке изображения путем обратного вейвлет преобразования, в котором в качестве ядра преобразования используют аналитические функции, описывающие производные используемых вейвлетов обратного преобразования по соответствующим координатам. После этого определяют модуль градиента яркости в каждой точке изображения, и формируют контуры объекта путем порогового преобразования модуля градиента яркости, в процессе которого на новой белой матрице черным цветом выделяют элементы, модуль градиента, для которых в соответствующих координатах изображения превышает порог преобразования.

Недостатком способа-прототипа является то, что вычисление прямого вейвлет-преобразования строк и столбцов цифрового полутонового изображения требует больших вычислительных затрат. Кроме того, данный способ демонстрирует слабую устойчивость к воздействию импульсных помех.

Задачей, на решение которой направлено изобретение, является создание средств выделения контуров полутоновых изображений в условиях импульсных помех, удовлетворяющих требованиям к высокой скорости обработки изображений.

Техническим результатом является повышение скорости выделения контуров полутоновых изображений в условиях импульсных помех.

Для решения указанной технической проблемы предлагается способ помехоустойчивого градиентного выделения контуров объектов на цифровых полутоновых изображениях, который состоит в том, что сначала с учетом уровня зашумленности выбирают коэффициент сглаживания, вычисляют коэффициенты сглаживающих кубических B-сплайнов вдоль каждой строки и каждого столбца изображения. Затем формируют две матрицы 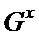и компонент градиента яркости в каждой точке изображения путем суммирования сглаживающих параболических B-сплайнов с найденными ранее коэффициентами сглаживающих кубических B-сплайнов для строк и столбцов соответственно. Далее определяют модуль градиента яркости в каждой точке изображения. После этого формируют контуры объекта путем порогового преобразования модуля градиента яркости, в процессе которого на новой белой матрице черным цветом выделяют элементы, модуль градиента для которых в соответствующих координатах изображения превышает порог преобразования.

Таким образом, предлагаемый способ имеет следующие отличительные признаки и последовательность его реализации от способа-прототипа, которые приведены в таблице 1.

Таблица 1

Способ-прототип Предлагаемый способ 1. С учетом уровня зашумленности изображения выбирают коэффициент сглаживания 2. Вычисляют коэффициенты сглаживающих кубических B-сплайнов вдоль каждой строки и каждого столбца изображения 1. Вычисляют прямое вейвлет-преобразование строк и столбцов цифрового полутонового изображения 2. Формируют две матрицы и компонент градиента яркости в каждой точке изображения
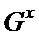
2.1 путем обратного вейвлет-преобразования, в котором в качестве ядра преобразования используют аналитические функции, описывающие производные используемых вейвлетов обратного преобразования по соответствующим координатам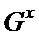 3. Формируют две матрицы и компонент градиента яркости в каждой точке изображения путем
3.1 суммирования сглаживающих параболических B-сплайнов с найденными ранее коэффициентами сглаживающих кубических B-сплайнов для строк и столбцов соответственно 3. Определяют модуль градиента яркости в каждой точке изображения 4. Определяют модуль градиента яркости в каждой точке изображения 4. Формируют контуры объекта путем порогового преобразования модуля градиента яркости, в процессе которого на новой белой матрице черным цветом выделяют элементы, модуль градиента для которых в соответствующих координатах изображения превышает порог преобразования 5. Формируют контуры объекта путем порогового преобразования модуля градиента яркости, в процессе которого на новой белой матрице черным цветом выделяют элементы, модуль градиента для которых в соответствующих координатах изображения превышает порог преобразования

Из представленной таблицы 1 сравнения последовательностей реализации способа-прототипа и предлагаемого способа видно, что в предлагаемом способе введены операции:

− с учетом уровня зашумленности изображения выбирают коэффициент сглаживания;

− вычисляют коэффициенты сглаживающих кубических B-сплайнов вдоль каждой строки и каждого столбца изображения.

А также изменен режим выполнения одной операции:

− две матрицы 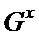и компонент градиента яркости в каждой точке изображения формируют путем суммирования сглаживающих параболических B-сплайнов с найденными ранее коэффициентами сглаживающих кубических B-сплайнов для строк и столбцов соответственно.

Введение двух операций и изменение режима одной операции позволяет обеспечить достижение технического результата, а именно, повышение скорости формирования контуров полутоновых изображений в условиях импульсных помех.

Предлагаемое изобретение не известно из анализа уровня техники, а также не известны источники информации, содержащие сведения об аналогичных технических решениях, имеющих признаки, сходные с признаками, отличающими заявляемое решение от прототипа, а также свойства, совпадающие со свойствами заявляемого решения, поэтому можно считать, что оно обладает существенными отличиями, вытекает из них неочевидным образом и, следовательно, соответствует критериям «новизна» и «изобретательский уровень».

Сущность предлагаемого способа раскрывается фигурами 1-5.

На Фиг. 1 приведена структурная схема устройства, реализующего предлагаемый способ помехоустойчивого градиентного выделения контуров объектов на цифровых полутоновых изображениях.

На Фиг. 2 показано исходное цифровое полутоновое изображение (фиг. 2а) и результат выделения контуров данного изображения при отсутствии шумов (фиг. 2б).

На Фиг. 3 показаны тестовые цифровые полутоновые изображения с наложенным на них импульсным шумом (на фиг. 3а на исходное изображение наложен импульсный шум «битые пиксели» с вероятностью 0,5, на фиг. 3б − «соль-перец» также с вероятностью 0,5).

На Фиг. 4 приведены изображения, иллюстрирующие результаты выделения контуров на зашумленных изображениях при помощи маски Собеля (результаты на фиг. 4а соответствуют импульсному шуму «битые пиксели» с вероятностью 0,5, а на рис. 4б − «соль-перец» с вероятностью 0,5).

На Фиг. 5 отображены результаты выделения контуров предлагаемым способом (результаты на фиг. 5а соответствуют импульсному шуму «битые пиксели» с вероятностью 0,5, а на рис. 5б − «соль-перец» с вероятностью 0,5).

При реализации данного способа выполняется следующая последовательность операций:

- с учетом уровня зашумленности изображения выбирают коэффициент сглаживания − 1;

- вычисляют коэффициенты сглаживающих кубических B-сплайнов вдоль каждой строки и каждого столбца изображения – 2;

- формируют две матрицы 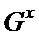и компонент градиента яркости в каждой точке изображения путем суммирования сглаживающих параболических B-сплайнов с найденными ранее коэффициентами сглаживающих кубических B-сплайнов для строк и столбцов соответственно − 3;

- определяют модуль градиента яркости в каждой точке изображения − 4;

- формируют контуры объекта путем порогового преобразования модуля градиента яркости, в процессе которого на новой белой матрице черным цветом выделяют элементы, модуль градиента для которых в соответствующих координатах изображения превышает порог преобразования − 5.

Прежде чем рассмотреть работу устройства выделения контуров для обоснования способа изложим следующее.

Пусть задана матрица изображения размером . Тогда строке изображения может быть поставлена в соответствие некоторая функция . В области входные данные можно представить в виде совокупности равноотстоящих отсчетов координат с шагом , заданных так, что

; (1)

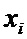
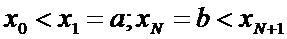
и соответствующих им значений яркости изображения .

Представим входной сигнал в виде сплайн-аппроксимации в базисе сглаживающих кубических нормализованных В-сплайнов дефекта 1 [7 Завьялов Ю.С., Квасов Б.И., Мирошниченко B.JI. Методы сплайн-функций. -М.: Наука, 1980. 350 с.]

(2)

где − коэффициент -го сплайна;

(3)

(4)

− координаты середины носителя -сплайна;

− степень сплайна.

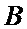
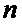
Рассмотрим теперь участок и осуществим привязку коэффициентов сплайна к середине соответствующего носителя. Тогда для этого участка, с учетом (4), выражение (5) примет вид [7]:

(5)

Введем нормализованную координату , тогда выражение (5) можно представить в виде:

(6)

После несложных арифметических преобразований получим аналитическое выражение для сплайна на участке в виде:

(7)

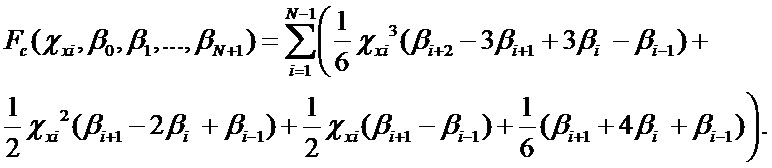
Коэффициенты сплайна найдем из решения задачи минимизации функционала [8 Лапчик М.П. Численные методы .-М: Академия, 2008, 381с.]:

(8)

где − коэффициент сглаживания;

− значение сплайна в точке ;

− модуль второй производной сплайна.

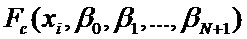
Коэффициент сглаживания выбирают равным величине среднеквадратического отклонения шума на изображении. В случае, если статистические характеристики шума неизвестны, то эффект сглаживания шумов наблюдается при .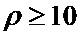

С учетом представления сплайна в виде (7) функционал (8) можно представить в виде

(9)

С учетом (7) представляет собой линейную функцию от :

(10)

В узловых точках , откуда

(11)

(12)

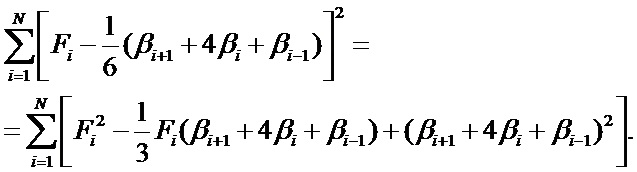
Для формирования результирующей системы уравнений относительно неизвестных коэффициентов продифференцируем (9) по каждому элементу вектора и приравняем к нулю полученное выражение. Например, первое уравнение можно записать в виде

(13)

После дифференцирования по каждому из коэффициентов получим систему уравнений вида

, (14)

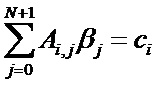
где − квадратная семидиагональная матрица ранга ;

− вектор правых частей, который строится на основе входного массива .

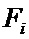
В работе [9 Безуглов Д.А., Крутов В.А., Швачко О.В. Метод дифференцирования сигналов с использованием сплайн-аппроксимации // Фундаментальные исследования, 2017, № 4-1, С.24-28] ненулевые элементы матрицы были получены в виде:

(15)

(16)

(17)

, (18)

а вектор был записан в виде:

. (19)

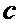
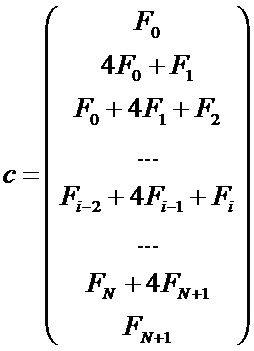
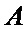
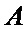
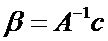
Анализ системы уравнений позволяет заключить, что матрица всегда хорошо обусловлена, что обеспечивает существование единственного решения системы уравнений. При этом матрица зависит только от коэффициента сглаживания. Это позволяет найти обратную матрицу и использовать ее для расчета искомых коэффициентов всех строк и столбцов изображения по формуле

. (20)

Система уравнений вида (14) может быть решена для каждой строки и столбца изображения. В результате получим матрицы и , которые в каждой строке хранят массивы коэффициентов сглаживающих кубических -сплайнов, аппроксимирующих распределения яркости вдоль строк и столбцов входного изображения соответственно. Например, матрица в строке с номером содержит вектор коэффициентов сплайна , найденных в результате решения системы уравнений (14) по распределению яркости вдоль соответствующей строки матрицы , а матрица в строке с номером содержит вектор коэффициентов сплайна , найденных по данным соответствующего столбца матрицы .

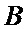
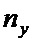
С учетом выражения (7) сплайн, описывающий производную одномерной функции 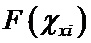, может быть записан в виде:

(21)

Данный сплайн называют сглаживающим параболическим -сплайном.

Отсюда следует, что компоненты градиента яркости входного изображения могут быть найдены по формулам:

(22)

(23)

Как и в прототипе, модуль градиента яркости найдем по формуле

. (24)

При этом пороговое преобразование описывается соотношением:

(25)

Здесь − значение порога.

В качестве примера рассмотрим задачу выделения контуров на цифровом полутоновом изображении в условиях импульсных шумов. Следует отметить, что способ-прототип обеспечивает эффективное подавление шумов, распределенных по нормальному закону, и не предназначен для выделения контуров на зашумленном изображении. В связи с этим работоспособность предлагаемого способа выделения контуров производилась в сравнении с получившим практическое распространение методом выделения контуров, основанном на применении маски Собеля (детектор границ «Canny»). Сравнение предлагаемого способа и способа-прототипа произведем по быстродействию.

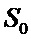
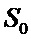
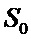
Для формирования тестовых изображений использовался следующий алгоритм. Матрица яркости исходного полутонового изображения, в котором отсутствовали шумы, обрабатывалась детектором границ «Canny». В результате было получено изображение контуров , соответствующее матрице яркости при отсутствии шумов. Изображения, соответствующие матрицам и приведены на фиг.2 (фиг. 2а и 2б соответственно).

Далее в исходное цифровое полутоновое изображение был добавлен шум (матрица ). В качестве модели шума использовался импульсный шум «битые пиксели» и «соль-перец» с вероятностью . В результате были получены изображения, которым соответствуют матрицы яркости , представленные на фиг. 3 (фиг. 3а и 3б соответственно).

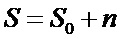
На фиг. 4 приведены матрицы 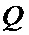контуров, по результатам обработки оператором Собеля зашумленных изображений, представленных на фиг. 3 (фиг. 4а отражает результаты выделения контуров изображения на фиг. 3а, а фиг. 4б − фиг. 3б).

Анализ полученных изображений позволяет заключить, что оператор Собеля неработоспособен для выделения контуров на изображениях, полученных в условиях импульсных шумов.

На фиг. 5 приведены изображения матриц контуров, полученные при помощи предлагаемого способа с использованием сплайн дифференцирования. Изображение на фиг.5а соответствует модели шумов «битые пиксели», а на фиг. 5б − «соль-перец». Приведенные на фиг. 5 изображения подтверждают работоспособность предлагаемого способа выделения контуров при наличии импульсных шумов.

С целью количественной оценки эффективности предлагаемого способа по сравнению с прототипом использовалось три показателя.

Первый состоял в том, что определялась величина среднеквадратического отклонения (СКО) между изображениями контуров , полученными предлагаемым способом, а также способом прототипа и изображением контура , полученным при отсутствии шумов.

Оценка СКО осуществлялась по формуле:

. (26)

Второй показатель представляет собой оценку отношения сигнал/шум (ОСШ), рассчитываемую по формулам:

, (27)

, (28)

где − максимальное значение яркости в полутоновых изображениях, которое обычно равно 255.

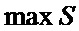
Значения третьего показателя для оценки эффективности предлагаемого способа для подавления импульсных помех получают при помощи соотношения

; (29)

где - СКО фона;

(30)

− среднее значение фона; n1, m1- координаты выбранной площадки фона размером на исследуемом изображении ,

. (31)

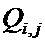
Результаты данного сопоставления применительно к модели импульсного шума типа «битые пиксели» при различных вероятностях шума и значениях коэффициента сглаживания приведены в таблице 2. Аналогичные результаты, относящиеся к импульсному шуму «соль-перец», представлены в таблице 3.

Таблица 2

Показатель 1, выигрыш по среднеквадратическому отклонению еско , дБ Вероятность шума Коэффициент сглаживания сплайн-функций 5 10 50 100 0,3 1,8 2,01 2,22 2,23 0,5 2,03 2,31 2,6 2,64 0,7 2,13 2,42 2,75 2,79 Показатель 2, выигрыш по отношению пиковый сигнал/шум SNR, дБ Вероятность шума Коэффициент сглаживания сплайн-функций 5 10 50 100 0,3 3,47 4,09 5,22 5,48 0,5 3,76 4,57 5,87 6,32 0,7 3,97 4,85 6,45 6,87 Показатель 3, выигрыш по отношению пиковый сигнал/шум по СКО фона SNRF, дБ Вероятность шума Коэффициент сглаживания сплайн-функций 5 10 50 100 0,3 5,23 6,08 8,11 8,9 0,5 5,41 6,34 8,15 8,94 0,7 5,63 6,65 8,73 9,4

Таблица 3

Показатель 1, выигрыш по среднеквадратическому отклонению еско , дБ Вероятность шума Коэффициент сглаживания сплайн-функций 5 10 50 100 0,2 2,15 2,28 2,33 2,33 0,3 2,51 2,69 2,83 2,81 0,5 2,95 3,23 3,5 3,53 0,7 3,22 3,55 3,92 3,96 Показатель 2, выигрыш по отношению пиковый сигнал/шум SNR, дБ Вероятность шума Коэффициент сглаживания сплайн-функций 5 10 50 100 0,2 4,86 5,43 5,94 6,06 0,3 5,13 5,77 6,57 6,56 0,5 5,4 6,15 7,16 7,44 0,7 5,65 6,46 7,78 8,07 Показатель 3, выигрыш по отношению пиковый сигнал/шум по СКО фона SNRF, дБ Вероятность шума Коэффициент сглаживания сплайн-функций 5 10 50 100 0,2 6,05 6,93 8,7 9,59 0,3 6,17 7,08 9 9,69 0,5 6,07 7,05 8,99 9,79 0,7 6,12 7,14 9,32 10,12

Оценим выигрыш предлагаемого способа по сравнению со способом-прототипом по быстродействию.

Пусть распределение яркости изображения задает квадратная матрица 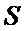размером MЧM.

При этом прямое дискретное вейвлет-преобразование для строк и столбцов в способе-прототипе осуществляется по формулам

, (32)

(33)

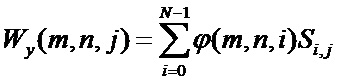
соответственно.

Здесь − вейвлет.

В этом случае объем вычислительных затрат 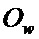при реализации прямого вейвлет-преобразования будет равен:

. (34)

В выражении (34) учтено, что .

Если выбранному виду вейвлета соответствует его производная, то обратное преобразование, позволяющее получить компоненты градиента яркости исходного изображения, можно найти по формулам

(35)

(36)

где − коэффициент нормировки для обратного вейвлет-преобразования (для приведенных соотношений данный коэффициент равен единице).

Обратное преобразование потребует также операций. С учетом того, что модуль градиента яркости изображения будем определять по формуле (19) итоговое количество операций для выделения контуров будет составлять

. (37)

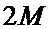
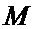
Для реализации предлагаемого способа выделения контуров с использованием сплайн-аппроксимации необходимо раз решить систему линейных уравнений размерностью вида (14). Для обращения матрицы такой системы уравнений потребуется порядка операций. Так как коэффициенты матрицы совпадают для всех строк и столбцов, то матрицу необходимо обратить один раз. Так как матрицу можно обратить заранее, для всех вычислений используется одна матрица, изменяется только правая часть системы уравнений (14). Для вычисления контура необходимо еще операций. В результате общее число операций при реализации предлагаемого способа составит

. (38)

Отсюда следует, что выигрыш в вычислительной эффективности, равный отношению числа операций в способе-прототипе и предлагаемом способе будет равен:

(39)

Как правило, . В этом случае

. (40)

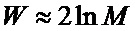
Например, при выигрыш составит раз.

Таким образом, известные авторам способы выделения контуров на полутоновых изображениях неэффективны в условиях импульсных помех, а способ-прототип, обеспечивающий решение задачи выделение контуров на зашумленных изображениях, способен бороться с гауссовым шумом и обладает низким быстродействием. Напротив, предлагаемый способ является устойчивым к воздействию импульсных помех и позволяет увеличить скорость выделения контуров полутоновых изображений.

Рассмотрим функционирование устройства выделения контуров, реализующее способ.

В состав устройства выделения контуров (фиг. 1) входят блоки определения коэффициентов сплайнов исходного изображения (БОКС) 1 и 2, блоки вычисления матриц и и компонент градиента яркости изображения (БВКГ) 3 и 4, блок определения модуля градиента яркости изображения (БОМГ) 5, блок порогового преобразования (БПП) 6.

Общим входом устройства являются входы БОКС 1 и БОКС 2, выход БОКС 1 подключен ко входу БВКГ 3, выход которого соединен с первым входом БОМГ 5, выход БОКС 2 соединен со входом БВКГ 4, выход которого подключен ко второму входу БОМГ 5, выход БОМГ 5 соединен со входом БПП 6, выход которого является выходом устройства.

Устройство работает следующим образом.

На входы БОКС 1 и БОКС 2 поступает двумерное распределение яркости сигнала, задаваемое матрицей яркости цифрового полутонового изображения. В БОКС 1 осуществляют вычисление коэффициентов сплайнов из решения систем линейных уравнений вида (14) по формуле (15) для каждой строки входной матрицы . Полученные коэффициенты сплайнов с выхода БОКС 1 поступают на вход БВКГ 3, в котором преобразование сигналов осуществляют по формуле (21). На выходе БВКГ 3 формируют двумерную матрицу , элементы которой содержат значения производных яркости в каждой точке изображения вдоль строки. Данные сигналы поступают на первый вход БОМГ 5.

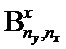
В БОКС 2 осуществляют вычисление коэффициентов сплайнов из решения систем линейных уравнений вида (14) по формуле (20) для каждого столбца матрицы . Полученные коэффициенты сплайнов с выхода БОКС 2 поступают на вход БВКГ 4, в котором преобразование сигналов осуществляют по формуле (21). На выходе БВКГ 4 формируют двумерную матрицу , элементы которой содержат значения производных яркости в каждой точке изображения вдоль строки. Данные сигналы поступают на второй вход БОМГ 5. В БОМГ 5 осуществляют процедуру расчета модуля градиента яркости по формуле (24). В результате получают двумерную матрицу , описывающую распределение модуля градиента яркости входной матрицы , соответствующее каждому ее элементу. Матрица поступает на вход БПП 6, в котором осуществляют формирование двумерной матрицы контуров по формуле (20). Полученная матрица поступает на выход устройства, где может быть визуализирована или сохранена в памяти ЭВМ.

В качестве блоков 1-6 рассмотренного устройства обработки изображений могут быть использованы описанные в [10 − АйфичерЭ.С., Джервис Б.У. Цифровая обработка сигналов: практический подход. 2-е издание. - М.: Вильямс, 2004. 992 с.; 11 − Куприянов М.С., Матюшкин Б.Л. Техническое обеспечение цифровой обработки сигналов. Справочник. - М.: Наука и техника, 2000. 752 с.], а также любые аналогичные известные из уровня техники технические устройства (программируемые и непрограммируемые процессоры цифровой обработки сигналов и изображений), реализующие соответствующие математические функции (15)-(20).

В БОКС 1 и БОКС 2 осуществляется операция умножения матрицы на вектор. Эта операция аналогична сверточной фильтрации, которая широко применяется в устройствах цифровой обработки сигналов [10], [11].

В БВКГ 3 и БВКГ 4 для расчета компонентов градиента выполняются операции умножения матрицы на матрицу, которая также распространена в устройствах цифровой обработки сигналов [10],[11].

БОМГ 5 и БПП 6 могут быть реализованы аналогично способу прототипу в соответствии с описанием в источниках [10], [11].

Приведенные выше материалы подтверждают соответствие критерию “промышленная применимость” предложенного способа.

Это означает, что техническим результатом изобретения является повышение скорости выделения контуров полутоновых изображений в условиях импульсных помех.

Изобретение относится к обработке изображений и может быть использовано в фото, видео, оптико-локационной и оптико-электронной технике при решении задач распознавания образов по их контурам на изображениях. Техническим результатом изобретения является повышение скорости выделения контуров полутоновых изображений в условиях импульсных помех. Суть способа заключается в том, что учетом уровня зашумленности изображения выбирают коэффициент сглаживания, вычисляют коэффициенты сглаживающих кубических B-сплайнов вдоль каждой строки и каждого столбца изображения. Затем формируют две матрицы 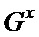и 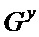компонент градиента яркости в каждой точке изображения путем суммирования сглаживающих параболических B-сплайнов с найденными ранее коэффициентами сглаживающих кубических B-сплайнов для строк и столбцов. Далее определяют модуль градиента яркости в каждой точке изображения. После этого формируют контуры объекта путем преобразования модуля градиента яркости, в процессе которого на новой белой матрице черным цветом выделяют элементы, модуль градиента для которых в координатах изображения превышает порог преобразования. 3 табл., 5 ил.

Способ помехоустойчивого градиентного выделения контуров объектов на цифровых полутоновых изображениях, при котором формируют две матрицы и компонент градиента яркости в каждой точке изображения, определяют модуль градиента яркости в каждой точке изображения, формируют контуры объекта путем порогового преобразования модуля градиента яркости, в процессе которого на новой белой матрице черным цветом выделяют элементы, модуль градиента для которых в соответствующих координатах изображения превышает порог преобразования, отличающийся тем, что перед формированием матриц и компонент градиента яркости с учетом уровня зашумленности изображения выбирают коэффициент сглаживания и вычисляют коэффициенты сглаживающих кубических B-сплайнов вдоль каждой строки и каждого столбца изображения, а две матрицы и компонент градиента яркости в каждой точке изображения формируют путем суммирования сглаживающих параболических B-сплайнов с найденными ранее коэффициентами сглаживающих кубических B-сплайнов для строк и столбцов соответственно.