Область применения
Изобретение относится к области реализации моделей нейронных сетей на базе связанных осцилляторов, в том числе на базе оксидных структур с эффектом электрического переключения, представляющих собой импульсные осцилляторные нейронные сети, которые могут использоваться для распознавания образов.
Уровень техники
Искусственные нейронные сети [1] активно применяются в задачах распознавания изображений и речи [2], где использование традиционных вычислительных систем сопряжено рядом трудностей. Для успешного решения подобных задач необходимо изучение режимов функционирования и обучения осцилляторных нейронных сетей (ОНС), например, на основе слабо связанных фазовых осцилляторов (модель Курамото) [3], а также импульсных осцилляторов [4]. Одним из ключевых аспектов в функционировании ОНС является эффект синхронизации, который зачастую используется как маркер произведенного действия ОНС, например, акта распознавания вектор-образа. В ОНС при определенной величине управляющих параметров, которыми могут быть как параметры схемы осциллятора, так и силы связи между ними, система демонстрирует частотную и фазовую синхронизацию [5]-[8], а также синхронизацию высокого порядка [9]—[11], на базе которой и основывается предлагаемый в настоящем патенте способ запоминания и распознавания вектор-образов.
Существует способ запоминания информации, основанный на разности фаз между сигналами связанных осцилляторов, представленный в патенте [12]. Для реализации данного способа кодирования применяется полносвязный массив из N осцилляторов имеющий И2 связей, а также устройства фазовой автоподстройки частоты. Вход каждого осциллятора связан со всеми выходами N осцилляторов с помощью соединений с
настраиваемыми весами, через суммирующие устройства и полосовые фильтры. В такой схеме частоты осцилляторов одинаковы, но при этом варьируют разности фаз, величины которых могут принимать определенные устойчивые значения, что применяется для решения задач распознавания вектор-образов. Определенная комбинация разностей фаз задается с помощью матрицы (вектора) весов по правилу Хэбба и является записанным образом. Такой способ кодирования позволяет запоминать более одного образа, а их максимальное количество будет определяться размером сети (количеством осцилляторов). Тестовый образ в такой системе задается вектором начальной разности фаз между осцилляторами, а процесс распознавания заключается во временном переходе системы от начальной разности фаз к одной из устойчивых комбинаций разностей фаз, которая будет наиболее близка к тестовой. Для задания начальной разности фаз используется правило Хэбба, а процесс распознавания является двухстадиным: на первой стадии веса в системе устанавливаются таким образом, чтобы получить начальную, соответствующую тестовому образу, разность фаз, а на второй стадии веса переключаются на таковые, которые соответствуют запомненным образам. По времени перехода из начального состояния к устойчивому определяют степень соответствия тестового и запомненного образов.
Недостатком данного способа является наличие К2 связей с настраиваемыми весами, а также наличие двухстадийной процедуры распознавания образов.
Известен способ запоминания информации с помощью амплитуд гармоник сложного квазипериодического сигнала, подаваемого на массив осцилляторов, представленный в патенте [13]. Данный способ предполагает наличие N осцилляторов, соединённых по топологии общая шина, каждый из которых должен иметь различные частоты. В невозмущенном состоянии такая система не является синхронизованной. Однако, если в систему подается квазипериодический сигнал, содержащий в своем спектре гармоники, соответствующие разности частот между каждым из осцилляторов, то такая система может синхронизоваться и будет эквивалентна полносвязной сети с фазовым кодированием [12].
В этом случае амплитуды гармоник внешнего сигнала, соответствующих разностным частотам, будут являться весовыми коэффициентами связи и определяют возможные устойчивые состояния системы с определёнными векторами разностей фаз осцилляторов, соответствующие записываемым образам. Тестовый образ по аналогии с [12] будет также задаваться вектором разностей фаз, а схема распознавания будет двухстадийной: вначале на массив осцилляторов должен воздействовать внешний квазипериодический сигнал, соответствующий тестовому образу, а после установления тестовой разности фаз, он должен измениться, чтобы соответствовать целевым запомненным образам.
Недостатком данного способа является необходимость генерации сложного квазипериодического сигнала, а также наличие двухстадийной процедуры распознавания образов.
Наиболее близким к заявляемому способом, который принят за прототип, является способ кодирования для ассоциативной памяти, представленный в патенте [14], основанный на смещении частот. Для реализации способа используется массив связанных осцилляторов, управляемых напряжением или током в соответствии с некоторым шаблоном, который задает смещение частот осцилляторов относительно центральной частоты синхронизации массива осцилляторов (подразумевается синхронизация всех осцилляторов на частоте первой гармоники). В начальном состоянии частоты связанных осцилляторов не различаются или различаются слабо, что приводит к их синхронизации на частоте первой гармоники. Запоминаемый информационный образ кодируется с помощью векторов изменения напряжений или токов питания осцилляторов, что приводит к рассинхронизации связанных осцилляторов и смещению частот каждого отдельного осциллятора от центральной частоты. Тестовый образ задается вектором изменений токов или напряжений для обратного смещения частот осцилляторов. При совпадении тестового и запомненного образа (или при их незначительном отличии) происходит возврат частот осцилляторов к центральной частоте и их синхронизация на частоте первой гармоники, в то время как, различие тестового и запомненного образа исключает синхронизацию на первой гармонике. Данный способ позволяет использовать схему соединения осцилляторов звездой, с общей шиной, и задействует N связей для N осцилляторов.
Основным недостатком данного способа является то, что данный способ позволяет запоминать для последующего распознавания только один образ, кодируемый через вектор смещений частот связанных осцилляторов, относительно момента их синхронизации на первой гармонике.
Технический результат предлагаемого изобретения состоит в том, что массив связанных осцилляторов позволяет запоминать и распознавать множество образов, а их требуемое количество (емкость запоминания) можно выбирать в зависимости от количества осцилляторов К, диапазона управляющих параметров, топологии сети, силы связи между осцилляторами и интенсивности шума в системе связанных осцилляторов.
Достигается технический результат за счет того, что на этапе запоминания в рабочем сигнале выделяют гармоники высокого порядка к1:к2:..кN и используют эффект синхронизации на этих гармониках при котором в осцилляторной нейронной сети возникают NS синхронных состояний, соответствующих различным наборам гармоник к1:к2:к3:…кN, при этом с помощью питающих токов (I1, I2…IN) или напряжений (U1, U2…UN) осцилляторов осцилляторную нейронную сеть устанавливают в несинхронное состояние S, при котором векторы смещения питающих токов (ΔI1, ΔI2…ΔIN) или напряжений (ΔU1, ΔU2…ΔUN) относительно NS синхронных состояний соответствуют NS запомненным образам, затем на этапе распознавания изменяют питающие токи или напряжения осцилляторов на векторную величину соответствующую тестируемому образу, и при возникновении синхронизации в осцилляторной нейронной сети устанавливают совпадение с одним из NS запомненных образов.
Перечень фигур
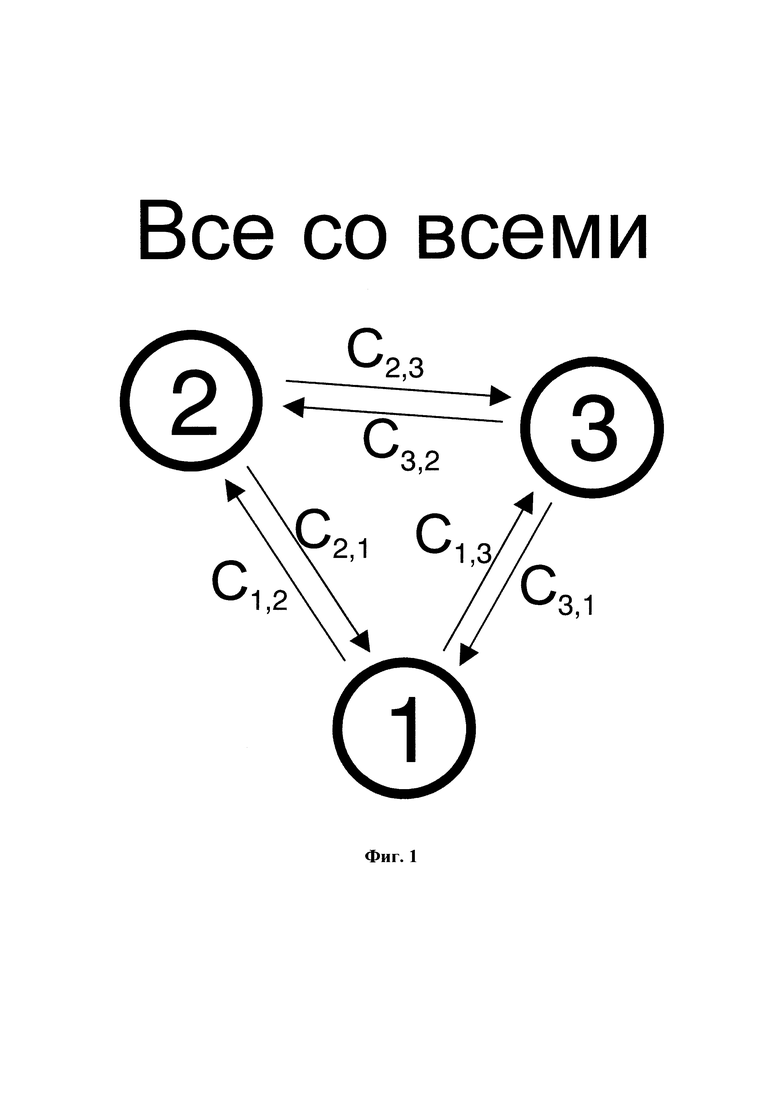
Фиг. 1 Пример соединения трех осцилляторов по топологии "все со всеми", Ci,j - сила связи между i-м и j-м осцилляторами
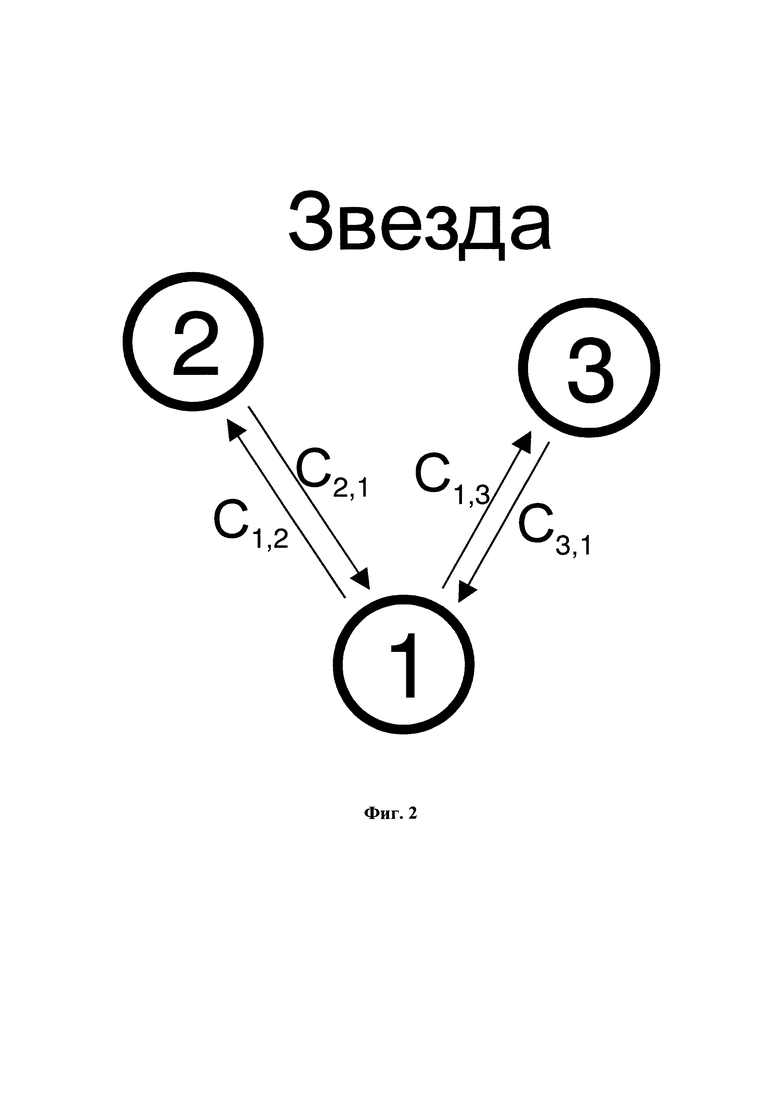
Фиг. 2 Пример соединения трех осцилляторов по топологии "звезда", Ci,j - сила связи между i-м и j-м осцилляторами
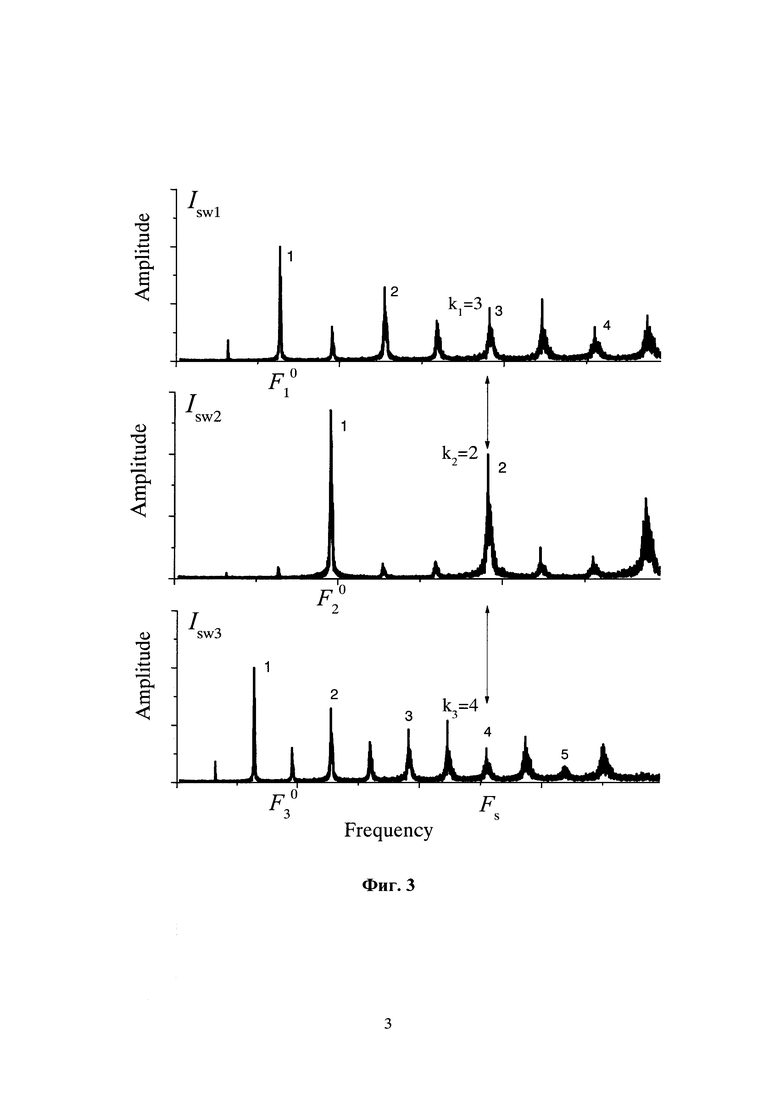
Фиг. 3 Пример спектров осцилляций при синхронизации порядка к1:к2:к3=3:2:4, где кi -номера гармоник на основной частоте синхронизации Fs, Ci,j - сила связи между i-м и j-м осцилляторами, Isw - спектральная амплитуда тока в осцилляторе, F0- частота первой гармоники.
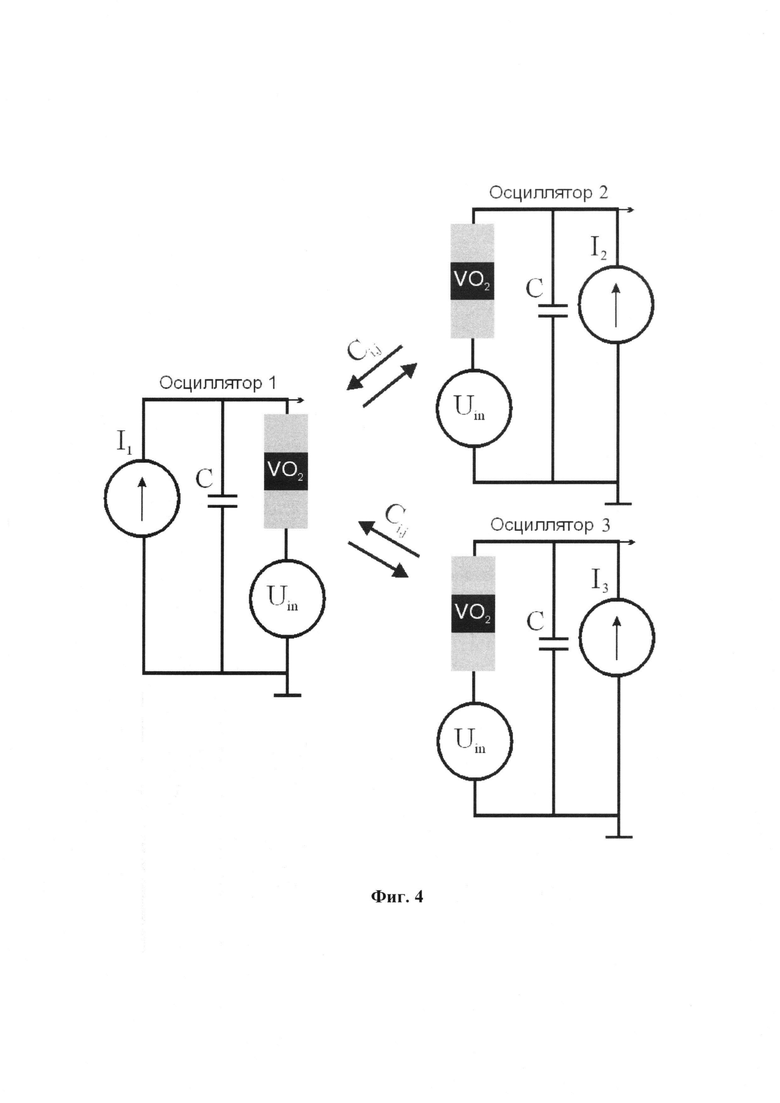
Фиг. 4 Пример исполнения нейронной сети на базе трех осциляторных контуров с переключателем на основе диоксида ванадия (VO2), соединенных термической связью по типу "звезда", Ci,j - сила связи между i-ым и j-ым осцилляторами, Ii - генератор питающего тока i-того осциллятора, Uin -генератор шума в осцилляторном контуре, С - величина емкости в осцилляторном контуре.
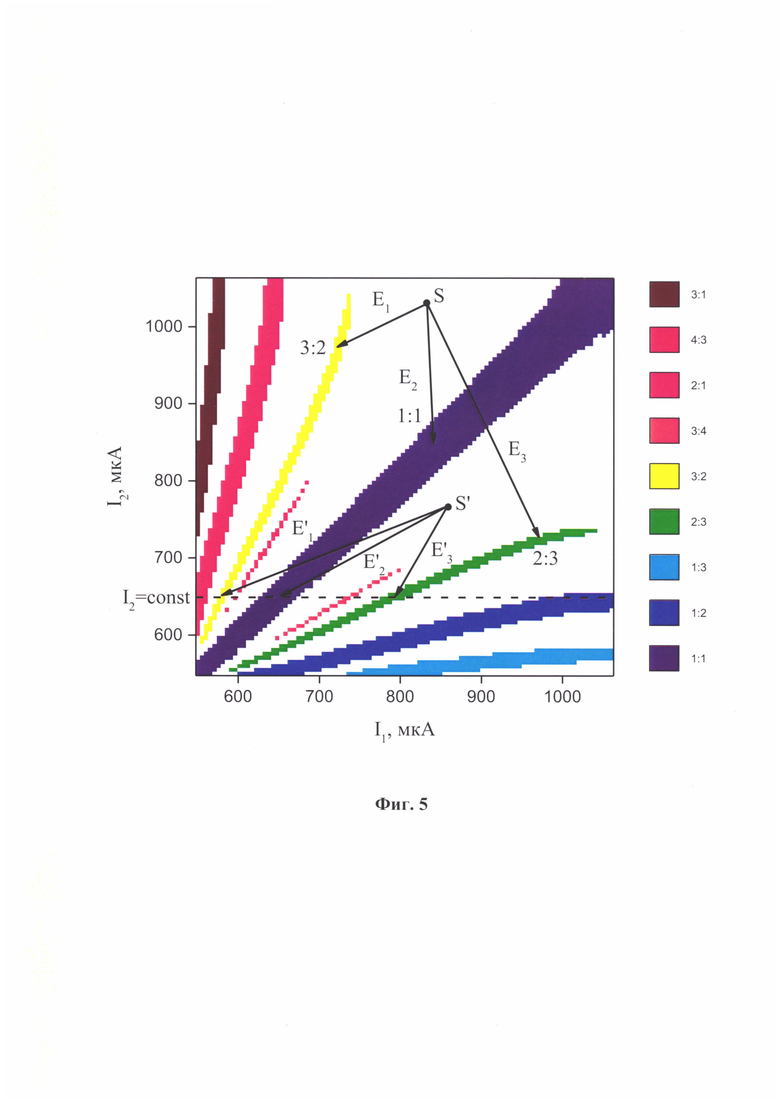
Фиг. 5 Пример областей синхронизации для двух осцилляторов, соединенных по топологии "звезда". Векторами указаны отдельные запомненные образы Е1-Е3 и Е'1-Е'з относительно начальных точек S и S', соответственно.
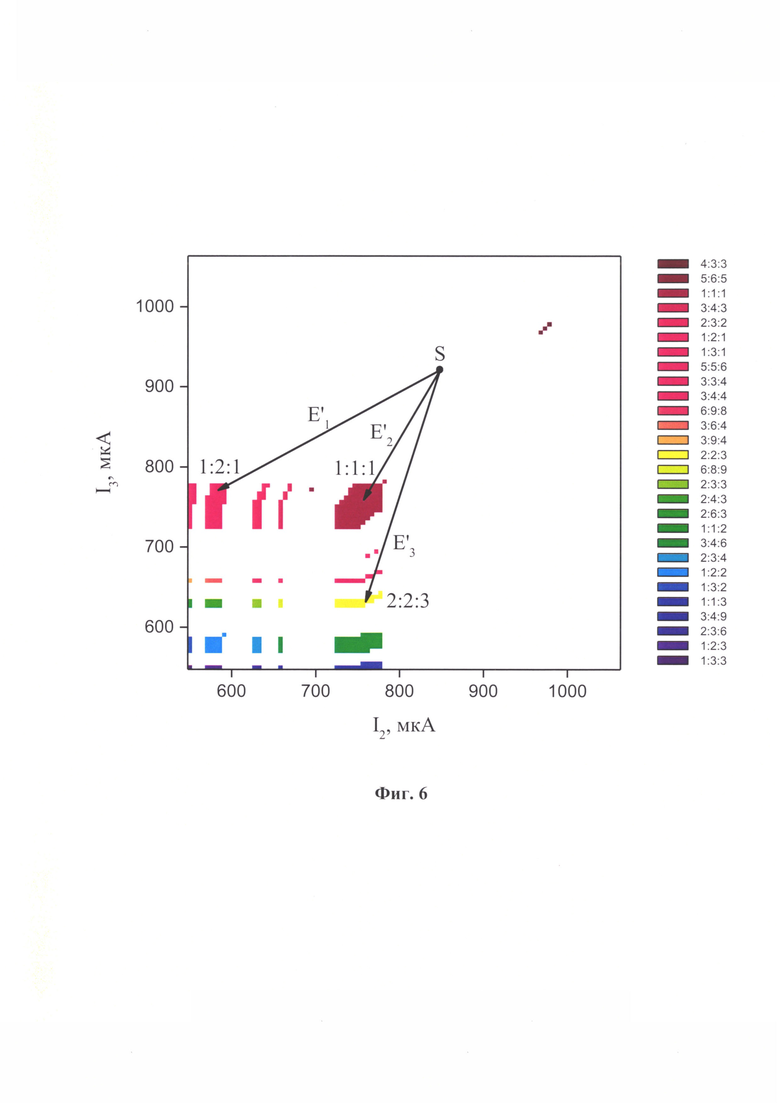
Фиг. 6 Пример областей синхронизации для трех осцилляторов, соединенных по топологии "звезда". Векторами указаны отдельные запомненные образы Е'1 - Е'з относительно начальной точки S.
Осцилляторная нейронная сеть в представленном изобретении представляет собой систему из N связанных осцилляторов. В зависимости от физического механизма взаимодействия осцилляторов они могут быть соединены, электрической (через резисторы и конденсаторы) [15], [16], термической связью [9], [10], оптической связями [17]. В общем случае существует матрица сил связей Ci,j (весов), где i,j - номера взаимодействующих осцилляторов, а Ci,j обозначает величину воздействия i-го осциллятора на j-й. Сеть осцилляторов может образовывать различные топологи: полносвязные - все со всеми, и неполносвязные - общая шина, звезда, кольцо. Следует отметить, что неполносвязная топология позволяет использовать меньшее количество связей по отношению к полносвязной топологии. На Фиг. 1 и Фиг. 2 приведены примеры топологий "все со всеми" и "звезда" трех осцилляторов, и обозначены силы связи.
Известно [9]—[11], что осцилляторы в сети могут испытывать эффект синхронизации, и, кроме синхронизации на основной (первой) гармонике, можно наблюдать синхронные режимы высокого порядка, в случае если спектр сигнала осциллятора имеет несколько гармоник. В общем случае синхронизация высокого порядка определяется отношением к1:к2:к3:..кN , где кi - номер гармоники i-го осциллятора на общей частоте синхронизации сети Fs. В качестве примера на Фиг. 3 приведены спектры трех осцилляторов имеющие синхронизацию порядка 3:2:4. Следует заметить следующее правило, что если все осцилляторы попарно имеют различные частоты синхронизации на произвольных гармониках, то всегда найдется общая частота синхронизации Fs для всей системы (всех пар), и синхронное состояние сети будет также определяться отношением к1:к2:к3:..кN на общей частоте синхронизации.
Переход из одного синхронного состояния в другое возможен при варьировании управляющих параметров осцилляторной сети. Например, в электрических осцилляторах, работающих по схеме релаксационного генератора (см. Фиг. 4) на базе переключателя на основе диоксида ванадия (VO2) основными параметрами являются токи питания осцилляторов, их вариация приводит к изменению основной частоты генерации осцилляторов. Тем не менее, в отдельных случаях, переход между состояниями возможно осуществить и вариацией сил связи или интенсивности шума.
Диапазон изменения управляющих параметров, при котором синхронизация не изменяет своего состояния, называется областью синхронизации. Существует целое семейство областей синхронизации, которые (для случая двух осцилляторов) принято называть языками Арнольда. Пример областей синхронизации для двух- и трех-осцилляторной схем, соединенных по топологии "звезда" показаны на Фиг. 5 и Фиг. 6. Здесь управляющими параметрами являются токи питания осцилляторов.
Количество возможных вариантов синхронных состояний (областей синхронизации), в которых система может пребывать при варьировании основных управляющих параметров, назовем емкостью запоминания NS. Величина NS зависит от количества осцилляторов N, диапазона управляющих параметров, топологии сети, силы связи между осцилляторами и интенсивности шума в системе (на Фиг. 5 NS=9, на Фиг. 6 NS=28). Ранее было показано [9], что NS имеет максимум для определенных значениях силы связи между осцилляторами и спадает при увеличении амплитуды шума в системе. При значительном увеличении силы связи величина NS уменьшается, что происходит из-за эффекта объединения близ лежащих областей синхронизации.
Методика кодирования и распознавания образов в системе испытывающей синхронизацию высокого порядка состоит из нескольких этапов.
Во-первых, необходимо вывести нейронную сеть в такую начальную точку управляющих параметров (S), которая лежит вне области синхронизации системы (см. Фиг. 5 и Фиг. 6). Находясь в несинхронном состоянии, система потенциально может прийти в одно из NS различных состояний синхронизации. Таким образом, в любой точке, лежащей вне синхронных областей система хранит NS образов, обозначим их векторами как E1, E2…ENs. Размерность векторов запомненных образов в этом случае равна числу осцилляторов N, а координаты векторов определяют смещения управляющих параметров осцилляторов, например, токов Е1=(ΔI1, ΔI2…ΔIN), относительно начальной точки S. Недостатком здесь является то, что области синхронизации имеют большую протяженность (с формой языков Арнольда, см. Фиг 5), поэтому возникает широкий диапазон координат векторов запомненных образов приводящих систему к определённому синхронному состоянию. Выходом из этой ситуации и сужению разброса координат векторов запомненных образов является использование векторов Е'1=(ΔI1, ΔI2…ΔIN-1) размерности на один меньше, чем количество осцилляторов (N-1). На практике это означает то, что фиксируется ток на одном осцилляторе, а варьируем токи остальных. Таким образом, исключается неоднозначность определения синхронизации по одной из координат вектора запомненного образа и области возможной синхронизации сужаются. Для примера на Фиг. 5 показано сечение области управляющих параметров для двух осцилляторной схемы при I2=соnst, при этом векторы запомненных образов Е'1, Е'2, Е'3 имеют меньший разброс параметров чем векторы образов Е1, Е2, Е3. Сечение областей синхронизации для системы, состоящей из трех осцилляторов, при фиксированном значении тока на первом осцилляторе I1=соnst, показано на Фиг. 6.
Таким образом, для запоминания конкретных образов, необходимо установить начальную точку системы в такое несинхронное состояние, что бы векторные расстояния от нее до существующих синхронных состояний соответствовали запоминаемым образам.
Во-вторых, после установления начальной точки, для распознавания тестового образа с вектором Т необходимо подать на управляющие параметры вектор смещения, соответствующий одному из запомненных образов. Если будет соблюдаться одно из условий (Т=Е1 или Т=Е2... или Т=ЕNs), произойдет переход в синхронное состояние и, непосредственно, акт распознавания соответствующего запомненного образа. Существование областей синхронизации гарантирует распознавание образа даже при незначительном отклонении его координат от запомненного образа.
Пример исполнения
В качестве примера реализации представлено 3 осциллятора, на базе VO2-переключателей, соединенных звездой как на Фиг 4. Управляющими параметрами здесь являются токи источников питания I1, I2, I3, а синхронизация осуществляется термическим образом [9], [10], при этом силы связей осцилляторов №1 и №2, а также №1 и №3 одинаковы и равны Сi,j =0.2 В. Параметры ВАХ переключателей (Uth=5 В, Uh=1.5 В Ucf=0.82 В, Roff=9.1 кОм, Rоп= 615 Ом), а также схем (емкость С=100 нФ и амплитуда шума Uin=20 мВ) для каждого осцилляторного контура одинаковы.
Используя численную модель, представленную в работе [9], было промоделировано сечение областей синхронизации см. Фиг. 6. Сечение представляет собой зависимость порядка синхронизации от величин тока I2 и I3 при постоянном значении тока I1=соnst=750 мкА. Всего в данной конфигурации насчитывается NS=28 синхронных состояний, некоторые из которых выделены на Фиг. 6.
Если, например, необходимо запомнить 3 образа с векторами Е'1 = (-264 мкА, -151 мкА), Е'2 = (-91 мкА, -163 мкА) и Е'3 = (-88 мкА, -290 мкА), то тогда следует установить начальную точку S в координату S = (847 мкА, 921 мкА), где отсутствует синхронное состояние. Следует заметить, что количество координат в каждом векторе на единицу меньше количества осцилляторов и равно 2, что, как объяснялось выше, необходимо для сужения области возможной синхронизации и снижения неопределенности распознавания.
При подаче тестового образа с вектором Т=Е'1 нейронная сеть переходит в синхронное состояние с синхронизацией порядка 1:2:1 (см. Фиг. 6).
При подаче тестового образа с вектором Т=Е'2 нейронная сеть переходит в синхронное состояние с синхронизацией порядка 1:1:1 (см. Фиг 6).
При подаче тестового образа с вектором Т=Е'3 нейронная сеть переходит в синхронное состояние с синхронизацией порядка 2:2:3 (см. Фиг. 6).
При отклонении координат вектора Т тестового образа от значений векторов Е' запомненных образов, как минимум в пределах ~1 мкА, тестовый образ также уверенно распознается.
Таким образом, осуществляется запись и распознавание трех различных образов, хотя емкость данной системы значительно выше и позволяет записывать одновременно до 28 образов.
Количество запоминаемых образов зависит от количества осцилляторов N, диапазона управляющих параметров, топологии сети, силы связи между осцилляторами и интенсивности шума в системе связанных осцилляторов.
БИБЛИОГРАФИЯ
[1] J. Heaton, Artificial intelligence for humans. Charleston: Createspace Independent Publishing, 2015.
[2] С.M. Bishop, Neural networks for pattern recognition. New York: Clarendon Press, 1995.
[3] S.H. Strogatz, "From Kuramoto to Crawford: exploring the onset of synchronization in populations of coupled oscillators," Phys. D Nonlinear Phenom., vol. 143, no. 1-4, pp. 1-20, Sep. 2000.
[4] H. Nakano and T. Saito, "Grouping Synchronization in a Pulse-Coupled Network of Chaotic Spiking Oscillators," IEEE Trans. Neural Networks, vol. 15, no. 5, pp. 1018-1026, Sep. 2004.
[5] F.C. Hoppensteadt and E. M. Izhikevich, "Pattern recognition via synchronization in phase-locked loop neural networks," IEEE Trans. Neural Networks, vol. 11, no. 3, pp. 734-738, May 2000.
[6] F.C. Hoppensteadt and E. M. Izhikevich, "Oscillatory Neurocomputers with Dynamic Connectivity," Phys. Rev. Lett., vol. 82, no. 14, pp. 2983-2986, Apr. 1999.
[7] E.M. Izhikevich, "Weakly pulse-coupled oscillators, FM interactions, synchronization, and oscillatory associative memory," IEEE Trans. Neural Networks, vol. 10, no. 3, pp. 508-526, May 1999.
[8] D.E. Nikonov et al., "Coupled-Oscillator Associative Memory Array Operation for Pattern Recognition," IEEE J. Explor. Solid-State Comput. Devices Circuits, vol. 1, pp. 85-93, Dec. 2015.
[9] A. Velichko, V. Putrolaynen, and M. Belyaev, "Effects of Higher Order and Long-Range Synchronizations for Classification and Computing in Oscillator-Based Spiking Neural Networks," Apr. 2018.
[10] A. Velichko, M. Belyaev, V. Putrolaynen, V. Perminov, and A. Pergament, "Thermal coupling and effect of subharmonic synchronization in a system of two VO2 based oscillators," Solid. State. Electron., vol. 141, pp. 40-49, Mar. 2018.
[11] A. Pikovsky, М. Rosenblum, and J. Kurths, Synchronization: a universal concept in nonlinear sciences. Cambridge University Press, 2001.
[12] F.C. Hoppensteadt and E. M. Izhikevich, "Phase-locked loop oscillatory neurocomputer," US 7280989 B1, 09.10.2007
[13] F.C. Hoppensteadt and E. Izhikevich, "Oscillatary neurocomputers with dynamic connectivity," US 6957204 B1, 18.10.2005.
[14] G.I. Bourianoff and D.E. Nikonov, "Associative memory oscillator array," US 8897047 B2, 25.11.2014.
[15] N. Shukla et al, "Synchronized charge oscillations in correlated electron systems" Sci. Rep., vol. 4, no. 1, p. 4964, May 2015.
[16] A. Velichko, M. Belyaev, V. Putrolaynen, A. Pergament, and V. Perminov, "Switching dynamics of single and coupled VO2-based oscillators as elements of neural networks," Int. J. Mod. Phys. B, vol. 31, no. 2, p. 1650261, Jan. 2017.
[17] F.C. Hoppensteadt and E.M. Izhikevich, "Synchronization of laser oscillators, associative memory, and optical neurocomputing," Phys. Rev. E, vol. 62, no. 3, pp. 4010-4013, Sep. 2000.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ обработки информации в импульсной нейронной сети | 2019 |
|
RU2709168C1 |
| Способ взаимодействия в системе связанных осцилляторов на базе оксидных структур с эффектом электрического переключения | 2017 |
|
RU2663546C1 |
| НЕЙРОН, МОДЕЛИРУЮЩИЙ СВОЙСТВА РЕАЛЬНОГО НЕЙРОНА | 2014 |
|
RU2597495C2 |
| ВОССТАНОВЛЕНИЕ СЕНСОМОТОРНОЙ ФУНКЦИИ С ПОМОЩЬЮ СИСТЕМЫ НЕЙРОПРОТЕЗИРОВАНИЯ И СПОСОБ ЕЕ РЕАЛИЗАЦИИ | 2020 |
|
RU2772637C2 |
| СПОСОБ ИНТЕЛЛЕКТУАЛЬНОЙ МНОГОУРОВНЕВОЙ ОБРАБОТКИ ИНФОРМАЦИИ В НЕЙРОННОЙ СЕТИ | 2020 |
|
RU2737227C1 |
| ИМПУЛЬСНЫЙ НЕЙРОН, БЛИЗКИЙ К РЕАЛЬНОМУ | 2015 |
|
RU2598298C2 |
| ОДНОСЛОЙНЫЙ ПЕРЦЕПТРОН, МОДЕЛИРУЮЩИЙ СВОЙСТВА РЕАЛЬНОГО ПЕРЦЕПТРОНА | 2015 |
|
RU2597496C1 |
| СПОСОБ ЗАЩИЩЕННОЙ ПЕРЕДАЧИ ИНФОРМАЦИИ С ИСПОЛЬЗОВАНИЕМ ИМПУЛЬСНОГО КОДИРОВАНИЯ | 2011 |
|
RU2493659C2 |
| СПОСОБ НЕМЕДИКАМЕНТОЗНОЙ КОРРЕКЦИИ ПСИХОЭМОЦИОНАЛЬНОГО, НЕЙРОГОРМОНАЛЬНОГО И ИММУННОГО СТАТУСОВ ЧЕЛОВЕКА | 2006 |
|
RU2314132C1 |
| РАСПОЗНАВАНИЕ СОБЫТИЙ НА ФОТОГРАФИЯХ С АВТОМАТИЧЕСКИМ ВЫДЕЛЕНИЕМ АЛЬБОМОВ | 2020 |
|
RU2742602C1 |
Изобретение относится к области реализации моделей нейронных сетей, а в частности сетей на базе связанных осцилляторов, представляющих собой импульсные осцилляторные нейронные сети, которые могут использоваться для распознавания образов. Техническим результатом является обеспечение запоминания и распознавания множества образов. Способ распознавания образов осуществляется за счет использования синхронизации осцилляторов на различных гармониках высокого порядка. Запись запоминаемых образов производится выбором исходного несинхронного состояния осцилляторов, а распознавание с помощью выявления синхронного состояния при векторных смещениях управляющих параметров осцилляторов. Представленный способ может быть реализован при различных топологиях связей в сети, таких «все со всеми», звезда, кольцо. 6 ил.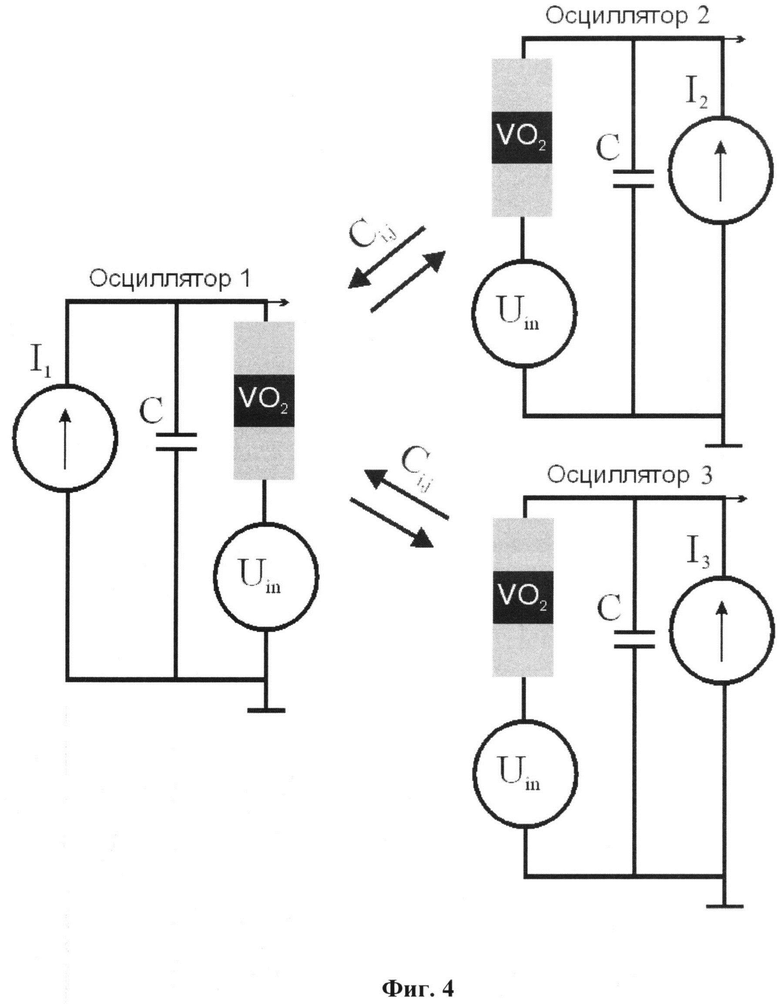
Способ запоминания и распознавания образов в системе связанных осцилляторов, состоящей из N осцилляторов, включающий: на этапе запоминания установление управляющих параметров осцилляторов, при которых осцилляторная нейронная сеть находится в несинхронном состоянии S, где набор векторных смещений относительно синхронного состояния соответствует одному запомненному образу; на этапе распознавания последующее векторное смещение управляющих параметров осцилляторов на величину, соответствующую тестируемому образу, при котором совпадение запомненного и тестируемого образа приводит к синхронизации осцилляторной нейронной сети, отличающийся тем, что на этапе запоминания в рабочем сигнале выделяют гармоники высокого порядка k1:k2:…kN и используют эффект синхронизации на этих гармониках, при котором в осцилляторной нейронной сети возникают NS синхронных состояний, соответствующих различным наборам гармоник k1:k2:k3:…kN, при этом с помощью питающих токов (I1, I2…IN) осцилляторов осцилляторную нейронную сеть устанавливают в несинхронное состояние S, при котором векторы смещения питающих токов (ΔI1, ΔI2…ΔIN) относительно NS синхронных состояний соответствуют NS запомненным образам, затем на этапе распознавания изменяют питающие токи осцилляторов на векторную величину, соответствующую тестируемому образу, и при возникновении синхронизации в осцилляторной нейронной сети устанавливают совпадение с одним из NS запомненных образов.
| US 8897047 B2, 25.11.2014 | |||
| WO 00/29970 A1, 25.05.2000 | |||
| US 7280989 B1, 09.10.2007 | |||
| Токарный резец | 1924 |
|
SU2016A1 |
| RU 97111217 A, 10.07.1999. | |||
Авторы
Даты
2019-08-21—Публикация
2018-06-29—Подача