Изобретение относится к нейрокомпьютерной технике и предназначено для классификации классов чисел по заданному модулю р. Наиболее близким по технической сущности (прототипом к предполагаемому изобретению) является устройство (патент РФ №2279132, МКИ G06N 3/04, Б.И. 18, 2006 г.), содержащее входной слой и скрытый слой, выходной слой.
Недостаток прототипа - большие аппаратурные затраты. Это связано с тем, что нейронная сеть содержит входной слой, который служит для фиксирования исходного числа. При этом существенно увеличивается требуемое число нейронов в сети.
Задача, на решение которой направлено заявляемое устройство состоит в повышении надежности перспективных образцов нейрокомпьютерной техники.
Технический результат выражается в сокращении аппаратурных затрат при классификации классов чисел по заданному модулю p.
Технический результат достигается тем, что в устройство, содержащее входной слой, предназначенный хранения числа, представленного в позиционной системе счисления, скрытый слой нейронов, предназначенный для взвешенного суммирования сохраненных чисел по формуле
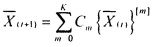 ,
,
где  является оператором извлечения m-го разряда двоичного представления числа, полученного после t-й итерации; K - старший разряд двоичного числа, полученного после t-й итерации;
является оператором извлечения m-го разряда двоичного представления числа, полученного после t-й итерации; K - старший разряд двоичного числа, полученного после t-й итерации;  - константа соответственно для каждой итерации и выходной слой, предназначенный для формирования на своих выходах вычетов числа z по выбранному модулю p суммирования, при этом выходы нейронов входного слоя подключены ко входам нейронов скрытого слоя, соединенных попарно между собой, выходы нейронов скрытого слоя соединены со входами нейронов выходного слоя, отличающаяся тем, что в нее введены первый и второй регистры, группа блоков элементов И, причем информационный вход кода исходного числа соединен с информационным входом первого регистра, вход начала вычислений устройства соединен с входами записи первого и второго регистров, а информационный вход нулевого разряда второго регистра соединен с входом записи второго регистра,
- константа соответственно для каждой итерации и выходной слой, предназначенный для формирования на своих выходах вычетов числа z по выбранному модулю p суммирования, при этом выходы нейронов входного слоя подключены ко входам нейронов скрытого слоя, соединенных попарно между собой, выходы нейронов скрытого слоя соединены со входами нейронов выходного слоя, отличающаяся тем, что в нее введены первый и второй регистры, группа блоков элементов И, причем информационный вход кода исходного числа соединен с информационным входом первого регистра, вход начала вычислений устройства соединен с входами записи первого и второго регистров, а информационный вход нулевого разряда второго регистра соединен с входом записи второго регистра, 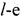 выходы разрядов первого регистра
выходы разрядов первого регистра
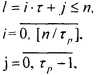
где: n - число двоичных разрядов первого регистра;
τp - период повторения остатков по модулю p весов разрядов в двоичном коде, соединены с соответствующими первыми входами i-х блоков элементов И группы, вторые входы которых соединены с i-ми выходами второго регистра, а выходы - с соответствующими j-ми нейронами входного слоя, причем

где K - старший разряд исходного двоичного числа, полученного после t-й итерации;
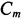 - константа соответственно для каждой итерации.
- константа соответственно для каждой итерации.
Сущность изобретения основывается на использовании периодичности остатков от чисел 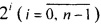 для определенного модуля p, где n - разрядность исходного двоичного числа. Представим число A в двоичной системе счисления
для определенного модуля p, где n - разрядность исходного двоичного числа. Представим число A в двоичной системе счисления
 , где ai=0 или 1.
, где ai=0 или 1.
Как следует из малой теоремы Ферма всегда существует такой наименьший показатель степени τp, что 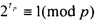 . Это положение свидетельствует о цикличности остатков по модулю p в разложении числа А. Для определения периода повторения применим теорию индексов, откуда
. Это положение свидетельствует о цикличности остатков по модулю p в разложении числа А. Для определения периода повторения применим теорию индексов, откуда
τp=(p-1)/I2,
где I2 - индекс числа 2 по модулю устройства p. Отметим, что если число 2 является первообразным корнем по модулю p, то I2=1 и τp=p-1.
Например для модуля p=5 имеем следующую последовательность чередования остатков
20=1, 21=2, 22=4, 23=3, 24=1, … (τ5=4)
Таким образом для определения класса числа по модулю p число А (начиная с младшего разряда) разбивается на части, длина которых равна периоду повторения τp и последовательному суммированию промежуточных модульных остатков периода по модулю p.
При этом входной слой нейронной сети состоит всего из τp нейронов, выходные сигналы которых образуют связи для первого скрытого слоя. Число скрытых слоев определяется величиной [log2τp] и не зависит от числа разрядов исходного числа А. В частности, для p=5 их число равно двум. Веса связей определяются константами Ci=2'(modp), где 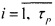 . Скрытые слои рекурсивно объединяются, а выходные сигналы последнего скрытого слоя подаются на входы выходного слоя, который представляет собой арифметический элемент, имеющий характеристику оператора по модулю.
. Скрытые слои рекурсивно объединяются, а выходные сигналы последнего скрытого слоя подаются на входы выходного слоя, который представляет собой арифметический элемент, имеющий характеристику оператора по модулю.
Время преобразования в прототипе определяется (log2n) - циклами синхронизации. В предлагаемом изобретении, после вычисления во входном слое, на его входы поступает второй период числа А и так далее. Таким образом достигается полная загрузка нейронной сети, а время вычислений равно  - циклов синхронизации.
- циклов синхронизации.
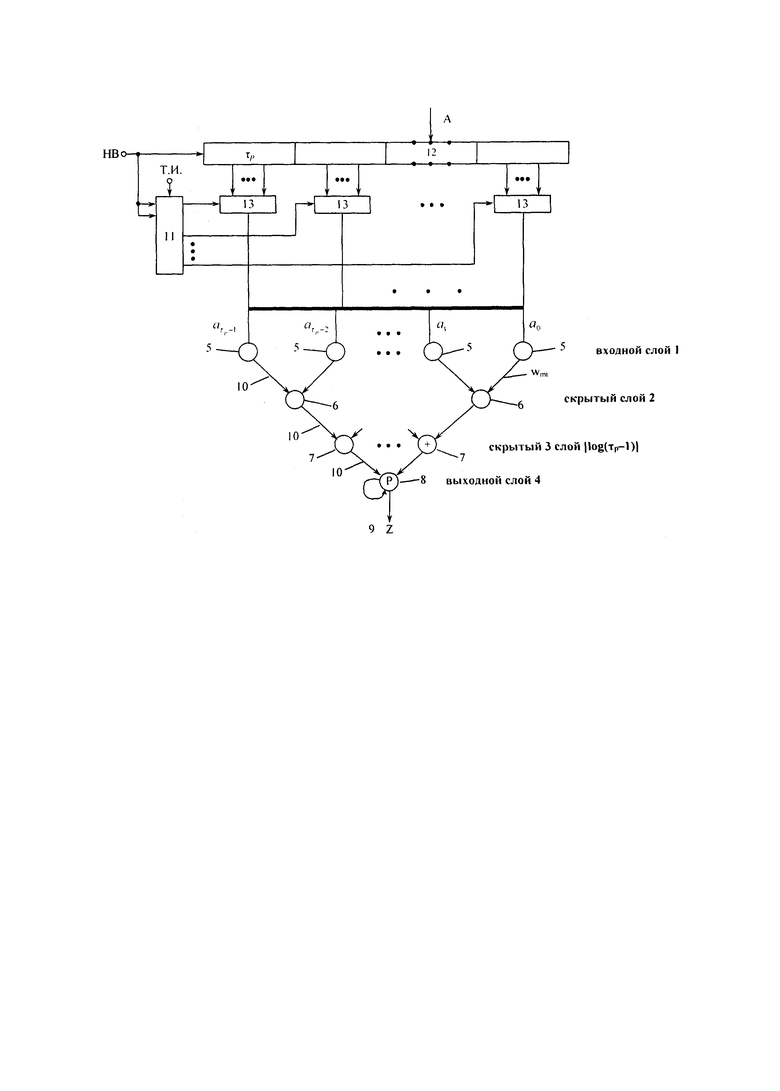
На фиг. 1 представлена структурная схема предлагаемого устройства, где 1 - выходной слой, 2 и 3 - скрытые слои, 4 - выходной слой, 5 - нейроны выходного слоя 1, 6 и 7 - нейроны скрытых слоев 2 и 3 соответственно, 8 - нейроны выходного слоя 4, 9 - вычет Z, 10 - связи между слоями нейронов, 11 - второй регистр, 12 - первый регистр, 13 группа блоков элементов И.
Информационный код исходного числа соединен с информационным входом первого 12 регистра, вход начала вычислений устройства соединен с входами записи первого 12 и второго 11 регистров, а информационной вход нулевого разряда второго 11 регистра соединен с входом записи второго 11 регистра, 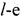 выходы разрядов первого 12 регистра
выходы разрядов первого 12 регистра
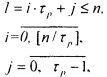
где: n - число двоичных разрядов первого регистра,
τp - период повторения остатков по модулю p весов разрядов в двоичном коде,
соединены с соответствующими первыми входами i-x блоков элементов И группы 13, вторые входы которых соединены с i-ми входами второго 11 регистра, а выходы - с соответствующими j-ми нейронами 5 входного слоя 1, причем
где: K - старший разряд исходного двоичного числа, полученного после t-й итерации;
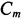 -константа соответственно для каждой итерации,
-константа соответственно для каждой итерации,
а выходы нейронов 5 входного слоя 1 подключены ко входам нейронов 6 и 7 скрытых слоев 2 и 3 соответственно, соединенных попарно между собой, выходы которых соединены с входами нейрона выходного слоя 4.
Рассмотрим работу устройства. В исходном состоянии все регистры обнулены. После подачи кода числа А на информационный вход первого 12 регистра на вход начала вычислений (НВ) подают импульс, который поступает на информационный вход нулевого разряда второго 11 регистра и входы записи регистров 11 и 12. Производится запись кода числа А в первый регистр 12 и единицы в нулевой разряд второго 11 регистра, сигнал с выхода нулевого разряда второго 11 регистра, сигнал с выхода нулевого разряда которого поступает на второй вход нулевого блока 13 элементов И группы. Первый период повторения остатков по модулю p весов разрядов с выходов нулевого блока 13 элементов И группы поступает в двоичном коде на соответствующие нейроны 5 входного слоя 1, где происходит сложение разрядных произведений αiCi по рекурсивному принципу. Затем результаты передаются на нейроны 6 скрытого слоя 2, а сигнал с выхода первого разряда регистра 12 поступает на второй вход первого блока 13 элементов И группы. Второй период повторения остатков по модулю p поступает на соответствующие нейроны 5 входного слоя 1. Процесс повторяется до тех пор, пока единица не окажется в 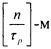 разряде регистра 12. Выходной слой 4, нейроны 8 представляют, как и в прототипе параллельный сумматор с обратной связью, обеспечивающий суммирование чисел 20 по модулю р. Процесс повторяется от слоя к слою.
разряде регистра 12. Выходной слой 4, нейроны 8 представляют, как и в прототипе параллельный сумматор с обратной связью, обеспечивающий суммирование чисел 20 по модулю р. Процесс повторяется от слоя к слою.
Классифицируемые вычеты Z на основании входной информации определяются вычетами 9, представленными двоичным кодом. Весовые коэффициенты 10 (связи между нейронами) определяются константами Ci. Изобретение предназначено для рационального построения блоков модулярного нейрокомпьютера.
Пример: пусть дано число 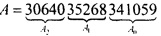 (для лучшего понимания представлено в десятичной системе счисления).
(для лучшего понимания представлено в десятичной системе счисления).
При p=7 имеем С0=1, С1=10=3, С2=102=2, С3=103=-1(mod7), С4=104=-3, С5=105=-2(mod7).
Найдем
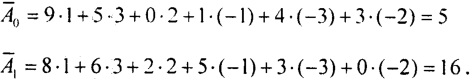
Далее число 16 преобразуем по модулю 7: 6⋅1+1⋅3=9=2(mod7).
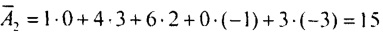
Далее число 15 преобразуем по модулю 7: 5⋅1+1⋅3=1(mod7).
Производим сложение остатков трех периодов по модулю 7 и получаем 5+2+1=8(mod7)=1(mod7).
Таким образом, в данном примере при проведении операции по модулю 7 имеем следующие преобразования периодов исходного числа А
341059,5; 035268,16,9,2; 3064,15,8,3.
Рассмотрим сокращение аппаратурных затрат (числа нейронов) при реализации данного устройства. Пусть исходное число А имеет 16 двоичных разрядов. Для построения нейронной сети в прототипе (p=5) требуется N1=31 нейрон, а в данном варианте N2=7 нейронов. Также использование данного подхода способствует унификации оборудования, т.к. связи между слоями нейронов (Ci) постоянны, при заданном модуле операции, независимо от величины исходного числа.
Полученное устройство отражает принципы построения нейросетей на основе модулярной системы счисления. Примененный подход позволяет реализовать соответствующие вычислительные системы более эффективным способом.
| название | год | авторы | номер документа |
|---|---|---|---|
| НЕЙРОННАЯ СЕТЬ КОНЕЧНОГО КОЛЬЦА | 2020 |
|
RU2759964C1 |
| НЕЙРОННАЯ СЕТЬ КОНЕЧНОГО КОЛЬЦА | 2003 |
|
RU2279132C2 |
| НЕЙРОННАЯ СЕТЬ УСКОРЕННОГО МАСШТАБИРОВАНИЯ МОДУЛЯРНЫХ ЧИСЕЛ | 2007 |
|
RU2359325C2 |
| Система надежного облачного хранения с регулируемой избыточностью данных | 2021 |
|
RU2782681C1 |
| ПАРАЛЛЕЛЬНЫЙ СУММАТОР-ВЫЧИТАТЕЛЬ В ТРОИЧНОЙ СИСТЕМЕ СЧИСЛЕНИЯ НА НЕЙРОНАХ | 2010 |
|
RU2453900C2 |
| НЕЙРОННАЯ СЕТЬ С ПОРОГОВОЙ (k, t) СТРУКТУРОЙ ДЛЯ ПРЕОБРАЗОВАНИЯ ОСТАТОЧНОГО КОДА В ДВОИЧНЫЙ ПОЗИЦИОННЫЙ КОД | 2008 |
|
RU2380751C1 |
| УСТРОЙСТВО ДЛЯ ПРЕОБРАЗОВАНИЯ ДВОИЧНОГО КОДА В КОД СИСТЕМЫ ОСТАТОЧНЫХ КЛАССОВ (СОК) | 2009 |
|
RU2413279C1 |
| ПАРАЛЛЕЛЬНЫЙ СУММАТОР-ВЫЧИТАТЕЛЬ НА НЕЙРОНАХ СО СКВОЗНЫМ ПЕРЕНОСОМ | 2012 |
|
RU2523942C2 |
| НЕЙРОННАЯ СЕТЬ ДЛЯ ПРЕОБРАЗОВАНИЯ ОСТАТОЧНОГО КОДА В ДВОИЧНЫЙ ПОЗИЦИОННЫЙ КОД | 2006 |
|
RU2318238C1 |
| УСТРОЙСТВО ДЛЯ ОСНОВНОГО ДЕЛЕНИЯ МОДУЛЯРНЫХ ЧИСЕЛ | 2013 |
|
RU2559771C2 |
Изобретение относится к нейронным сетям конечного кольца. Технический результат заключается в повышении надежности нейрокомпьютерной техники. Нейронная сеть конечного кольца для классификации чисел по заданному модулю р, содержит выходной слой, предназначенный для хранения числа, представленного в позиционной системе счисления, скрытый слой нейронов, предназначенный для взвешенного суммирования сохраненных чисел и выходной слой, предназначенный для формирования своих входах вычетов числа z по выбранному модулю р суммирования, при этом выходы нейронов входного слоя подключены ко входам нейронов скрытого слоя, соединенных попарно между собой, выходы нейронов скрытого слоя соединены со входами нейронов выходного слоя, при этом в сеть введены первый и второй регистры, группа блоков элементов И, причем информационный вход кода исходного числа соединен с информационным входом первого регистра, вход начала вычислений устройства соединен с входами записи первого и второго регистров, а информационный вход нулевого разряда второго регистра соединен с входом записи второго регистра. 1 ил.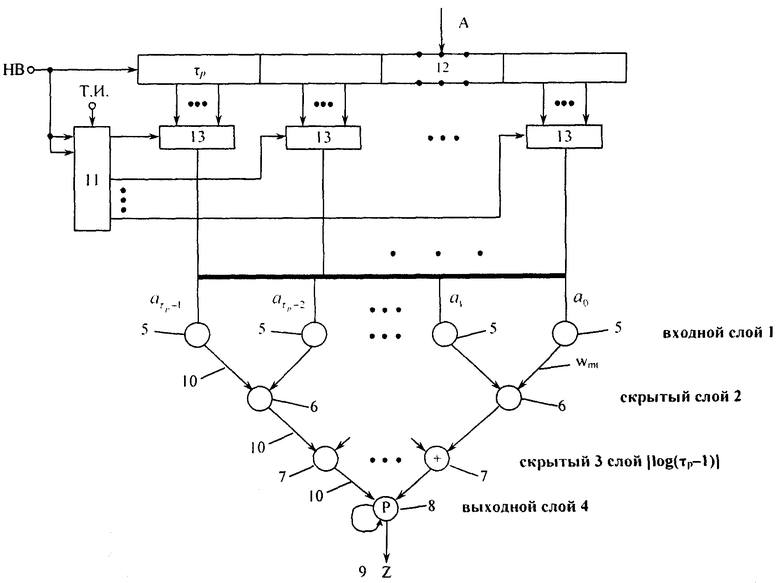
Нейронная сеть конечного кольца для классификации чисел по заданному модулю р, содержащая выходной слой, предназначенный для хранения числа, представленного в позиционной системе счисления, скрытый слой нейронов, предназначенный для взвешенного суммирования сохраненных чисел по формуле

где 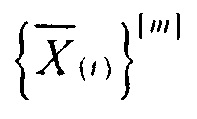 является оператором извлечения m-го разряда двоичного представления числа, полученного после t-й итерации; K - старший разряд двоичного числа, полученного после t-й итерации; Cm - константа соответственно для каждой итерации и выходной слой, предназначенный для формирования своих входах вычетов числа z по выбранному модулю р суммирования, при этом выходы нейронов входного слоя подключены ко входам нейронов скрытого слоя, соединенных попарно между собой, выходы нейронов скрытого слоя соединены со входами нейронов выходного слоя, отличающаяся тем, что в нее введены первый и второй регистры, группа блоков элементов И, причем информационный вход кода исходного числа соединен с информационным входом первого регистра, вход начала вычислений устройства соединен с входами записи первого и второго регистров, а информационный вход нулевого разряда второго регистра соединен с входом записи второго регистра,
является оператором извлечения m-го разряда двоичного представления числа, полученного после t-й итерации; K - старший разряд двоичного числа, полученного после t-й итерации; Cm - константа соответственно для каждой итерации и выходной слой, предназначенный для формирования своих входах вычетов числа z по выбранному модулю р суммирования, при этом выходы нейронов входного слоя подключены ко входам нейронов скрытого слоя, соединенных попарно между собой, выходы нейронов скрытого слоя соединены со входами нейронов выходного слоя, отличающаяся тем, что в нее введены первый и второй регистры, группа блоков элементов И, причем информационный вход кода исходного числа соединен с информационным входом первого регистра, вход начала вычислений устройства соединен с входами записи первого и второго регистров, а информационный вход нулевого разряда второго регистра соединен с входом записи второго регистра, 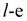 выходы разрядов первого регистра
выходы разрядов первого регистра
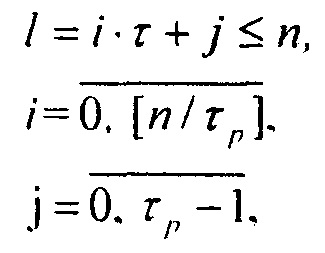
где: n - число двоичных разрядов первого регистра;
τр - период повторения остатков по модулю р весов разрядов в двоичном коде, соединены с соответствующими первыми входами i-x блоков элементов И группы, вторые входы которых соединены с i-ми выходами второго регистра, а выходы - с соответствующими j-ми нейронами входного слоя, причем
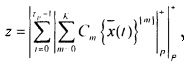
где K - старший разряд исходного двоичного числа, полученного после t-й итерации;
Cm - константа соответственно для каждой итерации.
| НЕЙРОННАЯ СЕТЬ КОНЕЧНОГО КОЛЬЦА | 2003 |
|
RU2279132C2 |
| US 6243490 B1, 05.06.2001 | |||
| НЕЙРОННАЯ СЕТЬ ДЛЯ ДЕЛЕНИЯ ЧИСЕЛ, ПРЕДСТАВЛЕННЫХ В СИСТЕМЕ ОСТАТОЧНЫХ КЛАССОВ | 2006 |
|
RU2318239C1 |
| НЕЙРОННАЯ СЕТЬ ДЛЯ ПРЕОБРАЗОВАНИЯ ОСТАТОЧНОГО КОДА В ДВОИЧНЫЙ ПОЗИЦИОННЫЙ КОД | 2006 |
|
RU2318238C1 |
| НЕЙРОННАЯ СЕТЬ УСКОРЕННОГО МАСШТАБИРОВАНИЯ МОДУЛЯРНЫХ ЧИСЕЛ | 2007 |
|
RU2359325C2 |
Авторы
Даты
2019-09-24—Публикация
2018-09-20—Подача