Предлагаемое изобретение относится к области нейрокомпьютерной техники и предназначено для классификации чисел по заданному модулю р. Классом по данному модулю р называется множество всех целых чисел, сравнимых с некоторым данным целым числом А. Число классов по модулю р конечно и равно р, а каждый класс содержит бесконечное множество чисел, но в силу конечности машинного диапазона чисел, самое большое число из класса будет определяться максимальным числом машинного диапазона, а самое малое - 0. Будем обозначать такой класс знаком 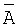 . Таким образом,
. Таким образом, 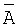 обозначает множество всех тех чисел х, которое удовлетворяет сравнению
обозначает множество всех тех чисел х, которое удовлетворяет сравнению 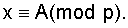 Класс чисел, сравнимых с А по модулю р, совпадает со значением линейной функции А + pt при целых значениях аргумента t. Если какое-то число класса по модулю р имеет при делении на р остаток, равный α, то все числа класса имеют вид α+pt, где аргумент t принимает любые целые значения. Вычетом класса называется любое из чисел, принадлежащее этому классу. Наименьший неотрицательный вычет класса
Класс чисел, сравнимых с А по модулю р, совпадает со значением линейной функции А + pt при целых значениях аргумента t. Если какое-то число класса по модулю р имеет при делении на р остаток, равный α, то все числа класса имеют вид α+pt, где аргумент t принимает любые целые значения. Вычетом класса называется любое из чисел, принадлежащее этому классу. Наименьший неотрицательный вычет класса 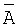 по модулю р равен остатку от деления А на р.
по модулю р равен остатку от деления А на р.
Известна нейронная сеть для классификации сигналов или символьной информации (заявка 19917957, МПК 7 G 06 F 15/18, опубликована 26.10.2000, немецкий), содержащая входной, выходной, скрытый слои и связи между ними. Классифицируемые символы или символьная информация определяется, соответственно, классами А, В, С, D, Е, F и G нейронами выходного слоя. Однако такие нейронные сети предназначены для классификации целей радиолокатора. Целью данного изобретения является расширение возможностей известной нейронной сети для классификации вычетов. Это достигается тем, что в нейронную сеть введены арифметические элементы, которые имеют характеристики взвешенного суммирования, и элемент, который имеет характеристику оператора по модулю, а не обычные нелинейные функции активации, применяемые при обучении нейронной сети. Таким образом, нейронная сеть будет состоять из входного слоя, служащего для фиксирования исходного числа, выходные сигналы которого образуют связи для первого скрытого слоя. Число скрытых слоев определяется величиной [log2n], где n - число разрядов исходного двоичного числа А. Веса связей определяются константами

для данного модуля, где i=1,2...n. Скрытые слои рекурсивно объединяются, организуя логарифмическое суммирование. Выходные сигналы скрытого слоя [log2n] подаются на входы выходного слоя, который представляет собой арифметический элемент, имеющий характеристику оператора по модулю. Выходной сигнал скрытого слоя определяет вычет или наименьший неотрицательный остаток α≡Amodp.
Введем следующие обозначения:
р - модуль, который представляет из себя простое число;
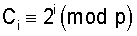 - константа, определенная номером двоичного разряда.
- константа, определенная номером двоичного разряда.
Пусть число Х записано в двоичной системе счисления, т.е.
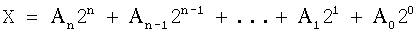 или
или 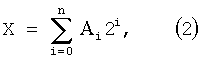
где при всех i: 0≤Аi≤1.
Далее подставляя значения Сi(1) в выражение (2) и учитывая свойства сравнений, получим
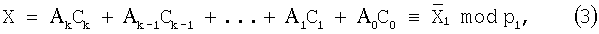
где 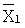 является классом Х.
является классом Х.
Преобразование (3) позволило уменьшить разрядность исходного числа Х.
Далее, аналогичную операцию проведем с 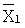 . В результате получим
. В результате получим 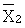 меньшей разрядности, чем
меньшей разрядности, чем 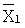 и т.д.
и т.д.
При практической реализации данного метода необходимо определить остатки от деления на р степеней основания 2, которые дадут набор чисел Сi. Если остаток от деления степени основания 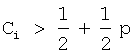 , то в качестве значения Сi необходимо взять число, дополняющее до значения р со знаком «минус». Значения Сi являются константами и вычисляются заранее. Количество Сi определяется разрядностью исходных чисел. Затем цифры исходного числа умножают на соответствующие Сi. Полученная сумма
, то в качестве значения Сi необходимо взять число, дополняющее до значения р со знаком «минус». Значения Сi являются константами и вычисляются заранее. Количество Сi определяется разрядностью исходных чисел. Затем цифры исходного числа умножают на соответствующие Сi. Полученная сумма
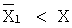 .
.
По значению 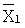 можно узнать класс числа по модулю р, что равносильно определению остатка от деления числа Х на модуль р. Если
можно узнать класс числа по модулю р, что равносильно определению остатка от деления числа Х на модуль р. Если 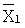 имеет количество разрядов больше, чем р, то вновь разряды числа
имеет количество разрядов больше, чем р, то вновь разряды числа 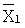 необходимо умножить на числа Сi, полученная сумма
необходимо умножить на числа Сi, полученная сумма 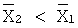 . По значению
. По значению 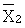 можно узнать, каков остаток от деления числа Х на р. Этот процесс преобразования числа Х необходимо продолжать до тех пор, пока полученное число
можно узнать, каков остаток от деления числа Х на р. Этот процесс преобразования числа Х необходимо продолжать до тех пор, пока полученное число 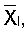 где l - количество итераций, не окажется вычетом числа Х по модулю р.
где l - количество итераций, не окажется вычетом числа Х по модулю р.
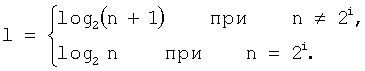
Создание нового метода основывается на двух новых идеях. Первая заключается в преобразовании числа большой разрядности в число малой разрядности. Вторая идея заключается в нахождении вычета по модулю р исходного числа путем определения наименьшего неотрицательного вычета от полученного, в результате первой идеи, малоразрядного числа.
Пример: пусть дано число Х=269341059 (для лучшего понимания число представлено в десятичной системе счисления).
При р=7 имеем 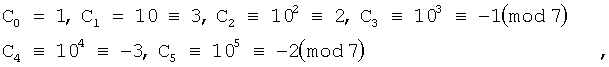
а далее все эти значения Сi периодически повторяются.
Найдем 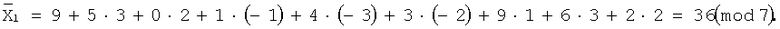
Далее найдем 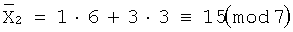 и
и 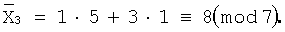
Далее число 8 преобразуем по модулю 7 и получим остаток, равный 1.
Таким образом, в данном примере по модулю 7 класс 1 состоит из чисел:
269341059,36,15,8,1.
Нейронная сеть конечного кольца может реализовываться как аппаратным, так и программным способом. Рассмотрим реализацию нейронной сети конечного кольца аппаратным способом. В основе данного изобретения лежит нейронная сеть для классификации вычетов (остатков), которая относительно проста и относительно быстра в обработке. Структура нейронной сети зависит от разрядности исходного числа и величины модуля. Посредством весовых коэффициентов Сi нейронная сеть осуществляет классификацию, при этом структура нейронной сети не изменяется.
В процессе классификации слои нейронной сети осуществляют сложение разрядных произведений AiСi по рекурсивному принципу, от слоя к слою, вследствие чего происходит быстрая обработка классифицируемых вычетов. Функционирование нейронной сети зависит от весовых коэффициентов и величины модуля, которые определяются заранее перед процессом классификации.
В данном изобретении обучение для классификации классов и определение остатков сети осуществляют весовыми коэффициентами. Если возникает необходимость данную нейронную сеть использовать для нескольких различных модулей, то константы сi хранятся в памяти и в зависимости от необходимости устанавливаются необходимые весовые коэффициенты.
Принцип работы данного изобретения излагается ниже. Нейронная сеть конечного кольца приведена на чертеже (а) (на чертеже (б) показано символическое изображение) и классифицирует входную информацию 1. Входная информация в двоичном n-разрядном коде, где n - количество двоичных разрядов исходного числа (а0,а1,...an), поступает на нейроны 6, расположенные во входном слое 2, а распознанный остаток появляется в выходном слое 5 в нейроне 9. Между входным слоем 2 и выходным слоем 5 расположены скрытые слои 3, 4, состоящие из нейронов 7, 8, выполняющие операции взвешенного суммирования, связи между слоями нейронов wij, wjk и wlk обозначены 11.
Входной слой 2, нейроны 6, представляют собой n-разрядный регистр, где n - количество разрядов исходного двоичного числа А, и предназначены для временного хранения этого числа. Выходной слой 5, нейроны 9, представляют собой параллельный сумматор с обратной связью, обеспечивающий суммирование чисел по модулю р, а нейроны, реализующие эти функции, являются арифметическими элементами, которые имеют характеристики оператора по модулю, что и отличает их от обычных нейронов (например, персептронов), где используется функция активации. В скрытых слоях 7 и 8 используются нейроны, представляющие собой традиционные сумматоры, которые предназначены для суммирования двоичных чисел, т.е. эти нейроны являются арифметическими элементами, которые имеют характеристики взвешенного суммирования, т.е. суммирования чисел, представленных в позиционной системе счисления.
Классифицируемые вычеты amodp на основании входной информации 1 определяются вычетами z 10, представленными двоичным кодом, нейрон 9. Весовые коэффициенты wij, wjk и wlk определяются константами Сi, соответственно, для каждой итерации. Классификация входных данных 1 происходит на основании итеративного применения вычислительной модели (3) взвешенного суммирования, которая повторяется в слоях 3, 4. На выходе каждого скрытого слоя разрядность полученного числа уменьшается за счет свертки числа с помощью выражения
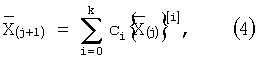
где j означает номер итерации;
k - старший разряд двоичного числа, полученного после j-й итерации;
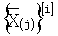 - оператор извлечения i-го разряда двоичного представления числа, полученного после j-й итерации.
- оператор извлечения i-го разряда двоичного представления числа, полученного после j-й итерации.
Выходной слой реализует вычислительную модель суммирования по модулю
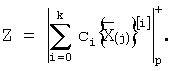
Данное устройство может быть применено для определения остатков по любому количеству различных модулей. При этом определенные внешние параметры для разных значений модулей будут заданы в виде весовых коэффициентов wij, wjk и wlk и хранятся в памяти.
Классификация данных реализуется с помощью иерархической нейронной сети, основанной на базовых процессорных элементах с характеристиками взвешенного суммирования и оператора по модулю. Число слоев нейронов определяется рекурсивным сдваиванием и логарифмическим суммированием, как [log2n], и время преобразования будет определяться 0(log2n) - циклами синхронизации.
Изобретение преимущественно предназначено для построения функциональных блоков модулярного нейрокомпьютера.
| название | год | авторы | номер документа |
|---|---|---|---|
| Нейронная сеть конечного кольца | 2018 |
|
RU2701064C1 |
| НЕЙРОННАЯ СЕТЬ КОНЕЧНОГО КОЛЬЦА | 2020 |
|
RU2759964C1 |
| НЕЙРОННАЯ СЕТЬ С ПОРОГОВОЙ (k, t) СТРУКТУРОЙ ДЛЯ ПРЕОБРАЗОВАНИЯ ОСТАТОЧНОГО КОДА В ДВОИЧНЫЙ ПОЗИЦИОННЫЙ КОД | 2008 |
|
RU2380751C1 |
| КОНВЕЙЕРНАЯ НЕЙРОННАЯ СЕТЬ КОНЕЧНОГО КОЛЬЦА | 2006 |
|
RU2317584C1 |
| НЕЙРОННАЯ СЕТЬ ДЛЯ РАСШИРЕНИЯ КОРТЕЖА ЧИСЛОВОЙ СИСТЕМЫ ВЫЧЕТОВ | 2003 |
|
RU2256226C2 |
| НЕЙРОННАЯ СЕТЬ ДЛЯ ОБНАРУЖЕНИЯ, ЛОКАЛИЗАЦИИ И ИСПРАВЛЕНИЯ ОШИБОК В СИСТЕМЕ ОСТАТОЧНЫХ КЛАССОВ | 2005 |
|
RU2301442C2 |
| НЕЙРОННАЯ СЕТЬ ДЛЯ ПРЕОБРАЗОВАНИЯ ОСТАТОЧНОГО КОДА В ДВОИЧНЫЙ ПОЗИЦИОННЫЙ КОД | 2006 |
|
RU2318238C1 |
| НЕЙРОННАЯ СЕТЬ ДЛЯ ПРЕОБРАЗОВАНИЯ ПОЛИАДИЧЕСКОГО КОДА В КОД СИСТЕМЫ ОСТАТОЧНЫХ КЛАССОВ | 2003 |
|
RU2258257C2 |
| АДАПТИВНАЯ ПАРАЛЛЕЛЬНО-КОНВЕЙЕРНАЯ НЕЙРОННАЯ СЕТЬ ДЛЯ КОРРЕКЦИИ ОШИБОК | 2003 |
|
RU2279131C2 |
| НЕЙРОННАЯ СЕТЬ ДЛЯ ДЕЛЕНИЯ ЧИСЕЛ, ПРЕДСТАВЛЕННЫХ В СИСТЕМЕ ОСТАТОЧНЫХ КЛАССОВ | 2006 |
|
RU2318239C1 |
Изобретение относится к нейрокомпьютерной технике и предназначено для классификации классов чисел по заданному модулю р. Техническим результатом является расширение возможностей известной нейронной сети для классификации вычетов. Для этого нейронная сеть содержит входной слой, скрытый слой, к которому рекурсивно попарно подсоединен входной слой, и выходной слой. 1 ил.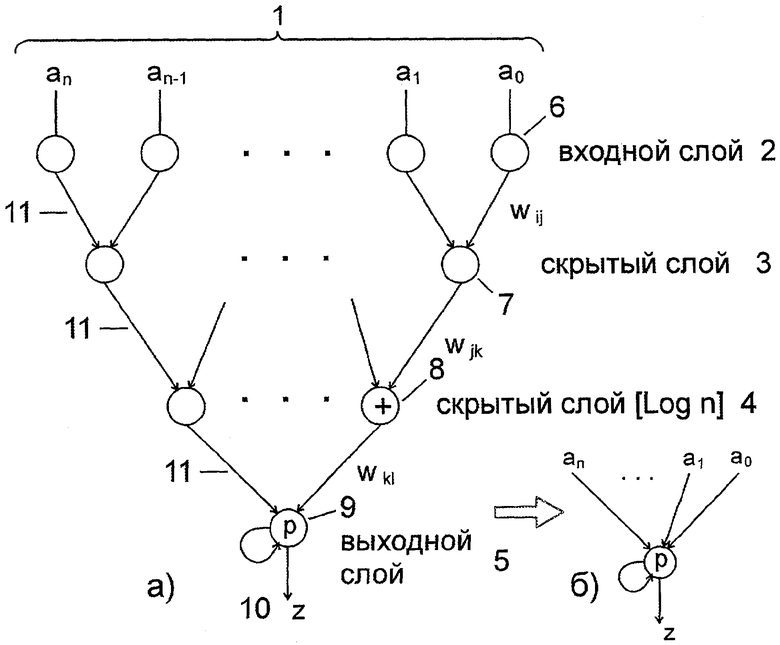
Нейронная сеть конечного кольца для классификации чисел по модулю, содержащая входной слой, предназначенный для хранения исходного числа, представленного в позиционной системе счисления, отличающаяся тем, что в нее введены скрытый слой нейронов, предназначенный для взвешенного суммирования сохраненных исходных чисел по формуле 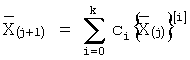 ,
,
где 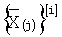 является оператором извлечения i-го разряда двоичного представления числа, полученной после j-й итерации;
является оператором извлечения i-го разряда двоичного представления числа, полученной после j-й итерации;
k - старший разряд двоичного числа, полученного после j-й итерации;
ci - константа соответственно для каждой итерации,
и выходной слой, предназначенный для формирования на своих выходах вычетов числа Z по выбранному модулю р суммирования 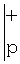 , в соответствии с формулой
, в соответствии с формулой 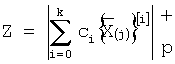 , при этом выходы входного слоя подключены ко входам нейронов скрытого слоя, соединенных рекурсивно попарно между собой, выходы нейронов скрытого слоя соединены со входами нейронов выходного слоя.
, при этом выходы входного слоя подключены ко входам нейронов скрытого слоя, соединенных рекурсивно попарно между собой, выходы нейронов скрытого слоя соединены со входами нейронов выходного слоя.
| ЧЕРВЯКОВ Н.И | |||
| и др | |||
| Оптимизация структуры нейронных сетей конечного кольца | |||
| Нейрокомпьютеры: разработка, применение | |||
| Перекатываемый затвор для водоемов | 1922 |
|
SU2001A1 |
| US 5719955 A, 17.02.1998 | |||
| US 6243490 B1, 05.06.2001 | |||
| Походная разборная печь для варки пищи и печения хлеба | 1920 |
|
SU11A1 |
Авторы
Даты
2006-06-27—Публикация
2003-08-07—Подача