Изобретение относится к вычислительным модулярным системам и предназначено для выполнения основного деления чисел, представленных в системе остаточных классов (СОК).
В СОК обычное целое число представляется в виде остатков от деления на набор модулей. Арифметические операции над числами заменяются операциями над остатками. Выполнение операций происходит параллельно и без межразрядных переносов, что позволяет очень быстро реализовать сложение, вычитание и умножение. Однако операция деления представляет определенные трудности, которые исследователи стараются упростить, предлагая новые архитектуры вычислений и аппаратные реализации.
Известна «Нейронная сеть для деления чисел, представленных в системе остаточных классов» (патент RU 2318239, G06F, опубликовано 27.02.2008), содержащая нейронную сеть для расширения кортежа числовой системы вычетов, нейронные сети конечного кольца для суммирования и умножения.
Недостатком устройства является низкая скорость деления чисел и ограниченная функциональная возможность, так как в качестве делителя выбирается один их модулей системы остаточных классов (СОК).
Наиболее близкой к изобретению является «Нейронная сеть основного деления модулярных чисел» (патент RU 2400813, G06F 3/02, G06F 7/72, опубликовано 27.04.2010). Недостатком устройства является большой объем оборудования. Известная нейронная сеть предназначена для деления модулярных чисел в случае, когда в качестве делителя используется целое положительное число, попарно простое с р1, р2,…, pn, либо целое положительное число, представляющее собой произведение чисел, попарно простых с pi. Для выполнения этого условия возникает необходимость нахождения приблизительного делителя путем использования обобщенной позиционной системы счисления (ОПСС). Для нахождения приблизительного делителя необходимо дополнительное оборудование и время.
Техническим результатом изобретения является расширение функциональных возможностей, что выражается в отсутствии накладываемых условий на делимое, делитель и выбор набора модулей СОК, сокращение оборудования и повышение скорости при выполнении операции деления.
Указанный технический результат достигается тем, что устройство для основного деления модулярных чисел содержит (фиг. 1): входные шины для определения начала процесса «деления», шину 31, входные шины для подачи делимого 1 и делителя 2 и выходную шину частного 30; схему умножения 7, предназначенную для умножения делителя на высшую степень аппроксимационного ряда частного; схему мультиплексора 8, на вход которого поступают данные либо непосредственно делителя, шина 2, либо делителя, умноженного на высшую степень аппроксимационного ряда частного, шина 32; схему сравнения 11 (патент на изобретение №2503992, опубл. 10.01.2014) для сравнения относительных значений делимого и делителя, поступивших по шинам 1 и 33; сумматоры делимого 37 и делителя 10, предназначенные для суммирования произведений констант выбранной СОК на разряды соответственно делимого и делителя, поступивших по шинам 26 и 25; кроме того, на сумматор делимого 37 поступает остаток от вычитания из делимого степеней членов ряда, поступающий по шине 39; вычитатель 14 для вычитания из сумматора делимого 37, шина 38, соответствующих значений степеней аппроксимационного ряда частного, поступивших по шине 34; регистр сдвига 9, предназначенный для сдвига делителя «влево» до появления переноса в знаковый разряд в случае аппроксимации ряда частного или сдвига «вправо» в случае уточнения аппроксимационного ряда частного, поступившего по шине 23; регистр 36 хранения остатка при вычитании из делимого членов ряда частного, предназначенный для временного хранения результатов вычитания (вычитатель 14) из делимого соответствующих степеней ряда частного, поступивших по шине 41 в случае отсутствия запрещающего сигнала по шине 27; схему «запрета» 35, предназначенную для запрета прохождения результата вычитателя 14 шина 40, если значение результата отрицательное, т.е. в случае действия запрещающего сигнала по шине 27; схему «запрета» 12, предназначенную для прохождения значений соответствующих степеней, если они входят в уточненный ряд частного, поступивших по шине 28; шина 27 служит для подачи сигналов на запрещающие входы схем «запрета» 12 и 35, если в знаковом разряде вычитателя 14 записана «1», то есть число отрицательное; счетчик 4, предназначенный для счета тактовых импульсов, поступивших по шине 17, соответствующих количеству сдвигов регистра сдвига 9; память 5 (количество ячеек памяти определяется выражением i=logP, где Р=p1p2…pn) предназначена для хранения степеней двойки qi mod pj, j=1,2,…,n, представленных в СОК, которые подаются по шине 24 через ключ 6 на информационный вход схемы «запрета» 12 по шине 28 и далее на вход сумматора 13 по шине 29, считывание которых осуществляется по адресной шине 21 после поступления сигнала «Разрешение считывания» по шине 22 (остановка счетчика 4 и «Разрешение считывания» определяется в момент переноса единицы в знаковый разряд регистра сдвига 9); ключ 6 для прохождения степеней ряда на вход схемы умножения 7 и схемы «запрета» 12 при поступлении тактовых импульсов с шины 16; схема управления 3 предназначена для формирования тактовых, синхронизирующих импульсов и сигналов установки в «0» элементов устройства деления (шины 15, 16, 17, 18); сумматор 13 частного предназначен для суммирования степеней ряда, представленных в СОК, поступивших по шине 29, либо по шине 42 в случае а=b; сигналы с выхода схемы сравнения 11 поступают на вход схемы управления: в случае, если а>b, шина 20, в случае если а<b, шина 19.
Известные алгоритмы деления чисел, представленных в СОК, базируются на абсолютных значениях делимого и делителя. В изобретении предлагается использовать не абсолютные значения, а их относительные величины.
Рассмотрим модификацию алгоритма основного деления чисел, представленных в системе остаточных классов в случае, когда и делимое и делитель представляют собой произвольные целые числа и делитель не приводится к случаю попарно простого с модулями СОК. Модификация основана на использовании делимого и делителя, представленных в относительных величинах.
В последнее время проявляется значительный интерес к СОК, обладающей высоким уровнем естественного параллелизма при выполнении арифметических операций, высокой точностью, надежностью и стойкостью.
Специализированные процессоры на основе арифметики СОК могут сыграть важную роль в высокоскоростных системах обработки данных в режиме реального времени. Операции сложения, вычитания и умножения, называемые модульными операциями, могут быть реализованы очень быстро, без распространения межразрядных переносов. Немодульные операции деления, сравнения чисел, определения знака и переполнения диапазона остаются сравнительно медленными. Любое улучшение скорости этих медленных алгоритмов значительно улучшает производительность многомодульных арифметико-логических устройств (АЛУ). Обычно при рассмотрении деления в СОК выделяют три категории: деление с нулевым остатком, масштабирование и деление в общем случае. Проблема деления в общем виде в СОК привлекает внимание многих исследователей для разработки высокопроизводительных многомодульных АЛУ. Известные алгоритмы деления в СОК, основанные на использовании преобразования в ОПСС, масштабировании, округлении, расширении и других операциях, являются медленными и требуют выполнения большого количества арифметических действий. Большинство известных алгоритмов основаны на сравнении делимого с делителем или с его удвоенным значением, которые представляют определенную сложность. В связи с этим возникает необходимость упростить структуру вычислений при сравнении модулярных чисел. Одним из направлений упрощения операции сравнения модулярных чисел является подход с использованием приближенного метода вычисления позиционной характеристики модулярного числа, который позволяет абсолютно правильно реализовать основные классы процедур принятия решений: проверка равенства (неравенства) двух значений; сравнение двух значений (больше, меньше) и другие, которые обеспечивают решение основного круга задач, возникающих при аппаратной или программной реализации вычислений в системе остаточных классов.
Суть приближенного метода вычисления позиционной характеристики модулярного числа и его использование для деления модулярных чисел основаны на использовании относительных величин анализируемых чисел к полному диапазону, определяемому Китайской теоремой об остатках, которая связывает позиционное число а с его представлением в остатках (α1, α2,…,αn„), где αi - наименьшие неотрицательные вычеты числа, относительно модулей системы остаточных классов р1, р2,…,pn следующим выражением

где 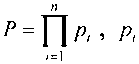 - модули СОК,
- модули СОК, 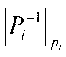 - мультипликативная инверсия Pi относительно pi, и
- мультипликативная инверсия Pi относительно pi, и 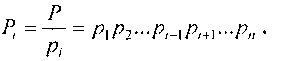
Если разделить левую и правую части выражения (1) на константу Р, соответствующую диапазону чисел, то получим приближенное значение
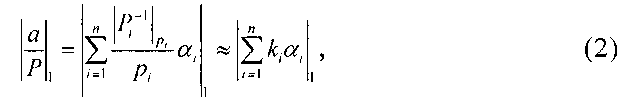
где 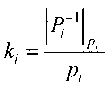 - константы выбранной системы, а αi - разряды числа, представленного в СОК по модулям pi, где i=1, 2,…,n, при этом значение суммы (2) будет в интервале [0,1). Конечный результат суммы определяется после суммирования и отбрасывания целой части числа с сохранением дробной части суммы. Дробная величина
- константы выбранной системы, а αi - разряды числа, представленного в СОК по модулям pi, где i=1, 2,…,n, при этом значение суммы (2) будет в интервале [0,1). Конечный результат суммы определяется после суммирования и отбрасывания целой части числа с сохранением дробной части суммы. Дробная величина 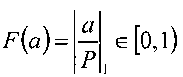 содержит как информацию о величине числа, так и о его знаке. Если
содержит как информацию о величине числа, так и о его знаке. Если 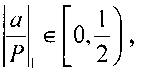 то число a - положительное и F(a) равна величине числа а, разделенной на Р. В противном случае a - отрицательное число, и 1 - F(a) показывает относительную величину числа а. Округление величины F{a) до 2-1 бита будем обозначать как
то число a - положительное и F(a) равна величине числа а, разделенной на Р. В противном случае a - отрицательное число, и 1 - F(a) показывает относительную величину числа а. Округление величины F{a) до 2-1 бита будем обозначать как 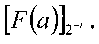 Точное значение величины F(a) определяется неравенствами
Точное значение величины F(a) определяется неравенствами 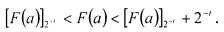 Целая часть числа, полученная в результате суммирования констант ki, представляет собой ранг числа, то есть такую непозиционную характеристику, которая показывает, сколько раз диапазон системы р был превзойден при переходе от представления чисел в системе остаточных классов к его позиционному представлению. При необходимости определение ранга может производиться непосредственно в процессе выполнения операции суммирования констант ki. Дробная часть может быть записана также как A mod 1, потому что
Целая часть числа, полученная в результате суммирования констант ki, представляет собой ранг числа, то есть такую непозиционную характеристику, которая показывает, сколько раз диапазон системы р был превзойден при переходе от представления чисел в системе остаточных классов к его позиционному представлению. При необходимости определение ранга может производиться непосредственно в процессе выполнения операции суммирования констант ki. Дробная часть может быть записана также как A mod 1, потому что  Количество разрядов дробной части числа определяется максимально возможной разностью между соседними числами. При точном сравнении, которое широко используется при делении чисел, необходимо вычислить значение, которое является эквивалентом преобразования из СОК в позиционную систему счисления. Для решения задачи сравнения чисел а и b достаточно приблизительно знать относительные значения чисел
Количество разрядов дробной части числа определяется максимально возможной разностью между соседними числами. При точном сравнении, которое широко используется при делении чисел, необходимо вычислить значение, которое является эквивалентом преобразования из СОК в позиционную систему счисления. Для решения задачи сравнения чисел а и b достаточно приблизительно знать относительные значения чисел 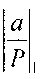 и
и 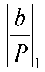 по отношению к динамическому диапазону [0,l), что выполняется достаточно просто, но при этом верно определяются соотношения А=В, А>В или А<В.
по отношению к динамическому диапазону [0,l), что выполняется достаточно просто, но при этом верно определяются соотношения А=В, А>В или А<В.
Пример 1. Пусть дана система оснований р1=2, р2=3, р3=5, р4=7, объем диапазона Р=2·3·5·7=210. Допустим, что в заданной СОК будут представлены только положительные числа. Определим величины 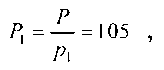
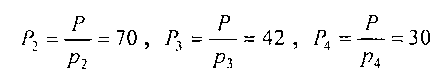 и сравним два числа а=25 и 6=30, представленные в СОК по основаниям р1, р2, р3, р4. Определим числа а и b в СОК: а=(1,1,0,4), 6=(0,0,0,2). Для реализации предлагаемого алгоритма найдем константы
и сравним два числа а=25 и 6=30, представленные в СОК по основаниям р1, р2, р3, р4. Определим числа а и b в СОК: а=(1,1,0,4), 6=(0,0,0,2). Для реализации предлагаемого алгоритма найдем константы 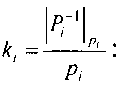
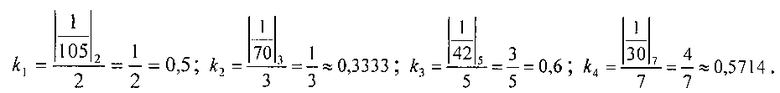
Далее, используя выражение (2) найдем функции F(a) и F(b)
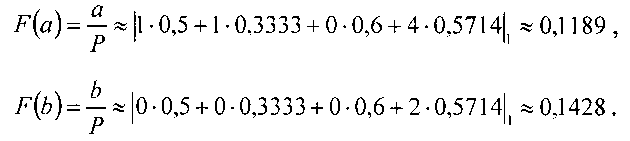
Так как  то есть 0,1428>0,1189, то b>а, и действительно 30>25.
то есть 0,1428>0,1189, то b>а, и действительно 30>25.
Алгоритм деления целых чисел 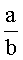
Алгоритм деления можно описать следующими правилами.
Конструируется некоторое правило φ, которое каждой паре целых положительных чисел а и b ставит в соответствие некоторое положительное число qi, где i - номер итерации, такое что a-bq1=r1≥0, то есть a > bql. Тогда деление а на b осуществляется по следующему правилу: согласно операции φ паре чисел а и b ставится в соответствие число q1=qi, такое что а-bq1=r1≥0, то есть a ≥ bq1. В качестве qi примем значения 2i, которые поместим в память в виде констант qi=(2i mod р1,2i mod р2,…,2i mod pn). При этом i+1 операция не зависит от i-й операции, что позволяет итерации выполнять параллельно. Кроме того, в каждой итерации выполняются только две операции: умножение делителя на константу 2i и сравнение полученного значения с делимым.
Если r1,<b1, то деление закончено, если же r1≥b1, то согласно правилу φ паре чисел (r1, b) ставится в соответствие q2 такое, что a-bq2=r2≥0, то есть a≥bq2. Если r2<b, то деление завершается, если же r2≥b, то согласно правилу φ паре чисел {r2, b) ставится в соответствие q3 такое, что а-bq3=r3≥0 и т.д. Так как последовательное применение операции φ приводит к убывающей последовательности целых чисел а>r1>r2>…≥0, то алгоритм реализуется за конечное число шагов. Пусть на n -м шаге зафиксирован случай а<bqn, что означает окончание операции деления. Тогда в итоге получим а≅(q1+q2+…+qn)b+rn, где ряд q1+q2+…+qn есть аппроксимация частного, которое может содержать лишние qi. Далее необходимо провести уточнение полученного аппроксимирующего ряда.
Уточнение начнем со старшего qn. Если a>bqn, то qn является членом аппроксимирующего ряда образованного частного. Далее берем (qn+n+1), если a>b(qn+qn-1), то qn-1 вносится в ряд, иначе, если a<b(qn+qn-1), то qn-1 исключается из ряда и т.д. После проверки всех частное определяется оставшимися членами ряда. Тогда искомое частное определяется выражением
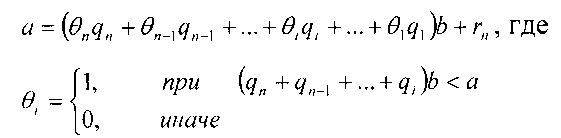
Данный алгоритм легко модифицируется в модулярную форму, причем абсолютные значения величин заменяются их относительными значениями. При этом структура алгоритма основана на сравнении относительных значений, которое выполняется с использованием операции вычитания. Однако некоторые операции в системе остаточных классов, такие как сравнение чисел и деление, весьма сложные. С целью сокращения временной сложности при использовании модулярной формы абсолютные величины делимого и делителя заменим на их относительные значения к общему диапазону системы остаточных классов.
Известные алгоритмы деления определяют частное на основе итерации A′=A-QD, где А и А′, соответственно, текущее и следующее делимое, D - делитель, Q1 - частное, которое генерируется на каждой итерации из полного диапазона СОК, а не выбирается из небольшого множества констант. В предлагаемом алгоритме частное определяется на основе итерации ri=А-b2i, где А - некоторое делимое, 6 - делитель, а 2' является членом аппроксимирующего ряда частного.
Сравнение алгоритмов показывает, что деление во всех итерациях не меняется, а делитель умножается на константу, что существенно уменьшает вычислительную сложность. Приведенный выше алгоритм легко модифицируется в систему остаточных классов с применением приближенного метода сравнения модулярных чисел. При итерационном процессе деления в позиционной системе счисления для поиска старшей степени ряда аппроксимации частного и для уточнения аппроксимирующего ряда сравниваются делимое с удвоенными делителями или с суммой членов ряда. Применение этого принципа для СОК может привести к ошибке процесса деления, так как при переполнении динамического диапазона восстановленное число выходит за пределы рабочего диапазона, числа которого будут меньше делимого, что не соответствует действительности, так как на самом деле числа будут превышать диапазон Р. Например, если модули СОК равны р1=2, р2=3, р3=5, р4=7, тогда диапазон Р=2·3·5·7=210. Допустим при восстановлении получили число А=220. В СОК Л=220=(0,1,0,3). Диапазон Р превышен на число 10, которое в СОК равно (0,1,0,3). При использовании относительных значений число А=220 выражается как А′=10, что не соответствует действительности.
Для преодоления этой трудности необходимо в СОК сравнивать результаты текущих значений итераций с предыдущими, что позволяет правильно определить большее или меньшее число. Итак, факт переполнения динамического диапазона в СОК можно использовать для принятия решения «больше-меньше». На первой итерации происходит сравнение делимого с делителем, а на остальных итерациях происходит сравнение удвоенных значений делителей qib<qj+1b. На каждой новой итерации происходит сравнение текущего значения с предыдущим. Количество требуемых итераций зависит от величин делимого и делителя. Последовательное применение этой операции приводит к формированию последовательности целых чисел bq1<bq2<…<bqn>bqn+1. Таким образом, алгоритм реализуется за конечное число итераций. Пусть на n+1 итерации зафиксирован случай bqn>bqn+1, что соответствует переполнению диапазона СОК, то есть bqn+l>Р и а<bqn+l. На этом процесс формирования интерполяции частного двоичным рядом или набором констант в СОК завершается. Итак, процесс аппроксимации частного может осуществляться путем сравнения только удвоенных соседних приближенных делителей.
Рассмотрим алгоритм деления на примере. Действия будут производиться как над десятичными числами, так и над числами, представленными в системе остаточных классов.
Пример 2. Найти частное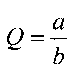 от деления числа а=201 на число b=8. Выберем СОК с основаниями 2, 3, 5, 7, тогда Р=р1р2р3р4=210. Константы ki соответственно равны: k1=0,5; k2=0,3333; k3=0,6; k4=0,5714.
от деления числа а=201 на число b=8. Выберем СОК с основаниями 2, 3, 5, 7, тогда Р=р1р2р3р4=210. Константы ki соответственно равны: k1=0,5; k2=0,3333; k3=0,6; k4=0,5714.
Представим в СОК числа а и b.
а10=201→(l,0,l,5)сок,
b10=8→(0,2,3,l)сок.
Относительные значения этих чисел, соответственно, равны:
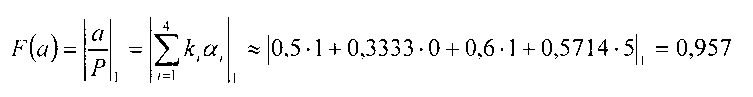
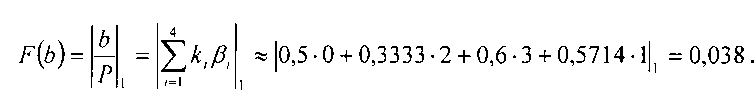
Решение. Деление а на b осуществляется по следующему алгоритму. Для интерполяции частного определим степени 2i, представленные в СОК.
I. Поиск старшей степени при аппроксимации частного двоичным рядом.
1. На первой итерации сравниваем 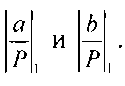 Если
Если 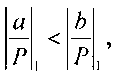 то в память ничего не записывается, так как в этом случае делитель больше делимого и на этом процесс деления заканчивается и частное равно 0. Если
то в память ничего не записывается, так как в этом случае делитель больше делимого и на этом процесс деления заканчивается и частное равно 0. Если 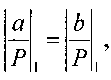 то в память записываем константу q1=2°, а если
то в память записываем константу q1=2°, а если  то реализуется итерационный процесс деления.
то реализуется итерационный процесс деления.
Допустим, что делимое а и делитель b имеют следующие значения:
а10=201→(1,0,l,5)сок, b10=8→(0,2,3,1)сок.
Найдем частное от деления 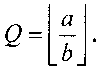
Тогда,

отсюда 0,957>0,038, то есть
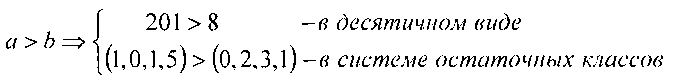
В память записываем константы, представленные в двоичном коде q1=2° и в СОК q1=(1,1,1,1).
2. Далее во всех остальных итерациях будем сравнивать текущие значения с предыдущими. Так, на второй итерации умножаем знаменатель на 21, то есть q2=2, если 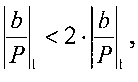 то в память запишем 21.
то в память запишем 21.
Тогда
b1}=8·2=16, b1=16→(0,2,3,l)·(0,2,2,2)=(0,l,l,2).
Сравнение дает следующий результат:
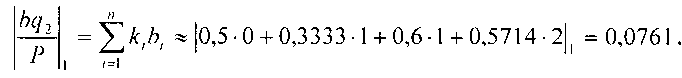
Тогда 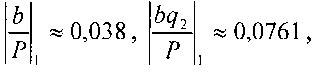 так как 0,038<0,0761, то
так как 0,038<0,0761, то 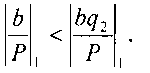
В память записываем число в двоичном коде q2=21, а в СОК q2=(0,2,2,2).
3. Аналогично получим результаты сравнения на следующих итерациях.
На третьей итерации умножаем знаменатель b на q3=22, если 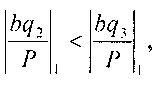 то в память запишем 22.
то в память запишем 22.
Так как b2=8·4=32, b2=32→(0,2,3,l)·(0,l,4,4)=(0,2,2,4).
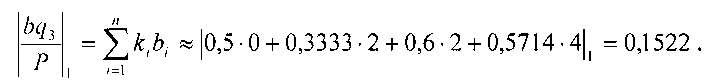
Тогда 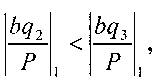 так как 0,0761<0,1522.
так как 0,0761<0,1522.
В память записываем число в двоичном коде q3=22, а в СОК q3=(0,1,4,4).
4. На четвертой итерации получим результат
b3=8·8=64; b3=64→(0,2,3,1)·(0,2,3,1)=(0,1,4,1).
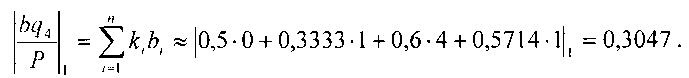
Тогда 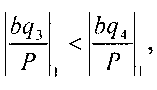 так как 0,1522<0,3047.
так как 0,1522<0,3047.
В память записываем число в двоичном коде q4=23, а в СОК q4=(0,2,3,1).
5. На пятой итерации получим следующий результат
b4=8·16=128, b4=128→(0,2,3,l)·(0,l,l,2)=(0,2,3,2).

Тогда 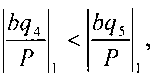 так как 0,3047<0,6094.
так как 0,3047<0,6094.
В память записываем число в двоичном коде q5=24, а в СОК qs=(0,1,1,2).
6. На шестой итерации получим следующий результат
b5=8·32=256, b5=256→(0,2,3,1)·(0,2,2,4)=(0,1,1,4).
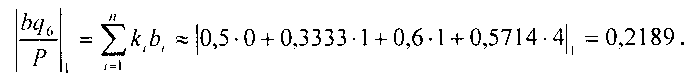
Тогда 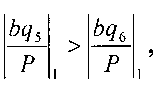 так как 0,6094>0,2189.
так как 0,6094>0,2189.
Таким образом, произошло переполнение, и в память ничего не записывается. Процесс формирования аппроксимационного ряда частного завершается.
Итак, первое неравенство 0,957>0,038 определяет начало итерационного процесса деления, а последовательность последующих неравенств 0,0761>0,038; 0,1522>0,0761; 0,3047>0,1522; 0,6094>0,3047, или 0,038<0,0761<0,1522<0,3047<0,6094>0,2189 определяет количество итераций. Отсюда видно, что на шестом шаге заканчивается возрастающая последовательность. Этот факт сигнализирует об окончании итераций, так как полученный путем последовательного умножения на 2 делитель превысил делимое.
II. Уточнение аппроксимирующего ряда частного от деления а на b начнем со старшего qn.
1. Из памяти выбираем старшую степень, то есть q5=(0,1,1,2), умножаем на знаменатель b=(0,2,3,1) и сравниваем с а. Тогда
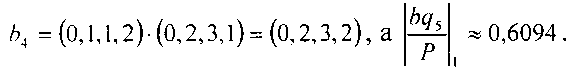
Так как 0,957>0,6094, то в качестве старшей степени берем 24, а в СОК (0,1,1,2).
2. Из памяти выбираем степень 23 и вычисляем (24+23)·8=192, а в СОК ((0,1,1,2)+(0,2,3,1))·(0,2,3,1)=(0,0,2,3). Тогда
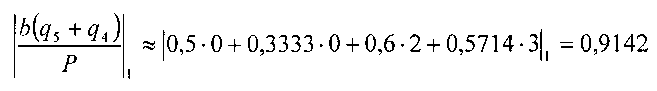
Так как 0,9142>0,6094 и 0,957>0,9142, то в качестве следующего члена ряда берем 23, а в СОК (0,2,3,1).
3. Из памяти берем 22 и вычисляем (24+23+22)·8=224. Тогда ((0,1,1,2)+(0,2,3,1)+(0,1,4,4))·(0,2,3.1)=(0,2,4,0),
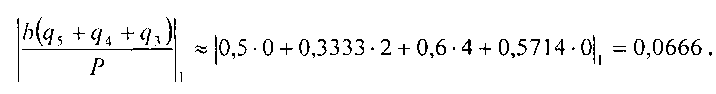
Так как 0,0666<0,9142, то произошло переполнение диапазона Р и степень 22, или в СОК (0,1,4,4), из аппроксимационного ряда исключается.
4. Из памяти берем 21 и вычисляем (24+23+21)·8=208. Тогда ((0,1,1,2)+(0,2,3 J)+(0,2,2,2))·(0,2,3, l)=(0,1,3,5),

Так как 0,957<0,9903, то степень 21 или (0,2,2,2) из аппроксимационного ряда исключается.
5. Из памяти берем 20 и вычисляем (24+23+20)·8=200. Тогда ((0,l,l,2)+(0,2,3,l)+(l,l,l,l))·(0,2,3,l)=(0,2,0,4),a
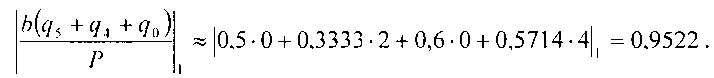
Так как 0,957>0,9522, поэтому в качестве младшей степени берем 20 или в СОК (1,1,1,1) Следовательно, частное равно (0,l,l,2)+(0,2,3,l)+(l,l,l,l)=(l,l,0,4).
Для определения частного необходимо сложить оставшиеся члены аппроксимационного ряда. Из приведенного примера видно, что остались следующие члены ряда: (0,1,1,2), (0,2,3,1) и (l,1,1,1). Тогда частное определяется путем суммирования членов ряда:
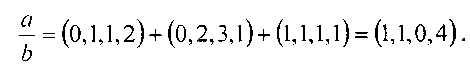
По остаткам частного восстановим позиционное число с помощью выражения (1), тогда
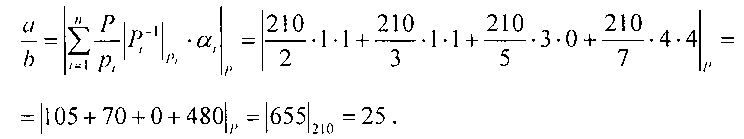
Действительно 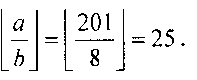
Результат в СОК и в позиционной системе счисления совпадают, что говорит о правильности проведенного деления.
Новый алгоритм основного деления модулярных чисел.
Улучшенный алгоритм деления модулярных чисел на основе приближенного метода сравнения чисел состоит из следующих шагов.
1. Вычисляем приближенные значения делимого F(a) и делителя F(b), и сравниваем их. Если F(a)<F(b), то процесс деления заканчивается и частное 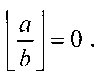 Если F(a)=F(b), то процесс деления заканчивается и частное
Если F(a)=F(b), то процесс деления заканчивается и частное 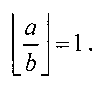 Если F(a)>F(b), то осуществляется поиск старшей степени 2k при аппроксимации частного двоичным кодом.
Если F(a)>F(b), то осуществляется поиск старшей степени 2k при аппроксимации частного двоичным кодом.
2. Сдвигаем функцию F(b) влево до появления переноса старшего значащего разряда в знаковый разряд. Количество сдвигов определяет старшую степень, которая регистрируется счетчиком импульсов.
3. Из памяти 5 выбираем константу 2k (старшая степень ряда), умножаем ее на делитель F1(b)=b2k и подаем на вход схемы сравнения.
4. Находим Δi=F(a)-F1(b). Если в знаковом разряде Δi стоит «1», то соответствующая степень ряда отбрасывается, если стоит «0», то в сумматор частного 13 добавляем значение члена ряда с этой степенью, то есть 2k.
5. Сдвигаем F1(b) «вправо» и проверяем член ряда со степенью 2k-1.
6. Находим Δ2=Δ1-F1{b) и выполняем действия в соответствии с пунктом 4.
7. Аналогично проверяем все оставшиеся члены ряда до нулевой степени. Полученный остаток Δi=Δi-1-Fi-1(b)≈0. В случае, когда делитель принимает значение, равное нескольким единицам, то порог Δi можно взять больше нуля, что позволит сократить количество итераций при делении большого делимого и маленького делителя. В процессе этих преобразований суммируем все разрешенные члены ряда.
Процесс сдвига и вычитания завершается проверкой нулевой степени ряда. В накопительном сумматоре суммируются только разрешенные члены аппроксимирующего ряда частного. После последнего шага устройство устанавливается в исходное состояние.
Новый упрощенный алгоритм для деления модулярных чисел основан на использовании приближенного метода сравнения, который значительно снижает вычислительную сложность алгоритма. Он требует лишь одну операцию приближенного сравнения, одну операцию умножения и по числу шагов операции сдвига и вычитания. При реализации известных алгоритмов в каждой итерации используются операции сравнения, умножения и сложения. Исходя из этого можно сказать, что на сегодняшний день предложенный алгоритм является лучшим решением выполнения операции деления, что позволит в целом упростить реализацию аппаратно-логических модулярных схем.
Пример 3. Рассмотрим работу устройства деления на конкретном примере. Используем делимое и делитель из примера 2, где а=201=(1,0,1,5) и b=(0,2,3,1). Найдем частное от деления числа а на число b 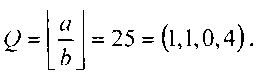
1. На вход 1 подается делимое a=(l,0,l,5), а на вход 2 - делитель b=(0,2,3,l). Выберем из LUT-таблиц схемы сравнения 11 значения kiαi и kiβi которые используются для сравнения модулярных чисел схемой сравнения и выдаются схемой сравнения для суммирования по модулю 1 в сумматорах делимого 37 и делителя 10. Эти операции осуществляются параллельно в схеме сравнения и сумматорах делимого 37 и делителя 10. Так как F(a)=0,957 и F(b)=0,038, то схема сравнения 11 формирует сигнал а>b, а в сумматорах формируются значения в двоичной форме соответственно F(a)=0,11110 и F(b)=0,00001.
2. В регистре сдвига 9 сдвигаем F(b) на 5 разрядов влево F(b)c=1,00000, счетчик 4 формирует состояние, соответствующее высшей степени ряда 24.
3. Умножаем делитель b=8=(0,2,3,1) на 24=16=(0,1,1,2), тогда b·24=(0,2,3,1.)(0,1,1,2)=(0,2,3,2).
4. Вычисляем F(b·24)≈0,6094.
5. Вычисляем F(a)-F(b·24)≈0,957-0,6094=0,3476. Разность положительная, в знаковом разряде «0», который разрешает прохождение члена ряда (0,1,1,2) через схему «запрета» 12 на вход сумматора 13 частного и разности F(a)-f(b·24)≈0,3476 на вход регистра 36 хранения остатка при вычитании из делимого членов ряда частного через схему «запрета» 35, которая далее поступает на второй вход сумматора делимого 37. В регистре сдвига 9 запишем значение функции F(b·24), причем регистр сдвига 9 переведен в режим сдвига «вправо».
6. В регистре сдвига 9 F(b·24) сдвигаем на 1 разряд «вправо», то есть уменьшаем число в 2 раза, при этом Fc(b·24)≈0,3047, и результат подаем на первые входы вычитателя 14, а на вторые входы вычитателя 14 поступает разность F(a)-F(b·24)≈0,3476. На выходе вычитателя 14 получаем F(a)-F(b·24)-F(b·23)≈0,3476-0,3047=0,0429. Так как число положительное, то в схеме происходят процессы, аналогичные пункту 5 и в сумматоре 13 частного содержимое (0,1,1,2) суммируется с 23=8=(0,2,3,1), то есть (0,l,l,2)+(0,2,3,l)=(0,0,4,3), а в сумматор делимого 37 записываются новые данные 0,0429.
7. Содержимое регистра сдвига 9 F(b·23) сдвигаем вправо и получаем F(b·22). Тогда на первом входе вычитателя будет число 0,1524, а на втором 0,0429. Результат вычитания будет отрицательным и схемы «запрета» 12 и 35 не пропустит данные на вход регистра 36 хранения. Содержимое сумматора частного 13 и регистра 36 хранения сохраняется, а степень 22 удаляется.
Далее происходит сдвиг содержимого регистра сдвига 9, то есть получаем F(b·21), тогда на первом входе вычитателя будет число 0,0762, а на втором 0,0429. При вычитании процесс повторяется, как и для степени 22, то есть степень 21 тоже удаляется. Новый сдвиг дает число F(b·20). Тогда на первом входе вычитателя будет число 0,0381, а на втором 0,0429. При вычитании результат будет положительным и к содержимому сумматора частного 13 (0,0,4,3) добавляется (1,1,1,1), то есть (0,0,4,3)+(l,1,1,l)=(1,1,0,4).
Получили частное Q=(1,1,0,4) от деления числа а=(1,0,1,5) на число b=(0,2,3,1).
В таблице 1 приведены исходные и промежуточные величины работы алгоритма. В алгоритме использованы двоичные значения F(a) и F(b). Округление F(a) и F(b) проведено до t -го бита, где t - первый значащий разряд F(b). Вычислительная сложность нового алгоритма деления представлена в таблице 1. Сравнительный анализ работы нового алгоритма с модифицированными показал преимущества первого. Если все операции свести к элементарным действиям типа побитового сложения и сдвига, то выигрыш нового алгоритма по вычислительной сложности примерно равен 5.
На чертеже представлена схема для деления модулярных чисел. Принцип работы изобретения излагается ниже. Устройство для деления модулярных чисел позволяет выполнять операцию деления при произвольных значениях делимого и делителя без каких-либо дополнительных предварительных операций, кроме операций, устанавливающих устройство в исходное состояние.
Режим аппроксимации частного двоичным рядом
В исходном состоянии схема управления 3 по шине 18 выдает сигнал «установка в 0», по которому регистр сдвига 9, счетчик 4 и сумматоры делителя 10 и частного 13, вычитатель 14 устанавливаются в начальное состояние, а мультиплексор 8 (сигнал поступает на адресный вход) коммутирует шину 2 на вход схемы сравнения 11, шина 33.
Делимое и делитель, представленные в системе остаточных классов по модулям p1,p2,…,pn соответственно, по шинам 1 и 33 поступают на вход схемы сравнения 11, в которой происходит сравнение относительных значений делимого и делителя. Если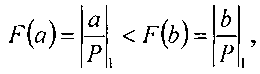 то схема сравнения формирует сигнал по шине 19, который поступает на вход схемы управления 3, и устройство устанавливается в начальное состояние. Частное (шина 30) равно нулю. Если
то схема сравнения формирует сигнал по шине 19, который поступает на вход схемы управления 3, и устройство устанавливается в начальное состояние. Частное (шина 30) равно нулю. Если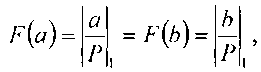 то схема сравнения 11 выдает сигнал равенства делимого и делителя по шине 42 на вход сумматора частного 13, в который записывается константа «1». Если
то схема сравнения 11 выдает сигнал равенства делимого и делителя по шине 42 на вход сумматора частного 13, в который записывается константа «1». Если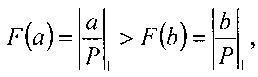 то схема сравнения 11 формирует сигнал по шине 20, под действием которого схема управления 3 переводит устройство в режим аппроксимации ряда частного. Значения kiβi и kiαi с выходов LUT-таблиц схемы сравнения 11 по шинам 25 и 26 соответственно поступают на вход сумматоров делителя 10 и делимого 37. Относительное значение делимого, представленное в дополнительном коде, выход сумматора делимого 37, по шине 38 поступает на вход вычитателя 14.
то схема сравнения 11 формирует сигнал по шине 20, под действием которого схема управления 3 переводит устройство в режим аппроксимации ряда частного. Значения kiβi и kiαi с выходов LUT-таблиц схемы сравнения 11 по шинам 25 и 26 соответственно поступают на вход сумматоров делителя 10 и делимого 37. Относительное значение делимого, представленное в дополнительном коде, выход сумматора делимого 37, по шине 38 поступает на вход вычитателя 14.
Относительное значение делителя, выход сумматора делителя 10, по шине 23 поступает на вход регистра сдвига 9. Под действием тактовых импульсов схемы управления 3 (шина 17) происходит сдвиг содержимого регистра сдвига 9 и счет этих импульсов счетчиком 4. Как только старший значащий разряд делителя становится знаковым, т.е. произошло переполнение, то эта единица по шине 22 останавливает счет импульсов счетчиком 4 и активируется сигнал «разрешение считывания» информации из памяти 5. Счетчик 4 регистрирует состояние, формирующее высшую степень 2k ряда частного. В регистре 36 хранения остатка при вычитании из делимого членов ряда частного в это время во всех разрядах записано значение «0» и он не оказывает никакого влияния на сумматор делимого 37. На этом режим интерполяции частного заканчивается. Итак, для интерполяции частного потребовалась одна итерация сравнения, одна операция суммирования и одна операция сдвига на k разрядов.
Операция сдвига эквивалентна одной итерации известного алгоритма. В каждую итерацию входит операция удвоения делителя и операция сравнения результата удвоения со значением делителя. Замена абсолютных значений их относительными значениями позволила при интерполяции частного получить выигрыш по сравнению с рассмотренными выше алгоритмами в k раз, где k - количество сдвигов до появления переполнения.
Режим уточнения аппроксимирующего ряда частного отделения а на b.
Схема управления 3 формирует сигналы по шинам 15 и 17, которые подаются на адресные входы мультиплексора 8 и коммутирует умноженное значение делителя на высшую степень ряда частного (шина 32) на выход мультиплексора 8 и переводит регистр сдвига 9 в режим сдвига «вправо». Ключ 6 (шина 28)под действием двух сигналов, поступивших на его вход по шинам 16 и 24, подает на вход схемы умножения 7 и схемы «запрета» 12 значение высшей степени ряда. Поступившие данные на вход схемы сравнения 11 сравниваются. Если 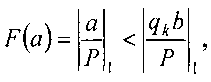 то схема сравнения 11 выдает сигнал по шине 19 и устанавливает устройство в исходное состояние. Если
то схема сравнения 11 выдает сигнал по шине 19 и устанавливает устройство в исходное состояние. Если 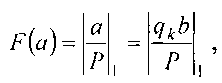 то формируется сигнал а=b и по шине 42 записывает в сумматор «единицу», а устройство переходит в исходное состояние. Если
то формируется сигнал а=b и по шине 42 записывает в сумматор «единицу», а устройство переходит в исходное состояние. Если 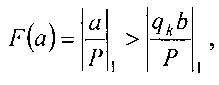 то сигнал по шине 20 устанавливает устройство в режим уточнения аппроксимационного ряда частного.
то сигнал по шине 20 устанавливает устройство в режим уточнения аппроксимационного ряда частного.
Значения умноженного на высшую степень делителя и делимого, как в случае интерполяции ряда, поступают на вход сумматоров делителя 10 и делимого 37. Содержимое сумматора делителя 10 по шине 23 подается на вход регистра сдвига 9, стирает старую информацию и записывает новое значение и далее по шине 34 подается на вход вычитателя 14, а содержимое сумматора делимого 37 в дополнительном коде подается на вторые входы вычитателя 14, где происходит вычитание умноженного делителя на высшую степень из содержимого делимого. Делимое и делитель, как и ранее, представлены своими относительными значениями. Если в знаковом разряде результата вычитания в вычитателе 14 стоит «ноль», то есть делимое больше делителя, тогда на запрещающих входах схем «запрета» 12 и 35 формируются «нули» и высшая степень частного по шине 28 через схему «запрета» 12 поступает на вход сумматора частного 13 по шине 29, а результат вычитания вычитателя 14, то есть остаток делимого, приходящий на остальные степени по шине 40 через схему «запрета» 35, подается на вход регистра 36 хранения остатка при вычитании из делимого членов ряда частного и далее по шине 39 поступает на вход сумматора делимого 37, где удаляется старое содержимое и записывается новое значение. Далее происходит сдвиг «вправо» содержимого регистра сдвига 9 и процесс происходит аналогично вышеизложенному. При этом, если в знаковом разряде результата вычитания в вычитателе 14 будет стоять «1», то есть относительное значение делителя больше делимого, то появившаяся единица, поступающая на запрещающие входы схемы «запрета» 12 и 35, запрещает прохождение соответствующей степени на сумматор частного 13 и результата вычитания вычитателя 14 на вход регистра 36 хранения остатка при вычитании из делимого членов ряда частного, то есть регистр сохраняет прежнее значение результата суммирования. Таким образом, на вход сумматора частного 13 поступают только те уточненные степени, которые являются членами ряда частного. Процесс преобразования заканчивается после анализа степени 20. Таким образом, при уточнении итеративно удаляются лишние члены аппроксимационного ряда частного путем несложных преобразований, состоящих из операций сдвига и сложения. В известном алгоритме при уточнении используются такие сложные операции, как умножение и сравнение, которые входят в каждую итерацию.
Итак, основное деление модулярных чисел осуществляется примерно за 2 итерации сравнения и k-1 операций сдвига и сложения, а в известном алгоритме необходимо 2k итераций сравнения, k операций умножения и 2k операций суммирования. Выигрыш в скорости деления модулярных чисел достигает примерно k итераций. Это лучший на сегодняшний день алгоритм основного деления модулярных чисел. Это достоинство предложенного алгоритма по сравнению с известным достигается тесной связью архитектурных вычислений с аппаратной реализацией, что позволило значительно сократить вычислительную сложность деления модулярных чисел. Предложенный алгоритм отличается от известных простотой его реализации, который требует меньшего объема вычислений по сравнению с существующими алгоритмами.
Сравнительный анализ по сложности и времени деления модулярных чисел изобретения с известными (патент RU 2400813, опубликованный 27.09.2010, Бюл. №27) показал значительные преимущества по аппаратным и временным ресурсам.
Так, в известном изобретении используются:
схема для преобразования в ОПСС;
схема для нахождения приблизительного делителя;
схема для деления с нулевым остатком; схема памяти;
схема расширения оснований СОК;
схема ключей;
схема сравнения, умножения и вычитания.
Сложность всех перечисленных схем пропорциональна n, где n - число оснований СОК, то есть сложность всего устройства определяется как N=O(zn), где z - количество схем, перечисленных выше.
В предложенном устройстве для деления чисел используются:
схема сравнения модулярных чисел;
схема умножения, сложения;
схемы регистров и счетчик;
схемы мультиплексоров;
схемы ключей.
Сложность устройства определяется как 0(5k), где k - количество двоичных разрядов относительных значений делимого и делителя.
При нежестком допущении о равенстве количества разрядов двоичного представления СОК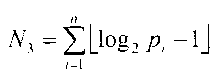 и разрядов относительных величин делимого и делителя выигрыш в аппаратурных затратах равен 1,4 раза.
и разрядов относительных величин делимого и делителя выигрыш в аппаратурных затратах равен 1,4 раза.
По временным ресурсам на конкретном примере (один и тот же пример рассмотрен в известном и предложенном устройстве) выигрыш примерно равен 5. Все итерации в предложенном устройстве состоят из операций сдвига и сложения. На сегодняшний день это лучшее решение.
| название | год | авторы | номер документа |
|---|---|---|---|
| НЕЙРОННАЯ СЕТЬ ОСНОВНОГО ДЕЛЕНИЯ МОДУЛЯРНЫХ ЧИСЕЛ | 2008 |
|
RU2400813C2 |
| УСТРОЙСТВО ДЛЯ ОСНОВНОГО ДЕЛЕНИЯ МОДУЛЯРНЫХ ЧИСЕЛ В ФОРМАТЕ СИСТЕМЫ ОСТАТОЧНЫХ КЛАССОВ | 2013 |
|
RU2559772C2 |
| Устройство для деления чисел в модулярной системе счисления | 1990 |
|
SU1756887A1 |
| Устройство деления модулярных чисел | 2016 |
|
RU2628179C1 |
| УСТРОЙСТВО ДЕЛЕНИЯ И ИЗВЛЕЧЕНИЯ КВАДРАТНОГО КОРНЯ | 2012 |
|
RU2510072C1 |
| Двоичное устройство деления | 1975 |
|
SU541171A2 |
| Устройство для деления двоичных чисел | 1982 |
|
SU1084785A1 |
| ПОСЛЕДОВАТЕЛЬНЫЙ ДЕЛИТЕЛЬ ТРОИЧНЫХ ЦЕЛЫХ ЧИСЕЛ | 2023 |
|
RU2810609C1 |
| Устройство для деления в системе остаточных классов | 1983 |
|
SU1141400A1 |
| Устройство для деления чисел в системе остаточных классов | 1985 |
|
SU1287152A1 |


Изобретение относится к вычислительной технике и может быть использовано в вычислительных системах, функционирующих в системе остаточных классов. Техническим результатом является повышение скорости деления чисел, сокращение оборудования и повышение функциональных возможностей устройства за счет выполнения операции деления при произвольных значениях делимого и делителя без предварительного анализа исходных операндов. Устройство содержит умножитель, мультиплексор, схему сравнения, регистры, счетчик, сумматоры, вычитатель, память, схему управления, элементы запрета, ключ. 1 ил., 1 табл. 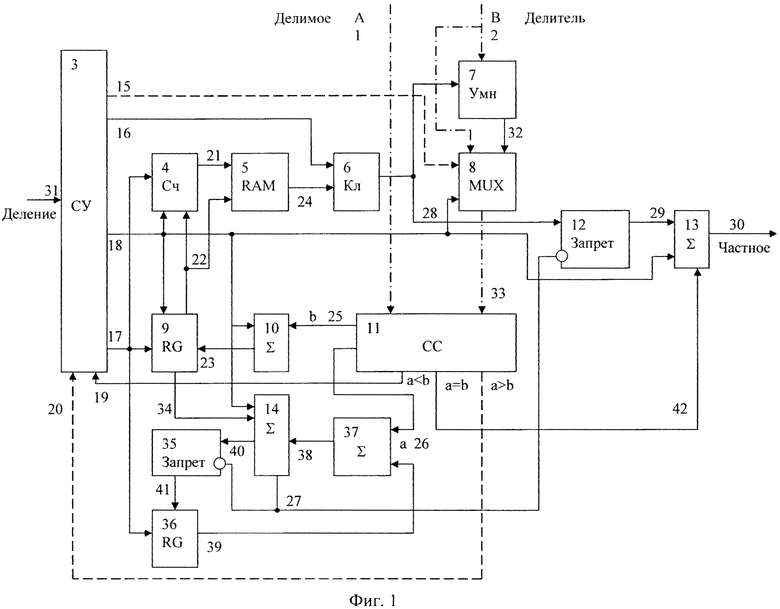
Устройство для основного деления модулярных чисел, содержащее входные шины делимого и делителя, которые подают делимое непосредственно, а делитель через схему умножения, либо через мультиплексор на вход схемы сравнения модулярных чисел, выходы которой реализуют вычислительную модель а<b, а>b или а=b, где а - делимое, b - делитель; управляющие выходы схемы сравнения а<b, а>b соединены со схемой управления, выходы которой соединены с адресными входами мультиплексора, входами управления счетчика, регистров сдвига и хранения, сумматоров частного, делителя и вычитателя, а также с одним из входов ключей, вторые входы которых соединены с выходом памяти, входы которой соединены с регистром сдвига, а выход а=b схемы сравнения соединен со входом сумматора частного, помещая в него «единицу», а информационные выходы соединены со схемами сумматоров делимого и делителя, выходы которого соединены регистром сдвига влево, выход которого соединен со счетчиком определения высшей степени аппроксимационного ряда частного, выход счетчика соединен с адресными входами памяти, выходы которой через схему ключей и запрет подают на вход сумматора частного степень члена ряда, входящего в уточненный член ряда частного и на вход схемы умножения высшей степени ряда на делитель, выход которой через мультиплексор соединен со схемой сравнения, выходы которой соединены с сумматорами делимого и делителя; выход сумматора делителя соединен со входом регистра сдвига вправо, выход которого соединен со схемой вычитателя, на второй вход которого подключен выход сумматора делимого, выход вычитателя соединен с регистром хранения остатка при вычитании из делимого членов ряда частного, выход которого соединен через сумматор делимого с вычитателем, выход которого соединен со схемой запрета, выходы которой соединены с регистром хранения остатка при вычитании из делимого членов ряда частного и схемой сумматора частного.
| НЕЙРОННАЯ СЕТЬ ОСНОВНОГО ДЕЛЕНИЯ МОДУЛЯРНЫХ ЧИСЕЛ | 2008 |
|
RU2400813C2 |
| НЕЙРОННАЯ СЕТЬ ДЛЯ ДЕЛЕНИЯ ЧИСЕЛ, ПРЕДСТАВЛЕННЫХ В СИСТЕМЕ ОСТАТОЧНЫХ КЛАССОВ | 2006 |
|
RU2318239C1 |
| Устройство для деления чисел в модулярной системе счисления | 1990 |
|
SU1756887A1 |
| Арифметическое устройство по модулю | 1989 |
|
SU1633400A1 |
| US 2008114820 A1, 15.05.2008 | |||
| US 2005038845 A1, 17.02.2005 | |||
| US 6470372 B1, 22.10.2002 | |||
Авторы
Даты
2015-08-10—Публикация
2013-10-30—Подача