Изобретение относится к нейрокомпьютерной технике и предназначено для классификации классов чисел по заданному модулю р.
Близким по технической сущности (аналогом к предлагаемому изобретению) является устройство (патент РФ №2279132, МКИ G06N 3/04, Б.И. №18, 2006 г.), содержащее входной и скрытый слой нейронов, выходной слой нейронной сети.
Недостаток аналога - низкое быстродействие при классификации классов чисел по заданному модулю р.
Наиболее близким (прототипом к предлагаемому изобретению является устройство (патент РФ №2701064, МКИ G06N 3/04, Б.И. №27, 2019 г.), содержащее входной, скрытый и выходной слои нейронов, два регистра и группу блоков элементов И).
Недостаток прототипа - низкое быстродействие классификации чисел по заданному модулю, ввиду того, что скрытые слои рекурсивно объединяются, организуя логарифмическое суммирование. При этом в процессе участвуют все элементы входного слоя. Однако не учитывается двойственность распределения остатков в периоде повторения, т.е. остатки, парные суммы которых равны р, что позволяет исключить соответствующие разряды в двоичном представлении исходного числа. Это позволяет минимум в два раза уменьшить число проводимых рекурсий, т.к. сложение с нулем представляет собой фактически не бинарную, а унарную операцию. Тем самым существенно увеличивается быстродействие проводимой операции.
Задача, на решение которой направлено заявляемое устройство, состоит в повышении производительности перспективных образцов нейрокомпьютерной техники.
Технический результат выражается в повышении быстродействия (уменьшении временных затрат) при классификации чисел по заданному модулю р.
Технический результат достигается тем, что в устройство, содержащее нейронную сеть конечного кольца для классификации чисел по модулю, содержащая входной слой, предназначенный для хранения числа, представленного в позиционной системе счисления, скрытый слой нейронов, предназначенный для взвешенного суммирования сохраненных чисел по формуле
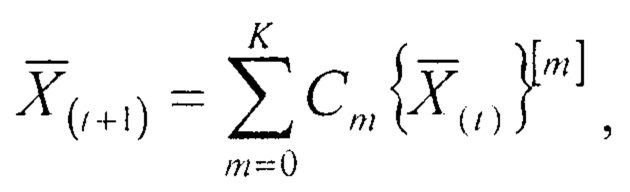
где 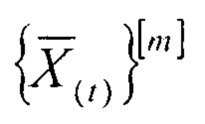 является оператором извлечения m-го разряда двоичного представления числа, полученного после t-й итерации; K - старший разряд двоичного числа, полученного после t-й итерации; Cm - константа соответственно для каждой итерации; выходной слой, предназначенный для формирования на своих выходах вычетов числа Z по выбранному модулю р суммирования; первый и второй регистры, группу блоков элементов И, при этом выходы нейронов входного слоя подключены ко входам нейронов скрытого слоя, соединенных попарно между собой, выходы нейронов скрытого слоя соединены со входами нейронов выходного слоя, информационный вход кода исходного числа соединен с информационным входом первого регистра, вход начала вычислений устройства соединен с входами записи первого и второго регистров, а информационный вход нулевого разряда второго регистра соединен с входом записи второго регистра, l-е выходы разрядов первого регистра
является оператором извлечения m-го разряда двоичного представления числа, полученного после t-й итерации; K - старший разряд двоичного числа, полученного после t-й итерации; Cm - константа соответственно для каждой итерации; выходной слой, предназначенный для формирования на своих выходах вычетов числа Z по выбранному модулю р суммирования; первый и второй регистры, группу блоков элементов И, при этом выходы нейронов входного слоя подключены ко входам нейронов скрытого слоя, соединенных попарно между собой, выходы нейронов скрытого слоя соединены со входами нейронов выходного слоя, информационный вход кода исходного числа соединен с информационным входом первого регистра, вход начала вычислений устройства соединен с входами записи первого и второго регистров, а информационный вход нулевого разряда второго регистра соединен с входом записи второго регистра, l-е выходы разрядов первого регистра
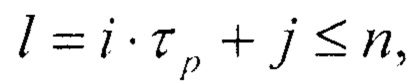
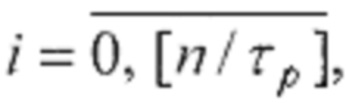
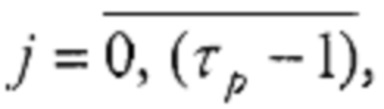
где: n - число двоичных разрядов первого регистра, τр - период повторения остатков по модулю р весов разрядов в двоичном коде,
соединены с соответствующими первыми входами i-x блоков элементов И группы, вторые входы которых соединены с i-ми выходами второго регистра, а выходы - с соответствующими j-ми нейронами входного слоя, причем
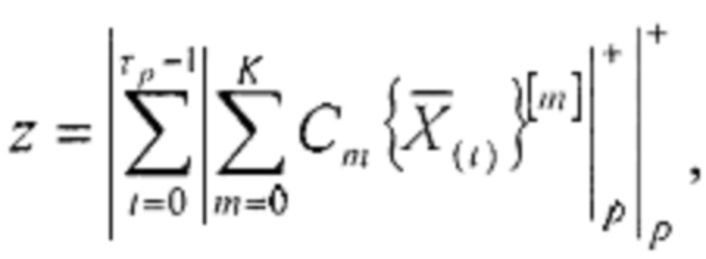
где K - старший разряд исходного двоичного числа, полученного после t-й итерации, Cm - константа соответственно для каждой итерации, отличающаяся тем, что в нее введены (τр/2) групп элементов И, причем первые входы d-x элементов И q-й группы
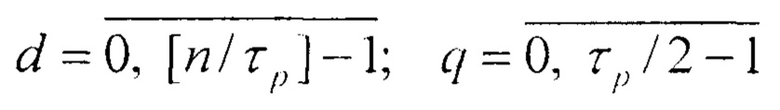
соединены с выходами (q+d⋅τp)-x разрядов первого регистра, выходы 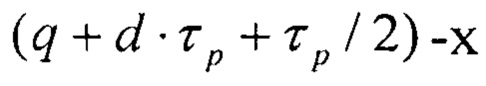 разрядов которых соединены с входами установки в ноль
разрядов которых соединены с входами установки в ноль 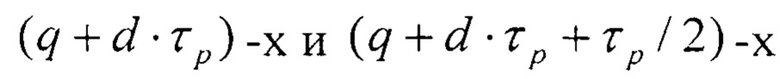 разрядов первого регистра.
разрядов первого регистра.
Сущность изобретения заключается в следующем. Если модуль р является простым числом, то вторая половина периода повторения остатков от чисел 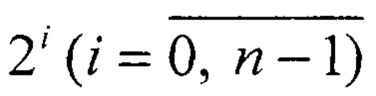 оказывается двойственной к первой. Из теории чисел известно, что последовательность чисел |2i|p имеет некоторый период повторения равный τр. В общем виде
оказывается двойственной к первой. Из теории чисел известно, что последовательность чисел |2i|p имеет некоторый период повторения равный τр. В общем виде
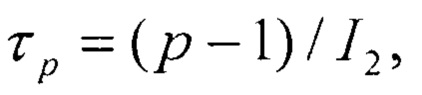
где I2 - индекс числа 2 по модулю устройства р. Рассмотрим возможность повышения быстродействия проведения операции, связанную с закономерностями распределения остатков внутри периода. Ввиду того, что
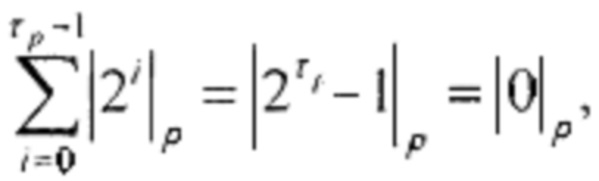
как это следует из малой теоремы Ферма, сумма остатков внутри периода хр кратна величине модуля. В частности при р=5 имеем
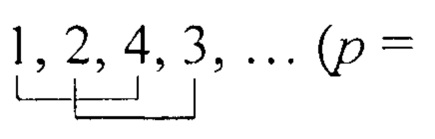
Горизонтальными линиями отмечены остатки, парные суммы которых равны р, что позволяет исключить соответствующие разряды в двоичном представлении числа А. При этом число рекурсий уменьшается, а их оставшееся число (максимально τр/2) не представляет бинарную операцию, т.к. производится сложение с нулем.
Определим расстояние μр между двоичными разрядами, модульные остатки которых в сумме составляют величину р
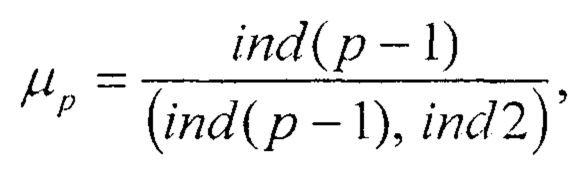
где (ind(p-1), ind2) - наибольший общий делитель соответствующих чисел. Неравенство τр≠μp является удобным критерием двойственности остатков в периоде. Он позволил уточнить, что g=2 (g - первообразный корень) не является существенным условием симметрии относительно модуля распределения остатков периода τр. Например при р=17 имеем следующее распределение остатков
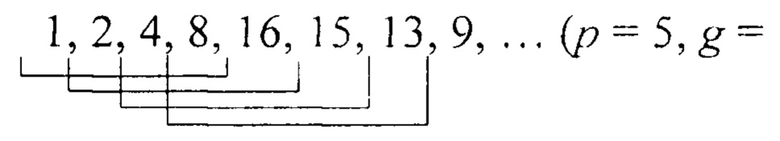
Ввиду того, что при g≠2 τр<(р-1), что позволяет использовать подобные числа в высокопроизводительных устройствах формирования конечных полей.
Дальнейшим развитием данного подхода может служить сброс в ноль оставшихся двойственных пар единиц в различных периодах повторения, составляющих в сумме величину р.
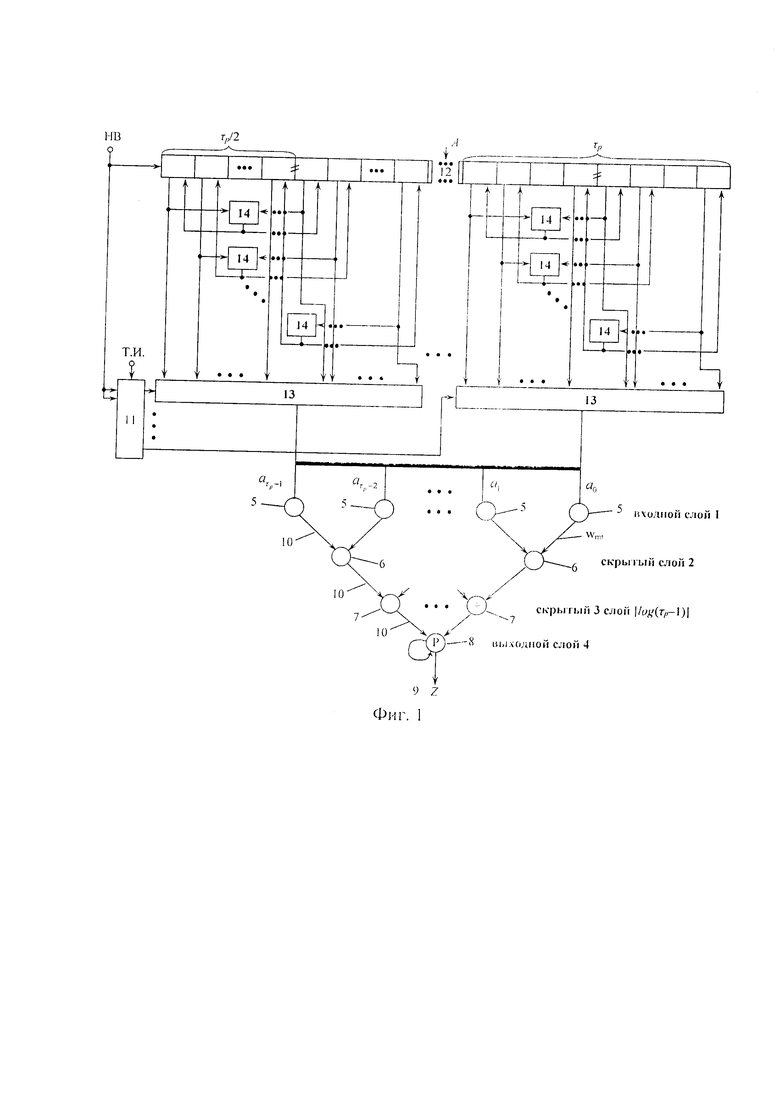
На фиг. 1 представлена структурная схема предлагаемого устройства, где: 1 - входной слой; 2 и 3 - скрытые слои; 4 - выходной слой; 5 - нейроны входного слоя 1; 6 и 7 - нейроны скрытых слоев 2 и 3 соответственно; 8 - нейроны выходного слоя 4; 9 - вычет Z; 10 - связи между слоями нейронов; 11 - второй регистр; 12 - первый регистр; 13 - группа блоков элементов И; 14 - группы элементов И.
Информационный вход исходного числа соединен с информационным входом первого 12 регистра, вход начала вычислений устройства соединен с входами записи первого 12 и второго 11 регистров, а информационный вход нулевого разряда второго 11 регистра соединен с входом записи второго 11 регистра l-е выходы разрядов первого 12 регистра
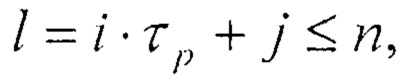
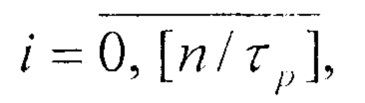
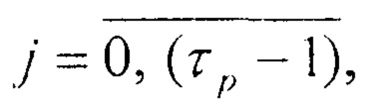
где: n - число двоичных разрядов первого регистра, τр - период повторения остатков по модулю р весов разрядов в двоичном коде, соединены с соответствующими первыми входами i-х блоков элементов И группы 13, вторые входы которых соединены с i-ми выходами второго 11 регистра, а выходы - с соответствующими j-ми нейронами входного слоя, первые входы d-x элементов И q-й группы
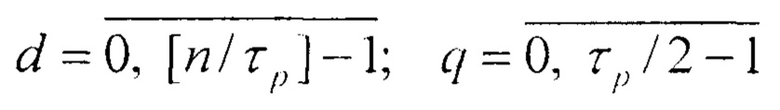
соединены с выходами (q+d⋅τp)-x разрядов первого 12 регистра, выходы 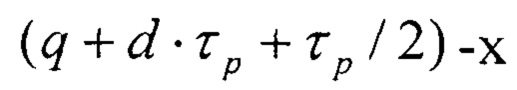 разрядов которых соединены с входами установки в ноль
разрядов которых соединены с входами установки в ноль 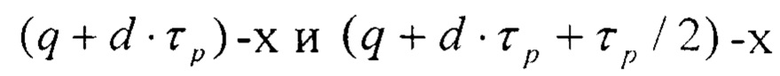 разрядов первого 12 регистра.
разрядов первого 12 регистра.
Рассмотрим работу устройства. В исходном состоянии все регистры обнулены. После подачи кода числа А на информационный вход первого 12 регистра на вход начала вычислений (НВ) подают импульс, который поступает на информационный вход нулевого разряда второго 11 регистра и входы записи регистров 11 и 12.
Производится запись кода числа А в первый регистр 12 и единицы в нулевой разряд второго 11 регистра, сигнал с выхода которого поступает на второй нулевого блока 13 элементов И группы. Двойственные пары единиц разрядов регистра 12 (при их наличии) поступают соответственно на первые и вторые входы соответствующего элемента И 14 данной группы. На выходе И 14 появляется сигнал, который поступает на входы установки в ноль соответствующей пары разрядов регистра 12. Первый период повторения остатков по модулю р весов разрядов в преобразованном виде с выходов нулевого блока 13 элементов И группы поступает на соответствующие нейроны 5 входного слоя 1. Затем результаты передаются на нейроны 6 скрытого слоя 2, а сигнал с выхода первого разряда регистра 11 поступает на второй вход первого блока 13 элементов И группы. Второй период повторения остатков по модулю р (после преобразования) поступает на соответствующие нейроны 5 входного слоя 1. Процесс повторяется до тех пор, пока единица не окажется в [n/τр]-м разряде регистра 11. Выходной слой 4, нейроны 8 представляют, как обычно, параллельный сумматор по модулю р с обратной связью.
Отметим, что число единиц входного слоя 1 не превышает величины τр/2 в худшем случае. Классифицируемые вычеты Z определяются вычетами 9. Весовые коэффициенты 10 (связи между нейронами) определяются константами Ci.
Рассмотрим пример выполнения операции по модулю р=5 от числа 72710 при n=10.
Первоначально производится запись числа А=111_1011_01 в регистр 12. Сигналы с выходов нулевого и четвертого разрядов регистра 12 (см. фиг. 1) поступают на первые входы нулевых элементов И 14 соответственно нулевой и первой групп, на вторые входы которых поступают сигналы соответственно с выходов второго и шестого разрядов регистра 12. С выходов указанных элементов И 14 поступают сигналы на вход установки в ноль разрядов регистра 12, которые обнуляют разряды с номерами 0, 2, 4 и 6. Следовательно, состояние регистра 12 будет равно 0100_0001_01. Отметим, что число единиц при этом уменьшилось с 8 до 3. Первоначально на нейронную сеть поступает период числа А, равный 0100. Здесь не требуется взвешенного суммирования и получим на входе нейрона 8 число 4. На следующем такте получим период 0001, которому без проведения суммирования 8 сети соответствует число 1. Последний такт содержит неполный период 01хх (где знаками х отмечены отсутствующие разряды). Данному случаю соответствует число 2. Таким образом вычет Z от числа А равен |4+1+2|5=2, т.е. |A|5=|727|5=|2|5.
Отметим, что, проводя второй этап обнуления двойственных пар в двух периодах, можно получить число А=0000_0000_01, т.е. также равно числу 2, т.е. Z=|2|5.
| название | год | авторы | номер документа |
|---|---|---|---|
| Нейронная сеть конечного кольца | 2018 |
|
RU2701064C1 |
| НЕЙРОННАЯ СЕТЬ КОНЕЧНОГО КОЛЬЦА | 2003 |
|
RU2279132C2 |
| УСТРОЙСТВО ДЛЯ ФОРМИРОВАНИЯ ОСТАТКА ПО МОДУЛЮ ОТ ЧИСЛА | 2000 |
|
RU2209460C2 |
| Система надежного облачного хранения с регулируемой избыточностью данных | 2021 |
|
RU2782681C1 |
| НЕЙРОННАЯ СЕТЬ УСКОРЕННОГО МАСШТАБИРОВАНИЯ МОДУЛЯРНЫХ ЧИСЕЛ | 2007 |
|
RU2359325C2 |
| КОНВЕЙЕРНАЯ НЕЙРОННАЯ СЕТЬ КОНЕЧНОГО КОЛЬЦА | 2006 |
|
RU2317584C1 |
| НЕЙРОННАЯ СЕТЬ С ПОРОГОВОЙ (k, t) СТРУКТУРОЙ ДЛЯ ПРЕОБРАЗОВАНИЯ ОСТАТОЧНОГО КОДА В ДВОИЧНЫЙ ПОЗИЦИОННЫЙ КОД | 2008 |
|
RU2380751C1 |
| УСТРОЙСТВО ДЛЯ ОСНОВНОГО ДЕЛЕНИЯ МОДУЛЯРНЫХ ЧИСЕЛ | 2013 |
|
RU2559771C2 |
| НЕЙРОННАЯ СЕТЬ ДЛЯ ОБНАРУЖЕНИЯ, ЛОКАЛИЗАЦИИ И ИСПРАВЛЕНИЯ ОШИБОК В СИСТЕМЕ ОСТАТОЧНЫХ КЛАССОВ | 2005 |
|
RU2301442C2 |
| НЕЙРОННАЯ СЕТЬ ДЛЯ ПРЕОБРАЗОВАНИЯ ОСТАТОЧНОГО КОДА В ДВОИЧНЫЙ ПОЗИЦИОННЫЙ КОД | 2006 |
|
RU2318238C1 |
Изобретение относится к нейрокомпьютерной технике и предназначено для классификации классов чисел по заданному модулю р. Техническим результатом является повышение быстродействия нейронной сети при классификации вычетов. Устройство содержит входной, скрытый и выходной слои нейронов, два регистра, группу блоков элементов И и группы элементов И. 1 ил.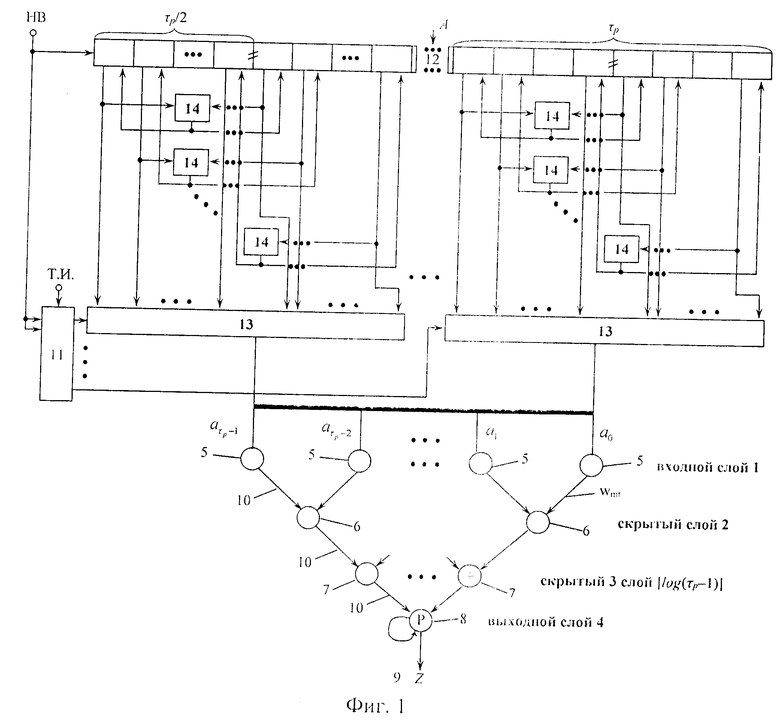
Нейронная сеть конечного кольца для классификации чисел по модулю, содержащая входной слой, предназначенный для хранения числа, представленного в позиционной системе счисления, скрытый слой нейронов, предназначенный для взвешенного суммирования сохраненных чисел по формуле
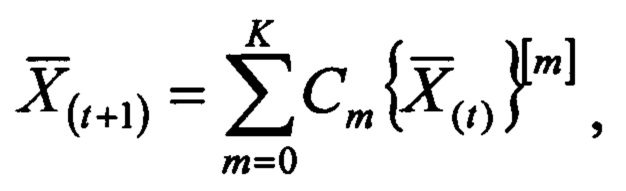
где 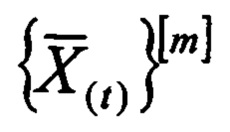 является оператором извлечения m-го разряда двоичного представления числа, полученного после t-й итерации; K - старший разряд двоичного числа, полученного после t-й итерации; Cm - константа соответственно для каждой итерации; выходной слой, предназначенный для формирования на своих выходах вычетов числа Z по выбранному модулю р суммирования; первый и второй регистры, группу блоков элементов И, при этом выходы нейронов входного слоя подключены ко входам нейронов скрытого слоя, соединенных попарно между собой, выходы нейронов скрытого слоя соединены со входами нейронов выходного слоя, информационный вход кода исходного числа соединен с информационным входом первого регистра, вход начала вычислений устройства соединен с входами записи первого и второго регистров, а информационный вход нулевого разряда второго регистра соединен с входом записи второго регистра, l-е выходы разрядов первого регистра
является оператором извлечения m-го разряда двоичного представления числа, полученного после t-й итерации; K - старший разряд двоичного числа, полученного после t-й итерации; Cm - константа соответственно для каждой итерации; выходной слой, предназначенный для формирования на своих выходах вычетов числа Z по выбранному модулю р суммирования; первый и второй регистры, группу блоков элементов И, при этом выходы нейронов входного слоя подключены ко входам нейронов скрытого слоя, соединенных попарно между собой, выходы нейронов скрытого слоя соединены со входами нейронов выходного слоя, информационный вход кода исходного числа соединен с информационным входом первого регистра, вход начала вычислений устройства соединен с входами записи первого и второго регистров, а информационный вход нулевого разряда второго регистра соединен с входом записи второго регистра, l-е выходы разрядов первого регистра
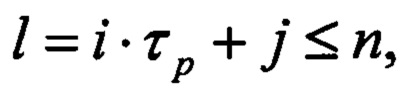
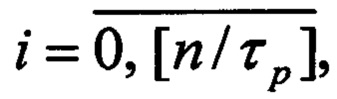
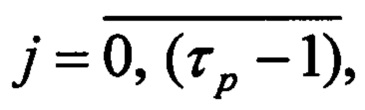
где: n - число двоичных разрядов первого регистра, τр - период повторения остатков по модулю р весов разрядов в двоичном коде,
соединены с соответствующими первыми входами i-x блоков элементов И группы, вторые входы которых соединены с i-ми выходами второго регистра, а выходы - с соответствующими j-ми нейронами входного слоя, причем
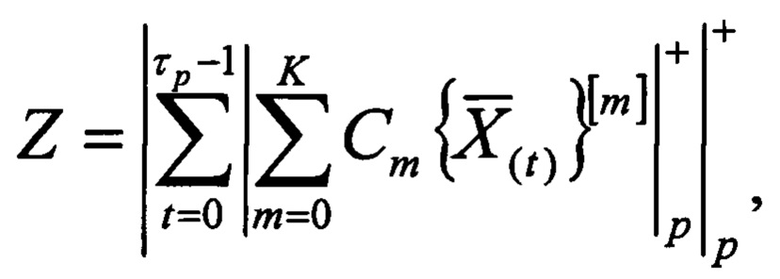
где K - старший разряд исходного двоичного числа, полученного после t-й итерации, Cm - константа соответственно для каждой итерации, отличающаяся тем, что в нее введены (τр/2) групп элементов И, причем первые входы d-x элементов И q-й группы
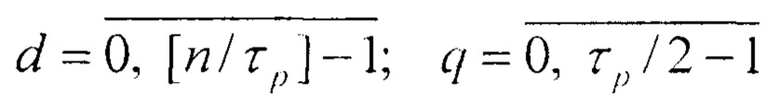
соединены с выходами (q+d⋅τp)-х разрядов первого регистра, выходы 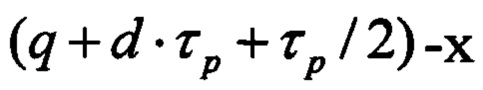 разрядов которых соединены с входами установки в ноль
разрядов которых соединены с входами установки в ноль 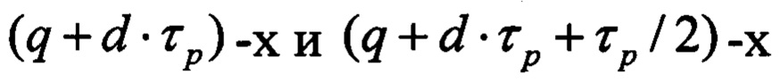 разрядов первого регистра.
разрядов первого регистра.
| Нейронная сеть конечного кольца | 2018 |
|
RU2701064C1 |
| НЕЙРОННАЯ СЕТЬ КОНЕЧНОГО КОЛЬЦА | 2003 |
|
RU2279132C2 |
| Устройство для вычисления сумм парных произведений в полиномиальной системе классов вычетов | 2016 |
|
RU2622881C1 |
| НЕЙРОННАЯ СЕТЬ ДЛЯ ВЫЧИСЛЕНИЯ ПОЗИЦИОННОЙ ХАРАКТЕРИСТИКИ РАНГА ЧИСЛА, ПРЕДСТАВЛЕННОГО В СИСТЕМЕ ОСТАТОЧНЫХ КЛАССОВ | 2003 |
|
RU2271569C2 |
| US 20180218275 A1, 02.08.2018. | |||
Авторы
Даты
2021-11-19—Публикация
2020-08-12—Подача