Способ передачи данных на основе кодов с низкой плотностью проверок на четность Российский патент 2019 года по МПК H03M13/11 H04L1/16 

Изобретение относится к области теории кодирования, в частности, к системам для объединенного кодирования с исправлением и обнаружением ошибок с целью повышения эффективности использования спектра при передаче данных в цифровой системе радиосвязи.

Актуальной является задача не только исправление ошибок при канальном кодировании, но и обнаружения неисправленных ошибок и организация автоматического запроса повторения (АЗП) с целью исправить подобные ошибки за счет дополнительной передачи минимально возможного числа кодовых символов. Основной характеристикой помехоустойчивого кодирования является скорость кодирования равная отношению число информационных символов к кодовым, поскольку кодирование вносит избыточность, скорость кодирования .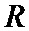

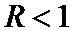
Широко известен параллельный сверточный турбокод [ Berrou C. Near Shannon limit error – correcting coding and decoding / C. Berrou, A. Glaviex, P. Thitimajshina // IEEE International Communications Conference : Proc. 1993. – Geneva (Switzerland), 1993. – P. 1064–1070], позволивший приблизиться к потенциально достижимым характеристикам помехоустойчивого кодирования. Способ характеризуется следующим. На вход первого кодера подается информационная последовательность, на вход второго подается та же последовательность, но после перемежителя. Тем самым достигается статистическая независимость, особенно при больших размерах кодового блока. Итеративный подход заключается в том, что результаты одного декодирования с мягким выходом могут использоваться при другом декодировании, как априорная информация. Однако турбокод не является более эффективным, чем сверточный код, декодируемый по алгоритму Витерби, при размере фрейма менее 200 бит.

Аналогом заявляемого способа является продукт фирмы Trellis Ware код F-LDPC [Halford, Thomas & Bayram, Metin & Kose, Cenk & M. Chugg, Keith & Polydoros, Andreas. (2008). The F-LDPC Family: High-Performance Flexible Modern Codes for Flexible Radio. 376 - 380. 10.1109/ISSSTA.2008.75.]. Достоинством этого решения является глубокая интеграция протокола автоматического запроса повторной передачи (АЗП) с алгоритмом помехоустойчивого кодирования. Утверждается, что решение обладает максимально гибкими возможностями, одно ядро кодер/декодер поддерживает 40 кодовых скоростей (1/2–32/33), при этом допустимые размеры фрейма: 128, 256, 512, …, 16384 бит. Однако, например, для голосовых данных, размеры фреймов, производимые вокодером, могут составлять 16, 40, 80, 172 бита, таким образом невозможность работать с блоками от 20 бит является недостатком кода F-LDPC.

Классическая АЗП (ARQ), которая при ошибочном декодировании кадра предусматривает стирание принятых данных, полную повторную передачу кадра и независимое декодирование вновь полученного кадра не эффективна, т.к. приводит к слишком большой избыточной передаче данных. В настоящее время все большое распространение получает гибридная повторная передача [Error Control Coding: Fundamentals and Applications/ S. Lin, D. J. Costello, Jr. – NJ: Englewood Cliffs. – 1983. – 603 p.]. Суть метода в том, что более эффективной является такая стратегия, которая предусматривает при ошибочном декодировании сохранение данных кадра, получение от передатчика некоторой дополнительной информации, и повторное декодирование кадра с использованием этой дополнительной информации. Если объем дополнительной информации меньше объема целого кадра, то эффективность использования канала связи существенно увеличивается. Данный подход исследован Хагенауэром [J. Hagenauer. Rate Compatible Punctured Convolutional Codes (RCPC Codes) and their Applications. // IEEE Trans. Commun. – Vol. 36. – Apr. 1988. – P. 389-400.] и Чейзом [D. Chase. Code Combining ­ A Maximum­Likelihood Decoding Approach for Combining an Arbitrary Number of Noisy Packets. // IEEE Trans. Comm. – Vol. 33. – May 1985. – P. 385­393] с разных позиций.

Рассмотрим классификацию рассмотренных схем АЗП (ARQ):

• Гибридная АЗП Типа 1 (НARQ-1 – суммирование Чейза). Данная стратегия повторной передачи характеризуется тем, что повторно передается тот же самый кадр.

• Гибридная АЗП Типа 2 (НARQ-2 – наращивание избыточности). Данная стратегия повторной передачи характеризуется тем, что число бит для повторной передачи меньше, чем в исходном кадре. Копия для повторной передачи не может быть декодируема самостоятельно.

• Гибридная АЗП Типа 3 (НARQ-3). Копия для повторной передачи может декодироваться самостоятельно. Однако кадр для повторной передачи может отличаться от первоначально переданного кадра, то есть может быть закодирован другим кодом.

Данную классификацию можно обобщить следующим образом:

• АЗП (ARQ) с полной передачей (к ней относится Тип 1 и Тип 3).

• АЗП (ARQ) с частичной передачей (Тип 2).

Темой дальнейшего исследования будет частичная передача – гибридная АЗП типа 2 (HARQ-2).

Возможны несколько подходов к реализации подобной стратегии АЗП (ARQ):

1. Повторная передача части ранее переданных кодовых символов кадра и их оптимальное сложение с кодовыми символами, сохраненными в памяти приемника.

2. Использование кодов с нарастающей сложностью. В случае ошибочного декодирования на передающей стороне вычисляются новые (дополнительные) проверочные символы, которые передаются приемнику.

Известен способ [Пат. 2427491 CA (0237743 WO), МКИ H04L1/18. Automatic Request Protocol Based Packet Transmission Using Punctured Codes / R. Wang, Ming J., A. Garmonov, A. Savinkov, A. Zhdanov. –PST Gazette. – 2002, May 19. – P. 9340], где подобная стратегия не приводит к снижению пропускной способности поскольку дополнительные кодовые символы или частичную повторную передача передают в составе следующего пакета, где проводят дополнительное перфорирование, освобождая место для проверочных кодовых символов для пакета в котором обнаружена ошибка, таким образом, ошибка в одном пакете исправляется за счет избыточности другого.

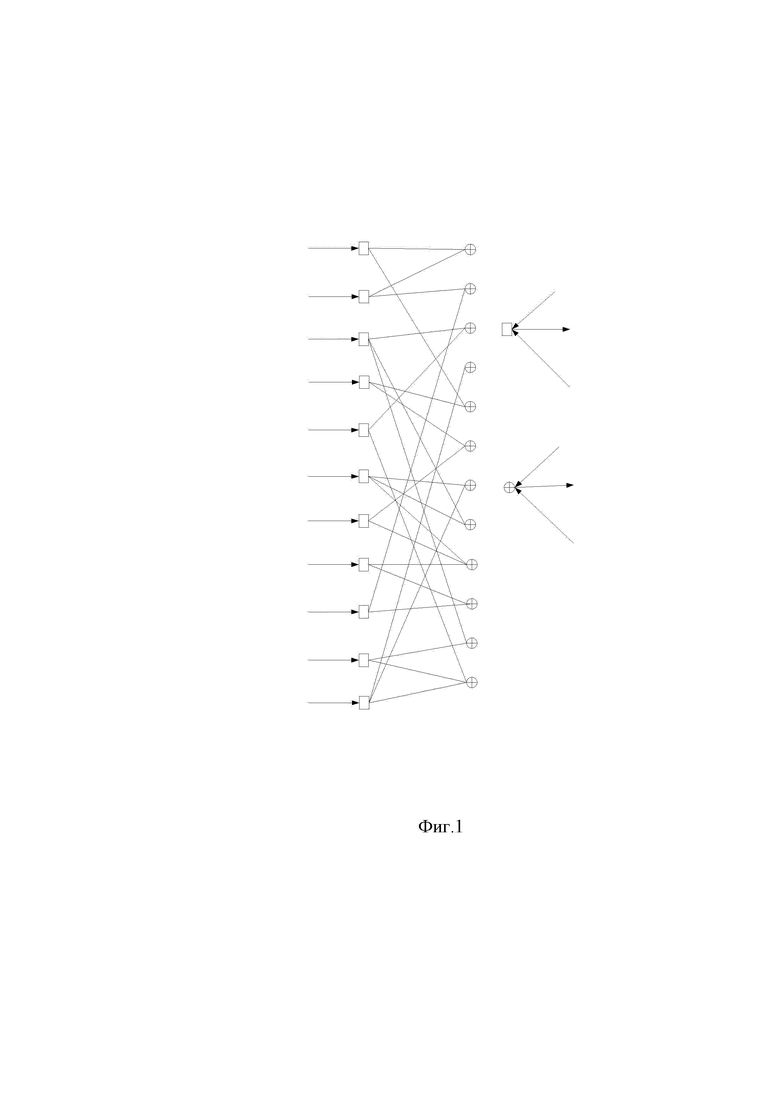
В классе линейных блоковых кодов можно особо выделить подкласс кодов с низкой плотностью проверок на четность [Gallager R. “Low Density Parity Check Codes”// MIT Press 1963], превосходящий по своим характеристикам турбокод. Особенностью данного кода является наличие простой графической модели алгоритма декодирования определяемого как декодирование на графе (фиг. 1). Декодирование на графе следует понимать в том смысле, что граф определяет разбиение всего кодового слова на более короткие коды, причем короткие коды могут перекрываться друг с другом. Избежать данных перекрытий можно путем повторения перекрывающихся кодовых символов. Разные копии принятого кодового символа или мягкого решения об этом символе входят в различные кодовые слова более короткого кода, при этом все кодовые слова короткого кода могут быть декодированы независимо. Такая структура может быть представлена в виде двудольного графа, один тип вершин которого ассоциирован с кодовыми символами, причем количество ребер исходящих из каждой вершины соответствует количеству повторений кодового символа (переменная вершина – обозначена прямоугольником). Другой тип вершин соответствует коротким кодам, причем каждая вершина есть кодовое слово с количеством кодовых символов равным числу входящих ребер (проверочная вершина – обозначена кругом). Каждой проверочной вершине может быть приписана контрольная сумма, как индикатор наличия ошибок в коротком коде. Переменные вершины могут быть соединены только с проверочными вершинами, и, наоборот, проверочные вершины могут быть соединены только с переменными вершинами, что позволяет рассматривать граф как двудольный.

Такой двудольный граф называют графом Таннера [Tanner R.M. A Recursive Approach to Low Complexity Codes / R.M. Tanner // IEEE Transaction on Information Theory. – 1981. –Vol. IT­27, № 9. – P. 533­547]. По сути, для линейного блокового кода, граф Таннера является графическим представлением проверочной матрицы. Безошибочное декодирование характеризуется равенством нулю всех контрольных сумм – кодовых ограничений.

Код с низкой плотностью проверок на четность может быть декодирован в мягких решениях, используя алгоритм обмена сообщений (фиг. 1). Алгоритм обмена сообщениями [Gallager R. “Low Density Parity Check Codes”// MIT Press 1963] инициализируют каждый переменную вершину информацией о достоверности приема каждого символа (мягким решением), полученной из канала.

1. Вычисляют значение исходящего сообщения от переменной вершины равного апостериорной вероятности для кодового символа принять определенное значение кодового символа, отнесенного к этому переменной вершине для каждого ребра двудольного графа.

2. В каждом проверочной вершине модифицируют исходящие сообщения от тех переменных вершин, с которым они связаны ребром двудольного графа, и для которого они являются входящими, ставя в соответствие каждому ребру исходящие сообщения проверочной вершине, которые равны второму набору вероятностей для кодового символа принять определенное значение.

3. Обновляют исходящие сообщение переменной вершине входящими сообщениями, которые являются исходящими сообщениями проверочной вершине.

4. Повторяют итерации определенное число раз или до тех пор, пока кодовые ограничения не будут выполнены.

Знак исходящего сообщения выбирают таким, чтобы удовлетворить кодовым ограничениям. Абсолютное значение исходящего сообщения вычисляют при помощи функции . Эта функция является решающей функцией или логарифмом отношения правдоподобия. Функция обладает коммутативностью:

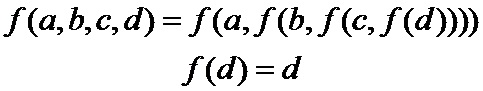
Есть несколько методов для определения функции 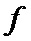. Наиболее простой известен как алгоритм “min-sum”. Абсолютное значение исходящего сообщения равно минимальному абсолютному значению среди входящих сообщений за исключением сообщения от той вершины, для которого предназначено данное исходящее сообщение:

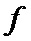
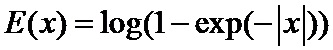
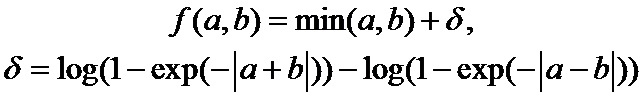
Другой метод задания функции состоит в определении функции через функцию , применяемую в LOG MAP алгоритме [Pietrobon S.S. Implementation and Performance of a Turbo/MAP Decoder / S.S. Pietrobon // International J. of Satellite Communication. – 1998. Vol. 16 (Jan-Feb). – P. 23-46]. Функция может быть задана как:

Где функция 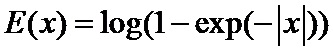, может быть представлена в виде таблицы.

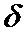
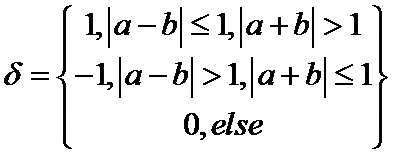
Существует модификация предложенного метода, где дополнительное слагаемое определено как:

Модификации этого алгоритма приведена в [W.K Leung,W.L Lee,A.Wu,L.Ping,“ Efficient implementation technique of LDPC decoder ”Electron.Lett..,vol.37(20),pp.1231-1232,Sept2001]. Данный метод не требует таблицы, но приводит к некоторому ухудшению характеристик, но зато позволяет сократить число операций при декодировании.

Таким образом, операции на графе Таннера, представляющего собой графическую модель разбиения кода на подкоды могут быть описаны в виде повторения, перемежения, группирования, а шаблоны повторения, группирования и правило перемежения однозначно задают двудольный граф.

Так турбокоды удобнее описывать в терминах повторения и перемежения, а коды с низкой плотностью проверок на четность – в виде двудольного графа.

Учитывая пример с линейным блоковым кодом, где короткий код – это проверка на четность или сложения всех кодовых символов по модулю 2, будем называть применяемый короткий код на графе обобщенной проверкой на четность, которая будет заключаться в суммировании всех кодовых символов в поле Галуа или суммировании чисел по заданному модулю. Если в процессе передачи ошибок нет, то все подобные контрольные суммы должны быть равны нулю.

В настоящее время широкую известность получил класс “турбо-образных” (“turbo-like”) кодов, среди которых выделяются коды с “повторением – накоплением”, известные из [H. Jin, A. Khandekar and R. J. McEliece, “Irregular repeat-accumulate codes," Proceedings of the Second International Symposium on Turbo Codes and Related Topics, pp. 1-8, Brest, France, September 2000]. Кодирование кодов с “повторением – накоплением” осуществляют в следующем порядке: повторение каждого информационного символа, перемежение повторенных символов, накопление суммы по модулю 2 перемеженных символов. Данные коды обладают свойствами, как турбо-кодов, так и кодов с низкой плотностью проверок на четность и могут быть декодированы как в параллельном режиме – алгоритм обмена сообщениями, так и в последовательном режиме – алгоритм MAP. Следует отметить, что в последнем случае алгоритм по существу является гибридным, состоящим из MAP алгоритма декодирования сверточного кода с двумя состояниями и алгоритма обмена сообщениями с неравномерно повторенными информационными символами [J. Li, Low-Complexity, Capacity-Approaching Coding Schemes: Design, Analysis and Applications, Ph.D. dissertation, Texas A&M University, 2002. ]. Из [ H. Jin, A. Khandekar and R. J. McEliece, “Irregular repeat-accumulate codes," Proceedings of the Second International Symposium on Turbo Codes and Related Topics, pp. 1-8, Brest, France, September 2000] известно, что наибольшая эффективность от применения достигается неравномерным или иррегулярным повторением информационных символов. Кроме того, характеристики кодов повторения с накоплением в большой степени характеризуются перемежителем, который совместно с шаблоном иррегулярного повторения и шаблоном накопления контрольных сумм определяют граф Таннера для данного кода. Требования к перемежителю заключаются в том, чтобы обеспечить достаточное разнесение повторенных символов, обеспечив тем самым отсутствие или малое число кодовых слов с низким весом.

Пример подобного кода приведен на фиг. 7. Это систематический код, состоящий из 7 переменных узлов, из которых 4 информационные, и 3 проверочные узлы. Такому коду соответствует проверочная матрица вида:

Шаблон иррегулярных повторений представляет собой соответствие между количеством символов и числом их повторений. Для кода с фиг. 7 два информационных повторены один раз, один информационный символ повторен два раза, один информационный символ повторен три раза. Компактно шаблон повторений может быть записан в виде двух массивов: , где первый массив отражает количество повторений, а второй число повторенных символов. Закон перемежения или перестановку задают последовательностью неповторяющихся чисел, каждое из которых задействовано ровно один раз, таких, что они могут образовать натуральный ряд чисел (каждое последующее число на единицу больше предыдущего), если их расположить по возрастанию. Числа в виде натурального ряда – это последовательность до перемежения, эти же числа в виде псевдослучайной последовательности – это последовательность после перемежения.

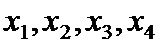
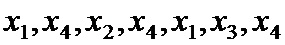
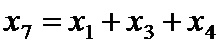
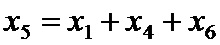
Рассмотрим процедуру кодирования. Пусть информационные символы будут и индекс соответствует номеру переменного узла. Тогда после повторения последовательность символов примет вид . Общее число повторенных символов семь. После перемежения по закону имеем последовательность вида . Добиваясь того, чтобы контрольная сумма на узле 3 была нулевой, формируем кодовый символ . Далее следуя "зигзаг" паттерну, добиваемся равенству нулю остальных контрольных сумм: , .

Шаблон накопления контрольных сумм, аналогично шаблону повторения кодовых символов может быть записан в виде двух массивов 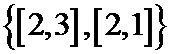, где первый массив отражает количество накоплений путем суммирования по модулю 2, а второй число накопленных символов.

При кодировании перемежение выполняется только среди повторенных информационных символов, а при декодировании к ним добавляют избыточные кодовые символы, полученные согласно паттерну "зигзаг". Говоря о перемежителе, обычно имеется ввиду перемежитель только информационных символов, так как только он несет псевдослучайную составляющую. Актуальной является задача построения частично параллельного перемежителя, в котором за один такт работы перемежают сразу символов, где - коэффициент параллельности перемежителя. Чем он больше, тем больше пропускная способность устройства. Для того чтобы схема параллельного перемежения была реализуемой, работа каждого из процессоров не должна приводить к конфликтам при доступе к памяти. К числу таких конфликтов можно, например, отнести попытку одновременной записи и чтения отдельной ячейки памяти. Память обычно реализуют в виде блоков (“банков”) памяти, таким образом, что к каждому блоку за один квант времени возможен либо доступ на запись (по указанному адресу), либо доступ на чтение.

Известен способ [Пат. 2427491 CA (0237743 WO), МКИ H04L1/18. Automatic Request Protocol Based Packet Transmission Using Punctured Codes / R. Wang, Ming J., A. Garmonov, A. Savinkov, A. Zhdanov. –PST Gazette. – 2002, May 19. – P. 9340], где подобная стратегия не приводит к снижению пропускной способности поскольку дополнительные кодовые символы или частичную повторную передача передают в составе следующего пакета, где проводят дополнительное перфорирование, освобождая место для проверочных кодовых символов для пакета в котором обнаружена ошибка, таким образом, ошибка в одном пакете исправляется за счет избыточности другого.

В основе способа классический иррегулярный код повторений с накоплениями с низкой плотностью проверок на четность [D. Divsalar, H. Jin, and R. J. McEliece. "Coding theorems for ‘turbo-like’ codes." Proc. 36th Allerton Conf. on Communication, Control and Computing, Allerton, Illinois, Sept. 1998, pp. 201–210.], где применен новый эффективный перемежитель, и производят оценку качества декодирования, то есть выносится решение о правильности приема

Недостатком классической схемы при декодировании по алгоритму "распространение сообщений" является то, что затруднено согласование скоростей посредством перфорирования или выкалывания. При замене выколотого символа нулем и приходе этого нуля на проверочный узел декодирования в качестве исходящего сообщения будут выданы все нули, что снижает эффективность декодирования.

Наиболее близким аналогом по технической сущности к предлагаемому является способ передачи голосовых данных в системе цифровой радиосвязи по патенту РФ 2323520, H03M 13/00, принятый за прототип.

Особенностью способа-прототипа является то, что производят оценку качества декодирования без применения циклической контрольной суммы. Для чего рассматривают последовательность не равных нулю контрольных сумм. При превышении значения порога пакет объявляет декодированным недостоверно.

Способ-прототип заключается в следующем.

На передающей стороне:

• формируют пакеты данных, каждый из которых содержит упорядоченную последовательность информационных символов;

• каждый информационный символ повторяют определенное число раз, в зависимости от его номера по порядку в последовательности символов, формируя последовательность повторенных информационных символов, причем количество повторений определяется заранее;

• осуществляют перемежение в последовательности повторенных информационных символов, добиваясь достаточного разнесения идущих подряд повторенных информационных символов, и формируя последовательность перемеженных повторенных информационных символов;

• разбивают перемеженные повторенные информационные символы на группы таким образом, что первый проверочный символ получают путем суммирования по заданному модулю начального значения переменной суммирования со всеми перемеженными повторенными информационными символами из первой группы, а проверочный символ путем суммирования по заданному модулю проверочного символа со всеми перемеженными повторенными информационными символами из группы ;

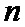
• запоминают полученные проверочные символы;

• формируют кодовое слово путем добавления проверочных символов к информационным символам;

на приемной стороне:

• формируют принятые корреляционные отклики на каждый из переданных кодовых символов;

• выполняют оценку шумового параметра смеси сигнал плюс шум, которая приближенно равна величине стандартного отклонения эквивалентного гауссовского белого шума, которым аппроксимируются помехи в канале;

• формируют мягкие решения о принятых кодовых символах, используя полученную оценку шумового параметра смеси сигнал плюс шум;

• разделяют мягкие решения о принятых кодовых символах на решения об информационных символах и решения о проверочных символах;

• повторяют мягкие решения об информационных символах в соответствии с шаблоном повторения информационных символов;

• повторяют мягкие решения о проверочных символах, по крайней мере, два раза за исключением последнего проверочного символа;

• для мягких решений об информационных символах выполняют перемежение аналогичное перемежению на передающей стороне;

• формируют группы перемеженных мягких решений об информационных символах аналогичные группам соответствующих информационных символов на передающей стороне;

• первую группу перемеженных мягких решений дополняют мягким решением, соответствующим начальному значению переменной суммирования, и первой копией мягкого решения о первом проверочном символе, образуя первое кодовое слово кода обобщенной проверки на четность;

• группу перемеженных мягких решений дополняют второй копией проверочного символа и первой копией мягкого решения об проверочном символе, образуя кодовое слово кода обобщенной проверки на четность;

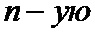
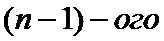
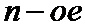
• для каждого мягкого решения, входящего в каждое кодовое слово кода обобщенной проверки на четность, формируют модифицированное мягкое решение, которое является исходящим сообщением кодового слова кода обобщенной проверки на четность, таким образом, что исходящее сообщение кодового слова кода обобщенной проверки на четность представляет собой результат функционального преобразования исходных мягких решений - входящих сообщений кодового слова кода обобщенной проверки на четность;

• деперемежают исходящие сообщения кодового слова кода обобщенной проверки на четность таким образом, что каждой копии мягкого решения о кодовом символе ставят в соответствие исходящее сообщение кодового слова кода обобщенной проверки на четность соответствующее копии мягкого решения об этом символе;

• группируют исходящие сообщения кодового слова кода обобщенной проверки на четность с мягкими решениями о принятых кодовых символах, так что в каждую группу входят мягкое решение о соответствующем кодовом символе и исходящие сообщение кодового слова кода обобщенной проверки на четность, соответствующее копии мягкого решения об этом символе, формируя, таким образом, кодовое слово обобщенного кода повторения, ставя каждое кодовое слово обобщенного кода повторения в соответствие кодовому символу, таким образом, что каждое исходящее сообщения кодового слова кода обобщенной проверки на четность является входящим сообщением кодового слова обобщенного кода повторения;

• для каждого мягкого решения входящего в каждое кодовое слово обобщенного кода повторения формируют модифицированное мягкое решение, которое является исходящим сообщением кодового обобщенного кода повторения представляющее собой результат функционального преобразования над входящими сообщениями кодового слова обобщенного кода повторения;

• итеративно повторяют процесс обмена исходящими и входящими сообщениями таким образом, что исходящее сообщение кодового слова обобщенного кода повторений является входящим сообщением кодового слова кода обобщенной проверки на четность, а исходящее сообщение кода обобщенной проверки на четность является входящим сообщением кодового слова обобщенного кода повторений формируя на каждой итерации последовательность модифицированных мягких решений;

• из последовательности модифицированных мягких решений формируют декодированные кодовые слова;

• умножают каждое декодированное кодовое слово на проверочную матрицу, получая упорядоченную последовательность контрольных сумм;

• если все контрольные суммы равны нулю, то кодовое слово считают декодированным верно;

• если количество контрольных сумм отличных от нуля нечетно и последняя контрольная сумма отлична от нуля, то заменяют ее нулем;

• если количество контрольных сумм отличных от нуля нечетно и последняя в последовательности контрольная сумма равна нулю, то ее заменяют любым отличным от нуля значением;

• разбивают последовательность контрольных сумм на пары, в которые входят элементы последовательности, идущие подряд, причем каждая контрольная сумма входит только в единственную пару;

• в каждой паре вычисляют разность номеров контрольных сумм;

• складывают все полученные разности номеров контрольных сумм;

• сравнивают полученное число с заданным порогом, если число превышает установленный порог, то информационную часть кодового слова считают декодированной неверно;

• если полученное число меньше заданного порога, то информационную часть кодового слова считают декодированной верно.

В прототипе реализована не только функция исправления ошибок, но также функция обнаружения ошибок без циклической контрольной суммы. Однако эффективность обнаружения ошибок существенно уступает алгоритму с циклической контрольной суммой. Тем не менее, функция обнаружения ошибок может быть использована для увеличения энергетического выигрыша кодирования путем применения алгоритма гибридного запроса-повторения без потери пропускной способности и, не прибегая к перфорированию последовательности кодовых символов.

Таким образом, задача увеличения энергетического выигрыша кодирования путем применения алгоритма гибридного запроса-повторения исключительно на физическом уровне является актуальной.

Для решения поставленной задачи в способе передачи данных в цифровой системе связи, заключающемся в том, что на передающей стороне формируют пакеты данных, каждый из которых содержит упорядоченную последовательность информационных символов, каждый информационный символ повторяют в соответствии с шаблоном повторения , где первый массив отражает количество повторений, а второй число повторенных символов, формируя последовательность повторенных информационных символов, осуществляют перемежение в последовательности повторенных информационных символов перемежителем размером , где первые символа образуют последовательность , а остальные номера получают по формуле , формируя последовательность перемеженных повторенных информационных символов, разбивают перемеженные повторенные информационные символы на группы таким образом, что первый проверочный символ получают путем суммирования по заданному модулю начального значения переменной суммирования со всеми перемеженными повторенными информационными символами из первой группы, а проверочный символ путем суммирования по заданному модулю проверочного символа со всеми перемеженными повторенными информационными символами из группы , запоминают полученные проверочные символы, формируют кодовое слово путем добавления проверочных символов к информационным символам, на приемной стороне формируют принятые корреляционные отклики на каждый из переданных кодовых символов, выполняют оценку шумового параметра смеси сигнал плюс шум, формируют мягкие решения о принятых кодовых символах, используя полученную оценку шумового параметра смеси сигнал плюс шум, разделяют мягкие решения о принятых кодовых символах на решения об информационных символах и решения о проверочных символах, повторяют мягкие решения об информационных символах в соответствии с шаблоном повторения информационных символов, повторяют мягкие решения о проверочных символах, по крайней мере, два раза за исключением последнего проверочного символа, для мягких решений об информационных символах выполняют перемежение аналогичное перемежению на передающей стороне, формируют группы перемеженных мягких решений об информационных символах, аналогичные группам соответствующих информационных символов на передающей стороне, первую группу перемеженных мягких решений дополняют мягким решением, соответствующим начальному значению переменной суммирования, и первой копией мягкого решения о первом проверочном символе, образуя первое кодовое слово кода обобщенной проверки на четность, группу перемеженных мягких решений дополняют второй копией проверочного символа и первой копией мягкого решения об проверочном символе, образуя кодовое слово кода обобщенной проверки на четность, для каждого мягкого решения, входящего в каждое кодовое слово кода обобщенной проверки на четность, формируют модифицированное мягкое решение, которое является исходящим сообщением кодового слова кода обобщенной проверки на четность таким образом, что исходящее сообщение кодового слова кода обобщенной проверки на четность представляет собой результат функционального преобразования исходных мягких решений, представляющих собой входящие сообщения кодового слова кода обобщенной проверки на четность, деперемежают исходящие сообщения кодового слова кода обобщенной проверки на четность таким образом, что каждой копии мягкого решения о кодовом символе ставят в соответствие исходящее сообщение кодового слова кода обобщенной проверки на четность соответствующее копии мягкого решения об этом символе, группируют исходящие сообщения кодового слова кода обобщенной проверки на четность с мягкими решениями о принятых кодовых символах, так что в каждую группу входят мягкое решение о соответствующем кодовом символе и исходящие сообщение кодового слова кода обобщенной проверки на четность, соответствующее копии мягкого решения об этом символе, формируя, таким образом, кодовое слово обобщенного кода повторения, ставя каждое кодовое слово обобщенного кода повторения в соответствие кодовому символу, таким образом, что каждое исходящее сообщение кодового слова кода обобщенной проверки на четность является входящим сообщением кодового слова обобщенного кода повторения, для каждого мягкого решения, входящего в каждое кодовое слово обобщенного кода повторения, формируют модифицированное мягкое решение, которое является исходящим сообщением кодового обобщенного кода повторения, представляющее собой результат функционального преобразования над входящими сообщениями кодового слова обобщенного кода повторения, итеративно повторяют процесс обмена исходящими и входящими сообщениями таким образом, что исходящее сообщение кодового слова обобщенного кода повторений является входящим сообщением кодового слова кода обобщенной проверки на четность, а исходящее сообщение кода обобщенной проверки на четность является входящим сообщением кодового слова обобщенного кода повторений, формируя на каждой итерации последовательность модифицированных мягких решений, из последовательности модифицированных мягких решений формируют декодированные кодовые слова, умножают каждое декодированное кодовое слово на проверочную матрицу, получая упорядоченную последовательность контрольных сумм, если все контрольные суммы равны нулю, то кодовое слово считают декодированным верно, если количество контрольных сумм отличных от нуля нечетно и последняя контрольная сумма отлична от нуля, то заменяют ее нулем, если количество контрольных сумм отличных от нуля нечетно, и последняя в последовательности контрольная сумма равна нулю, то ее заменяют любым отличным от нуля значением, разбивают последовательность контрольных сумм на пары, в которые входят элементы последовательности, идущие подряд, причем каждая контрольная сумма входит только в единственную пару, в каждой паре вычисляют разность номеров контрольных сумм, складывают все полученные разности номеров контрольных сумм, сравнивают полученное число с заданным порогом, если число превышает установленный порог, то информационную часть кодового слова считают декодированной неверно, если полученное число меньше заданного порога, то информационную часть кодового слова считают декодированной верно, согласно изобретению, формируют сигнал запроса повторной передачи по каналу обратной связи для передающей стороны, если информационная часть кодового слова декодирована неверно, на передающей стороне при получении сигнала запроса повторной передачи формируют пакет с кодово-сопряженной частью, для чего в очередном кодированном пакете часть кодовых символов заменяют их суммой по модулю два с кодовыми символами ранее переданного и ошибочно декодированого пакета, формируя тем самым кодово-сопряженную часть, при получении текущего пакета с кодово-сопряженной частью декодируют его совместно с ранее принятым ошибочно декодированным пакетом для чего восстанавливают, возможно, с ошибками, последовательность мягких решений ошибочного пакета, модифицируют мягкие решения в кодово-сопряженной части в тех позициях, в которых заменяли кодовые символы суммой символов разных пакетов для чего заменяют знак на противоположный у принятого мягкого решения, если восстановленный кодовый символ предыдущего пакета соответствует логической единице, получая мягкие решения текущего пакета, декодируют мягкие решения текущего пакета, восстанавливают последовательность мягких решений текущего пакета, модифицируют мягкие решения в кодово-сопряженной части в тех позициях, в которых заменяли кодовые символы суммой символов разных пакетов для чего заменяют знак на противоположный у принятого мягкого решения, если восстановленный кодовый символ текущего пакета соответствует логической единице, получая модифицированную последовательность мягких решений для ошибочного пакета, повторно декодируют ошибочный пакет, используя модифицированную последовательность мягких решений для ошибочного пакета как дополнительную информацию в тех позициях, в которых заменяли кодовые символы суммой символов разных пакетов, передают по каналу обратной связи сигналы, характеризующие результативность декодирования кодово-сопряженных пакетов.

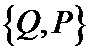
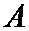
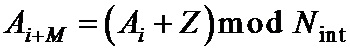
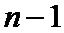
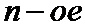
Графические материалы, используемые в описании:

фиг. 1 – алгоритм декодирования на графе: обмен сообщениями;

фиг. 2 – граф Петерсона и заданный на нем код по способу Таннера;

фиг. 3 – вариант реализации приемопередающего устройства;

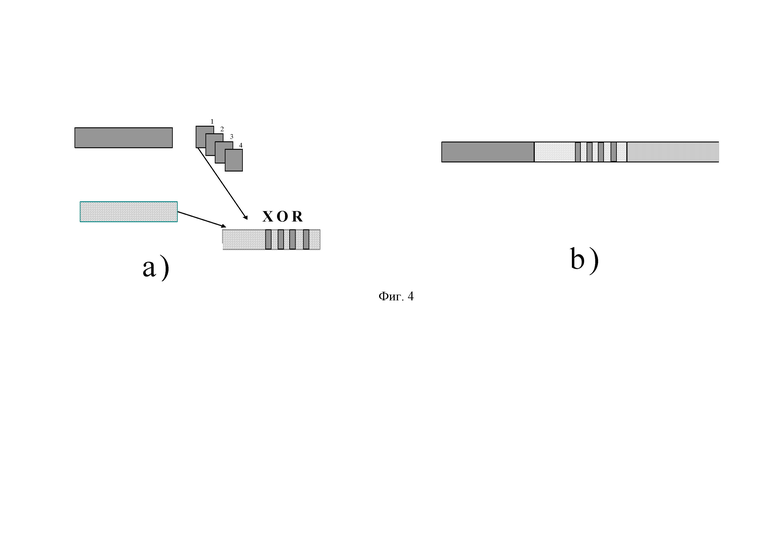
фиг. 4 – структура пакета с кодово-сопряженной частью;

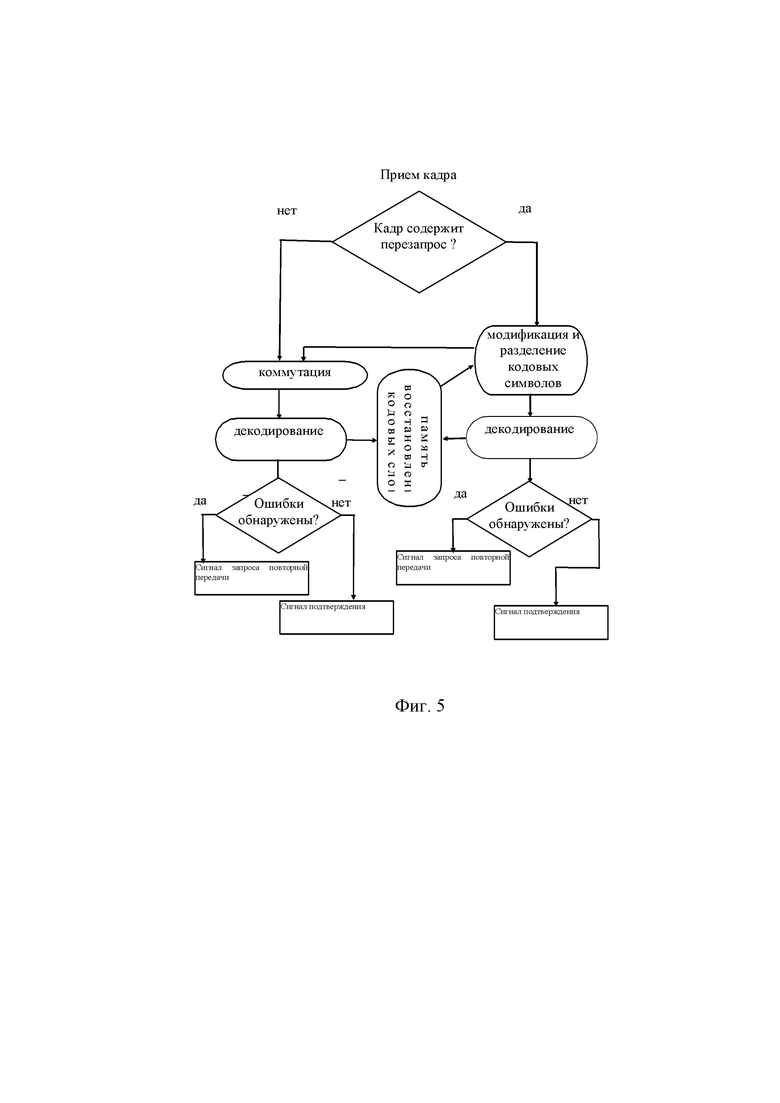
фиг. 5 – алгоритм декодирования пакетов;

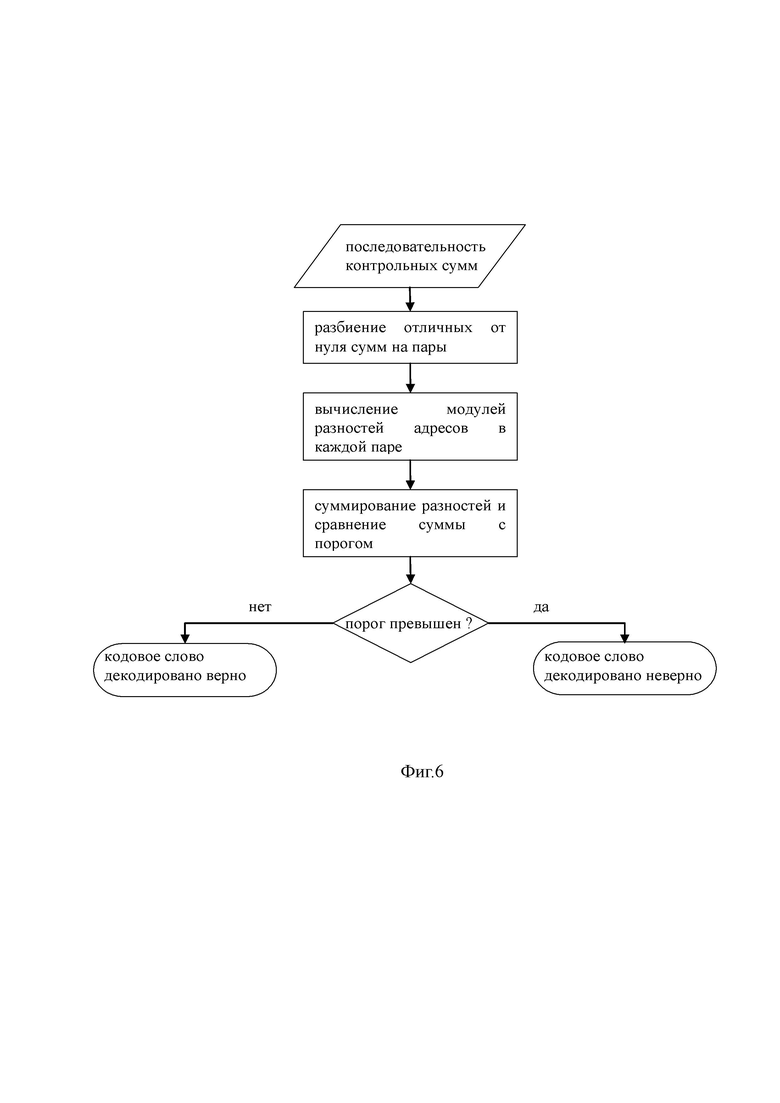
фиг. 6 – способ обнаружения ошибок без CRC;

фиг. 7 – пример кода перемежений с накоплениями;

фиг. 8 – результаты моделирования: зависимость битовой ошибки от отношения сигнал-шум для ;

фиг. 9 – результаты моделирования для .

Заявляемый способ передачи данных в цифровой системе связи, заключается в том, что

на передающей стороне:

– формируют пакеты данных, каждый из которых содержит упорядоченную последовательность 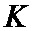информационных символов;

– каждый информационный символ повторяют в соответствии с шаблоном повторения 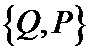, где первый массив отражает количество повторений, а второй число повторенных символов, формируя последовательность повторенных информационных символов,;

– осуществляют перемежение в последовательности повторенных информационных символов перемежителем размером , где первые символа образуют последовательность ,

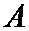
а остальные номера получают по формуле 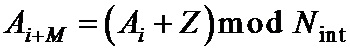добиваясь достаточного разнесения идущих подряд повторенных информационных символов;

– разбивают перемеженные повторенные информационные символы на группы таким образом, что первый проверочный символ получают путем суммирования по заданному модулю начального значения переменной суммирования со всеми перемеженными повторенными информационными символами из первой группы, а проверочный символ путем суммирования по заданному модулю проверочного символа со всеми перемеженными повторенными информационными символами из группы ;

– запоминают полученные проверочные символы;

– формируют кодовое слово путем добавления проверочных символов к информационным символам;

на приемной стороне:

– формируют принятые корреляционные отклики на каждый из переданных кодовых символов;

– выполняют оценку шумового параметра смеси сигнал плюс шум, которая приближенно равна величине стандартного отклонения эквивалентного гауссовского белого шума, которым аппроксимируются помехи в канале;

– формируют мягкие решения о принятых кодовых символах, используя полученную оценку шумового параметра смеси сигнал плюс шум;

– разделяют мягкие решения о принятых кодовых символах на решения об информационных символах и решения о проверочных символах;

– повторяют мягкие решения о информационных символах в соответствии с шаблоном повторения информационных символов;

– повторяют мягкие решения о проверочных символах по крайней мере два раза за исключением последнего проверочного символа;

– для мягких решений об информационных символах выполняют перемежение аналогичное перемежению на передающей стороне;

– формируют группы перемеженных мягких решений об информационных символах аналогичные группам соответствующих информационных символов на передающей стороне;

– первую группу перемеженных мягких решений дополняют мягким решением, соответствующим начальному значению переменной суммирования, и первой копией мягкого решения о первом проверочном символе, образуя первое кодовое слово кода обобщенной проверки на четность;

– группу перемеженных мягких решений дополняют второй копией проверочного символа и первой копией мягкого решения об проверочном символе, образуя кодовое слово кода обобщенной проверки на четность;

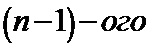
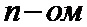
– для каждого мягкого решения, входящего в каждое кодовое слово кода обобщенной проверки на четность, формируют модифицированное мягкое решение, которое является исходящим сообщением кодового слова кода обобщенной проверки на четность, таким образом, что исходящее сообщение кодового слова кода обобщенной проверки на четность представляет собой результат функционального преобразования исходных мягких решений – входящих сообщений кодового слова кода обобщенной проверки на четность;

– деперемежают исходящие сообщения кодового слова кода обобщенной проверки на четность таким образом, что каждой копии мягкого решения о кодовом символе ставят в соответствие исходящее сообщение кодового слова кода обобщенной проверки на четность соответствующее копии мягкого решения об этом символе;

– группируют исходящие сообщения кодового слова кода обобщенной проверки на четность с мягкими решениями о принятых кодовых символах, так что в каждую группу входят мягкое решение о соответствующем кодовом символе и исходящие сообщение кодового слова кода обобщенной проверки на четность, соответствующее копии мягкого решения об этом символе, формируя, таким образом, кодовое слово обобщенного кода повторения, ставя каждое кодовое слово обобщенного кода повторения в соответствие кодовому символу, таким образом, что каждое исходящее сообщения кодового слова кода обобщенной проверки на четность является входящим сообщением кодового слова обобщенного кода повторения;

– для каждого мягкого решения входящего в каждое кодовое слово обобщенного кода повторения формируют модифицированное мягкое решение, которое является исходящим сообщением кодового обобщенного кода повторения, представляющее собой результат функционального преобразования над входящими сообщениями кодового слова обобщенного кода повторения;

– итеративно повторяют процесс обмена исходящими и входящими сообщениями таким образом, что исходящее сообщение кодового слова обобщенного кода повторений является входящим сообщением кодового слова кода обобщенной проверки на четность, а исходящее сообщение кода обобщенной проверки на четность является входящим сообщением кодового слова обобщенного кода повторений, формируя на каждой итерации последовательность модифицированных мягких решений;

– из последовательности модифицированных мягких решений формируют декодированные кодовые слова;

– умножают каждое декодированное кодовое слово на проверочную матрицу, получая упорядоченную последовательность контрольных сумм;

– если все контрольные суммы равны нулю, то кодовое слово считают декодированным верно;

– если количество контрольных сумм отличных от нуля нечетно и последняя контрольная сумма отлична от нуля, то заменяют ее нулем;

– если количество контрольных сумм отличных от нуля нечетно и последняя в последовательности контрольная сумма равна нулю, то ее заменяют любым отличным от нуля значением;

– разбивают последовательность контрольных сумм на пары, в которые входят элементы последовательности идущие подряд, причем каждая контрольная сумма входит только в единственную пару;

– в каждой паре вычисляют разность номеров контрольных сумм;

– складывают все полученные разности номеров контрольных сумм;

– сравнивают полученное число с заданным порогом, если число превышает установленный порог, то информационную часть кодового слова считают декодированной неверно;

– если полученное число меньше заданного порога, то информационную часть кодового слова считают декодированной верно;

– если информационная часть кодового слова декодирована неверно то формируют сигнал запроса повторной передачи по каналу обратной связи для передающей стороны;

– на передающей стороне при получении сигнала запроса повторной передачи формируют пакет с кодово-сопряженной частью, для чего в очередном кодированном пакете часть кодовых символов заменяют их суммой по модулю два с кодовыми символами ошибочно декодированного пакета;

– при получении текущего пакета с кодово-сопряженной частью декодируют его совместно с ранее принятым ошибочно декодированным пакетом для чего восстанавливают, возможно, с ошибками, последовательность мягких решений ошибочного пакета;

– модифицируют мягкие решения в кодово-сопряженной части в тех позициях, в которых заменяли кодовые символы суммой символов разных пакетов для чего заменяют знак на противоположный у принятого мягкого решения если восстановленный кодовый символ предыдущего пакета соответствует логической единице, получая мягкие решения текущего пакета;

– декодируют мягкие решения текущего пакета;

– восстанавливают последовательность мягких решений текущего пакета;

– модифицируют мягкие решения в кодово-сопряженной части в тех позициях, в которых заменяли кодовые символы суммой символов разных пакетов для чего заменяют знак на противоположный у принятого мягкого решения если восстановленный кодовый символ текущего пакета соответствует логической единице, получая модифицированную последовательность мягких решений для ошибочного пакета

– повторно декодируют ошибочный пакет, используя модифицированную последовательность мягких решений для ошибочного пакета как дополнительную информацию, в тех позициях, в которых заменяли кодовые символы суммой символов разных пакетов;

– передают по каналу обратной связи сигналы, характеризующие результативность декодирования кодово-сопряженных пакетов.

Для реализации заявляемого способа может быть использована система связи, содержащая передающую и приемную части представленная на фиг. 3, где введены следующие обозначения:

1 – источник информации;

2 – кодер;

3, 8 – первый и второй декодеры;

4 – блок памяти восстановленных кодовых слов;

5 – блок памяти для выравнивания;

6 – получатель информации;

7 – блок памяти кодированных пакетов;

9 – блок формирования кодово-сопряженных пакетов;

10 – блок модификации и разделения кодовых символов;

11 – модулятор;

12 – канал связи;

13 – демодулятор.

Устройство содержит последовательно соединенные источник информации 1, кодер 2, блок формирования кодово-сопряженных пакетов 9, модулятор 11, канал связи 12 и демодулятор 13,выход которого соединен с входом блока модификации и разделения кодовых символов 10. При этом выход блока модификации и разделения кодовых символов 10 через последовательно соединенные второй декодер 8, блок памяти восстановленных кодовых слов 4 и первый декодер 3 соединен с первым входом блока памяти для выравнивания 5, второй вход которого подключен к другому выходу второго декодера 8. Выход блока памяти для выравнивания 5 соединен с входом получателя информации 6. Кроме того, выход кодера 2 через блок памяти кодированных пакетов 7 соединен с соответствующим входом блока формирования кодово-сопряженных пакетов 9. Выход-вход блока модификации и разделения кодовых символов 10 соединен с входом-выходом блока памяти восстановленных кодовых слов 4. Соединение соответствующих входов блока 9 и 10 и второго выхода второго декодера 8, а также соединение соответствующих входов блока 9 и 10 и второго выхода первого декодера 3 образуют канал обратной связи (на фиг. 3 изображены пунктиром).

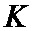
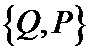
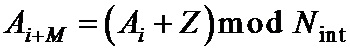
Работает устройство следующим образом: источник информации 1 формируют пакеты данных, каждый из которых содержит упорядоченную последовательность информационных символов, которые кодирует кодер 2 для чего каждый информационный символ повторяют в соответствии с шаблоном повторения , где первый массив отражает количество повторений, а второй – число повторенных символов, формируя последовательность повторенных информационных символов, осуществляют перемежение в последовательности повторенных информационных символов перемежителем размером , где первые символа образуют последовательность , а остальные номера получают по формуле , разбивают перемеженные повторенные информационные символы на группы таким образом, что первый проверочный символ получают путем суммирования по заданному модулю начального значения переменной суммирования со всеми перемеженными повторенными информационными символами из первой группы, а проверочный символ путем суммирования по заданному модулю проверочного символа со всеми перемеженными повторенными информационными символами из группы ; запоминают полученные проверочные символы в блоке памяти кодированных пакетов 7 и хранят их там до получения сигнала об успешном декодировании данного пакета по каналу обратной связи. В блоке формирования кодово-сопряженных пакетов 9 на передающей стороне при получении сигнала запроса повторной передачи формируют пакет с кодово-сопряженной частью, для чего в очередном кодированном пакете часть кодовых символов заменяют их суммой по модулю два с кодовыми символами ошибочно декодированного пакета, который был сохранен в блоке памяти кодированных пакетов 7. Модулируют полученную последовательность в модуляторе 11 и передают ее через канал связи 12. В демодуляторе 13 формируют принятые корреляционные отклики на каждый из переданных кодовых символов; выполняют оценку шумового параметра смеси сигнал плюс шум, которая приближенно равна величине стандартного отклонения эквивалентного гауссовского белого шума, которым аппроксимируются помехи в канале; формируют мягкие решения о принятых кодовых символах, используя полученную оценку шумового параметра смеси сигнал плюс шум. В блоке модификации и разделения кодовых символов 10, если передают пакет с кодово-сопряженной частью, модифицируют мягкие решения в кодово-сопряженной части в тех позициях, в которых заменяли кодовые символы суммой по модулю 2 символов разных пакетов для чего заменяют знак на противоположный у принятого мягкого решения, если восстановленный кодовый символ предыдущего пакета соответствует логической единице, получая мягкие решения текущего пакета. Декодируют мягкие решения текущего пакета вторым декодером 8 и сохраняют восстановленные последовательность мягких решений текущего пакета в блоке памяти восстановленных кодовых слов 4. Используя сохраненные кодовые символы, в блоке модификации и разделения кодовых символов 10 модифицируют мягкие решения в кодово-сопряженной части в тех позициях, в которых заменяли кодовые символы суммой символов разных пакетов, для чего заменяют знак на противоположный у принятого мягкого решения, если восстановленный кодовый символ текущего пакета соответствует логической единице, получая модифицированную последовательность мягких решений для ошибочного пакета и повторно декодируют ошибочный пакет в декодере 3, используя модифицированную последовательность мягких решений для ошибочного пакета как дополнительную информацию, в тех позициях, в которых заменяли кодовые символы суммой символов разных пакетов; передают по каналу обратной связи сигналы, характеризующие результативность декодирования кодово-сопряженных пакетов. Сохраняют декодированные без ошибок информационные пакеты в блоке памяти для выравнивания 5 для выдачи их получателю информации 6 в правильном порядке.

Структура пакета с кодово-сопряженной частью показана на фиг. 4. где в части а) показан процесс формирования кодово-сопряженного пакета, состоящий в том, что часть кодовых символов заменяют их суммой по модулю два с кодовыми символами ошибочно декодированного пакета, который был сохранен в блоке памяти кодированных пакетов, а в части б) показан процесс передачи последовательсти кодовых пакетов.

Алгоритм декодирования пакета с кодово-сопряженной частью показан на фиг. 5, где модифицируют мягкие решения в кодово-сопряженной части в тех позициях, в которых заменяли кодовые символы суммой по модулю 2 символов разных пакетов для чего заменяют знак на противоположный у принятого мягкого решения, если восстановленный кодовый символ предыдущего пакета соответствует логической единице, получая мягкие решения текущего пакета. В свою очередь, используя сохраненные кодовые символы текущего пакета модифицируют мягкие решения в кодово-сопряженной части в тех позициях, в которых заменяли кодовые символы суммой символов разных пакетов для чего заменяют знак на противоположный у принятого мягкого решения, если восстановленный кодовый символ текущего пакета соответствует логической единице, получая модифицированную последовательность мягких решений для ошибочного пакета и повторно декодируют ошибочный пакет. Если кадр не содержит перезапрос, то его просто декодируют, при этом если обнаружены ошибки, то сохраняют восстановленные кодовые символы и формируют сигнал запроса повторной передачи.

Алгоритм обнаружения ошибок в кодовом слове представлен на фиг. 6.

Обнаружение ошибок в заявляемом способе передачи данных в цифровой системе связи может быть пояснено следующим примером. Пусть мы имеем код “повторение с накоплением” заданный двудольным регулярным графом. Рассмотрим различные конфигурации ошибок. Отметим случай, когда существуют ошибочно декодированные переменные вершины, но все контрольные суммы равны нулю. Это случай необнаружимой ошибки. Рассмотрим также случай, когда ошибки только в проверочной части кодового слова. Заметим, что каждая ошибка в проверочной части вызывает неравенство нулю двух соседних контрольных сумм. Однако неравные нулю контрольные суммы при ошибке в информационной части разнесены на расстояние пропорциональное параметру разнесения интерливера (перемежителя). Таким образом, при наличии единственной ошибки легко определить к какому символу она относится: информационному или проверочному. Для этого достаточно рассмотреть разность номеров проверочных вершин соответствующих неравным нулю контрольным суммам. Если таковая разность равна 1, то ошибочный символ однозначно можно отнести к проверочным символам, если больше, то ошибочный символ информационный.

Переходя к случаю многих ошибок, алгоритм состоит в следующем:

• если число отличных от нуля контрольных сумм нечетно, то изменяют контрольное значение последней суммы, добиваясь четного числа контрольных сумм;

• последовательно разбивают контрольные суммы на пары, вычисляют сумму разностей адресов проверочных вершин;

• сравнивают полученное значение с порогом, если оно меньше порога, то относят ошибки только к проверочным символам.

Таким образом, обнаружение ошибок осуществляют без CRC, тем самым повышая качество радиосвязи за счет снижения количества избыточных передаваемых кодовых символов, обеспечивая одновременно обнаружение и исправление ошибок.

Все блоки, входящие в систему связи могут быть реализованы на процессоре, ПЛИС, специализированной микросхеме.

Отличительными (новыми) признаками заявляемого способа передачи данных в цифровой системе радиосвязи относительно прототипа являются следующие признаки:

-новый способ кодового сопряжения пакетов;

-новый способ декодирования кодово-сопряженных пакетов.

Сопоставительный анализ заявляемого способа с прототипом показывает, что предлагаемое изобретение существенно отличается от известных решений, так как позволяет повысить качество радиосвязи за счет снижения количества избыточных передаваемых кодовых символов, путем кодового сопряжения пакетов при автоматическом запросе-повторении, а также используя новый, оптимизированный способ перемежения, увеличить быстродействие и пропускную способность устройства за счет параллельной обработки пакетов данных.

Таким образом, технический результат состоит в получении энергетического выигрыша кодирования в среднем 0.5 дБ.

Для этого в способе применяют кодовое сопряжение пакетов и новый способ перемежения кодовых символов.

Таким образом, заявляемый способ позволяет достичь энергетического выигрыша кодирования в среднем 0.5 дБ по сравнению с прототипом. Кроме того, заявляемый способ допускает параллельную реализацию декодирующего устройства без потери характеристик помехоустойчивости.

Изобретение относится к области теории кодирования, в частности к системам для объединенного кодирования с исправлением и обнаружением ошибок. Технический результат - повышение эффективности использования спектра при передаче данных в цифровой системе радиосвязи. Для этого в способе применяют кодовое сопряжение пакетов. Таким образом, заявляемый способ позволяет получить энергетический выигрыш кодирования в среднем 0.5 дБ. Кроме того, способ допускает параллельную реализацию декодирующего устройства без потери характеристик помехоустойчивости. 8 з.п. ф-лы, 9 ил.

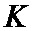
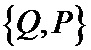
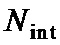
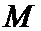
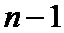
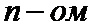
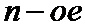
1. Способ передачи данных в цифровой системе связи, заключающийся в том, что на передающей стороне формируют пакеты данных, каждый из которых содержит упорядоченную последовательность информационных символов, каждый информационный символ повторяют в соответствии с шаблоном повторения , где первый массив отражает количество повторений, а второй – число повторенных символов, формируя последовательность повторенных информационных символов, осуществляют перемежение в последовательности повторенных информационных символов перемежителем размером , где первые символа образуют последовательность , а остальные номера получают по формуле , формируя последовательность перемеженных повторенных информационных символов, разбивают перемеженные повторенные информационные символы на группы таким образом, что первый проверочный символ получают путем суммирования по заданному модулю начального значения переменной суммирования со всеми перемеженными повторенными информационными символами из первой группы, а проверочный символ путем суммирования по заданному модулю проверочного символа со всеми перемеженными повторенными информационными символами из группы , запоминают полученные проверочные символы, формируют кодовое слово путем добавления проверочных символов к информационным символам; на приемной стороне формируют принятые корреляционные отклики на каждый из переданных кодовых символов, выполняют оценку шумового параметра смеси сигнал плюс шум, формируют мягкие решения о принятых кодовых символах, используя полученную оценку шумового параметра смеси сигнал плюс шум, разделяют мягкие решения о принятых кодовых символах на решения об информационных символах и решения о проверочных символах, повторяют мягкие решения об информационных символах, в соответствии с шаблоном повторения информационных символов повторяют мягкие решения о проверочных символах, по крайней мере, два раза за исключением последнего проверочного символа, для мягких решений об информационных символах выполняют перемежение аналогичное перемежению на передающей стороне, формируют группы перемеженных мягких решений об информационных символах аналогичные группам соответствующих информационных символов на передающей стороне, первую группу перемеженных мягких решений дополняют мягким решением, соответствующим начальному значению переменной суммирования, и первой копией мягкого решения о первом проверочном символе, образуя первое кодовое слово кода обобщенной проверки на четность, группу перемеженных мягких решений дополняют второй копией проверочного символа и первой копией мягкого решения об проверочном символе, образуя кодовое слово кода обобщенной проверки на четность, для каждого мягкого решения, входящего в каждое кодовое слово кода обобщенной проверки на четность, формируют модифицированное мягкое решение, которое является исходящим сообщением кодового слова кода обобщенной проверки на четность таким образом, что исходящее сообщение кодового слова кода обобщенной проверки на четность представляет собой результат функционального преобразования исходных мягких решений, представляющих собой входящие сообщения кодового слова кода обобщенной проверки на четность, деперемежают исходящие сообщения кодового слова кода обобщенной проверки на четность таким образом, что каждой копии мягкого решения о кодовом символе ставят в соответствие исходящее сообщение кодового слова кода обобщенной проверки на четность соответствующее копии мягкого решения об этом символе, группируют исходящие сообщения кодового слова кода обобщенной проверки на четность с мягкими решениями о принятых кодовых символах, так что в каждую группу входят мягкое решение о соответствующем кодовом символе и исходящие сообщение кодового слова кода обобщенной проверки на четность, соответствующее копии мягкого решения об этом символе, формируя, таким образом, кодовое слово обобщенного кода повторения, ставя каждое кодовое слово обобщенного кода повторения в соответствие кодовому символу, таким образом, что каждое исходящее сообщения кодового слова кода обобщенной проверки на четность является входящим сообщением кодового слова обобщенного кода повторения, для каждого мягкого решения входящего в каждое кодовое слово обобщенного кода повторения формируют модифицированное мягкое решение, которое является исходящим сообщением кодового обобщенного кода повторения, представляющее собой результат функционального преобразования над входящими сообщениями кодового слова обобщенного кода повторения, итеративно повторяют процесс обмена исходящими и входящими сообщениями таким образом, что исходящее сообщение кодового слова обобщенного кода повторений является входящим сообщением кодового слова кода обобщенной проверки на четность, а исходящее сообщение кода обобщенной проверки на четность является входящим сообщением кодового слова обобщенного кода повторений, формируя на каждой итерации последовательность модифицированных мягких решений, из последовательности модифицированных мягких решений формируют декодированные кодовые слова, умножают каждое декодированное кодовое слово на проверочную матрицу, получая упорядоченную последовательность контрольных сумм, если все контрольные суммы равны нулю, то кодовое слово считают декодированным верно, если количество контрольных сумм отличных от нуля нечетно и последняя контрольная сумма отлична от нуля, то заменяют ее нулем, если количество контрольных сумм отличных от нуля нечетно и последняя в последовательности контрольная сумма равна нулю, то ее заменяют любым отличным от нуля значением, разбивают последовательность контрольных сумм на пары, в которые входят элементы последовательности, идущие подряд, причем каждая контрольная сумма входит только в единственную пару, в каждой паре вычисляют разность номеров контрольных сумм, складывают все полученные разности номеров контрольных сумм, сравнивают полученное число с заданным порогом, если число превышает установленный порог, то информационную часть кодового слова считают декодированной неверно, если полученное число меньше заданного порога, то информационную часть кодового слова считают декодированной верно, отличающийся тем, что формируют сигнал запроса повторной передачи по каналу обратной связи для передающей стороны, если информационная часть кодового слова декодирована неверно, на передающей стороне при получении сигнала запроса повторной передачи формируют пакет с кодово-сопряженной частью, для чего в очередном кодированном пакете часть кодовых символов заменяют суммой по модуля два с кодовыми символами ранее переданного и ошибочно декодированного пакета, формируя тем самым кодово-сопряженную часть, при получении текущего пакета с кодово-сопряженной частью декодируют его совместно с ранее принятым ошибочно декодированным пакетом для чего восстанавливают, возможно, с ошибками, последовательность мягких решений ошибочного пакета, модифицируют мягкие решения в кодово-сопряженной части в тех позициях, в которых заменяли кодовые символы суммой символов разных пакетов для чего заменяют знак на противоположный у принятого мягкого решения, если восстановленный кодовый символ предыдущего пакета соответствует логической единице, получая мягкие решения текущего пакета, декодируют мягкие решения текущего пакета, восстанавливают последовательность мягких решений текущего пакета, модифицируют мягкие решения в кодово-сопряженной части в тех позициях, в которых заменяли кодовые символы суммой символов разных пакетов для чего заменяют знак на противоположный у принятого мягкого решения, если восстановленный кодовый символ текущего пакета соответствует логической единице, получая модифицированную последовательность мягких решений для ошибочного пакета, повторно декодируют ошибочный пакет, используя модифицированную последовательность мягких решений для ошибочного пакета, как дополнительную информацию в тех позициях, в которых заменяли кодовые символы суммой символов разных пакетов, передают по каналу обратной связи сигналы, характеризующие результативность декодирования кодово-сопряженных пакетов.

2. Способ по п. 1, отличающийся тем, что оценку шумового параметра смеси сигнал плюс шум, определяют как величину стандартного отклонения эквивалентного гауссовского белого шума, которым аппроксимируются помехи в канале.

3. Способ по п. 1, отличающийся тем, что для получения скорости кодирования перемеженные повторенные информационные символы накапливают по 6.

4. Способ по п. 1, отличающийся тем, что для получения скорости кодирования перемеженные повторенные информационные символы накапливают по 3.

5. Способ по п. 1, отличающийся тем, что для получения скорости кодирования 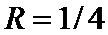перемеженные повторенные информационные символы накапливают по 2.

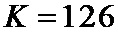
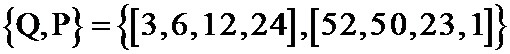
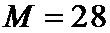
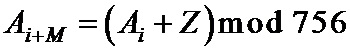
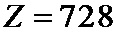
6. Способ по п. 1, отличающийся тем, что число информационных символов , шаблон повторения информационных символов размер перемежителя , первые символа перемежителя остальные получают как , где .

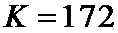
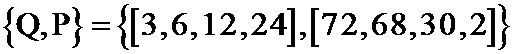
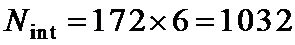
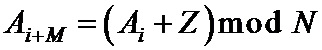
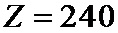
7. Способ по п. 1, отличающийся тем, что число информационных символов , шаблон повторения размер перемежителя , первые символа перемежителя , а остальные получают как , где .

8. Способ по п. 1, отличающийся тем, что число информационных символов , шаблон повторения размер перемежителя , первые символа перемежителя , а остальные получают как , где .

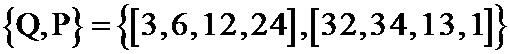
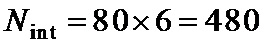
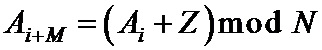
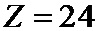
9. Способ по п. 1 , отличающийся тем, что кодово-сопряженную часть составляет каждый 9-ый проверочный символ.