Изобретение относится к сборке зубчатых планетарных передач, которые широко применяются в машиностроении.
Известен способ сборки зубчатых передач, при котором скорость вращения входного и выходного звеньев передачи оказываются разными (Артоболевский И.И. / Теория механизмов и машин / изд. «Наука» 1988 г., стр. 153, рисунок 7.19). Пары колес 1-2, 2-3, 3'-4, 4'-5 последовательно вводятся в зацепление, в результате чего скорость вращения входного звена 1 передачи и выходного звена 5 оказываются разными и именно этим добиваются уменьшения скорости (редукции) входного звена передачи.
Недостатком такой передачи является ее громоздкость в осевом направлении. При любом наращивании такой передачи новыми ступенями колес, габариты и объем передачи увеличиваются.
Известен способ устранения этого недостатка ступенчатых зубчатых передач, при котором передача собирается соосной, т.е. геометрические оси входного колеса и выходного звена совмещаются (Артоболевский И.И. / Теория механизмов и машин / изд. «Наука» 1988 г., стр. 156, рисунок 7.23). Однако это достигается тем, что одно из колес, а именно колесо 2 выполняется с подвижной геометрической осью. Это колесо называют сателлитом, рычаг, которым сателлит связывается с неподвижной опорой - водилом, а всю передачу - планетарной. Недостатком такого способа соединения колес является то, что вся передача при этом оказывается неуравновешенной. Эта неуравновешенность возникает из-за того, что центр тяжести сателлита становится подвижным, а потому в нем возникает сила инерции, определяющаяся массой сателлита и нормальным ускорением центра этой массы.
Наиболее близким к предлагаемому изобретению является способ сборки соосных планетарных передач с установкой на водило «Н» нескольких сателлитов - 2, 2',2'' и таким образом, что инерционные силы сателлитов взаимоуравновешиваются (Артоболевский И.И. / Теория механизмов и машин / изд. «Наука» 1988 г., стр. 502, рисунок 24.3). Этот способ имеет самое широкое применение в практике. Однако и у этого способа имеется важный недостаток. Дело в том, что если на водило установлено два и более сателлитов, то передача становится принципиально неработоспособной. Уже при двух сателлитах, теоретически, подвижность системы оказывается равной нулю, т.е. она становится неподвижной. Действительно, подвижность такой плоской системы определяется известной формулой Чебышева П.Л., (Артоболевский И.И. / Теория механизмов и машин/ изд. «Наука» 1988 г. стр. 40 под номером 2,6)

где, n - число звеньев цепи,
p5 - число шарниров в цепи,
p4 - число высших пар, т.е. пар зацеплений колес.
Приведенная формула Чебышева П.Л. полностью описывает подвижность планетарной передачи, что доказывается ее использованием профессором Руденко Н.Ф. в его монографии (Руденко Н.Ф. /Планетарные передачи/ изд. «Машгиз» 1947 г., стр. 5, формула 1), а также профессором Кудрявцевым В.Н. в справочнике (Кудрявцев В.Н., Кирдяшев Ю.И. / Планетарные передачи, справочник/ изд. «Машиностроение» 1977 г., стр. 311, формула 19.2).
Для односателлитной передачи, показанной на рисунке 7.23 (Артоболевский И.И. / Теория механизмов и машин/ изд. «Наука» 1988 г., стр. 156), где число подвижных звеньев n=3 (центральное колесо 3, сателлит 2 и водило Н), число шарниров p5=3 и число пар зацепления колес p4=2, по приведенной формуле W=1. Если же установить на водило Н два сателлита, т.е. принять nс=2, nс - число сателлитов, то число звеньев передачи станет равным 4, число пар пятого класса p5=4 и число пар четвертого класса - пар зацепления p4=4. Подвижность передачи при этом по формуле Чебышева П.Л. станет равной нулю W=12-8-4=0? что означает невозможность движения колес. При числе сателлитов, равным трем (nс=3) рис. 24.3 (Артоболевский И.И. / Теория механизмов и машин/ изд. «Наука» 1988 г., стр. 502), передача становится не только неподвижной, но и статически неопределимой (W=-l). При увеличении числа сателлитов до четырех (nс=4)подвижность передачи становится W=-2, т.е. она оказывается дважды статически неопределимой.
В действительности - по опыту, такие передачи остаются подвижными но лишь потому, что передача сил в них осуществляется одним сателлитом, а у остальных сателлитов возникают зазоры с зубьями центральных колес. Это обстоятельство доказано профессором Кудрявцевым В.Н. в его монографии (Кудрявцев В.Н. / Планетарные передачи, монография / изд. «Машиностроение» 1966 г.). В ней на стр. 215, профессор Кудрявцев В.Н. записывает: «В реальной передаче с фиксированными осями центральных колес и водила, вследствие неизбежности погрешностей, касание будет только с одним сателлитом (с сателлитом 1) рисунок 105в, стр. 212. В зацеплении с остальными сателлитами будут зазоры Δ2, Δ3 ... Δαр)».
Таким образом, при сборке широко применяемых в практике многосателлитных передач, во-первых, установка второго, третьего и т.д. сателлитов не повышает передаваемой мощности передачи и, во-вторых, изготовление и установка дополнительных сателлитов требует неоправданных экономических затрат.
Техническая проблема, решаемая предлагаемым изобретением, заключается в сборке планетарной передачи с самоустанавливающимися сателлитами, способными устранять все возможные зазоры и передавать мощность всеми сателлитами без исключения.
Техническая проблема решается тем, что в предлагаемом способе сборки зубчатых передач путем соосного соединения ведущего центрального зубчатого колеса через сателлиты с неподвижным зубчатым колесом и выходным звеном-водилом, согласно изобретению, входное центральное колесо, выходное звено - водило и сателлиты соединяют дополнительными рычагами в кинематическую цепь, в которой сателлиты передачи вместе с дополнительными рычагами образуют между собой единую статически определимую группу звеньев, имеющую возможность самоустанавливаться между входным звеном и неподвижным колесом с выбором всех зазоров между звеньями.
Технический результат, получаемый при использовании предлагаемого изобретения, заключается в том, что сателлиты нагружаются одинаково, т.е. вся мощность передается через все сателлиты, и каждый из них нагружается равными усилиями. По предлагаемому способу в состав передачи входят центральное колесо, водило, сателлиты и дополнительные рычаги, при этом входное центральное колесо, выходное звено - водило, сателлиты и рычаги собираются в единую кинематическую цепь, в которой все сателлиты нагружаются одинаково.
Предлагаемый способ сборки зубчатых планетарных передач имеет строгое аналитическое доказательство, заключающееся в том, что если собирается планетарная передача с (1+nдс) сателлитами, где nдс - дополнительные к первому сателлиты, то общее число подвижных звеньев в ней становится

где 2 - это входное звено - центральное зубчатое колесо и выходное звено - водило, а nдр - число дополнительных рычагов. При этом, число (1+nдс) сателлитов образуют (1+nдс) шарниров, входное колесо и водило добавляют в цепь два шарнира в их соединении с неподвижным колесом - стойкой и требуется еще nдр шарниров для присоединения к цепи дополнительных рычагов, т.е. всего кинематических пар - шарниров требуется

Кроме того, каждый из сателлитов, входящих в зацепление с центральным колесом, добавляет в цепь по две высших кинематических пары, т.е. всего

При этих условиях зависимость (1) для группы звеньев нулевой подвижности (W=0) преобразуется к виду
3[(1+nдс)+2+nдр]-2[(1+nдс)+2+nдр]-2(1+nдс)=0 откуда, раскрывая скобки и группируя члены, получим, что nдр=nдс.
Таким образом, чтобы обеспечить определенность движения всех звеньев планетарной зубчатой передачи при увеличении числа сателлитов, в кинематическую цепь передачи необходимо вводить дополнительные рычаги числом, равным числу дополнительных сателлитов.
На фигуре, иллюстрирующей способ, показан пример сборки трехсателлитной самоустанавливающейся планетарной передачи.
Способ предусматривает установку сателлита I с шарниром А, соединение его трехшарнирным рычагом 1 в шарнир В с сателлитом II. Третьим шарниром С трехшарнирный рычаг 1 соединяется со вторым (2) трехшарнирным рычагом, которым в свою очередь шарниром D соединяется с третьим сателлитом (III), а шарниром Е с рычагом - водилом (3) передачи, входящим в шарнир с неподвижной опорой О.
В этой цепи всего шесть звеньев (I, II, III, 1,2,3), шесть шарниров (A,B,C,D,E,O), шесть кинематических пар зацепления колес (m,n,f,g,k,e,). По формуле (1) при n=6, р5=6, р4=6 подвижность всей цепи W=18-12-6=0, то есть обозначенная цепь является самоустанавливающейся, не распадающейся на более простые группы. Ее особым свойством является то, что через нее обеспечивается движение от ведущего колеса на водило, при гарантированном зацеплении всех трех сателлитов с центральным колесом.
С увеличением числа сателлитов до четырех, пяти, шести и т.д. необходимо вводить соответственно шарниры и пары зацепления (р5 и р4) числом 8, 10, 12 и т.д., при этом нагрузка, передаваемая каждым из сателлитов от центрального колеса к водилу, будет уменьшаться пропорционально числу сателлитов (чем больше сателлитов, тем меньше нагрузка на каждый из них).
Положительный эффект, получаемый при сборке таких передач, заключается в том, что сателлиты передачи соединяются с водилом в кинематическую цепь, включающую в свой состав сателлиты и дополнительные рычажные звенья - рычаги, являющуюся не распадающейся на более простые группы звеньев нулевой подвижности.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ СБОРКИ МНОГОСАТЕЛЛИТНОЙ УРАВНОВЕШЕННОЙ ПЛАНЕТАРНОЙ ПЕРЕДАЧИ | 2020 |
|
RU2728880C1 |
| ПЛАНЕТАРНАЯ ПЕРЕДАЧА С НЕСКОЛЬКИМИ ВЫХОДНЫМИ ВАЛАМИ | 2023 |
|
RU2822630C1 |
| САМОУСТАНАВЛИВАЮЩАЯСЯ ПЯТИСАТЕЛЛИТНАЯ ПЛАНЕТАРНАЯ ПЕРЕДАЧА | 2018 |
|
RU2701296C1 |
| САМОУСТАНАВЛИВАЮЩИЙСЯ ПЛАНЕТАРНЫЙ МЕХАНИЗМ | 2007 |
|
RU2342573C1 |
| ДВУХСАТЕЛЛИТНАЯ ПЛАНЕТАРНАЯ ПЕРЕДАЧА СО СДВОЕННЫМИ КОЛЕСАМИ | 2024 |
|
RU2837945C1 |
| Самоустанавливающаяся пятисателлитная планетарная передача | 2015 |
|
RU2622731C1 |
| САМОУСТАНАВЛИВАЮЩАЯСЯ ШЕСТИСАТЕЛЛИТНАЯ ПЛАНЕТАРНАЯ ПЕРЕДАЧА | 2017 |
|
RU2662604C1 |
| Уравновешенный самоустанавливающийся планетарный механизм | 2024 |
|
RU2837603C1 |
| ДВУХСАТЕЛЛИТНЫЙ ПЛАНЕТАРНЫЙ РЕДУКТОР | 2023 |
|
RU2807784C1 |
| САМОУСТАНАВЛИВАЮЩИЙСЯ ПЛАНЕТАРНЫЙ МЕХАНИЗМ | 2010 |
|
RU2419006C1 |

Изобретение относится к машиностроению. Способ сборки зубчатых планетарных передач включает этап соосного соединения ведущего центрального зубчатого колеса через сателлиты с неподвижным зубчатым колесом и выходным звеном-водилом. При увеличении числа сателлитов входное центральное колесо, выходное звено-водило и вновь вводимые сателлиты соединяют дополнительными рычагами в кинематическую цепь, в которой сателлиты передачи вместе с дополнительными рычагами образуют между собой единую статически определимую группу звеньев, имеющую возможность самоустанавливаться между входным звеном и неподвижным колесом с выбором всех зазоров между звеньями. Число вводимых дополнительных рычагов соответственно равно числу вводимых дополнительных сателлитов. Обеспечивается сборка планетарной передачи без зазоров, с равномерно нагружаемыми сателлитами. 1 ил.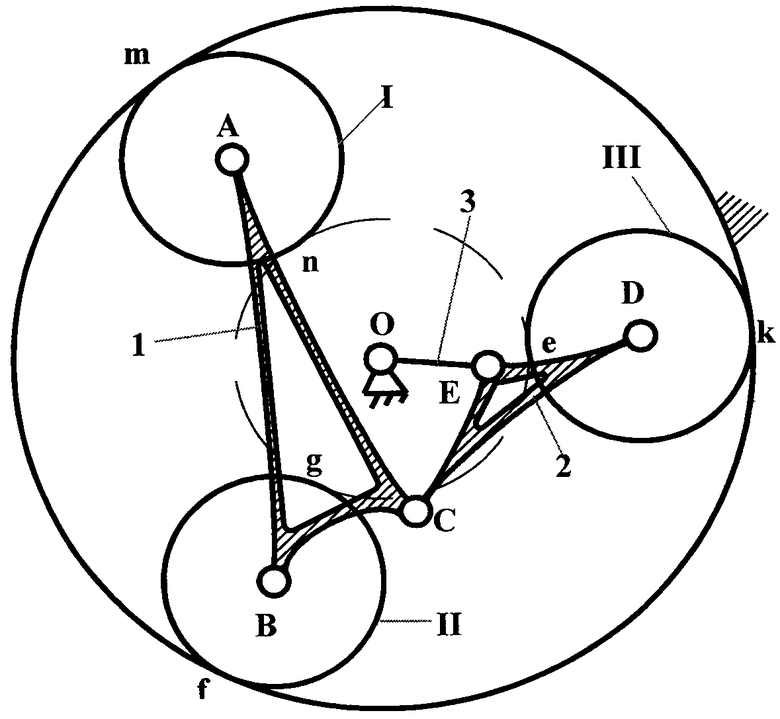
Способ сборки зубчатых планетарных передач, путем соосного соединения ведущего центрального зубчатого колеса через сателлиты с неподвижным зубчатым колесом и выходным звеном-водилом, отличающийся тем, что при увеличении числа сателлитов входное центральное колесо, выходное звено-водило и вновь вводимые сателлиты соединяют дополнительными рычагами в кинематическую цепь, в которой сателлиты передачи вместе с дополнительными рычагами образуют между собой единую статически определимую группу звеньев, имеющую возможность самоустанавливаться между входным звеном и неподвижным колесом с выбором всех зазоров между звеньями, причем число вводимых дополнительных рычагов соответственно равно числу вводимых дополнительных сателлитов.
| САМОУСТАНАВЛИВАЮЩИЙСЯ ТРЕХСАТЕЛЛИТНЫЙ ПЛАНЕТАРНЫЙ РЕДУКТОР | 2013 |
|
RU2541049C1 |
| САМОУСТАНАВЛИВАЮЩАЯСЯ ЧЕТЫРЁХСАТЕЛЛИТНАЯ ПЛАНЕТАРНАЯ ПЕРЕДАЧА | 2015 |
|
RU2583320C1 |
| US 6206800 B1, 27.03.2001. | |||
Авторы
Даты
2020-01-22—Публикация
2018-05-04—Подача