Изобретение относится к измерительной технике, в частности к измерению сверхвысокочастотных параметров материалов в свободном пространстве.
Известен способ измерения тангенса угла диэлектрических потерь tgδ в объемном резонаторе на фиксированной частоте, когда образец измеряется в двух положениях: на поршне и на подставке (Е.Б. Зальцман. Измерение tgδ диэлектриков методом передачи через резонатор. // Приборы и техника эксперимента, 1965, №6, с.101-104).
Недостатком способа является узкополосность производимых измерений. При измерении параметров tgδ материалов в резонаторе измерения производятся на образце специальной формы и с толщиной, настроенной на фиксированную частоту. При увеличении частоты измерения размеры резонатора уменьшаются, как и размеры образца, что снижает точность измерения.
Наиболее близким техническим решением является способ измерения относительной диэлектрической проницаемости и тангенса угла диэлектрических потерь (Р.А.Чирков, А.Е.Жителев, Р.А.Миронов, М.О.Забежайлов. Исследование диэлектрических характеристик материалов методами свободного пространства. Тезисы докладов XVI международного семинара структурные основы модифицирования материалов МНТ-XVI. /ИАЕЭ НИЯУ МИФИ, 2021, Обнинск, стр.74-77).
Этот способ включает измерение с помощью СВЧ измерителя ширины частотной кривой амплитуды на уровне 3 дБ, по которой рассчитывается тангенс угла диэлектрических потерь.
Недостатком способа является невысокая точность определения тангенса угла диэлектрических потерь, связанная с недостаточной точностью определения амплитуды на уровне 3 дБ.
Задачей настоящего изобретения является повышение точности определения тангенса угла диэлектрических потерь материалов.
Поставленная задача достигается тем, что предложен способ определения тангенса угла диэлектрических потерь плоского образца материала полуволновой толщины, включающий определение тангенса угла диэлектрических потерь в частотной области и измерение частоты, соответствующей минимуму амплитуды отраженной волны от образца, отличающийся тем, что дополнительно измеряют частоту, соответствующую середине скачка фазы отраженной волны от образца, рассчитывают разницу между частотами и определяют тангенс угла диэлектрических потерь по формуле:
 ,
,
где 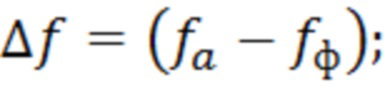
 - частота, соответствующая минимуму амплитуды отраженной волны от образца;
- частота, соответствующая минимуму амплитуды отраженной волны от образца;
 - частота, соответствующая середине скачка фазы отраженной волны от образца;
- частота, соответствующая середине скачка фазы отраженной волны от образца;
 - постоянные коэффициенты.
- постоянные коэффициенты.
Для анализа условий проведения определения тангенса угла диэлектрических потерь авторы использовали задачу нормального падения электромагнитной волны на бесконечную пластину диэлектрика, в которой амплитуда и фаза отраженной волны в зависимости от частоты рассчитывались с учетом относительной диэлектрической проницаемости и тангенса угла диэлектрических потерь:

где i - мнимая единица;
 - мнимая часть диэлектрической проницаемости;
- мнимая часть диэлектрической проницаемости;
 - относительная диэлектрическая проницаемость,
- относительная диэлектрическая проницаемость,
 - значение тангенса угла диэлектрических потерь.
- значение тангенса угла диэлектрических потерь.
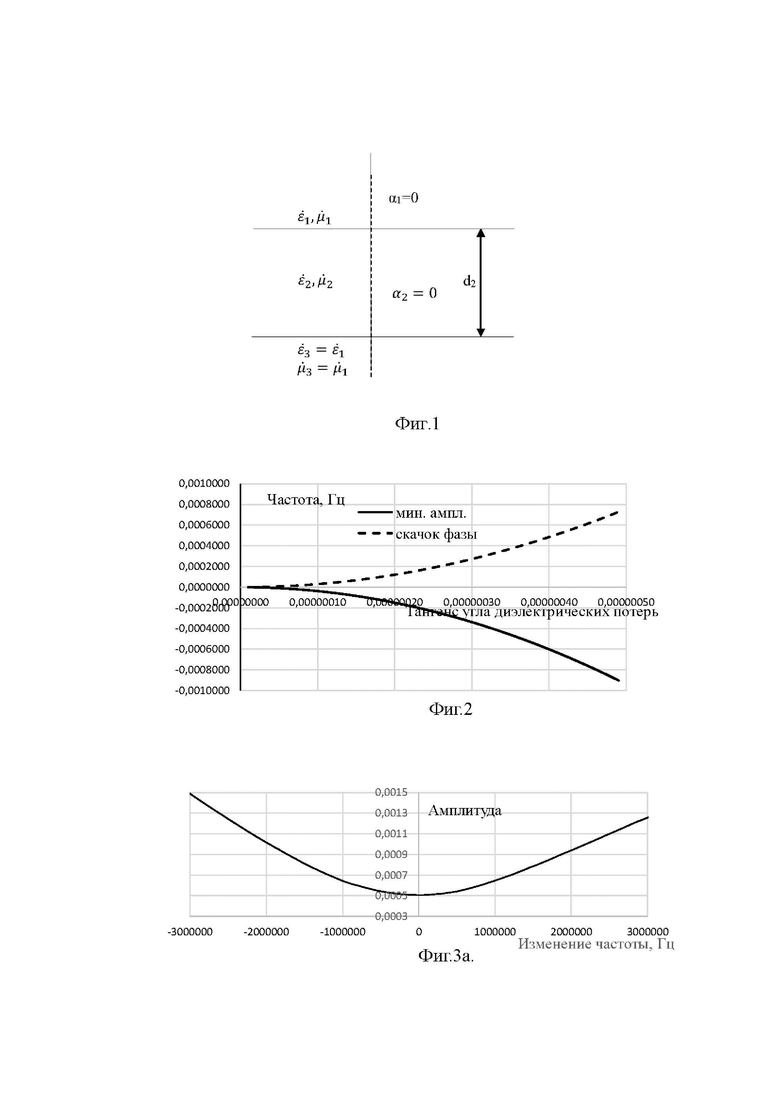
Параметры образца, как пластины, указаны на фиг. 1. Между первой и третьей средами с электродинамическими параметрами  ;
;  ; и
; и  ;
; 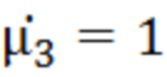 ,
,
где 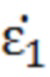 ,
, 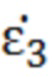 - относительные комплексные диэлектрические проницаемости сред;
- относительные комплексные диэлектрические проницаемости сред;
 ,
,  -относительные комплексные магнитные проницаемости сред, располагается исследуемый плоский образец с относительной комплексной диэлектрической проницаемостью
-относительные комплексные магнитные проницаемости сред, располагается исследуемый плоский образец с относительной комплексной диэлектрической проницаемостью 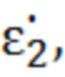 относительной комплексной магнитной проницаемостью
относительной комплексной магнитной проницаемостью  и геометрической толщиной
и геометрической толщиной 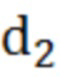 . Падающая волна изображена в виде луча, совпадающего с перпендикуляром к границе пластины - угол
. Падающая волна изображена в виде луча, совпадающего с перпендикуляром к границе пластины - угол  .
.
Модель расчета коэффициента отражения для задачи в рамках геометрической оптики построена на основе матричного метода для плоского образца (Борн М., Вольф Э. Основы оптики. Изд. 2-е. М.: Из-во «Наука», Главная редакция физико-математической литературы, 1973., 720 с.).
В рамках геометрической оптики по предложенной модели рассчитывались:
- положение на частотной оси минимума амплитуды отраженной волны по формуле:

где: 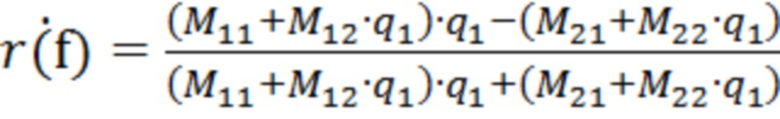 - расчетная частотная зависимость комплексного коэффициента отраженной волны;
- расчетная частотная зависимость комплексного коэффициента отраженной волны;
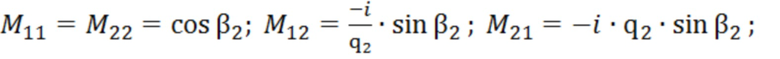
 -параметр, соответствующий плоскому образцу толщиной
-параметр, соответствующий плоскому образцу толщиной 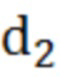 ;
;
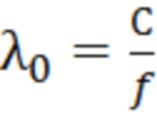 - длина волны;
- длина волны;
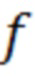 - частота измерений;
- частота измерений;
C - скорость света;
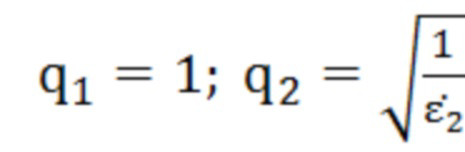 ;
;
- положение на частотной оси средней фазы в скачке наблюдаемого в отраженной волне от образца полуволновой толщины, которое определялось из измеренной частотной зависимости фазы коэффициента отражения Френеля и соответствующего расчетной фазе, по формуле:
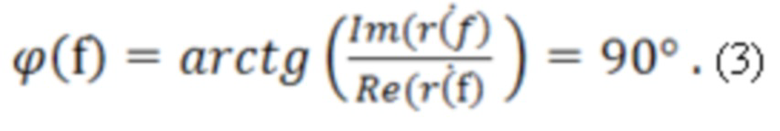
Анализируя результаты теоретических и экспериментальных исследований, авторы представили связь между формулами определения фазы и амплитуды отраженной волны из измеряемых параметров отраженной волны в виде:
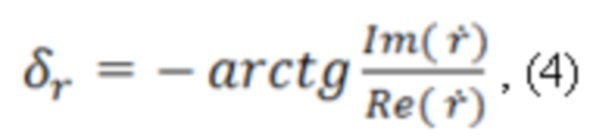
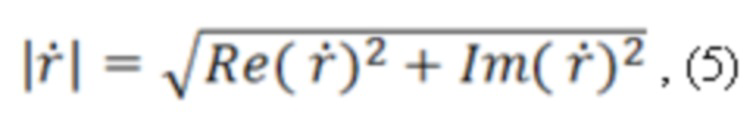
из которых можно делать вывод, что скачок фазы электромагнитной волны на 180° происходит тогда, когда выполняется условие равенства нулю действительной части амплитуды:
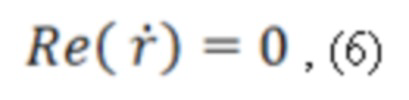
а условие минимума амплитуды при равенстве нулю модуля амплитуды:

выполняется только при условии равенства нулю действительной и мнимой частей амплитуды электромагнитной волны:
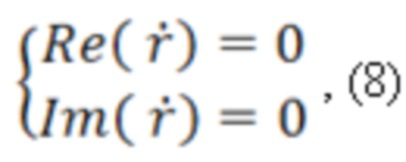
поэтому, как видно из сравнения условий (4) и (6) в общем случае точки минимума амплитуды и скачка фазы на 180° не должны совпадать. Но так как в основе математического описания электромагнитных амплитуд лежат гармонические функции, то очевидно, что для среды с электромагнитными параметрами с диэлектрическими и магнитными потерями это приводит к их несовпадению при положении на частотной оси.
Разница в частотных положениях минимума амплитуды и скачка фазы на 180° отраженной волны наблюдается в экспериментах и увеличивается пропорционально увеличению тангенса угла диэлектрических потерь в материале образца.
Для оценки влияния увеличения тангенса угла диэлектрических потерь на величину разницы в частотных положениях минимума амплитуды и скачка фазы на 180° отраженной волны от образца полуволновой толщины были проведены расчеты с использованием программной платформы Microsoft Visual Studio стандарта FORTRAN 2008 с применением дополнительных опций для чисел с плавающими запятыми для уменьшения ошибок расчетов при моделировании задачи падения электромагнитной волны на бесконечную пластину из однородного диэлектрического материала с потерями для образца с относительной диэлектрической проницаемостью  и в зависимости от малых значений тангенса угла диэлектрических потерь, которые представлены на фиг.2. Из фиг.2 видно, что с увеличением тангенса угла диэлектрических потерь разница между положением минимума амплитуды и положением скачка фазы отраженной волны увеличивается пропорционально увеличению тангенса угла диэлектрических потерь даже для столь малых значений.
и в зависимости от малых значений тангенса угла диэлектрических потерь, которые представлены на фиг.2. Из фиг.2 видно, что с увеличением тангенса угла диэлектрических потерь разница между положением минимума амплитуды и положением скачка фазы отраженной волны увеличивается пропорционально увеличению тангенса угла диэлектрических потерь даже для столь малых значений.
Для проверки реализации предложенного способа проведены экспериментальные измерения частотных зависимостей амплитуды и фазы отраженной волны от образца в виде пластины размерами 200х200 мм толщиной  мм.
мм.
На фиг.3a представлена экспериментальная частотная зависимость амплитуды отраженной волны от образца полуволновой толщины с относительной диэлектрической проницаемостью 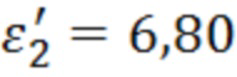 и тангенсом угла диэлектрических потерь
и тангенсом угла диэлектрических потерь  в котором частота соответствующая минимуму амплитуды, равна
в котором частота соответствующая минимуму амплитуды, равна 
На фиг.3б представлена экспериментальная частотная зависимость фазы отраженной волны от того же образца, что и на фиг.3 а, в котором частота соответствующая середине скачка фазы 90° равна 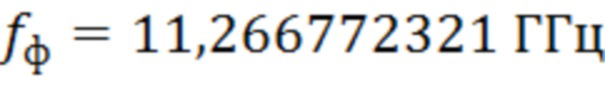
Из экспериментальных данных видно, что величина тангенса угла диэлектрических потерь 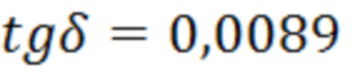 для экспериментально измеренного образца соответствует разнице по частоте
для экспериментально измеренного образца соответствует разнице по частоте 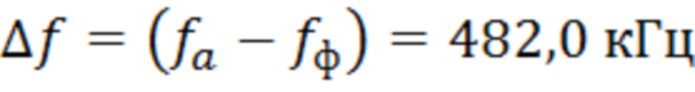 .
.
Для определения в широком диапазоне изменений тангенса угла диэлектрических потерь материала образца от разницы частот положения минимума амплитуды и скачка фазы были проведены теоретические расчеты параметров отраженной волны, а результаты расчетов для двух диапазонов изменения тангенса угла диэлектрических потерь представлены на фиг. 4 а, для tgδ в диапазоне от 0,0001 до 0,02, и 4б, для tgδ в диапазоне от 0,02 до 0,1. На фиг. 4а и 4б представлены аппроксимирующие кривые, найденные из расчетов с помощью метода наименьших квадратов с представлением кривой в виде зависимости:

где 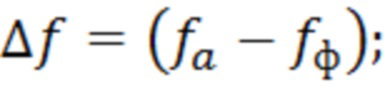
 - частота, соответствующая минимуму амплитуды отраженной волны от образца;
- частота, соответствующая минимуму амплитуды отраженной волны от образца;
 - частота, соответствующая середине скачка фазы отраженной волны от образца;
- частота, соответствующая середине скачка фазы отраженной волны от образца;
 - постоянные коэффициенты.
- постоянные коэффициенты.
Значения постоянных коэффициентов для двух диапазонов изменения тангенса угла диэлектрических потерь представлены в таблице, в которой для каждого диапазона указана размерность по частоте, для которой определялась аппроксимирующая зависимость.

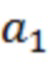
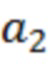

Таким образом, авторы установили, что предлагаемый способ позволяет с более высокой точностью определить величину тангенса угла диэлектрических потерь за счет использования измерений в частотной области.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ определения диэлектрической проницаемости материала | 2019 |
|
RU2713162C1 |
| Способ измерения относительной комплексной диэлектрической проницаемости материала с потерями | 2022 |
|
RU2789626C1 |
| Способ определения сверхвысокочастотных параметров материала в полосе частот и устройство для его осуществления | 2018 |
|
RU2688588C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ОТНОСИТЕЛЬНОЙ ДИЭЛЕКТРИЧЕСКОЙ ПРОНИЦАЕМОСТИ И ТАНГЕНСА УГЛА ДИЭЛЕКТРИЧЕСКИХ ПОТЕРЬ ДИЭЛЕКТРИЧЕСКОЙ СТРУКТУРЫ | 2019 |
|
RU2716600C1 |
| Способ измерения диэлектрических свойств материала и устройство для его осуществления | 2017 |
|
RU2665593C1 |
| Способ измерения комплексной диэлектрической проницаемости материала в диапазоне СВЧ | 2022 |
|
RU2797142C1 |
| УСТРОЙСТВО ДЛЯ ОПРЕДЕЛЕНИЯ ДИЭЛЕКТРИЧЕСКОЙ ПРОНИЦАЕМОСТИ ОБРАЗЦА МАТЕРИАЛА ПРИ ВОЗДЕЙСТВИИ ВНЕШНИХ ФАКТОРОВ | 2011 |
|
RU2453856C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ПАРАМЕТРОВ МАГНИТНОЙ ЖИДКОСТИ | 2017 |
|
RU2679457C1 |
| Устройство для неразрушающего измерения на СВЧ комплексной диэлектрической проницаемости материала диэлектрических пластин | 2023 |
|
RU2822306C1 |
| УСТРОЙСТВО ДЛЯ ОПРЕДЕЛЕНИЯ ПАРАМЕТРОВ НИЗКОИМПЕДАНСНЫХ МАТЕРИАЛОВ НА СВЧ С ПОМОЩЬЮ КОАКСИАЛЬНОГО РЕЗОНАТОРА | 2007 |
|
RU2326392C1 |

Изобретение относится к измерительной технике, а именно к измерению сверхвысокочастотных параметров материалов в свободном пространстве. Технический результат: повышение точности измерения тангенса угла диэлектрических потерь материала плоского образца полуволновой толщины в свободном пространстве. Сущность: измеряют частоту, соответствующую минимуму амплитуды отраженной волны от образца, и частоту, соответствующую середине скачка фазы отраженной волны от образца. Рассчитывают разницу между частотами. Определяют тангенс угла диэлектрических потерь по формуле

где 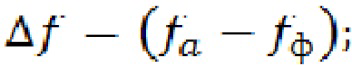
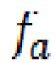 - частота, соответствующая минимуму амплитуды отраженной волны от образца;
- частота, соответствующая минимуму амплитуды отраженной волны от образца;  - частота, соответствующая середине скачка фазы отраженной волны от образца;
- частота, соответствующая середине скачка фазы отраженной волны от образца; 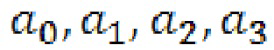 - постоянные коэффициенты. 4 ил.
- постоянные коэффициенты. 4 ил.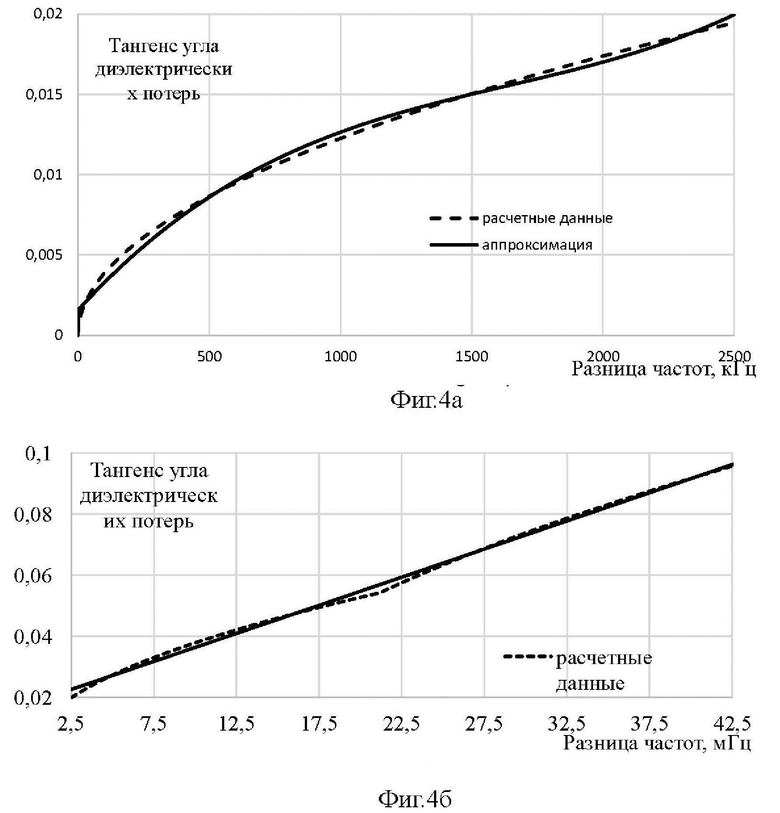
Способ определения тангенса угла диэлектрических потерь плоского образца материала полуволновой толщины, включающий определение тангенса угла диэлектрических потерь в частотной области и измерение частоты, соответствующей минимуму амплитуды отраженной волны от образца, отличающийся тем, что дополнительно измеряют частоту, соответствующую середине скачка фазы отраженной волны от образца, рассчитывают разницу между частотами и определяют тангенс угла диэлектрических потерь по формуле
 ,
,
где 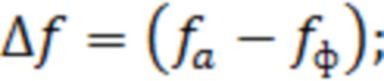
 - частота, соответствующая минимуму амплитуды отраженной волны от образца;
- частота, соответствующая минимуму амплитуды отраженной волны от образца;
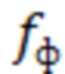 - частота, соответствующая середине скачка фазы отраженной волны от образца;
- частота, соответствующая середине скачка фазы отраженной волны от образца;
 - постоянные коэффициенты.
- постоянные коэффициенты.
| Способ измерения параметров плоскопараллельных диэлектриков | 1983 |
|
SU1166012A1 |
| Способ определения сверхвысокочастотных параметров материала в полосе частот и устройство для его осуществления | 2018 |
|
RU2688588C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ОТНОСИТЕЛЬНОЙ ДИЭЛЕКТРИЧЕСКОЙ ПРОНИЦАЕМОСТИ И ТАНГЕНСА УГЛА ДИЭЛЕКТРИЧЕСКИХ ПОТЕРЬ ДИЭЛЕКТРИЧЕСКОЙ СТРУКТУРЫ | 2019 |
|
RU2716600C1 |
| JP 11166952 A, 22.06.1999 | |||
| US 10309909 B2, 04.06.2019. | |||
Авторы
Даты
2023-01-11—Публикация
2022-04-07—Подача