Изобретение относится к вычислительной технике и может быть использовано в телепередающих и радиопередающих, телеприемных и радиоприемных устройствах, измерительной технике, фазометрических системах, а также в различных областях информационных технологий.
Известен способ сжатия вектора изображения (Патент РФ №(19)2646348, Опубликовано: 02.03.2018 Бюл. №7), )включающий создание эталонного вектора целевых характеристик изображения на основе вектора изображения, причем эталонный вектор включает информацию о целевых характеристиках изображения из вектора изображения; сжатие вектора изображения с помощью автокодировщика с получением сжатого вектора изображения на основе вектора изображения; распаковку сжатого вектора изображения с помощью автокодировщика с получением вектора изображения с потерями на основе сжатого вектора изображения; создание вектора целевых характеристик изображения с потерями на основе вектора изображения с потерями; сравнение эталонного вектора целевых характеристик изображения с вектором целевых характеристик изображения с потерями путем определения параметра расхождения и использование параметра расхождения для обучения автокодировщика так, что потери информации в векторе изображения с потерями, связанной с целевыми характеристиками, снижаются за счет повышенных потерь информации, связанной с дополнительными характеристиками изображения.
Однако в данном патенте нет информации, как создается эталонный вектор целевых характеристик изображения на основе вектора изображения. В современных технологиях этот вектор создается обычно с использованием системы Хаара, тригонометрической системы и вейвлетанализа [1, 2]. А вот с помощью автокодировщика происходит получение вектора изображения с потерями на основе вектора изображения. Как правило, это получается путем удаления маленьких коэффициентов при разложении по системе Хаара, тригонометрической системе и вейвлет систем и меньшие потери достигаются с помощью удаления меньших (по абсолютной величине) коэффициентов при разложении по указанным системам. У нас же другой принцип сжатия образов. У нас идет просто приближение (создание эталонного вектора целевых характеристик изображения) на основе вектора изображения к тому же с целочисленными компонентами, и при этом начальные компоненты приближенного вектора остаются и добавляются последующие, если исходное приближение нас не устраивает. Возможно, это будет оптимальное приближение исходя из установленного заранее количества компонент вектора.
Также известен способ сжатия цифровой информации с помощью эталонного электрического сигнала (патент РФ №2482604, опубликовано: 20.05.2013 бюл. №14) с помощью эталонного электрического сигнала, в котором используют предварительно выбранные эталонный электрический сигнал сжатия S (N) и эталонный электрический сигнал ключей восстановления K (N), которые изменяют с помощью арифметическо-логического устройства (АЛУ) электрическими сигналами, которые соответствуют элементам информации, цифровые коды которых сжимают и в результате получают измененный эталонный электрический сигнал сжатия S(n) и измененный эталонный электрический сигнал ключей восстановления K(n), с помощью которых впоследствии выполняют восстановление исходных электрических сигналов, которые соответствуют элементам информации, цифровые коды которых были сжаты, при этом в процессе сжатия цифровые разряды эталонного электрического сигнала отображают любые изменения эталонного сигнала и, следовательно, содержат полную информацию об электрических сигналах, которые поступили для сжатия.
Однако, здесь, сжатие образов получается за счет того что при разложении по указанным выше системам исходного сигнала многие коэффициенты просто равны нулю.
Наиболее близким является способ сжатия цифровой информации с помощью сжатия одномерных образов путем приближения элементов пространств Lp по системам сжатий и сдвигов одной функции рядами типа Фурье с целыми коэффициентами (патент РФ №2681367, опубликовано: 06.03.2019, бюл. №7). В то время, как в [2] рассматриваются другие системы функций, для которых целочисленные коэффициенты получить не возможно и ошибки при вычислении коэффициетов искажают исходный сигнал. При этом получается сжатие образов без отбрасывания малых коэффициентов и коэффициенты или 0 или больше 1 по абсолютной величине.
В заявляемом способе реализовано приближение - создание эталонного многомерного вектора целевых характеристик изображения на основе вектора изображения, к тому же, с целочисленными компонентами, и при этом начальные компоненты приближенного вектора остаются и добавляются последующие, если исходное приближение нас не устраивает. Таким образом, теперь можно сжимать изображения.
Техническая проблема заключается в необходимости создания алгоритмов, при которых при кодировании многомерных сигналов получается вектор с целочисленными компонентами, чего до этого не было.
Технический результат настоящего изобретения заключается в том, что сжатие многомерных образов можно осуществить за счет того, что при кодировании получаются целочисленные коэффициенты и много коэффициентов равно нулю. В то время, как в [2] рассматриваются другие системы функций, для которых целочисленные коэффициенты получить не возможно и ошибки при вычислении коэффициетов искажают исходный сигнал. При этом мы получаем сжатие многомерных образов без отбрасывания малых коэффициентов. У нас коэффициенты или 0 или больше 1 по абсолютной величине.
В заявляемом способе реализовано просто приближение (создание эталонного многомерного вектора целевых характеристик изображения) на основе вектора изображения к тому же с целочисленными компонентами, и при этом начальные компоненты приближенного многомерного вектора остаются и добавляются последующие, если исходное приближение нас не устраивает. Использованы новые системы функций [3-7] и по-другому вычисляются коэффициенты кодируемого сигнала. Таким образом, обеспечивается оптимальное приближение исходя из установленного заранее количества компонент вектора. Заметим, что в [7] коэффициенты не целочисленные и получают их иначе. К тому же, в заявляемом способе при промежуточных вычислениях, допускается неточность вычислений, которая корректируется в последующих вычислениях.
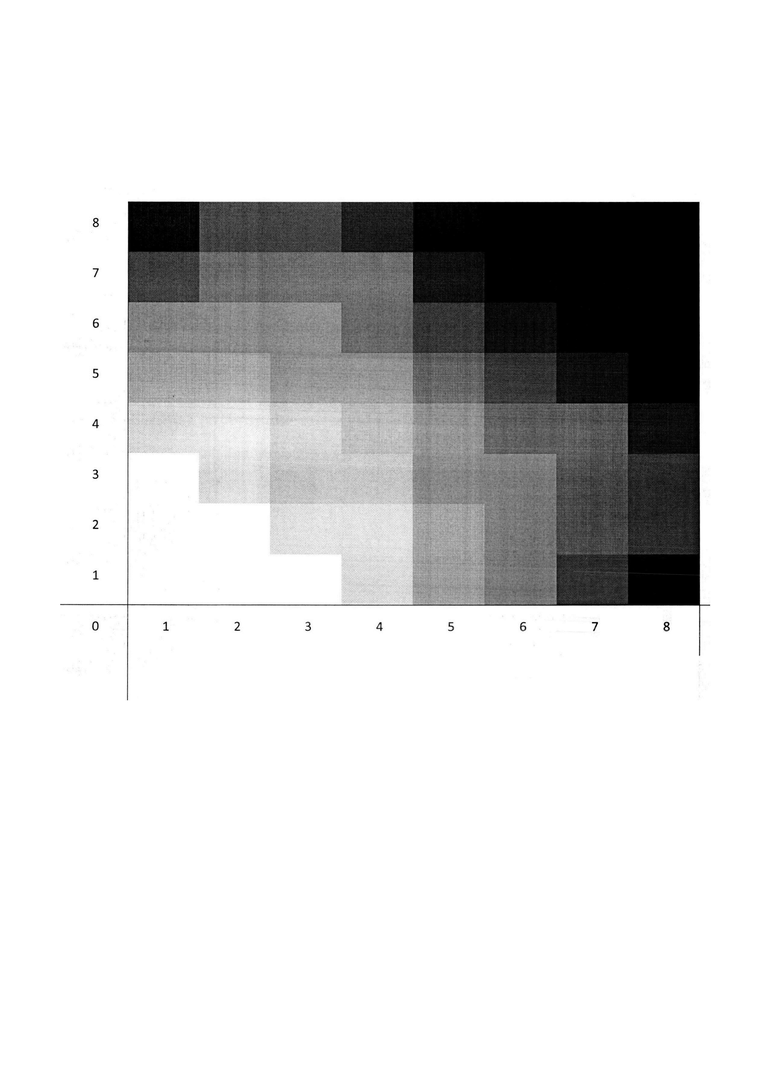
Способ поясняется чертежом: фиг. - пример практической реализации сжатия цифрового сигнала, полученного из функции многих переменных, где ступенчатая функция (квадраты разного цвета) - это полученное приближение исходного сигнала, а исходный сигнал, очевидно, будет изображаться постепенным изменением цвета на том же рисунке, где белый цвет соответствует значению «0», следующий по шкале - 1/8, далее - 2/8 и т.д.
Также автором предлагается (см. пример 2) рассмотрение разных многомерных сигналов в одном многомодулярном [8] пространстве. Способ сжатия многомерных образов путем приближения элементов пространств Lp{(0,1]m}, 1≤p<∞, m∈N, по системам сжатий и сдвигов одной функции рядами типа Фурье с целыми коэффициентами реализуют следующим образом.
Цифровой сигнал ƒ в виде функции многих переменных с выхода исследуемого объекта поступает как элемент пространства Lp{(0,1]m} на вход персонального компьютера. Как правило, это вектор изображения или таблица, где указано, на каком множестве какие значения эта функция принимает. Как правило, эти множества в виде n-мерных кубов или n-мерных параллелепипедов. Затем в электронно-вычислительный блок записывают последовательность значений этой функции.
Затем в электронно-вычислительном блоке осуществляют приближение элементов пространств Lp{(0,1]m} по системам из сжатий и сдвигов одной функции рядами типа Фурье с целыми коэффициентами. Для этого принимают, например, допущения: по осям ox и oy изображение в момент времени tl (таких моментов, например, может быть 24 в 1 секунду), точность приближения ε>0. Вводят функцию ψ (как образующую функцию для системы кодирования) в виде таблицы или формулы. При этом
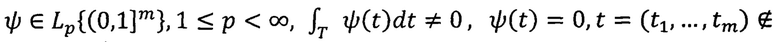
Т, Т=(0,1]×(0,1]×…×(0,1] - m-мерный куб, т.о. обеспечивают большой выбор систем, по которым осуществляют обработку исходного сигнала f. Затем вычисляют
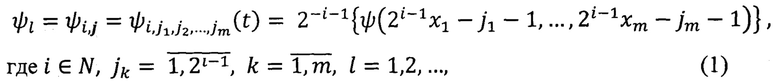
- элементы системы, по которой будет кодироваться сигнал.
Покажем, как l согласуется с номерами n и 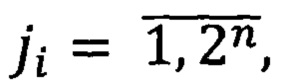
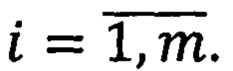 Предлагаем следующую нумерацию. Пусть n=1, 2, …. Далее для каждого фиксированного n номер ji изменяется от 1 до 2n. Совокупность этих элементов (при фиксированном n) назовем пачкой. Легко видеть, что элементов системы (1) в -ой пачке 2m(n-1). Очевидно, что при n=1 элементов в пачке 1. Поэтому l=1=r1. Далее переходим ко второй пачке и к номеру r1 добавляем номера во второй пачке. Для этого пусть n=2 и все ji=1,
Предлагаем следующую нумерацию. Пусть n=1, 2, …. Далее для каждого фиксированного n номер ji изменяется от 1 до 2n. Совокупность этих элементов (при фиксированном n) назовем пачкой. Легко видеть, что элементов системы (1) в -ой пачке 2m(n-1). Очевидно, что при n=1 элементов в пачке 1. Поэтому l=1=r1. Далее переходим ко второй пачке и к номеру r1 добавляем номера во второй пачке. Для этого пусть n=2 и все ji=1, 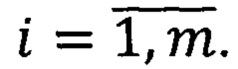 Это будет соответствовать номеру l=2=r1+1. Далее добавляем 1 к j1, то есть J1=2, а l=r1+2=3 и так далее до номера j1=2n-1. При этом l=r1+2=3. Затем задаем j2=2 а j1 изменяется от 1 до 22-1. Таким образом, l=4=r1+2+1, l=5=r1+2+2 и так далее. Очевидно, что для произвольного n≥3 нумерация начнется с номера l=5=r1+r2+…rn-1+1, где ji=1,
Это будет соответствовать номеру l=2=r1+1. Далее добавляем 1 к j1, то есть J1=2, а l=r1+2=3 и так далее до номера j1=2n-1. При этом l=r1+2=3. Затем задаем j2=2 а j1 изменяется от 1 до 22-1. Таким образом, l=4=r1+2+1, l=5=r1+2+2 и так далее. Очевидно, что для произвольного n≥3 нумерация начнется с номера l=5=r1+r2+…rn-1+1, где ji=1, 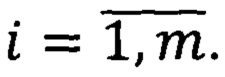 Затем для l=r1+r2+…rn-1+2 возьмем j1=2 и так далее.
Затем для l=r1+r2+…rn-1+2 возьмем j1=2 и так далее.
Пусть, теперь, рассматривается частный случай функции ψ(t):
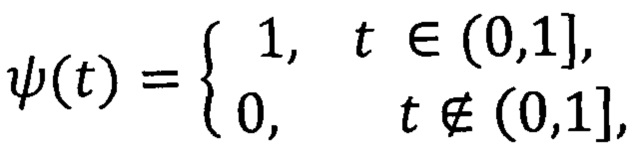
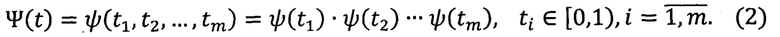
Для произвольной функции ƒ∈Lp{(0,1]m}, 1≤p<∞, построим ряд 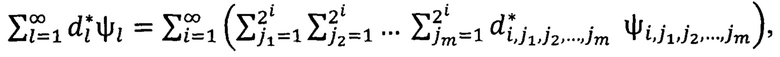
где
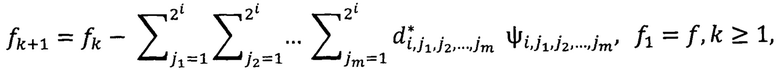
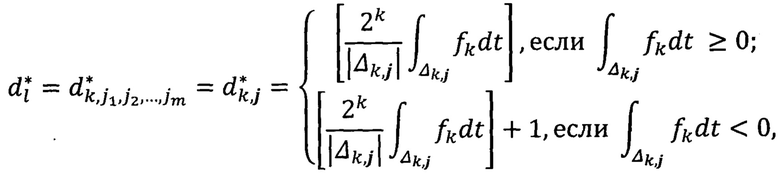
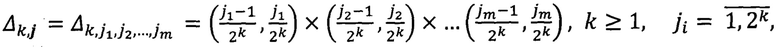
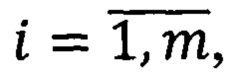 и [а] - целая часть числа а.
и [а] - целая часть числа а.
В общем случае, когда ψ∈Lp{(0,1]m}, 1≤p<∞, ∫T ψ(t)dt≠0, ψ(t)=0, t=(t1, …, tm)∉T, T=(0,1]×(0,1]×…×(0,1] промежуточные вычисления ƒk производят несколько иначе. Сама система (1) также рассматривается в несколько другом виде. Вводится параметр λ0,зависящий от функции ψ.
Математическими методами доказывается, что построенный ряд (как в частном случае, так и в общем случае) сходится по норме пространства Lp{(0,1]m}, 1≤p<∞, к рассматриваемой функции ƒ∈Lp{(0,1]m}, 1≤p<∞. Заметим, что нумерации элементов внутри пачки могут быть разные, но это не влияет на сходимость построенного ряда. Далее, для практического применения доказанных методов, рассматриваем частичные суммы построенного ряда. Задаем точность приближения ε>0. Проверяем точность приближения
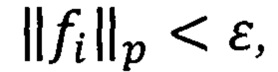
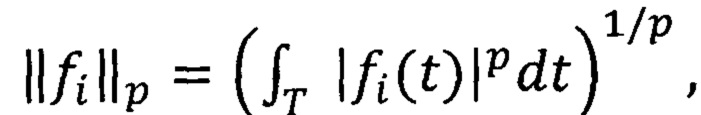
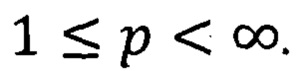
Если точность приближения достигнута, то вычисления прекращают, в противном случае формируют новый цикл с ƒi+1. Выводят для запоминания коэффициенты 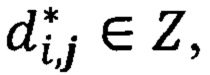 где Z - целые числа, т.е. кодируют сигнал. Так как коэффициенты целые и многие равны 0 (нулевые коэффициенты игнорируем), получают сжатие образа (сигнала). Затем восстанавливают (т.е. декодируют) путем составления суммы
где Z - целые числа, т.е. кодируют сигнал. Так как коэффициенты целые и многие равны 0 (нулевые коэффициенты игнорируем), получают сжатие образа (сигнала). Затем восстанавливают (т.е. декодируют) путем составления суммы
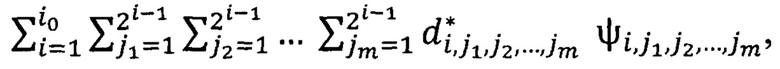
где 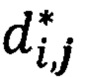 мы получили, а
мы получили, а 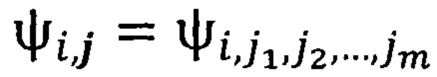 заранее известны, так как мы заранее установили, что кодирование и раскодирование происходит с участием системы
заранее известны, так как мы заранее установили, что кодирование и раскодирование происходит с участием системы 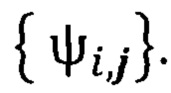 Таким образом, получаем удовлетворяющее поставленным условиям приближение
Таким образом, получаем удовлетворяющее поставленным условиям приближение
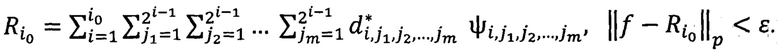
Заметим, что для некоторых ψ(t) имеем, что i=ni, i∈N, ni∈N, как в случае системы (1) для произвольной образующей функции ψ(t).
Пример 1. Для подтверждения практической реализации рассмотрим пример сжатия выходного сигнала в виде фрагмента поверхности эллиптического параболоида.
Рассмотрим функцию ƒ(x,y)=х2+y2, x∈[0,1], y∈[0,1]. Пусть ε=0.11 и
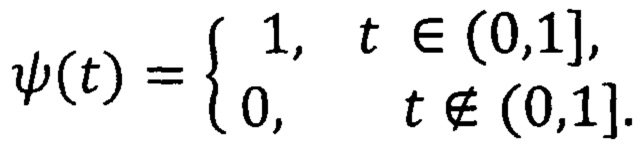
Пусть 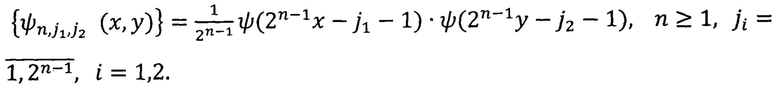
Построим сумму 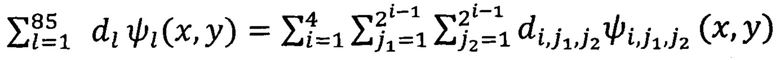
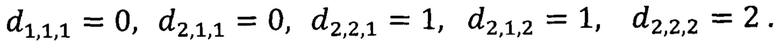
Строим функцию
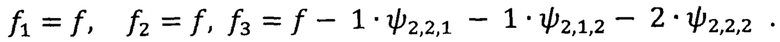
Вычисляем коэффициенты
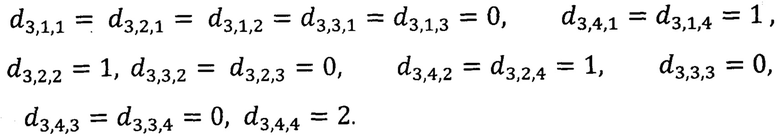
Строим функцию
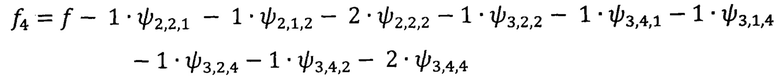
Вычисляем коэффициенты
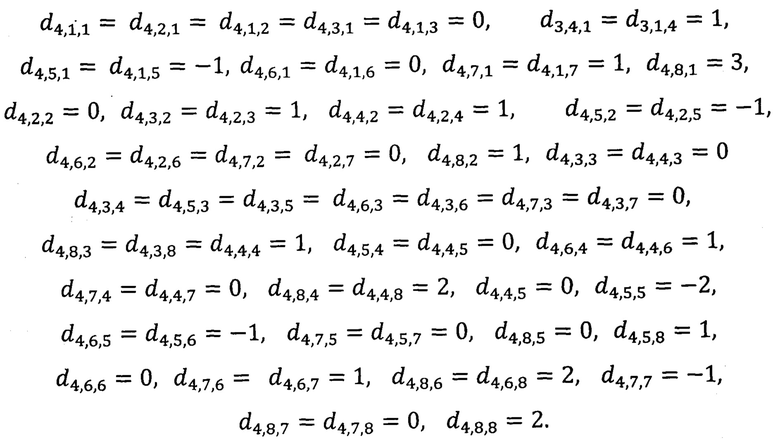
Строим функцию
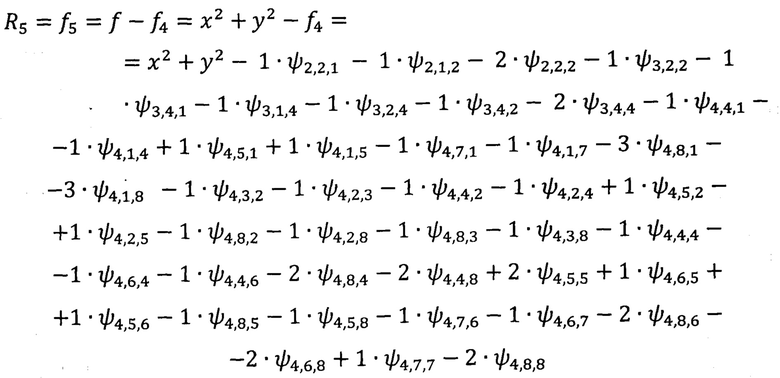
Как видим, из 85 коэффициентов 43 коэффициента не равны 0, а остальные все равны 0.
Погрешность приближения удовлетворяет заданной точности приближения в среднем и по норме пространства L2.
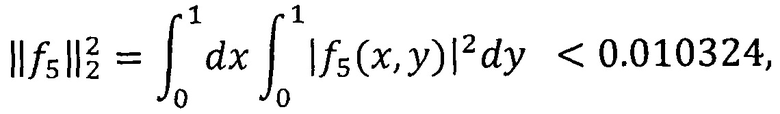
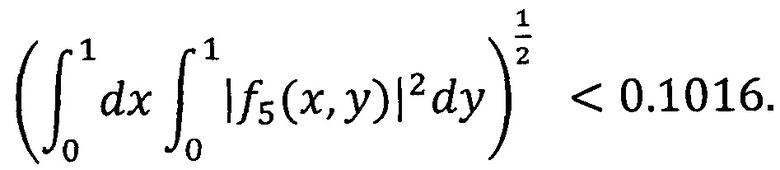
Частичная сумма ряда имеет вид:
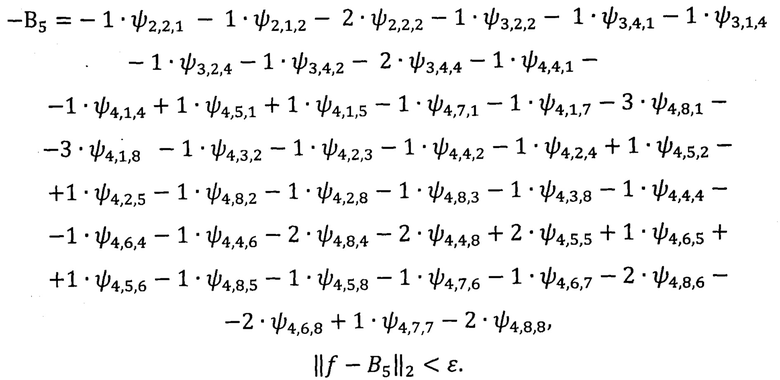
Этот пример поясняется чертежом: фиг.- пример практической реализации сжатия цифрового сигнала полученного из функции многих переменных, где ступенчатая функция (квадратики разного цвета) - это полученное приближение (В5) исходного сигнала 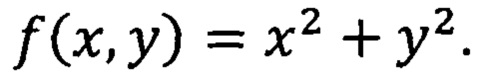 А исходный сигнал
А исходный сигнал 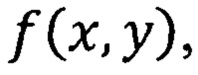 очевидно, будет изображаться постепенным изменением цвета на том же рисунке.
очевидно, будет изображаться постепенным изменением цвета на том же рисунке.
В вопросах сжатия образов [1, 2] возник интерес к системам типа
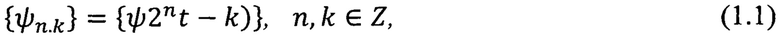
где ψ(t) - произвольная измеримая функция, определенная на R.
Системы из сжатий и сдвигов одной функции рассмотрены, в частности, в работах [1-7]. Но разложение с целыми коэффициентами по системам (1) нигде не рассматривалось, кроме, патента РФ №2681367, опубликованного: 06.03.2019, бюл. №7.
Пример 2. Покажем, как можно применить приведенные результаты с использованием многомодулярных пространств. Наша задача, например, трансляция или сохранение телевизионного аудио- и видео- сигнала с помощью его разложения на целые числа. Заметим, что при этом получается и сжатие образов.
Используя обозначения работы [8], в случае 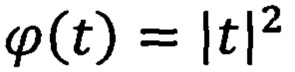 получим
получим 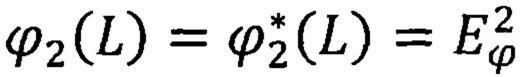 (заметим, что индекс 2 вверху и внизу означает, что рассматривается двумодулярное пространство), где
(заметим, что индекс 2 вверху и внизу означает, что рассматривается двумодулярное пространство), где 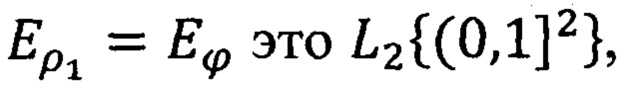 а
а 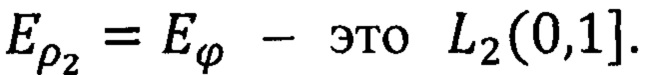 Пространство
Пространство 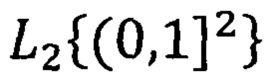 нами используется для приближения в нем изображений по системе (2) в фиксированный момент времени tl. Пространство L2(0,1]. Нами используется для приближения в нем звукового сигнала по системе (2) в течение момента времени (tl, tl+1). Таких моментов при обычной трансляции, например, может быть 24 в одну секунду. Если при этом в изображении много стационарных зон, то можно от момента к моменту передавать только информацию об измененных зонах. Рассмотрим систему функций
нами используется для приближения в нем изображений по системе (2) в фиксированный момент времени tl. Пространство L2(0,1]. Нами используется для приближения в нем звукового сигнала по системе (2) в течение момента времени (tl, tl+1). Таких моментов при обычной трансляции, например, может быть 24 в одну секунду. Если при этом в изображении много стационарных зон, то можно от момента к моменту передавать только информацию об измененных зонах. Рассмотрим систему функций 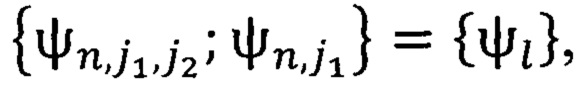 где l нумерует сначала элементы в n-ой пачке системы
где l нумерует сначала элементы в n-ой пачке системы 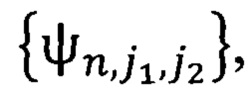 а затем в в n-ой пачке системы
а затем в в n-ой пачке системы 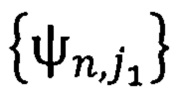 .
.
Назовем систему 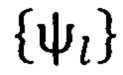 системой разложения (системой целочисленного разложения)} в пространстве
системой разложения (системой целочисленного разложения)} в пространстве 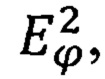 если существует ряд
если существует ряд 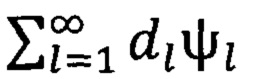
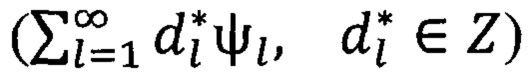 такой, что для любого элемента ƒ=(ƒ1(x1,х2), ƒ2(t)), где ƒ1(x1,x2) это изображение в момент времени tl, а ƒ2(t) это звуковой сигнал в период времени (tl, tl+1), который сходится по ϕ-норме пространства
такой, что для любого элемента ƒ=(ƒ1(x1,х2), ƒ2(t)), где ƒ1(x1,x2) это изображение в момент времени tl, а ƒ2(t) это звуковой сигнал в период времени (tl, tl+1), который сходится по ϕ-норме пространства 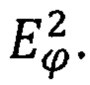 Заметим что сходимость по ϕ-норме эквивалента, в данном пространстве, с ρ-сходимостью, то есть со сходимостью в среднем в каждом из пространств, а значит и со сходимостью по норме. Учтем, так же, что норма является модуляром [8].
Заметим что сходимость по ϕ-норме эквивалента, в данном пространстве, с ρ-сходимостью, то есть со сходимостью в среднем в каждом из пространств, а значит и со сходимостью по норме. Учтем, так же, что норма является модуляром [8].
Пусть конкретно ƒ1(x1,x2)=х2+y2, x∈(0,1], y∈(0,1], ƒ2(t)=t3, t∈(0,1]. Воспользуемся вычислениями в примере 1 и примере из [9] (патент РФ №2681367, опубликовано: 06.03.2019, бюл. №7).
Таким образом, при задании погрешности приближения ε=0.1>0 мы можем построить сумму 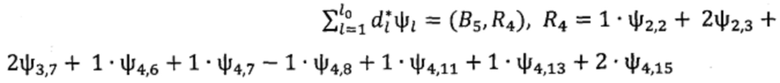
такую, что
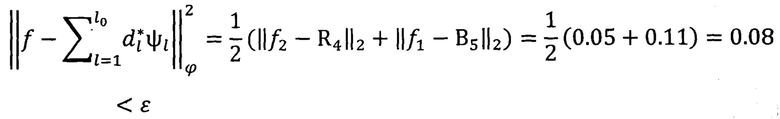
при этом в этой сумме будет много нулевых коэффициентов 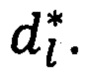 Уменьшая ε, получаем более четкое изображение и более четкий звук. Затем транслируем или запоминаем номера коэффициентов и их значения (целочисленные).
Уменьшая ε, получаем более четкое изображение и более четкий звук. Затем транслируем или запоминаем номера коэффициентов и их значения (целочисленные).
В качестве метрики в данном двумодулярном пространстве можно рассмотреть и следующую метрику:
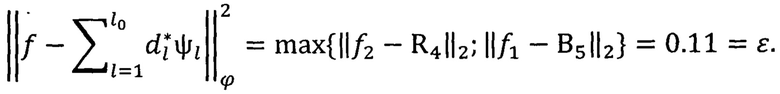
Таким образом, в заявляемом изобретении осуществляется просто приближение (создание эталонного одномерного вектора целевых характеристик изображения) на основе многомерного вектора изображения к тому же с целочисленными компонентами, и при этом начальные компоненты приближенного вектора остаются и добавляются последующие, если исходное приближение нас не устраивает. Используются новые системы функций [3-7] и по-другому вычисляются коэффициенты кодируемого сигнала. Этот способ является оптимальным приближением исходя из установленного заранее количества компонент вектора. К тому же, у нас, при промежуточных вычислениях, допускается возможная неточность промежуточных вычислений, которая корректируется в последующих вычислениях. Заметим, что и у нас и в [1, 2, 7] используются системы функций, полученные из сжатий и сдвигов одной функции. Что составляет основу современных технологий в этой области. Системы функций, рассмотренные нами, не являются ортонормированными.
Рассуждения из примера 2 легко переносятся на общий случай рассмотрения n-модулярного пространства.
Литература
[1] Jia R.Q., and Micchelli С. Using the refinement equation for the construction of pre-wavelets 2: Powers of two, in "Curves and Surfaces (P.J. Laurent, A. LeMehaute, and L.L. Schumaker, Eds.). Academic Press. New York. 1991. P. 209-246.
[2] Daubechies I. Ten lectures on wavelets. SIAM. Philadelphia. 1992.
[3] Filippov V.I. On the completeness and other properties of some functionsystemin Lp, 0<p<∞. // Journal of Approximation Theory. 1998. V. 94. P. 42-53.
[4] Филиппов В.И. Системы представления, полученные из сжатий и сдвигов одной функции в многомерных пространствах Еϕ// Изв. РАН, сер. матем. 2012. Т. 76. N 6. С. 193-206.
[5] Филиппов В.И. Об обобщениях системы Хаара и других систем функций в пространствах Еϕ // Известия Вузов. Математика, 2018, 62:1, 87-92.
[6] Fillipov V.I., and Oswald P. Representation in Lp by series of translates anddilates of one function // Journal of ApproximationTheory. 1995. V. 82. №1. P. 15-29.
[7] Kudryavtsev A. Yu. On the rate of convergence of orthorecursive expansionsovernon-orthogonal wavelets/Izvestiya: Mathematics, 2012, 76(4): 688-701.
[8] Филиппов В.И. Многомодулярные пространства и их свойства // Известия Вузов. Математика. 2017. 61:12. С. 57-65.
[9] Филиппов В.И. Способ сжатия одномерных образов путем приближения элементов пространств Lp по системам сжатий и сдвигов одной функции рядами типа Фурье с целыми коэффициентами // (патент РФ №2681367, опубликовано: 06.03.2019 бюл. №7).
Изобретение относится к области вычислительной техники, в частности к способам сжатия многомерных образов. Техническим результатом является возможность сжатия многомерных образов без искажения исходного сигнала. Технический результат заявляемого технического решения достигается за счет того, что при кодировании получаются целочисленные коэффициенты. Для этого в заявленном способе предусмотрены этапы, на которых осуществляют приближение элементов пространств Lp по системам из сжатий и сдвигов одной функции рядами типа Фурье с целыми коэффициентами, вводят функцию ψ как образующую функцию для системы кодирования в виде таблицы или формулы, вычисляют элементы системы, по которым кодируют сигнал; для произвольной функции строят ряд; проверяют точность приближения, если точность приближения достигнута, то вычисления прекращают, в противном случае формируют новый цикл; производят декодирование и получают удовлетворяющее поставленным условиям приближение. 1 з.п. ф-лы, 1 ил.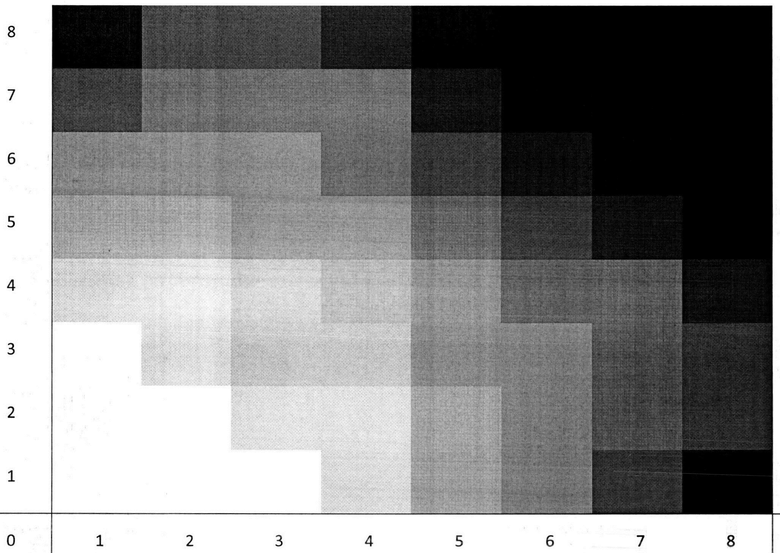
1. Способ сжатия многомерных образов путем приближения элементов пространств Lp{(0,1]m}, 1≤p<∞, по системам сжатий и сдвигов одной функции рядами типа Фурье с целыми коэффициентами и целочисленное разложение элементов многомодулярных пространств, включающий запись цифрового многомерного сигнала с выхода исследуемого объекта как элемента пространства Lp{(0,1]m} в виде значений этой функции, затем в электронно-вычислительном блоке осуществляют приближение элементов пространств Lp{(0,1]m} по системам из сжатий и сдвигов одной функции рядами типа Фурье с целыми коэффициентами, вводят функцию ψ как образующую функцию для системы кодирования в виде таблицы или формулы, при этом ψ∈Lp{(0,1]m}; 1≤p<∞, ∫T ψ(t)dt≠0, ψ(t)=0, t=(t1, …, tm)∉Т, Т=(0,1]×(0,1]×…×(0,1] - m-мерный куб, затем вычисляют
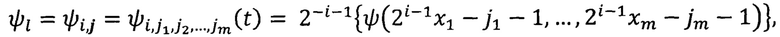
где i∈N, 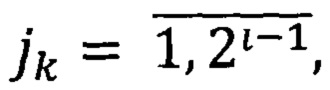
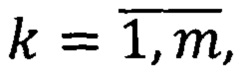
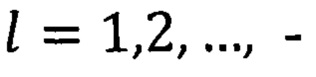
элементы системы, по которым кодируют сигнал, затем для произвольной функции ƒ∈Lp{(0,1]m}, 1≤p<∞, строят ряд 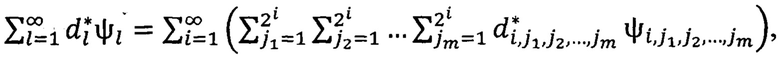 где
где
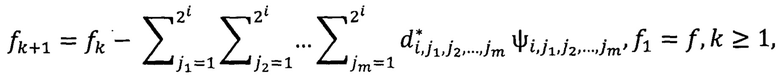
при рассмотрении частного случая функции ψ(t):
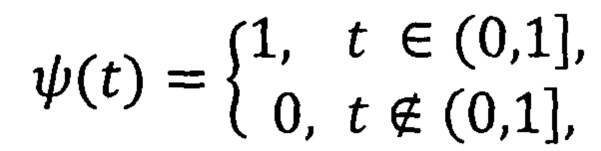
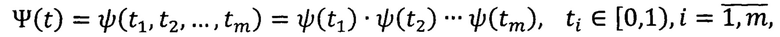 коэффициенты
коэффициенты 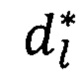 вычисляют по формулам
вычисляют по формулам
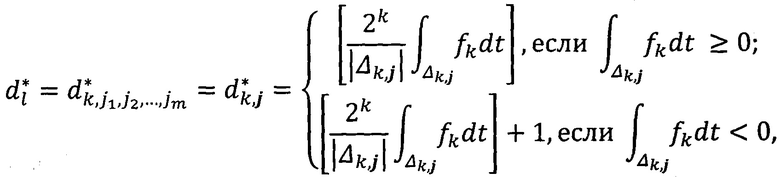
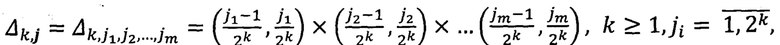
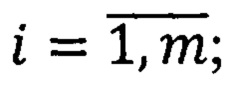 в общем случае, когда ψ∈Lp{(0,1]m}, 1≤p<∞, ∫T ψ(t)dt≠0, ψ(t)=0, t=(t1, …, tm)∉T, T=(0,1]×(0,1]×…×(0,1], промежуточные вычисления ƒk, k≥2, производят несколько иначе; при этом систему элементов, по которым кодируют сигнал, также рассматривают в несколько другом виде, вводят параметр λ0, зависящий от функции ψ; затем проверяют точность приближения
в общем случае, когда ψ∈Lp{(0,1]m}, 1≤p<∞, ∫T ψ(t)dt≠0, ψ(t)=0, t=(t1, …, tm)∉T, T=(0,1]×(0,1]×…×(0,1], промежуточные вычисления ƒk, k≥2, производят несколько иначе; при этом систему элементов, по которым кодируют сигнал, также рассматривают в несколько другом виде, вводят параметр λ0, зависящий от функции ψ; затем проверяют точность приближения 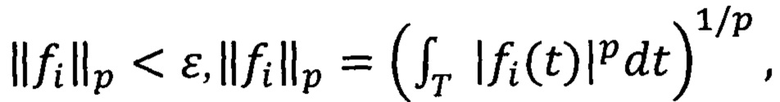 1≤p<∞, если точность приближения достигнута, то вычисления прекращают, в противном случае формируют новый цикл с ƒi+1; затем декодируют путем составления суммы
1≤p<∞, если точность приближения достигнута, то вычисления прекращают, в противном случае формируют новый цикл с ƒi+1; затем декодируют путем составления суммы 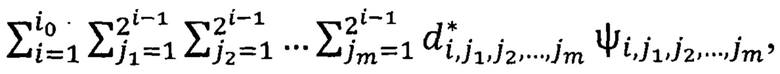 и получают удовлетворяющее поставленным условиям приближение
и получают удовлетворяющее поставленным условиям приближение
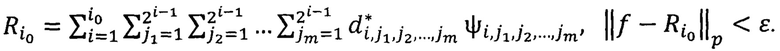
2. Способ сжатия многомерных образов путем приближения элементов пространств Lp{(0,1]m}, 1≤p<∞, по системам сжатий и сдвигов одной функции рядами типа Фурье с целыми коэффициентами и целочисленное разложение элементов многомодулярных пространств по п. 1, отличающийся тем, что приближение разных частей объекта (например, видеоизображение и звук) можно объединить в одном многомодулярном пространстве, приближая поочередно каждую часть.
| RU 2012107969 A, 10.09.2013 | |||
| СЖАТИЕ РАЗЛОЖЕННЫХ ПРЕДСТАВЛЕНИЙ ЗВУКОВОГО ПОЛЯ | 2014 |
|
RU2668059C2 |
| ФИЛИППОВ В.И.: "Системы представления, полученные из сжатий и сдвигов одной функции в многомерных пространствах Еϕ", РАН, серия математическая, 2012, Т | |||
| Аппарат, предназначенный для летания | 0 |
|
SU76A1 |
| Приспособление для точного наложения листов бумаги при снятии оттисков | 1922 |
|
SU6A1 |
| ФИЛИППОВ В.И.: "Об обобщениях системы Хаара и других систем функций в пространствах Еϕ", Известия Вузов | |||
| Математика, | |||
Авторы
Даты
2020-05-28—Публикация
2019-04-16—Подача