Изобретение относится к области точного приборостроения и может быть использовано для измерения градиентов гравитационного поля.
Известен гравитационный градиентометр Чена-Пайка, содержащий два акселерометра, оси чувствительности которых расположены на одной оси, направленной под углом к вертикали, а также поворотное и регистрирующее устройства /Physical Review D, 1987, v. 35, N 12/.
Недостатком аналога является ограниченность его применения случаем лабораторных условий.
Известен градиентометр, принятый за прототип, содержащий два идентичных акселерометра в герметичном цилиндрическом корпусе, с расположенными в нем чувствительными элементами акселерометров, выполненными с возможностью перемещения вдоль оси корпуса в виде механоэлектрических преобразовательных элементов (МЭПЭ) с инерционными массами, а также электронный блок и схему съема информации, при этом оси чувствительностей акселерометров ориентированы вдоль оси цилиндрического корпуса, закрепленного на поворотном устройстве, ось вращения которого ортогональна оси корпуса /RU N 2033632/.
Данный гравитационный градиентометр можно применять в условиях эксплуатации.
Недостатками прототипа являются его сложность, недостаточная чувствительность и относительная дороговизна.
Техническим результатом, получаемым от внедрения изобретения, является устранение недостатков прототипа, т.е. удешевление, упрощение и повышение чувствительности прибора.
Данный технический результат достигают за счет того, что в известном градиентометре, содержащем два идентичных акселерометра в герметичном цилиндрическом корпусе, с расположенными в нем чувствительными элементами акселерометров, выполненными с возможностью перемещения вдоль оси корпуса в виде механоэлектрических преобразовательных элементов с инерционными массами, а также электронный блок и схему съема информации, при этом оси чувствительностей акселерометров ориентированы вдоль оси цилиндрического корпуса, закрепленного на поворотном устройстве, ось вращения которого ортогональна оси корпуса, механоэлектрические преобразовательные элементы акселерометров выполнены в виде пьезоэлементов, установленных с инерционными массами на торцах цилиндрического корпуса в едином модуле, образующем дифференциальный акселерометр, подключенный выходом через схему съема информации к электронному блоку, при этом пьезоэлементы механически соединены между собой по направлению осей чувствительностей акселерометров.
Пьезоэлементы выполнены в виде биморфов, центры которых связаны между собой струной.
Пьезоэлементы с инерционными массами связаны с корпусом посредством плоских пружин.
Электронный блок выполнен в виде двух усилителей, один из которых с регулируемым усилением, и сумматора, при этом выходы механоэлектрических преобразователей соединены с входами усилителей, подключенных выходами к входам сумматора.
Пьезоэлектрические преобразователи (ПП) широко используются в виброметрии, где МЭПЭ в виде пьезокерамики, работающей на сжатие, сдвиг или кручение, входят в состав различных вибропреобразователей, обеспечивая, благодаря пьезоэффекту, преобразование механических деформаций, возникающих в них при колебательных движениях, в электрические сигналы на частотах до десятков килогерц. Являясь преобразователями силы пассивного типа с большим динамическим диапазоном (до 200 дБ), они выгодно отличаются от прототипа простотой своей технической реализации, малыми габаритами, надежностью и незначительным объемом требуемого электронного оборудования.
Пьезоэлектрические МЭПЭ - это преобразователи контактного типа. Их жесткость входит в жесткость механической подвески инерционной массы (ИМ) является доминирующей для всех подвесок, кроме низкочастотных, где в целях уменьшения собственных шумов подвески и увеличения чувствительности пьезопреобразователей предпринимаются специальные меры снижения собственной частоты подвесок путем применения биморфных преобразователей. Биморфные МЭПЭ являются преобразователями изгибных деформаций, обладают малой по сравнению с другими типами пьезоэлементов жесткостью, малым пироэлектрическим эффектом и большим коэффициентом преобразования, что позволяет рассматривать их в качестве одного из возможных типов МЭПЭ для высокочувствительного унифицированного градиентометра.
Оценим предельные возможности пьезоэлектрического биморфного преобразователя с наиболее широко распространенным последовательным соединением пластин, имеющего длину l, ширину в и толщину h, свободно опертого по краям и нагруженного по центру силой F. Напряжение на обкладках пьезоэлемента U при его поперечных (изгибных) деформациях будет удовлетворять уравнению:

где d31 и ε - пьезомодуль и диэлектрическая проницаемость материала биморфа, соответственно; ε0=8.85×10-12 ф/м. Откуда коэффициент преобразования биморфного пьезоэлемента по силе:

При работе биморфа в качестве МЭПЭ в градиентометре величинами наиболее полно его характеризующими, являются коэффициент преобразования по перемещению Кn(х) и жесткость биморфа. При принятой схеме нагружения биморфа, его жесткость может быть представлена выражением:

где Е - модуль упругости материала биморфа;
Воспользовавшись соотношением F=W×x и подставив его в (2), найдем Кn(х):
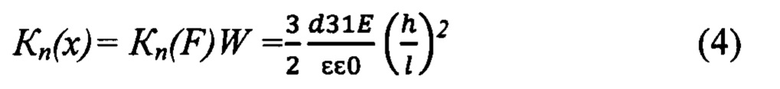
Подставив в (4) значения пьезоэлектрических постоянных для наиболее распространенной пьезокерамики ЦТС-19 (d31=157×10-12 Кл/Н, Е=7,2×1010Н/м2, ε=1540), получим выражение, позволяющее численно оценивать коэффициенты преобразования биморфных пьезоэлементов:

Из (5) видно, что биморфные пьезоэлементы являются одними из самых чувствительных преобразователей перемещения. Так, например, чувствительность биморфа с размерами h=1 мм, l=40 мм, равна 7,5×105 В/м, что во много раз больше максимально достижимого коэффициента преобразования прототипа. При этом малая жесткость биморфов позволяет на их основе создавать достаточно низкочастотные подвески. Так, биморф с указанными параметрами и шириной 2 мм имеет жесткость W=9×103 Н/м, что в ПП с инерционной массой 0,5 кг дает возможность получить собственную частоту подвески, равную 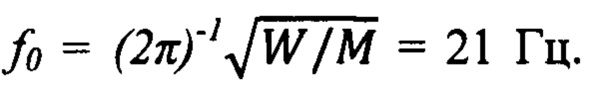 Ясно, что уменьшить соответствующим образом размеры биморфа (3), можно снизить и ƒ0, однако, следует учитывать, что при этом будет уменьшаться и Кn(х) (5), причем относительное уменьшение Кn(х) будет происходить быстрее, например, снижение приведет к уменьшению Кn в 3 раза.
Ясно, что уменьшить соответствующим образом размеры биморфа (3), можно снизить и ƒ0, однако, следует учитывать, что при этом будет уменьшаться и Кn(х) (5), причем относительное уменьшение Кn(х) будет происходить быстрее, например, снижение приведет к уменьшению Кn в 3 раза.
Для оценки предельной разрешающей способности биморфных МЭПЭ найдем выражение для его собственных шумов, для чего используем эквивалентную схему пьезоэлектрического МЭПЭ в виде емкости С, нагруженной на сопротивление потерь R. Спектральная плотность мощности напряжения тепловых шумов такой схемы определяется выражением:
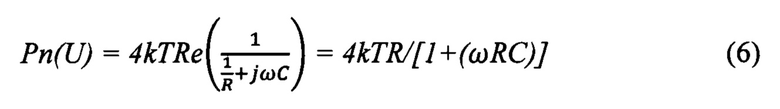
Специально проведенными исследованиями доказано, что величина равная tgδ, где tgδ - тангенс угла диэлектрических потерь, а также С - частотно независимы до 0,1 Гц. Учитывая это обстоятельство, а также то, что абсолютное значение tgδ для всех пьезокерамик мало, выражение (6) можно переписать в виде:

откуда видно, что определяющим параметром при оценке собственных шумов, проводимых на выходе пьезоэлектрического МЭПЭ, является их емкость, увеличение которой ведет к снижению Pn(U). Шумы пьезоэлементов частотно зависимы. Их абсолютное значение растет с уменьшением частоты.
Воспользовавшись (4) и (7), а также очевидным соотношением С=εε0bl/h, получим общее выражение для спектральной плотности мощности шумовых колебательных перемещений на входе биморфного МЭПЭ:

где 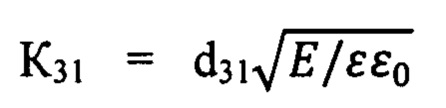 - коэффициент электромеханической связи пьезокерамики.
- коэффициент электромеханической связи пьезокерамики.
Выражение (8) показывает, что собственные шумы биморфных МЭПЭ, приведенные ко входу, определяются электромеханическими параметрами пьезокерамики (член tgδ/(К31)2) и жесткостью пьезоэлементов. Причем изменение собственных шумов МЭПЭ в широких пределах можно практически добиться только путем изменения жесткости биморфа, т.к. отличие коэффициента К31 для большинства известных составов пьезокерамик - незначительно. Поэтому, подставив в (8) значения электромеханических констант для состава ЦТС-19, получим упрощенное выражение, позволяющее оценивать величину спектральной плотности мощности эквивалентного шумового ускорения на входе биморфного пьезоэлемента 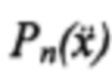 в зависимости от его жесткости:
в зависимости от его жесткости:
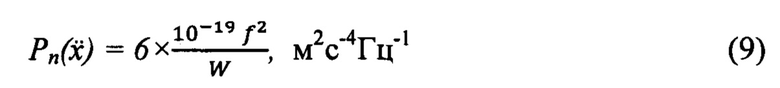
или геометрических размеров:
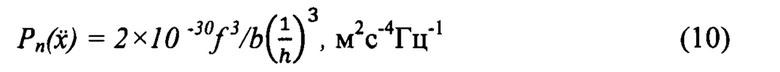
Используя (9), можно получить выражение для оценки минимального уровня собственных шумов 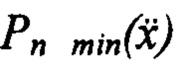 тех ПП, у которых величина суммарной жесткости определяется в основном жесткостью применяемых биморфов. Для того в (9) подставим вместо W его выражение W=(2πƒ0)2M и найдем
тех ПП, у которых величина суммарной жесткости определяется в основном жесткостью применяемых биморфов. Для того в (9) подставим вместо W его выражение W=(2πƒ0)2M и найдем  которое достигает минимального значения на резонансной частоте подвески ƒ0:
которое достигает минимального значения на резонансной частоте подвески ƒ0:

Выше и ниже резонансной частоты собственные шумы ПП будут возрастать. Выше- пропорционально ƒ3, ниже - обратно пропорционально ƒ. Это обусловлено наличием частотной зависимости собственных шумов у пьезоэлементов и передаточной функции подвески.
Изобретение поясняется чертежами. На фиг. 1 представлена конструктивная схема градиентометра, на фиг. 2 - состав его электронного блока.
Градиентометр содержит два идентичных акселерометра с единой осью чувствительности OO' в герметичном цилиндрическом корпусе 1 (фиг. 1) с расположенными в нем чувствительными элементами в виде МЭПЭ, выполненными ввиде пьезоэлементов 2, 2' с ИМ 3, 3', выполненных с возможностью перемещения вдоль оси OO' чувствительности. При этом пьезоэлементы 2, 2' выполнены в виде биморфов, центры которых связаны между собой, например, стержнем или струной 4, образуя дифференциальный акселерометр ввиде единого модуля.
Пьезоэлементы 2, 2' установлены на торцах цилиндрического корпуса 1 в едином модуле с помощью плоских пружин 5, 5'.
Корпус 1 закреплен на оси 6 поворотного устройства 7, ортогональной оси OO' чувствительности (оси цилиндрического корпуса 1).
Градиентометр установлен на основание 8.
Имеется также электронный блок (фиг. 2).
Информация с дифференциального акселерометра передается на электронный блок с помощью известной фотоэлектрической или магнитоэлектрической схемы съема информации. Электронный блок выполнен в виде двух усилителей, один из которых, например, 9 выполнен перестраевым по усилению.
Выходы усилителей 9, 10 подключены к входам сумматора 11 (фиг. 2).
Схема съема информации на чертежах не представлена ввиду ее известности из специальной литературы /SU N 1483499/.
Градиентометр предназначен для детального исследования областей с большими горизонтальными градиентами силы тяжести. При этом прибор измеряет вторые производные от гравитационного потенциала Земли, т.е. измеряет кривизны ее поверхности и горизонтальные градиенты силы тяжести.
Вторые производные определяют степень неоднородности гравитационного поля. Для характеристики этой неоднородности измеряют силы, действующие на две ИМ 3, 3' (фиг. 1).
В неоднородном гравитационном поле на ИМ 3, 3', будут действовать разные по величине и направлению силы, сумма которых регистрируется пьезоэлементами 2, 2', усиливается в усилителях 9, 10 и суммируется в сумматоре 11 (фиг. 2).
Определение измеряемых величин проводится при вращении цилиндрического корпуса 1, вокруг оси 6 с помощью поворотного устройства 7. При замене пьезоэлементов 2 и 2' на тензоэлементы, необходимость во вращении МЭПЭ отпадает.
Перед началом измерений прибор настраивается на ноль с помощью перестраевомого усилителя 9.
Градиентометр является более простым, надежным и малобюджетным прибором по сравнению с прототипом. Его предполагается использовать на микроспутниках.
Этим достигается поставленный технический результат.
| название | год | авторы | номер документа |
|---|---|---|---|
| ГРАВИТАЦИОННЫЙ ГРАДИЕНТОМЕТР | 2019 |
|
RU2724588C1 |
| ТРЕХКОМПОНЕНТНЫЙ ПЬЕЗОЭЛЕКТРИЧЕСКИЙ АКСЕЛЕРОМЕТР | 1995 |
|
RU2098830C1 |
| СЕЙСМОПРИЕМНИК | 1993 |
|
RU2076341C1 |
| Акселерометр | 1987 |
|
SU1478826A1 |
| ПЬЕЗОЭЛЕКТРИЧЕСКИЙ ДАТЧИК УСКОРЕНИЯ | 2002 |
|
RU2212672C1 |
| МАЛОГАБАРИТНЫЙ ДАТЧИК УДАРА | 2016 |
|
RU2621467C1 |
| Вертикальный сейсмоприемник | 1980 |
|
SU911406A1 |
| УСТРОЙСТВО ДЛЯ ИЗМЕРЕНИЯ ВИБРОУСКОРЕНИЙ, ВОЗНИКАЮЩИХ В ЭЛЕКТРОУСТАНОВКАХ | 2023 |
|
RU2829713C1 |
| ПЬЕЗОЭЛЕКТРИЧЕСКИЙ ПРИБОР И СПОСОБ ЕГО ИЗГОТОВЛЕНИЯ | 2011 |
|
RU2472253C1 |
| ЦИФРОВОЙ КОМБИНИРОВАННЫЙ ВЕКТОРНЫЙ ПРИЕМНИК С СИНТЕЗИРОВАННЫМИ КАНАЛАМИ | 2012 |
|
RU2509320C1 |

Изобретение относится к устройствам для измерения градиентов гравитационного поля. Сущность: градиентометр содержит цилиндрический герметичный корпус (1), электронный блок и схему съема информации. Корпус (1) закреплен на поворотном устройстве (7), ось (6) вращения которого ортогональна оси (О, О’) корпуса (1). Внутри корпуса (1) размещены два идентичных акселерометра. Механоэлектрические преобразовательные элементы акселерометров выполнены с возможностью перемещения вдоль оси (О, О’) корпуса (1). Оси чувствительности акселерометров ориентированы вдоль оси (О, О’) корпуса (1). При этом механоэлектрические преобразовательные элементы акселерометров выполнены в виде пьезоэлементов (2, 2’), установленных с инерционными массами (3, 3’) на торцах цилиндрического корпуса (1) в едином модуле, образующем дифференциальный акселерометр. Дифференциальный акселерометр подключен выходом через схему съема информации к электронному блоку. При этом пьезоэлементы (2, 2’) механически соединены между собой по направлению осей чувствительностей акселерометров. Технический результат: упрощение устройства и повышение его чувствительности. 3 з.п. ф-лы, 2 ил.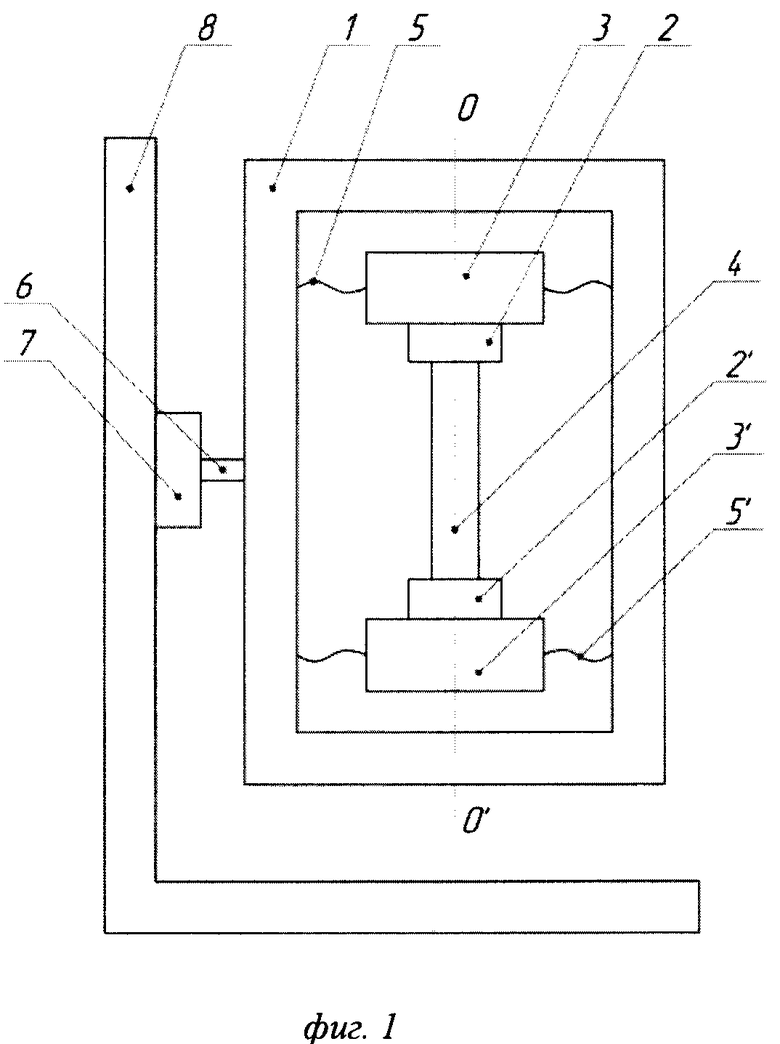
1. Градиентометр, содержащий два идентичных акселерометра в герметичном цилиндрическом корпусе, с расположенными в нем чувствительными элементами акселерометров, выполненными с возможностью перемещения вдоль оси корпуса в виде механоэлектрических преобразовательных элементов с инерционными массами, а также электронный блок и схему съема информации, при этом оси чувствительности акселерометров ориентированы вдоль оси цилиндрического корпуса, закрепленного на поворотном устройстве, ось вращения которого ортогональна оси корпуса, отличающийся тем, что механоэлектрические преобразовательные элементы акселерометров выполнены в виде пьезоэлементов, установленных с инерционными массами на торцах цилиндрического корпуса в едином модуле, образующем дифференциальный акселерометр, подключенный выходом через схему съема информации к электронному блоку, при этом пьезоэлементы механически соединены между собой по направлению осей чувствительностей акселерометров.
2. Градиентометр по п. 1, отличающийся тем, что пьезоэлементы выполнены в виде биморфов, центры которых связаны между собой струной.
3. Градиентометр по п. 1, отличающийся тем, что пьезоэлементы с инерционными массами связаны с корпусом посредством плоских пружин.
4. Градиентометр по п. 1, отличающийся тем, что электронный блок выполнен в виде двух усилителей, один из которых с регулируемым усилением, и сумматора, при этом выходы механоэлектрических преобразователей соединены с входами усилителей, подключенных выходами к входам сумматора.
| ГРАВИТАЦИОННЫЙ ТРЕХКОМПОНЕНТНЫЙ ГРАДИЕНТОМЕТР | 1990 |
|
RU2033632C1 |
| US 4841772 A, 27.06.1989 | |||
| ГРАВИТАЦИОННЫЙ ТРЕХКОМПОНЕНТНЫЙ ГРАДИЕНТОМЕТР | 1992 |
|
RU2046380C1 |
Авторы
Даты
2020-06-23—Публикация
2019-12-24—Подача