Область техники, к которой относится изобретение
Конкретные варианты осуществления направлены на беспроводную связь, а более конкретно, на проектные решения по коэффициентам сдвига на основе разреженного контроля по четности (LDPC) для нового стандарта радиосвязи (NR).
Введение
Согласованные по скорости коды разреженного контроля по четности (LDPC) являются важными для мобильной связи, поскольку они упрощают повторные передачи гибридного автоматического запроса на повторную передачу (HARQ) с нарастающей избыточностью. Конкретные коды также являются квазициклическими, что обеспечивает простое кодирование и декодирование. Квазициклические матрицы контроля по четности сегментируются на квадратные субблоки (субматрицы) размера ZxZ. Эти субматрицы представляют собой либо циклические перестановки единичной матрицы, либо нулевые субматрицы. Циклическая перестановочная матрица Pk получается из единичной матрицы ZxZ посредством цикличного сдвига столбцов вправо посредством k элементов. Матрица P0 представляет собой единичную матрицу ZxZ.
Структура квазициклического LDPC-кода может описываться через базовую матрицу. Базовая матрица имеет один элемент для каждого субблока ZxZ в соответствующей матрице контроля по четности. Элемент в базовой матрице может иметь значение 0, которое соответствует нулевому субблоку, или 1, которое может соответствовать любой сдвинутой единичной матрице ZxZ. В общем, базовая матрица может иметь элементы со значениями, большими 1, но такие базовые матрицы не рассматриваются здесь.
С учетом конкретной базовой матрицы, циклические сдвиги (также называемые "коэффициентами сдвига"), а также Z, задаются с возможностью указывать матрицу контроля по четности (PCM). Процесс выбора коэффициентов сдвига и указания матрицы контроля по четности для данной базовой матрицы называется "подъемом". Коэффициенты сдвига типично указываются через матрицу размера, идентичного размеру базовой матрицы, причем каждая запись Pi,j соответствует субматрице ZxZ в конечной PCM. Записи с Pi,j=-1 в матрице обозначают нолевые (нулевые) субматрицы, в то время как записи с Pi,j=k обозначают субматрицы, равные Pk. Эта матрица, которая вместе с Z указывает LDPC-код, может называться "проектным решением по коэффициентам сдвига". Конкретная матрица контроля по четности получается посредством выбора размера Z сдвига с соответствующим проектным решением по коэффициентам сдвига и замены каждой записи соответствующей матрицей ZxZ.
Один способ для конструирования матрицы контроля по четности представляет собой алгоритм на основе постепенного роста ребер (PEG). PEG-конструкция наращивает матрицу контроля по четности для LDPC-кода на основе ребер. Разновидность PEG-конструкции, которая учитывает внешнюю степень сообщений (EMD), описывается в работе "Selective avoidance of cycles in irregular LDPC code construction", in IEEE Transactions on Communications, издание 52, № 8, стр. 1242-1247, август 2004 года, авторов Tao Tian, C. R. Jones, J. D. Villasenor и R. D. Wesel. Способ используется для того, чтобы находить циклические сдвиги, которые обеспечивают высокие значения EMD с аппроксимированным циклом (ACE) для графа. Минимальное ACE-значение вычисляется для каждого цикла длины, меньшей или равной указанной длине.
ACE цикла длины 2d задается следующим образом:
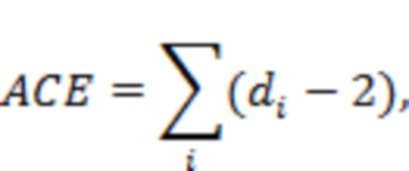 ,
,
где di является степенью i-ого переменного узла в цикле. Кроме того, LDPC-код имеет свойство (dACE, etaACE), если все циклы, длина которых составляет 2*dACE или меньше, имеет ACE-значения, по меньшей мере, etaACE.
Коэффициенты сдвига выбираются таким образом, что отсутствуют циклы на графе с ACE-значениями ниже указанного ACE-ограничения. Таким образом, вредные короткие циклы с низкой связываемостью с остальной частью графа могут исключаться.
Для данного размера Z сдвига, единичная матрица может сдвигаться вплоть до Z-1 раз без формирования идентичного субблока ZxZ. Это означает то, что каждый коэффициент сдвига может принимать любое значение между 0 и Z-1. Чем больше размер сдвига, тем большую свободу имеет алгоритм подъема для того, чтобы выбирать коэффициенты сдвига, и тем с большей вероятностью случается то, что короткие циклы с низкими ACE-значениями могут исключаться.
Одно возможное решение состоит в том, чтобы указывать одно проектное решение по коэффициентам сдвига для каждого размера сдвига, для которого указывается LDPC-код. Тем не менее, это требует хранения каждого проектного решения по коэффициентам сдвига как в передающем устройстве, так и в приемном устройстве. Другая альтернатива, которая рассматривается здесь, заключается в том, чтобы проектировать коэффициенты сдвига для набора размеров сдвига одновременно. Значение Pi,j сдвига может вычисляться посредством функции  =
= 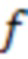 (
(  ,
,  ), где Vi,j является коэффициентом сдвига (i,j)-ого элемента в соответствующем проектном решении по коэффициентам сдвига. Один пример представляет собой функцию f, заданную следующим образом:
), где Vi,j является коэффициентом сдвига (i,j)-ого элемента в соответствующем проектном решении по коэффициентам сдвига. Один пример представляет собой функцию f, заданную следующим образом:
 ,
,
но также могут использоваться другие функции.
NR поддерживает размеры Z сдвига согласно таблице 1. Один набор значений Vi,j может указываться для каждого набора в таблице для каждой базовой матрицы. Конкретное проектное решение по коэффициентам сдвига для данного Z находится посредством применения функции выше к значениям Vi,j, которые указываются для набора, которому принадлежит Z.
Таблица 1. Размеры Z сдвига, которые должен поддерживать NR
Новый стандарт радиосвязи (NR) поддерживает LDPC-коды с двумя различными базовыми матрицами, называемыми "базовым графом 1" и "базовым графом 2" в 3GPP TS 38.212. Первая базовая матрица, базовая матрица #1, имеет размер 46×68 и 316 ребер. Вторая базовая матрица, базовая матрица #2, имеет размер 42×52 и 197 ребер. Базовые матрицы являются разреженными и указываются ниже. Ненулевые записи в базовом графе указываются посредством тройки (e, r, c). Тройки означают, что ненулевое ребро, пронумерованное e, находится в строке r и столбце c. Все ненулевые записи в базовом графе равны 1. Все элементы в базовой матрице, которые не указываются в разреженном описании, равны 0. Разреженный формат сжато описывает матрицы, из которых извлекаются проектные решения по коэффициентам сдвига.
Для общей базовой матрицы с N ребер, с ненулевыми записями, указываемыми посредством набора троек  и вектора
и вектора  длины N, Vi,j принимает значения
длины N, Vi,j принимает значения  для
для 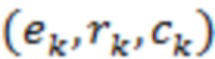 в наборе троек, и Vi,j=-1 для другого (i,j).
в наборе троек, и Vi,j=-1 для другого (i,j).
Чтобы описывать набор Vi,j для базовой матрицы #1, все, что необходимо, представляет собой вектор длины 316, записи которого являются целыми числами. Если вектор составляет [a_1, a_2, a_3...., a_316], это означает то, что Vi,j принимает значения  a_1,
a_1,  a_2,
a_2, 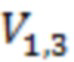 =a_3,
=a_3,  =a_4,
=a_4,  =a_5...,
=a_5...,  =a_316, для (i, j), приведенного в описании базовой матрицы, с
=a_316, для (i, j), приведенного в описании базовой матрицы, с 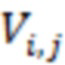 =-1 для другого (i, j). Вместе с формулой для определения Pi,j из Vi, jj и Z и набора Z, это полностью указывает PCM.
=-1 для другого (i, j). Вместе с формулой для определения Pi,j из Vi, jj и Z и набора Z, это полностью указывает PCM.
Базовая матрица #1 LDPC для NR
(1, 1, 1) (2, 1, 2) (3, 1, 3) (4, 1, 4) (5, 1, 6) (6, 1, 7)
(7, 1, 10) (8, 1, 11) (9, 1, 12) (10, 1, 13) (11, 1, 14) (12, 1, 16) (13, 1, 17)
(14, 1, 19) (15, 1, 20) (16, 1, 21) (17, 1, 22) (18, 1, 23) (19, 1, 24) (20, 2, 1)
(21, 2, 3) (22, 2, 4) (23, 2, 5) (24, 2, 6) (25, 2, 8) (26, 2, 9) (27, 2, 10)
(28, 2, 12) (29, 2, 13) (30, 2, 15) (31, 2, 16) (32, 2, 17) (33, 2, 18) (34, 2, 20)
(35, 2, 22) (36, 2, 23) (37, 2, 24) (38, 2, 25) (39, 3, 1) (40, 3, 2) (41, 3, 3)
(42, 3, 5) (43, 3, 6) (44, 3, 7) (45, 3, 8) (46, 3, 9) (47, 3, 10) (48, 3, 11)
(49, 3, 14) (50, 3, 15) (51, 3, 16) (52, 3, 18) (53, 3, 19) (54, 3, 20) (55, 3, 21)
(56, 3, 25) (57, 3, 26) (58, 4, 1) (59, 4, 2) (60, 4, 4) (61, 4, 5) (62, 4, 7)
(63, 4, 8) (64, 4, 9) (65, 4, 11) (66, 4, 12) (67, 4, 13) (68, 4, 14) (69, 4, 15)
(70, 4, 17) (71, 4, 18) (72, 4, 19) (73, 4, 21) (74, 4, 22) (75, 4, 23) (76, 4, 26)
(77, 5, 1) (78, 5, 2) (79, 5, 27) (80, 6, 1) (81, 6, 2) (82, 6, 4) (83, 6, 13)
(84, 6, 17) (85, 6, 22) (86, 6, 23) (87, 6, 28) (88, 7, 1) (89, 7, 7) (90, 7, 11)
(91, 7, 12) (92, 7, 14) (93, 7, 18) (94, 7, 19) (95, 7, 21) (96, 7, 29) (97, 8, 1)
(98, 8, 2) (99, 8, 5) (100, 8, 8) (101, 8, 9) (102, 8, 15) (103, 8, 30) (104, 9, 1)
(105, 9, 2) (106, 9, 4) (107, 9, 13) (108, 9, 17) (109, 9, 20) (110, 9, 22) (111, 9, 23)
(112, 9, 25) (113, 9, 31) (114, 10, 1) (115, 10, 2) (116, 10, 11) (117, 10, 12) (118, 10, 14)
(119, 10, 18) (120, 10, 19) (121, 10, 21) (122, 10, 32) (123, 11, 2) (124, 11, 3) (125, 11, 5)
(126, 11, 8) (127, 11, 9) (128, 11, 15) (129, 11, 33) (130, 12, 1) (131, 12, 2) (132, 12, 13)
(133, 12, 17) (134, 12, 22) (135, 12, 23) (136, 12, 24) (137, 12, 34) (138, 13, 1) (139, 13, 2)
(140, 13, 11) (141, 13, 12) (142, 13, 14) (143, 13, 19) (144, 13, 35) (145, 14, 1) (146, 14, 4)
(147, 14, 8) (148, 14, 21) (149, 14, 24) (150, 14, 36) (151, 15, 1) (152, 15, 13) (153, 15, 16)
(154, 15, 17) (155, 15, 18) (156, 15, 22) (157, 15, 37) (158, 16, 1) (159, 16, 2) (160, 16, 11)
(161, 16, 14) (162, 16, 19) (163, 16, 26) (164, 16, 38) (165, 17, 2) (166, 17, 4) (167, 17, 12)
(168, 17, 21) (169, 17, 23) (170, 17, 39) (171, 18, 1) (172, 18, 15) (173, 18, 17) (174, 18, 18)
(175, 18, 22) (176, 18, 40) (177, 19, 2) (178, 19, 13) (179, 19, 14) (180, 19, 19) (181, 19, 20)
(182, 19, 41) (183, 20, 1) (184, 20, 2) (185, 20, 8) (186, 20, 9) (187, 20, 11) (188, 20, 42)
(189, 21, 1) (190, 21, 4) (191, 21, 10) (192, 21, 12) (193, 21, 23) (194, 21, 43) (195, 22, 2)
(196, 22, 6) (197, 22, 17) (198, 22, 21) (199, 22, 22) (200, 22, 44) (201, 23, 1) (202, 23, 13)
(203, 23, 14) (204, 23, 18) (205, 23, 45) (206, 24, 2) (207, 24, 3) (208, 24, 11) (209, 24, 19)
(210, 24, 46) (211, 25, 1) (212, 25, 4) (213, 25, 5) (214, 25, 12) (215, 25, 23) (216, 25, 47)
(217, 26, 2) (218, 26, 7) (219, 26, 8) (220, 26, 15) (221, 26, 48) (222, 27, 1) (223, 27, 3)
(224, 27, 5) (225, 27, 16) (226, 27, 49) (227, 28, 2) (228, 28, 7) (229, 28, 9) (230, 28, 50)
(231, 29, 1) (232, 29, 5) (233, 29, 20) (234, 29, 22) (235, 29, 51) (236, 30, 2) (237, 30, 15)
(238, 30, 19) (239, 30, 26) (240, 30, 52) (241, 31, 1) (242, 31, 11) (243, 31, 14) (244, 31, 25)
(245, 31, 53) (246, 32, 2) (247, 32, 8) (248, 32, 23) (249, 32, 26) (250, 32, 54) (251, 33, 1)
(252, 33, 13) (253, 33, 15) (254, 33, 25) (255, 33, 55) (256, 34, 2) (257, 34, 3) (258, 34, 12)
(259, 34, 22) (260, 34, 56) (261, 35, 1) (262, 35, 8) (263, 35, 16) (264, 35, 18) (265, 35, 57)
(266, 36, 2) (267, 36, 7) (268, 36, 13) (269, 36, 23) (270, 36, 58) (271, 37, 1) (272, 37, 15)
(273, 37, 16) (274, 37, 19) (275, 37, 59) (276, 38, 2) (277, 38, 14) (278, 38, 24) (279, 38, 60)
(280, 39, 1) (281, 39, 10) (282, 39, 11) (283, 39, 13) (284, 39, 61) (285, 40, 2) (286, 40, 4)
(287, 40, 8) (288, 40, 20) (289, 40, 62) (290, 41, 1) (291, 41, 9) (292, 41, 18) (293, 41, 63)
(294, 42, 2) (295, 42, 4) (296, 42, 10) (297, 42, 19) (298, 42, 64) (299, 43, 1) (300, 43, 5)
(301, 43, 25) (302, 43, 65) (303, 44, 2) (304, 44, 17) (305, 44, 19) (306, 44, 26) (307, 44, 66)
(308, 45, 1) (309, 45, 8) (310, 45, 10) (311, 45, 23) (312, 45, 67) (313, 46, 2) (314, 46, 7)
(315, 46, 11) (316, 46, 68)
Базовая матрица #2 LDPC для NR
(1, 1, 1) (2, 1, 2) (3, 1, 3) (4, 1, 4) (5, 1, 7) (6, 1, 10)
(7, 1, 11) (8, 1, 12) (9, 2, 1) (10, 2, 4) (11, 2, 5) (12, 2, 6) (13, 2, 7)
(14, 2, 8) (15, 2, 9) (16, 2, 10) (17, 2, 12) (18, 2, 13) (19, 3, 1) (20, 3, 2)
(21, 3, 4) (22, 3, 5) (23, 3, 9) (24, 3, 11) (25, 3, 13) (26, 3, 14) (27, 4, 2)
(28, 4, 3) (29, 4, 5) (30, 4, 6) (31, 4, 7) (32, 4, 8) (33, 4, 9) (34, 4, 10)
(35, 4, 11) (36, 4, 14) (37, 5, 1) (38, 5, 2) (39, 5, 12) (40, 5, 15) (41, 6, 1)
(42, 6, 2) (43, 6, 6) (44, 6, 8) (45, 6, 12) (46, 6, 16) (47, 7, 1) (48, 7, 6)
(49, 7, 8) (50, 7, 10) (51, 7, 12) (52, 7, 17) (53, 8, 2) (54, 8, 6) (55, 8, 8)
(56, 8, 12) (57, 8, 14) (58, 8, 18) (59, 9, 1) (60, 9, 2) (61, 9, 13) (62, 9, 19)
(63, 10, 2) (64, 10, 9) (65, 10, 11) (66, 10, 12) (67, 10, 20) (68, 11, 1) (69, 11, 2)
(70, 11, 7) (71, 11, 8) (72, 11, 21) (73, 12, 1) (74, 12, 8) (75, 12, 10) (76, 12, 14)
(77, 12, 22) (78, 13, 2) (79, 13, 4) (80, 13, 12) (81, 13, 23) (82, 14, 1) (83, 14, 2)
(84, 14, 9) (85, 14, 14) (86, 14, 24) (87, 15, 2) (88, 15, 7) (89, 15, 12) (90, 15, 14)
(91, 15, 25) (92, 16, 1) (93, 16, 11) (94, 16, 12) (95, 16, 26) (96, 17, 2) (97, 17, 10)
(98, 17, 12) (99, 17, 13) (100, 17, 27) (101, 18, 2) (102, 18, 6) (103, 18, 12) (104, 18, 13)
(105, 18, 28) (106, 19, 1) (107, 19, 7) (108, 19, 8) (109, 19, 29) (110, 20, 1) (111, 20, 2)
(112, 20, 11) (113, 20, 30) (114, 21, 2) (115, 21, 5) (116, 21, 12) (117, 21, 31) (118, 22, 1)
(119, 22, 9) (120, 22, 14) (121, 22, 32) (122, 23, 2) (123, 23, 3) (124, 23, 33) (125, 24, 1)
(126, 24, 4) (127, 24, 6) (128, 24, 34) (129, 25, 2) (130, 25, 3) (131, 25, 10) (132, 25, 35)
(133, 26, 1) (134, 26, 6) (135, 26, 36) (136, 27, 3) (137, 27, 8) (138, 27, 13) (139, 27, 14)
(140, 27, 37) (141, 28, 1) (142, 28, 7) (143, 28, 38) (144, 29, 2) (145, 29, 3) (146, 29, 6)
(147, 29, 39) (148, 30, 1) (149, 30, 5) (150, 30, 40) (151, 31, 3) (152, 31, 6) (153, 31, 8)
(154, 31, 10) (155, 31, 41) (156, 32, 2) (157, 32, 14) (158, 32, 42) (159, 33, 1) (160, 33, 6)
(161, 33, 13) (162, 33, 43) (163, 34, 3) (164, 34, 8) (165, 34, 11) (166, 34, 44) (167, 35, 1)
(168, 35, 13) (169, 35, 14) (170, 35, 45) (171, 36, 2) (172, 36, 6) (173, 36, 12) (174, 36, 46)
(175, 37, 1) (176, 37, 3) (177, 37, 8) (178, 37, 47) (179, 38, 11) (180, 38, 14) (181, 38, 48)
(182, 39, 2) (183, 39, 6) (184, 39, 12) (185, 39, 49) (186, 40, 1) (187, 40, 8) (188, 40, 13)
(189, 40, 50) (190, 41, 3) (191, 41, 11) (192, 41, 14) (193, 41, 51) (194, 42, 2) (195, 42, 6)
(196, 42, 12) (197, 42, 52)
Проблема с существующими решениями состоит в том, что ACE-ограничения для полной матрицы контроля по четности (PCM) типично рассматриваются в процессе подъема. Тем не менее, ACE-значения, которые являются высокими для полной PCM с низкой кодовой скоростью, по-прежнему обеспечивают вредные циклы в высокоскоростной части согласованного по скорости LDPC-кода, который проектируется посредством расширения кода. Кроме того, ограничения задаются таким образом, что любые циклы конкретной длины или меньше должны удовлетворять определенному ACE-ограничению. Типично трудно находить циклические сдвиги, которые удовлетворяют жестким ACE-ограничениям для больших циклов, и ACE-ограничение, возможно, должно уменьшаться, за счет этого также обеспечивая вредные короткие циклы с более низкой связываемостью.
Сущность изобретения
Варианты осуществления, описанные в данном документе, включают в себя способ подъема с различными ограничениями по внешней степени сообщений с аппроксимированным циклом (ACE) для различных кодовых скоростей, которые соответствуют субматрицам матрицы контроля по четности. Конкретные варианты осуществления включают в себя различные ACE-ограничения для различных длин цикла, чтобы обеспечивать то, что короткие циклы имеют более высокую связываемость, чем более длинные менее вредные циклы. Кроме того, конкретные варианты осуществления указывают и оптимизируют ACE-ограничения для каждого размера сдвига отдельно, поскольку более высокие ACE-значения могут достигаться для больших размеров сдвига, чем для небольших.
Согласно некоторым вариантам осуществления, способ для использования в беспроводном передающем устройстве сети беспроводной связи содержит кодирование (например, LDPC-) информационных битов с использованием PCM и передачу кодированных информационных битов в беспроводное приемное устройство. PCM оптимизируется согласно двум или более ACE-ограничений.
Согласно некоторым вариантам осуществления, беспроводное передающее устройство содержит схему обработки, выполненную с возможностью кодировать (например, LDPC-) информационные биты с использованием PCM и передавать кодированные информационные биты в беспроводное приемное устройство. PCM оптимизируется согласно двум или более ACE-ограничений.
Согласно некоторым вариантам осуществления, способ для использования в беспроводном приемном устройстве сети беспроводной связи содержит прием кодированных информационных битов из беспроводного передающего устройства и декодирование информационных битов с использованием PCM. Декодирование использует PCM, оптимизированную согласно двум или более ACE-ограничений.
Согласно некоторым вариантам осуществления, беспроводное приемное устройство содержит схему обработки, выполненную с возможностью принимать кодированные информационные биты из беспроводного передающего устройства и декодировать информационные биты с использованием PCM. Декодирование использует PCM, оптимизированную согласно двум или более ACE-ограничений.
В конкретных вариантах осуществления, PCM поднимается из базовой матрицы, и коэффициенты сдвига, используемые для подъема, выбраны с возможностью удовлетворять конкретным ACE-ограничениям, которые варьируются для различных частей PCM. Два или более ACE-ограничения варьируются согласно кодовой скорости, длине цикла, размеру сдвига и/или систематическим битам и битам четности.
В конкретных вариантах осуществления, первая часть PCM оптимизируется согласно первому ACE-ограничению из двух или более ACE-ограничений, и вторая часть PCM оптимизируется согласно второму ACE-ограничению из двух или более ACE-ограничений. Первая часть PCM может содержать высокоскоростную часть, и вторая часть PCM может содержать низкоскоростную часть. Первая часть PCM может оптимизироваться согласно двум или более ACE-ограничений, и вторая часть PCM может оптимизироваться согласно двум или более ACE-ограничений.
В конкретных вариантах осуществления, беспроводное передающее устройство представляет собой сетевой узел или беспроводное устройство. Беспроводное передающее устройство может содержать сетевой узел или беспроводное устройство.
Согласно некоторым вариантам осуществления, беспроводное передающее устройство содержит модуль кодирования и передающий модуль. Модуль кодирования выполнен с возможностью кодировать информационные биты с использованием PCM. Передающий модуль выполнен с возможностью передавать кодированные информационные биты в беспроводное приемное устройство. PCM оптимизируется согласно двум или более ACE-ограничений.
Согласно некоторым вариантам осуществления, беспроводное приемное устройство содержит модуль декодирования и приемный модуль. Приемный модуль выполнен с возможностью принимать кодированные информационные биты из беспроводного передающего устройства. Модуль декодирования выполнен с возможностью декодировать информационные биты с использованием PCM. Декодирование использует PCM, оптимизированную согласно двум или более ACE-ограничений.
Также раскрыт компьютерный программный продукт. Компьютерный программный продукт содержит инструкции, сохраненные на энергонезависимых машиночитаемых носителях, которые, при выполнении посредством процессора, выполняют этапы кодирования (например, LDPC-) информационных битов с использованием PCM и передачи кодированных информационных битов в беспроводное приемное устройство. PCM оптимизируется согласно двум или более ACE-ограничений.
Другой компьютерный программный продукт содержит инструкции, сохраненные на энергонезависимых машиночитаемых носителях, которые, при выполнении посредством процессора, выполняют этапы приема кодированных информационных битов из беспроводного передающего устройства и декодирования информационных битов с использованием PCM. Декодирование использует PCM, оптимизированную согласно двум или более ACE-ограничений.
Преимущество способов подъема конкретных вариантов осуществления и LDPC-кодов, спроектированных с использованием этих способов, состоит в том, что повышается производительность по частоте ошибок по блокам, в частности, в области минимального уровня ошибки. Некоторые варианты осуществления могут включать в себя дополнительные или другие преимущества.
Краткое описание чертежей
Для более полного понимания вариантов осуществления и их признаков и преимуществ, следует обратиться к нижеприведенному подробному описанию, рассматриваемому вместе с чертежами, на которых:
Фиг. 1 является блок-схемой, иллюстрирующей примерную беспроводную сеть, согласно конкретному варианту осуществления;
Фиг. 2 является блок-схемой последовательности операций, иллюстрирующей примерный способ в беспроводном передающем устройстве, согласно конкретным вариантам осуществления;
Фиг. 3 является блок-схемой последовательности операций, иллюстрирующей примерный способ в беспроводном приемном устройстве, согласно конкретным вариантам осуществления;
Фиг. 4A является блок-схемой, иллюстрирующей примерный вариант осуществления беспроводного устройства;
Фиг. 4B является блок-схемой, иллюстрирующей примерные компоненты беспроводного устройства;
Фиг. 5A является блок-схемой, иллюстрирующей примерный вариант осуществления сетевого узла; и
Фиг. 5B является блок-схемой, иллюстрирующей примерные компоненты сетевого узла.
Подробное описание изобретения
Новый 5G-стандарт радиосвязи (NR) Партнерского проекта третьего поколения (3GPP) поддерживает коды разреженного контроля по четности (LDPC) с двумя различными базовыми матрицами. Первая базовая матрица имеет размер 46×68, и вторая базовая матрица имеет размер 42×52. Один способ для конструирования матрицы контроля по четности (PCM) из базовой матрицы представляет собой алгоритм на основе постепенного роста ребер (PEG). Разновидность PEG-конструкции, которая учитывает внешнюю степень сообщений (EMD), используется для того, чтобы находить циклические сдвиги, которые обеспечивают высокие значения EMD с аппроксимированным циклом (ACE) для графа. Минимальное ACE-значение вычисляется для каждого цикла длины, меньшей или равной указанной длине.
LDPC-код имеет свойство (dACE, etaACE), если все циклы, длина которых равна 2 · dACE или меньше имеют ACE-значения, по меньшей мере, etaACE. Коэффициенты сдвига выбираются таким образом, что отсутствуют циклы на графе с ACE-значениями ниже указанного ACE-ограничения. Таким образом, вредные короткие циклы с низкой связываемостью с остальной частью графа могут исключаться.
Одно возможное решение состоит в том, чтобы указывать одно проектное решение по коэффициентам сдвига для каждого размера сдвига, для которого указывается LDPC-код. Тем не менее, это требует хранения каждого проектного решения по коэффициентам сдвига как в передающем устройстве, так и в приемном устройстве. Другая альтернатива, которая рассматривается здесь, заключается в том, чтобы проектировать коэффициенты сдвига для набора размеров сдвига одновременно.
Проблема с существующими решениями состоит в том, что ACE-ограничения для полной PCM типично рассматриваются в процессе подъема. Тем не менее, ACE-значения, которые являются высокими для полной PCM с низкой кодовой скоростью, по-прежнему обеспечивают вредные циклы в высокоскоростной части согласованного по скорости LDPC-кода, который проектируется посредством расширения кода. Кроме того, ограничения задаются таким образом, что любые циклы конкретной длины или меньше должны удовлетворять определенному ACE-ограничению. Типично трудно находить циклические сдвиги, которые удовлетворяют жестким ACE-ограничениям для больших циклов, и ACE-ограничение, возможно, должно уменьшаться, за счет этого также обеспечивая вредные короткие циклы с более низкой связываемостью.
Варианты осуществления, описанные в данном документе, включают в себя способ подъема с различными ограничениями по внешней степени сообщений с аппроксимированным циклом (ACE) для различных кодовых скоростей, которые соответствуют субматрицам матрицы контроля по четности. Конкретные варианты осуществления включают в себя различные ACE-ограничения для различных длин цикла, чтобы обеспечивать то, что короткие циклы имеют более высокую связываемость, чем более длинные менее вредные циклы. Кроме того, конкретные варианты осуществления указывают и оптимизируют ACE-ограничения для каждого размера сдвига отдельно, поскольку более высокая связываемость может достигаться для больших размеров сдвига, чем для небольших.
Преимущество способов подъема конкретных вариантов осуществления и LDPC-кодов, спроектированных с использованием этих способов, состоит в том, что повышается производительность по частоте ошибок по блокам, в частности, в области минимального уровня ошибки.
Нижеприведенное описание излагает множество конкретных подробностей. Тем не менее, следует понимать, что варианты осуществления могут осуществляться на практике без этих конкретных подробностей. В других случаях, хорошо известные схемы, структуры и технологии подробно не показаны, чтобы не затруднять понимание данного описания. Специалисты в данной области техники, с использованием прилагаемых описаний, должны иметь возможность реализовывать соответствующую функциональность без чрезмерного экспериментирования.
Ссылки в подробном описании на "один вариант осуществления", "вариант осуществления", "примерный вариант осуществления" и т.д. указывают то, что описанный вариант осуществления может включать в себя конкретный признак, структуру или характеристику, но каждый вариант осуществления не обязательно может включать в себя конкретный признак, структуру или характеристику. Кроме этого, такие фразы не обязательно ссылаются на идентичный вариант осуществления. Дополнительно, когда конкретный признак, структура или характеристика описывается в связи с вариантом осуществления, заявляется, что реализация такого признака, структуры или характеристики в связи с другими вариантами осуществления, описанными или нет в явной форме, находится в пределах знаний специалистов в данной области техники.
Конкретные варианты осуществления описываются со ссылкой на фиг. 1-5B из числа чертежей, причем аналогичные номера используются для аналогичных и соответствующих частей различных чертежей. LTE и NR используется в ходе этого раскрытия сущности в качестве примерной системы сотовой связи, но идеи, представленные в данном документе, также могут применяться к другим системам беспроводной связи.
Фиг. 1 является блок-схемой, иллюстрирующей примерную беспроводную сеть, согласно конкретному варианту осуществления. Беспроводная сеть 100 включает в себя одно или более беспроводных устройств 110 (таких как мобильные телефоны, смартфоны, переносные компьютеры, планшетные компьютеры, MTC-устройства, V2X-устройства или любые другие устройства, которые могут предоставлять беспроводную связь), и множество сетевых узлов 120 (таких как базовые станции, усовершенствованные узлы B, gNB и т.д.). Беспроводное устройство 110 также может называться "UE". Сетевой узел 120 обслуживает зону 115 покрытия (также называемую "сотой 115").
В общем, беспроводные устройства 110, которые находятся в пределах покрытия сетевого узла 120 (например, в соте 115, обслуживаемой посредством сетевого узла 120), обмениваются данными с сетевым узлом 120 посредством передачи и приема беспроводных сигналов 130. Например, беспроводные устройства 110 и сетевой узел 120 могут передавать беспроводные сигналы 130, содержащие речевой трафик, трафик данных и/или управляющие сигналы.
Сетевой узел 120, передающий речевой трафик, трафик данных и/или управляющие сигналы в беспроводное устройство 110, может называться "обслуживающим сетевым узлом 120" для беспроводного устройства 110. Связь между беспроводным устройством 110 и сетевым узлом 120 может называться "сотовой связью". Беспроводные сигналы 130 могут включать в себя обе передачи по нисходящей линии связи (из сетевого узла 120 в беспроводные устройства 110) и передачи по восходящей линии связи (из беспроводных устройств 110 в сетевой узел 120). В LTE, интерфейс для обмена беспроводными сигналами между сетевым узлом 120 и беспроводным устройством 110 может называться "Uu-интерфейсом".
Каждый сетевой узел 120 может иметь одно передающее устройство или несколько передающих устройств для передачи сигналов 130 в беспроводные устройства 110. В некоторых вариантах осуществления, сетевой узел 120 может содержать систему со многими входами и многими выходами (MIMO). Беспроводной сигнал 130 может содержать один или более лучей. Конкретные лучи могут подвергаться формированию диаграммы направленности в конкретном направлении. Аналогично, каждое беспроводное устройство 110 может иметь одно приемное устройство или несколько приемных устройств для приема сигналов 130 из сетевых узлов 120 или других беспроводных устройств 110. Беспроводное устройство может принимать один или более лучей, содержащих беспроводной сигнал 130.
Беспроводные устройства 110 могут обмениваться данными между собой (т.е. D2D-режим работы) посредством передачи и приема беспроводных сигналов 140. Например, беспроводное устройство 110a может обмениваться данными с беспроводным устройством 110b с использованием беспроводного сигнала 140. Беспроводной сигнал 140 также может называться "боковой линией 140 связи". Связь между двумя беспроводными устройствами 110 может называться "D2D-связью" или "связью в боковой линии связи". В LTE, интерфейс для обмена данными беспроводного сигнала 140 между беспроводными устройствами 110 может называться "PC5-интерфейсом".
Беспроводные сигналы 130 и 140 могут передаваться в частотно-временных ресурсах. Частотно-временные ресурсы могут сегментироваться на радиокадры, субкадры, временные кванты и/или временные миникванты. Данные могут диспетчеризоваться для передачи на основе сегментов. Например, передачи данных могут диспетчеризоваться на основе субкадра, временного кванта или временного миникванта. Беспроводные сигналы 130 могут включать в себя опорные сигналы, такие как DM-RS.
Беспроводные сигналы 130 и 140 могут кодироваться с использованием LDPC. Конкретный LDPC может определяться посредством способа подъема, в котором коэффициенты сдвига определяются на основе ACE-ограничений, которые могут варьироваться на основе числа различных кодовых скоростей, размера Z сдвига, различных длин цикла и/или отдельно для систематических битов и битов четности. Ниже описываются более конкретные примеры.
Беспроводное устройство 110, сетевой узел 120 или любой другой компонент сети 100, который передает беспроводные сигналы, может называться "беспроводным передающим устройством". Беспроводное устройство 110, сетевой узел 120 или любой другой компонент сети 100, который принимает беспроводные сигналы, может называться "беспроводным приемным устройством".
В беспроводной сети 100, каждый сетевой узел 120 может использовать любую подходящую технологию радиодоступа, такую как стандарт долгосрочного развития (LTE), 5G NR, усовершенствованный стандарт LTE, UMTS, HSPA, GSM, CDMA2000, NR, WiMAX, Wi-Fi и/или другая подходящая технология радиодоступа. Беспроводная сеть 100 может включать в себя любую подходящую комбинацию одной или более технологий радиодоступа. Для примерных целей, различные варианты осуществления могут описываться в контексте определенных технологий радиодоступа. Тем не менее, объем раскрытия сущности не ограничен примерами, и другие варианты осуществления могут использовать другие технологии радиодоступа.
Как описано выше, варианты осуществления беспроводной сети могут включать в себя одно или более беспроводных устройств и один или более различных типов сетевых радиоузлов, допускающих обмен данными с беспроводными устройствами. Сеть также может включать в себя любые дополнительные элементы, подходящие для того, чтобы поддерживать связь между беспроводными устройствами или между беспроводным устройством и другим устройством связи (к примеру, проводным телефоном). Беспроводное устройство может включать в себя любую подходящую комбинацию аппаратных средств и/или программного обеспечения. Например, в конкретных вариантах осуществления, беспроводное устройство, такое как беспроводное устройство 110, может включать в себя компоненты, описанные относительно фиг. 4A ниже. Аналогично, сетевой узел может включать в себя любую подходящую комбинацию аппаратных средств и/или программного обеспечения. Например, в конкретных вариантах осуществления, сетевой узел, такой как базовый сетевой узел 120, может включать в себя компоненты, описанные относительно фиг. 5A ниже.
В конкретных вариантах осуществления, способ подъема для квазициклических кодов выбирает коэффициенты сдвига для одной ненулевой записи в базовой матрице (также называемой "базовым графом") за один раз. Для каждой ненулевой записи в базовой матрице, коэффициент сдвига выбирается случайно (т.е. выбирается значение между 0 и Z-1). Алгоритм ACE-обнаружения, описанный во введении, используется для того, чтобы исключать циклы, которые не удовлетворяют конкретным ACE-ограничениям. Это может выполняться посредством проверки всех ACE-ограничений на предмет ребер в матрице, которые уже выбраны, включающих в себя ребра, соответствующие коэффициенту сдвига, который в данный момент рассматривается. Если циклы, не удовлетворяющие ограничениям, добавляются на граф через последний выбранный коэффициент сдвига, вместо этого новое случайное значение этого коэффициента сдвига рассматривается. Эта процедура продолжается до тех пор, пока коэффициент сдвига, который удовлетворяет всем ACE-ограничениям, не будет найден.
Конкретные варианты осуществления включают в себя преимущества по сравнению с традиционными способами подъема, поскольку: (a) ACE-ограничения могут указываться для определенного числа различных кодовых скоростей; (b) ACE-ограничения могут указываться для каждого размера Z сдвига; (c) ACE-ограничения могут указываться для нескольких различных длин цикла; и (d) ACE-ограничения могут указываться отдельно для систематических битов и битов четности.
Примерная базовая матрица указывается в таблице 2. Пример представляет собой субматрицу базовой матрицы #2, описанной выше.

Таблица 2 включает в себя два различных прямоугольника. Меньший прямоугольник в верхнем левом углу соответствует более высокой кодовой скорости, и полная базовая матрица соответствует более низкой кодовой скорости. Способ подъема конкретных вариантов осуществления основан на поиске коэффициентов сдвига, которые удовлетворяют определенным ACE-ограничениям. Поскольку ACE-значение для цикла зависит от степени переменного узла, вычисляемой как весовой коэффициент столбца базовой матрицы, очевидно, что большая базовая матрица, которая соответствует более низкой кодовой скорости, имеет более высокие степени переменных узлов и в силу этого также более высокие ACE-значения. Посредством ограничения ACE-значений для различных кодовых скоростей, т.е. субматриц различного размера, конкретные варианты осуществления обеспечивают то, что подъем является оптимальным не только для наименьшей кодовой скорости, которую задает базовая матрица, но также и для более высоких кодовых скоростей.
Размер сдвига также важен при выборе ACE-ограничений, которые должны удовлетворяться для выбранного проектного решения по коэффициентам сдвига. Поскольку алгоритм подъема имеет большую свободу в выборе коэффициентов сдвига, если размер сдвига является большим, проектные решения по коэффициентам сдвига, которые удовлетворяют более высоким ACE-ограничениям для определенной длины цикла или которые удовлетворяют ACE-ограничениям для больших длин цикла, могут быть найдены, если размер Z сдвига увеличивается. Конкретные варианты осуществления в силу этого указывают отдельные ACE-ограничения для каждого размера Z сдвига. Это позволяет полностью использовать свобода выбора коэффициентов сдвига для каждого размера сдвига и достигать более высоких ACE-значений, которые тесно связаны с повышенной производительностью по BLER для больших размеров сдвига.
Кроме того, способ подъема на основе ACE, описанный во введении, использует одно ACE-значение, которому должны удовлетворять все циклы указанной длины или меньше. Конкретные варианты осуществления, описанные в данном документе, задают определенное число ACE-ограничений для различных длин цикла, чтобы позволять налагать более жесткие ограничения (большие требуемые ACE-значения) на более короткие циклы и немного ослаблять их для более длинных циклов. Поскольку невозможно исключать все циклы, это упрощает оптимизацию связываемости циклов различных длин.
Конкретные варианты осуществления включают в себя базовые матрицы, которые имеют специальную субматричную структуру в первом наборе битов четности следующей формы:
или:
,
где коэффициенты сдвига выбираются следующим образом, так что A и B являются целыми числами между 0 и Z-1. Типично необходимо выбирать A=1 и B=0:
или:
Эта субматричная структура показана в таблице 2 в полужирных элементах.
Эта структура обуславливает Z циклов длины 2d, где d является числом строк в (квадратной) субматрице с ACE=1 для кодовых скоростей с использованием этой части матрицы. Следовательно, невозможно удовлетворять более высоким ограничениям, чем etaACE=1 для dACE=4, даже если другие коэффициенты сдвига могут выбираться таким образом, что циклы, заключающие в себе соответствующие переменные узлы, имеют более высокую ACE.
Даже если справедливо короткие циклы с низким ACE-значением не могут исключаться при использовании этой структуры, она зачастую используется в любом случае вследствие простой процедуры кодирования, которая может использоваться. Нижеприведенное описание предполагает, что A=1, B=0, и что все коэффициенты сдвига для сдвоенной диагонали, показанной в специальной субматричной структуре, задаются равными 0. Кроме того, коэффициенты сдвига для части расширения по диагонали базовой матрицы (нижнего правого угла матрицы) задаются равными 0. Коэффициенты сдвига, выбранные для части расширения по диагонали, не являются важными для производительности по BLER кода, поскольку они соответствуют переменным узлам степени 1 и не могут составлять часть циклов. Оптимизация этих коэффициентов сдвига в силу этого не требуется.
Тем не менее, вследствие цикла длины 8 (dACE=4) с etaACE=1, который уже присутствует в матрице, невозможно задавать более жесткие ограничения для этой длины цикла или более и для наибольшей кодовой скорости, для которой указывается матрица. Тем не менее, можно исключать циклы, которые содержат три самых правых столбца в вышеприведенной структуре и другие столбцы в матрице. Такие столбцы находятся в систематической части базовой матрицы, которые соответствуют столбцам, оставшимся в матрице со специальной субматричной структурой, помеченной полужирным. Чтобы иметь возможность исключать эти циклы в оптимизации коэффициентов сдвига, конкретные варианты осуществления указывают различные ACE-ограничения при начале ACE-обнаружения из переменных узлов в систематической части и из переменных узлов в части четности, в которой ACE-ограничения с началом в систематической части могут быть более высокими.
Для обеих базовых матриц 1 и 2, описанных выше, весовые коэффициенты столбцов для первых двух столбцов (или эквивалентно переменных узлов) выше, чем для других столбцов. Типично, хорошо исключать, по меньшей мере, все циклы длины 4. Тем не менее, для небольших размеров Z сдвига, при которых свобода в выборе коэффициентов сдвига является небольшой, это может быть невозможным. Для этой кодовой скорости, в этом случае может быть преимущественным обеспечивать только циклы длины 4, заключающие в себе два первых переменных узла базовой матрицы, которые имеют наибольшую степень переменного узла. Это может принудительно активироваться посредством выбора ACE-ограничения с dACE=2 и выбора etaACE таким образом, что циклы длины 4, содержащие другие переменные узлы, автоматически нарушают это ограничение. Если рассматривается более низкая скорость, соответствующая использованию большего числа строк базовой матрицы, более высокая etaACE типично может достигаться, поскольку степени переменных узлов являются более высокими для этой субматрицы. Тем не менее, аналогичное ограничение etaACE может выбираться для этой скорости, чтобы принудительно активировать то, что любые циклы длины 4 заключают в себе узлы только из первых двух столбцов.
Для большего размера Z сдвига, может быть возможным исключать все циклы длины 4. Следовательно, преимущественно иметь различные ACE-ограничения для различных размеров сдвига. В этом небольшом примере, конкретные варианты осуществления, например, могут выбирать коэффициенты сдвига для размера сдвига Z>10, которые исключают все циклы длины 4, т.е. dACE=2 и etaACE=Infinity (также обозначается посредством Inf ниже).
Чтобы находить надлежащие ограничения etaACE для задания, попробовано несколько начальных ACE-ограничений. Проектные решения по коэффициентам сдвига, удовлетворяющие, в общем, более высоким ACE-ограничениям, выбраны, если способ находит подходящий возможный вариант. Из возможных вариантов с аналогичными ACE-ограничениями, конечный выбор PCM выполняется после изучения производительности по BLER PCM. Следует отметить, что ACE-ограничения, отличающиеся в различных размерах сдвига или dACE, легко не упорядочиваются, поскольку наложение более высоких ограничений на конкретную кодовую скорость или значение Z может приводить к трудности при удовлетворении другим ограничениям. Следовательно, конечный выбор осуществлен из числа PCM, удовлетворяющих примерно аналогичным ограничениям.
Матрицы, принадлежащие набору #3 для базового графа 1, удовлетворяют следующим ограничениям etaACE для различных кодовых скоростей (соответствующих использованию меньшей субматрицы), когда ACE-обнаружение начинается в систематическом переменном узле для Z=40.
Матрицы, принадлежащие набору #3 для базового графа 1, удовлетворяют следующим ограничениям etaACE для различных кодовых скоростей (соответствующих использованию меньшей субматрицы) и размеров сдвига, когда ACE-обнаружение начинается в систематическом переменном узле для Z=80.
Матрицы, принадлежащие набору #3 для базового графа 1, удовлетворяют следующим ограничениям etaACE для различных кодовых скоростей (соответствующих использованию меньшей субматрицы), когда ACE-обнаружение начинается в систематическом переменном узле для Z=160.
Матрицы, принадлежащие набору #3 для базового графа 1, удовлетворяют следующим ограничениям etaACE для различных кодовых скоростей (соответствующих использованию меньшей субматрицы), когда ACE-обнаружение начинается в систематическом переменном узле для Z=320.
Матрицы, принадлежащие набору #3 для базового графа 1, удовлетворяют следующим ограничениям etaACE для различных кодовых скоростей (соответствующих использованию меньшей субматрицы), когда ACE-обнаружение начинается в переменном узле четности для Z=40.
Матрицы, принадлежащие набору #3 для базового графа 1, удовлетворяют следующим ограничениям etaACE для различных кодовых скоростей (соответствующих использованию меньшей субматрицы), когда ACE-обнаружение начинается в переменном узле четности для Z=80.
Матрицы, принадлежащие набору #3 для базового графа 1, удовлетворяют следующим ограничениям etaACE для различных кодовых скоростей (соответствующих использованию меньшей субматрицы), когда ACE-обнаружение начинается в переменном узле четности для Z=160.
Матрицы, принадлежащие набору #3 для базового графа 1, удовлетворяют следующим ограничениям etaACE для различных кодовых скоростей (соответствующих использованию меньшей субматрицы), когда ACE-обнаружение начинается в переменном узле четности для Z=320.
Начальные ограничения для матриц, принадлежащих набору #3 для базового графа 1, для различных кодовых скоростей (соответствующих использованию меньшей субматрицы), когда ACE-обнаружение начинается в систематическом переменном узле для Z=40, где
Начальные ограничения для матриц, принадлежащих набору #3 для базового графа 1, для различных кодовых скоростей (соответствующих использованию меньшей субматрицы), когда ACE-обнаружение начинается в систематическом переменном узле для Z=80, где
Начальные ограничения для матриц, принадлежащих набору #3 для базового графа 1, для различных кодовых скоростей (соответствующих использованию меньшей субматрицы), когда ACE-обнаружение начинается в систематическом переменном узле для Z=160, где
Начальные ограничения для матриц, принадлежащих набору #3 для базового графа 1, для различных кодовых скоростей (соответствующих использованию меньшей субматрицы), когда ACE-обнаружение начинается в систематическом переменном узле для Z=320, где
Начальные ограничения для субматриц, содержащих первые четыре узла четности, в базовом графе, принадлежащем набору #3 для базового графа 1, для различных кодовых скоростей (соответствующих использованию меньшей субматрицы), когда ACE-обнаружение начинается в переменном узле четности для Z=40, где
Начальные ограничения для субматриц, содержащих первые четыре узла четности, в базовом графе, принадлежащем набору #3 для базового графа 1, для различных кодовых скоростей (соответствующих использованию меньшей субматрицы), когда ACE-обнаружение начинается в переменном узле четности для Z=80, где
Начальные ограничения для субматриц, содержащих первые четыре узла четности, в базовом графе, принадлежащем набору #3 для базового графа 1, для различных кодовых скоростей (соответствующих использованию меньшей субматрицы), когда ACE-обнаружение начинается в переменном узле четности для Z=160, где
Начальные ограничения для субматриц, содержащих первые четыре узла четности, в базовом графе, принадлежащем набору #3 для базового графа 1, для различных кодовых скоростей (соответствующих использованию меньшей субматрицы), когда ACE-обнаружение начинается в переменном узле четности для Z=320, где
Следует отметить, что переменные узлы в базовом графе и переменные узлы в полной PCM после подъема не являются идентичными. В общем, если предусмотрено N переменных узлов в базовом графе, после подъема должно быть предусмотрено N*Z переменных узлов.
Новый стандарт радиосвязи (NR) включает в себя две различных базовых матрицы, которые описывают структуру LDPC-кодов. Тем не менее, соответствующие проектные решения по коэффициентам сдвига, которые являются очень важными для производительности LDPC-кодов, не указаны. Конкретные варианты осуществления используют ACE-ограничения, чтобы находить проектное решение по коэффициентам сдвига с хорошей производительностью, которое исключает вредные циклы и повышает производительность по BLER. В конкретных вариантах осуществления, различные ACE-ограничения могут использоваться для систематических битов и битов четности. Нижеприведенные примеры представляют собой результат применения алгоритма подъема к базовой матрицы #1 и #2, указываемой для NR. Формат нижеприведенных примерных векторов описывается выше во введении.
BG#1: Вектор для набора 1:
4, 175, 110, 199, 65, 149, 58, 24, 234, 204, 230, 154, 79, 207, 97, 124, 124, 1, 0, 116, 3, 42, 255, 57, 250, 165, 73, 104, 242, 111, 77, 144, 253, 234, 94, 0, 0, 0, 28, 50, 136, 83, 151, 172, 40, 78, 19, 131, 243, 222, 42, 210, 51, 156, 120, 0, 0, 251, 216, 5, 27, 91, 25, 103, 76, 20, 201, 9, 19, 61, 112, 71, 99, 14, 1, 0, 60, 124, 0, 33, 128, 140, 26, 113, 168, 203, 0, 158, 177, 174, 245, 144, 213, 145, 43, 0, 201, 247, 40, 232, 253, 55, 0, 120, 58, 11, 146, 46, 190, 12, 219, 21, 0, 106, 186, 143, 174, 243, 15, 136, 250, 0, 106, 240, 79, 200, 209, 13, 0, 93, 135, 20, 42, 133, 54, 52, 0, 103, 54, 47, 12, 110, 34, 0, 254, 58, 15, 224, 98, 0, 195, 179, 155, 162, 244, 113, 0, 95, 172, 183, 53, 100, 233, 0, 172, 108, 191, 112, 111, 0, 105, 122, 96, 98, 4, 0, 17, 218, 229, 135, 141, 0, 80, 235, 219, 245, 189, 0, 44, 219, 82, 103, 103, 0, 15, 236, 70, 1, 38, 0, 220, 101, 28, 105, 0, 218, 74, 201, 199, 0, 198, 228, 51, 117, 47, 0, 45, 73, 90, 209, 0, 100, 239, 137, 45, 0, 191, 176, 244, 0, 47, 87, 218, 5, 0, 12, 67, 191, 141, 0, 75, 22, 163, 180, 0, 207, 11, 253, 201, 0, 63, 113, 10, 122, 0, 0, 25, 89, 21, 0, 206, 119, 238, 45, 0, 112, 253, 183, 161, 0, 76, 43, 104, 22, 0, 28, 153, 35, 0, 130, 176, 193, 159, 0, 20, 100, 23, 221, 0, 190, 158, 38, 0, 127, 136, 185, 239, 0, 139, 109, 85, 0, 234, 210, 198, 0, 0, 106, 206, 66, 24, 0, 204, 223, 47, 0
BG#1: Вектор для набора 2:
307, 19, 50, 369, 181, 216, 317, 288, 109, 17, 357, 215, 106, 242, 180, 330, 346, 1, 0, 76, 76, 73, 288, 144, 331, 331, 178, 295, 342, 217, 99, 354, 114, 331, 112, 0, 0, 0, 205, 250, 328, 332, 256, 161, 267, 160, 63, 129, 200, 88, 53, 131, 240, 205, 13, 0, 0, 276, 87, 0, 275, 199, 153, 56, 132, 305, 231, 341, 212, 304, 300, 271, 39, 357, 1, 0, 332, 181, 0, 195, 14, 115, 166, 241, 51, 157, 0, 278, 257, 1, 351, 92, 253, 18, 225, 0, 9, 62, 316, 333, 290, 114, 0, 307, 179, 165, 18, 39, 224, 368, 67, 170, 0, 366, 232, 321, 133, 57, 303, 63, 82, 0, 101, 339, 274, 111, 383, 354, 0, 48, 102, 8, 47, 188, 334, 115, 0, 77, 186, 174, 232, 50, 74, 0, 313, 177, 266, 115, 370, 0, 142, 248, 137, 89, 347, 12, 0, 241, 2, 210, 318, 55, 269, 0, 13, 338, 57, 289, 57, 0, 260, 303, 81, 358, 375, 0, 130, 163, 280, 132, 4, 0, 145, 213, 344, 242, 197, 0, 187, 206, 264, 341, 59, 0, 205, 102, 328, 213, 97, 0, 30, 11, 233, 22, 0, 24, 89, 61, 27, 0, 298, 158, 235, 339, 234, 0, 72, 17, 383, 312, 0, 71, 81, 76, 136, 0, 194, 194, 101, 0, 222, 19, 244, 274, 0, 252, 5, 147, 78, 0, 159, 229, 260, 90, 0, 100, 215, 258, 256, 0, 102, 201, 175, 287, 0, 323, 8, 361, 105, 0, 230, 148, 202, 312, 0, 320, 335, 2, 266, 0, 210, 313, 297, 21, 0, 269, 82, 115, 0, 185, 177, 289, 214, 0, 258, 93, 346, 297, 0, 175, 37, 312, 0, 52, 314, 139, 288, 0, 113, 14, 218, 0, 113, 132, 114, 168, 0, 80, 78, 163, 274, 0, 135, 149, 15, 0
BG#1: Вектор для набора 3:
247, 198, 124, 265, 245, 5, 266, 57, 319, 30, 150, 76, 312, 257, 213, 234, 156, 1, 0, 97, 156, 89, 173, 236, 184, 261, 55, 298, 311, 170, 219, 30, 52, 49, 253, 0, 0, 0, 121, 62, 121, 216, 106, 238, 215, 108, 242, 82, 90, 124, 285, 147, 179, 141, 40, 0, 0, 74, 153, 109, 215, 136, 99, 213, 111, 176, 179, 213, 143, 119, 88, 43, 56, 86, 1, 0, 261, 247, 0, 32, 285, 3, 256, 73, 45, 268, 0, 310, 232, 149, 98, 151, 17, 83, 255, 0, 69, 303, 214, 308, 160, 143, 0, 36, 105, 140, 38, 144, 38, 45, 237, 293, 0, 162, 318, 53, 265, 252, 143, 111, 263, 0, 248, 299, 214, 227, 298, 159, 0, 98, 101, 27, 88, 162, 56, 293, 0, 57, 31, 106, 81, 20, 305, 0, 7, 216, 244, 284, 222, 0, 316, 57, 217, 55, 186, 92, 0, 255, 170, 81, 302, 48, 140, 0, 222, 211, 288, 143, 24, 0, 24, 296, 20, 102, 212, 0, 189, 13, 164, 315, 83, 0, 207, 214, 15, 195, 301, 0, 290, 64, 126, 79, 7, 0, 104, 182, 139, 70, 127, 0, 221, 60, 126, 74, 0, 210, 284, 122, 290, 0, 300, 140, 128, 191, 28, 0, 287, 193, 297, 248, 0, 72, 305, 3, 46, 0, 15, 99, 30, 0, 139, 309, 304, 9, 0, 231, 49, 162, 128, 0, 84, 278, 163, 194, 0, 33, 96, 132, 58, 0, 210, 175, 146, 181, 0, 90, 252, 227, 307, 0, 28, 3, 98, 6, 0, 98, 79, 274, 227, 0, 189, 184, 129, 252, 0, 225, 271, 184, 0, 210, 28, 311, 68, 0, 201, 223, 313, 272, 0, 48, 56, 233, 0, 280, 74, 221, 319, 0, 141, 235, 126, 0, 303, 242, 52, 91, 0, 302, 265, 181, 160, 0, 237, 307, 40, 0
BG#1: Вектор для набора 4:
126, 197, 52, 193, 176, 190, 51, 129, 47, 21, 187, 2, 86, 170, 196, 46, 53, 1, 0, 44, 87, 21, 163, 117, 17, 107, 127, 148, 114, 20, 8, 40, 23, 69, 71, 0, 0, 0, 216, 104, 134, 19, 12, 17, 143, 68, 145, 160, 65, 98, 178, 91, 210, 173, 75, 0, 0, 37, 158, 111, 134, 117, 138, 139, 59, 146, 149, 197, 117, 48, 28, 127, 71, 177, 1, 0, 88, 99, 0, 14, 179, 106, 132, 129, 149, 60, 0, 145, 92, 127, 172, 62, 79, 59, 58, 0, 207, 32, 216, 209, 118, 69, 0, 169, 209, 123, 223, 189, 214, 47, 85, 111, 0, 32, 77, 81, 17, 18, 169, 157, 6, 0, 201, 87, 166, 83, 34, 52, 0, 204, 196, 45, 44, 196, 91, 124, 0, 119, 129, 43, 28, 16, 206, 0, 35, 131, 153, 218, 195, 0, 62, 86, 28, 91, 7, 4, 0, 31, 1, 63, 167, 152, 216, 0, 132, 105, 108, 156, 110, 0, 44, 78, 155, 218, 173, 0, 172, 211, 12, 199, 219, 0, 105, 135, 56, 74, 103, 0, 208, 159, 190, 182, 199, 0, 125, 209, 202, 18, 0, 0, 108, 28, 118, 20, 0, 31, 203, 179, 96, 0, 217, 183, 68, 84, 35, 0, 174, 42, 38, 121, 0, 125, 25, 109, 92, 0, 108, 61, 188, 0, 174, 70, 49, 142, 0, 180, 17, 104, 156, 0, 71, 52, 27, 42, 0, 130, 89, 138, 216, 0, 207, 54, 220, 50, 0, 28, 148, 165, 78, 0, 206, 32, 156, 50, 0, 2, 132, 119, 213, 0, 64, 193, 99, 23, 0, 216, 124, 150, 0, 164, 41, 123, 23, 0, 29, 29, 43, 111, 0, 85, 28, 223, 0, 57, 211, 115, 62, 0, 184, 111, 30, 0, 47, 126, 189, 26, 0, 20, 187, 38, 137, 0, 41, 186, 135, 0
BG#1: Вектор для набора 5:
2, 233, 219, 231, 113, 201, 126, 58, 228, 225, 181, 28, 71, 255, 174, 13, 63, 1, 0, 141, 144, 144, 149, 82, 125, 247, 211, 16, 276, 183, 215, 115, 111, 208, 101, 0, 0, 0, 234, 143, 6, 157, 37, 13, 107, 186, 11, 6, 218, 257, 225, 100, 133, 150, 58, 0, 0, 276, 148, 142, 278, 88, 16, 2, 217, 150, 227, 11, 133, 12, 72, 127, 145, 41, 1, 0, 214, 147, 0, 11, 184, 238, 169, 30, 33, 63, 0, 158, 116, 78, 152, 46, 186, 130, 155, 0, 279, 70, 15, 176, 228, 144, 0, 187, 279, 181, 265, 10, 49, 45, 146, 128, 0, 67, 230, 107, 63, 36, 64, 154, 162, 0, 244, 274, 178, 0, 40, 77, 0, 38, 181, 49, 109, 109, 199, 167, 0, 131, 34, 212, 242, 142, 11, 0, 118, 213, 130, 147, 279, 0, 123, 30, 275, 95, 184, 219, 0, 89, 77, 287, 114, 134, 262, 0, 161, 72, 157, 271, 65, 0, 7, 241, 201, 214, 280, 0, 180, 133, 99, 225, 208, 0, 176, 5, 278, 99, 95, 0, 52, 145, 28, 280, 241, 0, 240, 61, 82, 183, 251, 0, 82, 64, 218, 118, 0, 280, 64, 209, 66, 0, 90, 54, 15, 241, 253, 0, 130, 149, 62, 250, 0, 236, 225, 132, 133, 0, 113, 278, 116, 0, 135, 100, 67, 283, 0, 60, 240, 115, 67, 0, 197, 171, 54, 184, 0, 144, 64, 61, 105, 0, 102, 27, 33, 129, 0, 243, 163, 138, 138, 0, 116, 37, 189, 169, 0, 2, 107, 197, 46, 0, 133, 270, 144, 183, 0, 13, 99, 239, 0, 122, 10, 79, 134, 0, 59, 40, 43, 133, 0, 172, 34, 83, 0, 1, 188, 19, 78, 0, 5, 40, 147, 0, 187, 155, 176, 180, 0, 272, 198, 183, 237, 0, 270, 29, 100, 0
BG#1: Вектор для набора 6:
74, 41, 309, 17, 133, 68, 327, 282, 181, 153, 85, 343, 153, 4, 253, 113, 44, 1, 0, 18, 260, 68, 321, 188, 127, 131, 345, 197, 44, 302, 191, 191, 161, 3, 239, 0, 0, 0, 135, 123, 338, 313, 65, 256, 160, 179, 56, 264, 47, 158, 100, 148, 146, 75, 250, 0, 0, 129, 279, 294, 214, 207, 297, 266, 70, 39, 149, 307, 229, 0, 97, 45, 324, 338, 1, 0, 158, 116, 0, 292, 37, 269, 87, 21, 233, 75, 0, 135, 332, 328, 31, 321, 348, 28, 170, 0, 177, 155, 53, 284, 205, 207, 0, 83, 234, 125, 106, 71, 256, 324, 15, 195, 0, 291, 110, 22, 6, 53, 316, 345, 175, 0, 285, 302, 25, 286, 252, 332, 0, 107, 67, 139, 158, 32, 232, 307, 0, 285, 160, 249, 154, 5, 49, 0, 195, 99, 331, 276, 41, 0, 125, 191, 238, 339, 171, 244, 0, 349, 28, 0, 275, 350, 110, 0, 11, 15, 308, 246, 293, 0, 279, 284, 284, 2, 166, 0, 253, 122, 310, 43, 127, 0, 69, 21, 340, 155, 146, 0, 297, 6, 141, 25, 304, 0, 216, 203, 116, 119, 220, 0, 256, 154, 338, 207, 0, 168, 309, 195, 143, 0, 67, 255, 179, 316, 116, 0, 349, 166, 283, 277, 0, 119, 338, 19, 111, 0, 195, 252, 108, 0, 21, 128, 231, 346, 0, 207, 222, 234, 286, 0, 151, 100, 174, 143, 0, 326, 296, 153, 200, 0, 157, 244, 131, 196, 0, 312, 110, 146, 60, 0, 266, 268, 306, 95, 0, 129, 300, 274, 165, 0, 235, 188, 230, 279, 0, 11, 117, 68, 0, 160, 124, 340, 173, 0, 104, 302, 110, 248, 0, 9, 250, 63, 0, 24, 327, 48, 185, 0, 345, 348, 250, 0, 155, 71, 99, 233, 0, 203, 194, 185, 245, 0, 280, 218, 171, 0
BG#1: Вектор для набора 7:
18, 42, 124, 101, 177, 196, 133, 181, 205, 201, 168, 86, 95, 86, 201, 193, 172, 1, 0, 117, 55, 192, 46, 167, 97, 110, 167, 129, 198, 75, 49, 200, 200, 178, 168, 0, 0, 0, 121, 30, 63, 84, 83, 96, 121, 31, 94, 141, 163, 20, 56, 85, 19, 90, 12, 0, 0, 162, 1, 14, 119, 125, 21, 154, 83, 73, 53, 121, 63, 111, 187, 174, 98, 35, 1, 0, 80, 21, 0, 158, 94, 134, 189, 203, 54, 24, 0, 8, 183, 32, 189, 124, 75, 105, 94, 0, 102, 61, 69, 142, 44, 121, 0, 203, 171, 155, 105, 11, 3, 40, 22, 139, 0, 83, 73, 39, 23, 148, 95, 58, 148, 0, 160, 21, 173, 91, 46, 2, 0, 64, 126, 133, 74, 32, 83, 184, 0, 65, 174, 82, 52, 49, 18, 0, 70, 66, 130, 41, 122, 0, 3, 92, 155, 110, 0, 99, 0, 122, 36, 75, 148, 76, 59, 0, 117, 71, 193, 65, 129, 0, 115, 189, 41, 180, 27, 0, 7, 121, 47, 75, 194, 0, 4, 164, 72, 45, 84, 0, 178, 49, 141, 107, 66, 0, 70, 81, 83, 196, 53, 0, 75, 193, 109, 89, 0, 10, 11, 105, 168, 0, 26, 89, 206, 66, 32, 0, 16, 151, 141, 73, 0, 114, 119, 15, 19, 0, 95, 125, 97, 0, 112, 19, 118, 38, 0, 97, 19, 31, 11, 0, 47, 8, 139, 46, 0, 152, 151, 136, 28, 0, 101, 187, 29, 156, 0, 50, 126, 121, 133, 0, 189, 174, 177, 171, 0, 39, 110, 200, 32, 0, 14, 205, 29, 131, 0, 62, 196, 177, 0, 51, 129, 155, 162, 0, 199, 196, 109, 19, 0, 122, 82, 170, 0, 168, 98, 66, 47, 0, 128, 202, 192, 0, 145, 56, 101, 201, 0, 177, 189, 108, 64, 0, 141, 154, 90, 0
BG#1: Вектор для набора 8:
76, 22, 133, 38, 162, 197, 52, 166, 214, 199, 144, 93, 139, 192, 134, 1, 124, 1, 0, 148, 67, 90, 54, 215, 220, 66, 222, 225, 83, 220, 226, 215, 140, 167, 59, 0, 0, 0, 154, 57, 212, 232, 44, 27, 213, 191, 203, 54, 123, 164, 0, 217, 79, 230, 90, 0, 0, 150, 123, 133, 196, 125, 58, 18, 206, 131, 42, 105, 0, 223, 131, 69, 149, 173, 1, 0, 118, 63, 0, 153, 195, 59, 200, 202, 19, 146, 0, 150, 115, 12, 52, 175, 180, 111, 95, 0, 135, 195, 125, 25, 163, 88, 0, 149, 69, 7, 43, 63, 82, 50, 26, 124, 0, 37, 191, 72, 3, 178, 13, 169, 209, 0, 187, 198, 24, 20, 189, 217, 0, 192, 179, 10, 73, 36, 139, 235, 0, 68, 238, 194, 57, 175, 44, 0, 158, 169, 5, 56, 227, 0, 42, 201, 94, 108, 73, 154, 0, 25, 186, 79, 194, 99, 182, 0, 71, 14, 114, 16, 96, 0, 160, 61, 215, 47, 36, 0, 15, 18, 91, 154, 71, 0, 196, 124, 122, 128, 189, 0, 3, 53, 42, 101, 103, 0, 94, 119, 174, 212, 199, 0, 107, 37, 7, 206, 0, 207, 93, 143, 39, 0, 171, 36, 124, 41, 124, 0, 138, 61, 14, 203, 0, 43, 108, 47, 176, 0, 167, 166, 144, 0, 114, 71, 182, 181, 0, 99, 73, 26, 81, 0, 152, 45, 71, 70, 0, 140, 190, 85, 123, 0, 74, 213, 52, 43, 0, 61, 206, 42, 45, 0, 135, 231, 140, 95, 0, 218, 211, 44, 181, 0, 147, 223, 21, 154, 0, 231, 82, 161, 0, 174, 224, 52, 111, 0, 63, 226, 187, 143, 0, 74, 227, 179, 0, 151, 189, 127, 179, 0, 199, 115, 188, 0, 51, 149, 42, 38, 0, 3, 215, 216, 72, 0, 37, 132, 212, 0
BG#2: Вектор для набора 1:
251, 21, 141, 195, 196, 158, 1, 0, 113, 36, 178, 173, 114, 104, 160, 81, 0, 0, 168, 237, 214, 109, 163, 0, 0, 0, 153, 55, 167, 51, 96, 109, 112, 101, 1, 0, 129, 153, 147, 0, 39, 215, 128, 109, 31, 0, 177, 22, 133, 164, 72, 0, 180, 178, 186, 64, 209, 0, 114, 246, 38, 0, 147, 180, 77, 24, 0, 193, 215, 100, 222, 0, 243, 92, 170, 183, 0, 223, 119, 229, 0, 204, 184, 13, 49, 0, 198, 199, 138, 209, 0, 87, 40, 98, 0, 24, 103, 23, 78, 0, 71, 249, 149, 40, 0, 123, 99, 45, 0, 13, 222, 140, 0, 117, 224, 108, 0, 28, 168, 213, 0, 149, 62, 0, 181, 217, 156, 0, 114, 196, 228, 0, 104, 0, 0, 204, 114, 187, 51, 0, 113, 233, 0, 114, 213, 194, 0, 233, 191, 0, 167, 94, 67, 9, 0, 216, 217, 0, 93, 209, 218, 0, 216, 96, 171, 0, 142, 125, 164, 0, 68, 0, 243, 0, 99, 246, 20, 0, 205, 36, 0, 241, 146, 27, 0, 138, 228, 53, 0, 85, 14, 254, 0, 78, 205, 70, 0
BG#2: Вектор для набора 2:
86, 338, 258, 27, 328, 265, 1, 0, 183, 11, 213, 329, 272, 155, 89, 214, 0, 0, 382, 288, 4, 377, 72, 0, 0, 0, 318, 13, 91, 80, 173, 116, 305, 9, 1, 0, 281, 189, 23, 0, 94, 256, 328, 100, 105, 0, 356, 333, 372, 109, 215, 0, 294, 63, 362, 30, 188, 0, 206, 39, 330, 0, 29, 77, 284, 241, 0, 135, 60, 12, 14, 0, 111, 259, 328, 196, 0, 256, 218, 319, 0, 369, 302, 238, 288, 0, 275, 357, 336, 115, 0, 186, 100, 215, 0, 289, 300, 9, 365, 0, 12, 284, 112, 248, 0, 69, 368, 331, 0, 333, 324, 314, 0, 322, 121, 188, 0, 321, 75, 5, 0, 47, 37, 0, 278, 381, 240, 0, 256, 201, 311, 0, 78, 191, 0, 52, 179, 92, 213, 0, 298, 81, 0, 45, 36, 189, 0, 120, 56, 0, 311, 214, 332, 155, 0, 48, 15, 0, 185, 89, 216, 0, 13, 48, 364, 0, 194, 116, 52, 0, 16, 56, 283, 0, 102, 307, 321, 0, 356, 246, 0, 363, 334, 259, 0, 291, 164, 334, 0, 82, 225, 104, 0, 363, 131, 294, 0
BG#2: Вектор для набора 3:
104, 183, 45, 64, 143, 245, 1, 0, 295, 49, 30, 209, 24, 209, 7, 51, 0, 0, 220, 14, 158, 297, 308, 0, 0, 0, 12, 253, 82, 185, 43, 267, 193, 95, 1, 0, 17, 80, 219, 0, 141, 237, 276, 91, 275, 0, 8, 74, 247, 288, 247, 0, 231, 95, 73, 235, 102, 0, 7, 258, 80, 0, 85, 58, 319, 55, 0, 229, 194, 139, 78, 0, 189, 0, 29, 176, 0, 245, 64, 91, 0, 297, 104, 298, 139, 0, 191, 114, 232, 94, 0, 116, 255, 176, 0, 43, 39, 72, 257, 0, 109, 157, 103, 306, 0, 156, 204, 93, 0, 213, 137, 207, 0, 37, 272, 65, 0, 61, 71, 287, 0, 305, 228, 0, 136, 142, 178, 0, 291, 89, 21, 0, 284, 254, 0, 0, 202, 190, 249, 0, 159, 138, 0, 217, 116, 236, 0, 160, 97, 0, 37, 155, 219, 74, 0, 237, 222, 0, 95, 0, 299, 0, 62, 199, 235, 0, 112, 17, 276, 0, 61, 4, 103, 0, 183, 112, 171, 0, 207, 138, 0, 20, 201, 6, 0, 173, 289, 153, 0, 308, 7, 218, 0, 4, 294, 97, 0
BG#2: Вектор для набора 4:
72, 110, 23, 181, 95, 8, 1, 0, 53, 156, 115, 156, 115, 200, 29, 31, 0, 0, 152, 131, 46, 191, 91, 0, 0, 0, 185, 6, 36, 124, 124, 110, 156, 133, 1, 0, 200, 16, 101, 0, 185, 138, 170, 219, 193, 0, 123, 55, 31, 222, 209, 0, 103, 13, 105, 150, 181, 0, 147, 43, 152, 0, 2, 30, 184, 83, 0, 174, 150, 8, 56, 0, 99, 138, 110, 99, 0, 46, 217, 109, 0, 37, 113, 143, 140, 0, 36, 95, 40, 116, 0, 116, 200, 110, 0, 75, 158, 134, 97, 0, 48, 132, 206, 2, 0, 68, 16, 156, 0, 35, 138, 86, 0, 6, 20, 141, 0, 80, 43, 81, 0, 49, 1, 0, 156, 54, 134, 0, 153, 88, 63, 0, 211, 94, 0, 90, 6, 221, 6, 0, 27, 118, 0, 216, 212, 193, 0, 108, 61, 0, 106, 44, 185, 176, 0, 147, 182, 0, 108, 21, 110, 0, 71, 12, 109, 0, 29, 201, 69, 0, 91, 165, 55, 0, 1, 175, 83, 0, 40, 12, 0, 37, 97, 46, 0, 106, 181, 154, 0, 98, 35, 36, 0, 120, 101, 81, 0
BG#2: Вектор для набора 5:
275, 93, 240, 20, 275, 55, 1, 0, 158, 123, 216, 68, 260, 238, 247, 164, 0, 0, 124, 243, 183, 31, 116, 0, 0, 0, 15, 268, 237, 210, 170, 64, 180, 217, 1, 0, 276, 119, 153, 0, 193, 50, 270, 5, 111, 0, 226, 78, 73, 170, 224, 0, 272, 68, 161, 122, 197, 0, 162, 92, 127, 0, 108, 17, 175, 82, 0, 29, 1, 118, 269, 0, 96, 23, 83, 161, 0, 18, 98, 19, 0, 50, 46, 277, 66, 0, 19, 158, 87, 84, 0, 207, 40, 225, 0, 15, 117, 201, 218, 0, 116, 237, 283, 216, 0, 283, 82, 61, 0, 238, 142, 19, 0, 13, 189, 75, 0, 41, 81, 229, 0, 23, 175, 0, 207, 285, 61, 0, 227, 26, 128, 0, 183, 212, 0, 131, 222, 17, 190, 0, 64, 257, 0, 139, 117, 153, 0, 69, 62, 0, 131, 81, 160, 238, 0, 53, 236, 0, 85, 269, 37, 0, 94, 225, 192, 0, 213, 16, 246, 0, 50, 215, 175, 0, 40, 70, 142, 0, 184, 43, 0, 225, 112, 9, 0, 246, 181, 204, 0, 115, 105, 245, 0, 267, 222, 162, 0
BG#2: Вектор для набора 6:
49, 301, 326, 81, 216, 202, 1, 0, 303, 167, 145, 45, 69, 117, 139, 129, 0, 0, 139, 172, 19, 309, 270, 0, 0, 0, 310, 156, 148, 153, 118, 222, 2, 5, 1, 0, 203, 299, 343, 0, 35, 53, 304, 325, 36, 0, 153, 68, 27, 232, 76, 0, 107, 136, 265, 205, 124, 0, 202, 269, 122, 0, 127, 103, 290, 23, 0, 104, 64, 319, 215, 0, 49, 156, 71, 224, 0, 203, 81, 157, 0, 193, 221, 74, 92, 0, 327, 146, 252, 217, 0, 199, 20, 319, 0, 18, 12, 230, 125, 0, 285, 91, 245, 317, 0, 253, 50, 105, 0, 269, 107, 121, 0, 279, 252, 67, 0, 109, 19, 225, 0, 117, 236, 0, 256, 100, 267, 0, 114, 162, 127, 0, 213, 277, 0, 210, 208, 308, 106, 0, 130, 30, 0, 332, 92, 52, 0, 9, 217, 0, 129, 206, 208, 218, 0, 98, 135, 0, 186, 178, 136, 0, 286, 84, 160, 0, 265, 46, 78, 0, 162, 35, 281, 0, 278, 52, 203, 0, 196, 332, 0, 5, 211, 1, 0, 314, 300, 194, 0, 321, 203, 271, 0, 82, 70, 229, 0
BG#2: Вектор для набора 7:
84, 189, 77, 26, 112, 156, 1, 0, 170, 27, 124, 115, 141, 151, 91, 174, 0, 0, 95, 131, 118, 133, 114, 0, 0, 0, 26, 31, 89, 85, 39, 62, 190, 14, 1, 0, 103, 54, 29, 0, 28, 82, 90, 51, 200, 0, 166, 48, 146, 138, 109, 0, 8, 86, 137, 103, 30, 0, 84, 195, 26, 0, 112, 6, 37, 106, 0, 102, 147, 9, 171, 0, 58, 9, 64, 192, 0, 7, 84, 168, 0, 114, 76, 182, 85, 0, 181, 114, 7, 15, 0, 166, 114, 148, 0, 188, 85, 171, 20, 0, 109, 76, 167, 9, 0, 171, 37, 50, 0, 97, 140, 194, 0, 24, 154, 158, 0, 22, 17, 137, 0, 101, 98, 0, 132, 90, 62, 0, 77, 44, 91, 0, 47, 120, 0, 81, 71, 49, 159, 0, 150, 87, 0, 18, 94, 61, 0, 197, 192, 0, 37, 79, 106, 125, 0, 168, 40, 0, 35, 81, 0, 0, 69, 17, 83, 0, 94, 160, 40, 0, 129, 5, 135, 0, 75, 86, 164, 0, 110, 139, 0, 70, 203, 139, 0, 23, 199, 94, 0, 189, 139, 207, 0, 135, 118, 155, 0
BG#2: Вектор для набора 8:
116, 157, 79, 101, 237, 13, 1, 0, 80, 89, 38, 24, 10, 156, 226, 99, 0, 0, 83, 84, 139, 155, 158, 0, 0, 0, 72, 220, 151, 176, 154, 161, 147, 66, 1, 0, 154, 224, 214, 0, 64, 27, 108, 85, 130, 0, 87, 107, 107, 19, 65, 0, 137, 35, 237, 124, 30, 0, 20, 10, 65, 0, 231, 224, 179, 108, 0, 24, 38, 236, 174, 0, 33, 207, 105, 33, 0, 10, 30, 200, 0, 210, 30, 41, 207, 0, 65, 105, 231, 154, 0, 76, 169, 210, 0, 203, 62, 26, 95, 0, 169, 27, 94, 67, 0, 101, 213, 201, 0, 120, 29, 188, 0, 233, 123, 68, 0, 178, 200, 13, 0, 160, 230, 0, 172, 142, 126, 0, 198, 95, 216, 0, 64, 197, 0, 227, 116, 95, 61, 0, 55, 113, 0, 62, 163, 113, 0, 110, 132, 0, 65, 192, 5, 84, 0, 0, 197, 0, 227, 131, 61, 0, 24, 80, 30, 0, 158, 29, 127, 0, 132, 76, 92, 0, 70, 224, 206, 0, 22, 199, 0, 52, 95, 239, 0, 101, 206, 226, 0, 122, 102, 72, 0, 80, 63, 122, 0
Примерное представление матрицы  для базового графа #1 для набора 2 приведено ниже. Записи в одном ряду разделены запятой, а ряды разделены точкой с запятой.
для базового графа #1 для набора 2 приведено ниже. Записи в одном ряду разделены запятой, а ряды разделены точкой с запятой.
[307, 19, 50, 369, -1, 181, 216, -1, -1, 317, 288, 109, 17, 357, -1, 215, 106, -1, 242, 180, 330, 346, 1, 0, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1; 76, -1, 76, 73, 288, 144, -1, 331, 331, 178, -1, 295, 342, -1, 217, 99, 354, 114, -1, 331, -1, 112, 0, 0, 0, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1; 205, 250, 328, -1, 332, 256, 161, 267, 160, 63, 129, -1, -1, 200, 88, 53, -1, 131, 240, 205, 13, -1, -1, -1, 0, 0, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1; 276, 87, -1, 0, 275, -1, 199, 153, 56, -1, 132, 305, 231, 341, 212, -1, 304, 300, 271, -1, 39, 357, 1, -1, -1, 0, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1; 332, 181, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, 0, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1; 195, 14, -1, 115, -1, -1, -1, -1, -1, -1, -1, -1, 166, -1, -1, -1, 241, -1, -1, -1, -1, 51, 157, -1, -1, -1, -1, 0, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1; 278, -1, -1, -1, -1, -1, 257, -1, -1, -1, 1, 351, -1, 92, -1, -1, -1, 253, 18, -1, 225, -1, -1, -1, -1, -1, -1, -1, 0, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1; 9, 62, -1, -1, 316, -1, -1, 333, 290, -1, -1, -1, -1, -1, 114, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, 0, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1; 307, 179, -1, 165, -1, -1, -1, -1, -1, -1, -1, -1, 18, -1, -1, -1, 39, -1, -1, 224, -1, 368, 67, -1, 170, -1, -1, -1, -1, -1, 0, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1; 366, 232, -1, -1, -1, -1, -1, -1, -1, -1, 321, 133, -1, 57, -1, -1, -1, 303, 63, -1, 82, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, 0, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1; -1, 101, 339, -1, 274, -1, -1, 111, 383, -1, -1, -1, -1, -1, 354, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, 0, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1; 48, 102, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, 8, -1, -1, -1, 47, -1, -1, -1, -1, 188, 334, 115, -1, -1, -1, -1, -1, -1, -1, -1, -1, 0, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1; 77, 186, -1, -1, -1, -1, -1, -1, -1, -1, 174, 232, -1, 50, -1, -1, -1, -1, 74, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, 0, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1; 313, -1, -1, 177, -1, -1, -1, 266, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, 115, -1, -1, 370, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, 0, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1; 142, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, 248, -1, -1, 137, 89, 347, -1, -1, -1, 12, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, 0, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1; 241, 2, -1, -1, -1, -1, -1, -1, -1, -1, 210, -1, -1, 318, -1, -1, -1, -1, 55, -1, -1, -1, -1, -1, -1, 269, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, 0, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1; -1, 13, -1, 338, -1, -1, -1, -1, -1, -1, -1, 57, -1, -1, -1, -1, -1, -1, -1, -1, 289, -1, 57, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, 0, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1; 260, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, 303, -1, 81, 358, -1, -1, -1, 375, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, 0, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1; -1, 130, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, 163, 280, -1, -1, -1, -1, 132, 4, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, 0, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1; 145, 213, -1, -1, -1, -1, -1, 344, 242, -1, 197, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, 0, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1; 187, -1, -1, 206, -1, -1, -1, -1, -1, 264, -1, 341, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, 59, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, 0, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1; -1, 205, -1, -1, -1, 102, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, 328, -1, -1, -1, 213, 97, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, 0, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1; 30, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, 11, 233, -1, -1, -1, 22, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, 0, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1; -1, 24, 89, -1, -1, -1, -1, -1, -1, -1, 61, -1, -1, -1, -1, -1, -1, -1, 27, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, 0, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1; 298, -1, -1, 158, 235, -1, -1, -1, -1, -1, -1, 339, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, 234, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, 0, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1; -1, 72, -1, -1, -1, -1, 17, 383, -1, -1, -1, -1, -1, -1, 312, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, 0, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1; 71, -1, 81, -1, 76, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, 136, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, 0, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1; -1, 194, -1, -1, -1, -1, 194, -1, 101, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, 0, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1; 222, -1, -1, -1, 19, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, 244, -1, 274, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, 0, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1; -1, 252, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, 5, -1, -1, -1, 147, -1, -1, -1, -1, -1, -1, 78, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, 0, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1; 159, -1, -1, -1, -1, -1, -1, -1, -1, -1, 229, -1, -1, 260, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, 90, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, 0, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1; -1, 100, -1, -1, -1, -1, -1, 215, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, 258, -1, -1, 256, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, 0, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1; 102, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, 201, -1, 175, -1, -1, -1, -1, -1, -1, -1, -1, -1, 287, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, 0, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1; -1, 323, 8, -1, -1, -1, -1, -1, -1, -1, -1, 361, -1, -1, -1, -1, -1, -1, -1, -1, -1, 105, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, 0, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1; 230, -1, -1, -1, -1, -1, -1, 148, -1, -1, -1, -1, -1, -1, -1, 202, -1, 312, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, 0, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1; -1, 320, -1, -1, -1, -1, 335, -1, -1, -1, -1, -1, 2, -1, -1, -1, -1, -1, -1, -1, -1, -1, 266, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, 0, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1; 210, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, 313, 297, -1, -1, 21, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, 0, -1, -1, -1, -1, -1, -1, -1, -1, -1; -1, 269, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, 82, -1, -1, -1, -1, -1, -1, -1, -1, -1, 115, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, 0, -1, -1, -1, -1, -1, -1, -1, -1; 185, -1, -1, -1, -1, -1, -1, -1, -1, 177, 289, -1, 214, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, 0, -1, -1, -1, -1, -1, -1, -1; -1, 258, -1, 93, -1, -1, -1, 346, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, 297, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, 0, -1, -1, -1, -1, -1, -1; 175, -1, -1, -1, -1, -1, -1, -1, 37, -1, -1, -1, -1, -1, -1, -1, -1, 312, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, 0, -1, -1, -1, -1, -1; -1, 52, -1, 314, -1, -1, -1, -1, -1, 139, -1, -1, -1, -1, -1, -1, -1, -1, 288, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, 0, -1, -1, -1, -1; 113, -1, -1, -1, 14, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, 218, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, 0, -1, -1, -1; -1, 113, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, 132, -1, 114, -1, -1, -1, -1, -1, -1, 168, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, 0, -1, -1; 80, -1, -1, -1, -1, -1, -1, 78, -1, 163, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, 274, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, 0, -1; -1, 135, -1, -1, -1, -1, 149, -1, -1, -1, 15, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, 0]
Примерное представление матрицы для базового графа #2 для набора 4 приведено ниже. Записи в одном ряду разделены запятой, а ряды разделены точкой с запятой.
[72, 110, 23, 181, -1, -1, 95, -1, -1, 8, 1, 0, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1; 53, -1, -1, 156, 115, 156, 115, 200, 29, 31, -1, 0, 0, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1; 152, 131, -1, 46, 191, -1, -1, -1, 91, -1, 0, -1, 0, 0, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1; -1, 185, 6, -1, 36, 124, 124, 110, 156, 133, 1, -1, -1, 0, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1; 200, 16, -1, -1, -1, -1, -1, -1, -1, -1, -1, 101, -1, -1, 0, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1; 185, 138, -1, -1, -1, 170, -1, 219, -1, -1, -1, 193, -1, -1, -1, 0, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1; 123, -1, -1, -1, -1, 55, -1, 31, -1, 222, -1, 209, -1, -1, -1, -1, 0, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1; -1, 103, -1, -1, -1, 13, -1, 105, -1, -1, -1, 150, -1, 181, -1, -1, -1, 0, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1; 147, 43, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, 152, -1, -1, -1, -1, -1, 0, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1; -1, 2, -1, -1, -1, -1, -1, -1, 30, -1, 184, 83, -1, -1, -1, -1, -1, -1, -1, 0, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1; 174, 150, -1, -1, -1, -1, 8, 56, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, 0, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1; 99, -1, -1, -1, -1, -1, -1, 138, -1, 110, -1, -1, -1, 99, -1, -1, -1, -1, -1, -1, -1, 0, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1; -1, 46, -1, 217, -1, -1, -1, -1, -1, -1, -1, 109, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, 0, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1; 37, 113, -1, -1, -1, -1, -1, -1, 143, -1, -1, -1, -1, 140, -1, -1, -1, -1, -1, -1, -1, -1, -1, 0, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1; -1, 36, -1, -1, -1, -1, 95, -1, -1, -1, -1, 40, -1, 116, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, 0, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1; 116, -1, -1, -1, -1, -1, -1, -1, -1, -1, 200, 110, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, 0, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1; -1, 75, -1, -1, -1, -1, -1, -1, -1, 158, -1, 134, 97, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, 0, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1; -1, 48, -1, -1, -1, 132, -1, -1, -1, -1, -1, 206, 2, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, 0, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1; 68, -1, -1, -1, -1, -1, 16, 156, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, 0, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1; 35, 138, -1, -1, -1, -1, -1, -1, -1, -1, 86, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, 0, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1; -1, 6, -1, -1, 20, -1, -1, -1, -1, -1, -1, 141, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, 0, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1; 80, -1, -1, -1, -1, -1, -1, -1, 43, -1, -1, -1, -1, 81, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, 0, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1; -1, 49, 1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, 0, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1; 156, -1, -1, 54, -1, 134, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, 0, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1; -1, 153, 88, -1, -1, -1, -1, -1, -1, 63, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, 0, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1; 211, -1, -1, -1, -1, 94, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, 0, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1; -1, -1, 90, -1, -1, -1, -1, 6, -1, -1, -1, -1, 221, 6, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, 0, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1; 27, -1, -1, -1, -1, -1, 118, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, 0, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1; -1, 216, 212, -1, -1, 193, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, 0, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1; 108, -1, -1, -1, 61, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, 0, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1; -1, -1, 106, -1, -1, 44, -1, 185, -1, 176, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, 0, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1; -1, 147, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, 182, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, 0, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1; 108, -1, -1, -1, -1, 21, -1, -1, -1, -1, -1, -1, 110, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, 0, -1, -1, -1, -1, -1, -1, -1, -1, -1; -1, -1, 71, -1, -1, -1, -1, 12, -1, -1, 109, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, 0, -1, -1, -1, -1, -1, -1, -1, -1; 29, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, 201, 69, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, 0, -1, -1, -1, -1, -1, -1, -1; -1, 91, -1, -1, -1, 165, -1, -1, -1, -1, -1, 55, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, 0, -1, -1, -1, -1, -1, -1; 1, -1, 175, -1, -1, -1, -1, 83, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, 0, -1, -1, -1, -1, -1; -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, 40, -1, -1, 12, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, 0, -1, -1, -1, -1; -1, 37, -1, -1, -1, 97, -1, -1, -1, -1, -1, 46, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, 0, -1, -1, -1; 106, -1, -1, -1, -1, -1, -1, 181, -1, -1, -1, -1, 154, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, 0, -1, -1; -1, -1, 98, -1, -1, -1, -1, -1, -1, -1, 35, -1, -1, 36, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, 0, -1; -1, 120, -1, -1, -1, 101, -1, -1, -1, -1, -1, 81, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, 0]
Не только ACE-значения являются важными, но и число циклов, удовлетворяющих ACE по принципу наихудшего случая. Необходимо уменьшать это число за счет попытки добавлять ребра, удовлетворяющие более сложным ограничениям, и временного понижения этих ограничений, в случае неуспешности. Дополнительная оптимизация кода включает в себя начало с указанных ограничений, но прибавление 1 к каждому etaACE-значению. Если коэффициент сдвига, который удовлетворяет всем ограничениям, не может быть найден, то необходимо уменьшать некоторые значения etaACE для этого конкретного переменного узла на 1 (обратно к исходному заданному значению) и пробовать еще раз до тех пор, пока не будет найден коэффициент сдвига, который удовлетворяет ограничениям.
Примеры конкретных вариантов осуществления включают в себя следующее: (a) использование LDPC-кода, который удовлетворяет следующим ограничениям (dACE_sys, etaACE_sys) со следующим числом систематических переменных узлов, точно удовлетворяющих ограничению и не удовлетворяющих ограничению (dACE_sys, etaACE_sys+1); (b) использование LDPC-кода, который удовлетворяет следующим ограничениям (dACE_par, etaACE_par) со следующим числом систематических переменных узлов, точно удовлетворяющих ограничению и не удовлетворяющих ограничению (dACE_par, etaACE_par+1); (c) предыдущие варианты осуществления более чем с одним ограничением (dACE_sys, etaACE_sys) и/или (dACE_par, etaACE_par); и (d) предыдущие варианты осуществления с различными ограничениями (dACE_sys, etaACE_sys) и/или (dACE_par, etaACE_par) для различных субматриц PCM (соответствующих различным скоростям и/или различному числу сокращенных столбцов).
Примеры и варианты осуществления, описанные выше, могут обобщаться посредством блок-схем последовательности операций способа на фиг. 2 и 3.
Фиг. 2 является блок-схемой последовательности операций, иллюстрирующей примерный способ в беспроводном передающем устройстве, согласно некоторым вариантам осуществления. В конкретных вариантах осуществления, один или более этапов по фиг. 2 могут выполняться посредством сетевых элементов (например, беспроводного устройства 110, сетевого узла 120 и т.д.) сети 100, описанной относительно фиг. 1.
Способ может начинаться на этапе 210, на котором беспроводное передающее устройство получает информационные биты. Например, сетевой узел 120 может получать информационные биты (например, пользовательские данные) из верхнего уровня для беспроводной передачи в беспроводное устройство 110.
На этапе 212, беспроводное передающее устройство кодирует информационные биты с использованием PCM. PCM поднимается из базовой матрицы, и коэффициенты сдвига, используемые для подъема, выбраны с возможностью удовлетворять конкретным ACE-ограничениям, которые варьируются для различных частей PCM, согласно любому из примеров или вариантов осуществления, описанных выше. Например, сетевой узел 120 может кодировать информационные биты с использованием PCM, указываемой согласно стандартным спецификациям. PCM может описываться посредством вектора, такого как вектор 1, описанный выше. Вектор может формироваться посредством использования ACE-ограничений, которые варьируются на основе кодовой скорости, длины цикла, размера сдвига, систематических битов или битов четности.
На этапе 714, беспроводное передающее устройство передает кодированные информационные биты в беспроводное приемное устройство. Например, сетевой узел 120 может передавать кодированные информационные биты в беспроводное устройство 110.
Модификации, добавления или опускания могут вноситься в способ 200, проиллюстрированный на фиг. 2. Дополнительно, один или более этапов в способе 2 могут выполняться параллельно или в любом подходящем порядке. Этапы могут повторяться во времени при необходимости.
Фиг. 3 является блок-схемой последовательности операций, иллюстрирующей примерный способ в беспроводном приемном устройстве, согласно некоторым вариантам осуществления. В конкретных вариантах осуществления, один или более этапов по фиг. 3 могут выполняться посредством сетевых элементов (например, беспроводного устройства 110, сетевого узла 120 и т.д.) сети 100, описанной относительно фиг. 1.
Способ начинается на этапе 312, на котором беспроводное приемное устройство принимает информационные биты, кодированные с использованием PCM. Например, беспроводное устройство 110 может принимать информационные биты из сетевого узла 120. Прием кодированных информационных битов может означать прием беспроводного сигнала, соответствующего кодированным информационным битам, такого как беспроводной сигнал, передаваемый, например, на этапе 214 по фиг. 2.
На этапе 314, беспроводное приемное устройство декодирует информационные биты с использованием PCM. PCM поднята из базовой матрицы с использованием коэффициентов сдвига, выбранных с возможностью удовлетворять конкретным ACE-ограничениям, и конкретные ACE-ограничения варьируются для различных частей PCM, согласно любому из примеров или вариантов осуществления, описанных выше. Например, беспроводное устройство 110 может декодировать информационные биты с использованием PCM, указываемой согласно стандартным спецификациям. PCM может описываться посредством вектора, такого как вектор 1, описанный выше. Вектор может формироваться посредством использования ACE-ограничений, которые варьируются на основе кодовой скорости, длины цикла, размера сдвига, систематических битов или битов четности. Декодирование информационных битов может означать декодирование беспроводного сигнала, соответствующего кодированным информационным битам, приводящее к исходным кодированным информационным битам, например, на этапе 212 по фиг. 2.
Модификации, добавления или опускания могут вноситься в способ 300, проиллюстрированный на фиг. 3. Дополнительно, один или более этапов в способе 3 могут выполняться параллельно или в любом подходящем порядке. Этапы могут повторяться во времени при необходимости.
Фиг. 4A является блок-схемой, иллюстрирующей примерный вариант осуществления беспроводного устройства. Беспроводное устройство представляет собой пример беспроводных устройств 110, проиллюстрированных на фиг. 1. В конкретных вариантах осуществления, беспроводное устройство допускает кодирование и/или декодирование информационных битов с использованием PCM, поднятой из базовой матрицы с использованием коэффициентов сдвига, выбранных с возможностью удовлетворять конкретным ACE-ограничениям, и конкретные ACE-ограничения варьируются для различных частей PCM, согласно любому из примеров и вариантов осуществления, описанных выше.
Конкретные примеры беспроводного устройства включают в себя мобильный телефон, смартфон, PDA (персональное цифровое устройство), портативный компьютер (например, переносной компьютер, планшетный компьютер), датчик, модем, устройство машинной связи (MTC)/устройство межмашинной связи (M2M), встроенное в переносной компьютер устройство (LEE), установленное в переносном компьютере устройство (LME), аппаратные USB-ключи, устройство с поддержкой связи между устройствами, устройство с поддержкой связи между транспортными средствами или любое другое устройство, которое может предоставлять беспроводную связь. Беспроводное устройство включает в себя приемо-передающее устройство 910, схему 920 обработки, запоминающее устройство 930 и источник 940 мощности. В некоторых вариантах осуществления, приемо-передающее устройство 910 упрощает передачу беспроводных сигналов и прием беспроводных сигналов в/из беспроводного сетевого узла 120 (например, через антенну), схема 920 обработки выполняет инструкции, чтобы предоставлять часть или всю функциональность, описанную в данном документе как предоставляемую посредством беспроводного устройства, и запоминающее устройство 930 сохраняет инструкции, выполняемые посредством схемы 920 обработки. Источник 940 мощности подает электрическую мощность в один или более компонентов беспроводного устройства 110, таких как приемо-передающее устройство 910, схема 920 обработки и/или запоминающее устройство 930.
Схема 920 обработки включает в себя любую подходящую комбинацию аппаратных средств и программного обеспечения, реализованных в одной или более интегральных схем или модулей, чтобы выполнять инструкции и обрабатывать данные, чтобы выполнять некоторые или все описанные функции беспроводного устройства. В некоторых вариантах осуществления, схема 920 обработки может включать в себя, например, один или более компьютеров, одно или более программируемых логических устройств, один или более центральных процессоров (CPU), один или более микропроцессоров, одно или более приложений и/или другую логику и/или любую подходящую комбинацию вышеозначенного. Схема 920 обработки может включать в себя аналоговую и/или цифровую схему, выполненную с возможностью выполнять некоторые или все описанные функции беспроводного устройства 110. Например, схема 920 обработки может включать в себя резисторы, конденсаторы, индукторы, транзисторы, диоды и/или любые другие подходящие схемные компоненты.
Запоминающее устройство 930, в общем, выполнено с возможностью сохранять машиноисполняемый код и данные. Примеры запоминающего устройства 930 включают в себя компьютерное запоминающее устройство (например, оперативное запоминающее устройство (RAM) или постоянное запоминающее устройство (ROM)), носители хранения данных большой емкости (например, жесткий диск), съемные носители хранения данных (например, компакт-диск (CD) или цифровой видеодиск (DVD)) и/или любые другие энергозависимые или энергонезависимые, энергонезависимые машиночитаемые и/или машиноисполняемые запоминающие устройства, которые сохраняют информацию.
Источник 940 мощности, в общем, выполнен с возможностью подавать электрическую мощность в компоненты беспроводного устройства 110. Источник 940 мощности может включать в себя любой подходящий тип аккумулятора, к примеру, литий-ионный, литий-воздушный, литий-полимерный, никель-кадмиевый, никель-металлогидридный или любой другой подходящий тип аккумулятора для подачи мощности в беспроводное устройство.
Другие варианты осуществления беспроводного устройства могут включать в себя дополнительные компоненты (помимо компонентов, показанных на фиг. 4A), отвечающих за предоставление конкретных аспектов функциональности беспроводного устройства, включающей в себя любое из функциональности, описанной выше, и/или любой дополнительной функциональности (включающей в себя любую функциональность, необходимую для того, чтобы поддерживать решение, описанное выше).
Фиг. 4B является блок-схемой, иллюстрирующей примерные компоненты беспроводного устройства 110. Компоненты могут включать в себя приемный модуль 950, модуль 952 кодирования/декодирования и передающий модуль 954.
Приемный модуль 950 может выполнять функции приема беспроводного устройства 110. Например, приемный модуль 950 может принимать кодированные информационные биты. В конкретных вариантах осуществления, приемный модуль 950 может включать в себя или быть включен в схему 920 обработки. В конкретных вариантах осуществления, приемный модуль 950 может обмениваться данными с модулем 952 кодирования/декодирования и передающим модулем 954.
Модуль 952 кодирования/декодирования может выполнять функции кодирования и декодирования беспроводного устройства 110. Например, модуль 952 кодирования/декодирования может кодировать или декодировать информационные биты с использованием PCM. PCM поднимается из базовой матрицы, и коэффициенты сдвига, используемые для подъема, выбраны с возможностью удовлетворять конкретным ACE-ограничениям, которые варьируются для различных частей PCM, согласно любому из примеров и вариантов осуществления, описанных выше. В конкретных вариантах осуществления, модуль 952 кодирования/декодирования может включать в себя или быть включен в схему 920 обработки. В конкретных вариантах осуществления, модуль 952 кодирования/декодирования может обмениваться данными с приемным модулем 950 и передающим модулем 954.
Некоторые варианты осуществления, такие как устройства с низкой сложностью, могут включать в себя только модуль кодирования или модуль декодирования, но не оба из них. Хотя функциональные модули проиллюстрированы в качестве одного модуля, схема кодирования содержит часть цепочки передающих устройств, и схема декодирования содержит часть цепочки приемных устройств.
Передающий модуль 954 может выполнять функции передачи беспроводного устройства 110. Например, передающий модуль 954 может передавать кодированные информационные биты. В конкретных вариантах осуществления, передающий модуль 954 может включать в себя или быть включен в схему 920 обработки. В конкретных вариантах осуществления, передающий модуль 954 может обмениваться данными с приемным модулем 950 и модулем 952 кодирования/декодирования.
Фиг. 5A является блок-схемой, иллюстрирующей примерный вариант осуществления сетевого узла. Сетевой узел представляет собой пример сетевого узла 120, проиллюстрированного на фиг. 1. В конкретных вариантах осуществления, сетевой узел допускает кодирование и/или декодирование информационных битов с использованием PCM, поднятой из базовой матрицы с использованием коэффициентов сдвига, выбранных с возможностью удовлетворять конкретным ACE-ограничениям, и конкретные ACE-ограничения варьируются для различных частей PCM, согласно любому из примеров и вариантов осуществления, описанных выше.
Сетевой узел 120 может представлять собой усовершенствованный узел B, узел B, gNB, базовую станцию, точку беспроводного доступа (например, точку Wi-Fi-доступа), узел с низким уровнем мощности, базовую приемо-передающую станцию (BTS), точку или узел передачи, удаленный RF-блок (RRU), удаленную радиоголовку (RRH) или другой узел радиодоступа. Сетевой узел включает в себя, по меньшей мере, одно приемо-передающее устройство 1010, по меньшей мере, одну схему 1020 обработки, по меньшей мере, одно запоминающее устройство 1030 и, по меньшей мере, один сетевой интерфейс 1040. Приемо-передающее устройство 1010 упрощает передачу беспроводных сигналов и прием беспроводных сигналов в/из беспроводного устройства, такого как беспроводные устройства 110 (например, через антенну); схема 1020 обработки выполняет инструкции, чтобы предоставлять часть или всю функциональность, описанную выше как предоставляемую посредством сетевого узла 120; запоминающее устройство 1030 сохраняет инструкции, выполняемые посредством схемы 1020 обработки; и сетевой интерфейс 1040 передает сигналы во внутренние интерфейсные сетевые компоненты, такие как шлюз, коммутатор, маршрутизатор, Интернет, коммутируемая телефонная сеть общего пользования (PSTN), контроллер и/или другие сетевые узлы 120. Схема 1020 обработки и запоминающее устройство 1030 могут иметь идентичные типы, как описано относительно схемы 920 обработки и запоминающего устройства 930 по фиг. 4A выше.
В некоторых вариантах осуществления, сетевой интерфейс 1040 функционально соединяется со схемой 1020 обработки и означает любое подходящее устройство, выполненное с возможностью принимать ввод для сетевого узла 120, отправлять вывод из сетевого узла 120, выполнять подходящую обработку ввода или вывода либо и того, и другого, обмениваться данными с другими устройствами или любую комбинацию предыдущего. Сетевой интерфейс 1040 включает в себя соответствующие аппаратные средства (например, порт, модем, сетевую интерфейсную плату и т.д.) и программное обеспечение, включающее в себя характеристики преобразования протоколов и обработки данных, чтобы обмениваться данными через сеть.
Другие варианты осуществления сетевого узла 120 могут включать в себя дополнительные компоненты (помимо компонентов, показанных на фиг. 5A), отвечающие за предоставление конкретных аспектов функциональности сетевого узла, включающей в себя любое из функциональности, описанной выше, и/или любой дополнительной функциональности (включающей в себя любую функциональность, необходимую для того, чтобы поддерживать решение, описанное выше). Всевозможные типы сетевых узлов могут включать в себя компоненты, имеющие идентичные физические аппаратные средства, но сконфигурированные (например, через программирование) с возможностью поддерживать различные технологии радиодоступа, или могут представлять частично или полностью различные физические компоненты.
Фиг. 5B является блок-схемой, иллюстрирующей примерные компоненты сетевого узла 120. Компоненты могут включать в себя приемный модуль 1050, модуль 1052 кодирования/декодирования и передающий модуль 1054.
Приемный модуль 1050 может выполнять функции приема сетевого узла 120. Например, приемный модуль 1050 может принимать кодированные информационные биты. В конкретных вариантах осуществления, приемный модуль 1050 может включать в себя или быть включен в схему 1020 обработки. В конкретных вариантах осуществления, приемный модуль 1050 может обмениваться данными с модулем 1052 кодирования/декодирования и передающим модулем 1054.
Модуль 1052 кодирования/декодирования может выполнять функции кодирования и декодирования сетевого узла 120. Например, модуль 1052 кодирования/декодирования может кодировать или декодировать информационные биты с использованием PCM. PCM поднимается из базовой матрицы, и коэффициенты сдвига, используемые для подъема, выбраны с возможностью удовлетворять конкретным ACE-ограничениям, которые варьируются для различных частей PCM, согласно любому из примеров и вариантов осуществления, описанных выше. В конкретных вариантах осуществления, модуль 1052 кодирования/декодирования может включать в себя или быть включен в схему 1020 обработки. В конкретных вариантах осуществления, модуль 1052 кодирования/декодирования может обмениваться данными с приемным модулем 1050 и передающим модулем 1054.
Некоторые варианты осуществления, такие как устройства с низкой сложностью, могут включать в себя только модуль кодирования или модуль декодирования, но не оба из них. Хотя функциональные модули проиллюстрированы в качестве одного модуля, схема кодирования содержит часть цепочки передающих устройств, и схема декодирования содержит часть цепочки приемных устройств.
Передающий модуль 1054 может выполнять функции передачи сетевого узла 120. Например, передающий модуль 1054 может передавать кодированные информационные биты. В конкретных вариантах осуществления, передающий модуль 1054 может включать в себя или быть включен в схему 1020 обработки. В конкретных вариантах осуществления, передающий модуль 1054 может обмениваться данными с приемным модулем 1050 и модулем 1052 определения местоположений сигналов.
Модификации, добавления или опускания могут вноситься в системы и оборудование, раскрытые в данном документе, без отступления от объема изобретения. Компоненты систем и оборудования могут быть интегрированными или разделенными. Кроме того, операции систем и оборудования могут выполняться посредством большего числа, меньшего числа или других компонентов. Дополнительно, операции систем и оборудования могут выполняться с использованием любой подходящей логики, содержащей программное обеспечение, аппаратные средства и/или другую логику. При использовании в этом документе, "каждый" означает каждый элемент набора или каждый элемент поднабора набора.
Модификации, добавления или опускания могут вноситься в способы, раскрытые в данном документе, без отступления от объема изобретения. Способы могут включать в себя большее число, меньшее число или другие этапы. Дополнительно, этапы могут выполняться в любом подходящем порядке.
Хотя это раскрытие сущности описывается с точки зрения конкретных вариантов осуществления, изменения и перестановки вариантов осуществления должны становиться очевидными для специалистов в данной области техники. Соответственно, вышеприведенное описание вариантов осуществления не ограничивает это раскрытие сущности. Другие изменения, подстановки и изменения являются возможными без отступления от сущности и объема этого раскрытия сущности, заданного посредством нижеприведенной формулы изобретения.
Сокращения, используемые в вышеприведенном описании, включают в себя:
3GPP – Партнерский проект третьего поколения
ACE – EMD с аппроксимированным циклом
BTS – базовая приемо-передающая станция
D2D – между устройствами
EMD – внешняя степень сообщений
eNB – усовершенствованный узел B
FDD – дуплекс с частотным разделением каналов
LDPC – разреженный контроль по четности
LTE – стандарт долгосрочного развития
MAC – управление доступом к среде
M2M – межмашинный
MIMO – со многими входами и многими выходами
MTC – машинная связь
NR – новый стандарт радиосвязи
OFDM – мультиплексирование с ортогональным частотным разделением каналов
PCM – матрица контроля по четности
PDSCH – физический совместно используемый канал нисходящей линии связи
PUCCH – физический канал управления восходящей линии связи
RAN – сеть радиодоступа
RAT – технология радиодоступа
RBS – базовая радиостанция
RNC – контроллер радиосети
RRC – уровень управления радиоресурсами
RRH – удаленная радиоголовка
RRH – удаленный радиоблок
SINR – отношение "сигнал-к-помехам-и-шуму"
TDD – дуплекс с временным разделением каналов
UE – абонентское устройство
UL – восходящая линия связи
URLLC – стандарт сверхнадежной связи с низкой задержкой
UTRAN – сеть универсального наземного радиодоступа
WAN – беспроводная сеть доступа
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ДЛЯ ВЫПОЛНЕНИЯ КОДИРОВАНИЯ НА ОСНОВЕ МАТРИЦЫ КОНТРОЛЯ ПО ЧЕТНОСТИ LDPC-КОДА В СИСТЕМЕ БЕСПРОВОДНОЙ СВЯЗИ И ТЕРМИНАЛ С ЕГО ИСПОЛЬЗОВАНИЕМ | 2018 |
|
RU2730444C1 |
| СПОСОБ ДЛЯ ВЫПОЛНЕНИЯ КОДИРОВАНИЯ НА ОСНОВЕ МАТРИЦЫ КОНТРОЛЯ ПО ЧЕТНОСТИ КОДА РАЗРЕЖЕННОГО КОНТРОЛЯ ПО ЧЕТНОСТИ (LDPC) В СИСТЕМЕ БЕСПРОВОДНОЙ СВЯЗИ И ТЕРМИНАЛ С ЕГО ИСПОЛЬЗОВАНИЕМ | 2018 |
|
RU2719688C1 |
| ВЫСОКОСКОРОСТНЫЕ ДЛИННЫЕ LDPC КОДЫ | 2017 |
|
RU2733826C1 |
| СПОСОБЫ СОГЛАСОВАНИЯ СКОРОСТИ ДЛЯ LDPC-КОДОВ | 2017 |
|
RU2730434C1 |
| СПОСОБ ОБРАБОТКИ ИНФОРМАЦИИ И УСТРОЙСТВО СВЯЗИ | 2017 |
|
RU2740151C1 |
| АППАРАТУРА, СПОСОБ ОБРАБОТКИ ИНФОРМАЦИИ И АППАРАТУРА СВЯЗИ | 2018 |
|
RU2758968C2 |
| КОДИРОВАНИЕ И ДЕКОДИРОВАНИЕ LDPC ПАКЕТОВ ПЕРЕМЕННЫХ РАЗМЕРОВ | 2008 |
|
RU2443053C2 |
| УЛУЧШЕННОЕ ВЫКАЛЫВАНИЕ И СТРУКТУРА КОДА С МАЛОЙ ПЛОТНОСТЬЮ ПРОВЕРОК НА ЧЕТНОСТЬ (LDPC) | 2017 |
|
RU2718171C1 |
| HARQ-ОБРАБОТКА ДЛЯ УЗЛОВ С ПЕРЕМЕННЫМИ ВРЕМЕНАМИ ОБРАБОТКИ | 2018 |
|
RU2737481C1 |
| СПОСОБ ПЕРЕДАЧИ УПРАВЛЯЮЩЕГО СООБЩЕНИЯ ПО ВОСХОДЯЩЕЙ ЛИНИИ СВЯЗИ | 2010 |
|
RU2538180C2 |


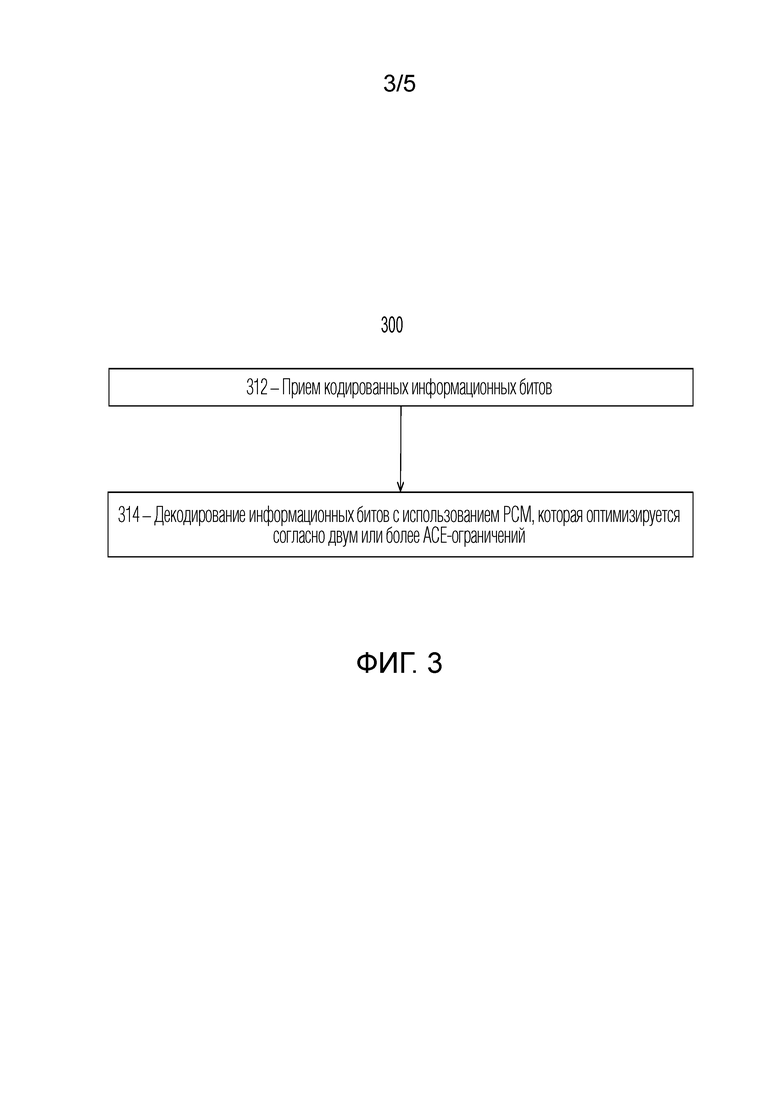
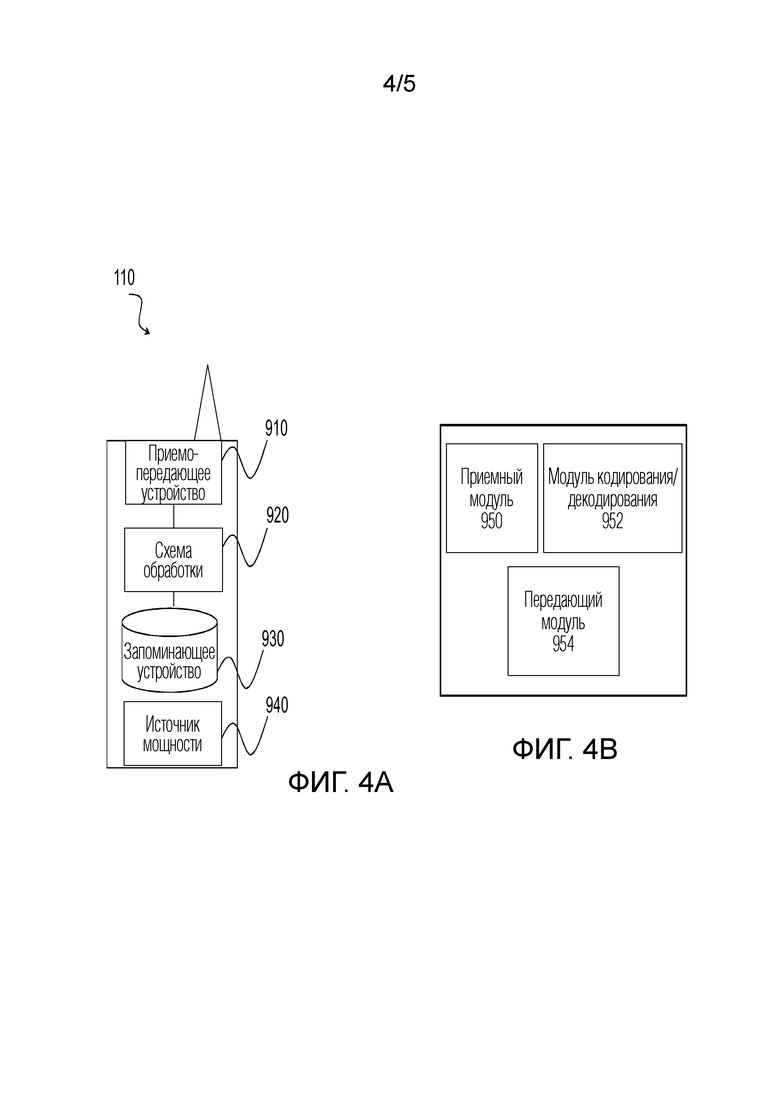
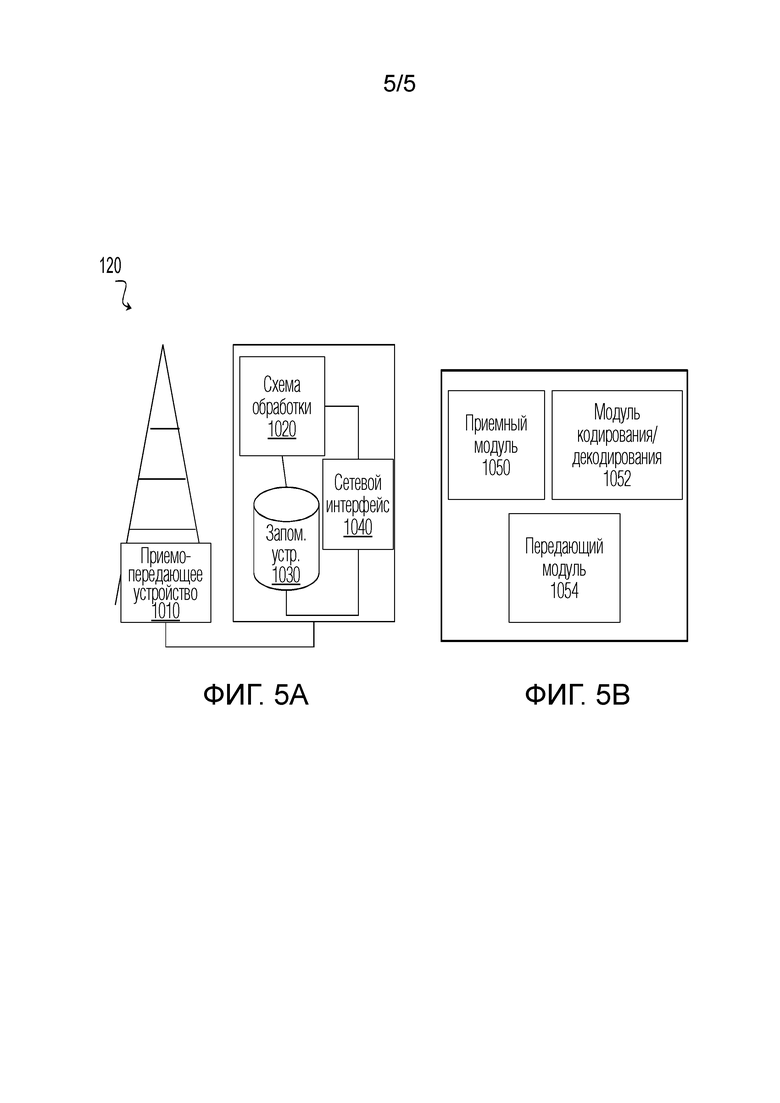
Изобретение относится к беспроводной связи. Технический результат – определение циклических сдвигов, обеспечивающих высокие значения внешней степени сообщений (EMD) c аппроксимированным циклом (ACE). Согласно некоторым вариантам осуществления способ для использования в беспроводном передающем устройстве сети беспроводной связи содержит кодирование информационных битов с использованием матрицы контроля по четности (PCM) и передачу кодированных информационных битов в беспроводное приемное устройство. Матрица контроля по четности (PCM) оптимизируется согласно двум или более ограничениям по внешней степени сообщений с аппроксимированным циклом (ACE). В некоторых вариантах осуществления первая часть PCM оптимизируется согласно первому ACE-ограничению и вторая часть PCM оптимизируется согласно второму ACE-ограничению. 8 н. и 8 з.п. ф-лы, 7 ил., 2 табл.
1. Беспроводное передающее устройство (110, 120), содержащее схему (920, 1020) обработки, выполненную с возможностью:
- кодировать информационные биты с использованием матрицы контроля по четности (PCM) кода разреженного контроля по четности (LDPC), причем PCM сегментируется на квадратные субматрицы размера ZxZ и описывается посредством базовой матрицы и вектора сдвига с использованием размера сдвига Z=3*2', где j составляет одно из 0, 1, 2, 3, 4, 5, 6 и 7; и
- передавать кодированные информационные биты в беспроводное приемное устройство (110, 120),
при этом базовая матрица имеет одну запись для каждой субматрицы ZxZ, причем запись равна 0 согласно субматрице, представляющей собой нулевую матрицу, и причем запись равна 1 согласно субматрице, представляющей собой циклическую перестановочную матрицу, полученную из единичной матрицы ZxZ посредством циклического сдвига столбцов вправо на k элементов,
при этом базовая матрица имеет размер 46×68 и ненулевые записи в базовой матрице описываются посредством троек (e, r, c), обозначающих то, что ненулевая запись с номером e находится в строке r и столбце c базовой матрицы, причем тройки задаются следующим образом:
(1, 1, 1) (2, 1, 2) (3, 1, 3) (4, 1, 4) (5, 1, 6) (6, 1, 7) (7, 1, 10) (8, 1, 11) (9, 1, 12) (10, 1, 13) (11, 1, 14) (12, 1, 16) (13, 1, 17) (14, 1, 19) (15, 1, 20) (16, 1, 21) (17, 1, 22) (18, 1, 23) (19, 1, 24) (20, 2, 1) (21, 2, 3) (22, 2, 4) (23, 2, 5) (24, 2, 6) (25, 2, 8) (26, 2, 9) (27, 2, 10) (28, 2, 12) (29, 2, 13) (30, 2, 15) (31, 2, 16) (32, 2, 17) (33, 2, 18) (34, 2, 20) (35, 2, 22) (36, 2, 23) (37, 2, 24) (38, 2, 25) (39, 3, 1) (40, 3, 2) (41, 3, 3) (42, 3, 5) (43, 3, 6) (44, 3, 7) (45, 3, 8) (46, 3, 9) (47, 3, 10) (48, 3, 11) (49, 3, 14) (50, 3, 15) (51, 3, 16) (52, 3, 18) (53, 3, 19) (54, 3, 20) (55, 3, 21) (56, 3, 25) (57, 3, 26) (58, 4, 1) (59, 4, 2) (60, 4, 4) (61, 4, 5) (62, 4, 7) (63, 4, 8) (64, 4, 9) (65, 4, 11) (66, 4, 12) (67, 4, 13) (68, 4, 14) (69, 4, 15) (70, 4, 17) (71, 4, 18) (72, 4, 19) (73, 4, 21) (74, 4, 22) (75, 4, 23) (76, 4, 26) (77, 5, 1) (78, 5, 2) (79, 5, 27) (80, 6, 1) (81, 6, 2) (82, 6, 4) (83, 6, 13) (84, 6, 17) (85, 6, 22) (86, 6, 23) (87, 6, 28) (88, 7, 1) (89, 7, 7) (90, 7, 11) (91, 7, 12) (92, 7, 14) (93, 7, 18) (94, 7, 19) (95, 7, 21) (96, 7, 29) (97, 8, 1) (98, 8, 2) (99, 8, 5) (100, 8, 8) (101, 8, 9) (102, 8, 15) (103, 8, 30) (104, 9, 1) (105, 9, 2) (106, 9, 4) (107, 9, 13) (108, 9, 17) (109, 9, 20) (110, 9, 22) (111, 9, 23) (112, 9, 25) (113, 9, 31) (114, 10, 1) (115, 10, 2) (116, 10, 11) (117, 10, 12) (118, 10, 14) (119, 10, 18) (120, 10, 19) (121, 10, 21) (122, 10, 32) (123, 11, 2) (124, 11, 3) (125, 11, 5) (126, 11, 8) (127, 11, 9) (128, 11, 15) (129, 11, 33) (130, 12, 1) (131, 12, 2) (132, 12, 13) (133, 12, 17) (134, 12, 22) (135, 12, 23) (136, 12, 24) (137, 12, 34) (138, 13, 1) (139, 13, 2) (140, 13, 11) (141, 13, 12) (142, 13, 14) (143, 13, 19) (144, 13, 35) (145, 14, 1) (146, 14, 4) (147, 14, 8) (148, 14, 21) (149, 14, 24) (150, 14, 36) (151, 15, 1) (152, 15, 13) (153, 15, 16) (154, 15, 17) (155, 15, 18) (156, 15, 22) (157, 15, 37) (158, 16, 1) (159, 16, 2) (160, 16, 11) (161, 16, 14) (162, 16, 19) (163, 16, 26) (164, 16, 38) (165, 17, 2) (166, 17, 4) (167, 17, 12) (168, 17, 21) (169, 17, 23) (170, 17, 39) (171, 18, 1) (172, 18, 15) (173, 18, 17) (174, 18, 18) (175, 18, 22) (176, 18, 40) (177, 19, 2) (178, 19, 13) (179, 19, 14) (180, 19, 19) (181, 19, 20) (182, 19, 41) (183, 20, 1) (184, 20, 2) (185, 20, 8) (186, 20, 9) (187, 20, 11) (188, 20, 42) (189, 21, 1) (190, 21, 4) (191, 21, 10) (192, 21, 12) (193, 21, 23) (194, 21, 43) (195, 22, 2) (196, 22, 6) (197, 22, 17) (198, 22, 21) (199, 22, 22) (200, 22, 44) (201, 23, 1) (202, 23, 13) (203, 23, 14) (204, 23, 18) (205, 23, 45) (206, 24, 2) (207, 24, 3) (208, 24, 11) (209, 24, 19) (210, 24, 46) (211, 25, 1) (212, 25, 4) (213, 25, 5) (214, 25, 12) (215, 25, 23) (216, 25, 47) (217, 26, 2) (218, 26, 7) (219, 26, 8) (220, 26, 15) (221, 26, 48) (222, 27, 1) (223, 27, 3) (224, 27, 5) (225, 27, 16) (226, 27, 49) (227, 28, 2) (228, 28, 7) (229, 28, 9) (230, 28, 50) (231, 29, 1) (232, 29, 5) (233, 29, 20) (234, 29, 22) (235, 29, 51) (236, 30, 2) (237, 30, 15) (238, 30, 19) (239, 30, 26) (240, 30, 52) (241, 31, 1) (242, 31, 11) (243, 31, 14) (244, 31, 25) (245, 31, 53) (246, 32, 2) (247, 32, 8) (248, 32, 23) (249, 32, 26) (250, 32, 54) (251, 33, 1) (252, 33, 13) (253, 33, 15) (254, 33, 25) (255, 33, 55) (256, 34, 2) (257, 34, 3) (258, 34, 12) (259, 34, 22) (260, 34, 56) (261, 35, 1) (262, 35, 8) (263, 35, 16) (264, 35, 18) (265, 35, 57) (266, 36, 2) (267, 36, 7) (268, 36, 13) (269, 36, 23) (270, 36, 58) (271, 37, 1) (272, 37, 15) (273, 37, 16) (274, 37, 19) (275, 37, 59) (276, 38, 2) (277, 38, 14) (278, 38, 24) (279, 38, 60) (280, 39, 1) (281, 39, 10) (282, 39, 11) (283, 39, 13) (284, 39, 61) (285, 40, 2) (286, 40, 4) (287, 40, 8) (288, 40, 20) (289, 40, 62) (290, 41, 1) (291, 41, 9) (292, 41, 18) (293, 41, 63) (294, 42, 2) (295, 42, 4) (296, 42, 10) (297, 42, 19) (298, 42, 64) (299, 43, 1) (300, 43, 5) (301, 43, 25) (302, 43, 65) (303, 44, 2) (304, 44, 17) (305, 44, 19) (306, 44, 26) (307, 44, 66) (308, 45, 1) (309, 45, 8) (310, 45, 10) (311, 45, 23) (312, 45, 67) (313, 46, 2) (314, 46, 7) (315, 46, 11) (316, 46, 68),
при этом для ненулевой записи с номером e число k задается посредством коэффициента сдвига, предоставленного посредством mod(Ve, Z), причем Ve обозначает e-й элемент вектора сдвига и вектор сдвига представляет собой следующее:
[307, 19, 50, 369, 181, 216, 317, 288, 109, 17, 357, 215, 106, 242, 180, 330, 346, 1, 0, 76, 76, 73, 288, 144, 331, 331, 178, 295, 342, 217, 99, 354, 114, 331, 112, 0, 0, 0, 205, 250, 328, 332, 256, 161, 267, 160, 63, 129, 200, 88, 53, 131, 240, 205, 13, 0, 0, 276, 87, 0, 275, 199, 153, 56, 132, 305, 231, 341, 212, 304, 300, 271, 39, 357, 1, 0, 332, 181, 0, 195, 14, 115, 166, 241, 51, 157, 0, 278, 257, 1, 351, 92, 253, 18, 225, 0, 9, 62, 316, 333, 290, 114, 0, 307, 179, 165, 18, 39, 224, 368, 67, 170, 0, 366, 232, 321, 133, 57, 303, 63, 82, 0, 101, 339, 274, 111, 383, 354, 0, 48, 102, 8, 47, 188, 334, 115, 0, 77, 186, 174, 232, 50, 74, 0, 313, 177, 266, 115, 370, 0, 142, 248, 137, 89, 347, 12, 0, 241, 2, 210, 318, 55, 269, 0, 13, 338, 57, 289, 57, 0, 260, 303, 81, 358, 375, 0, 130, 163, 280, 132, 4, 0, 145, 213, 344, 242, 197, 0, 187, 206, 264, 341, 59, 0, 205, 102, 328, 213, 97, 0, 30, 11, 233, 22, 0, 24, 89, 61, 27, 0, 298, 158, 235, 339, 234, 0, 72, 17, 383, 312, 0, 71, 81, 76, 136, 0, 194, 194, 101, 0, 222, 19, 244, 274, 0, 252, 5, 147, 78, 0, 159, 229, 260, 90, 0, 100, 215, 258, 256, 0, 102, 201, 175, 287, 0, 323, 8, 361, 105, 0, 230, 148, 202, 312, 0, 320, 335, 2, 266, 0, 210, 313, 297, 21, 0, 269, 82, 115, 0, 185, 177, 289, 214, 0, 258, 93, 346, 297, 0, 175, 37, 312, 0, 52, 314, 139, 288, 0, 113, 14, 218, 0, 113, 132, 114, 168, 0, 80, 78, 163, 274, 0, 135, 149, 15, 0].
2. Беспроводное передающее устройство (110, 120), содержащее схему (920, 1020) обработки, выполненную с возможностью:
- кодировать информационные биты с использованием матрицы контроля по четности (PCM) кода разреженного контроля по четности (LDPC), причем PCM сегментируется на квадратные субматрицы размера ZxZ и описывается посредством базовой матрицы и вектора сдвига с использованием размера сдвига Z=7*2', где j составляет одно из 0, 1, 2, 3, 4 и 5; и
- передавать кодированные информационные биты в беспроводное приемное устройство (110, 120),
при этом базовая матрица имеет одну запись для каждой субматрицы ZxZ, причем запись равна 0 согласно субматрице, представляющей собой нулевую матрицу, и причем запись равна 1 согласно субматрице, представляющей собой циклическую перестановочную матрицу, полученную из единичной матрицы ZxZ посредством сдвига столбцов вправо на k элементов,
при этом базовая матрица имеет размер 42×52 и ненулевые записи в базовой матрице описываются посредством троек (e, r, c), обозначающих то, что ненулевая запись с номером e находится в строке r и столбце c базовой матрицы, причем тройки задаются следующим образом:
(1, 1, 1) (2, 1, 2) (3, 1, 3) (4, 1, 4) (5, 1, 7) (6, 1, 10) (7, 1, 11) (8, 1, 12) (9, 2, 1) (10, 2, 4) (11, 2, 5) (12, 2, 6) (13, 2, 7) (14, 2, 8) (15, 2, 9) (16, 2, 10) (17, 2, 12) (18, 2, 13) (19, 3, 1) (20, 3, 2) (21, 3, 4) (22, 3, 5) (23, 3, 9) (24, 3, 11) (25, 3, 13) (26, 3, 14) (27, 4, 2) (28, 4, 3) (29, 4, 5) (30, 4, 6) (31, 4, 7) (32, 4, 8) (33, 4, 9) (34, 4, 10) (35, 4, 11) (36, 4, 14) (37, 5, 1) (38, 5, 2) (39, 5, 12) (40, 5, 15) (41, 6, 1) (42, 6, 2) (43, 6, 6) (44, 6, 8) (45, 6, 12) (46, 6, 16) (47, 7, 1) (48, 7, 6) (49, 7, 8) (50, 7, 10) (51, 7, 12) (52, 7, 17) (53, 8, 2) (54, 8, 6) (55, 8, 8) (56, 8, 12) (57, 8, 14) (58, 8, 18) (59, 9, 1) (60, 9, 2) (61, 9, 13) (62, 9, 19) (63, 10, 2) (64, 10, 9) (65, 10, 11) (66, 10, 12) (67, 10, 20) (68, 11, 1) (69, 11, 2) (70, 11, 7) (71, 11, 8) (72, 11, 21) (73, 12, 1) (74, 12, 8) (75, 12, 10) (76, 12, 14) (77, 12, 22) (78, 13, 2) (79, 13, 4) (80, 13, 12) (81, 13, 23) (82, 14, 1) (83, 14, 2) (84, 14, 9) (85, 14, 14) (86, 14, 24) (87, 15, 2) (88, 15, 7) (89, 15, 12) (90, 15, 14) (91, 15, 25) (92, 16, 1) (93, 16, 11) (94, 16, 12) (95, 16, 26) (96, 17, 2) (97, 17, 10) (98, 17, 12) (99, 17, 13) (100, 17, 27) (101, 18, 2) (102, 18, 6) (103, 18, 12) (104, 18, 13) (105, 18, 28) (106, 19, 1) (107, 19, 7) (108, 19, 8) (109, 19, 29) (110, 20, 1) (111, 20, 2) (112, 20, 11) (113, 20, 30) (114, 21, 2) (115, 21, 5) (116, 21, 12) (117, 21, 31) (118, 22, 1) (119, 22, 9) (120, 22, 14) (121, 22, 32) (122, 23, 2) (123, 23, 3) (124, 23, 33) (125, 24, 1) (126, 24, 4) (127, 24, 6) (128, 24, 34) (129, 25, 2) (130, 25, 3) (131, 25, 10) (132, 25, 35) (133, 26, 1) (134, 26, 6) (135, 26, 36) (136, 27, 3) (137, 27, 8) (138, 27, 13) (139, 27, 14) (140, 27, 37) (141, 28, 1) (142, 28, 7) (143, 28, 38) (144, 29, 2) (145, 29, 3) (146, 29, 6) (147, 29, 39) (148, 30, 1) (149, 30, 5) (150, 30, 40) (151, 31, 3) (152, 31, 6) (153, 31, 8) (154, 31, 10) (155, 31, 41) (156, 32, 2) (157, 32, 14) (158, 32, 42) (159, 33, 1) (160, 33, 6) (161, 33, 13) (162, 33, 43) (163, 34, 3) (164, 34, 8) (165, 34, 11) (166, 34, 44) (167, 35, 1) (168, 35, 13) (169, 35, 14) (170, 35, 45) (171, 36, 2) (172, 36, 6) (173, 36, 12) (174, 36, 46) (175, 37, 1) (176, 37, 3) (177, 37, 8) (178, 37, 47) (179, 38, 11) (180, 38, 14) (181, 38, 48) (182, 39, 2) (183, 39, 6) (184, 39, 12) (185, 39, 49) (186, 40, 1) (187, 40, 8) (188, 40, 13) (189, 40, 50) (190, 41, 3) (191, 41, 11) (192, 41, 14) (193, 41, 51) (194, 42, 2) (195, 42, 6) (196, 42, 12) (197, 42, 52),
при этом для ненулевой записи с номером e число k задается посредством коэффициента сдвига, предоставленного посредством mod(Ve, Z), причем Ve обозначает e-й элемент вектора сдвига и вектор сдвига представляет собой следующее:
[72, 110, 23, 181, 95, 8, 1, 0, 53, 156, 115, 156, 115, 200, 29, 31, 0, 0, 152, 131, 46, 191, 91, 0, 0, 0, 185, 6, 36, 124, 124, 110, 156, 133, 1, 0, 200, 16, 101, 0, 185, 138, 170, 219, 193, 0, 123, 55, 31, 222, 209, 0, 103, 13, 105, 150, 181, 0, 147, 43, 152, 0, 2, 30, 184, 83, 0, 174, 150, 8, 56, 0, 99, 138, 110, 99, 0, 46, 217, 109, 0, 37, 113, 143, 140, 0, 36, 95, 40, 116, 0, 116, 200, 110, 0, 75, 158, 134, 97, 0, 48, 132, 206, 2, 0, 68, 16, 156, 0, 35, 138, 86, 0, 6, 20, 141, 0, 80, 43, 81, 0, 49, 1, 0, 156, 54, 134, 0, 153, 88, 63, 0, 211, 94, 0, 90, 6, 221, 6, 0, 27, 118, 0, 216, 212, 193, 0, 108, 61, 0, 106, 44, 185, 176, 0, 147, 182, 0, 108, 21, 110, 0, 71, 12, 109, 0, 29, 201, 69, 0, 91, 165, 55, 0, 1, 175, 83, 0, 40, 12, 0, 37, 97, 46, 0, 106, 181, 154, 0, 98, 35, 36, 0, 120, 101, 81, 0].
3. Беспроводное передающее устройство (110, 120) по п. 1 или 2,
при этом беспроводное передающее устройство (110, 120) представляет собой сетевой узел.
4. Беспроводное передающее устройство (110, 120) по п. 1 или 2,
при этом беспроводное передающее устройство (110, 120) представляет собой беспроводное устройство.
5. Беспроводное приемное устройство (110, 120), содержащее схему (920, 1020) обработки, выполненную с возможностью:
- принимать кодированные информационные биты из беспроводного передающего устройства (110, 120); и
- декодировать информационные биты с использованием матрицы контроля по четности (PCM) кода разреженного контроля по четности (LDPC), причем PCM сегментируется на квадратные субматрицы размера ZxZ и описывается посредством базовой матрицы и вектора сдвига с использованием размера сдвига Z=3*2', где j составляет одно из 0, 1, 2, 3, 4, 5, 6 и 7,
при этом базовая матрица имеет одну запись для каждой субматрицы ZxZ, причем запись равна 0 согласно субматрице, представляющей собой нулевую матрицу, и причем запись равна 1 согласно субматрице, представляющей собой циклическую перестановочную матрицу, полученную из единичной матрицы ZxZ посредством сдвига столбцов вправо на k элементов,
при этом базовая матрица имеет размер 46×68 и ненулевые записи в базовой матрице описываются посредством троек (e, r, c), обозначающих то, что ненулевая запись с номером e находится в строке r и столбце c базовой матрицы, причем тройки задаются следующим образом:
(1, 1, 1) (2, 1, 2) (3, 1, 3) (4, 1, 4) (5, 1, 6) (6, 1, 7) (7, 1, 10) (8, 1, 11) (9, 1, 12) (10, 1, 13) (11, 1, 14) (12, 1, 16) (13, 1, 17) (14, 1, 19) (15, 1, 20) (16, 1, 21) (17, 1, 22) (18, 1, 23) (19, 1, 24) (20, 2, 1) (21, 2, 3) (22, 2, 4) (23, 2, 5) (24, 2, 6) (25, 2, 8) (26, 2, 9) (27, 2, 10) (28, 2, 12) (29, 2, 13) (30, 2, 15) (31, 2, 16) (32, 2, 17) (33, 2, 18) (34, 2, 20) (35, 2, 22) (36, 2, 23) (37, 2, 24) (38, 2, 25) (39, 3, 1) (40, 3, 2) (41, 3, 3) (42, 3, 5) (43, 3, 6) (44, 3, 7) (45, 3, 8) (46, 3, 9) (47, 3, 10) (48, 3, 11) (49, 3, 14) (50, 3, 15) (51, 3, 16) (52, 3, 18) (53, 3, 19) (54, 3, 20) (55, 3, 21) (56, 3, 25) (57, 3, 26) (58, 4, 1) (59, 4, 2) (60, 4, 4) (61, 4, 5) (62, 4, 7) (63, 4, 8) (64, 4, 9) (65, 4, 11) (66, 4, 12) (67, 4, 13) (68, 4, 14) (69, 4, 15) (70, 4, 17) (71, 4, 18) (72, 4, 19) (73, 4, 21) (74, 4, 22) (75, 4, 23) (76, 4, 26) (77, 5, 1) (78, 5, 2) (79, 5, 27) (80, 6, 1) (81, 6, 2) (82, 6, 4) (83, 6, 13) (84, 6, 17) (85, 6, 22) (86, 6, 23) (87, 6, 28) (88, 7, 1) (89, 7, 7) (90, 7, 11) (91, 7, 12) (92, 7, 14) (93, 7, 18) (94, 7, 19) (95, 7, 21) (96, 7, 29) (97, 8, 1) (98, 8, 2) (99, 8, 5) (100, 8, 8) (101, 8, 9) (102, 8, 15) (103, 8, 30) (104, 9, 1) (105, 9, 2) (106, 9, 4) (107, 9, 13) (108, 9, 17) (109, 9, 20) (110, 9, 22) (111, 9, 23) (112, 9, 25) (113, 9, 31) (114, 10, 1) (115, 10, 2) (116, 10, 11) (117, 10, 12) (118, 10, 14) (119, 10, 18) (120, 10, 19) (121, 10, 21) (122, 10, 32) (123, 11, 2) (124, 11, 3) (125, 11, 5) (126, 11, 8) (127, 11, 9) (128, 11, 15) (129, 11, 33) (130, 12, 1) (131, 12, 2) (132, 12, 13) (133, 12, 17) (134, 12, 22) (135, 12, 23) (136, 12, 24) (137, 12, 34) (138, 13, 1) (139, 13, 2) (140, 13, 11) (141, 13, 12) (142, 13, 14) (143, 13, 19) (144, 13, 35) (145, 14, 1) (146, 14, 4) (147, 14, 8) (148, 14, 21) (149, 14, 24) (150, 14, 36) (151, 15, 1) (152, 15, 13) (153, 15, 16) (154, 15, 17) (155, 15, 18) (156, 15, 22) (157, 15, 37) (158, 16, 1) (159, 16, 2) (160, 16, 11) (161, 16, 14) (162, 16, 19) (163, 16, 26) (164, 16, 38) (165, 17, 2) (166, 17, 4) (167, 17, 12) (168, 17, 21) (169, 17, 23) (170, 17, 39) (171, 18, 1) (172, 18, 15) (173, 18, 17) (174, 18, 18) (175, 18, 22) (176, 18, 40) (177, 19, 2) (178, 19, 13) (179, 19, 14) (180, 19, 19) (181, 19, 20) (182, 19, 41) (183, 20, 1) (184, 20, 2) (185, 20, 8) (186, 20, 9) (187, 20, 11) (188, 20, 42) (189, 21, 1) (190, 21, 4) (191, 21, 10) (192, 21, 12) (193, 21, 23) (194, 21, 43) (195, 22, 2) (196, 22, 6) (197, 22, 17) (198, 22, 21) (199, 22, 22) (200, 22, 44) (201, 23, 1) (202, 23, 13) (203, 23, 14) (204, 23, 18) (205, 23, 45) (206, 24, 2) (207, 24, 3) (208, 24, 11) (209, 24, 19) (210, 24, 46) (211, 25, 1) (212, 25, 4) (213, 25, 5) (214, 25, 12) (215, 25, 23) (216, 25, 47) (217, 26, 2) (218, 26, 7) (219, 26, 8) (220, 26, 15) (221, 26, 48) (222, 27, 1) (223, 27, 3) (224, 27, 5) (225, 27, 16) (226, 27, 49) (227, 28, 2) (228, 28, 7) (229, 28, 9) (230, 28, 50) (231, 29, 1) (232, 29, 5) (233, 29, 20) (234, 29, 22) (235, 29, 51) (236, 30, 2) (237, 30, 15) (238, 30, 19) (239, 30, 26) (240, 30, 52) (241, 31, 1) (242, 31, 11) (243, 31, 14) (244, 31, 25) (245, 31, 53) (246, 32, 2) (247, 32, 8) (248, 32, 23) (249, 32, 26) (250, 32, 54) (251, 33, 1) (252, 33, 13) (253, 33, 15) (254, 33, 25) (255, 33, 55) (256, 34, 2) (257, 34, 3) (258, 34, 12) (259, 34, 22) (260, 34, 56) (261, 35, 1) (262, 35, 8) (263, 35, 16) (264, 35, 18) (265, 35, 57) (266, 36, 2) (267, 36, 7) (268, 36, 13) (269, 36, 23) (270, 36, 58) (271, 37, 1) (272, 37, 15) (273, 37, 16) (274, 37, 19) (275, 37, 59) (276, 38, 2) (277, 38, 14) (278, 38, 24) (279, 38, 60) (280, 39, 1) (281, 39, 10) (282, 39, 11) (283, 39, 13) (284, 39, 61) (285, 40, 2) (286, 40, 4) (287, 40, 8) (288, 40, 20) (289, 40, 62) (290, 41, 1) (291, 41, 9) (292, 41, 18) (293, 41, 63) (294, 42, 2) (295, 42, 4) (296, 42, 10) (297, 42, 19) (298, 42, 64) (299, 43, 1) (300, 43, 5) (301, 43, 25) (302, 43, 65) (303, 44, 2) (304, 44, 17) (305, 44, 19) (306, 44, 26) (307, 44, 66) (308, 45, 1) (309, 45, 8) (310, 45, 10) (311, 45, 23) (312, 45, 67) (313, 46, 2) (314, 46, 7) (315, 46, 11) (316, 46, 68),
при этом для ненулевой записи с номером e число k задается посредством коэффициента сдвига, предоставленного посредством mod(Ve, Z), причем Ve обозначает e-й элемент вектора сдвига и вектор сдвига представляет собой следующее:
[307, 19, 50, 369, 181, 216, 317, 288, 109, 17, 357, 215, 106, 242, 180, 330, 346, 1, 0, 76, 76, 73, 288, 144, 331, 331, 178, 295, 342, 217, 99, 354, 114, 331, 112, 0, 0, 0, 205, 250, 328, 332, 256, 161, 267, 160, 63, 129, 200, 88, 53, 131, 240, 205, 13, 0, 0, 276, 87, 0, 275, 199, 153, 56, 132, 305, 231, 341, 212, 304, 300, 271, 39, 357, 1, 0, 332, 181, 0, 195, 14, 115, 166, 241, 51, 157, 0, 278, 257, 1, 351, 92, 253, 18, 225, 0, 9, 62, 316, 333, 290, 114, 0, 307, 179, 165, 18, 39, 224, 368, 67, 170, 0, 366, 232, 321, 133, 57, 303, 63, 82, 0, 101, 339, 274, 111, 383, 354, 0, 48, 102, 8, 47, 188, 334, 115, 0, 77, 186, 174, 232, 50, 74, 0, 313, 177, 266, 115, 370, 0, 142, 248, 137, 89, 347, 12, 0, 241, 2, 210, 318, 55, 269, 0, 13, 338, 57, 289, 57, 0, 260, 303, 81, 358, 375, 0, 130, 163, 280, 132, 4, 0, 145, 213, 344, 242, 197, 0, 187, 206, 264, 341, 59, 0, 205, 102, 328, 213, 97, 0, 30, 11, 233, 22, 0, 24, 89, 61, 27, 0, 298, 158, 235, 339, 234, 0, 72, 17, 383, 312, 0, 71, 81, 76, 136, 0, 194, 194, 101, 0, 222, 19, 244, 274, 0, 252, 5, 147, 78, 0, 159, 229, 260, 90, 0, 100, 215, 258, 256, 0, 102, 201, 175, 287, 0, 323, 8, 361, 105, 0, 230, 148, 202, 312, 0, 320, 335, 2, 266, 0, 210, 313, 297, 21, 0, 269, 82, 115, 0, 185, 177, 289, 214, 0, 258, 93, 346, 297, 0, 175, 37, 312, 0, 52, 314, 139, 288, 0, 113, 14, 218, 0, 113, 132, 114, 168, 0, 80, 78, 163, 274, 0, 135, 149, 15, 0].
6. Беспроводное приемное устройство (110, 120), содержащее схему (920, 1020) обработки, выполненную с возможностью:
- принимать кодированные информационные биты из беспроводного передающего устройства (110, 120); и
- декодировать информационные биты с использованием матрицы контроля по четности (PCM) кода разреженного контроля по четности (LDPC), причем PCM сегментируется на квадратные субматрицы размера ZxZ и описывается посредством базовой матрицы и вектора сдвига с использованием размера сдвига Z=7*2', где j составляет одно из 0, 1, 2, 3, 4 и 5,
при этом базовая матрица имеет одну запись для каждой субматрицы ZxZ, причем запись равна 0 согласно субматрице, представляющей собой нулевую матрицу, и причем запись равна 1 согласно субматрице, представляющей собой циклическую перестановочную матрицу, полученную из единичной матрицы ZxZ посредством сдвига столбцов вправо на k элементов,
при этом базовая матрица имеет размер 42×52 и ненулевые записи в базовой матрице описываются посредством троек (e, r, c), обозначающих то, что ненулевая запись с номером e находится в строке r и столбце c базовой матрицы, причем тройки задаются следующим образом:
(1, 1, 1) (2, 1, 2) (3, 1, 3) (4, 1, 4) (5, 1, 7) (6, 1, 10) (7, 1, 11) (8, 1, 12) (9, 2, 1) (10, 2, 4) (11, 2, 5) (12, 2, 6) (13, 2, 7) (14, 2, 8) (15, 2, 9) (16, 2, 10) (17, 2, 12) (18, 2, 13) (19, 3, 1) (20, 3, 2) (21, 3, 4) (22, 3, 5) (23, 3, 9) (24, 3, 11) (25, 3, 13) (26, 3, 14) (27, 4, 2) (28, 4, 3) (29, 4, 5) (30, 4, 6) (31, 4, 7) (32, 4, 8) (33, 4, 9) (34, 4, 10) (35, 4, 11) (36, 4, 14) (37, 5, 1) (38, 5, 2) (39, 5, 12) (40, 5, 15) (41, 6, 1) (42, 6, 2) (43, 6, 6) (44, 6, 8) (45, 6, 12) (46, 6, 16) (47, 7, 1) (48, 7, 6) (49, 7, 8) (50, 7, 10) (51, 7, 12) (52, 7, 17) (53, 8, 2) (54, 8, 6) (55, 8, 8) (56, 8, 12) (57, 8, 14) (58, 8, 18) (59, 9, 1) (60, 9, 2) (61, 9, 13) (62, 9, 19) (63, 10, 2) (64, 10, 9) (65, 10, 11) (66, 10, 12) (67, 10, 20) (68, 11, 1) (69, 11, 2) (70, 11, 7) (71, 11, 8) (72, 11, 21) (73, 12, 1) (74, 12, 8) (75, 12, 10) (76, 12, 14) (77, 12, 22) (78, 13, 2) (79, 13, 4) (80, 13, 12) (81, 13, 23) (82, 14, 1) (83, 14, 2) (84, 14, 9) (85, 14, 14) (86, 14, 24) (87, 15, 2) (88, 15, 7) (89, 15, 12) (90, 15, 14) (91, 15, 25) (92, 16, 1) (93, 16, 11) (94, 16, 12) (95, 16, 26) (96, 17, 2) (97, 17, 10) (98, 17, 12) (99, 17, 13) (100, 17, 27) (101, 18, 2) (102, 18, 6) (103, 18, 12) (104, 18, 13) (105, 18, 28) (106, 19, 1) (107, 19, 7) (108, 19, 8) (109, 19, 29) (110, 20, 1) (111, 20, 2) (112, 20, 11) (113, 20, 30) (114, 21, 2) (115, 21, 5) (116, 21, 12) (117, 21, 31) (118, 22, 1) (119, 22, 9) (120, 22, 14) (121, 22, 32) (122, 23, 2) (123, 23, 3) (124, 23, 33) (125, 24, 1) (126, 24, 4) (127, 24, 6) (128, 24, 34) (129, 25, 2) (130, 25, 3) (131, 25, 10) (132, 25, 35) (133, 26, 1) (134, 26, 6) (135, 26, 36) (136, 27, 3) (137, 27, 8) (138, 27, 13) (139, 27, 14) (140, 27, 37) (141, 28, 1) (142, 28, 7) (143, 28, 38) (144, 29, 2) (145, 29, 3) (146, 29, 6) (147, 29, 39) (148, 30, 1) (149, 30, 5) (150, 30, 40) (151, 31, 3) (152, 31, 6) (153, 31, 8) (154, 31, 10) (155, 31, 41) (156, 32, 2) (157, 32, 14) (158, 32, 42) (159, 33, 1) (160, 33, 6) (161, 33, 13) (162, 33, 43) (163, 34, 3) (164, 34, 8) (165, 34, 11) (166, 34, 44) (167, 35, 1) (168, 35, 13) (169, 35, 14) (170, 35, 45) (171, 36, 2) (172, 36, 6) (173, 36, 12) (174, 36, 46) (175, 37, 1) (176, 37, 3) (177, 37, 8) (178, 37, 47) (179, 38, 11) (180, 38, 14) (181, 38, 48) (182, 39, 2) (183, 39, 6) (184, 39, 12) (185, 39, 49) (186, 40, 1) (187, 40, 8) (188, 40, 13) (189, 40, 50) (190, 41, 3) (191, 41, 11) (192, 41, 14) (193, 41, 51) (194, 42, 2) (195, 42, 6) (196, 42, 12) (197, 42, 52),
при этом для ненулевой записи с номером e число k задается посредством коэффициента сдвига, предоставленного посредством mod(Ve, Z), причем Ve обозначает e-й элемент вектора сдвига и вектор сдвига представляет собой следующее:
[72, 110, 23, 181, 95, 8, 1, 0, 53, 156, 115, 156, 115, 200, 29, 31, 0, 0, 152, 131, 46, 191, 91, 0, 0, 0, 185, 6, 36, 124, 124, 110, 156, 133, 1, 0, 200, 16, 101, 0, 185, 138, 170, 219, 193, 0, 123, 55, 31, 222, 209, 0, 103, 13, 105, 150, 181, 0, 147, 43, 152, 0, 2, 30, 184, 83, 0, 174, 150, 8, 56, 0, 99, 138, 110, 99, 0, 46, 217, 109, 0, 37, 113, 143, 140, 0, 36, 95, 40, 116, 0, 116, 200, 110, 0, 75, 158, 134, 97, 0, 48, 132, 206, 2, 0, 68, 16, 156, 0, 35, 138, 86, 0, 6, 20, 141, 0, 80, 43, 81, 0, 49, 1, 0, 156, 54, 134, 0, 153, 88, 63, 0, 211, 94, 0, 90, 6, 221, 6, 0, 27, 118, 0, 216, 212, 193, 0, 108, 61, 0, 106, 44, 185, 176, 0, 147, 182, 0, 108, 21, 110, 0, 71, 12, 109, 0, 29, 201, 69, 0, 91, 165, 55, 0, 1, 175, 83, 0, 40, 12, 0, 37, 97, 46, 0, 106, 181, 154, 0, 98, 35, 36, 0, 120, 101, 81, 0].
7. Беспроводное приемное устройство (110, 120) по п. 5 или 6,
при этом беспроводное приемное устройство (110, 120) представляет собой сетевой узел.
8. Беспроводное приемное устройство (110, 120) по п. 5 или 6,
при этом беспроводное приемное устройство (110, 120) представляет собой беспроводное устройство.
9. Способ для использования в беспроводном передающем устройстве сети беспроводной связи, при этом способ содержит этапы, на которых:
- кодируют (212) информационные биты с использованием матрицы контроля по четности (PCM) кода разреженного контроля по четности (LDPC), причем PCM сегментируется на квадратные субматрицы размера ZxZ и описывается посредством базовой матрицы и вектора сдвига с использованием размера сдвига Z=3*2', где j составляет одно из 0, 1, 2, 3, 4, 5, 6 и 7; и
- передают (214) кодированные информационные биты в беспроводное приемное устройство,
при этом базовая матрица имеет одну запись для каждой субматрицы ZxZ, причем запись равна 0 согласно субматрице, представляющей собой нулевую матрицу, и причем запись равна 1 согласно субматрице, представляющей собой циклическую перестановочную матрицу, полученную из единичной матрицы ZxZ посредством сдвига столбцов вправо на k элементов,
при этом базовая матрица имеет размер 46×68 и ненулевые записи в базовой матрице описываются посредством троек (e, r, c), обозначающих то, что ненулевая запись с номером e находится в строке r и столбце c базовой матрицы, причем тройки задаются следующим образом:
(1, 1, 1) (2, 1, 2) (3, 1, 3) (4, 1, 4) (5, 1, 6) (6, 1, 7) (7, 1, 10) (8, 1, 11) (9, 1, 12) (10, 1, 13) (11, 1, 14) (12, 1, 16) (13, 1, 17) (14, 1, 19) (15, 1, 20) (16, 1, 21) (17, 1, 22) (18, 1, 23) (19, 1, 24) (20, 2, 1) (21, 2, 3) (22, 2, 4) (23, 2, 5) (24, 2, 6) (25, 2, 8) (26, 2, 9) (27, 2, 10) (28, 2, 12) (29, 2, 13) (30, 2, 15) (31, 2, 16) (32, 2, 17) (33, 2, 18) (34, 2, 20) (35, 2, 22) (36, 2, 23) (37, 2, 24) (38, 2, 25) (39, 3, 1) (40, 3, 2) (41, 3, 3) (42, 3, 5) (43, 3, 6) (44, 3, 7) (45, 3, 8) (46, 3, 9) (47, 3, 10) (48, 3, 11) (49, 3, 14) (50, 3, 15) (51, 3, 16) (52, 3, 18) (53, 3, 19) (54, 3, 20) (55, 3, 21) (56, 3, 25) (57, 3, 26) (58, 4, 1) (59, 4, 2) (60, 4, 4) (61, 4, 5) (62, 4, 7) (63, 4, 8) (64, 4, 9) (65, 4, 11) (66, 4, 12) (67, 4, 13) (68, 4, 14) (69, 4, 15) (70, 4, 17) (71, 4, 18) (72, 4, 19) (73, 4, 21) (74, 4, 22) (75, 4, 23) (76, 4, 26) (77, 5, 1) (78, 5, 2) (79, 5, 27) (80, 6, 1) (81, 6, 2) (82, 6, 4) (83, 6, 13) (84, 6, 17) (85, 6, 22) (86, 6, 23) (87, 6, 28) (88, 7, 1) (89, 7, 7) (90, 7, 11) (91, 7, 12) (92, 7, 14) (93, 7, 18) (94, 7, 19) (95, 7, 21) (96, 7, 29) (97, 8, 1) (98, 8, 2) (99, 8, 5) (100, 8, 8) (101, 8, 9) (102, 8, 15) (103, 8, 30) (104, 9, 1) (105, 9, 2) (106, 9, 4) (107, 9, 13) (108, 9, 17) (109, 9, 20) (110, 9, 22) (111, 9, 23) (112, 9, 25) (113, 9, 31) (114, 10, 1) (115, 10, 2) (116, 10, 11) (117, 10, 12) (118, 10, 14) (119, 10, 18) (120, 10, 19) (121, 10, 21) (122, 10, 32) (123, 11, 2) (124, 11, 3) (125, 11, 5) (126, 11, 8) (127, 11, 9) (128, 11, 15) (129, 11, 33) (130, 12, 1) (131, 12, 2) (132, 12, 13) (133, 12, 17) (134, 12, 22) (135, 12, 23) (136, 12, 24) (137, 12, 34) (138, 13, 1) (139, 13, 2) (140, 13, 11) (141, 13, 12) (142, 13, 14) (143, 13, 19) (144, 13, 35) (145, 14, 1) (146, 14, 4) (147, 14, 8) (148, 14, 21) (149, 14, 24) (150, 14, 36) (151, 15, 1) (152, 15, 13) (153, 15, 16) (154, 15, 17) (155, 15, 18) (156, 15, 22) (157, 15, 37) (158, 16, 1) (159, 16, 2) (160, 16, 11) (161, 16, 14) (162, 16, 19) (163, 16, 26) (164, 16, 38) (165, 17, 2) (166, 17, 4) (167, 17, 12) (168, 17, 21) (169, 17, 23) (170, 17, 39) (171, 18, 1) (172, 18, 15) (173, 18, 17) (174, 18, 18) (175, 18, 22) (176, 18, 40) (177, 19, 2) (178, 19, 13) (179, 19, 14) (180, 19, 19) (181, 19, 20) (182, 19, 41) (183, 20, 1) (184, 20, 2) (185, 20, 8) (186, 20, 9) (187, 20, 11) (188, 20, 42) (189, 21, 1) (190, 21, 4) (191, 21, 10) (192, 21, 12) (193, 21, 23) (194, 21, 43) (195, 22, 2) (196, 22, 6) (197, 22, 17) (198, 22, 21) (199, 22, 22) (200, 22, 44) (201, 23, 1) (202, 23, 13) (203, 23, 14) (204, 23, 18) (205, 23, 45) (206, 24, 2) (207, 24, 3) (208, 24, 11) (209, 24, 19) (210, 24, 46) (211, 25, 1) (212, 25, 4) (213, 25, 5) (214, 25, 12) (215, 25, 23) (216, 25, 47) (217, 26, 2) (218, 26, 7) (219, 26, 8) (220, 26, 15) (221, 26, 48) (222, 27, 1) (223, 27, 3) (224, 27, 5) (225, 27, 16) (226, 27, 49) (227, 28, 2) (228, 28, 7) (229, 28, 9) (230, 28, 50) (231, 29, 1) (232, 29, 5) (233, 29, 20) (234, 29, 22) (235, 29, 51) (236, 30, 2) (237, 30, 15) (238, 30, 19) (239, 30, 26) (240, 30, 52) (241, 31, 1) (242, 31, 11) (243, 31, 14) (244, 31, 25) (245, 31, 53) (246, 32, 2) (247, 32, 8) (248, 32, 23) (249, 32, 26) (250, 32, 54) (251, 33, 1) (252, 33, 13) (253, 33, 15) (254, 33, 25) (255, 33, 55) (256, 34, 2) (257, 34, 3) (258, 34, 12) (259, 34, 22) (260, 34, 56) (261, 35, 1) (262, 35, 8) (263, 35, 16) (264, 35, 18) (265, 35, 57) (266, 36, 2) (267, 36, 7) (268, 36, 13) (269, 36, 23) (270, 36, 58) (271, 37, 1) (272, 37, 15) (273, 37, 16) (274, 37, 19) (275, 37, 59) (276, 38, 2) (277, 38, 14) (278, 38, 24) (279, 38, 60) (280, 39, 1) (281, 39, 10) (282, 39, 11) (283, 39, 13) (284, 39, 61) (285, 40, 2) (286, 40, 4) (287, 40, 8) (288, 40, 20) (289, 40, 62) (290, 41, 1) (291, 41, 9) (292, 41, 18) (293, 41, 63) (294, 42, 2) (295, 42, 4) (296, 42, 10) (297, 42, 19) (298, 42, 64) (299, 43, 1) (300, 43, 5) (301, 43, 25) (302, 43, 65) (303, 44, 2) (304, 44, 17) (305, 44, 19) (306, 44, 26) (307, 44, 66) (308, 45, 1) (309, 45, 8) (310, 45, 10) (311, 45, 23) (312, 45, 67) (313, 46, 2) (314, 46, 7) (315, 46, 11) (316, 46, 68),
при этом для ненулевой записи с номером e число k задается посредством коэффициента сдвига, предоставленного посредством mod(Ve, Z), причем Ve обозначает e-й элемент вектора сдвига и вектор сдвига представляет собой следующее:
[307, 19, 50, 369, 181, 216, 317, 288, 109, 17, 357, 215, 106, 242, 180, 330, 346, 1, 0, 76, 76, 73, 288, 144, 331, 331, 178, 295, 342, 217, 99, 354, 114, 331, 112, 0, 0, 0, 205, 250, 328, 332, 256, 161, 267, 160, 63, 129, 200, 88, 53, 131, 240, 205, 13, 0, 0, 276, 87, 0, 275, 199, 153, 56, 132, 305, 231, 341, 212, 304, 300, 271, 39, 357, 1, 0, 332, 181, 0, 195, 14, 115, 166, 241, 51, 157, 0, 278, 257, 1, 351, 92, 253, 18, 225, 0, 9, 62, 316, 333, 290, 114, 0, 307, 179, 165, 18, 39, 224, 368, 67, 170, 0, 366, 232, 321, 133, 57, 303, 63, 82, 0, 101, 339, 274, 111, 383, 354, 0, 48, 102, 8, 47, 188, 334, 115, 0, 77, 186, 174, 232, 50, 74, 0, 313, 177, 266, 115, 370, 0, 142, 248, 137, 89, 347, 12, 0, 241, 2, 210, 318, 55, 269, 0, 13, 338, 57, 289, 57, 0, 260, 303, 81, 358, 375, 0, 130, 163, 280, 132, 4, 0, 145, 213, 344, 242, 197, 0, 187, 206, 264, 341, 59, 0, 205, 102, 328, 213, 97, 0, 30, 11, 233, 22, 0, 24, 89, 61, 27, 0, 298, 158, 235, 339, 234, 0, 72, 17, 383, 312, 0, 71, 81, 76, 136, 0, 194, 194, 101, 0, 222, 19, 244, 274, 0, 252, 5, 147, 78, 0, 159, 229, 260, 90, 0, 100, 215, 258, 256, 0, 102, 201, 175, 287, 0, 323, 8, 361, 105, 0, 230, 148, 202, 312, 0, 320, 335, 2, 266, 0, 210, 313, 297, 21, 0, 269, 82, 115, 0, 185, 177, 289, 214, 0, 258, 93, 346, 297, 0, 175, 37, 312, 0, 52, 314, 139, 288, 0, 113, 14, 218, 0, 113, 132, 114, 168, 0, 80, 78, 163, 274, 0, 135, 149, 15, 0].
10. Способ для использования в беспроводном передающем устройстве сети беспроводной связи, при этом способ содержит этапы, на которых:
- кодируют (212) информационные биты с использованием матрицы контроля по четности (PCM) кода разреженного контроля по четности (LDPC), причем PCM сегментируется на квадратные субматрицы размера ZxZ и описывается посредством базовой матрицы и вектора сдвига с использованием размера сдвига Z=7*2', где j составляет одно из 0, 1, 2, 3, 4 и 5; и
- передают (214) кодированные информационные биты в беспроводное приемное устройство,
при этом базовая матрица имеет одну запись для каждой субматрицы ZxZ, причем запись равна 0 согласно субматрице, представляющей собой нулевую матрицу, и причем запись равна 1 согласно субматрице, представляющей собой циклическую перестановочную матрицу, полученную из единичной матрицы ZxZ посредством сдвига столбцов вправо на k элементов,
при этом базовая матрица имеет размер 42×52 и ненулевые записи в базовой матрице описываются посредством троек (e, r, c), обозначающих то, что ненулевая запись с номером e находится в строке r и столбце c базовой матрицы, причем тройки задаются следующим образом:
(1, 1, 1) (2, 1, 2) (3, 1, 3) (4, 1, 4) (5, 1, 7) (6, 1, 10) (7, 1, 11) (8, 1, 12) (9, 2, 1) (10, 2, 4) (11, 2, 5) (12, 2, 6) (13, 2, 7) (14, 2, 8) (15, 2, 9) (16, 2, 10) (17, 2, 12) (18, 2, 13) (19, 3, 1) (20, 3, 2) (21, 3, 4) (22, 3, 5) (23, 3, 9) (24, 3, 11) (25, 3, 13) (26, 3, 14) (27, 4, 2) (28, 4, 3) (29, 4, 5) (30, 4, 6) (31, 4, 7) (32, 4, 8) (33, 4, 9) (34, 4, 10) (35, 4, 11) (36, 4, 14) (37, 5, 1) (38, 5, 2) (39, 5, 12) (40, 5, 15) (41, 6, 1) (42, 6, 2) (43, 6, 6) (44, 6, 8) (45, 6, 12) (46, 6, 16) (47, 7, 1) (48, 7, 6) (49, 7, 8) (50, 7, 10) (51, 7, 12) (52, 7, 17) (53, 8, 2) (54, 8, 6) (55, 8, 8) (56, 8, 12) (57, 8, 14) (58, 8, 18) (59, 9, 1) (60, 9, 2) (61, 9, 13) (62, 9, 19) (63, 10, 2) (64, 10, 9) (65, 10, 11) (66, 10, 12) (67, 10, 20) (68, 11, 1) (69, 11, 2) (70, 11, 7) (71, 11, 8) (72, 11, 21) (73, 12, 1) (74, 12, 8) (75, 12, 10) (76, 12, 14) (77, 12, 22) (78, 13, 2) (79, 13, 4) (80, 13, 12) (81, 13, 23) (82, 14, 1) (83, 14, 2) (84, 14, 9) (85, 14, 14) (86, 14, 24) (87, 15, 2) (88, 15, 7) (89, 15, 12) (90, 15, 14) (91, 15, 25) (92, 16, 1) (93, 16, 11) (94, 16, 12) (95, 16, 26) (96, 17, 2) (97, 17, 10) (98, 17, 12) (99, 17, 13) (100, 17, 27) (101, 18, 2) (102, 18, 6) (103, 18, 12) (104, 18, 13) (105, 18, 28) (106, 19, 1) (107, 19, 7) (108, 19, 8) (109, 19, 29) (110, 20, 1) (111, 20, 2) (112, 20, 11) (113, 20, 30) (114, 21, 2) (115, 21, 5) (116, 21, 12) (117, 21, 31) (118, 22, 1) (119, 22, 9) (120, 22, 14) (121, 22, 32) (122, 23, 2) (123, 23, 3) (124, 23, 33) (125, 24, 1) (126, 24, 4) (127, 24, 6) (128, 24, 34) (129, 25, 2) (130, 25, 3) (131, 25, 10) (132, 25, 35) (133, 26, 1) (134, 26, 6) (135, 26, 36) (136, 27, 3) (137, 27, 8) (138, 27, 13) (139, 27, 14) (140, 27, 37) (141, 28, 1) (142, 28, 7) (143, 28, 38) (144, 29, 2) (145, 29, 3) (146, 29, 6) (147, 29, 39) (148, 30, 1) (149, 30, 5) (150, 30, 40) (151, 31, 3) (152, 31, 6) (153, 31, 8) (154, 31, 10) (155, 31, 41) (156, 32, 2) (157, 32, 14) (158, 32, 42) (159, 33, 1) (160, 33, 6) (161, 33, 13) (162, 33, 43) (163, 34, 3) (164, 34, 8) (165, 34, 11) (166, 34, 44) (167, 35, 1) (168, 35, 13) (169, 35, 14) (170, 35, 45) (171, 36, 2) (172, 36, 6) (173, 36, 12) (174, 36, 46) (175, 37, 1) (176, 37, 3) (177, 37, 8) (178, 37, 47) (179, 38, 11) (180, 38, 14) (181, 38, 48) (182, 39, 2) (183, 39, 6) (184, 39, 12) (185, 39, 49) (186, 40, 1) (187, 40, 8) (188, 40, 13) (189, 40, 50) (190, 41, 3) (191, 41, 11) (192, 41, 14) (193, 41, 51) (194, 42, 2) (195, 42, 6) (196, 42, 12) (197, 42, 52),
при этом для ненулевой записи с номером e число k задается посредством коэффициента сдвига, предоставленного посредством mod(Ve, Z), причем Ve обозначает e-й элемент вектора сдвига и вектор сдвига представляет собой следующее:
[72, 110, 23, 181, 95, 8, 1, 0, 53, 156, 115, 156, 115, 200, 29, 31, 0, 0, 152, 131, 46, 191, 91, 0, 0, 0, 185, 6, 36, 124, 124, 110, 156, 133, 1, 0, 200, 16, 101, 0, 185, 138, 170, 219, 193, 0, 123, 55, 31, 222, 209, 0, 103, 13, 105, 150, 181, 0, 147, 43, 152, 0, 2, 30, 184, 83, 0, 174, 150, 8, 56, 0, 99, 138, 110, 99, 0, 46, 217, 109, 0, 37, 113, 143, 140, 0, 36, 95, 40, 116, 0, 116, 200, 110, 0, 75, 158, 134, 97, 0, 48, 132, 206, 2, 0, 68, 16, 156, 0, 35, 138, 86, 0, 6, 20, 141, 0, 80, 43, 81, 0, 49, 1, 0, 156, 54, 134, 0, 153, 88, 63, 0, 211, 94, 0, 90, 6, 221, 6, 0, 27, 118, 0, 216, 212, 193, 0, 108, 61, 0, 106, 44, 185, 176, 0, 147, 182, 0, 108, 21, 110, 0, 71, 12, 109, 0, 29, 201, 69, 0, 91, 165, 55, 0, 1, 175, 83, 0, 40, 12, 0, 37, 97, 46, 0, 106, 181, 154, 0, 98, 35, 36, 0, 120, 101, 81, 0].
11. Способ по п. 9 или 10,
в котором беспроводное передающее устройство (110, 120) представляет собой сетевой узел.
12. Способ по п. 9 или 10,
в котором беспроводное передающее устройство (110, 120) представляет собой беспроводное устройство.
13. Способ для использования в беспроводном приемном устройстве сети беспроводной связи, при этом способ содержит этапы, на которых:
- принимают (312) кодированные информационные биты из беспроводного передающего устройства; и
- декодируют (314) информационные биты с использованием матрицы контроля по четности (PCM) кода разреженного контроля по четности (LDPC), причем PCM сегментируется на квадратные субматрицы размера ZxZ и описывается посредством базовой матрицы и вектора сдвига с использованием размера сдвига Z=3*2', где j составляет одно из 0, 1, 2, 3, 4, 5, 6 и 7,
при этом базовая матрица имеет одну запись для каждой субматрицы ZxZ, причем запись равна 0 согласно субматрице, представляющей собой нулевую матрицу, и причем запись равна 1 согласно субматрице, представляющей собой циклическую перестановочную матрицу, полученную из единичной матрицы ZxZ посредством сдвига столбцов вправо на k элементов,
при этом базовая матрица имеет размер 46×68 и ненулевые записи в базовой матрице описываются посредством троек (e, r, c), обозначающих то, что ненулевая запись с номером e находится в строке r и столбце c базовой матрицы, причем тройки задаются следующим образом:
(1, 1, 1) (2, 1, 2) (3, 1, 3) (4, 1, 4) (5, 1, 6) (6, 1, 7) (7, 1, 10) (8, 1, 11) (9, 1, 12) (10, 1, 13) (11, 1, 14) (12, 1, 16) (13, 1, 17) (14, 1, 19) (15, 1, 20) (16, 1, 21) (17, 1, 22) (18, 1, 23) (19, 1, 24) (20, 2, 1) (21, 2, 3) (22, 2, 4) (23, 2, 5) (24, 2, 6) (25, 2, 8) (26, 2, 9) (27, 2, 10) (28, 2, 12) (29, 2, 13) (30, 2, 15) (31, 2, 16) (32, 2, 17) (33, 2, 18) (34, 2, 20) (35, 2, 22) (36, 2, 23) (37, 2, 24) (38, 2, 25) (39, 3, 1) (40, 3, 2) (41, 3, 3) (42, 3, 5) (43, 3, 6) (44, 3, 7) (45, 3, 8) (46, 3, 9) (47, 3, 10) (48, 3, 11) (49, 3, 14) (50, 3, 15) (51, 3, 16) (52, 3, 18) (53, 3, 19) (54, 3, 20) (55, 3, 21) (56, 3, 25) (57, 3, 26) (58, 4, 1) (59, 4, 2) (60, 4, 4) (61, 4, 5) (62, 4, 7) (63, 4, 8) (64, 4, 9) (65, 4, 11) (66, 4, 12) (67, 4, 13) (68, 4, 14) (69, 4, 15) (70, 4, 17) (71, 4, 18) (72, 4, 19) (73, 4, 21) (74, 4, 22) (75, 4, 23) (76, 4, 26) (77, 5, 1) (78, 5, 2) (79, 5, 27) (80, 6, 1) (81, 6, 2) (82, 6, 4) (83, 6, 13) (84, 6, 17) (85, 6, 22) (86, 6, 23) (87, 6, 28) (88, 7, 1) (89, 7, 7) (90, 7, 11) (91, 7, 12) (92, 7, 14) (93, 7, 18) (94, 7, 19) (95, 7, 21) (96, 7, 29) (97, 8, 1) (98, 8, 2) (99, 8, 5) (100, 8, 8) (101, 8, 9) (102, 8, 15) (103, 8, 30) (104, 9, 1) (105, 9, 2) (106, 9, 4) (107, 9, 13) (108, 9, 17) (109, 9, 20) (110, 9, 22) (111, 9, 23) (112, 9, 25) (113, 9, 31) (114, 10, 1) (115, 10, 2) (116, 10, 11) (117, 10, 12) (118, 10, 14) (119, 10, 18) (120, 10, 19) (121, 10, 21) (122, 10, 32) (123, 11, 2) (124, 11, 3) (125, 11, 5) (126, 11, 8) (127, 11, 9) (128, 11, 15) (129, 11, 33) (130, 12, 1) (131, 12, 2) (132, 12, 13) (133, 12, 17) (134, 12, 22) (135, 12, 23) (136, 12, 24) (137, 12, 34) (138, 13, 1) (139, 13, 2) (140, 13, 11) (141, 13, 12) (142, 13, 14) (143, 13, 19) (144, 13, 35) (145, 14, 1) (146, 14, 4) (147, 14, 8) (148, 14, 21) (149, 14, 24) (150, 14, 36) (151, 15, 1) (152, 15, 13) (153, 15, 16) (154, 15, 17) (155, 15, 18) (156, 15, 22) (157, 15, 37) (158, 16, 1) (159, 16, 2) (160, 16, 11) (161, 16, 14) (162, 16, 19) (163, 16, 26) (164, 16, 38) (165, 17, 2) (166, 17, 4) (167, 17, 12) (168, 17, 21) (169, 17, 23) (170, 17, 39) (171, 18, 1) (172, 18, 15) (173, 18, 17) (174, 18, 18) (175, 18, 22) (176, 18, 40) (177, 19, 2) (178, 19, 13) (179, 19, 14) (180, 19, 19) (181, 19, 20) (182, 19, 41) (183, 20, 1) (184, 20, 2) (185, 20, 8) (186, 20, 9) (187, 20, 11) (188, 20, 42) (189, 21, 1) (190, 21, 4) (191, 21, 10) (192, 21, 12) (193, 21, 23) (194, 21, 43) (195, 22, 2) (196, 22, 6) (197, 22, 17) (198, 22, 21) (199, 22, 22) (200, 22, 44) (201, 23, 1) (202, 23, 13) (203, 23, 14) (204, 23, 18) (205, 23, 45) (206, 24, 2) (207, 24, 3) (208, 24, 11) (209, 24, 19) (210, 24, 46) (211, 25, 1) (212, 25, 4) (213, 25, 5) (214, 25, 12) (215, 25, 23) (216, 25, 47) (217, 26, 2) (218, 26, 7) (219, 26, 8) (220, 26, 15) (221, 26, 48) (222, 27, 1) (223, 27, 3) (224, 27, 5) (225, 27, 16) (226, 27, 49) (227, 28, 2) (228, 28, 7) (229, 28, 9) (230, 28, 50) (231, 29, 1) (232, 29, 5) (233, 29, 20) (234, 29, 22) (235, 29, 51) (236, 30, 2) (237, 30, 15) (238, 30, 19) (239, 30, 26) (240, 30, 52) (241, 31, 1) (242, 31, 11) (243, 31, 14) (244, 31, 25) (245, 31, 53) (246, 32, 2) (247, 32, 8) (248, 32, 23) (249, 32, 26) (250, 32, 54) (251, 33, 1) (252, 33, 13) (253, 33, 15) (254, 33, 25) (255, 33, 55) (256, 34, 2) (257, 34, 3) (258, 34, 12) (259, 34, 22) (260, 34, 56) (261, 35, 1) (262, 35, 8) (263, 35, 16) (264, 35, 18) (265, 35, 57) (266, 36, 2) (267, 36, 7) (268, 36, 13) (269, 36, 23) (270, 36, 58) (271, 37, 1) (272, 37, 15) (273, 37, 16) (274, 37, 19) (275, 37, 59) (276, 38, 2) (277, 38, 14) (278, 38, 24) (279, 38, 60) (280, 39, 1) (281, 39, 10) (282, 39, 11) (283, 39, 13) (284, 39, 61) (285, 40, 2) (286, 40, 4) (287, 40, 8) (288, 40, 20) (289, 40, 62) (290, 41, 1) (291, 41, 9) (292, 41, 18) (293, 41, 63) (294, 42, 2) (295, 42, 4) (296, 42, 10) (297, 42, 19) (298, 42, 64) (299, 43, 1) (300, 43, 5) (301, 43, 25) (302, 43, 65) (303, 44, 2) (304, 44, 17) (305, 44, 19) (306, 44, 26) (307, 44, 66) (308, 45, 1) (309, 45, 8) (310, 45, 10) (311, 45, 23) (312, 45, 67) (313, 46, 2) (314, 46, 7) (315, 46, 11) (316, 46, 68),
при этом для ненулевой записи с номером e число k задается посредством коэффициента сдвига, предоставленного посредством mod(Ve, Z), причем Ve обозначает e-й элемент вектора сдвига и вектор сдвига представляет собой следующее:
[307, 19, 50, 369, 181, 216, 317, 288, 109, 17, 357, 215, 106, 242, 180, 330, 346, 1, 0, 76, 76, 73, 288, 144, 331, 331, 178, 295, 342, 217, 99, 354, 114, 331, 112, 0, 0, 0, 205, 250, 328, 332, 256, 161, 267, 160, 63, 129, 200, 88, 53, 131, 240, 205, 13, 0, 0, 276, 87, 0, 275, 199, 153, 56, 132, 305, 231, 341, 212, 304, 300, 271, 39, 357, 1, 0, 332, 181, 0, 195, 14, 115, 166, 241, 51, 157, 0, 278, 257, 1, 351, 92, 253, 18, 225, 0, 9, 62, 316, 333, 290, 114, 0, 307, 179, 165, 18, 39, 224, 368, 67, 170, 0, 366, 232, 321, 133, 57, 303, 63, 82, 0, 101, 339, 274, 111, 383, 354, 0, 48, 102, 8, 47, 188, 334, 115, 0, 77, 186, 174, 232, 50, 74, 0, 313, 177, 266, 115, 370, 0, 142, 248, 137, 89, 347, 12, 0, 241, 2, 210, 318, 55, 269, 0, 13, 338, 57, 289, 57, 0, 260, 303, 81, 358, 375, 0, 130, 163, 280, 132, 4, 0, 145, 213, 344, 242, 197, 0, 187, 206, 264, 341, 59, 0, 205, 102, 328, 213, 97, 0, 30, 11, 233, 22, 0, 24, 89, 61, 27, 0, 298, 158, 235, 339, 234, 0, 72, 17, 383, 312, 0, 71, 81, 76, 136, 0, 194, 194, 101, 0, 222, 19, 244, 274, 0, 252, 5, 147, 78, 0, 159, 229, 260, 90, 0, 100, 215, 258, 256, 0, 102, 201, 175, 287, 0, 323, 8, 361, 105, 0, 230, 148, 202, 312, 0, 320, 335, 2, 266, 0, 210, 313, 297, 21, 0, 269, 82, 115, 0, 185, 177, 289, 214, 0, 258, 93, 346, 297, 0, 175, 37, 312, 0, 52, 314, 139, 288, 0, 113, 14, 218, 0, 113, 132, 114, 168, 0, 80, 78, 163, 274, 0, 135, 149, 15, 0].
14. Способ для использования в беспроводном приемном устройстве сети беспроводной связи, при этом способ содержит этапы, на которых:
- принимают (312) кодированные информационные биты из беспроводного передающего устройства; и
- декодируют (314) информационные биты с использованием матрицы контроля по четности (PCM) кода разреженного контроля по четности (LDPC), причем PCM сегментируется на квадратные субматрицы размера ZxZ и описывается посредством базовой матрицы и вектора сдвига с использованием размера сдвига Z=7*2', где j составляет одно из 0, 1, 2, 3, 4 и 5,
при этом базовая матрица имеет одну запись для каждой субматрицы ZxZ, причем запись равна 0 согласно субматрице, представляющей собой нулевую матрицу, и причем запись равна 1 согласно субматрице, представляющей собой циклическую перестановочную матрицу, полученную из единичной матрицы ZxZ посредством сдвига столбцов вправо на k элементов,
при этом базовая матрица имеет размер 42×52 и ненулевые записи в базовой матрице описываются посредством троек (e, r, c), обозначающих то, что ненулевая запись с номером e находится в строке r и столбце c базовой матрицы, причем тройки задаются следующим образом:
(1, 1, 1) (2, 1, 2) (3, 1, 3) (4, 1, 4) (5, 1, 7) (6, 1, 10) (7, 1, 11) (8, 1, 12) (9, 2, 1) (10, 2, 4) (11, 2, 5) (12, 2, 6) (13, 2, 7) (14, 2, 8) (15, 2, 9) (16, 2, 10) (17, 2, 12) (18, 2, 13) (19, 3, 1) (20, 3, 2) (21, 3, 4) (22, 3, 5) (23, 3, 9) (24, 3, 11) (25, 3, 13) (26, 3, 14) (27, 4, 2) (28, 4, 3) (29, 4, 5) (30, 4, 6) (31, 4, 7) (32, 4, 8) (33, 4, 9) (34, 4, 10) (35, 4, 11) (36, 4, 14) (37, 5, 1) (38, 5, 2) (39, 5, 12) (40, 5, 15) (41, 6, 1) (42, 6, 2) (43, 6, 6) (44, 6, 8) (45, 6, 12) (46, 6, 16) (47, 7, 1) (48, 7, 6) (49, 7, 8) (50, 7, 10) (51, 7, 12) (52, 7, 17) (53, 8, 2) (54, 8, 6) (55, 8, 8) (56, 8, 12) (57, 8, 14) (58, 8, 18) (59, 9, 1) (60, 9, 2) (61, 9, 13) (62, 9, 19) (63, 10, 2) (64, 10, 9) (65, 10, 11) (66, 10, 12) (67, 10, 20) (68, 11, 1) (69, 11, 2) (70, 11, 7) (71, 11, 8) (72, 11, 21) (73, 12, 1) (74, 12, 8) (75, 12, 10) (76, 12, 14) (77, 12, 22) (78, 13, 2) (79, 13, 4) (80, 13, 12) (81, 13, 23) (82, 14, 1) (83, 14, 2) (84, 14, 9) (85, 14, 14) (86, 14, 24) (87, 15, 2) (88, 15, 7) (89, 15, 12) (90, 15, 14) (91, 15, 25) (92, 16, 1) (93, 16, 11) (94, 16, 12) (95, 16, 26) (96, 17, 2) (97, 17, 10) (98, 17, 12) (99, 17, 13) (100, 17, 27) (101, 18, 2) (102, 18, 6) (103, 18, 12) (104, 18, 13) (105, 18, 28) (106, 19, 1) (107, 19, 7) (108, 19, 8) (109, 19, 29) (110, 20, 1) (111, 20, 2) (112, 20, 11) (113, 20, 30) (114, 21, 2) (115, 21, 5) (116, 21, 12) (117, 21, 31) (118, 22, 1) (119, 22, 9) (120, 22, 14) (121, 22, 32) (122, 23, 2) (123, 23, 3) (124, 23, 33) (125, 24, 1) (126, 24, 4) (127, 24, 6) (128, 24, 34) (129, 25, 2) (130, 25, 3) (131, 25, 10) (132, 25, 35) (133, 26, 1) (134, 26, 6) (135, 26, 36) (136, 27, 3) (137, 27, 8) (138, 27, 13) (139, 27, 14) (140, 27, 37) (141, 28, 1) (142, 28, 7) (143, 28, 38) (144, 29, 2) (145, 29, 3) (146, 29, 6) (147, 29, 39) (148, 30, 1) (149, 30, 5) (150, 30, 40) (151, 31, 3) (152, 31, 6) (153, 31, 8) (154, 31, 10) (155, 31, 41) (156, 32, 2) (157, 32, 14) (158, 32, 42) (159, 33, 1) (160, 33, 6) (161, 33, 13) (162, 33, 43) (163, 34, 3) (164, 34, 8) (165, 34, 11) (166, 34, 44) (167, 35, 1) (168, 35, 13) (169, 35, 14) (170, 35, 45) (171, 36, 2) (172, 36, 6) (173, 36, 12) (174, 36, 46) (175, 37, 1) (176, 37, 3) (177, 37, 8) (178, 37, 47) (179, 38, 11) (180, 38, 14) (181, 38, 48) (182, 39, 2) (183, 39, 6) (184, 39, 12) (185, 39, 49) (186, 40, 1) (187, 40, 8) (188, 40, 13) (189, 40, 50) (190, 41, 3) (191, 41, 11) (192, 41, 14) (193, 41, 51) (194, 42, 2) (195, 42, 6) (196, 42, 12) (197, 42, 52),
при этом для ненулевой записи с номером e число k задается посредством коэффициента сдвига, предоставленного посредством mod(Ve, Z), причем Ve обозначает e-й элемент вектора сдвига и вектор сдвига представляет собой следующее:
[72, 110, 23, 181, 95, 8, 1, 0, 53, 156, 115, 156, 115, 200, 29, 31, 0, 0, 152, 131, 46, 191, 91, 0, 0, 0, 185, 6, 36, 124, 124, 110, 156, 133, 1, 0, 200, 16, 101, 0, 185, 138, 170, 219, 193, 0, 123, 55, 31, 222, 209, 0, 103, 13, 105, 150, 181, 0, 147, 43, 152, 0, 2, 30, 184, 83, 0, 174, 150, 8, 56, 0, 99, 138, 110, 99, 0, 46, 217, 109, 0, 37, 113, 143, 140, 0, 36, 95, 40, 116, 0, 116, 200, 110, 0, 75, 158, 134, 97, 0, 48, 132, 206, 2, 0, 68, 16, 156, 0, 35, 138, 86, 0, 6, 20, 141, 0, 80, 43, 81, 0, 49, 1, 0, 156, 54, 134, 0, 153, 88, 63, 0, 211, 94, 0, 90, 6, 221, 6, 0, 27, 118, 0, 216, 212, 193, 0, 108, 61, 0, 106, 44, 185, 176, 0, 147, 182, 0, 108, 21, 110, 0, 71, 12, 109, 0, 29, 201, 69, 0, 91, 165, 55, 0, 1, 175, 83, 0, 40, 12, 0, 37, 97, 46, 0, 106, 181, 154, 0, 98, 35, 36, 0, 120, 101, 81, 0].
15. Способ по п. 13 или 14,
в котором беспроводное приемное устройство (110, 120) представляет собой сетевой узел.
16. Способ по п. 13 или 14,
в котором беспроводное приемное устройство (110, 120) представляет собой беспроводное устройство.
| Приспособление для суммирования отрезков прямых линий | 1923 |
|
SU2010A1 |
| Приспособление для суммирования отрезков прямых линий | 1923 |
|
SU2010A1 |
| УСТРОЙСТВО И СПОСОБ КОДИРОВАНИЯ И ДЕКОДИРОВАНИЯ БЛОЧНОГО КОДА РАЗРЕЖЕННОГО КОНТРОЛЯ ЧЕТНОСТИ | 2005 |
|
RU2348103C2 |
| УСТРОЙСТВО ОБРАБОТКИ ДАННЫХ И СПОСОБ ОБРАБОТКИ ДАННЫХ | 2011 |
|
RU2574828C2 |
| СПОСОБ И УСТРОЙСТВО ДЛЯ КАНАЛЬНОГО КОДИРОВАНИЯ И ДЕКОДИРОВАНИЯ В СИСТЕМЕ СВЯЗИ, В КОТОРОЙ ИСПОЛЬЗУЮТСЯ КОДЫ КОНТРОЛЯ ЧЕТНОСТИ С НИЗКОЙ ПЛОТНОСТЬЮ | 2009 |
|
RU2450443C1 |
| US 8103931 B2, 24.01.2012 | |||
| US 8341492 B2, 25.12.2012 | |||
| CN 10241845 A, 11.04.2012 | |||
| Многоступенчатая активно-реактивная турбина | 1924 |
|
SU2013A1 |
Авторы
Даты
2020-09-08—Публикация
2018-06-26—Подача