Изобретение относится к вычислительной технике и электросвязи, предназначено для решения задач защиты компьютерной информации. Наиболее предпочтительной областью использования изобретения является реализация стохастических методов защиты информации.
В совокупности признаков заявленного изобретения используются следующие термины:
Design Obfuscation - технология, затрудняющая реверс-инжиниринг цифровых устройств в интегральном исполнении за счет «запутывания» логической схемы устройства и предназначенная для защиты от аппаратных троянов.
Конечное поле или поле Галуа GF(q) (GF - Galois Field, q=pn - число элементов поля, р - простое, n - натуральное) - конечное множество элементов, обладающее следующими свойствами: 1) в поле определены две операции, одна условно называется сложением, другая - умножением; 2) для элементов поля α, β, γ справедливы соотношения α+β=β+α, αβ=βα, (α+β)γ=αγ+βγ; 3) в поле существуют нулевой и единичный элементы, обозначаемые соответственно как 0 и 1, для которых справедливо 0+α=α, 0α=0, 1α=α; 4) в поле для любого α≠0 существует обратный ему элемент по сложению, обозначаемый (-α), для которого справедливо α+(-α)=0; и обратный ему элемент по умножению, обозначаемый α-1, для которого справедливо αα-1=1; 5) любой ненулевой элемент поля можно представить в виде степени примитивного элемента: ∀α≠0, α=ωi, таким образом, конечное поле можно представить в виде GF(q)={0, ω0=1, ω, ω2, …, ωq-2}.
Генераторы псевдослучайных чисел (ГПСЧ) - основа стохастических методов защиты информации, применение ГПСЧ обеспечивает непредсказуемое поведение объекта и средств защиты, позволяя тем самым защититься от активного противника.
Известен генератор псевдослучайных чисел, функционирующий в конечном поле GF(p), где р>2 - простое, состоящий из N регистров разрядности]log2p[, N блоков сложения в GF(p), N блоков умножения в GF(p), причем величина, на которую происходит умножение в (i+1)-м блоке умножения, равна коэффициенту ai характеристического многочлена ϕ(х)=(х-1)λ(х)=xN+aN-1+…+a2x2+а1х+а0, где i=0, 1, 2, …, (N-1), ai ∈ GF(p), λ(х) - многочлен степени (N-1), примитивный над GF(p), выходы N-го регистра соединены со входами всех блоков умножения, выходы j-x блоков умножения соединены с первыми входами j-x блоков сложения, выходы которых соединены со входами j-x регистров, где j=1, 2, N, вторые входы всех блоков сложения образуют N групп управляющих входов генератора, выходы k-х регистров соединены со третьими входами (k+1)-х блоков сложения, выходы которых соединены со входами (j+1)-х регистров, где k=1, 2, …, (N-1). (М.А. Ivanov, B.V. Kliuchnikova, Е.А. Salikov, A.V. Starikovskii. New class of non-binary pseudorandom number generators. - Proceedings of Intelligent Technologies in Robotics, Moscow, Russia, 2019, pp. 255-262).
Сумма по модулю p значений на управляющих входах ГПСЧ не должна равняться нулю по модулю р. В этом случае генератор формирует р-ичную псевдослучайную последовательность длиной (М-р+1), где M=pN-1. Диаграмма переключений известного генератора состоит из двух циклов длиной (М-р+1) и р. Устройство ориентировано на реализацию технологии Design Obfuscation. Недостатком известного генератора является низкая эффективность программной и аппаратной реализации, учитывая, что большинство современных компьютеров используют двоичную логику, а не p-ичную.
Таким образом, наиболее близким по своей технической сущности к заявленному устройству является генератор псевдослучайных чисел, функционирующий в конечном поле GF(2n), где n>1 - целое, состоящий из N регистров разрядности n, (N-1) блоков сложения в GF(2n), N блоков умножения в GF(2n), причем величина, на которую происходит умножение в (i+1)-м блоке умножения, равна коэффициенту ai характеристического многочлена ϕ(х)=xN+aN-1+…+а2х2+а1х+а0, где i=0, 1, 2, …, (N-1), ai ∈ GF(2n), ϕ(х) - многочлен степени N, примитивный над GF(2n), выходы N-го регистра соединены со входами всех блоков умножения, выходы (j+1)-х блоков умножения и выходы j-x регистров соединены соответственно с первыми и вторыми входами j-x блоков сложения, выходы которых соединены со входами (j+1)-х регистров, где j=1, 2, …, (N-1), входы первого регистра подключены к выходам первого блока умножения (Патент США №9298423, Methods and systems for determining characteristics of sequence of N-state symbols, Mar. 29, 2016, Fig. 1). Аналогичное устройство описано в учебном пособии «Стохастические методы и средства защиты информации в компьютерных системах и сетях / М.А. Иванов, И.В. Чугунков, Н.А. Мацук и др. - М.: Кудиц-Пресс, 2009», стр. 82, рис. 2.12в.
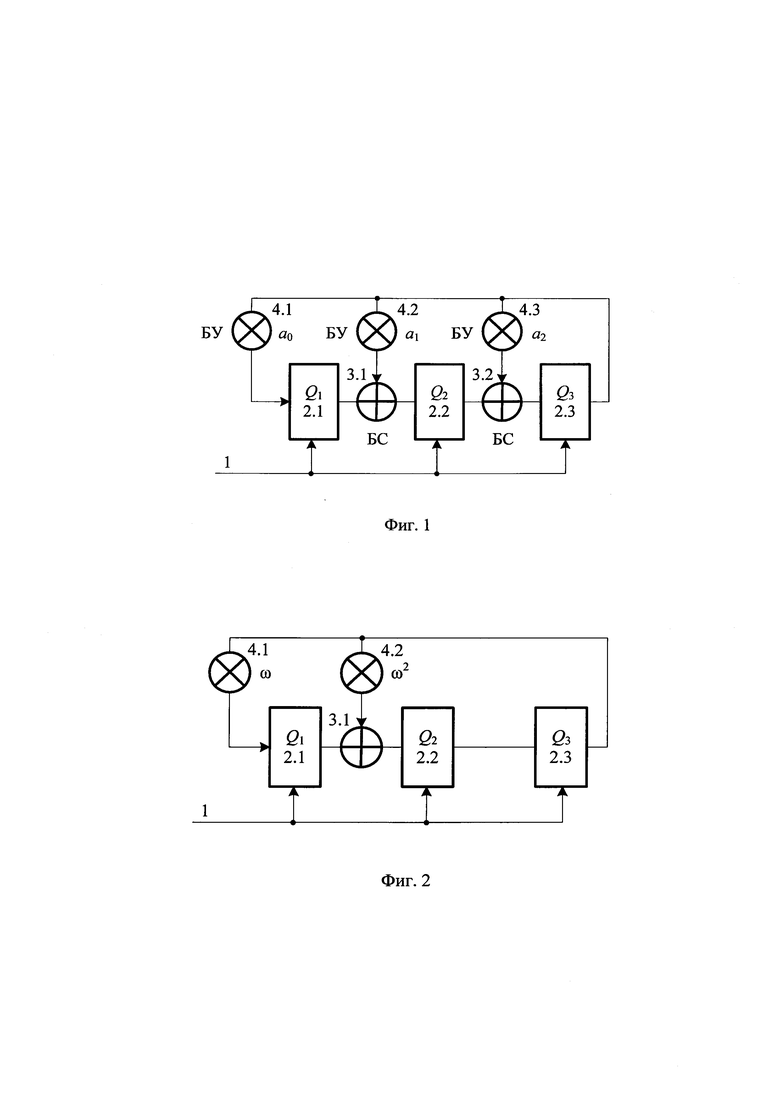
На фиг. 1 показана схема устройства-прототипа для случая N=3, ϕ(x)=x3+а2х2+а1х+а0, где ai ∈ GF(2n), 1 - тактовый вход генератора, 2.1, 2.2 и 2.3 - n-разрядные регистры, 3.1 и 3.2 - блоки сложения в поле GF(2n), 4.1, 4.2 и 4.3 - соответственно блоки умножения на а0, а1 и а2 в поле GF(2n).
На фиг. 2 показан пример устройства-прототипа для случая n=2, ϕ(х)=(х+1)(х2+х+ω)=х3+ω2х+ω, где λ(х)=х2+х+ω - многочлен, примитивный над GF(22)={0, 1, ω, ω2}, ω3=1, ω2+ω+1=0. Блок умножения 4.3 осуществляет умножение на а2=0, что эквивалентно отсутствию блоков 4.3 и 3.2. Диаграмма переключений устройства состоит из четырех циклов длиной 15 и четырех циклов длиной 1.
Техническим результатом изобретения является расширение функциональных возможностей устройства за счет повышения эффективности использования ГПСЧ, функционирующего в конечном поле GF(2n), при реализации технологии Design Obfuscation, ориентированной на защиту от аппаратных троянов за счет обфускации логической схемы защищаемого устройства.
Указанный технический результат обеспечивается за счет того, что генератор псевдослучайных чисел, состоящий из N регистров разрядности n, (N-1) блоков сложения в GF(2n), где n>1 - целое, N блоков умножения в GF(2n), причем величина, на которую происходит умножение в (i+1)-м блоке умножения, равна коэффициенту ai характеристического многочлена ϕ(х)=(х+1)λ(х)=xN+aN-1+…+а2х2+а1х+а0, где i=0, 1, 2, …, (N-1), ai ∈ GF(2n), λ(х) - многочлен степени (N-1), примитивный над GF(2n), выходы N-го регистра соединены со входами всех блоков умножения, выходы (j+1)-х блоков умножения и выходы j-x регистров соединены соответственно с первыми и вторыми входами j-x блоков сложения, выходы которых соединены со входами (j+1)-х регистров, где j=1, 2, …, (N-1), дополнительно содержит блок управляющих воздействий и N-й блок сложения в GF(2n), первые входы которого подключены к выходам первого блока умножения, а выходы соединены со входами первого регистра, вторые входы N-го блока сложения и третьи входы j-x блоков сложения подключены к соответствующим выходам блока управляющих воздействий.
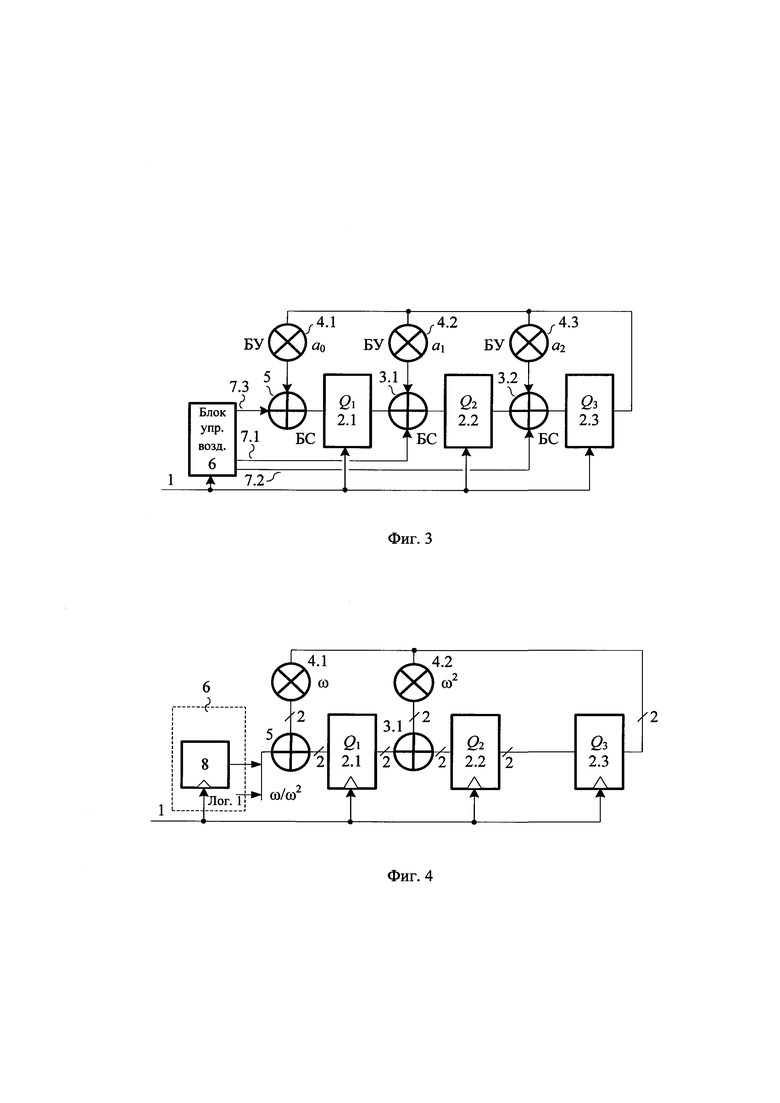
На фиг. 3 показана схема предлагаемого устройства для случая N=3, ϕ(х)=х3+а2х2+a1x+а0, где ai ∈ GF(2n), 1 - тактовый вход генератора, 2.1, 2.2 и 2.3 - n-разрядные регистры, 3.1 и 3.2 - блоки сложения в поле GF(2n), 4.1, 4.2 и 4.3 - соответственно блоки умножения на а0, а1 и а2 в поле GF(2n), 5 - третий блок сложения в поле GF(2n), 6 - блок управляющих воздействий, группы выходов 7.1, 7.2 и 7.3 блока 6 соединены со вторыми входами соответственно блоков сложения 3.1, 3.2 и 5.
ГПСЧ функционирует в конечном поле GF(2n), где n>1 - целое, и содержит N регистров 2.1, 2.2, …, 2.N разрядности n, (N-1) основных блоков 3.1, 3.2, …, 3.(N-1) сложения и один дополнительный блок 5 сложения, N блоков 4.1, 4.2, …, 4.N умножения, а также блок 6 управляющих воздействий. Выходы N-го регистра 2.N соединены со входами всех блоков 4.1, 4.2, …, 4.N умножения. Выходы (j+1)-х блоков 4.(j+1) умножения и выходы j-x регистров 2.j соединены соответственно с первыми и вторыми входами j-x блоков 3.j сложения. Выходы j-x блоков 3.j сложения соединены со входами (j+1)-х регистров 2.(N-1), где j=1, 2, …, (N-1). Первые входы дополнительного N-го блока 5 сложения, подключены к выходам первого блока 4.1 умножения, а выходы соединены со входами первого регистра 2.1, вторые входы дополнительного N-го блока 5 сложения и третьи входы j-х блоков 3.j сложения подключены к соответствующим выходам блока 6 управляющих воздействий.
На фиг. 4 показан пример предлагаемого устройства для случая n=2, ϕ(х)=(х+1)(х2+х+ω)=х3+ω2x+ω, где λ(х)=х2+х+ω - многочлен, примитивный над GF(22)={0, 1, ω, ω2}, ω3=1, ω2+ω+1=0. 2.1, 2.2 и 2.3 - двухразрядные регистры. 3.1 - двухвходовой блок сложения в поле GF(22). Блоки умножения 4.1 и 4.2 осуществляет умножение соответственно на ω и на ω2 в поле GF(22). Блок умножения 4.3 осуществляет умножение на а2=0, что эквивалентно отсутствию блоков 4.3 и 3.2. В рассматриваемом случае с выходов 7.1 и 7.2 блока 6 поступают нули, с выходов 7.3 - последовательность управляющих сигналов ω ω2 ω ω2 ω ω2…. Блок 6 состоит из Т-триггера 8, формирующего последовательность 0 1 0 1 0 1…. Диаграмма переключений устройства состоит из двух циклов длиной 60 и длиной 4.
По аналогии с известными генераторами (М-р+1) - последовательностями генераторы, показанные на фиг. 3 и 4 могут быть названы генератором (М-2n+1) - последовательности и генератором (М-3) - последовательности соответственно.
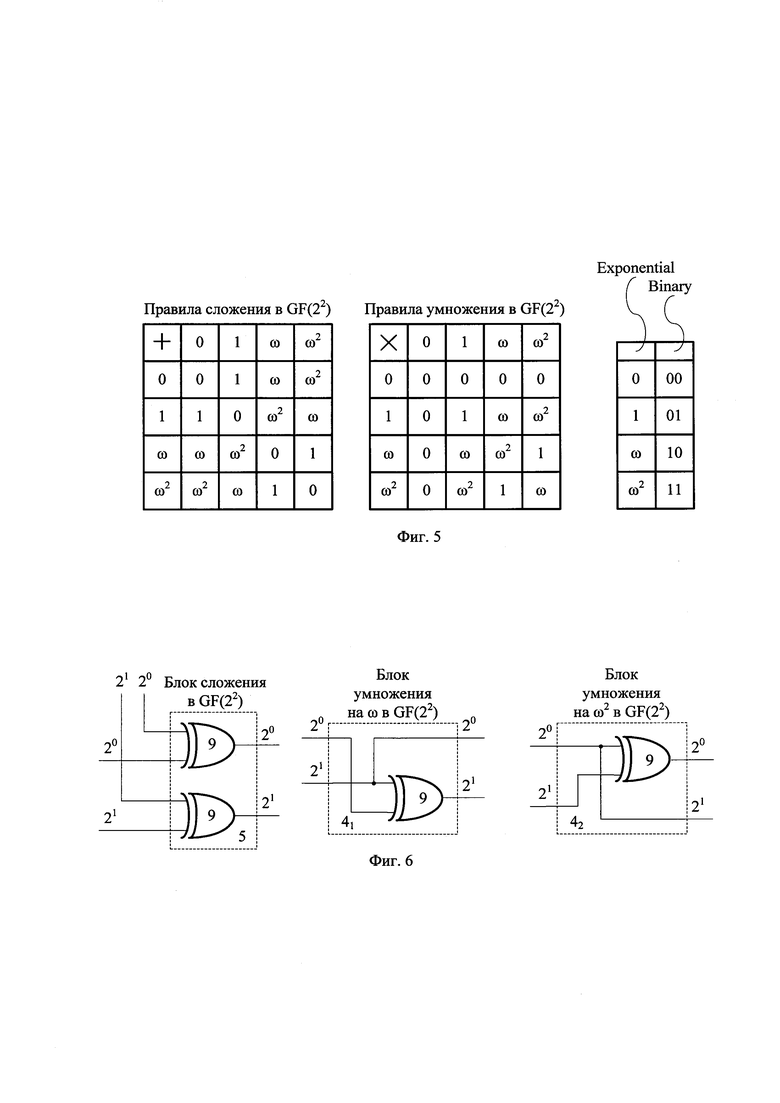
На фиг. 5 показаны правила сложения и умножения в поле GF(22)={0, 1, ω, ω2}, ω3=1, ω2+ω+1=0, а также соответствие между двумя формами представления элементов поля - в виде степеней примитивного элемента ω и в виде двухразрядных двоичных чисел.
На фиг. 6 показаны примеры реализации двухвходового блока сложения в поле GF(22), блока умножения на ω в поле GF(22) и блока умножения на ω2 в поле GF(22). Все эти блоки элементарно реализуются на двухвходовых элементах 9 исключающее ИЛИ, что подтверждает тезис об эффективной программной и аппаратной реализации заявленного устройства.
На фиг. 7 показана диаграмма переключений предлагаемого устройства для случая, показанного на рис. 4. Диаграмма состоит из двух циклов длиной 60 и 4. Жирным шрифтом выделены те состояния ГПСЧ, в которых на управляющем входе присутствует значение ω2.
В общем случае диаграмма переключений будет состоять из двух циклов длиной (М-2n+1) и 2n, где М=2nN-1. При реализации технологии Design Obfuscation это позволяет реализовать 2n скрытых функций (Hidden Functions) защищаемого устройства.
Устройство работает следующим образом. Перед началом работы все элементы памяти генератора устанавливаются в исходное состояние. Цепи установки в исходное состояние на фиг. 3 и 4 не показаны. Например, для случая, показанного на фиг. 4, все регистры 2.1, 2.2 и 2.3 и Т-триггер 8 устанавливаются в нулевое состояние.
В общем случае уравнения работы ГПСЧ имеют вид
Q1(t+1)=a0QN(t)+c1(t),
Qk(t+1)=ak-1QN(t)+Qk-1(t)+ck(t), k=2, 3, …, N,
где Qi(t) и Qi(t+1) - состояния i-го регистра генератора соответственно в моменты времени t и (t+1), ci(t) - управляющее воздействие в момент времени t, поступающее с соответствующего выхода блока 6, а все операции выполняются в поле GF(2n).
Для случая, рассмотренного на фиг. 4, уравнения принимают вид
Q1(t+1)=ωQ3(t)+ω в каждом нечетном такте,
Q1(t+1)=ωQ3(t)+ω2 в каждом четном такте,
Q2(t+1)=ω2Q3(t)+Q1(t),
Q3(t+1)=Q2(t),
где все операции выполняются в поле GF(22)={0, 1, ω, ω2}, ω3=1, ω2+ω+1=0.
Диаграмма переключений устройства, показанного на рис. 4, приведена на фиг. 7. Видно, что при корректной работе генератора значение свертки содержимого всех регистров меняется по закону 0 ω 1 ω2 0 ω 1 ω2 0 ω 1 ω2 ….
Важно отметить, что состояния генератора, попадающие в малое кодовое кольцо диаграммы переключений, зависят от вида управляющих воздействий с выхода блока 6.
Возможность достижения заявленного технического результата изобретения обуславливаются, во-первых, тем, что выбирая соответствующее значение n, можно реализовать любое количество скрытых функций в защищаемом устройстве, во-вторых, эффективной программной и аппаратной реализацией устройства, учитывая, что все операции в поле GF(2n) элементарно выполняются на элементах XOR, а само устройство за счет регулярной структуры легко реализуется в интегральном исполнении.
Таким образом, технический результат от использования изобретения заключается в повышении эффективности использования ГПСЧ при реализации технологии Design Obfuscation (Hardware Protection through Obfuscation. D. Forte, S. Bhunia, M.M. Tehranipoor editors. Springer International Publishing AG, 2017), ориентированной на защиту от аппаратных троянов за счет обфускации и рандомизации логической схемы защищаемого устройства.
В отличии от устройства-прототипа, диаграмма переключений которого состоит из двух циклов длиной 2nN-1 и 1, диаграмма переключений предлагаемого ГПСЧ состоит из двух циклов длиной (М-2n+1) и 2n, где М=2nN-1. При реализации технологии Design Obfuscation это позволяет реализовать 2n скрытых функций (Hidden Functions), при этом состояния ГПСЧ, входящие в малое кодовое кольцо, разрешают выполнение соответствующих функций защищаемого устройства.
| название | год | авторы | номер документа |
|---|---|---|---|
| ГЕНЕРАТОР ПСЕВДОСЛУЧАЙНЫХ ЧИСЕЛ | 2023 |
|
RU2815485C1 |
| ГЕНЕРАТОР ПСЕВДОСЛУЧАЙНЫХ ЧИСЕЛ | 2021 |
|
RU2776346C1 |
| УСТРОЙСТВО ДЛЯ ГЕНЕРАЦИИ ПСЕВДОСЛУЧАЙНЫХ ЧИСЕЛ | 2020 |
|
RU2761766C1 |
| УСТРОЙСТВО ДЛЯ ГЕНЕРАЦИИ ПСЕВДОСЛУЧАЙНЫХ ЧИСЕЛ | 2021 |
|
RU2774812C1 |
| ГЕНЕРАТОР ПСЕВДОСЛУЧАЙНЫХ ЧИСЕЛ | 2020 |
|
RU2756833C1 |
| СПОСОБ НЕЛИНЕЙНОГО ТРЕХМЕРНОГО МНОГОРАУНДОВОГО ПРЕОБРАЗОВАНИЯ ДАННЫХ RDOZEN | 2015 |
|
RU2591015C1 |
| СПОСОБ НЕЛИНЕЙНОГО ТРЕХМЕРНОГО МНОГОРАУНДОВОГО ПРЕОБРАЗОВАНИЯ ДАННЫХ DOZEN | 2012 |
|
RU2503994C1 |
| СПОСОБ НЕЛИНЕЙНОГО ТРЕХМЕРНОГО МНОГОРАУНДОВОГО ПРЕОБРАЗОВАНИЯ ДАННЫХ | 2017 |
|
RU2683689C1 |
| УСТРОЙСТВО ДЛЯ ГЕНЕРАЦИИ ПСЕВДОСЛУЧАЙНЫХ ЧИСЕЛ | 2022 |
|
RU2784684C1 |
| Устройство для деления многочленов | 1986 |
|
SU1483461A1 |

Изобретение относится к вычислительной технике и электросвязи, предназначено для решения задач защиты компьютерной информации. Генератор псевдослучайных чисел, функционирующий в конечном поле GF(2n), где n>1 - целое, содержащий N регистров 2.1, …, 2.N разрядности n, (N-1) блоков 3.1, …, 3.(N-1) сложения, N блоков 4.1, …, 4.N умножения, причем величина, на которую происходит умножение в (i+1)-м блоке умножения, равна коэффициенту аi характеристического многочлена ϕ(x)=(х+1)λ(x)=xN+aN-1+…+а2х2+а1х+a0, где i=0, 1, …, (N-1), аi ∈ GF(2n), λ(х) - многочлен степени (N-1), примитивный над GF(2n), выходы N-гo регистра 2.N соединены со входами всех блоков 4.1, …, 4.N умножения, выходы (j+1)-х блоков 4.(j+1) умножения и выходы j-x регистров 2.j соединены соответственно с первыми и вторыми входами j-x блоков 3.j сложения, выходы которых соединены со входами (j+1)-х регистров 2.(j+1), где j=1, 2, …, (N-1), дополнительно содержит блок 6 управляющих воздействий и N-й блок 5 сложения, первые входы которого подключены к выходам первого блока 4.1 умножения, а выходы соединены со входами первого регистра 2.1, вторые входы N-го блока 3.N сложения и третьи входы j-x блоков 3.j сложения подключены к соответствующим выходам блока 6 управляющих воздействий. Заявленное изобретение направлено на обеспечение защиты от аппаратных троянов за счет обфускации логической схемы защищаемого устройства. 7 ил.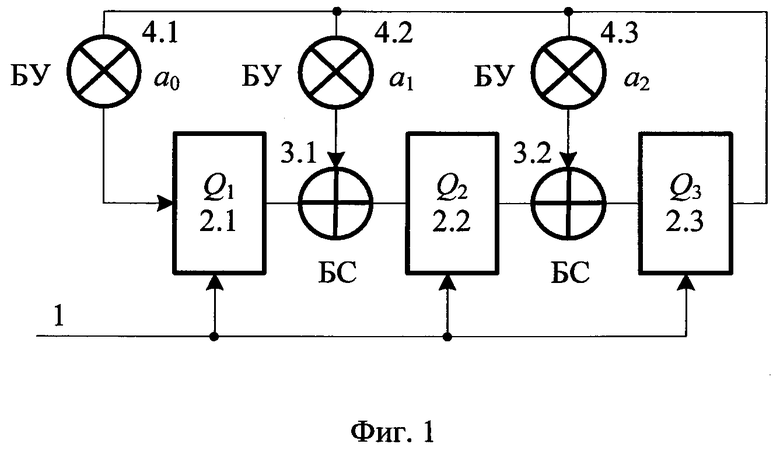
Генератор псевдослучайных чисел, состоящий из N регистров разрядности n, (N-1) блоков сложения в GF(2n), где n>1 - целое, N блоков умножения в GF(2n), причем величина, на которую происходит умножение в (i+1)-м блоке умножения, равна коэффициенту ai характеристического многочлена ϕ(x)=(х+1)λ(х)=xN+aN-1+…+а2х1+а1х+а0, где i=0, 1, 2, …, (N-1), ai ∈ GF(2n), λ(х) - многочлен степени (N-1), примитивный над GF(2n), выходы N-го регистра соединены со входами всех блоков умножения, выходы (j+1)-х блоков умножения и выходы j-х регистров соединены соответственно с первыми и вторыми входами j-x блоков сложения, выходы которых соединены со входами (j+1)-х регистров, где j=1, 2, (N-1), отличающийся тем, что он дополнительно содержит блок управляющих воздействий и N-й блок сложения в GF(2n), первые входы которого подключены к выходам первого блока умножения, а выходы соединены со входами первого регистра, вторые входы N-го блока сложения и третьи входы j-x блоков сложения подключены к соответствующим выходам блока управляющих воздействий.
| СПОСОБ ИЗГОТОВЛЕНИЯ КЕРАМИЧЕСКОГО КИРПИЧА | 1995 |
|
RU2101257C1 |
| US 6285761 B1, 04.09.2001 | |||
| US 6044388 A, 28.03.2000 | |||
| US 2003059045 A1, 28.03.2003. | |||
Авторы
Даты
2021-01-13—Публикация
2020-03-05—Подача