Изобретение относится к вычислительной технике и электросвязи, предназначено для решения задач защиты компьютерной информации. Наиболее предпочтительной областью использования изобретения является реализация стохастических методов защиты информации.
В совокупности признаков заявленного изобретения используются следующие термины:
Конечное поле или поле Галуа GF(q) (GF - Galois Field, q=pn - число элементов поля, р - простое, n - натуральное) - конечное множество элементов, обладающее следующими свойствами: 1) в поле определены две операции, одна условно называется сложением, другая - умножением; 2) для элементов поля α, β, γ справедливы соотношения α+β=β+α, αβ=βα, (α+β)γ=αγ+βγ; 3) в поле существуют нулевой и единичный элементы, обозначаемые соответственно как 0 и 1, для которых справедливо 0+α=α, 0α=0, 1α=α; 4) в поле для любого α≠0 существует обратный ему элемент по сложению, обозначаемый (-α), для которого справедливо α+(-α)=0; и обратный ему элемент по умножению, обозначаемый α-1, для которого справедливо αα-1=1; 5) любой ненулевой элемент поля можно представить в виде степени примитивного элемента ω: ∀α≠α=ωi, таким образом, конечное поле можно представить в виде GF(q)={0, ω0=1, ω, ω2, …, ωq-2}.
Стохастические алгоритмы преобразования данных (алгоритмы рандомизации) - алгоритмы, применяемые для решения задач защиты информации и обеспечивающие непредсказуемое поведение объектов и средств защиты. Используются для реализации нелинейных функций обратной связи или выхода генераторов псевдослучайных чисел (ГПСЧ) и функций хеширования. Отличительная особенность стохастических алгоритмов - интенсивное рассеивание и перемешивание информации.
ARX-алгоритмы - минималистские (Light-Weight) алгоритмы стохастического преобразования, основанные на использовании операций сложения (Add), циклического сдвига (Rotate) и исключающего ИЛИ (XOR), основные области применения которых - это RFID-системы и Интернет вещей.
Известен генератор псевдослучайных чисел, функционирующий в конечном поле GF(2n), где n>1 - целое, состоящий из N регистров разрядности n, (N-1) блоков сложения в GF(2n) и N блоков умножения в GF(2n), причем величина, на которую происходит умножение в (i+1)-м блоке умножения, равна коэффициенту ai характеристического многочлена ϕ(х)=xN+aN-1xN-1+…+а2х2+а1х+а0 над полем GF(2n). Выходы N-го регистра соединены со входами всех блоков умножения, выходы (j+1)-х блоков умножения и выходы j-x регистров соединены соответственно с первыми и вторыми входами j-x блоков сложения, выходы которых соединены со входами (j+1)-х регистров, где j=1, 2, …, (N-1), выходы первого блока умножения соединены со входами первого регистра [Иванов М.А., Саликов Е.А. Генератор псевдослучайных чисел. Патент РФ №2740339].
Недостатком известного генератора является линейный характер формируемых последовательностей, а значит предсказуемое поведение.
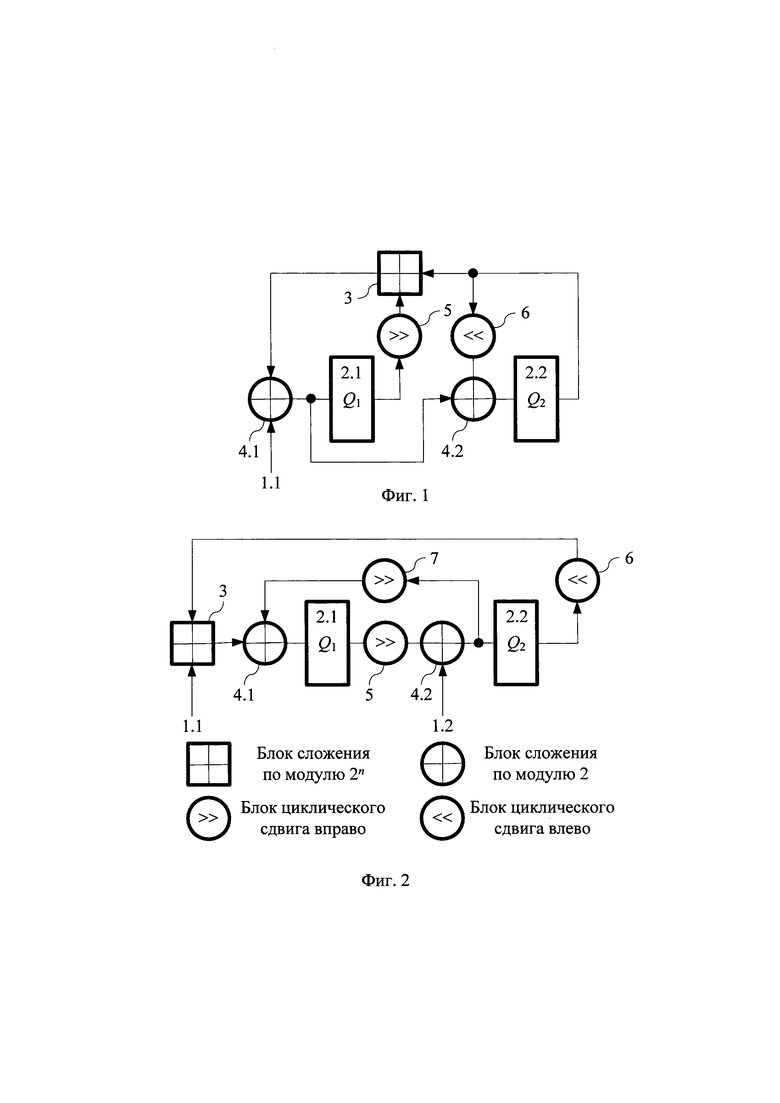
Таким образом, наиболее близким по своей технической сущности к заявленному является устройство для генерации псевдослучайных чисел, специфицированное в алгоритме SPEC32, состоящее из двух регистров разрядности n, двух блоков сложения в GF(2n), двух блоков циклического сдвига и блока сложения по модулю 2n, причем выходы первого блока сложения в GF(2n) соединены со входами первого регистра, выходы которого соединены со входами первого блока циклического сдвига, выходы второго блока сложения в GF(2n) соединены со входами второго регистра, выходы которого соединены со входами второго блока циклического сдвига; группа информационных входов устройства соединена с первыми входами первого блока сложения в GF(2n), вторые входы которого подключены к выходам блока сложения по модулю 2n, первые входы которого подключены к выходам второго регистра; выходы первого блока сложения в GF(2n) соединены с первыми входами второго блока сложения в GF(2n), вторые входы которого подключены к выходам второго блока циклического сдвига, выходы первого блока циклического сдвига соединены со вторыми входами блока сложения по модулю 2n. [Alex Biryukov, Vesselin Velichkov, and Yann Le Corre. Automatic Search for the Best Trails in ARX: Application to Block Cipher Speck. Cryptology ePrint Archive: Report 2016/409. https://eprint.iacr.org/2016/409.pdf].
На фиг. 1 показана схема устройства-прототипа, где 1 - группа ключевых входов; 2.1, 2.2 - n-разрядные регистры устройства Q1, Q2; 3 - блок сложения по модулю 2n; 4.1, 4.2 - блоки сложения в GF(2n); 5, 6 - соответственно первый и второй блоки циклического сдвига соответственно вправо и влево.
Техническим результатом изобретения является повышение эффективности устройства за счет повышения стойкости к линейному и дифференциальному анализу.
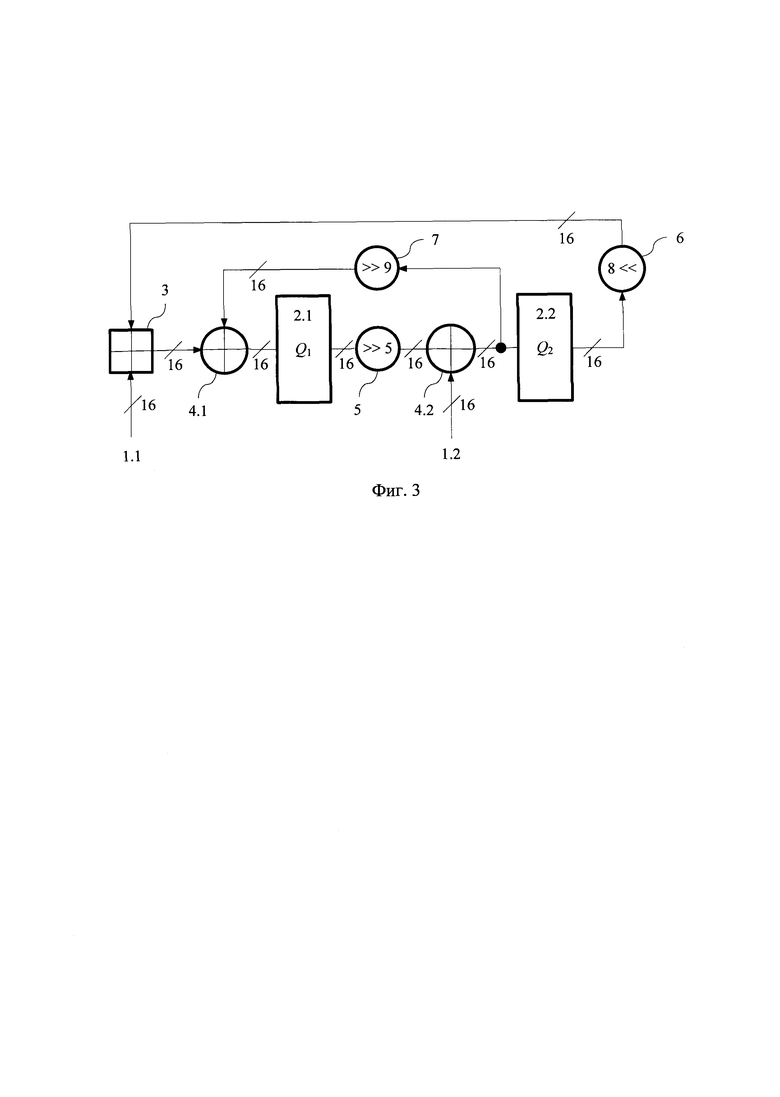
Поставленная цель достигается тем, что устройство для генерации псевдослучайных чисел, состоящее из двух регистров разрядности n, двух блоков сложения в GF(2n), блока сложения по модулю 2n, двух блоков циклического сдвига, причем выходы первого и второго блоков сложения в GF(2n) соединены со входами соответственно первого и второго регистров, выходы блока сложения по модулю 2n подключены к первой группе входов первого блока сложения в GF(2n), выходы первого и второго регистров соединены со входами соответственно первого и второго блоков циклического сдвига, дополнительно содержит третий блок циклического сдвига, входы и выходы которого соединены соответственно с выходами второго блока сложения в GF(2n) и второй группой входов первого блока сложения в GF(2n), выходы первого блока циклического сдвига соединены с первой группой входов второго блока сложения в GF(2n), выходы второго блока циклического сдвига соединены с первой группой входов блока сложения по модулю 2n, первая и вторая группы ключевых входов устройства соединены со вторыми группами входов соответственно блока сложения по модулю 2n и второго блока сложения в GF(2n).
Заявленный эффект обеспечивается за счет того, что в заявленном устройстве подмешивания ключевой информации осуществляется через разные операции (сложение по модулю 2n и сложение в GF(2n)), не образующие вместе с операцией циклического сдвига какой либо алгебраической структуры, это усложняет проведение статистического анализа с одной стороны, и обеспечивает более интенсивное перемешивание битов с другой.
В прототипе наоборот сложение с константой реализовано только в операции сложения в GF(2n) (XOR), поэтому, например, дифференциальный анализ там потенциально возможен. Результаты исследования прототипа показывают, что атаки на основе дифференциального анализа проходят до 14 раундов преобразования из 22.
На фиг. 2 показана схема предлагаемого устройства, где 1.1, 1.2 - группы ключевых входов устройства; 2.1, 2.2 - n-разрядные регистры устройства Q1, Q2; 3 - блок сложения по модулю 2n; 4.1, 4.2 - блоки сложения в GF(2n); 5, 6 и 7 - соответственно первый, второй и третий блоки циклического сдвига. На фиг. 3 показана схема устройства при n=16.
Выходы первого и второго блоков 4.1, 4.2 сложения в GF(2n) соединены со входами соответственно первого и второго регистров 4.1, 4.2. Первая группа 1.1 ключевых входов устройства подключена к первой группе входов блока 3 сложения по модулю 2n, выходы которого подключены к первой группе входов первого блока 4.1 сложения в GF(2n). Выходы второго регистра 2.2 соединены со входами первого блока 5 циклического сдвига. Входы и выходы третьего блока 7 циклического сдвига соединены соответственно с выходами первого регистра 2.1 и первой группой входов второго блока 4.2 сложения в GF(2n), вторая группа входов и выходы которого соединены соответственно со второй группой 1.2 ключевых входов устройства и входами второго блока 6 циклического сдвига, выходы которого соединены со второй группой входов первого блока 3.1 сложения в GF(2n). Выходы первого блока 5 циклического сдвига соединены со второй группой входов блока 3 сложения по модулю 2n.
Устройство работает следующим образом. Перед началом работы в регистры 2.1 и 2.2 записывается 2n-разрядный преобразуемый блок данных. Цепи загрузки на фиг. 2 не показаны. В каждом раунде преобразования (такте работы устройства) на входы 1.1 и 1.2 поступают раундовые ключи, обеспечивающие непредсказуемость результатов последующих операций. Тактовые входы регистров 2 объединены и образуют тактовый вход устройства, который также не показан на фиг. 2.
При поступлении тактовых импульсов устройство переключается в соответствии со схемой, показанной на фиг. 2. Суть выполняемого ARX-алгоритма - многократное повторение одного и того же раундового преобразования с разными ключами за счет чего обеспечивается рассеивание и перемешивание информации.
При использовании предлагаемого технического решения для реализации блока стохастического преобразования (фиг. 3) при решении задач стохастического кодирования [Иванов М.А. Способ обеспечения универсальной защиты информации, пересылаемой по каналу связи // Вопросы кибербезопасности. 2019, №3 (31), с. 45-50] оптимальное значение n равно 16, так как именно в этом случае обеспечивается 32-разрядное стохастическое преобразование, наиболее предпочтительное для большинства современных каналов связи [С.А. Осмоловский. Стохастические методы передачи данных. - М.: Радио и связь, 1991]. Блоки 5, 6 и 7 циклического сдвига в этом случае осуществляют сдвиг соответственно на 5 разрядов вправо, на 8 разрядов влево и на 9 разрядов вправо. Число раундов преобразования равно 20.
Таким образом, техническим результатом изобретения является повышение эффективности устройства за счет повышения стойкости к линейному и дифференциальному анализу.
С точки зрения аппаратных затрат формально число требуемых логических элементов не изменилось: один блок сложения по модулю 2n и два блока сложения в GF(2n), так как циклические сдвиги реализуются перекоммутацией соответвующих выходов, иначе говоря они не влияют на сложность реализации.
Схемотехнически самый сложный элемент во всей схеме это сложение по модулю 2n. В предлагаемом устройстве сложение по модулю 2n реализуется с константой. За счет этого можно уменьшить число тактов преобразования по сравнению с прототипом.
Кроме того сложение по модулю 2n с константой усложняет процедуру линейного анализа [А.А. Козлов, М.А. Иванов. Исследование возможности применения линейного анализа к ARX алгоритмам стохастического преобразования данных в зависимости от функции смешения с раундовым ключом // Безопасность информационных технологий, 2021 г., Том 28, №2, с. 62-69]. Использование подмешивания ключевой информации через разные операции (сложение по модулю 2n и сложения в GF(2n)), не образующие вместе с операцией циклического сдвига какой либо алгебраической структуры, усложняет проведение статистического анализа с одной стороны, и обеспечивает более интенсивное перемешивание битов с другой.
В Speck32 наоборот сложение с константой реализовано только в операции сложения в GF(2n), поэтому дифференциальный анализ там потенциально возможен. Исследования показывают, что атаки на основе дифференциального анализа для Speck32 проходят до 14-ти раундов (из 22-х).
Предлагаемое устройство ориентировано на использование в задачах стохастического кодирования информации. Стохастические коды С.А. Осмоловского - это единственный механизм, обеспечивающий решение всех задач защиты информации, пересылаемой по каналам связи, а именно задачи обнаружения и исправления случайных ошибок, вызванных помехами; задачи обеспечения секретности информации и задачи контроля целостности информации при ее умышленных искажениях. Кроме этого стохастические коды в отличие других существующих помехоустойчивых кодов, которые обеспечивающих обнаружение и исправление определенной доли ошибок, способны обеспечить наперед заданную вероятность правильного приема информации.
| название | год | авторы | номер документа |
|---|---|---|---|
| ГЕНЕРАТОР ПСЕВДОСЛУЧАЙНЫХ ЧИСЕЛ | 2021 |
|
RU2776346C1 |
| ГЕНЕРАТОР ПСЕВДОСЛУЧАЙНЫХ ЧИСЕЛ | 2020 |
|
RU2740339C1 |
| ГЕНЕРАТОР ПСЕВДОСЛУЧАЙНЫХ ЧИСЕЛ | 2020 |
|
RU2756833C1 |
| УСТРОЙСТВО ДЛЯ ГЕНЕРАЦИИ ПСЕВДОСЛУЧАЙНЫХ ЧИСЕЛ | 2020 |
|
RU2761766C1 |
| ГЕНЕРАТОР ПСЕВДОСЛУЧАЙНЫХ ЧИСЕЛ | 2023 |
|
RU2815485C1 |
| СПОСОБ ХЕШИРОВАНИЯ ИНФОРМАЦИИ | 2020 |
|
RU2747517C1 |
| УСТРОЙСТВО ДЛЯ ГЕНЕРАЦИИ ПСЕВДОСЛУЧАЙНЫХ ЧИСЕЛ | 2022 |
|
RU2784684C1 |
| СПОСОБ НЕЛИНЕЙНОГО ТРЕХМЕРНОГО МНОГОРАУНДОВОГО ПРЕОБРАЗОВАНИЯ ДАННЫХ DOZEN | 2012 |
|
RU2503994C1 |
| СПОСОБ ИТЕРАТИВНОГО КРИПТОГРАФИЧЕСКОГО ПРЕОБРАЗОВАНИЯ ДАННЫХ | 2012 |
|
RU2504911C1 |
| УСТРОЙСТВО ФОРМИРОВАНИЯ ТРИПЛЕКСНЫХ ЧИСЕЛ | 2023 |
|
RU2812412C1 |
Изобретение относится к устройству для генерации псевдослучайных чисел. Техническим результатом изобретения является повышение эффективности устройства за счет повышения стойкости к линейному и дифференциальному анализу. Устройство состоит из двух регистров 2.1 и 2.2 разрядности n, двух блоков сложения 4.1 и 4.2 в GF(2n), блока сложения 3 по модулю 2n, двух блоков 5 и 6 циклического сдвига, причем выходы первого и второго блоков сложения 4.1 и 4.2 в GF(2n) соединены с входами соответственно первого 2.1 и второго 2.2 регистров, выходы блока сложения 3 по модулю 2n подключены к первой группе входов первого блока сложения 4.1 в GF(2n), выходы первого 2.1 и второго 2.2 регистров соединены с входами соответственно первого 5 и второго 6 блоков циклического сдвига, и дополнительно содержит третий блок 7 циклического сдвига, входы и выходы которого соединены соответственно с выходами второго блока сложения 4.2 в GF(2n) и второй группой входов первого блока сложения 4.1 в GF(2n), выходы первого блока 5 циклического сдвига соединены с первой группой входов второго блока сложения 4.2 в GF(2n), выходы второго блока 6 циклического сдвига соединены с первой группой входов блока сложения 3 по модулю 2n, первая 1.1 и вторая 1.2 группы ключевых входов устройства соединены со вторыми группами входов соответственно блока сложения 3 по модулю 2n и второго блока сложения 4.2 в GF(2n). 3 ил.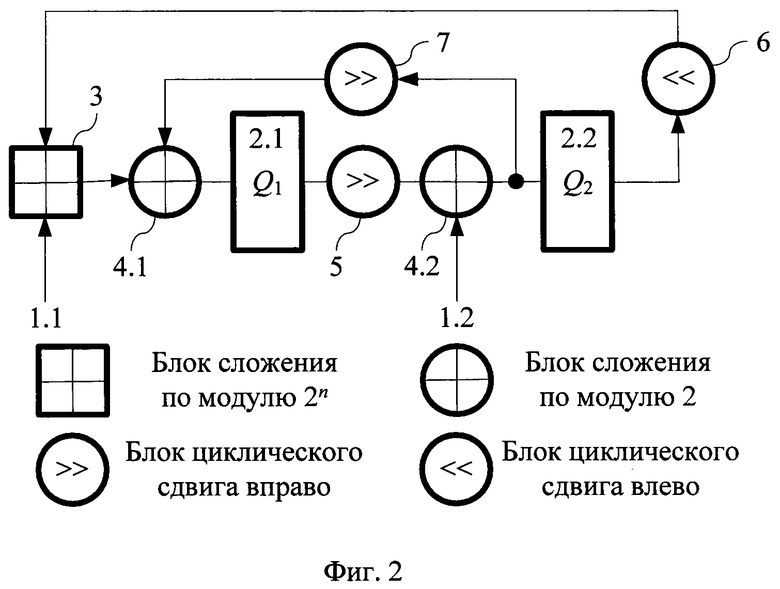
Устройство для генерации псевдослучайных чисел, состоящее из двух регистров разрядности n, двух блоков сложения в GF(2n), блока сложения по модулю 2n, двух блоков циклического сдвига, причем выходы первого и второго блоков сложения в GF(2n) соединены с входами соответственно первого и второго регистров, выходы блока сложения по модулю 2n подключены к первой группе входов первого блока сложения в GF(2n), выходы первого и второго регистров соединены с входами соответственно первого и второго блоков циклического сдвига, отличающееся тем, что оно дополнительно содержит третий блок циклического сдвига, входы и выходы которого соединены соответственно с выходами второго блока сложения в GF(2n) и второй группой входов первого блока сложения в GF(2n), выходы первого блока циклического сдвига соединены с первой группой входов второго блока сложения в GF(2n), выходы второго блока циклического сдвига соединены с первой группой входов блока сложения по модулю 2n, первая и вторая группы ключевых входов устройства соединены со вторыми группами входов соответственно блока сложения по модулю 2n и второго блока сложения в GF(2n).
| Alex Biryukov и др | |||
| Automatic Search for the Best Trails in ARX: Application to Block Cipher Speck, Fast Software Encryption, с | |||
| РЕЛЬСОВАЯ ПЕДАЛЬ | 1920 |
|
SU289A1 |
| ГЕНЕРАТОР ПСЕВДОСЛУЧАЙНЫХ ЧИСЕЛ | 2020 |
|
RU2740339C1 |
| 0 |
|
SU173172A1 | |
| СПОСОБ ИЗГОТОВЛЕНИЯ КЕРАМИЧЕСКОГО КИРПИЧА | 1995 |
|
RU2101257C1 |
| Способ восстановления спиралей из вольфрамовой проволоки для электрических ламп накаливания, наполненных газом | 1924 |
|
SU2020A1 |
| US 10078493 B2, 18.09.2018. | |||
Авторы
Даты
2022-06-23—Публикация
2021-07-08—Подача