Изобретение относится к вычислительной технике и электросвязи, предназначено для решения задач защиты компьютерной информации. Наиболее предпочтительной областью использования изобретения является реализация стохастических методов защиты информации.
В совокупности признаков заявленного изобретения используются следующие термины:
Регистры сдвига с линейной обратной связью (LFSR - Linear Feed-back Shift Register) - простейшие генераторы псевдослучайных чисел (ГПСЧ), активно используемые при решении различных задач защиты информации (см. [Стохастические методы и средства защиты информации в компьютерных системах и сетях / М.А. Иванов, А.В. Ковалев, И.В. Чугунков и др. - М.: КУДИЦ-ПРЕСС, 2009, 602 с.] или [Иванов М.А., Чугунков И.В. Криптографические методы защиты информации. - М.: НИЯУ МИФИ, 2012, ххх с, www.aha.ru/~msa]).
Конечное поле или поле Галуа GF(q) (GF - Galois Field, q=pn - число элементов поля, р - простое, n - натуральное) - конечное множество элементов, обладающее следующими свойствами: 1) в поле определены две операции, одна условно называется сложением, другая - умножением; 2) для элементов поля α, β, γ справедливы соотношения α+β = β+α, αβ = βα, (α+β)γ = αγ+βγ; 3) в поле существуют нулевой и единичный элементы, обозначаемые соответственно как 0 и 1, для которых справедливо 0+α=α, 0α=0, 1α=α; 4) в поле для любого α ≠ 0 существует обратный ему элемент по сложению, обозначаемый (-α), для которого справедливо α+(-α) = 0; и обратный ему элемент по умножению, обозначаемый α-1, для которого справедливо αα-1 = 1; 5) любой ненулевой элемент поля можно представить в виде степени примитивного элемента: ∀α ≠ 0 α =ωi, таким образом, конечное поле можно представить в виде GF(q) = {0, ω0 = 1, ω, ω2, …, αq-2}.
Генераторы псевдослучайных чисел (ГПСЧ) - основа стохастических методов защиты информации, применение ГПСЧ обеспечивает непредсказуемое поведение объекта и средств его защиты, позволяя тем самым защититься от активного противника.
Последовательности, формируемые двоичными генераторами на основе регистров сдвига с линейными обратными связями - LFSR (Linear Feedback Shift Register), являются важнейшим классом псевдослучайных последовательностей (ПСП). Основными достоинствами этих генераторов являются:
- простота программной и аппаратной реализации; удобство интегрального исполнения из-за регулярной структуры, максимальное быстродействие;
- хорошие статистические свойства формируемых последовательностей;
- возможность построения на их основе генераторов, обладающих свойствами, ценными при решении специфических задач защиты информации (формирование последовательностей произвольной длины, формирование последовательностей с предпериодом, формирование ПСП с произвольным законом распределения, построение генераторов, обладающих свойством самоконтроля, и т.п.).
Математический аппарат, лежащий в основе LFSR, - теория конечных полей или полей Галуа. Существует две конструкции LFSR - схема Фибоначчи и схема Галуа, при этом вторая конструкция имеет много интересных свойств, которые используются в заявленном техническом решении.
LFSR, к сожалению, не являются непредсказуемыми, поэтому применяются при решении задач криптографической защиты информации лишь в качестве строительных блоков.
Исходная информация для построения двоичного LFSR - так называемый образующий многочлен. Степень этого многочлена определяет разрядность регистра сдвига, а ненулевые коэффициенты - характер обратных связей.
Известно устройство для генерации псевдослучайных чисел, функционирующее в конечном поле GF(2), состоящее из N D-триггеров, где N - степень образующего двоичного многочлена Ф(х), сумматора по модулю два, выход которого соединен со входом первого D-триггер, а k входов подключены к выходам D-триггеров, номера которых определяются k старшими ненулевыми коэффициентами Ф(х), при этом k = m-1, где m - число ненулевых коэффициентов Ф(х), входы i-х D-триггеров подключены к выходам (i-1)-х D-триггеров, где i=2, 3, …, N (см. [SECURED PSEUDO-RANDOM NUMBER GENERATOR. United States Patent № US 10078493; Sep. 18, 2018; FIG. 4A]).
Данная конструкция LFSR называется схемой Фибоначчи. Ее недостатком является ограниченная область использования, так как выбор Ф(х) ограничен только примитивными многочленами. В этом случае LFSR формируют последовательности максимальной длины М = 2N-1, а сами LFSR носят название генераторов М-последовательностей. Кроме того двоичные генераторы Фибоначчи не могут использоваться для построения расширенных полей Галуа GF(2N).
Таким образом, наиболее близким по своей технической сущности к заявленному устройству является двоичное устройство для генерации псевдослучайных чисел, состоящее из N D-триггеров, (N-1) блоков умножения в поле GF(2) и (N-1) блоков сложения в поле GF(2), при этом выход N-го D-триггера подключен ко входу первого D-триггера и входам всех блоков умножения, выход i-го блока умножения подключен к первому входу (N-i)-го блока сложения, второй вход которого соединен с выходом (N-i)-го D-триггера, а выход подключен ко входу (N-i+1)-го D-триггера, i=1, 2, 3, …, (N-1). (см. [SECURED PSEUDO-RANDOM NUMBER GENERATOR. United States Patent № US 10078493; Sep. 18, 2018; FIG. 4D] или [APPARATUS AND METHOD FOR RANDOM NUMBER GENERATION. United States Patent № US 7028059; Apr. 11, 2006; FIG. 1, FIG. 1A] или [СПОСОБ ЛИНЕЙНОГО ПРЕОБРАЗОВАНИЯ (ВАРИАНТЫ). Описание изобретения к патенту Ru 2598781; 31.07.2015]).
Данная конструкция LFSR называется схемой Галуа. В случае ее использования выбор Ф(х) не ограничен только примитивными многочленами. Полезными свойствами обладают LFSR, соответствующими многочленам вида Ф(х)=(х+1)λ(х) и Ф(х)=(х+1)2λ(х), где λ(х) - примитивный. Кроме того двоичные N-разрядные генераторы Галуа могут использоваться для построения расширенных конечных полей вида GF(2N).
В общем случае двоичному образующему многочлену степени N
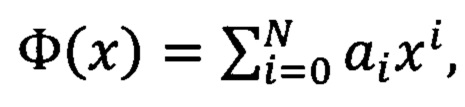
где aN=а0=1, aj ∈ {0,1}, j=1, 2, …, (N-1), соответствует генератор Галуа, уравнения работы которого имеют вид

где qi(t) и qi (t+1) - состояние i-го разряда регистра соответственно в моменты времени t и t+1, i = 1, 2, …, N; или в матричной форме
Q(t+1)=T⋅Q(t),
где 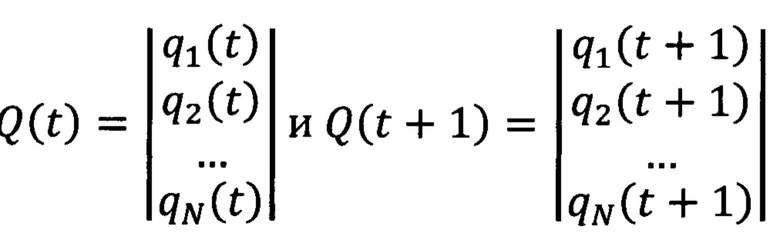 - состояния LFSR соответственно в моменты времени t и t+1, а T - квадратная матрица порядка N вида
- состояния LFSR соответственно в моменты времени t и t+1, а T - квадратная матрица порядка N вида

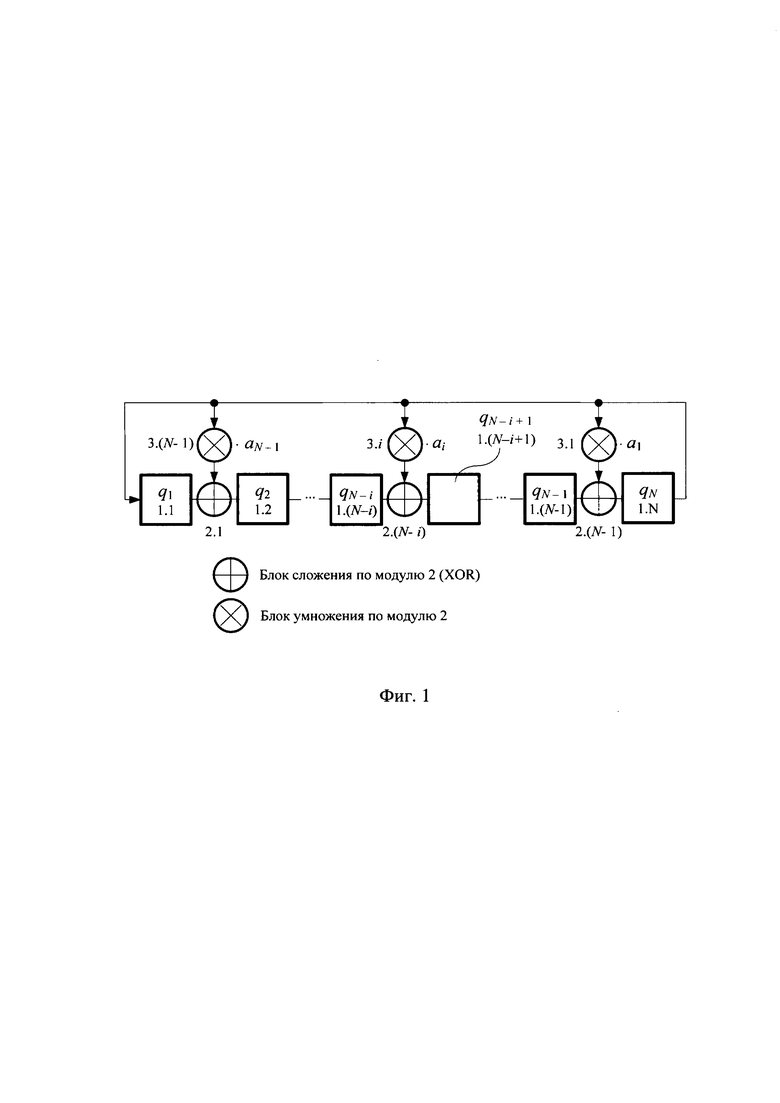
На фиг. 1 показана общая схема генератора Галуа, где 1.1, 1.2, 1.N - D-триггера, 2.1, 2.2, …, 2.(N-1) - блоки сложения в GF(2) (сумматоры по модулю два), 3.1, 3.2, …, 3.(N-1) - блоки умножения в GF(2). При ai=1 умножение на aj равносильно наличию связи, при ai = 0 умножение на aj, равносильно отсутствию связи, i = 1, 2, …, (N-1).
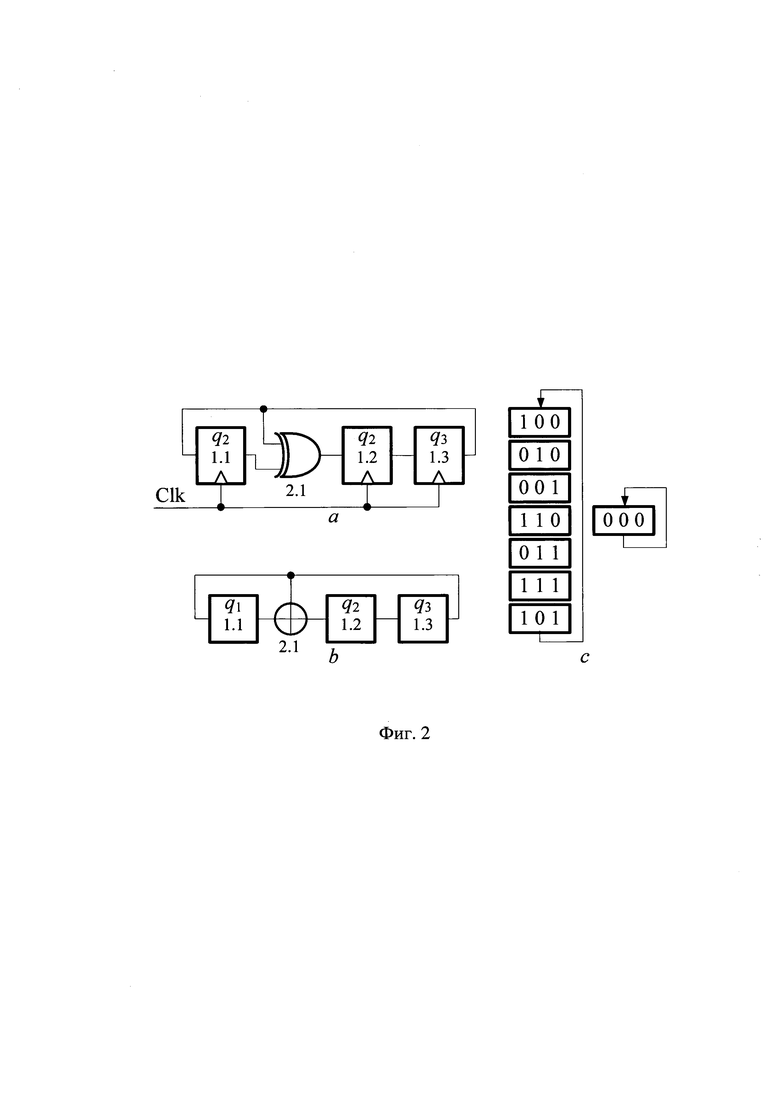
На фиг. 2 показан пример генератора Галуа для случая Ф(х) = х3+х2+1, где Ф(х) - примитивный над GF(2), 1.1, 1.2, 1.3 - D-триггера, 2.1 - сумматор по модулю два (элемент XOR): а и b - эквивалентные схемы устройства, с - диаграмма его переключений.
Если Ф(х) - примитивный двоичный многочлен степени N, то соответствующий N-разрядный LFSR будет иметь диаграмму переключений, включающую кодовое кольцо длиной 2N-1, в которое входят все ненулевые состояния генератора, и вырожденное состояние 00…0, переходящее само в себя (диаграмма (2N-1)-1). LFSR с диаграммой переключений вида (2N-1)-1 носят название генераторов М-последовательностей, а формируемые ими последовательности двоичных чисел длиной М=(2N-1) - М-последовательностями. Именно генераторы М-последовательностей чаще всего используются для генерации ПСП. Формируемая последовательность может сниматься с выхода любого разряда LFSR. Так, например, на выходе последнего разряда устройства, показанного на фиг. 2 и имеющего диаграмму переключений 7-1, формируется периодическая последовательность длиной 7 следующего вида …0010111…. На выходах других разрядов LFSR присутствуют сдвинутые копии той же последовательности.
Рассмотрим генераторы, соответствующие непримитивным многочленам вида Ф(х) = (х+1)λ(х), где λ(x) - примитивный двоичный многочлен. Выберем в качестве примера Ф(х) = (х+1)(х3+х+1). Раскрыв скобки и выполнив приведение подобных по модулю два, получим многочлен Ф(х) = х4+х3+х2+х+х+1 = х4+х3+х2+1, которому соответствует генератор Галуа, диаграмма переключений которого имеет вид 7-1-7-1, иначе говоря, содержит два кодовых кольца длиной 7 и два вырожденных состояния, переходящих самих в себя.
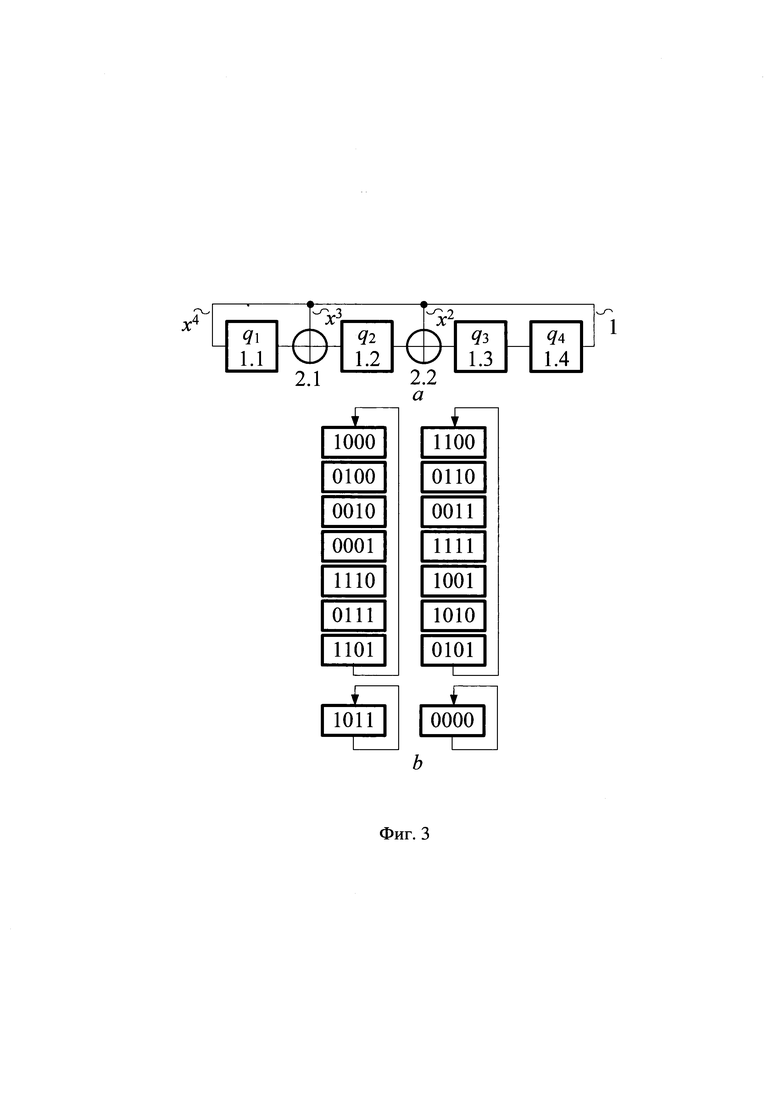
На фиг. 3 показана схема генератора Галуа, соответствующего многочлену Ф(х)=(х+1)(х3+х+1)=х4+х3+х2+1, где 1.1, 1.2, 1.3, 1.4 - D-триггера, 2.1, 2.2 - блоки сложения (сумматоры по модулю два): а - схема устройства, b - диаграмма переключений.
У генераторов Галуа, соответствующих Ф(х)=(х+1)λ(х), где λ(х) - примитивный двоичный полином, появляется интересное свойство - при правильной работе генератора свертка по модулю два содержимого всех разрядов не меняет своего значения. Действительно, на диаграмме переключений, показанной на фиг. 3, b, все состояния левого кодового кольца длиной 7 - нечетные, правого - четные. Данное свойство генератора позволяет в случае необходимости легко организовать самоконтроль правильности его работы, такие генераторы чаще всего используются для реализации счетчиков с самоконтролем (см. [Стохастические методы и средства защиты информации в компьютерных системах и сетях / М.А. Иванов, А.В. Ковалев, И.В. Чугунков и др. - М.: КУДИЦ-ПРЕСС, 2009, 602 с.]). В общем случае диаграмма переключений устройства имеет вид (2N-1-1)-1-(2N-1-1)-1.
Недостатком известного устройства являются ограниченные функциональные возможности из-за наличия двух запрещенных состояний.
Техническим результатом изобретения является расширение функциональных возможностей устройства за счет исключения ранее запрещенных состояний (состояния 1011 и 0000 на фиг. 3).
Указанный технический результат обеспечивается за счет того, что устройство для генерации псевдослучайных чисел, соответствующее образующему многочлену вида Ф(х) = (х+1)λ(х), где λ(х) - примитивный двоичный многочлен, состоящее из N D-триггеров, (N-1) блоков умножения в поле GF(2) и (N-1) блоков сложения в поле GF(2), при этом выход N-го D-триггера подключен ко входу первого D-триггера и входам всех блоков умножения, выход i-го блока умножения подключен к первому входу (N-i)-го блока сложения, второй вход которого соединен с выходом (N-i)-го D-триггера, а выход подключен ко входу (N-i+1)-го D-триггера, i=1, 2, 3, …, (N-1), дополнительно содержит дешифратор и четырехвходовой элемент ИЛИ, входы которого подключены к соответствующим выходам дешифратора, входы которого подключены к выходам всех D-триггеров, выход элемента ИЛИ подключен к дополнительным входам соответствующих блоков сложения, при этом число блоков сложения, к которым подключен выход элемента ИЛИ, всегда четное.
На фиг. 4 показан пример построения предлагаемого устройства, где 1.1, 1.2, 1.3, 1.4 - D-триггера, 2.1, 2.2 - блоки сложения (сумматоры по модулю два), селектор 4, дешифратор 5 и элемент 6 ИЛИ: а - схема исходного генератора Галуа (прототипа), соответствующего Ф(х) = х4+х3+х2+1, b - итоговая схема предлагаемого генератора, соответствующего Ф(х) = х4+х3+х2+1; с - исходная диаграмма переключений 7-1-7-1, d - диаграмма переключений 8-8 предлагаемого генератора.
Устройство работает следующим образом. Перед началом работы все D-триггера устанавливаются в исходное состояние. Цепь установки в исходное состояние на фиг. 4 не показана.
Для случая, рассмотренного на фиг. 4, уравнения генератора имеют вид
q1t+1)=q4(t)
q2(t+1)=q1(t)+q4(t)+z,
q3(t+1)=q2(t)+q4(t)
q4(t+1)=q3(t)+z,
где все операции выполняются в поле GF(2), a z - сигнал на выходе селектора 4. Тактовый вход (Clk) устройства соединен с тактовыми входами D-триггеров. На фиг. 4 эта цепь не показана.
Предположим, начальное состояние устройства нечетное и равно q4 q3 q2 q1 = 0001. Как только в процессе своего функционирования генератор окажется в состоянии q4 q3 q2 q1 = 1000 на выходе z селектора 4 сформируется единица, которая инвертирует значения на входах триггеров 1.2 и 1.4. В результате в следующем такте генератор окажется не в состоянии q4 q3 q2 q1 = 0111, а в состоянии q4 q3 q2 q1 =1101. Когда генератор находится в этом состоянии, на выходе z селектора 4 по-прежнему присутствует единичный сигнал, который опять инвертирует значения на входах триггеров 1.2 и 1.4. В результате в следующем такте генератор не останется в состоянии q4 q3 q2 q1 = 1101, а переключится в состояние q4 q3 q2 q1 - 0111. И таким образом вновь окажется в основном цикле, состоящем из нечетных состояний (левая часть диаграммы переключений на фиг. 4, d).
Предположим, начальное состояние устройства четное и равно q4 q3 q2 q1 = 0011. Как только в процессе своего функционирования генератор окажется в состоянии q4 q3 q2 q1 = 0101 на выходе z селектора 4 сформируется единица, которая инвертирует значения на входах триггеров 1.2 и 1.4. В результате в следующем такте генератор окажется не в состоянии q4 q3 q2 q1 = 1010, а в состоянии q4 q3 q2 q1 = 0000. Когда генератор находится в этом состоянии, на выходе z селектора 4 по-прежнему присутствует единичный сигнал, который опять инвертирует значения на входах триггеров 1.2 и 1.4. В результате в следующем такте генератор не останется в состоянии q4 q3 q2 q1 = 0000, а переключится в состояние q4 q3 q2 q1 = 0111. И таким образом вновь окажется в основном цикле, состоящем из четных состояний (правая часть диаграммы переключений на фиг. 4, d).
Возможность достижения заявленного технического результата изобретения обуславливаются тем, что исключаются два ранее запрещенных состояния, что увеличивает период формируемых последовательностей и повышается надежность устройства за счет исключения логики выхода генератора из запрещенных состояний, в котором устройство может оказаться в результате сбоя в работе. При этом ранее запрещенное четное состояние генератора оказывается в рабочем цикле, состоящем только из четных состояний, а ранее запрещенное нечетное состояние генератора оказывается в рабочем цикле, состоящем только из нечетных состояний. Иначе говоря, все свойства устройства, связанные с наличием двух рабочих циклов, в каждом из которых свертка по модулю два состояний всех элементов памяти при правильной работе генератора не меняет своего значения, сохранились, но появилось новое качество.
Таким образом, технический результат от использования изобретения заключается в расширении функциональных возможностей и как следствие, в увеличении длины формируемой последовательности и повышению надежности.
В отличие от устройства-прототипа, диаграмма переключений которого состоит из четырех циклов длиной (2N-1-1)-1-(2N-1-1)-1, диаграмма переключений предлагаемого устройства состоит из двух циклов длиной 2N-1.
| название | год | авторы | номер документа |
|---|---|---|---|
| ГЕНЕРАТОР ПСЕВДОСЛУЧАЙНЫХ ЧИСЕЛ | 2021 |
|
RU2776346C1 |
| ГЕНЕРАТОР ПСЕВДОСЛУЧАЙНЫХ ЧИСЕЛ | 2020 |
|
RU2756833C1 |
| ГЕНЕРАТОР ПСЕВДОСЛУЧАЙНЫХ ЧИСЕЛ | 2020 |
|
RU2740339C1 |
| ГЕНЕРАТОР ПСЕВДОСЛУЧАЙНЫХ ЧИСЕЛ | 2023 |
|
RU2815485C1 |
| УСТРОЙСТВО ДЛЯ ГЕНЕРАЦИИ ПСЕВДОСЛУЧАЙНЫХ ЧИСЕЛ | 2021 |
|
RU2774812C1 |
| Устройство для деления многочленов | 1986 |
|
SU1483461A1 |
| МНОГОКАНАЛЬНЫЙ СИГНАТУРНЫЙ АНАЛИЗАТОР | 1995 |
|
RU2087030C1 |
| Устройство для вычисления синдромов кода Рида-Соломона | 1990 |
|
SU1751860A1 |
| УСТРОЙСТВО ФОРМИРОВАНИЯ ТРИПЛЕКСНЫХ ЧИСЕЛ | 2023 |
|
RU2812412C1 |
| УСТРОЙСТВО КОДИРОВАНИЯ-ДЕКОДИРОВАНИЯ ИНФОРМАЦИИ | 1994 |
|
RU2115231C1 |

Изобретение относится к вычислительной технике и электросвязи, предназначено для решения задач защиты компьютерной информации. Технический результат заключается в расширении функциональных возможностей. Устройство для генерации псевдослучайных чисел состоит из из N D-триггеров, (N-1) блоков умножения в поле GF(2) и (N-1) блоков сложения в поле GF(2), при этом выход N-го D-триггера подключен ко входу первого D-триггера и входам всех блоков умножения, выход i-го блока умножения подключен к первому входу (N-i)-го блока сложения, второй вход которого соединен с выходом (N-i)-го D-триггера, а выход подключен ко входу (N-i+1)-го D-триггера, i=1, 2, 3, …, (N-1), дополнительно содержит дешифратор и четырехвходовый элемент ИЛИ, входы которого подключены к соответствующим выходам дешифратора, входы которого подключены к выходам всех D-триггеров, выход элемента ИЛИ подключен к дополнительным входам соответствующих блоков сложения, при этом число блоков сложения, к которым подключен выход элемента ИЛИ, всегда четное. 4 ил.
Устройство для генерации псевдослучайных чисел, соответствующее характеристическому многочлену вида Ф(х) = (х+1)λ(х), где λ(х) - примитивный двоичный многочлен, состоящее из N D-триггеров, (N-1) блоков умножения в поле GF(2) и (N-1) блоков сложения в поле GF(2), при этом выход N-го D-триггера подключен ко входу первого D-триггера и входам всех блоков умножения, выход i-го блока умножения подключен к первому входу (N-i)-го блока сложения, второй вход которого соединен с выходом (N-i)-го D-триггера, а выход подключен ко входу (N-i+1)-го D-триггера, i = 1, 2, 3, …, (N-1), отличающееся тем, что оно дополнительно содержит дешифратор и четырехвходовый элемент ИЛИ, входы которого подключены к соответствующим выходам дешифратора, входы которого подключены к выходам всех D-триггеров, выход элемента ИЛИ подключен к дополнительным входам соответствующих блоков сложения, при этом число блоков сложения, к которым подключен выход элемента ИЛИ, всегда четное.
| СПОСОБ ЛИНЕЙНОГО ПРЕОБРАЗОВАНИЯ (ВАРИАНТЫ) | 2015 |
|
RU2598781C1 |
| Способ получения цианистых соединений | 1924 |
|
SU2018A1 |
| СПОСОБ ПОТОЧНОГО КОДИРОВАНИЯ ДИСКРЕТНОЙ ИНФОРМАЦИИ | 2005 |
|
RU2296427C1 |
| СПОСОБ ПОТОЧНОГО КОДИРОВАНИЯ ДИСКРЕТНОЙ ИНФОРМАЦИИ | 2002 |
|
RU2205516C1 |
Авторы
Даты
2021-12-13—Публикация
2020-12-29—Подача