Изобретение относится к вычислительной технике и электросвязи, предназначено для решения задач защиты компьютерной информации. Наиболее предпочтительной областью использования изобретения является реализация стохастических методов защиты информации.
В совокупности признаков заявленного изобретения используются следующие термины:
Регистры сдвига с линейной обратной связью (LFSR - Linear Feedback Shift Register) - простейшие генераторы псевдослучайных чисел (ГПСЧ), активно используемые при решении различных задач защиты информации. Структура устройства определяется видом двоичного характеристического многочлена Ф(х) (см. [Стохастические методы и средства защиты информации в компьютерных системах и сетях / М.А. Иванов, А.В. Ковалев, И.В. Чугунков и др. - М.: КУДИЦ-ПРЕСС, 2009, 602 с.] или [Иванов М.А., Чугунков И.В. Криптографические методы защиты информации. - М.: НИЯУ МИФИ, 2012, www.aha.ru/~msa]).
Конечное поле или поле Галуа GF(q) (GF - Galois Field, q=pn - число элементов поля, р - простое, n - натуральное) - конечное множество элементов, обладающее следующими свойствами: 1) в поле определены две операции, одна условно называется сложением, другая - умножением; 2) для элементов поля α, β, γ справедливы соотношения α+β=β+α, αβ=βα, (α+β)γ=αγ+βγ; 3) в поле существуют нулевой и единичный элементы, обозначаемые соответственно как 0 и 1, для которых справедливо 0+α=α, 0α=0, 1α=α; 4) в поле для любого α≠0 существует обратный ему элемент по сложению, обозначаемый (-α), для которого справедливо α+(-α)=0; и обратный ему элемент по умножению, обозначаемый α-1, для которого справедливо αα-1=1; 5) любой ненулевой элемент поля можно представить в виде степени примитивного элемента ω: ∀α≠0 α=ωi, таким образом, конечное поле можно представить в виде GF(q)={0, ω0=1, ω, ω2, …, ωq-2}.
Генераторы псевдослучайных чисел (ГПСЧ) - основа стохастических методов защиты информации, применение ГПСЧ обеспечивает непредсказуемое поведение объекта и средств его защиты, позволяя тем самым защититься от активного противника.
Последовательности, формируемые генераторами на основе регистров сдвига с линейными обратными связями - LFSR (Linear Feedback Shift Register), функционирующих в конечных полях, являются важнейшим классом псевдослучайных последовательностей (ПСП). Основными достоинствами этих генераторов являются:
- простота программной и аппаратной реализации; удобство интегрального исполнения из-за регулярной структуры, максимальное быстродействие;
- гарантированно большой период и хорошие статистические свойства формируемых ПСП;
- возможность построения на их основе генераторов, обладающих свойствами, ценными при решении специфических задач защиты информации (формирование последовательностей произвольной длины, формирование последовательностей с предпериодом, формирование ПСП с произвольным законом распределения, построение генераторов, обладающих свойством самоконтроля, и т.п.).
Математический аппарат, лежащий в основе LFSR, - теория конечных полей или полей Галуа. Существует две конструкции LFSR - схема Фибоначчи и схема Галуа, при этом вторая конструкция имеет много интересных свойств, которые используются и в заявленном техническом решении.
LFSR, к сожалению, не являются непредсказуемыми, поэтому применяются при решении задач криптографической защиты информации лишь в качестве строительных блоков.
Исходная информация для построения двоичного LFSR - так называемый характеристический многочлен. Степень этого многочлена определяет разрядность регистра сдвига, а ненулевые коэффициенты - характер обратных связей.
Известен генератор псевдослучайных чисел, функционирующий в конечном поле GF(p), где р>2 - простое, состоящий из N регистров разрядности ]log2p[, N блоков сложения в GF(p), N блоков умножения в GF(p), причем величина, на которую происходит умножение в (i+1)-м блоке умножения, равна коэффициенту ai характеристического многочлена ϕ(х)=(х-1)λ(х)=xN-aN-1xN-1-…-а2х2-а1х-а0, где i=0, 1, 2, …, (N-1), ai∈GF(p), λ(х) - многочлен степени (N-1), примитивный над GF(p), выходы N-го регистра соединены со входами всех блоков умножения, выходы j-х блоков умножения соединены с первыми входами j-x блоков сложения, выходы которых соединены со входами j-x регистров, где j=1, 2, …, N, вторые входы всех блоков сложения образуют N групп управляющих входов генератора, выходы k-х регистров соединены со третьими входами (k+1)-х блоков сложения, выходы которых соединены со входами (j+1)-х регистров, где k=1, 2, (N-1). (М.А. Ivanov, B.V. Kliuchnikova, Е.А. Salikov, A.V. Starikovskii. New class of non-binary pseudorandom number generators. - Proceedings of Intelligent Technologies in Robotics, Moscow, Russia, 2019, pp. 255-262).
Недостатком известного генератора является сложность и зависимость длины формируемой последовательности от числа элементов поля, так как число запрещенных состояний устройства равно р.
Таким образом, наиболее близким по своей технической сущности к заявленному устройству является генератор псевдослучайных чисел, функционирующий в конечном поле GF(2n), где n>1 - целое, состоящий из N регистров разрядности n, N блоков сложения в GF(2n), блока управляющих воздействий и N блоков умножения в GF(2n), причем величина, на которую происходит умножение в (i+1)-м блоке умножения, равна коэффициенту ai характеристического многочлена ϕ(:с)=(х+1)λ(х)=xN+aN-1+…+а2х2+а1х+а0, где i=0, 1, 2, …, (N-1), ai∈GF(2n), λ(х) - многочлен степени (N-1), примитивный над GF(2n), Выходы N-го регистра соединены со входами всех блоков умножения, выходы (j+1)-х блоков умножения и выходы j-x регистров соединены соответственно с первыми и вторыми входами j-x блоков сложения, выходы которых соединены со входами (j+1)-х регистров, где j=1, 2, (N-1), первые входы N-го блока сложения в GF(2n) подключены к выходам первого блока умножения, а выходы соединены со входами первого регистра, вторые входы N-го блока сложения и третьи входы j-x блоков сложения подключены к соответствующим выходам блока управляющих воздействий [Иванов М.А., Саликов Е.А. Генератор псевдослучайных чисел. Патент РФ №2740339].
Известное устройство функционирует в конечном поле GF(2n) и формирует последовательность длиной 2nN-2n+1. Недостатком известного устройства является избыточная сложность из-за наличия блока управляющих воздействий, формирующего последовательности управляющих сигналов.
Техническим результатом изобретения является упрощение устройства и увеличение длины формируемой псевдослучайной последовательности.
Поставленная цель достигается тем, что генератор псевдослучайных чисел, функционирующий в конечном поле GF(2n), где n>1 - целое, состоящий из N регистров разрядности n, (N-1) блоков сложения в GF(2n), N блоков умножения в GF(2n), причем величина, на которую происходит умножение в (i+1)-м блоке умножения, равна коэффициенту ai характеристического многочлена
ϕ(x)=(х+1)λ(x)=xN+aN-1xN-1+…+a2x2+a1x+a0,
где i=0, 1, 2, …, (N-1), ai∈GF(2n), λ(х) - многочлен степени (N-1), примитивный над GF(2n), выходы N-го регистра соединены со входами всех блоков умножения, выходы (j+1)-х блоков умножения и выходы j-x регистров, где j=1, 2, (N-1), соединены соответственно с первыми и вторыми входами j-x блоков сложения, дополнительно содержит N сумматоров по модулю 2n, выходы (i+1)-х сумматоров по модулю 2n подключены ко входам (i+1)-х регистров, первые и вторые входы (i+1)-х сумматоров по модулю 2n подключены к выходам (i+1)-х блоков умножения и (i+1)-м группам управляющих входов генератора.
Заявленный эффект обеспечивается за счет того, что из схемы ГПСЧ исключается блок управляющих воздействий, так как все управляющие сигналы - это константы, а диаграмма переключений генератора включает в себя два цикла длиной 2nN - 2 и 2, т.е. длина формируемой последовательности не зависит от числа элементов поля.
На фиг. 1 показана схема генератора для случая GF(2n), N=3, где 1.1, 1.2, 1.3 - регистры генератора Q1, Q2, Q3; 2.1, 2.2 - блоки сложения в GF(2n); 3.1, 3.2 - блоки умножения в GF(2n), причем величина, на которую происходит умножение, определяется соответствующим коэффициентом характеристического многочлена; 4.1, 4.2, 4.3 - сумматоры по модулю 2n; 5.1, 5.2, 5.3 - группы управляющих входов генераторы, соответственно c1, с2, с3.
Генератор псевдослучайных чисел, в общем случае состоит из N регистров 1.1, 1.2, …, 1.N разрядности n, (N-1) блоков 2.1, 2.2, 2.(N-1) сложения в GF(2n), N блоков 3.1, 3.2, 3.N умножения в GF(2n), причем величина, на которую происходит умножение в (i+1)-м блоке умножения, равна коэффициенту а, характеристического многочлена
ϕ(х)=(х+1)λ(х)=xN+aN-1xN-1+…+а2х2+а1х+а0,
где i=0, 1, 2, …, (N-1), ai∈GF(2n), λ(х) - многочлен степени (N-1), примитивный над GF(2n), выходы N-го регистра 1.N соединены со входами всех блоков 3 умножения, выходы (j+1)-х блоков 3 умножения и выходы j-x регистров 1, где j=1, 2, …, (N-1), соединены соответственно с первыми и вторыми входами j-x блоков 2 сложения. Генератор содержит также N сумматоров 4.1, 4.2, …, 4.N по модулю 2n, выходы (i+1)-х сумматоров 4 по модулю 2n подключены ко входам (i+1)-х регистров 1, первые и вторые входы (i+1)-х сумматоров 4 по модулю 2п подключены к выходам (i+1)-х блоков 3 умножения и (i+1)-м группам управляющих входов 5 генератора.
Если какой-либо коэффициент а1, а2, …, aN-1 характеристического многочлена равен 1, это эквивалентно умножению на 1 в соответствующем блоке 3 умножения, иначе говоря, его отсутствию. Если какой-либо коэффициент а1, а2, …, aN-1 характеристического многочлена равен 0, это эквивалентно отсутствию соответствующих блока 2 сложения и блока 3 умножения. Таким образом, число блоков 3 умножения равно числу не равных нулю или единице коэффициентов характеристического многочлена (на фиг. 2 и 5 это число равно двум). Если какой-либо управляющий сигнал c1, с2, …, cN равен 0, это эквивалентно отсутствию соответствующего сумматора 4 по модулю 2n. Таким образом, число сумматоров 4 по модулю 2n равно числу не равных нулю управляющих сигналов 5 (на фиг. 2 и 5 это число равно единице).
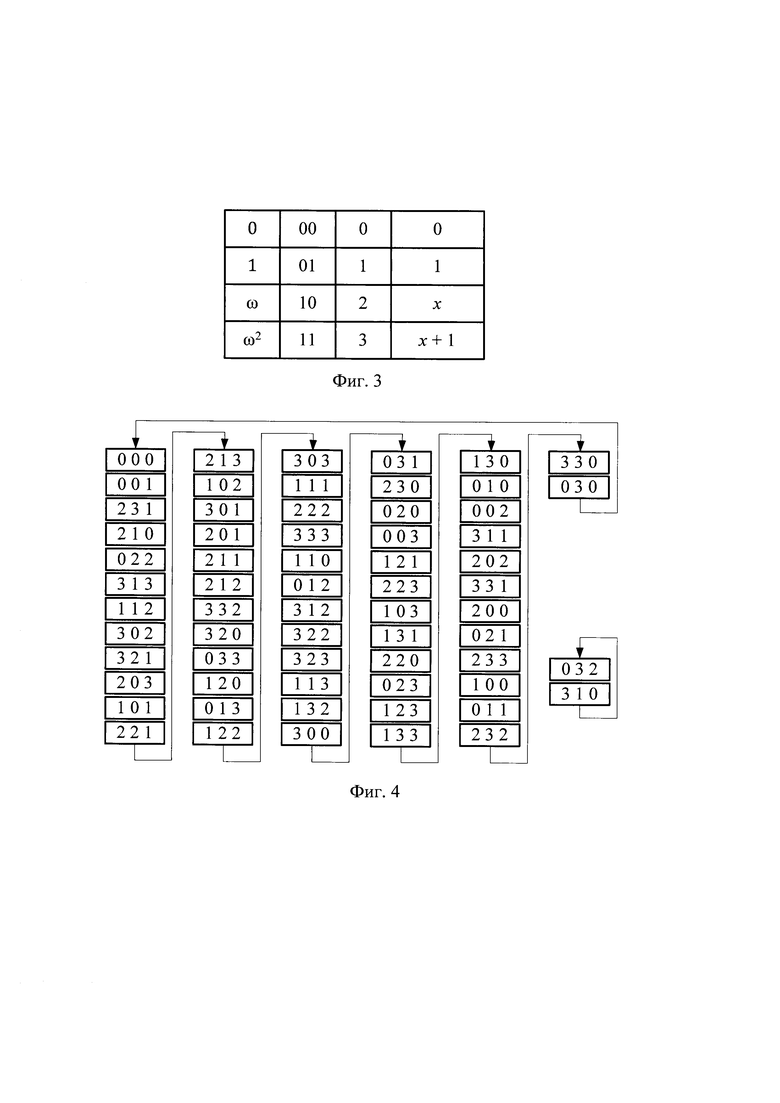
На фиг. 2 показан первый пример генератора для случая поля GF(22), когда характеристический многочлен степени N=3 имеет вид (х+1)(х2+х+ω)=х3+ω2х+ω, где х2+х+ω - многочлен, примитивный над GF(22). На фиг. 3 показано соответствие между различными формами представления элементов поля GF(22). На фиг. 4 показана диаграмма переключений генератора, схема которого приведена на фиг. 2.
На фиг. 5 показан второй пример генератора для случая поля GF(23), когда характеристический многочлен степени N=3 имеет вид (х+1)(х+ω)=х2+ω3х+ω, где х+ω - многочлен, примитивный над GF(23). На фиг. 6 показано соответствие между различными формами представления элементов поля GF(23). На фиг. 7 показана диаграмма переключений генератора, схема которого приведена на фиг. 5.
На фиг. 8 показан третий пример генератора для случая поля GF(22), когда характеристический многочлен степени N=2 имеет вид (х+1)(х+ω)=х2+ω2х+ω, где x+ω - многочлен, примитивный над GF(22). На фиг. 8 показаны также две диаграммы переключений вида 14-2 генератора для разных значений управляющих сигналов с1, с2.
Генератор псевдослучайных чисел (ГПСЧ) работает следующим образом. Перед началом работы регистры 1 генератора устанавливаются в одно из состояний цикла длиной 2nN-2. Два состояния, входящие в цикл длиной 2, являются запрещенными. Цепь установки в исходное состояние на фиг. 1 не показана. Тактовые входы регистров 1 объединены и образуют тактовый вход ГПСЧ, который также не показан на фиг. 1.
При поступлении тактовых импульсов ГПСЧ переключается в соответствии с уравнениями, приведенными на фиг. 1. Вне зависимости от используемого конечного поля GF(2n) диаграмма переключений генератора всегда имеет вид (2nN-2)-2, т.е. состоит из двух циклов длиной 2nN-2 и 2. Выходная псевдослучайная последовательность длиной 2nN-2 считывается с выходов одного из регистров 1 генератора. В примерах ГПСЧ, приведенных на фиг. 4 и 7 диаграммы переключений имеют вид 62-2. В примерах ГПСЧ, приведенных на фиг. 8, диаграммы переключений имеют вид 14-2. ГПСЧ, схема которого приведена на фиг. 2, формирует псевдослучайную последовательность длиной 62 над GF(22); ГПСЧ, схема которого приведена на фиг. 5, формирует псевдослучайную последова-тельность длиной 62 над GF(23); ГПСЧ, схема которого приведена на фиг. 8, формирует псевдослучайные последовательности длиной 14 над GF(22).
Таким образом, техническим результатом изобретения является упрощение устройства и увеличение длины формируемой последовательности.
В устройстве-прототипе требуется дополнительная логика для реализации блока управляющих сигналов, которые меняются в процессе работы устройства. Число запрещенных состояний в устройстве-прототипе растет с ростом n и равно 2n, в предлагаемом же изобретении число запрещенных состояний не зависит от n и всегда равно двум. Значения управляющих сигналов не меняются в процессе работы устройства и поэтому никакой дополнительной логики не требуется.
В устройстве-прототипе длина формируемой последовательности зависит от n и на 2n меньше максимально возможной длины, равной 2nN, в предлагаемом же изобретении длина формируемой последовательности не зависит от n и на 2 меньше максимально возможной длины, равной 2nN.
| название | год | авторы | номер документа |
|---|---|---|---|
| ГЕНЕРАТОР ПСЕВДОСЛУЧАЙНЫХ ЧИСЕЛ | 2020 |
|
RU2740339C1 |
| УСТРОЙСТВО ДЛЯ ГЕНЕРАЦИИ ПСЕВДОСЛУЧАЙНЫХ ЧИСЕЛ | 2020 |
|
RU2761766C1 |
| ГЕНЕРАТОР ПСЕВДОСЛУЧАЙНЫХ ЧИСЕЛ | 2023 |
|
RU2815485C1 |
| ГЕНЕРАТОР ПСЕВДОСЛУЧАЙНЫХ ЧИСЕЛ | 2020 |
|
RU2756833C1 |
| УСТРОЙСТВО ДЛЯ ГЕНЕРАЦИИ ПСЕВДОСЛУЧАЙНЫХ ЧИСЕЛ | 2021 |
|
RU2774812C1 |
| СПОСОБ НЕЛИНЕЙНОГО ТРЕХМЕРНОГО МНОГОРАУНДОВОГО ПРЕОБРАЗОВАНИЯ ДАННЫХ RDOZEN | 2015 |
|
RU2591015C1 |
| СПОСОБ НЕЛИНЕЙНОГО ТРЕХМЕРНОГО МНОГОРАУНДОВОГО ПРЕОБРАЗОВАНИЯ ДАННЫХ DOZEN | 2012 |
|
RU2503994C1 |
| УСТРОЙСТВО ДЛЯ ГЕНЕРАЦИИ ПСЕВДОСЛУЧАЙНЫХ ЧИСЕЛ | 2022 |
|
RU2784684C1 |
| УСТРОЙСТВО ФОРМИРОВАНИЯ ПСЕВДОСЛУЧАЙНЫХ КОМПЛЕКСНЫХ ЧИСЕЛ | 2022 |
|
RU2800190C1 |
| УСТРОЙСТВО ФОРМИРОВАНИЯ ТРИПЛЕКСНЫХ ЧИСЕЛ | 2023 |
|
RU2812412C1 |





Настоящее изобретение относится к области вычислительной техники для защиты информации. Технический результат заключается в упрощении устройства генератора псевдослучайных чисел и увеличении длины формируемой псевдослучайной последовательности. Технический результат достигается за счёт N регистров 1.1, 1.2, …, 1.N разрядности n, (N-1) блоков 2.1, 2.2, …, 2.(N-1) сложения в GF(2n), N блоков 3.1, 3.2, …, 3.N умножения в GF(2n), причем величина, на которую происходит умножение в (i+1)-м блоке умножения, равна коэффициенту аi характеристического многочлена ϕ(х)=(х+1)λ(х)=xN+aN-1xN-1+…+а2х2+а1х+а0, а также N сумматоров 4.1, 4.2, …, 4.N по модулю 2n. 8 ил.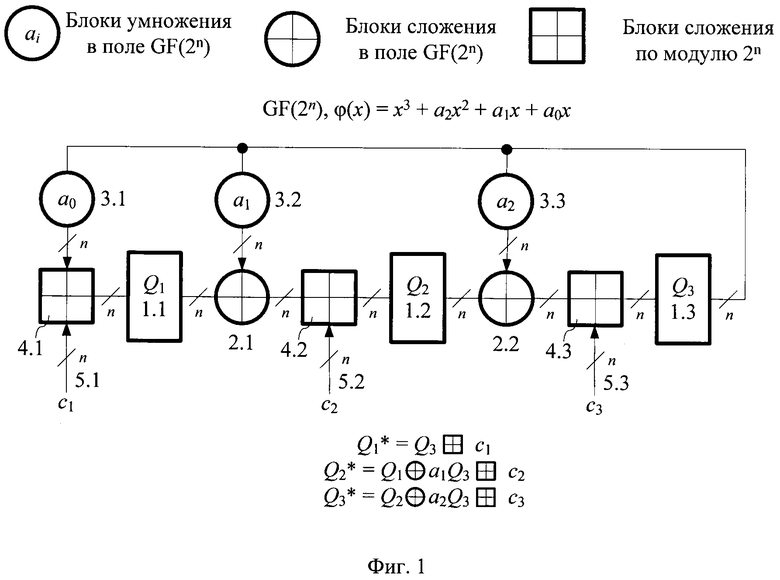
Генератор псевдослучайных чисел, состоящий из N регистров разрядности n, (N-1) блоков сложения в GF(2n), N блоков умножения в GF(2n), причем величина, на которую происходит умножение в (i+1)-м блоке умножения, равна коэффициенту ai характеристического многочлена ϕ(x)=(х+1)λ(х)=xN+aN-1xN-1+…+a2x2+а1х+a0, где i=0, 1, 2, …, (N-1), ai∈GF(2n), λ(х) - многочлен степени (N-1), примитивный над GF(2n), выходы N-го регистра соединены со входами всех блоков умножения, выходы (i+1)-х блоков умножения и выходы j-x регистров, где j=1, 2, …, (N-1), соединены соответственно с первыми и вторыми входами j-x блоков сложения, отличающийся тем, что он дополнительно содержит N сумматоров по модулю 2n, выходы (i+1)-х сумматоров по модулю 2n подключены ко входам (i+1)-х регистров, первые и вторые входы (i+1)-х сумматоров по модулю 2n подключены к выходам (i+1)-х блоков умножения и (i+1)-м группам управляющих входов генератора.
| ГЕНЕРАТОР ПСЕВДОСЛУЧАЙНЫХ ЧИСЕЛ | 2020 |
|
RU2740339C1 |
| US 8433740 B2, 30.04.2013 | |||
| US 6044388 A, 28.03.2000 | |||
| US 20050044119 A1, 24.02.2005 | |||
| EP 2000901 B1, 10.12.2008 | |||
| JP 6900176 B2, 15.06.2017. | |||
Авторы
Даты
2022-07-19—Публикация
2021-07-08—Подача