Изобретение относится к вычислительной технике и электросвязи, предназначено для решения задач защиты компьютерной информации. Наиболее предпочтительной областью использования изобретения является реализация стохастических методов защиты информации.
В совокупности признаков заявленного изобретения используются следующие термины.
Конечное поле или поле Галуа GF(g) (GF - Galois Field, q=pn - число элементов поля, р - простое, n - натуральное) - конечное множество элементов, обладающее следующими свойствами:
1) в поле определены две операции, одна условно называется сложением, другая - умножением;
2) для элементов поля α, β, γ справедливы соотношения α+β=β+α, αβ=βα, (α+β)γ=αγ+βγ;
3) в поле существуют нулевой и единичный элементы, обозначаемые соответственно как 0 и 1, для которых справедливо 0+α=α, 0α=0, 1α=α;
4) в поле для любого α≠0 существует обратный ему элемент по сложению, обозначаемый (-α), для которого справедливо α+(-α)=0; и обратный ему элемент по умножению, обозначаемый α-1, для которого справедливо αα-1=1;
5) любой ненулевой элемент поля можно представить в виде степени примитивного элемента: ∀α≠0 α=ωi,таким образом, конечное поле можно представить в виде GF(q)={0, ω0=:1, ω, ω2,…,ωq-2}.
Генераторы псевдослучайных чисел (ГПСЧ) - основа стохастических методов защиты информации, применение ГПСобеспечивает непредсказуемое поведение цифрового объекта и средств его защиты.
Известен генератор псевдослучайных чисел, функционирующий в конечном поле GF(2n), состоящий из N регистров разрядности n, N блоков сложения в GF(2n), где n>1 - целое, N блоков умножения в GF(2n), причем величина, на которую происходит умножение в (i+1)-м блоке умножения, равна коэффициенту ai характеристического многочлена ϕ(х)=(х+1)λ(x)=xN+aN-1+…+а2х2+а1х+а0, где i=0, 1, 2, …, (N-1), ai,∈GF(2n),λ(х) - многочлен степени (N-1), примитивный над GF(2n), блок управляющих воздействий, выходы N-го регистра соединены со входами всех блоков умножения, выходы (j+1)-х блоков умножения и выходы j-x регистров соединены соответственно с первыми и вторыми входами j-x блоков сложения, выходы которых соединены со входами (j+1)-х регистров, где j=1,2,… (N-1), первые входы N-го блоков сложения в GF(2n) подключены к выходам первого блока умножения, а выходы соединены со входами первого регистра, вторые входы N-го блока сложения и третьи входы j-x блоков сложения подключены к соответствующим выходам блока управляющих воздействий (Патент РФ №2740339, Генератор псевдослучайных чисел, БИ №2, 13.01.2021).
Недостатком известного устройства является сложность (требуется блок управляющих воздействий) и линейный закон формирования псевдослучайной последовательности (все вычисления выполняются в конечных полях).
В качестве прототипа выбран генератор псевдослучайных чисел, функционирующий в конечном поле GF(2n), где n>1 - целое, состоящий из N регистров разрядности n, (N-1) блоков сложения в GF(2n), N блоков умножения в GF(2n), причем величина, на которую происходит умножение в (i+1)-м блоке умножения, равна коэффициенту a характеристического многочлена степени N ϕ(х)=xN+aN-1+…+а2х2+а1х+а0, где i=0, 1, 2, …,(N-1), ai∈GF(2n), выходы N-го регистра соединены со входами всех блоковумножения, выходы (j+1)-х блоков умножения и выходы j-x регистров соединены соответственно с первыми и вторыми входами j-x блоков сложения, выходы которых соединены со входами (j+1)-х регистров, где j=1, 2, …(N-1), входы первого регистра подключены к выходам первого блока умножения (Патент США №9298423, Methods and systems for determining characteristics of sequence of N-state symbols, Mar. 29, 2016, Fig. 1). Аналогичное устройство описано в учебном пособии “Стохастические методы и средства защиты информации в компьютерных системах и сетях / М. А. Иванов, И. В. Чугунков, Н. А. Мацук и др. - М.: Кудиц-Пресс, 2009”, стр. 82, рис. 2.12в.
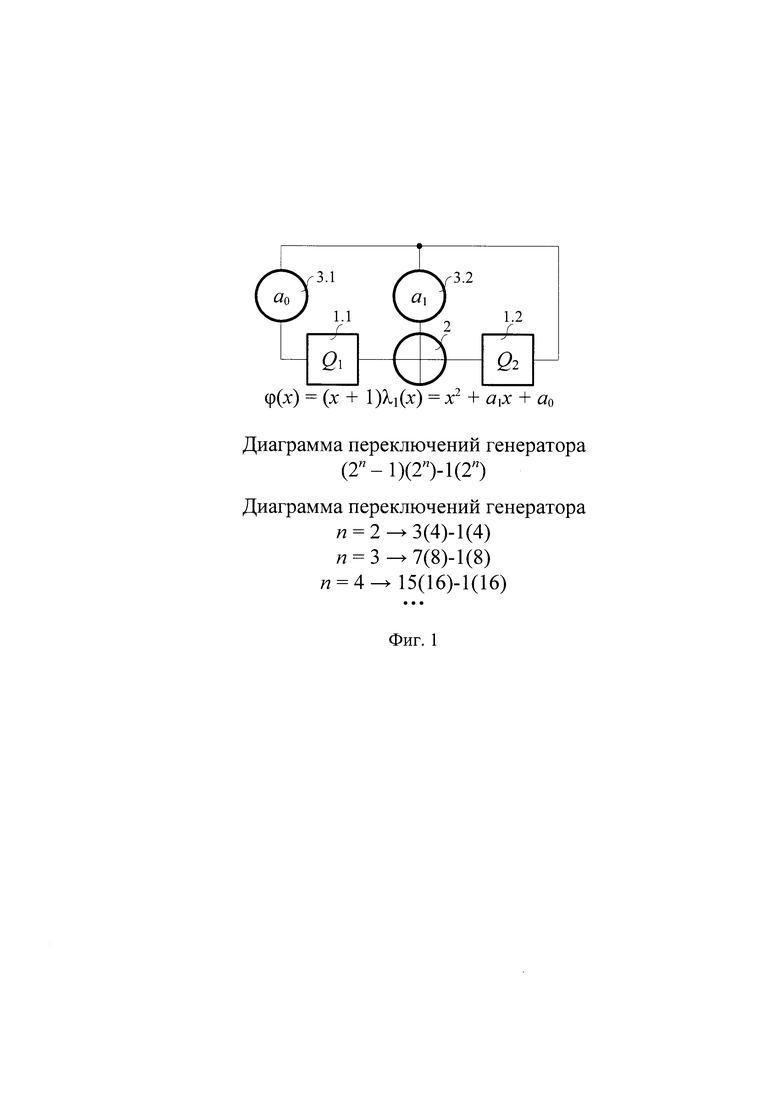
Если в качестве характеристического многочлена выбран многочлен вида ϕ(х)=(х+1)λ(х)=х2+а1х+а0, где λ(х) - многочлен первой степени, примитивный над GF(2n), диаграмма переключений устройства состоит из 2n циклов длиной 2n-1 и 2n циклов длиной 1, т.е. имеет вид (2n-1)(2n)-1(2n). Таким образом, несмотря на наличие 2n элементов памяти максимальная длина формируемой последовательности равна 2n-1, что сильно меньше потенциально возможной 22n.
Целью изобретения является увеличение длины формируемой последовательности до величины 2n (2n-1)=(22п-2n), т.е. в 2n раз большей, чем в прототипе.
Заявленный эффект обеспечивается за счет того, что диаграмма переключений генератора включает в себя не 2n+1 циклов как в прототипе, а всего лишь два цикла длиной (22n-2n) и 2n.
Поставленная цель достигается тем, что генератор псевдослучайных чисел, состоящий из двух регистров разрядности n, блока сложения в GF(2n), двух блоков умножения в GF(2n), где n>1 - целое, причем величины, на которые происходит умножение в первом и втором блоках умножения в GF(2n), равны соответственно коэффициентам а0 и а1 характеристического многочлена ϕ(х)=(х+1)λ(х)=х2+а1х+а0, где а1, а0∈GF(2n), λ(х) - многочлен первой степени, примитивный над GF(2n), выходы второго регистра соединены со входами блоков умножения в GF(2n), выходы первого блока умножения в GF(2n) соединены со входами первого регистра, выходы второго блока умножения в GF(2n) соединены с первыми входами блока сложения в GF(2n), вторые входы которого соединены с выходами первого регистра, дополнительно содержит второй блок сложения в GF(2n) и блок сложения по модулю 2n, причем выходы первого блока умножения в GF(2n) подключены к первым входам второго блока сложения в GF(2n) и третьим входам первого блока сложения в GF(2n), выходы которого соединены с первыми входами блока сложения по модулю 2n, вторые входы которого образуют управляющие входы генератора, вторые входы второго блока сложения в GF(2n) соединены с выходами блока сложения по модулю 2n, а выходы второго блока сложения в GF(2n) соединены со входами второго регистра.
На фиг. 1 показана схема устройства-прототипа при N=2, ϕ(х)=х2+а1х+а0, где 1.1, 1.2 - n-разрядные регистры; 2 - блок сложения в поле GF(2n); 3.1 и 3.2 - блоки умножения а0 и а1 в поле GF(2n) соответственно. На фиг. 1 показаны тип диаграммы переключений в общем случае и при n=2, 3 и 4.
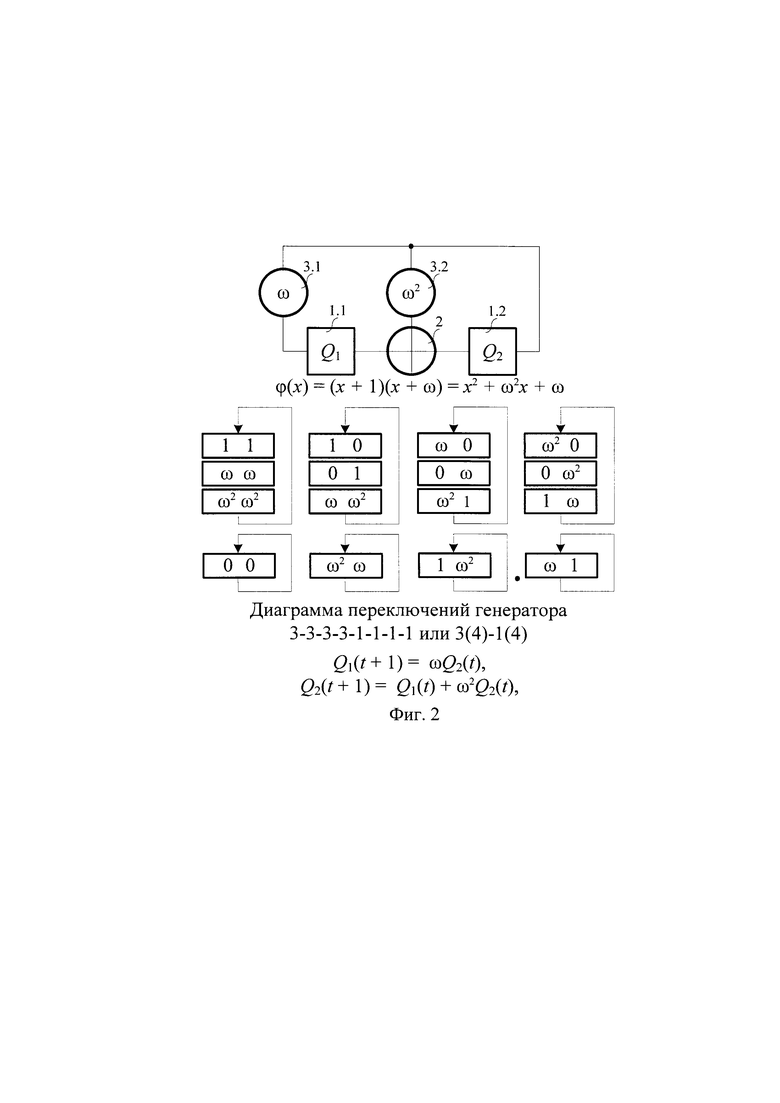
На фиг. 2 показаны пример устройства-прототипа для случая N=n=2, ϕ(х)=(х+1)(х+ω)=х2+ω2х+ω, где λ(х)=х+ω - многочлен, примитивный над GF(22)={0,1,ω, ω2}, ω3=1, ω2+ω+1=0, уравнения его работы, а также его диаграмма переключений, состоящая из четырех циклов длиной 3 и четырех циклов длиной 1.
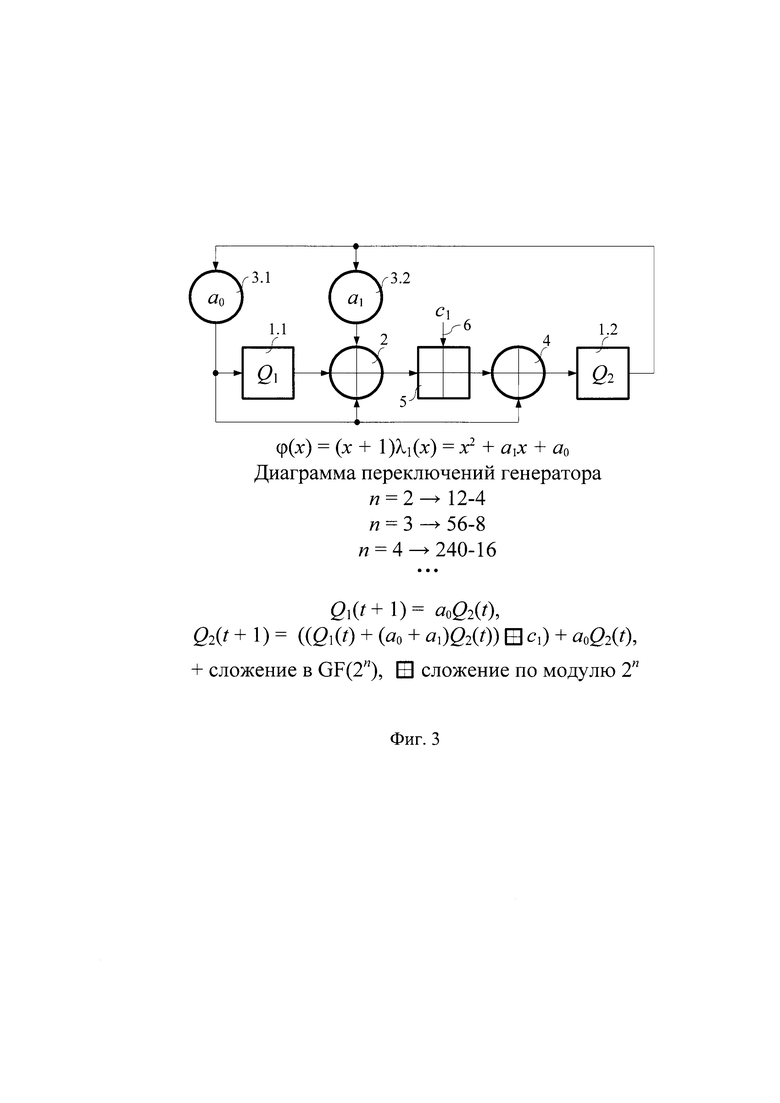
На фиг. 3 показана схема предлагаемого устройства для случая ω(х)=х2+а1х+а0, 1.1 и 1.2 - n-разрядные регистры, 2 - первый n-разрядный блок сложения в поле GF(2n), 3.1 и 3.2 - первый и второй n-разрядные блоки умножения в поле GF(2n), 4 - второй n-разрядный блок сложения в поле GF(2n), 5 - второй n-разрядный блок сложения по модулю 2n, 6 - управляющие входы генератора (количество которых равно n). Тактовый вход устройства соединен с тактовыми входами регистров и схеме непоказан. На фиг. 3 показаны также уравнения работы генератора и тип диаграммы его переключений при n=2, 3 и 4. Количество возможных значений на управляющих входах 6 равно количеству чисел, меньших и взаимно простых с числом 2n.
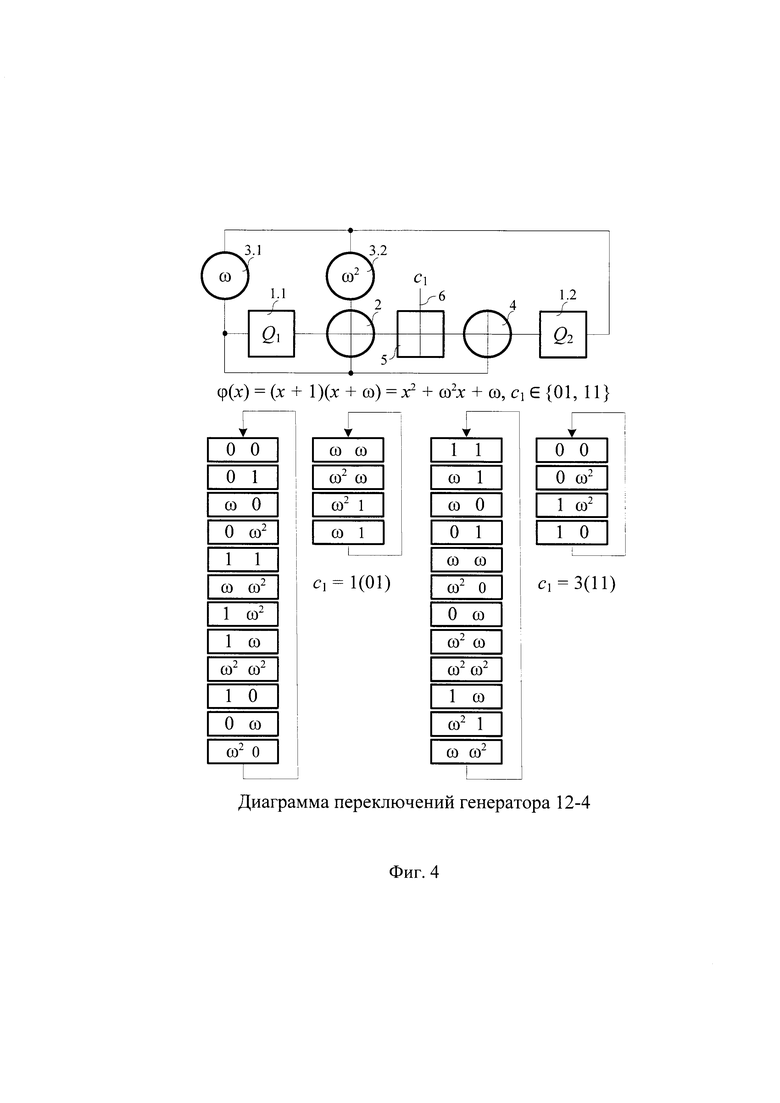
На фиг. 4 показан пример предлагаемого устройства для случая n=2, ϕ(х)=(х+1)(х+ω)=х2+ω2х+ω, где λ(х)=х+ω - многочлен, примитивный над GF(22)={0, 1, ω, ω2}, ω3=1,ω2+ω+1=0. 1.1 и 1.2 -двухразрядные регистры, 2 - двухразрядный первый блок сложения в поле GF(22), 3.1 и 3.2 - двухразрядные блоки умножения соответственно на ω и на ω2 в поле GF(22), 4 - двухразрядный второй блок сложения в поле GF(22), 5 - двухразрядный блок сложения по модулю 2n, 6 - управляющие входы генератора. Количество возможных значений на управляющих входах 6 равно двум, это 1 и 3 (в двоичном виде соответственно 01 и 11). На фиг. 4 показаны диаграммы переключений генератора при c1=1 и c1=3. B обоих случаях диаграмма переключений имеет вид 12-4, т.е. состоит из двух циклов длиной 12 и 4.
Устройство работает следующим образом. Перед началом работы все элементы памяти генератора устанавливаются в исходное состояние, которое должно принадлежать большему циклу диаграммы переключений. Цепи установки в исходное состояние на фиг.3 и 4 не показаны. Например, для случаев, показанных на фиг. 4, регистры 1.1, и 1.2 устанавливаются в любое состояние большого цикла диаграммы переключений (цикл длиной 12), например 00 (при с1=1) и 11 (с1=3). Выходная псевдослучайная последовательность считывается с выхода одного из регистров генератора.
В общем случае уравнения работы ГПСЧ имеют вид, показанный на фиг. 3, где Qi(t) и Qi(t+1) - состояния i-го регистра генератора соответственно в моменты времени t и (t+1),с1 - управляющее воздействие, i=1,2. Диаграмма переключений устройства имеет вид (22n-2n)-2n, т.е. состоит из двух кодовых колец длиной (22и-2n) и 2n.
Для случая, рассмотренного на фиг. 4, диаграмма переключений устройства имеет вид 12-4, т.е. состоит из двух кодовых колец длиной 12 и 4. Видно, что при корректной работе генератора значение свертки содержимого всех регистров меняется по закону 0 1 ω ω2 0 1 ω ω2 0 1 ω ω2… при с1=1 или по закону 0 ω2 ω 1 0 ω2 ω 1 0 ω2 ω 1… при с1=3, т.е. изменяется в каждом такте на 1 в первом случае и на ω2 - во втором.
Важно отметить, что состояния генератора, попадающие в малое кодовое кольцо диаграммы переключений, зависят от вида управляющего воздействия с1 и закон изменения свертки в малом кольце тот же, что и в большем кодовом кольце.
Генератор ориентирован на реализацию механизма скрытых функций, предполагающего что ГПСЧ интегрирован в структуру защищаемого цифрового устройства (ЦУ). Выполнение каждой функции защищаемого ЦУ разрешается при нахождении ГПСЧ в соответствующем состоянии, при этом состояния ГПСЧ, входящие в малое кодовое кольцо длиной 2n, разрешают выполнение скрытых, особо важных, функций защищаемого ЦУ.
Помимо достижения поставленной главной цели изобретения -увеличения периода формируемых последовательностей, можно отметить ряд дополнительных преимуществ предлагаемого технического решения:
- выбирая соответствующее значение n, можно реализовать разное количество скрытых функций в защищаемом ЦУ;
- устройство эффективно реализуется, не только программно, но и аппаратно, учитывая, что все операции в поле GF(2n) элементарно выполняются на элементах XOR, а само устройство за счет регулярной структуры легко реализуется в интегральном исполнении;
- отслеживая закон изменения свертки содержимого элементов памяти генератора, можно организовать самоконтроль правильности его функционирования в реальном масштабе времени;
- наличие сумматора по модулю 2n обеспечивает нелинейный характер закона формирования выходной последовательности, что усложняет задачуопределения структуры генератора по перехваченному фрагменту псевдослучайной последовательности конечной длины.
| название | год | авторы | номер документа |
|---|---|---|---|
| ГЕНЕРАТОР ПСЕВДОСЛУЧАЙНЫХ ЧИСЕЛ | 2020 |
|
RU2740339C1 |
| ГЕНЕРАТОР ПСЕВДОСЛУЧАЙНЫХ ЧИСЕЛ | 2021 |
|
RU2776346C1 |
| УСТРОЙСТВО ДЛЯ ГЕНЕРАЦИИ ПСЕВДОСЛУЧАЙНЫХ ЧИСЕЛ | 2020 |
|
RU2761766C1 |
| УСТРОЙСТВО ДЛЯ ГЕНЕРАЦИИ ПСЕВДОСЛУЧАЙНЫХ ЧИСЕЛ | 2021 |
|
RU2774812C1 |
| ГЕНЕРАТОР ПСЕВДОСЛУЧАЙНЫХ ЧИСЕЛ | 2020 |
|
RU2756833C1 |
| СПОСОБ НЕЛИНЕЙНОГО ТРЕХМЕРНОГО МНОГОРАУНДОВОГО ПРЕОБРАЗОВАНИЯ ДАННЫХ RDOZEN | 2015 |
|
RU2591015C1 |
| СПОСОБ НЕЛИНЕЙНОГО ТРЕХМЕРНОГО МНОГОРАУНДОВОГО ПРЕОБРАЗОВАНИЯ ДАННЫХ DOZEN | 2012 |
|
RU2503994C1 |
| УСТРОЙСТВО ФОРМИРОВАНИЯ ТРИПЛЕКСНЫХ ЧИСЕЛ | 2023 |
|
RU2812412C1 |
| СПОСОБ НЕЛИНЕЙНОГО ТРЕХМЕРНОГО МНОГОРАУНДОВОГО ПРЕОБРАЗОВАНИЯ ДАННЫХ | 2017 |
|
RU2683689C1 |
| УСТРОЙСТВО ФОРМИРОВАНИЯ ПСЕВДОСЛУЧАЙНЫХ КОМПЛЕКСНЫХ ЧИСЕЛ | 2022 |
|
RU2800190C1 |
Настоящее техническое решение относится к области вычислительной техники для электросвязи. Технический результат заключается в увеличении периода формируемой последовательности. Технический результат достигается за счёт того, что генератор псевдослучайных чисел, состоящий из двух регистров разрядности n, блока сложения в GF(2n), двух блоков умножения в GF(2n), где выходы второго регистра соединены со входами блоков умножения в GF(2n), выходы первого блока умножения в GF(2n) соединены со входами первого регистра, выходы второго блока умножения в GF(2n) соединены с первыми входами блока сложения в GF(2n), вторые входы которого соединены с выходами первого регистра, дополнительно содержит второй блок сложения в GF(2n) и блок сложения по модулю 2n, причем выходы первого блока умножения в GF(2n) подключены к первым входам второго блока сложения в GF(2W) и третьим входам первого блока сложения в GF(2n), выходы которого соединены с первыми входами блока сложения по модулю 2n, вторые входы которого образуют управляющие входы генератора, вторые входы второго блока сложения в GF(2n) соединены с выходами блока сложения по модулю 2n, а выходы второго блока сложения в GF(2n) соединены со входами второго регистра. 4 ил.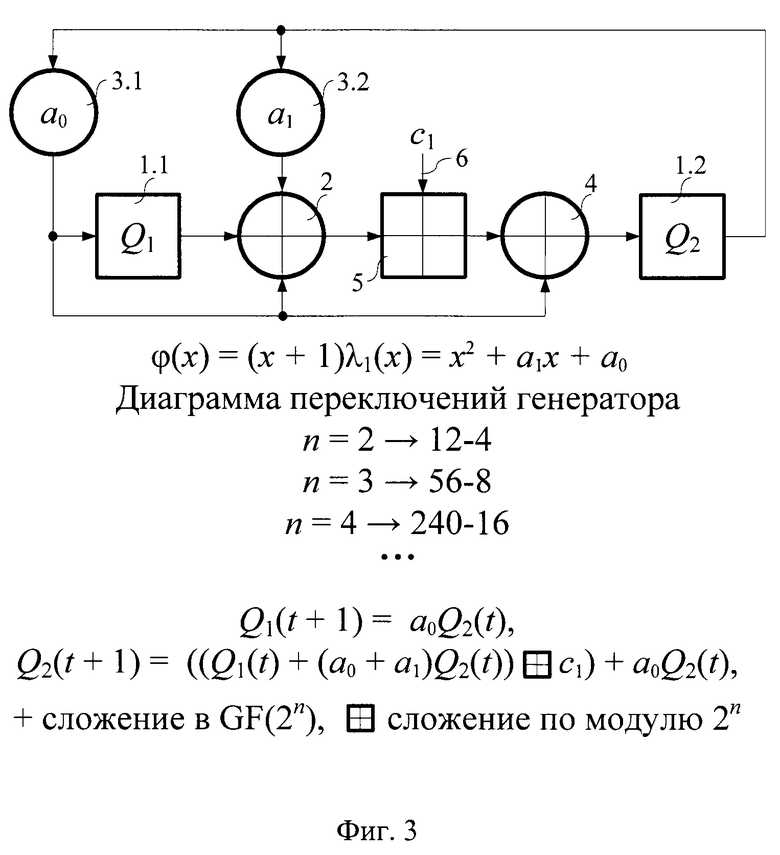
Генератор псевдослучайных чисел, состоящий из двух регистров разрядности n, блока сложения в GF(2n), двух блоков умножения в GF(2n), где n>1 - целое, причем величины, на которые происходит умножение в первом и втором блоках умножения в GF(2n), равны соответственно коэффициентам а0 и а1 характеристического многочлена ω(х)=(х+1)λ(х)=х2+а1х+а0, где а1, а0 ∈ GF(2n), λ(х) - многочлен первой степени, примитивный над GF(2n), выходы второго регистра соединены со входами блоков умножения в GF(2n), выходы первого блока умножения в GF(2n) соединены со входами первого регистра, выходы второго блока умножения в GF(2n) соединены с первыми входами блока сложения в GF(2n), вторые входы которого соединены с выходами первого регистра, отличающийся тем, что он дополнительно содержит второй блок сложения в GF(2n) и блок сложения по модулю 2n, причем выходы первого блока умножения в GF(2n) подключены к первым входам второго блока сложения в GF(2n) и третьим входам первого блока сложения в GF(2n), выходы которого соединены с первыми входами блока сложения по модулю 2n, вторые входы которого образуют управляющие входы генератора, вторые входы второго блока сложения в GF(2n) соединены с выходами блока сложения по модулю 2n, а выходы второго блока сложения в GF(2n) соединены со входами второго регистра.
| US 9298423 B2, 29.03.2016 | |||
| ГЕНЕРАТОР ПСЕВДОСЛУЧАЙНЫХ ЧИСЕЛ | 2020 |
|
RU2740339C1 |
| СПОСОБ ФОРМИРОВАНИЯ ПСЕВДОСЛУЧАЙНЫХ СИГНАЛОВ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2021 |
|
RU2769539C1 |
| US 7571200 B2, 04.08.2009 | |||
| JP 2014222394 A, 27.11.2014. | |||
Авторы
Даты
2024-03-18—Публикация
2023-10-09—Подача