Область техники
Изобретение «Способ имитации многоканальных рядов наблюдений, в том числе ЭКГ» (ИМРН) предназначен для тестирования систем обработки сигналов, в том числе медицинской техники. Способ ИМРН позволяет воспроизводить реализации многоканальных наблюдений, которые статистически подобны хранимым в базе данных реализациям, и может быть использован при обучении персонала.
Способ ИМРН может использоваться в подсистемах, входящих в состав гибридных интеллектуальных систем [20], например, для их тестирования.

Уровень техники
В основе способа ИМРН лежит представление сигналов на конечном интервале анализа (КИА) в ортонормированном базисе (ОНБ). Этот подход известен и описан в классических работах по теории сигналов, например в [1]. Широкое использование КИА в теории сигналов обусловлено, прежде всего, тремя обстоятельствами:
1. Возможностью использования хорошо развитого математического аппарата линейной алгебры [2], когда сигнал представляется точкой в многомерном унитарном (со скалярным произведением) векторном пространстве [3], размерность которого совпадает с числом отсчетов сигнала на КИА;
2. Хорошо развитыми вычислительными методами линейной алгебры [4];
3. Общедоступностью вычислительных мощностей и широким применением микро- и сигнальных процессоров [5].
В ряде полезных моделей, запатентованных авторами данной заявки, предложены технические решения, основанные на использовании ОНБ, состоящих из собственных векторов ковариационной матрицы на КИА. Эти технические решения различаются прежде всего тем, каким образом выбирается ансамбль КИА, используемый при вычислении ковариационной матрицы и при представлении сигнала для решения конкретной задачи. В анализаторе собственных векторов и компонент сигнала (АСВ и КС) [6] при анализе временного ряда (BP) используются все КИА заданного размера, которые получаются путем единичных сдвигов КИА вдоль оси дискретного времени. Последовательность полученных на таких КИА сегментов BP образует так называемую траекторную матрицу (ТМ) - частный случай матрицы ансамбля. На основе ТМ вычисляется ковариационная матрица (КМ), собственные векторы (СВ) которой и используются в АСВ и КС для обработки.
В кардиоайгеноскопе [7] - устройстве для анализа ЭКГ - также используется базис СВ, но ансамбль КИА формируется иначе. Здесь для анализа выбираются вполне определенные отрезки BP, которые синхронизированы с положениями R-зубцов ЭКГ. Из таких сегментов ЭКГ образуется так называемый синхронный ансамбль (СА), для которого рассчитывается КМ; ее СВ используются для представления элементов СА, полученного из ЭКГ.
В устройстве хранения и анализа ЭКГ (УХА ЭКГ) [8] СВ КМ СА используются для хранения ЭКГ в сжатом виде.
В [9] исследованы характеристики кардиоайгеноскопа при использовании как синхронного, так и асинхронного ансамбля (АСА) - для элиминирования медленной волны из ЭКГ.
Понятие ансамбля КИА достаточно продуктивно. Расширение типологии ансамблей, ковариационные матрицы которых используются для построения ОНБ собственных векторов, расширяет круг приложений айгеноскопии.
Понятие ансамбля связано с известными представлениями о наблюдении. Например, в [9] отмечается, что используя слово «ансамбль», мы хотим передать тот факт, что все наблюдения, объединенные в матрице ансамбля наблюдений (МАН), где каждое из наблюдений - столбец МАН, несут типичную информацию о макросостоянии объекта. МАН описывает макросостояние, а отдельные столбцы МАН - микросостояния объекта.
Формирование ансамбля [9] - целенаправленное действие, в рамках которого наблюдателем реализуется понимание того, что представляют собой макросостояние и микросостояние. Формируя ансамбль, наблюдатель реализует свое понимание сущности макросостояний и микросостояний.
Используя термины «наблюдение», «состояние», «целенаправленное действие», «объект», мы понимаем их так, как это описано в [11].
Так, в одних случаях целесообразно использовать ТМ [12, 13], в других - АСА [9, 14], в третьих - синхронный ансамбль [7, 8, 15, 16].
Удачное для данной задачи формирование ансамбля, как правило, уменьшает размерность описания, обеспечивающего заданную ошибку представления сигнала на КИА.
Если зафиксировать способ формирования ансамбля, то использование ОНБ, состоящего из СВ КМ ансамбля, требует минимально возможного числа ортогональных компонент (пропорциональных базисным векторам) для достижения заданной среднеквадратической ошибки (СКО) представления сигнала [9, 14, 16]. Это свойство в [9] названо «максимальная выразительность ОНБ, состоящего из СВ КМ». В то же самое время, разные способы построения ансамблей, сохраняя свою максимальную выразительность в рамках используемого способа формирования ансамбля, могут значительно отличаться друг от друга.
Например, для того, чтобы с использованием айгеноскопии удалить из ЭКГ медленную составляющую, достаточно двух-трех СВ КМ, полученной для ансамбля в виде ТМ или в виде АСА [9]. В то же самое время, когда в качестве объекта исследования выступает PQRST-комплекс, использование ТМ и АСА неэффективно, и целесообразно использование СА [7, 8].
В основе работы любого айгеноскопа лежит представление сигнала в виде линейной комбинации СВ КМ некоторого ансамбля, построенного из самого сигнала - в соответствии с представлением пользователя о том, что важно, а что неважно. Это свойство хорошо совместимо как с аксиоматикой «целеустремленности» [11], так и с «гибридным подходом» [20], позволяя решить дилемму «важно/неважно» человеку, а все остальное делегировать компьютеру.
Собственные векторы образуют ОНБ, который обладает (и только он) свойствами, отличающими его от других ОНБ. Ковариационная матрица - это матрица ковариаций, то есть матрица связей между изменениями. Формируя ансамбль, мы целеустремленно задаем некоторый шаблон наблюдений, в рамках которого айгеноскопия раскрывает имеющиеся взаимосвязи. Каждый собственный вектор задает в матрице ковариаций то есть в матрице, характеризующей связи между отсчетами в рамках заданного шаблона наблюдений, свой «слой» взаимных изменений, не влияющий на остальные «слои».
Уникальность свойств айгеноскопов состоит в том, что с их помощью становится возможным разделять компоненты, принадлежащие к разным «слоям», тогда как анализаторы, использующие любые другие ОНБ, смешивают, то есть одновременно реагируют на компоненты, принадлежащие различным «слоям» [21, 22].
Это свойство базиса СВ КМ (для любого ансамбля наблюдений) описывается так называемым поляризационным соотношением [9, 23]

где
KM×M - ковариационная матрица любого ансамбля на КИА, имеющем размерность М,
 - квадратные неотрицательно определенные матрицы размера М×М, представляющие собой «слои» КМ,
- квадратные неотрицательно определенные матрицы размера М×М, представляющие собой «слои» КМ,
 - СВ КМ,
- СВ КМ,
λi - СЗ КМ.
Соотношение (1) гарантирует представление любой КМ в виде линейной комбинации М матриц Ui, каждая из которых полностью определяется произведением ψi⋅ψ'i, а в качестве коэффициентов в комбинации выступают СЗ КМ. Соотношение (1) позволяет разложить взаимосвязи в ковариационной матрице заданного ансамбля в сумму отдельных взаимосвязей 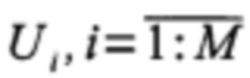 , информацию о которых несут соответствующие СВ, а коэффициенты разложения задаются соответствующими СЗ. Еще раз отметим, что (1) применимо к любой КМ, построенной для любого ансамбля.
, информацию о которых несут соответствующие СВ, а коэффициенты разложения задаются соответствующими СЗ. Еще раз отметим, что (1) применимо к любой КМ, построенной для любого ансамбля.
Айгеноскопия - самостоятельная область обработки сигналов; введение в практику айгеноскопов требует средств искусственного воссоздания ситуаций, в которых применяются эти анализаторы, то есть имитации.
Применительно к медико-биологическим сигналам имитаторы детерминированных сигналов представлены в работах [18, 19]. Их недостатком является то, что имитируемый сигнал - классический детерминированный сигнал в аддитивных шумах, не относящийся к области эффективного использования айгеноскопов.
Недостатки аналогов [18, 19] сводятся к следующему:
1. Необходимость до имитации строить детерминированную модель сигнала.
2. Невозможность введения в имитируемый сигнал новых недетерминированных компонент, некоррелированных с другими компонентами.
3. Невозможность независимого селективного и избирательного изменения уже существующих в сигнале уровней некоррелированных компонент.
Использование айгеноскопов позволяет воспроизвести недетерминированные сигналы, используя для представления сигнала собственные векторы, полученные непосредственно при обработке исходного экспериментального материала.
На фиг. 1 и фиг. 2 приведены конструкции УХА ЭКГ (прототип) и кардиоайгеноскопа (аналог), соответственно.
В состав УХА ЭКГ входят:
- блок авторизации и доступа 1;
- блок задания режимов работы, контроля сжатия, хранения и выборки 2;
- кардиоайгеноскоп 3.
В кардиоайгеноскоп (фиг. 2) входят:
- блок формирования ансамбля кардиоосцилляций 4;
- блок вычислителя матрицы смешанных моментов 5;
- блок вычислителя собственных векторов и собственных значений 6;
- блок восстановления кардиосигнала и анализа признаков 7.
Кардиоайгеноскоп [7] обрабатывает последовательные сегменты оцифрованной ЭКГ, в которую укладывается несколько десятков PQRST-комплексов, имеющих заданную длительность R0 дискретов. Размер КИА R0 выбирают заведомо большим длительности PQRST-комплекса. Формируют матрицу синхронного ансамбля  с размером R0×S,,где S - число элементов СА (число PQRST-комплексов в обрабатываемом сегменте ЭКГ). Все эти операции выполняются в блоке формирования ансамбля кардиоосцилляций 4.
с размером R0×S,,где S - число элементов СА (число PQRST-комплексов в обрабатываемом сегменте ЭКГ). Все эти операции выполняются в блоке формирования ансамбля кардиоосцилляций 4.
На основании матрицы ансамбля  в блоке вычислителя матрицы смешанных моментов 5 определяет КМ СА, задаваемую соотношением
в блоке вычислителя матрицы смешанных моментов 5 определяет КМ СА, задаваемую соотношением

где (…)' означает транспонирование матрицы.
Для КМ (2) находятся СВ и СЗ, удовлетворяющие соотношению [3]

где ψi - СВ (матрица-столбец),
λi - СЗ (число).
Количество СВ и СЗ совпадает с размером КМ и равно R0 [3]. КМ симметрична и неотрицательно определена [3], то есть 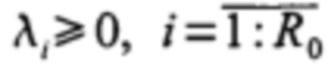 . СВ КМ образуют ОНБ [3], следовательно,ψ'i⋅ψj=0 если i≠j, а ψ'i⋅ψi=1.
. СВ КМ образуют ОНБ [3], следовательно,ψ'i⋅ψj=0 если i≠j, а ψ'i⋅ψi=1.
Все S PQRST-комплексов, записанные в виде столбцов в матрицу , могут быть представлены в виде
, могут быть представлены в виде

где
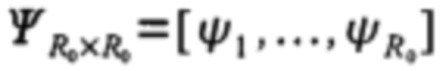 - квадратная матрица, в которую в качестве столбцов записаны все СВ по порядку,
- квадратная матрица, в которую в качестве столбцов записаны все СВ по порядку, 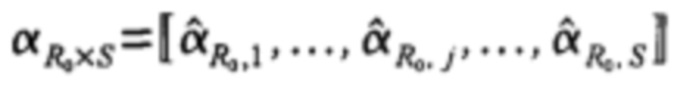 - матрица коэффициентов разложения элементов СА на КИА, j-ый столбец которой
- матрица коэффициентов разложения элементов СА на КИА, j-ый столбец которой
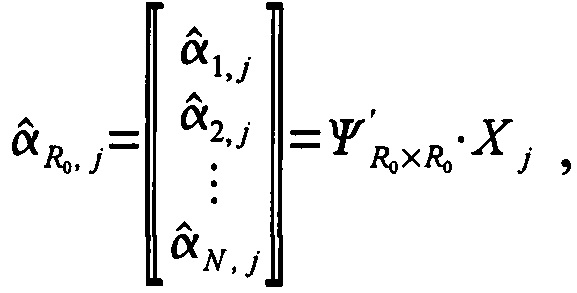
где Xj - j-ый столбец  , а вся матрица
, а вся матрица

Соотношения (4) и (5) дают точное представление PQRST-комплексов
Обычно при сжатии с приемлемой точностью достаточно использовать число СВ C<R0. в этом случае соотношения (4) и (5) имеют вид:


где
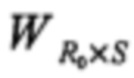 - аппроксимация
- аппроксимация  ,
,
QC×S - матрица коэффициентов аппроксимации С А с использованием C<R0 собственных векторов,
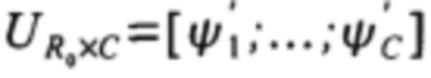 - матрица значимых СВ (ЗСВ), в которую ЗСВ записаны построчно.
- матрица значимых СВ (ЗСВ), в которую ЗСВ записаны построчно.
Обычно достаточно использовать число ЗСВ С равное четырем.
Очевидно, что используя ЗСВ и задавая случайные коэффициенты разложения и величины RR-интервалов так, чтобы они соответствовали статистическим свойствам реального BP, можно имитировать BP, статистически соответствующие исходным.
Раскрытие способа ИМРН
Цель изобретения и технический результат - за счет свойств ОНБ, состоящего из ЗСВ КМ ансамбля, построенного из реальных временных рядов многоканальных наблюдений (ВРМН), исключить необходимость построения аналитической модели и осуществлять имитирование ВРМН, используя в качестве образца реальные записи ВРМН, обеспечивая при этом статистическое подобие реального и имитируемого ВРМН.
Под статистическим подобием мы будем далее понимать эквивалентность [3] ковариационной матрицы ансамбля для исходного ВРМН и ВРМН, получаемого в результате имитации.
Как будет показано далее, эквивалентность достигается за счет того, что эти ковариационные матрицы имеют одни и те же собственные векторы и различаются только собственными значениями.
Технический результат, состоящий в отсутствии необходимости аналитического описания имитируемого сигнала и обеспечении его статистического подобия исходному, обеспечивается за счет:
1. Применимости ПС к любой КМ для любого ансамбля наблюдений;
2. Эквивалентности [3] ковариационных матриц имитируемого и реального ВРМН;
3. Универсальности представления ансамблей, построенных из любых ВРМН, в ОНБ СВ КМ этих ансамблей;
4. Независимости подхода от способа построения ансамбля.
В соответствии с первым пунктом формулы изобретения отличия способа имитации многоканальных рядов наблюдений состоят в том, что в способе ИМРН выполняют следующую последовательность действий:
1. На первом подготовительном этапе: задают покрытие многомерного временного ряда наблюдений с помощью множества реперных точек покрытия (РТП), после чего формируют ансамбль покрытия (АП), вычисляют ковариационную матрицу ансамбля покрытия (КМАП) и формируют матрицу значимых собственных векторов этой ковариационной матрицы, после чего вычисляют матрицу коэффициентов разложения столбцов матрицы ансамбля покрытия по ЗСВ; оценивают достаточные статистики коэффициентов разложения и интервалов между РТП,
2. На втором этапе имитации ВРМН: генерируют выборку реперных точек воспроизведения (РТВ), матрицу ансамбля коэффициентов воспроизведения (МАКВ) ансамбля воспроизведения (АВ) и саму матрицу ансамбля воспроизведения (МАВ), после чего формируют и заполняют парциальные матрицы воспроизведения (ПМВ), связанные с РТВ; далее путем усреднения парциальных матриц воспроизведения (ПМВ) вычисляют матрицу воспроизведения (MB) и осуществляют интерполяцию для недостающих точек дискретного времени.
Зависимые второй, третий и четвертый пункты формулы способа подробно детализируют варианты реализации первого независимого пункта способа, не выходя за его рамки. Проиллюстрируем работу способа ИМРН на частном примере имитации ВРМН ЭКГ, получаемой по многим отведениям, что соответствует зависимому четвертому пункту формулы способа ИМРН.
Пусть в одном из отведений (далее будем именовать его синхроотведением ЭКГ) определяется положение R-зубцов, которое далее используется для формирования ансамбля покрытия. То есть, положения R-зубцов - это характерные точки синхронизации 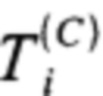 , принадлежащие интервалу дискретного времени от единицы до N.
, принадлежащие интервалу дискретного времени от единицы до N.
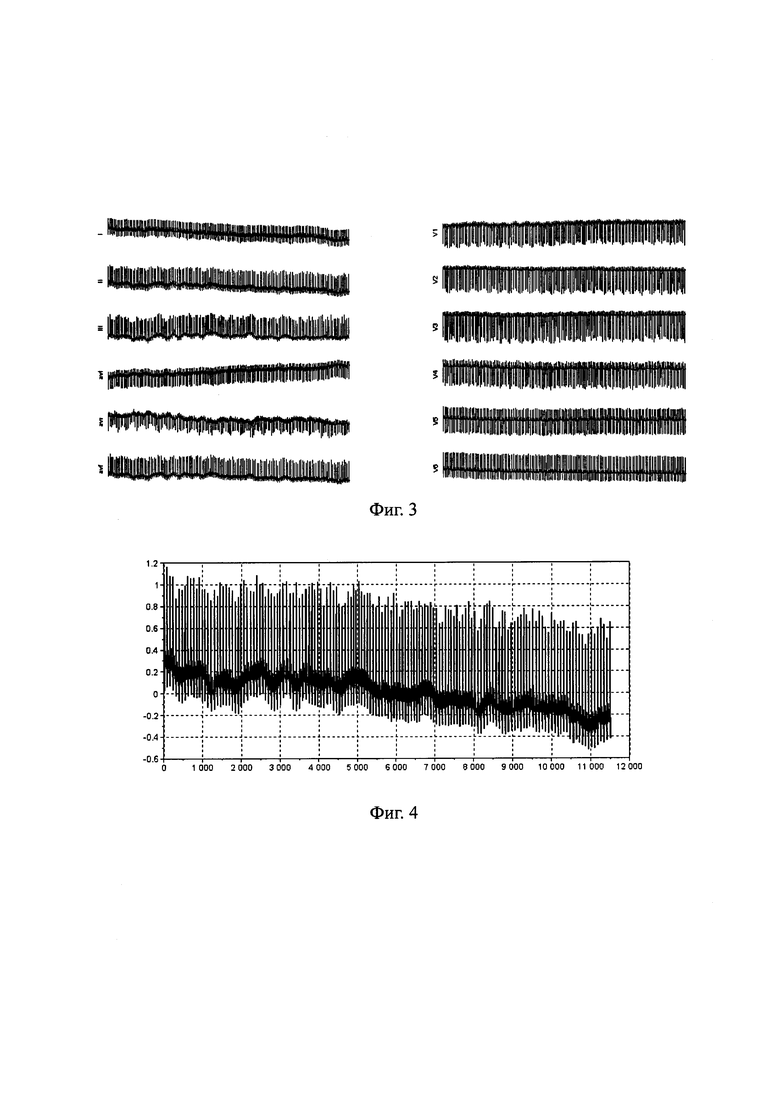
Фиг. 3-5 иллюстрируют процесс определения характерных точек синхронизации по одному из отведений ЭКГ. Как видно из графиков, для отрезка второго отведения ЭКГ с длительностью N=2500 дискретов сформировано NC=31 характерных точек синхронизации, которые задают функцию шаблона выборки (далее для уменьшения размерности задачи частота дискретизации в рассматриваемом примере была уменьшена вдвое).
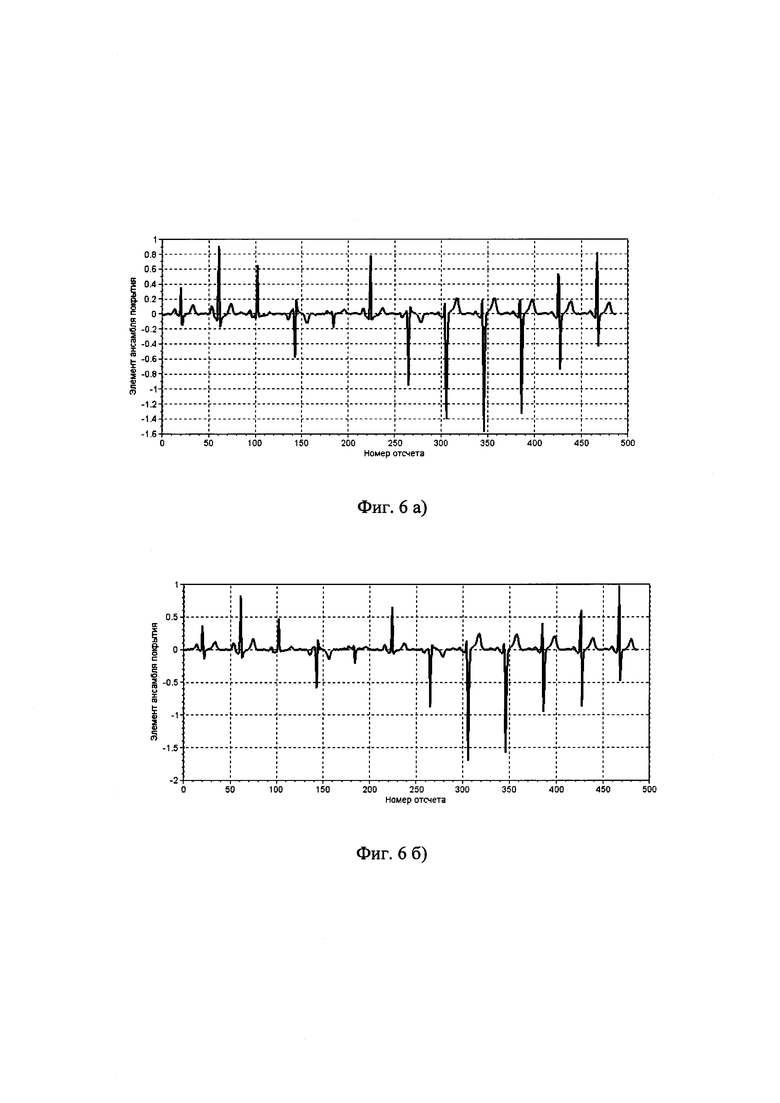
На фиг. 6 показан ансамбль покрытия

полученный из М=12 отведений, представленных на фиг. 3.
Каждая из подматриц, входящих в (8), представляет собой матрицу-столбец, которая получается из матрицы-строки соответствующего отведения (с номерами от 1 до 12) как сегмент этой матрицы, заданный на КИА 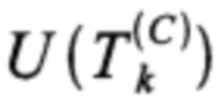 , состоящем из последовательности отсчетов вокруг соответствующей реперной точки
, состоящем из последовательности отсчетов вокруг соответствующей реперной точки  (характерной точки синхронизации).
(характерной точки синхронизации).
Общее число характерных точек синхронизации равно NC=31, левый и правый интервалы анализа TL=23 и TR=24 отсчета, соответственно, длина интервала анализа I=TL+TR=47 отсчетов, а величина R=I⋅M=47⋅12=564.
Границы интервалов 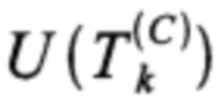 показаны на графиках фиг. 6 кружочками. Каждому столбцу матрицы (8) соответствует отдельный из множества элементов ансамбля, представленных на графике фиг. 6.
показаны на графиках фиг. 6 кружочками. Каждому столбцу матрицы (8) соответствует отдельный из множества элементов ансамбля, представленных на графике фиг. 6.
Посредством матричного умножения матрицы ансамбля покрытия (8) на транспонированную матрицу ансамбля покрытия с последующим делением результата матричного перемножения на число реперных точек рассчитывается ковариационная матрица ансамбля покрытия

и для нее вычисляются собственные векторы и собственные значения.
На фиг. 7 представлена зависимость величины первых десяти собственных значений ковариационной матрицы (9), отнесенных к следу ковариационной матрицы.
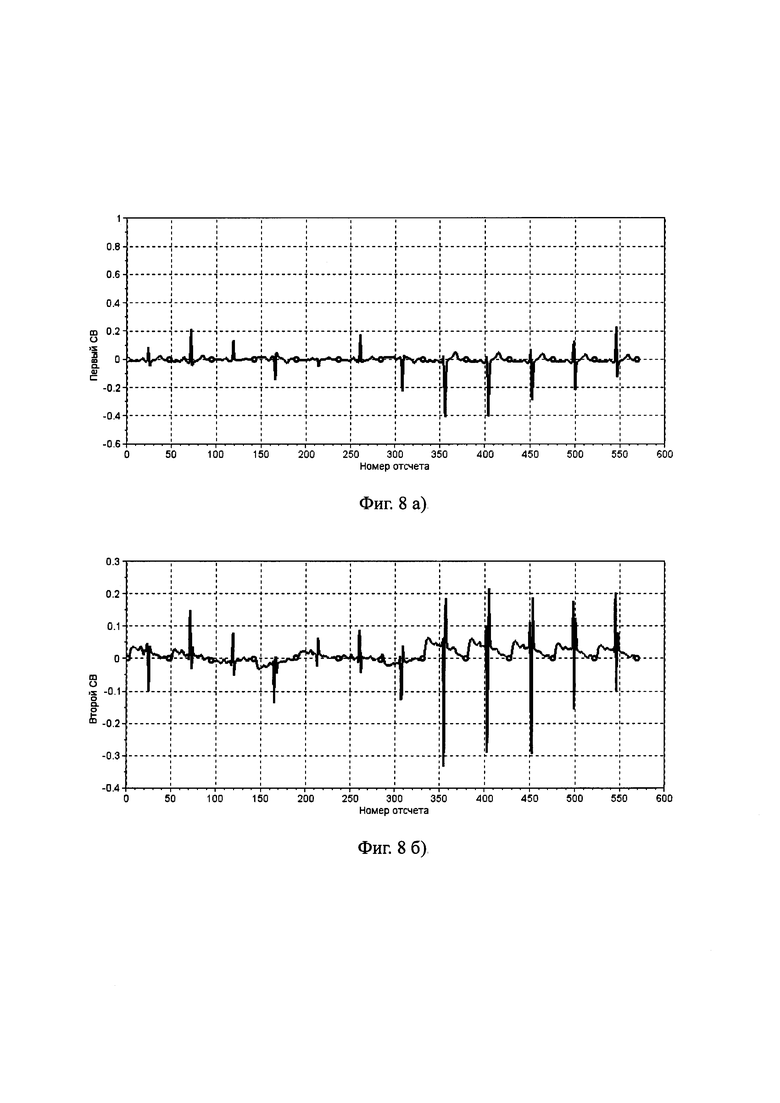
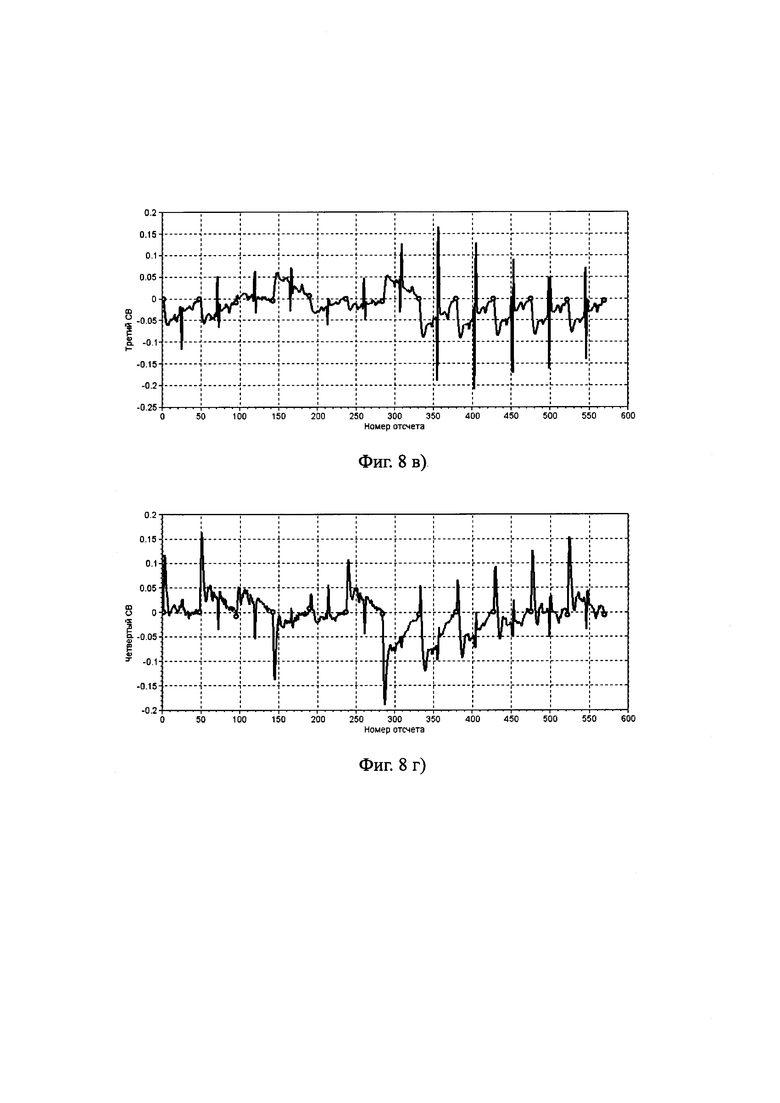
В качестве ЗСВ при критерии значимости собственного вектора 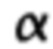 =0.005 отбирают первые четыре СВ, графики которых приведены на фиг. 8а)-8г). Эти ЗСВ построчно входят в матрицу U4×564.
=0.005 отбирают первые четыре СВ, графики которых приведены на фиг. 8а)-8г). Эти ЗСВ построчно входят в матрицу U4×564.
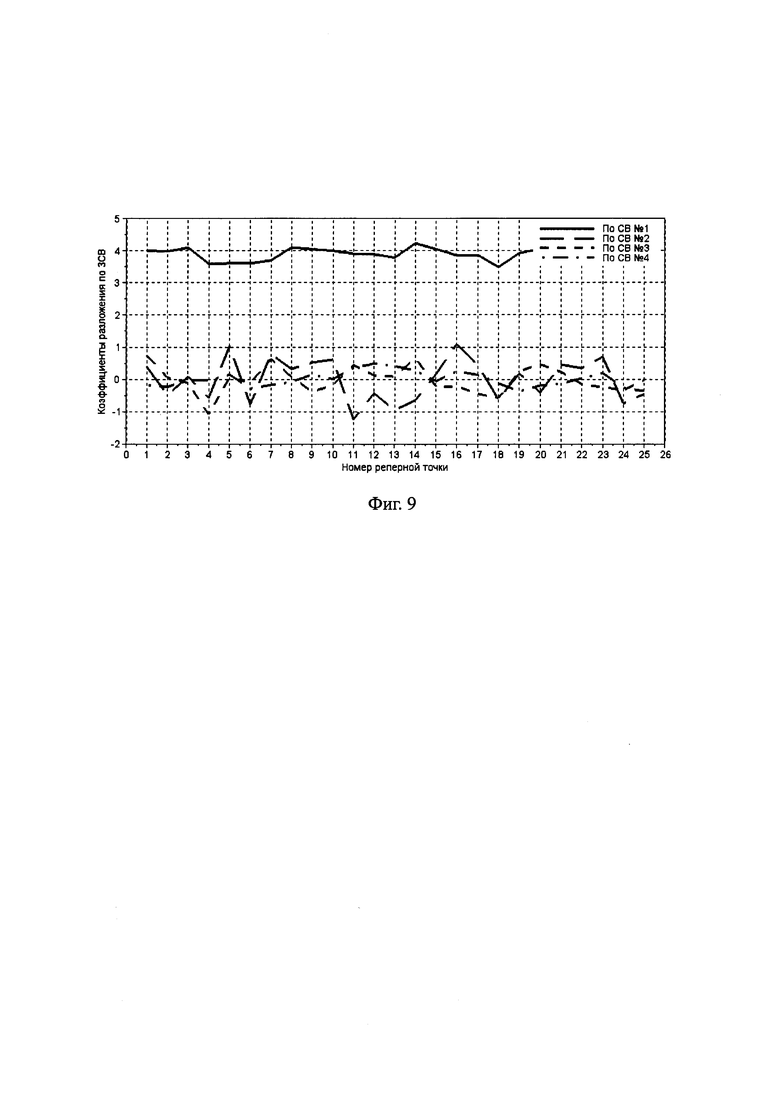
На фиг. 9 представлены коэффициенты Q4×31=U4×564⋅Z564×31 разложения по ЗСВ, а на фиг. 10а) и 10б) - даны ядерные оценки [25] плотностей вероятностей для этих же коэффициентов.
На этом первый подготовительный этап заканчивается.
Рассмотрим действия, производимые на втором этапе имитации временных рядов многомерных наблюдений.
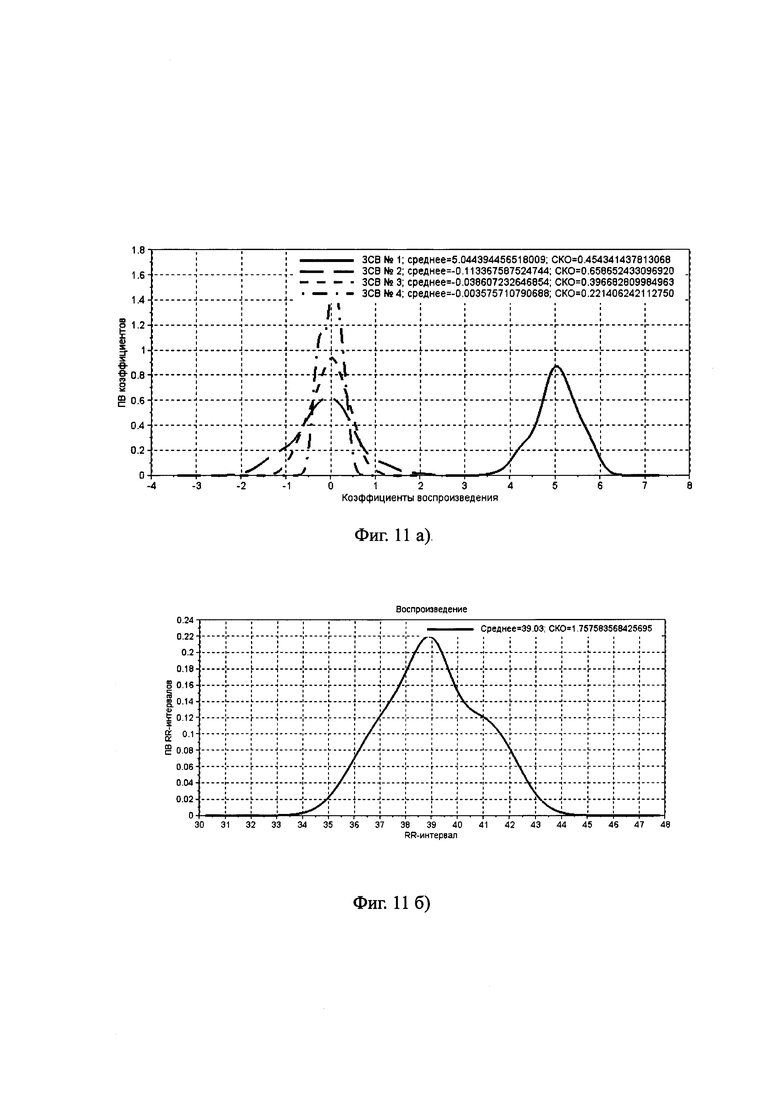
Число реперных точек воспроизведения было выбрано Н=50. На фиг. 11б) показана ядерная оценка плотности вероятностей для интервалов между реперными точками воспроизведения (RR-интервалами), полученных с использованием генераторов случайных нормальных чисел для среднего, равного сорока дискретам, и стандартного отклонения, равного двум дискретам.
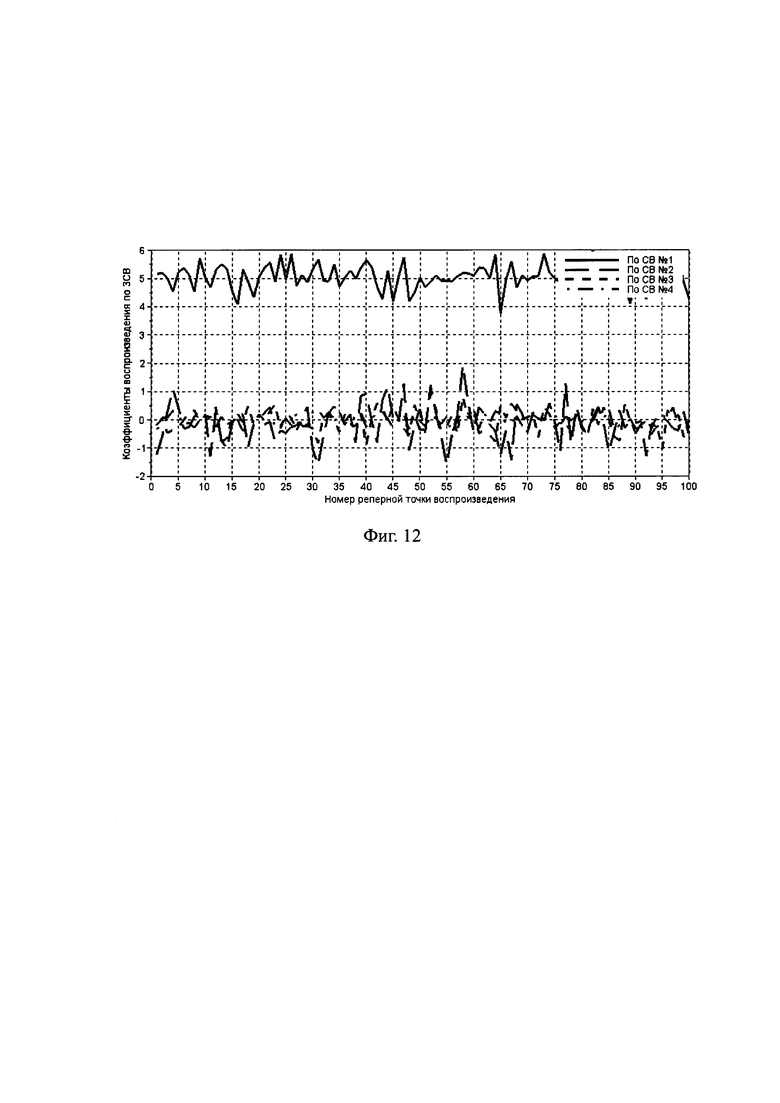
При моделировании коэффициентов воспроизведения W4×50 также использовались генераторы нормального распределения, При этом для первого коэффициента использовалось среднее равное пяти и стандартное отклонения 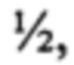 а средние и стандартные отклонения других трех коэффициентов полагались равными соответствующим параметрам исходного ВРМН. Графики ядерных оценок плотностей вероятностей этих коэффициентов представлены на фиг. 11а), а на фиг. 12 представлены реализации коэффициентов.
а средние и стандартные отклонения других трех коэффициентов полагались равными соответствующим параметрам исходного ВРМН. Графики ядерных оценок плотностей вероятностей этих коэффициентов представлены на фиг. 11а), а на фиг. 12 представлены реализации коэффициентов.
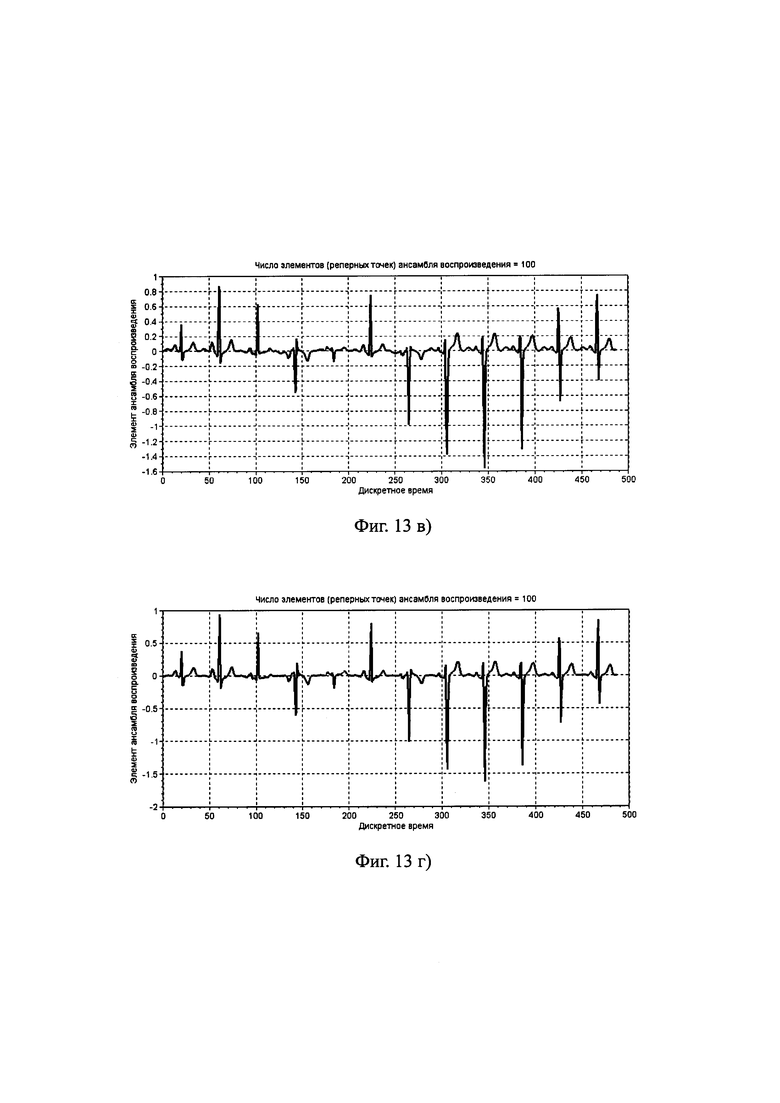
С использованием ЗСВ, представленных на фиг. 8а)-8г) и реализаций коэффициентов, представленных на фиг. 12, вычислялся ансамбль воспроизведения 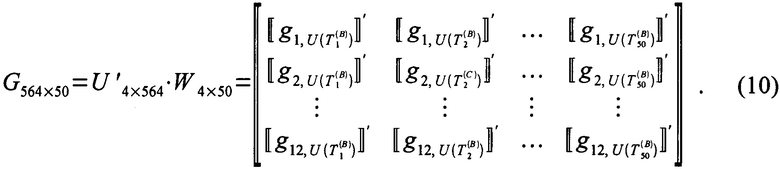
Каждый столбец (10) представляет собой элемент ансамбля воспроизведения. Весь ансамбль представлен на фиг. 13. Каждая из реализаций на этой фигуре соответствует одному столбцу (10).
Далее формировались пятьдесят парциальных матриц воспроизведения 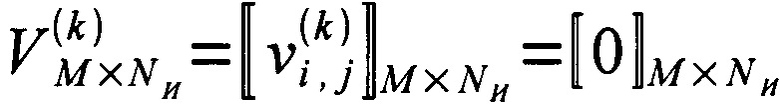 так, что общее число парциальных матриц воспроизведения совпадает с числом реперных точек воспроизведения; далее формируют парциальную матрицу воспроизведения в виде
так, что общее число парциальных матриц воспроизведения совпадает с числом реперных точек воспроизведения; далее формируют парциальную матрицу воспроизведения в виде

Из парциальных матриц воспроизведения формируют матрицу воспроизведения временного ряда 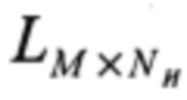 , для чего каждую строку матрицы воспроизведения временного ряда вычисляют как среднее всех строк парциальных матриц воспроизведения, то есть
, для чего каждую строку матрицы воспроизведения временного ряда вычисляют как среднее всех строк парциальных матриц воспроизведения, то есть 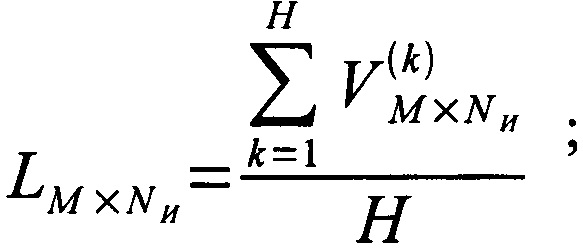 для каждой строки, входящей в матрицу воспроизведения временного ряда
для каждой строки, входящей в матрицу воспроизведения временного ряда 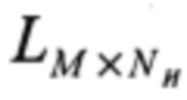 , осуществляют интерполяцию в точках, соответствующих оси дискретного времени, с использованием в качестве значений интерполируемой функции ненулевых значения строки, а в качестве аргумента - номер дискрета, соответствующий ненулевому значению; отправляют матрицу, полученную в результате интерполирования строк матрицы воспроизведения временного ряда, на хранение.
, осуществляют интерполяцию в точках, соответствующих оси дискретного времени, с использованием в качестве значений интерполируемой функции ненулевых значения строки, а в качестве аргумента - номер дискрета, соответствующий ненулевому значению; отправляют матрицу, полученную в результате интерполирования строк матрицы воспроизведения временного ряда, на хранение.
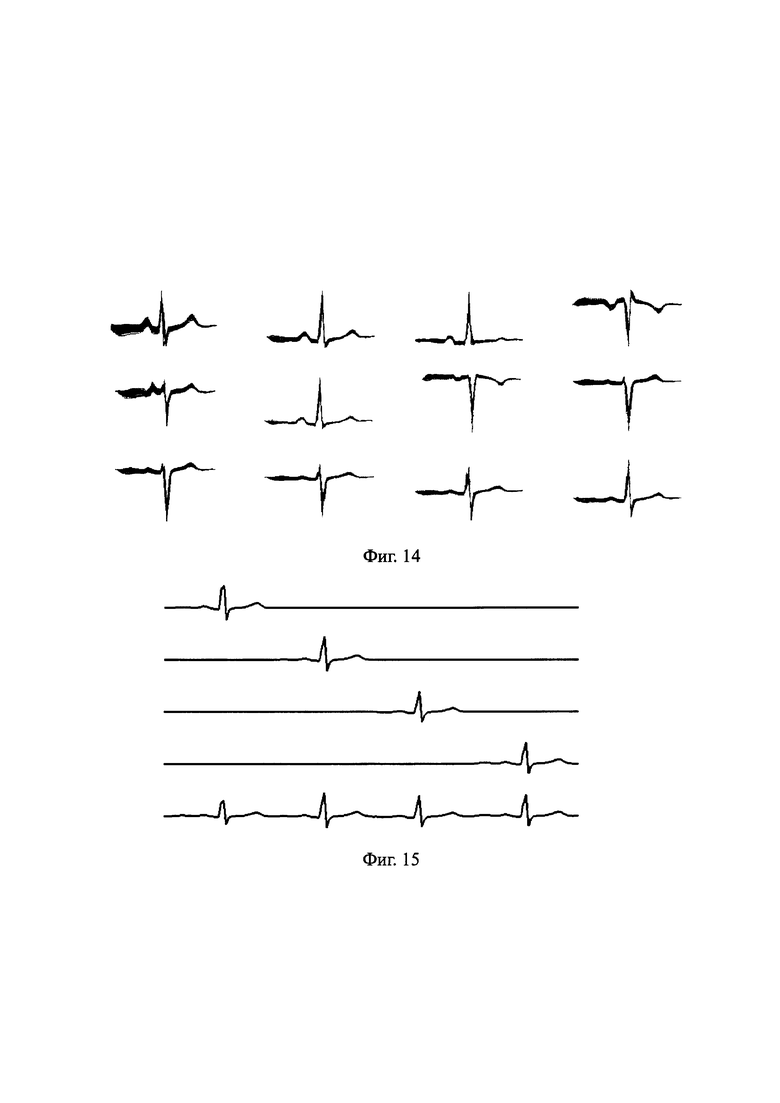
Фиг. 15 иллюстрирует процесс усреднения и последующей интерполяции для первого отведения. Первые четыре графика показывают сегменты первых четырех парциальных матриц воспроизведения, а на пятом графике приведен сегмент первой строки (соответствующей первому отведению) матрицы воспроизведения L12×2350.
Для того, чтобы убедиться, что ковариационные свойства ансамбля воспроизведения эквивалентны ковариационным свойствам ансамбля покрытия, покажем, что КМАП и КМАВ в рамках предлагаемого способа просто эквивалентны. Две матрицы А и В называются просто эквивалентными [3], если найдутся две матрицы S и D, такие, что A=S⋅B⋅D.
Пусть КМАП, определяемая формулой способа ИМРН равна 
и имеет собственные векторы  и собственные значения
и собственные значения 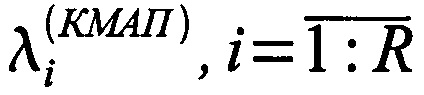 .
.
В соответствии с формулой способа ИМРН, при имитации рассматривается не матрица (12), а матрица, у которой оставлены только ЗСВ - то есть, в соответствии с ПС (1) матрица

где
С - число ЗСВ.
В соответствии с формулой способа ИМРН, ансамбль воспроизведения определяется соотношением

где
GR×H - МАВ, каждый столбец которой представляет собой элемент ансамбля воспроизведения, причем общее число элементов равно Н,
UC×R - матрица ЗСВ, в которую ЗСВ записаны в виде столбцов в порядке их следования в (13),
WC×H - матрица коэффициентов воспроизведения, все строки которой некоррелированы (или независимы).
В соответствии с (14) и правилами матричного умножения транспонированных матриц [3], КМАВ определится соотношением

Центральный множитель (15) представляет собой ковариационную матрицу коэффициентов воспроизведения, и в силу некоррелированности (или независимости) коэффициентов воспроизведения матрица

где
δi,j - символ Кронекера [3],
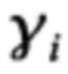 - второй выборочный момент i-го коэффициента воспроизведения.
- второй выборочный момент i-го коэффициента воспроизведения.
КМКВ диагональная, поэтому в соответствии с (16) и (15) 
Сравнение (13)и(17) позволяет сформулировать следующее утверждение: если КМКВ диагональная, то КМАП имеет те же самые СВ, что и матрица (13), но другие СЗ, которые совпадают с диагональными элементами КМКВ.
Очевидно, что матрицы (13) и (17) просто эквивалентны.
Действительно, если ввести в рассмотрение матрицу

то, используя (13), (17), (18) и условие ортонормированности ЗСВ, легко показать, что

Это означает, что КМАВ и КМАП просто эквивалентны, чем и достигается статистическое подобие имитируемого и исходного ВРМН.
Таким образом, для достижения технического результата достаточно реализовать последовательность действий, перечисленную в формуле способа ИМРН.
Реализация способа ИМРН
Способ ИМРН реализуют в виде программного или программно-аппаратного комплекса.
Описание чертежей
Фиг. 1. Устройство хранения и анализа ЭКГ [8]:
1 - блок авторизации и доступа;
2 - блок задания режимов работы, контроля сжатия, хранения и выборки;
3 - кардиоайгеноскоп.
Фиг. 2. Конструкция кардиоайгеноскопа [7]:
4 - блок формирования ансамбля кардиоосцилляций;
5 - блок вычислителя матрицы смешанных моментов;
6 - блок вычислителя собственных векторов и собственных значений;
7 - блок восстановления кардиосигнала и анализа признаков.
Фиг. 3. Многоканальные наблюдения ЭКГ - пациент №155 из группы «Здоров» [24]. Данные получены с использованием демонстрационной версии кардиоайгеноскопа [10].
Фиг. 4. Синхроотведение - второе отведение ЭКГ, показанной на фиг. 3. Данные получены с использованием демонстрационной версии кардиоайгеноскопа [10].
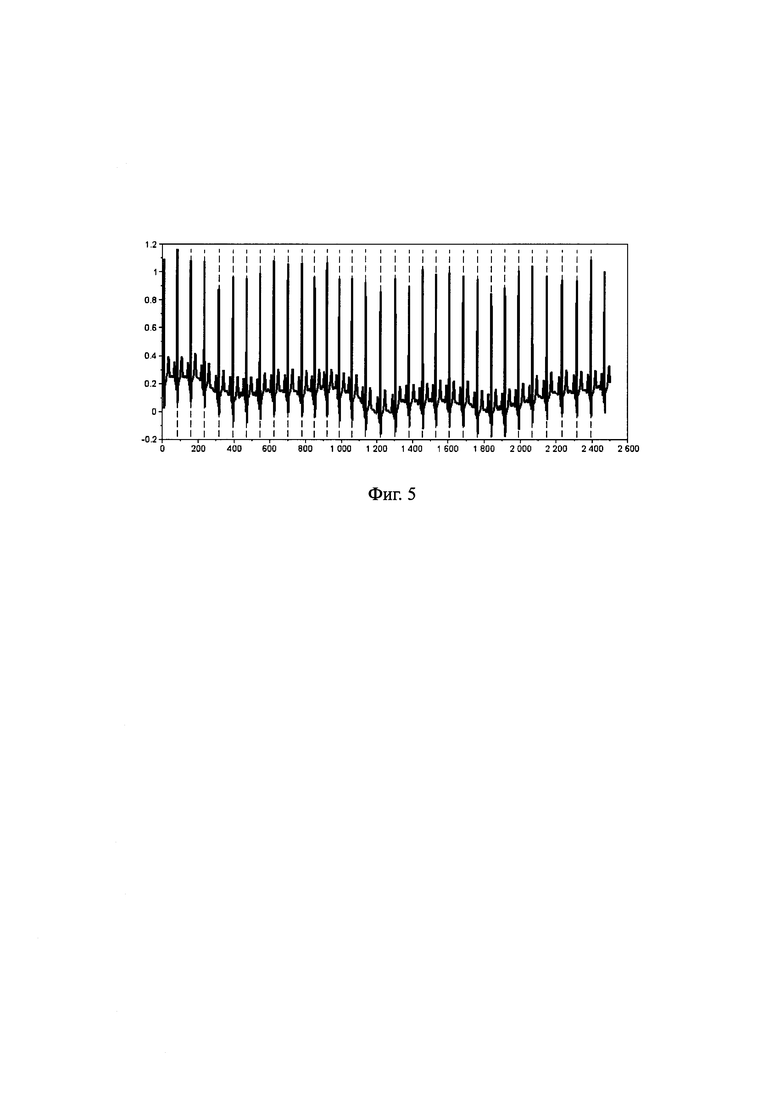
Фиг. 5. Определение характерных точек синхронизации  ,
,  , принадлежащих интервалу дискретного времени от единицы до N=2500, по синхроотведению, представленному на фиг. 4. Данные получены с использованием демонстрационной версии кардиоайгеноскопа [10]. Положение R- зубцов, соответствующее характерным точкам синхронизации, показано пунктирными линиями.
, принадлежащих интервалу дискретного времени от единицы до N=2500, по синхроотведению, представленному на фиг. 4. Данные получены с использованием демонстрационной версии кардиоайгеноскопа [10]. Положение R- зубцов, соответствующее характерным точкам синхронизации, показано пунктирными линиями.
Фиг. 6. Первые четыре элемента ансамбля покрытия для пациента №155 (группа «Здоров» в [24]) при использовании ЭКГ по 12 отведениям.
Фиг. 7. Сравнение собственных значений, отнесенных к следу ковариационной матрицы (масштаб - полулогарифмический) для случая покрытия с использованием СА только одного (первого) отведения (пунктир) и покрытия всех 12 отведений (сплошная линия) - для пациента №155 из [24]. Как видно из графика (сплошная линия), величине критерия значимости собственных векторов  =0.005 соответствуют четыре ЗСВ КМАП.
=0.005 соответствуют четыре ЗСВ КМАП.
Фиг. 8. Собственные векторы для ковариационной матрицы ансамбля покрытия, представленного на фиг. 3:
а) - первый ЗСВ КМАП; б) - второй ЗСВ КМАП; в) - третий ЗСВ КМАП; г) - четвертый ЗСВ КМАП. Кружочками показаны границы областей покрытия, соответствующие отведениям в порядке (слева направо): I, II, III, aVR, aVL, aVF, V1, V2, V3, V4, V5, V6.
Фиг. 9. Коэффициенты разложения элементов ансамбля покрытия, представленного на фиг. 3, по четырем значимым собственным векторам ковариационной матрицы ансамбля покрытия.
Фиг. 10. Оценки плотностей вероятностей:
а) - для коэффициентов разложения по ЗСВ КМАП элементов ансамбля, представленного на фиг. 3;
б) - для RR-интервалов.
Пациент №155 из [24].
Фиг. 11. Оценки плотностей вероятностей:
а) - для коэффициентов разложения, полученных с помощью генераторов нормального распределения;
б) - для RR-интервалов имитируемого ансамбля, полученных с помощью генератора нормального распределения.
Фиг. 12. Коэффициенты воспроизведения элементов ансамбля воспроизведения.
Фиг. 13. Первые четыре элемента ансамбля воспроизведения, полученный по четырем ЗСВ с использованием коэффициентов воспроизведения фиг. 12.
Фиг. 14. Синхронные ансамбли отведения (слева направо и сверху вниз - СА отведений в порядке: I, II, III, aVR, aVL, aVF, V1, V2, V3, V4, V5, V6), полученные из ансамбля покрытия, представленного на фиг. 13.
Фиг. 15. Формирование первых четырех парциальных матриц и сегмент усредненной парциальной матрицы (матрицы воспроизведения).
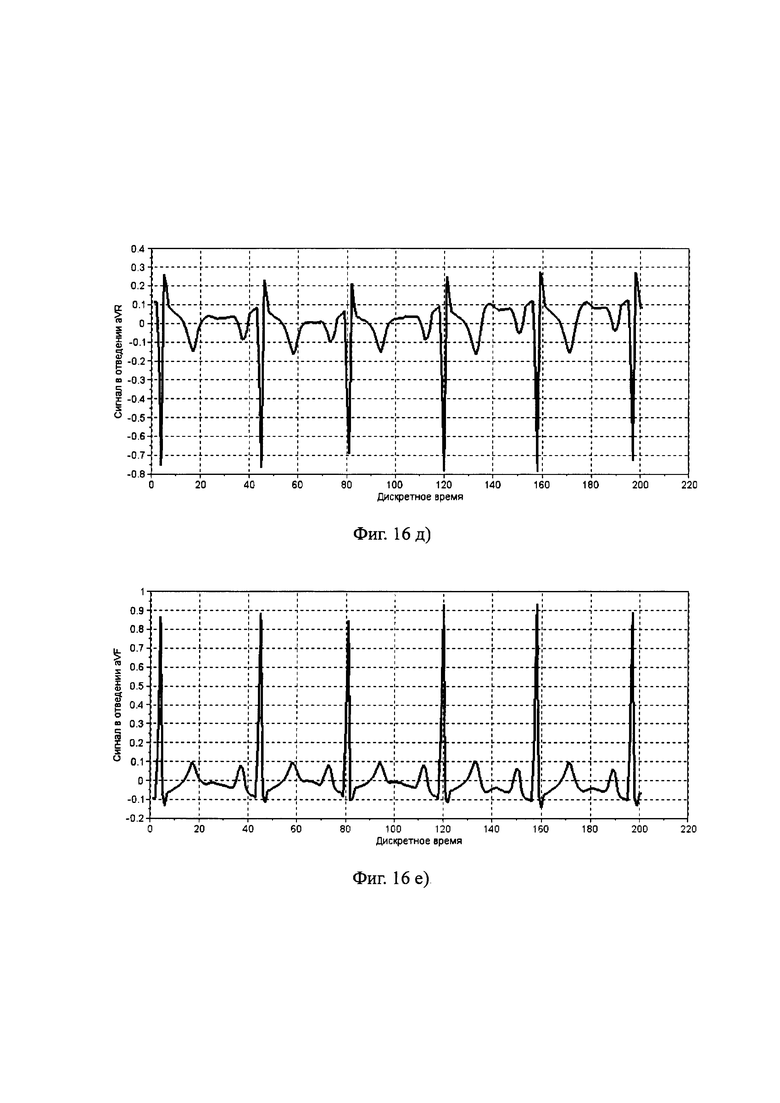
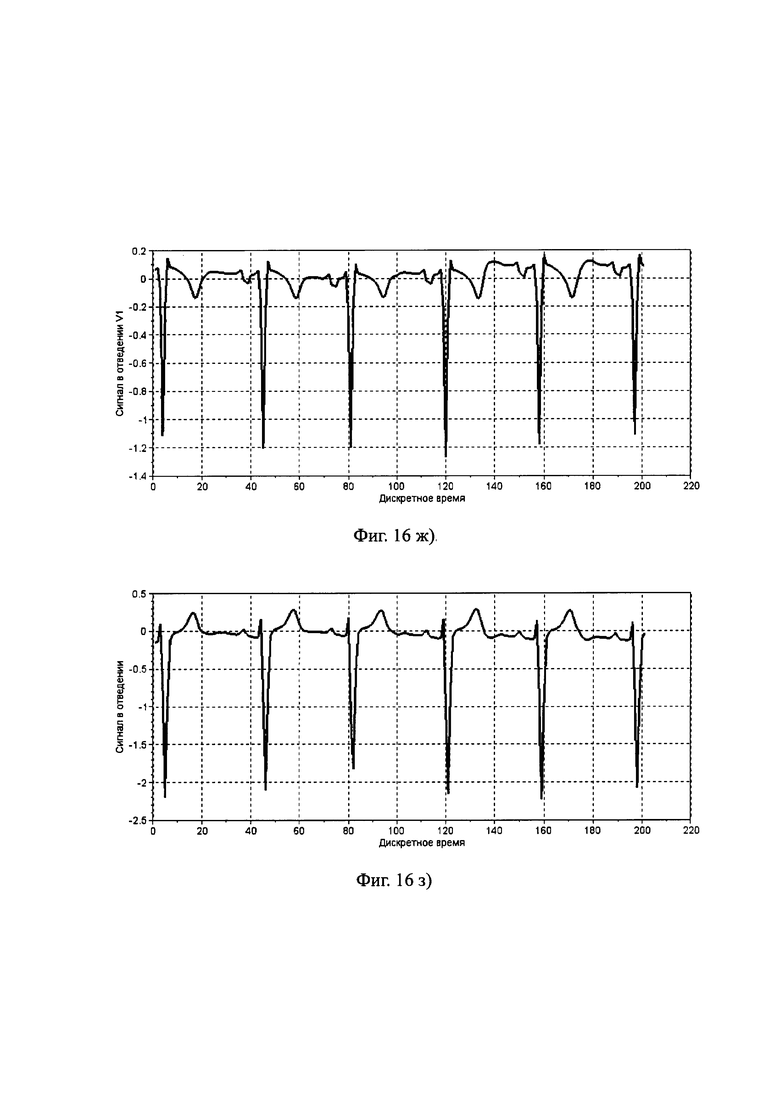
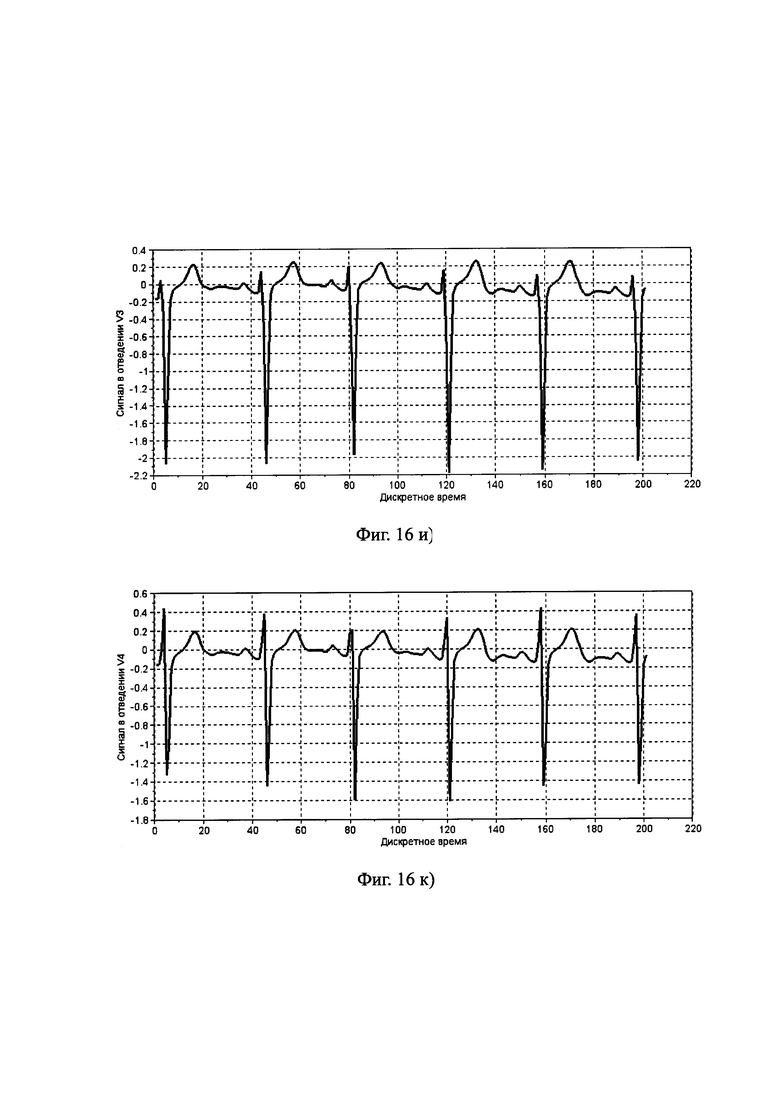
Фиг. 16. Компоненты многомерного временного ряда, полученные в результате имитации по предлагаемому способу для группы «Здоров» при использовании в качестве прототипа ЭКГ пациента №155 из [24]: а) - отведение I; б) - отведение II; в) - отведение III; г) - отведение aVL; д) - отведение aVR; е) - отведение aVF; ж) - отведение V1; з) - отведение V2; и) - отведение V3; к) - отведение V4; л) - отведение V5; м) - отведение V6.
Список литературы
1. Френкс Л. Теория сигналов. Пер. с английского под ред. Д.Е. Вакмана, М.: Сов. Радио. 1974. - 171 с.
2. Босс В. Лекции по математике. Т. 3: Линейная алгебра. Изд. 2-е стереотип. - М.: Книжный дом «ЛИБРОКОМ». 2009. - 224 с. ISBN 978-5-484-01058-5.
3. Корн Г., Корн Т. Справочник по математике (для научных работников и инженеров). М.: Наука. - 831 с.
4. Фаддеев Д.К., Фаддеева В.Н. Вычислительные методы линейной алгебры. М.: Издательство «Лань». 2009. - 736 с.
5. Смит С. Цифровая обработка сигналов. Практическое руководство для инженеров и научных работников. М.: Додэка-XXI, 2008. - 720 с. ISBN 978-5-94120-145-7.
6. Исакевич В.В., Исакевич Д.В., Грунская Л.В. Анализатор собственных векторов и компонент сигнала. Полезная модель №116242 RU.
7. Исакевич В.В., Исакевич Д.В., Батин А.С. Кардиоайгеноскоп. Полезная модель №128470 RU.
8. Исакевич В.В., Исакевич Д.В. Устройство хранения и анализа ЭКГ. Полезная модель №162110 RU.
9. Исакевич Д.В., Исакевич В.В. Кардиоайгеноскоп - новая полезная модель обработки ЭКГ. - М. Издательство Перо, 2014. - 138 с. ISBN 978-5-00086-280-3.
10. Исакевич В.В., Исакевич Д.В. Кардиоайгеноскоп: Демонстрационная версия на Scilab. - М. Издательство Перо, 2016.-133 с. ISBN 978-5-906851-75-8.
11. Акофф Р., Эмери Ф. О целеустремленных системах. Пер. с англ. Под ред. И.А. Ушакова. М.: Сов. радио, 1974. - 242 с.
12. Грунская Л.В., Исакевич В.В., Исакевич Д.В., Рубай Д.В. Анализ собственных векторов и главных компонент вертикальной составляющей электрического поля в приземном слое атмосферы: Частоты лунных приливов. М.: Издательство «Перо», 2015. - 356 с. ISBN 978-5-000868-04-1.
13. Грунская Л.В., Исакевич В.В., Исакевич Д.В. Айгеноскопия многолетних временных рядов электромагнитного поля в приземном слое атмосферы крайненизкочастотного диапазона на частотах двойных звездных систем. М. Издательство Перо, 2016. -276 с. ISBN 978-5-906927-50-7.
14. Исакевич Д.В. Основы анализа собственных векторов и компонент регулярных колебаний. М.: Издательство «Перо», 2014,138 с. ISBN 9-785000-8628035.
15. Аль-Барати Б., Исакевич В.В., Исакевич Д.В. И др. Формирование синхронного ансамбля кардиоосциляций при синусовом ритме. Ботехносфера. 2016, №6, стр. 28-32.
16. Аль-Барати Б.С., Исакевич В.В., Исакевич Д.В., Сушкова Л.Т. Айгеноскопия в задачах обработки электрокардиосигналов. Нелинейный мир. М.: Издательство Радиотехника, 2015. №6, с. 68-75.
17. Исакевич В.В., Исакевич Д.В., Грунская Л.В. О некоторых возможностях айгеноскопии / Приборы и системы разведочной геофизики. 2016, №2, с. 69-75.
18. Костенков С.Ю., Сидорова М.А. Электрофизиологические сигналы и автоматизированные средства их воспроизведения. - Пенза: Приволжский Дом знаний, 2015. - 104 с.
19. Костенков С.Ю., Пермяков А.В. Устройство имитационного моделирования элекирофизиологических сигналов. Полезная модель №163762 RU.
20. Колесников А.В. Гибридные интеллектуальные системы: Теория и технологии разработки. - СПБ: Издательство СпбГТУ, 2001. - 711 с.
21. Грунская Л.В., Исакевич В.В., Исакевич Д.В. Спектроайгеноскопия: Выявление спектрально локализованных некоррелированных компонент сигналов. 19-я Международная конференция «Цифровая обработка сигналов и ее применение» стр. 131-135. ISBN 978-5-905278-29-7.
22. Исакевич В.В., Исакевич Д.В., Грунская Л.В. Спектроайгеноскопия временных рядов электрического поля инфранизкочастотного диапазона на удвоенных частотах обращения двойных звездных систем / Журнал «Динамика сложных систем - XXI век» №1 за 2017 г., Стр. 56-64. - М.: Издательство "Радиотехника" ISSN 1999-7493.
23. Холево А.С. Квантовые системы, каналы, информация. МЦНМО, 2010.
24. The РТВ Diagnostic ECG Database - The РТВ Diagnostic ECG
Database - http://www.physionet.org/physiobank/database/ptbdb/
25. Kernel density estimation.
http//:en.m.wikipedia.org/wiki/Kernel_density_estimation
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ сжатия и воспроизведения ЭКГ | 2017 |
|
RU2746844C2 |
| Взаимно-базисный корректор | 1986 |
|
SU1403382A1 |
| СПОСОБ И СИСТЕМА УДАЛЕННОГО МОНИТОРИНГА ОБЪЕКТОВ | 2016 |
|
RU2649542C1 |
| СПОСОБ АДАПТИВНОЙ ПРОСТРАНСТВЕННОЙ КОМПЕНСАЦИИ ПОМЕХ ПРИ МОНОИМПУЛЬСНОМ АМПЛИТУДНОМ СУММАРНО-РАЗНОСТНОМ ПЕЛЕНГОВАНИИ И НАЛИЧИИ ОШИБОК КАЛИБРОВКИ ПРИЕМНЫХ КАНАЛОВ | 2011 |
|
RU2456631C1 |
| Способ релейной защиты энергообъекта | 2019 |
|
RU2720710C1 |
| ВЫПОЛНЯЕМЫЙ В ОКНЕ СТАТИСТИЧЕСКИЙ АНАЛИЗ ДЛЯ ОБНАРУЖЕНИЯ АНОМАЛИЙ В НАБОРАХ ГЕОФИЗИЧЕСКИХ ДАННЫХ | 2011 |
|
RU2554895C2 |
| СПОСОБ СОПРОВОЖДЕНИЯ ГРУППОВОЙ ВОЗДУШНОЙ ЦЕЛИ | 2006 |
|
RU2324952C1 |
| Способ диагностики острого коронарного синдрома | 2020 |
|
RU2733077C1 |
| СПОСОБ СОПРОВОЖДЕНИЯ ПИЛОТИРУЕМОЙ ВОЗДУШНОЙ ЦЕЛИ | 2009 |
|
RU2408031C2 |
| СПОСОБ И СИСТЕМА УДАЛЁННОЙ ИДЕНТИФИКАЦИИ И ПРОГНОЗИРОВАНИЯ РАЗВИТИЯ ЗАРОЖДАЮЩИХСЯ ДЕФЕКТОВ ОБЪЕКТОВ | 2018 |
|
RU2686257C1 |








Изобретение относится к медицинской технике. Технический результат заключается в исключении необходимости аналитического описания имитируемого сигнала и обеспечении его статистического подобия исходному. Способ имитации многоканальных рядов наблюдений, в том числе электрокардиограмм, заключается в том, что на первом подготовительном этапе: задают покрытие многомерного временного ряда наблюдений, после чего формируют ансамбль покрытия, вычисляют ковариационную матрицу ансамбля покрытия и формируют матрицу значимых собственных векторов, затем вычисляют матрицу коэффициентов разложения столбцов матрицы ансамбля покрытия по значимым собственным векторам; оценивают достаточные статистики коэффициентов разложения и интервалов между реперными точками; на втором этапе имитации временных рядов многомерных наблюдений: генерируют выборку реперных точек воспроизведения, матрицу ансамбля коэффициентов воспроизведения ансамбля воспроизведения и матрицу ансамбля воспроизведения, после чего формируют и заполняют парциальные матрицы воспроизведения, связанные с реперными точками воспроизведения; вычисляют матрицу воспроизведения и осуществляют интерполяцию для недостающих точек дискретного времени. 3 з.п. ф-лы, 1 табл., 38 ил.
1. Способ имитации многоканальных рядов наблюдений, в том числе электрокардиограмм, отличающийся тем, что над многомерным временным рядом наблюдений выполняют последовательность действий, такую, что на первом подготовительном этапе: задают покрытие многомерного временного ряда наблюдений с помощью множества реперных точек покрытия, после чего формируют ансамбль покрытия, вычисляют ковариационную матрицу ансамбля покрытия и формируют матрицу значимых собственных векторов этой ковариационной матрицы, затем вычисляют матрицу коэффициентов разложения столбцов матрицы ансамбля покрытия по значимым собственным векторам; оценивают достаточные статистики коэффициентов разложения и интервалов между реперными точками; на втором этапе имитации временных рядов многомерных наблюдений: генерируют выборку реперных точек воспроизведения, матрицу ансамбля коэффициентов воспроизведения ансамбля воспроизведения и саму матрицу ансамбля воспроизведения, после чего формируют и заполняют парциальные матрицы воспроизведения, связанные с реперными точками воспроизведения; далее путем усреднения парциальных матриц воспроизведения вычисляют матрицу воспроизведения и осуществляют интерполяцию для недостающих точек дискретного времени.
2. Способ имитации многоканальных рядов наблюдений, в том числе электрокардиограмм, по п. 1, отличающийся тем, что предлагаемую последовательность действий реализуют следующим образом: на первом подготовительном этапе представляют исходный многомерный временной ряд в виде
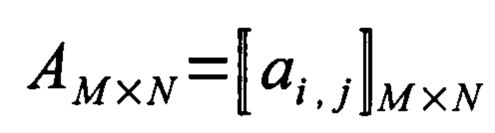 ,
,
где AM×N - прямоугольная матрица исходного временного ряда, имеющая М строк и N столбцов;
[…] - обозначение для любой прямоугольной матрицы;
M×N - размер матрицы;
М - число каналов наблюдения;
N - число дискретных моментов времени наблюдения;
a i,j - элемент матрицы, представляющий наблюдаемую величину в i-м канале наблюдения в j-й дискретный момент времени;
i - номер строки, меняется от единицы до М;
j - номер столбца, меняется от единицы до N;
после чего задают шаблон выборки, который представляет собой дискретную матричную функцию дискретного аргумента
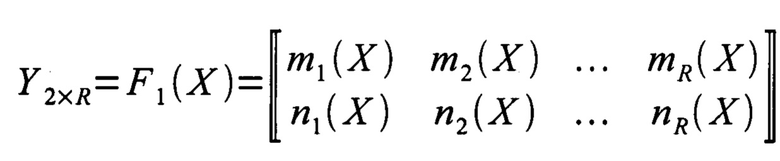 ,
,  ,
, 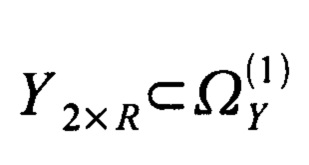 ,
,
где Y 2×R - значение функции, представляющее собой матрицу размера 2×R;
R - размерность шаблона выборки;
F1(X) - функция шаблона выборки;
X - аргумент функции шаблона выборки, имеющий целочисленную область определения  ;
;
mi(X) и ni(X) - соответственно некоторые номера строки и столбца матрицы AM×N исходного многомерного временного ряда;
 - аргумент X, принадлежит области определения
- аргумент X, принадлежит области определения  , которая является целочисленной, причем целые числа лежат в диапазоне от единицы до N;
, которая является целочисленной, причем целые числа лежат в диапазоне от единицы до N;
 - значения функции, принадлежат области значений
- значения функции, принадлежат области значений  , причем элементы первой строки матрицы Y2×R, представляют собой целые числа, лежащие в диапазоне от единицы до M, а элементы второй строки матрицы Y2×R представляют собой целые числа, лежащие в диапазоне от единицы до N;
, причем элементы первой строки матрицы Y2×R, представляют собой целые числа, лежащие в диапазоне от единицы до M, а элементы второй строки матрицы Y2×R представляют собой целые числа, лежащие в диапазоне от единицы до N;
 - знак включения элемента b в множество В;
- знак включения элемента b в множество В;
затем задают покрытие многомерного временного ряда наблюдений в виде упорядоченного по возрастанию множества, состоящего из S значений дискретного времени ti - реперных точек покрытия, входящих в область определения шаблона выборки; после чего формируют матрицу ансамбля покрытия ZR×S, число строк которой равно размерности шаблона выборки R, а число столбцов равно числу реперных точек покрытия S; формирование этой матрицы осуществляют следующим образом: с использованием функции шаблона покрытия вычисляют ее значение для каждой из S реперных точек
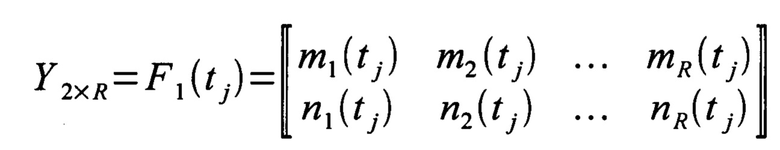 ,
,
а затем с использованием полученных значений путем выборки из матрицы
 формируют матрицу
формируют матрицу
 ;
;
затем вычисляют ковариационную матрицу ансамбля покрытия посредством матричного умножения матрицы ансамбля покрытия на транспонированную матрицу ансамбля покрытия с последующим делением результатов матричного перемножения на число реперных точек покрытия, то есть вычисляют
 ,
,
где KR×R - ковариационная матрица ансамбля покрытия;
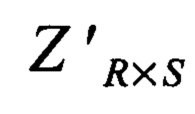 - матрица, получаемая из матрицы ZR×S путем транспонирования;
- матрица, получаемая из матрицы ZR×S путем транспонирования;
далее вычисляют след ковариационной матрицы ансамбля покрытия tR(KR×R), для чего суммируют ее диагональные элементы, и отправляют полученное значение следа ковариационной матрицы ансамбля покрытия на хранение; задают критерий значимости собственного вектора ковариационной матрицы ансамбля покрытия α<1; вычисляют собственные векторы ψi и собственные значения λi ковариационной матрицы ансамбля, число которых равно размерности шаблона выборки, и если собственное значение, поделенное на хранимый след ковариационной матрицы ансамбля покрытия, превышает критерий значимости собственного вектора α, то есть если выполняется неравенство
 ,
,
то записывают этот собственный вектор ψk в качестве следующей строки в матрицу значимых собственных векторов UC×R, где C - число значимых собственных векторов; далее вычисляют матрицу коэффициентов разложения столбцов матрицы ансамбля покрытия по значимым собственным векторам, для чего вычисляют матричное произведение матрицы значимых собственных векторов на матрицу ансамбля покрытия  ; оценивают и отправляют на хранение достаточные статистики, которые формируют из строк матрицы коэффициентов QC×S, и достаточную статистику для интервалов между соседними реперными точками; на втором этапе имитации временных рядов многомерных наблюдений: при генерировании имитирующих временных рядов многоканальных наблюдений задают достаточную статистику для интервалов между реперными точками воспроизведения и достаточные статистики для коэффициентов воспроизведения имитируемого многомерного временного ряда; на основе заданной достаточной статистики реперных точек воспроизведения с помощью генератора случайных чисел генерируют выборку реперных точек воспроизведения τi, общее число которых равно H, и отправляют выборку реперных точек воспроизведения на хранение; далее задают число отсчетов дискретного времени для имитируемого многомерного временного ряда NИ, согласуя величину NИ с положением реперных точек на оси дискретного времени; на основе шаблона выборки F1(Х) определяют шаблон воспроизведения F2(X), который отличается от F1(Х) только своими областью определения
; оценивают и отправляют на хранение достаточные статистики, которые формируют из строк матрицы коэффициентов QC×S, и достаточную статистику для интервалов между соседними реперными точками; на втором этапе имитации временных рядов многомерных наблюдений: при генерировании имитирующих временных рядов многоканальных наблюдений задают достаточную статистику для интервалов между реперными точками воспроизведения и достаточные статистики для коэффициентов воспроизведения имитируемого многомерного временного ряда; на основе заданной достаточной статистики реперных точек воспроизведения с помощью генератора случайных чисел генерируют выборку реперных точек воспроизведения τi, общее число которых равно H, и отправляют выборку реперных точек воспроизведения на хранение; далее задают число отсчетов дискретного времени для имитируемого многомерного временного ряда NИ, согласуя величину NИ с положением реперных точек на оси дискретного времени; на основе шаблона выборки F1(Х) определяют шаблон воспроизведения F2(X), который отличается от F1(Х) только своими областью определения  и областью значений
и областью значений  , то есть
, то есть
 ,
, 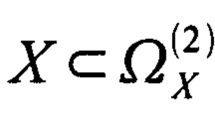 ,
, 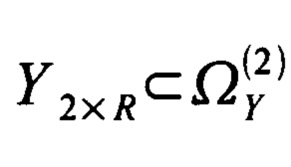 ,
,
где F2(X) - функция шаблона выборки воспроизведения;
X - аргумент функции шаблона выборки воспроизведения;
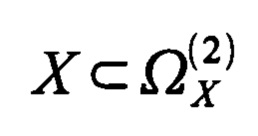 - аргумент X принадлежит области определения
- аргумент X принадлежит области определения  , которая является целочисленной, причем целые числа лежат в диапазоне от единицы до NИ;
, которая является целочисленной, причем целые числа лежат в диапазоне от единицы до NИ;
 - значения функции принадлежат области значений
- значения функции принадлежат области значений  , причем элементы первой строки матрицы Y2×R представляют собой целые числа, лежащие в диапазоне от единицы до M, а элементы второй строки матрицы Y2×R представляют собой целые числа, лежащие в диапазоне от единицы до NИ;
, причем элементы первой строки матрицы Y2×R представляют собой целые числа, лежащие в диапазоне от единицы до M, а элементы второй строки матрицы Y2×R представляют собой целые числа, лежащие в диапазоне от единицы до NИ;
затем на основе заданных величин достаточных статистик коэффициентов воспроизведения с помощью генераторов случайных чисел генерируют выборки некоррелированных коэффициентов воспроизведения имитируемого многомерного временного ряда, причем объемы этих выборок совпадают с числом реперных точек воспроизведения имитируемого многомерного временного ряда, а число выборок совпадает с числом строк в матрице значимых собственных векторов; записывают выборки некоррелированных коэффициентов воспроизведения в матрицу коэффициентов воспроизведения имитируемого многомерного временного ряда WC×H так, что номера строк матрицы выборок соответствуют номерам строк матрицы значимых собственных векторов; далее формируют и сохраняют матрицу ансамбля воспроизведения покрытий имитируемого многомерного временного ряда 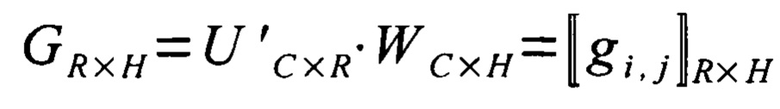 , для чего матрично перемножают транспонированную хранимую матрицу значимых собственных векторов ковариационной матрицы ансамбля покрытий на матрицу коэффициентов воспроизведения имитируемого многомерного временного ряда; для каждой из H реперных точек воспроизведения τk формируют нулевую парциальную матрицу воспроизведения
, для чего матрично перемножают транспонированную хранимую матрицу значимых собственных векторов ковариационной матрицы ансамбля покрытий на матрицу коэффициентов воспроизведения имитируемого многомерного временного ряда; для каждой из H реперных точек воспроизведения τk формируют нулевую парциальную матрицу воспроизведения  так, что общее число парциальных матриц воспроизведения совпадает с числом реперных точек воспроизведения и далее с использованием функции шаблона покрытия воспроизведения вычисляют значения функции для каждой из H реперных точек
так, что общее число парциальных матриц воспроизведения совпадает с числом реперных точек воспроизведения и далее с использованием функции шаблона покрытия воспроизведения вычисляют значения функции для каждой из H реперных точек
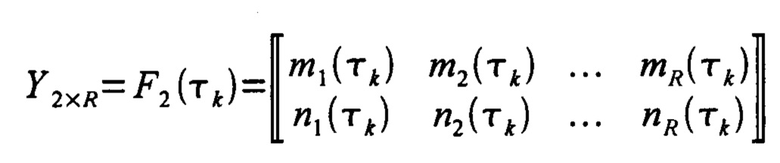 ,
,
а затем с использованием полученных значений заменяют отдельные элементы парциальной матрицы воспроизведения 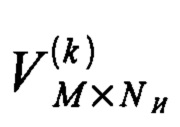 , для чего выполняют подстановку
, для чего выполняют подстановку
 ,
,
где gi,k - соответствующий элемент матрицы GR×H; после чего из матриц парциальных временных рядов формируют матрицу воспроизведения временного ряда
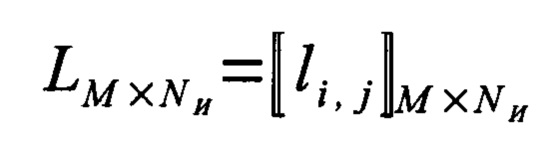 ,
,
для чего вычисляют среднее арифметическое всех матриц парциальных временных рядов, то есть
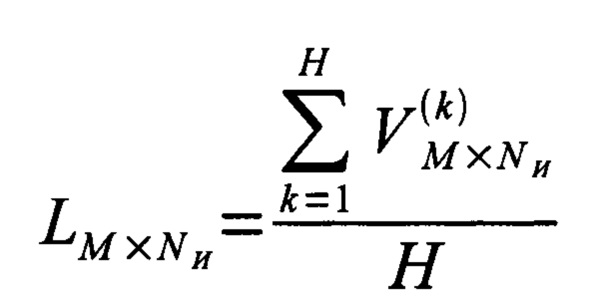 ;
;
далее для каждой строки, входящей в матрицу воспроизведения  , осуществляют интерполяцию в точках, соответствующих оси дискретного времени, с использованием в качестве значений интерполируемой функции ненулевых значений строки, а в качестве аргументов - номера дискрета, соответствующего ненулевому значению; после чего отправляют матрицу, полученную в результате интерполирования строк матрицы воспроизведения, на хранение.
, осуществляют интерполяцию в точках, соответствующих оси дискретного времени, с использованием в качестве значений интерполируемой функции ненулевых значений строки, а в качестве аргументов - номера дискрета, соответствующего ненулевому значению; после чего отправляют матрицу, полученную в результате интерполирования строк матрицы воспроизведения, на хранение.
3. Способ имитации многоканальных рядов наблюдений, в том числе электрокардиограмм, по п. 1, отличающийся тем, что предлагаемую последовательность действий реализуют следующим образом: на первом подготовительном этапе функцию шаблона выборки задают так: вводят конечный интервал анализа, представляющий собой последовательность отсчетов дискретного времени от единицы до I, где I - величина интервала анализа; задают область определения 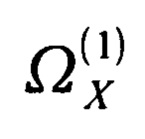 для функции шаблона покрытия как последовательность целых чисел от единицы до N-I+1; вводят функцию шаблона покрытия в виде
для функции шаблона покрытия как последовательность целых чисел от единицы до N-I+1; вводят функцию шаблона покрытия в виде
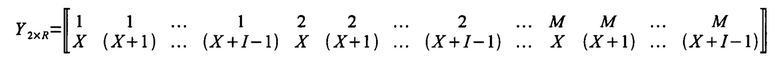 ,
,
имеющую размерность шаблона R=I⋅M; далее задают покрытие многомерного временного ряда в виде упорядоченного множества чисел, совпадающего с областью определения  с числом реперных точек покрытия S=N-I; с использованием функции шаблона покрытия формируют матрицу ансамбля покрытия
с числом реперных точек покрытия S=N-I; с использованием функции шаблона покрытия формируют матрицу ансамбля покрытия
 ;
;
после чего оценивают и отправляют на хранение достаточные статистики, которые формируют из строк матрицы коэффициентов QC×S; на втором этапе имитации временных рядов многомерных наблюдений: при генерировании имитирующих временных рядов многоканальных наблюдений в качестве реперных точек воспроизведения назначают числа от единицы до H=N-I; задают число отсчетов дискретного времени для имитируемого многомерного временного ряда NИ=N; определяют шаблон воспроизведения F2(X)=F1(X) при  и
и  ; на основе заданных величин достаточных статистик коэффициентов воспроизведения с помощью генераторов случайных чисел генерируют выборки некоррелированных коэффициентов воспроизведения имитируемого многомерного временного ряда, причем объемы этих выборок совпадают с величиной H=N-I, а число выборок совпадает с числом строк R=I⋅M в матрице значимых векторов; записывают выборки некоррелированных коэффициентов воспроизведения в матрицу коэффициентов воспроизведения имитируемого многомерного временного ряда WC×H так, что номера строк матрицы выборок соответствуют номерам строк матрицы значимых собственных векторов; сохраняют матрицу ансамбля воспроизведения покрытий имитируемого многомерного временного ряда, для чего матрично перемножают транспонированную хранимую матрицу значимых собственных векторов ковариационной матрицы ансамбля покрытий на матрицу коэффициентов воспроизведения имитируемого многомерного временного ряда;
; на основе заданных величин достаточных статистик коэффициентов воспроизведения с помощью генераторов случайных чисел генерируют выборки некоррелированных коэффициентов воспроизведения имитируемого многомерного временного ряда, причем объемы этих выборок совпадают с величиной H=N-I, а число выборок совпадает с числом строк R=I⋅M в матрице значимых векторов; записывают выборки некоррелированных коэффициентов воспроизведения в матрицу коэффициентов воспроизведения имитируемого многомерного временного ряда WC×H так, что номера строк матрицы выборок соответствуют номерам строк матрицы значимых собственных векторов; сохраняют матрицу ансамбля воспроизведения покрытий имитируемого многомерного временного ряда, для чего матрично перемножают транспонированную хранимую матрицу значимых собственных векторов ковариационной матрицы ансамбля покрытий на матрицу коэффициентов воспроизведения имитируемого многомерного временного ряда;

формируют парциальные матрицы воспроизведения, число которых совпадает с размером интервала анализа:
 ;
;
из матриц парциальных матриц воспроизведения формируют матрицу воспроизведения временного ряда
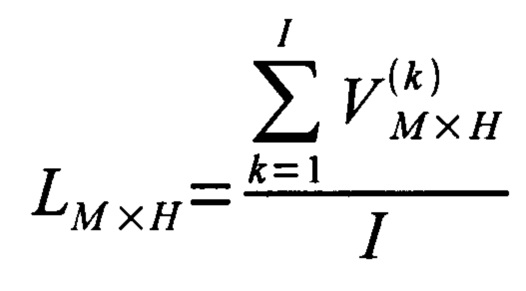
путем усреднения парциальных матриц воспроизведения; для каждой строки, входящей в матрицу воспроизведения LM×H, осуществляют интерполяцию в точках, соответствующих оси дискретного времени, с использованием в качестве значения интерполируемой функции ненулевого значения строки, а в качестве значения аргумента - номера дискрета, соответствующего ненулевому значению; отправляют матрицу, полученную в результате интерполирования строк матрицы воспроизведения, на хранение.
4. Способ имитации многоканальных рядов наблюдений, в том числе электрокардиограмм, по п. 1, отличающийся тем, что предлагаемую последовательность действий реализуют следующим образом: на первом подготовительном этапе: на основе характерных точек синхронизации 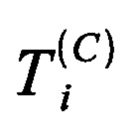 , принадлежащих интервалу дискретного времени от единицы до N, общее число которых составляет NC и которые поступают с внешнего устройства синхронизации, задают неявно функцию шаблона выборки, для чего определяют левый и правый интервалы анализа TL и TR так, что левый интервал анализа для конкретной точки синхронизации
, принадлежащих интервалу дискретного времени от единицы до N, общее число которых составляет NC и которые поступают с внешнего устройства синхронизации, задают неявно функцию шаблона выборки, для чего определяют левый и правый интервалы анализа TL и TR так, что левый интервал анализа для конкретной точки синхронизации 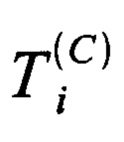 представляет собой последовательность отсчетов дискретного времени
представляет собой последовательность отсчетов дискретного времени 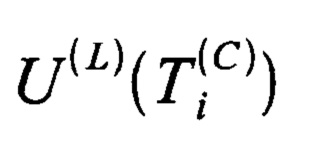 от
от до
до  , а правый - последовательность отсчетов дискретного времени
, а правый - последовательность отсчетов дискретного времени 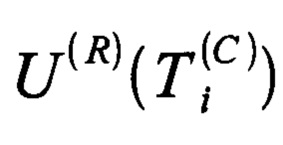 от
от  до
до 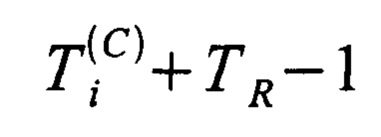 , а весь интервал анализа представляет собой последовательность отсчетов дискретного времени
, а весь интервал анализа представляет собой последовательность отсчетов дискретного времени 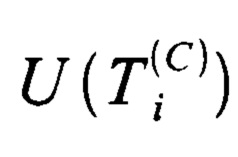 от
от  до
до  и имеет длительность
и имеет длительность 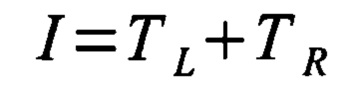 ;
;
затем проверяют условие вхождения левых границ левых интервалов и правых границ правых интервалов в интервал от единицы до N и отбрасывают точки синхронизации, для которых не выполняется или условие  , или условие
, или условие 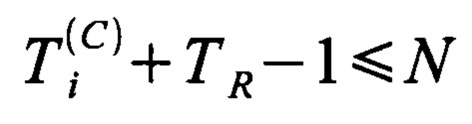 ; точки, для которых оба условия выполняются, рассматривают в качестве реперных точек покрытия, которые нумеруют по порядку их возрастания, присваивая новые номера от единицы до величины S, а в качестве области определения функции шаблона выборки
; точки, для которых оба условия выполняются, рассматривают в качестве реперных точек покрытия, которые нумеруют по порядку их возрастания, присваивая новые номера от единицы до величины S, а в качестве области определения функции шаблона выборки  определяют множество всех точек синхронизации; пользуясь неявно введенной функцией шаблона покрытия, состоящей в том, что каждой реперной точке в каждом из M каналов соответствует I отсчетов так, что размерность шаблона покрытия
определяют множество всех точек синхронизации; пользуясь неявно введенной функцией шаблона покрытия, состоящей в том, что каждой реперной точке в каждом из M каналов соответствует I отсчетов так, что размерность шаблона покрытия  , а сама матрица ансамбля покрытия
, а сама матрица ансамбля покрытия
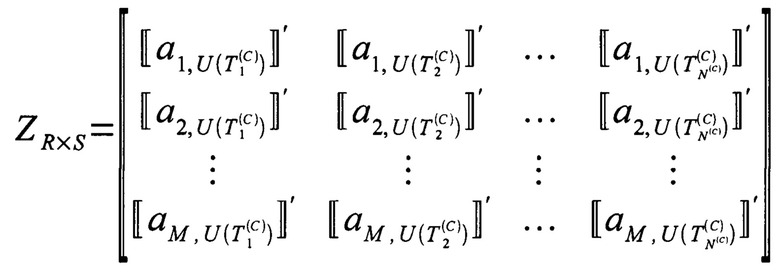 ,
,
где  - матрица-столбец, получаемая из элементов, стоящих в столбцах
- матрица-столбец, получаемая из элементов, стоящих в столбцах  в i-й строке матрицы исходного временного ряда;
в i-й строке матрицы исходного временного ряда;
вычисляют ковариационную матрицу ансамбля покрытия
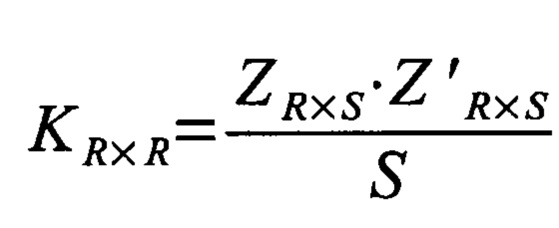
посредством матричного умножения матрицы ансамбля покрытия на транспонированную матрицу ансамбля покрытия с последующим делением результатов матричного умножения на число реперных точек;
на втором этапе имитации временных рядов многомерных наблюдений: на основе заданных величин достаточных статистик для интервалов между реперными точками воспроизведения с использованием генераторов случайных чисел генерируют последовательность упорядоченных по возрастанию реперных точек воспроизведения  ,
, 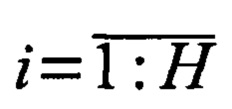 , общее число которых равно H, удовлетворяющих условию
, общее число которых равно H, удовлетворяющих условию 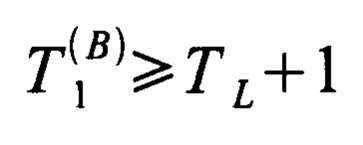 ; после чего производят вычитание из значений всех реперных точек воспроизведения величины
; после чего производят вычитание из значений всех реперных точек воспроизведения величины  ; задают число отсчетов дискретного времени для имитируемого многомерного временного ряда, равное
; задают число отсчетов дискретного времени для имитируемого многомерного временного ряда, равное 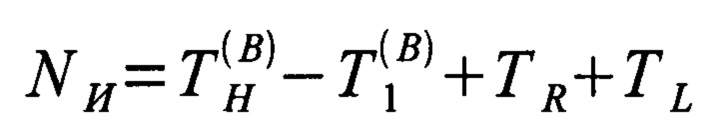 ; формируют и сохраняют матрицу ансамбля воспроизведения покрытий имитируемого многомерного временного ряда
; формируют и сохраняют матрицу ансамбля воспроизведения покрытий имитируемого многомерного временного ряда
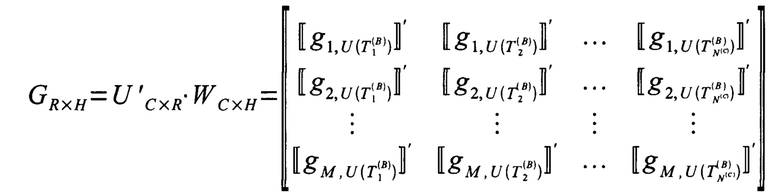 ;
;
для каждой реперной точки воспроизведения формируют нулевую парциальную матрицу воспроизведения 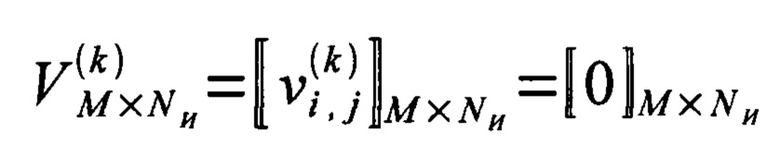 так, что общее число парциальных матриц воспроизведения совпадает с числом реперных точек воспроизведения; далее формируют парциальную матрицу воспроизведения в виде
так, что общее число парциальных матриц воспроизведения совпадает с числом реперных точек воспроизведения; далее формируют парциальную матрицу воспроизведения в виде
 ,
,
где штрих означает транспонирование;
из парциальных матриц воспроизведения формируют матрицу воспроизведения временного ряда 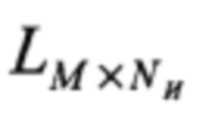 , для чего каждую строку матрицы воспроизведения временного ряда вычисляют как среднее всех парциальных матриц воспроизведения, то есть
, для чего каждую строку матрицы воспроизведения временного ряда вычисляют как среднее всех парциальных матриц воспроизведения, то есть
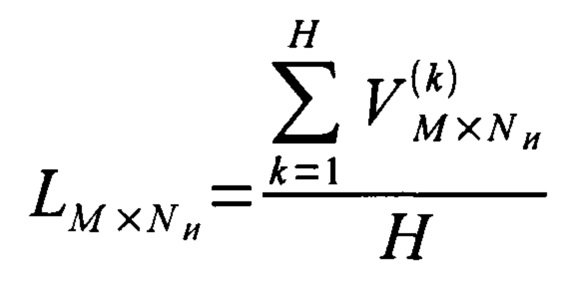 ;
;
для каждой строки, входящей в матрицу воспроизведения 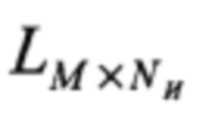 , осуществляют интерполяцию в точках, соответствующих оси дискретного времени, с использованием в качестве значения интерполируемой функции ненулевого значения строки, а в качестве значения аргумента - номера дискрета, соответствующего ненулевому значению; отправляют матрицу, полученную в результате интерполирования строк матрицы воспроизведения, на хранение.
, осуществляют интерполяцию в точках, соответствующих оси дискретного времени, с использованием в качестве значения интерполируемой функции ненулевого значения строки, а в качестве значения аргумента - номера дискрета, соответствующего ненулевому значению; отправляют матрицу, полученную в результате интерполирования строк матрицы воспроизведения, на хранение.
| US 8543195 B1, 24.09.2013 | |||
| Многоступенчатая активно-реактивная турбина | 1924 |
|
SU2013A1 |
| Устройство для накатывания наружных резьб | 1957 |
|
SU116242A1 |
| 0 |
|
SU162110A1 | |
| 0 |
|
SU163762A1 | |
Авторы
Даты
2021-05-14—Публикация
2017-11-08—Подача