Изобретение относится к области электротехники и может быть использовано в системах бездатчикового управления синхронным электродвигателем с постоянными магнитами.
Известен способ управления синхронным электродвигателем (Патент США №10291160, МПК Н02Р 6/06, дата приоритета 09.03.2018, дата публикации 14.05.2019), заключающийся в измерении мгновенных значений силы тока и напряжений фаз статора, использовании этих сигналов для оценивания угла поворота и скорости вращения ротора, после чего использования полученных оценок для выработки управляющего воздействия. Недостатком указанного способа является то, что при изменяющейся скорости вращения ротора появляется ошибка оценивания и регулирования угла поворота ротора.
Известен способ бездатчикового управления синхронным электродвигателем с постоянными магнитами (Н. Li, D. Ke, R. Zu, P. Tao and F. Wang, Sensorless Control of Permanent Magnet Synchronous Motor Based on An Improved Sliding Mode Observer, IEEE SCEMS, pp.1-6, 2018), основанный на алгоритме векторного управления, использующий наблюдатель со скользящим режимом для оценивания положения и скорости по противо-ЭДС. Для устранения осцилляций в системе предложена новая функция переключения, что позволяет компенсировать ошибку положения ротора, вызванную фильтром нижних частот, делая скорость вращения ротора и оценку положения более точной в широком диапазоне скоростей. Недостатком является то, что способ не применим на низких скоростях, где значение противо-ЭДС сравнимо с уровнем шума и помех измерения.
В качестве ближайшего аналога выбран способ бездатчикового управления синхронным электродвигателем на постоянных магнитах (D. Bazylev, S. Vukosavic, A. Bobtsov, A. Pyrkin, A. Stankovic and R. Ortega, Sensorless control of PM synchronous motors with a robust nonlinear observer, 2018 IEEE Industrial Cyber-Physical Systems (ICPS), St. Petersburg, 2018, pp. 304-309, doi: 10.1109/ICPHYS.2018.8387676), в котором, учитывая номинальные или измеренные параметры двигателя, выбранные значения настраиваемых параметров и заданного желаемого положения ротора θ*(t), сначала измеряют мгновенные значения силы тока в обмотках фаз статора, мгновенные значения напряжений на обмотках фаз статора, рассчитывают с помощью преобразования Кларк мгновенные значения силы тока i(t) и напряжения u(t) в двухфазной стационарной системе координат αβ, связанной со статором, определяют угол поворота ротора 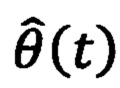 :
:
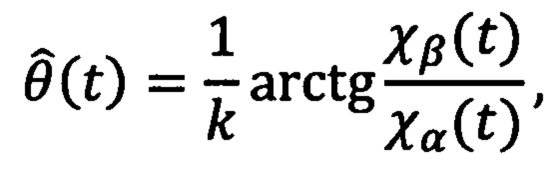
где k - количество пар полюсов, χα(t) и χβ(t) - компоненты оценки потокосцепления 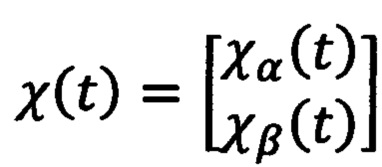 , создаваемого постоянными магнитами ротора в двухфазной системе координат αβ, оценивают скорость с помощью метода фазовой подстройки частоты ω(t). Далее используя три вложенных контура управления: по положению, по скорости, по току, рассчитывают значения желаемого напряжения во вращающейся системе координат dq, связанной с ротором. Для этого определяют ошибку регулирования углового положения ротора
, создаваемого постоянными магнитами ротора в двухфазной системе координат αβ, оценивают скорость с помощью метода фазовой подстройки частоты ω(t). Далее используя три вложенных контура управления: по положению, по скорости, по току, рассчитывают значения желаемого напряжения во вращающейся системе координат dq, связанной с ротором. Для этого определяют ошибку регулирования углового положения ротора 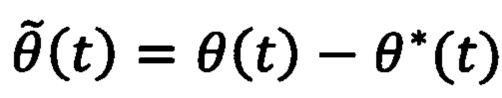 , определяют желаемую скорость ω*(t), с помощью пропорционально-интегрально-дифференциального регулятора, рассчитывают ошибку регулирования скорости вращения ротора
, определяют желаемую скорость ω*(t), с помощью пропорционально-интегрально-дифференциального регулятора, рассчитывают ошибку регулирования скорости вращения ротора  , определяют с помощью пропорционально-интегрально-дифференциального регулятора значение желаемой силы тока iq*(t) по поперечной оси во вращающейся системе координат dq, определяют значение сигналов силы тока во вращающейся системе координат dq: iq(t) и id(t), рассчитывают ошибки регулирования тока
, определяют с помощью пропорционально-интегрально-дифференциального регулятора значение желаемой силы тока iq*(t) по поперечной оси во вращающейся системе координат dq, определяют значение сигналов силы тока во вращающейся системе координат dq: iq(t) и id(t), рассчитывают ошибки регулирования тока 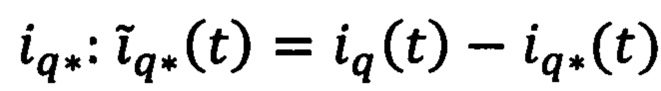 , определяют с помощью пропорционально-интегрально-дифференциального регулятора значения сигналов νd(t) и νq(t). После этого последовательно применяя обратное преобразования Парка и Кларк определяют значения требуемых напряжений для каждой фазы статора, которые подаются на блок широтно-импульсной модуляции, выходные сигналы которого подают на инвертор для формирования требуемого уровня напряжения на фазах статора.
, определяют с помощью пропорционально-интегрально-дифференциального регулятора значения сигналов νd(t) и νq(t). После этого последовательно применяя обратное преобразования Парка и Кларк определяют значения требуемых напряжений для каждой фазы статора, которые подаются на блок широтно-импульсной модуляции, выходные сигналы которого подают на инвертор для формирования требуемого уровня напряжения на фазах статора.
К недостаткам данного способа относится ухудшение качества регулирования положения при отклонении параметров двигателя от номинальных или наличии внешних возмущений.
Задачей, для решения которой предназначено изобретение, является улучшение качества управления положением ротора синхронного двигателя с постоянными магнитами при наличии параметрических и внешних возмущений.
Сущность предлагаемого способа заключается в том, для прямого бездатчикового управления положением ротора синхронного электродвигателя с постоянными магнитами, с учетом номинальных или измеренных значений сопротивления R, индуктивности L обмоток статора, количества пар полюсов k, момента инерции ротора j, коэффициента λm, связанного с потокосцеплением от постоянных магнитов, максимально допустимого фазного напряжения umax, выбранных значений настраиваемых параметров и заданного желаемого положения ротора θ*(t), сначала переходят к двухфазной системе координат для чего измеряют мгновенные значения силы тока в обмотках фаз статора, мгновенные значения напряжений на обмотках фаз статора, далее, применяя преобразования Кларк, рассчитывают мгновенные значения силы тока i(t) и напряжения u(t) в двухфазной стационарной системе координат αβ, связанной со статором. Далее по сигналам i(t) и u(t) определяют угол поворота ротора 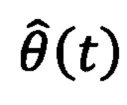 с помощью выражения:
с помощью выражения:

где k - количество пар полюсов, χα(t) и χβ(t) - компоненты оценки потокосцепления 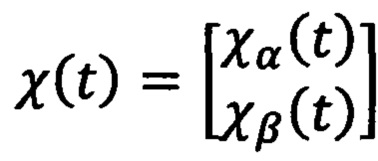 , создаваемого постоянными магнитами ротора в двухфазной системе координат αβ, которую определяют с помощью выражения:
, создаваемого постоянными магнитами ротора в двухфазной системе координат αβ, которую определяют с помощью выражения:
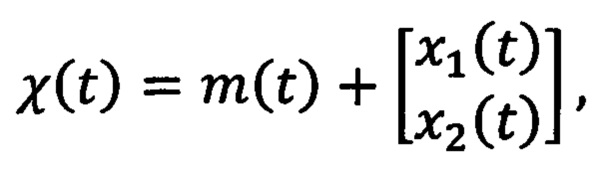
где
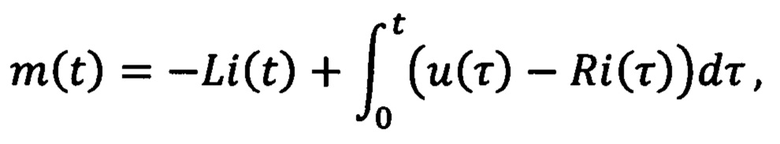
R и L - значения сопротивления и индуктивности обмоток статора соответственно, a x1(t) и x2(t) являются оценкой начальных условий χ(0), каждую из которых определяют с помощью скалярной версии алгоритма градиентного спуска:

где n принимает значения 1 и 2, γn>0 - настраиваемые коэффициенты усиления, ξ1(t)=ρ2(t)y(t)-q2(t)z(t), ξ2(t)=q1(t)z(t)-ρ1(t)y(t), φ(t)=ρ2(t)q1(t)-q2(t)ρ1(t), определяемые на основе фильтрованных сигналов mT(t)m(t) и 2m(t):
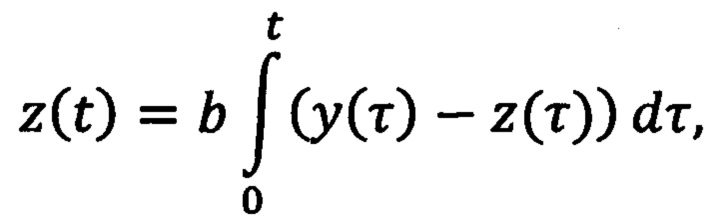

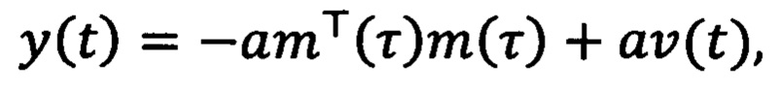
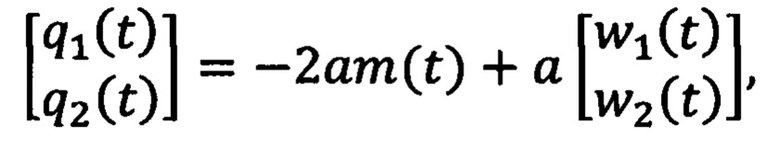
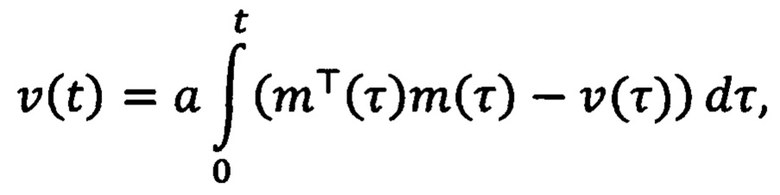
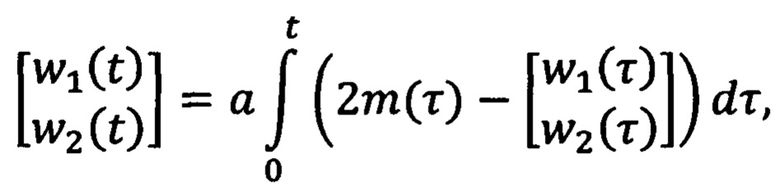
a>0 и b>0 - настраиваемые коэффициенты фильтрации. После определяют ошибку регулирования 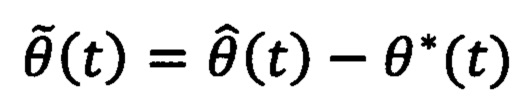 на основе оценки текущего углового положения ротора и заданного углового положения ротора. Далее формируют напряжения νd(t), νq(t) во вращающейся системе координат dq, причем продольную компоненту νd(t) принимают равной нулю, а поперечную компоненту νq(t) формируют путем суммирования двух напряжений νq1(t) и νq2(t), где νq1(t) меняют в зависимости от ошибки регулирования углового положения ротора
на основе оценки текущего углового положения ротора и заданного углового положения ротора. Далее формируют напряжения νd(t), νq(t) во вращающейся системе координат dq, причем продольную компоненту νd(t) принимают равной нулю, а поперечную компоненту νq(t) формируют путем суммирования двух напряжений νq1(t) и νq2(t), где νq1(t) меняют в зависимости от ошибки регулирования углового положения ротора 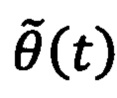 , a νq2(t) меняют в зависимости от известных параметров момента нагрузки, по следующим выражениям:
, a νq2(t) меняют в зависимости от известных параметров момента нагрузки, по следующим выражениям:
νq(t)=νq1(t)+νq2(t),
где стабилизирующее напряжение νq1(t) определяют с помощью выражения:
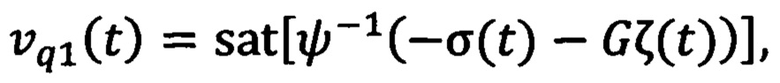
где G=(g1 g2 g3) - настраиваемые параметры регулятора, sat(⋅) - функция насыщения с выходным значениям в диапазоне [-umax, umax], ψ - ненулевая постоянная переменная, удовлетворяющая неравенству:
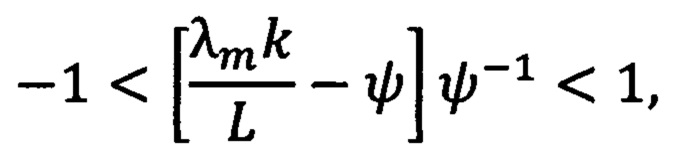
а вектор состояния расширенного наблюдателя  и σ(t) определяют с помощью выражений:
и σ(t) определяют с помощью выражений:
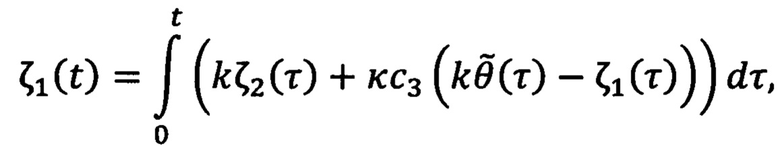
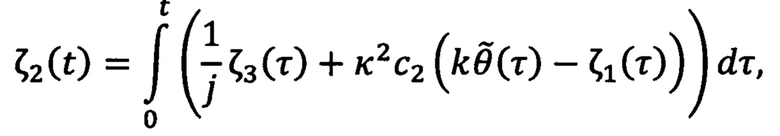
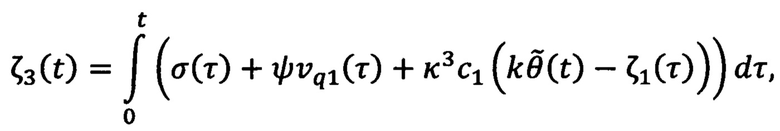
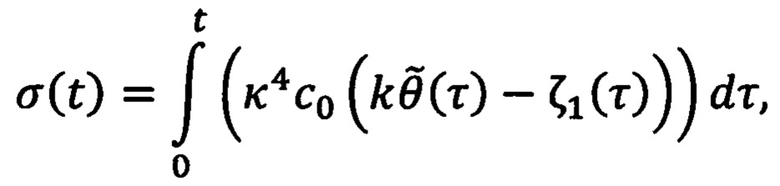
где с0, c1, c2, c3 и κ - настраиваемые параметры, 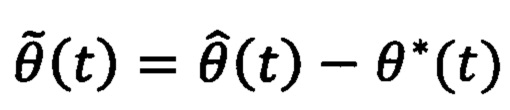 - ошибка регулирования углового положения ротора, а компенсирующее напряжение νq2(t) определяют с помощью выражения:
- ошибка регулирования углового положения ротора, а компенсирующее напряжение νq2(t) определяют с помощью выражения:
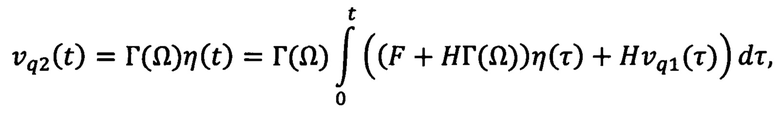
где η(t) - вектор состояния внутренней модели, F, Η - матрица состояния и вектор входа устойчивой системы в каноническом управляемом базисе соответственно, Γ(Ω) - вектор параметров, зависящих от номинальных значений частот гармоник момента нагрузки Ω. После к рассчитанным значениям νd(t) и νq(t) применяют последовательно обратные преобразования Парка и Кларк, для определения значения требуемых напряжений для каждой фазы статора, которые в свою очередь подаются на блок широтно-импульсной модуляции, выходные сигналы которого передаются на инвертор для формирования требуемого уровня напряжения на фазах статора.
Сущность заявляемого способа поясняется чертежами, где:
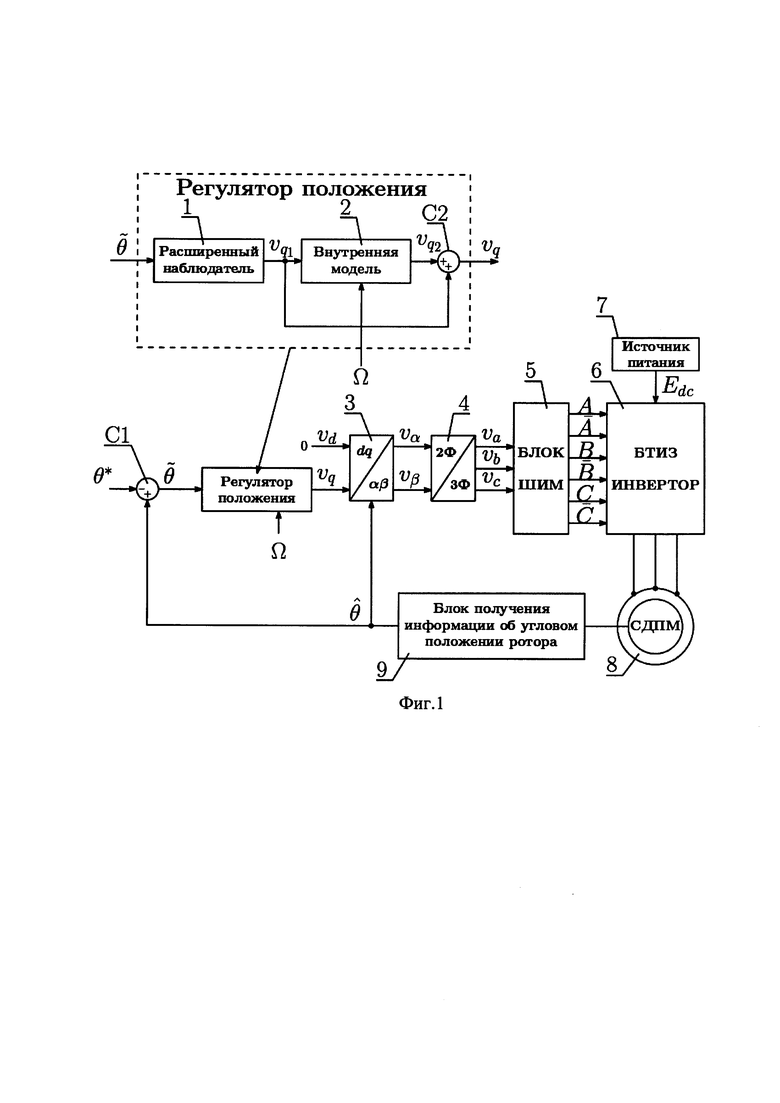
на фиг.1 представлена общая структура устройства системы управления синхронным двигателем с постоянными магнитами, включающая в себя предложенный регулятор положения ротора.
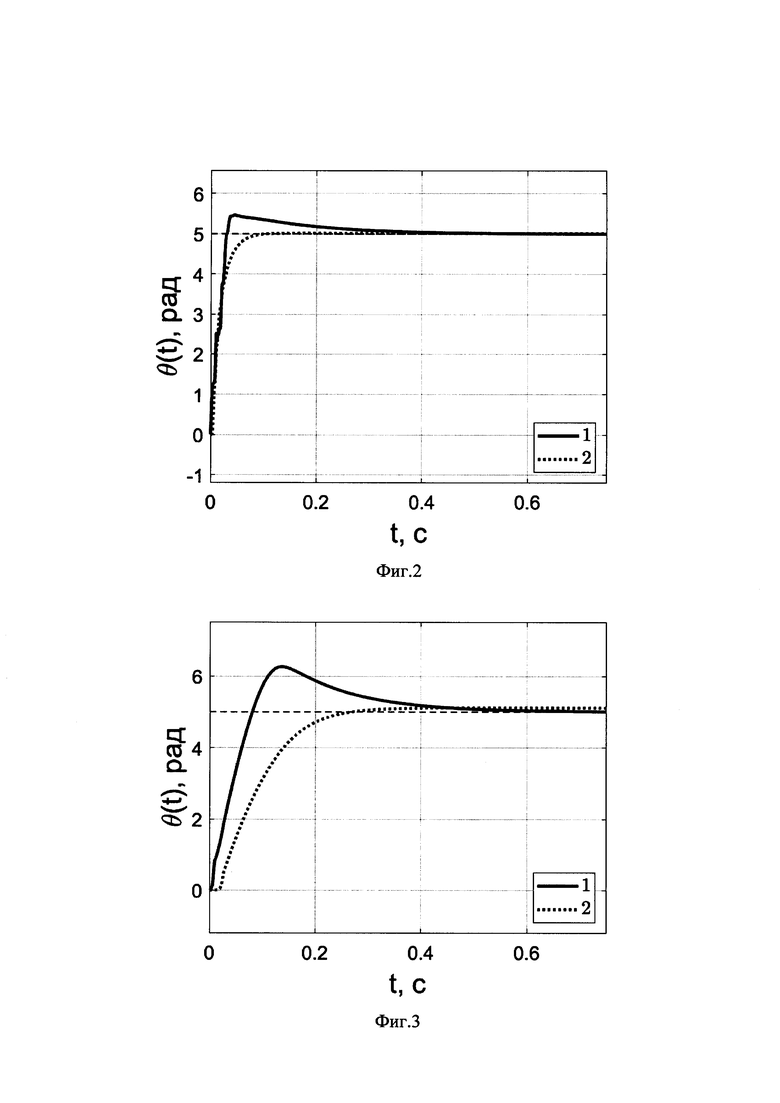
на фиг.2 приведен график углового положения ротора синхронного двигателя с постоянными магнитами при использовании предложенного способа управления (линия 1) и ближайшего аналога (линия 2) при номинальных параметрах двигателя, при отсутствии внешнего возмущающего воздействия и при θ*(t)=5 рад.
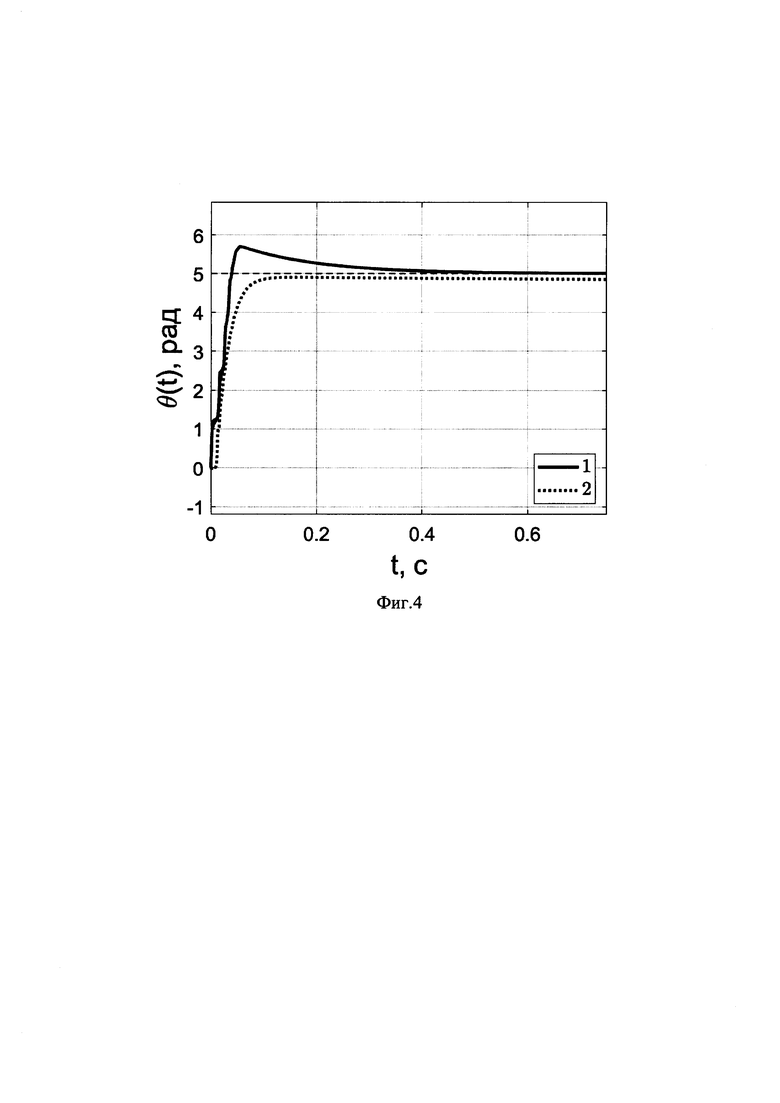
на фиг.3 приведен график углового положения ротора синхронного двигателя с постоянными магнитами при использовании предложенного способа управления (линия 1) и ближайшего аналога (линия 2) при наличии параметрического возмущения в виде увеличенных коэффициента вязкого трения со значением 0.6 Н⋅м⋅с/рад и момента инерции ротора 0.00059 кг⋅м2 при θ*(t)=5 рад.
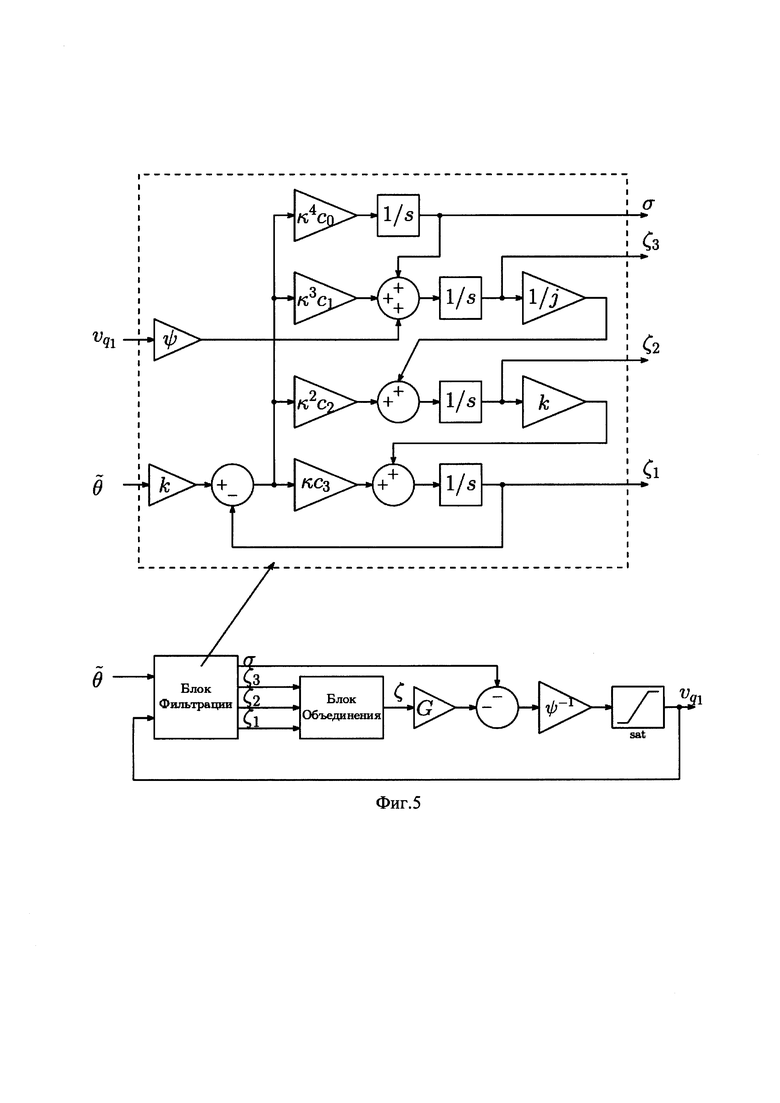
на фиг.4 приведен график углового положения ротора синхронного двигателя с постоянными магнитами при использовании предложенного способа управления (линия 1) и ближайшего аналога (линия 2) при наличии внешнего возмущения в виде момента внешней нагрузки, изменяющегося по закону τL(t)=1,5+2sin (t) Н⋅м, и при θ*(t)=5 рад.
на фиг.5 приведена схема блока с расширенным наблюдателем на усилителях, интеграторах и сумматорах. Обозначения являются стандартными для Matlab.
Устройство (фиг.1) содержит в себе регулятор положения, состоящий из блока с расширенным наблюдателем 1 (схема приведена на фиг.5) и блоком с внутренней моделью 2, блок 3, выполняющий обратное преобразование Парка, блок 4, выполняющий обратное преобразование Кларк, блок выработки сигнала широтно-импульсной модуляции 5, инвертор на основе биполярных транзисторов с изолированным затвором 6, источник питания 7, синхронный двигатель с постоянными магнитами 8, блок определения углового положения ротора 9 по сигналам силы тока i(t) и напряжения u(t) в двухфазной стационарной системе координат αβ. Также в устройство системы управления входит два сумматора С1 и С2, один задающий вход, на который подается желаемое угловое положение ротора θ*(t) и один вход, на который подается вектор номинальных значений частот гармоник момента нагрузки Ω.
Вход устройства для задания желаемого углового положения ротора θ*(t), соединен с входом сумматора С1, к инверсному входу которого, подключен выход блока получения информации об угловом положении ротора 9. Выход сумматора С1 подключен к расширенному наблюдателю 1, выход которого соединен с сумматором С2 и с внутренней моделью 2, которая имеет отдельный вход вектора номинальных значений частот гармоник момента нагрузки Ω и выход которой соединен с сумматором С2. Выход сумматора С2 соединен с входом блока 3, отдельный вход которого соединен с выходом блока получения информации об угловом положении ротора 9. Выходы блока 3 соединены с блоком 4, выходы которого соединены с блоком широтно-импульсной модуляции 5, выходы которого подключены на инвертор 6. Инвертор 6 имеет отдельный вход для подключения к выходу источника питания 7. Выходы инвертора 6 соединены с фазами синхронного двигателя с постоянными магнитами 8, к которому подключен блок 9.
Устройство с предложенным способом управления положением ротора синхронного электродвигателя с постоянными магнитами работает следующим образом.
Перед запуском устройства задается желаемое значение углового положения ротора θ*(t). Далее происходит запуск устройства, посредством подачи напряжения постоянного тока Edc с источника тока 7 на блок 6. С помощью блока получения информации об угловом положении ротора 9 определяется значение текущего углового положения ротора 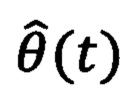 , которое подается на блок 3 и инверсный вход сумматора С1. Определяется разность между заданным желаемым значением углового положения ротора θ*(t) и значением текущего углового положения ротора
, которое подается на блок 3 и инверсный вход сумматора С1. Определяется разность между заданным желаемым значением углового положения ротора θ*(t) и значением текущего углового положения ротора 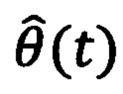 с использованием сумматора С1. Полученное значение ошибки углового положения ротора
с использованием сумматора С1. Полученное значение ошибки углового положения ротора 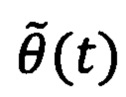 поступает на блок с расширенным наблюдателем 1 для расчета стабилизирующего напряжения νq1(t), который далее принимается блоком с внутренней моделью 2 для определения компенсирующего напряжения νq2(t). Оба полученных напряжения νq1(t) и νq2(t) складываются с помощью сумматора С2 и формируют поперечную компоненту напряжения νq(t) во вращающейся системе координат dq, подаваемое на блок 3, в котором (с учетом того, что продольная компонента напряжения νd(t) равна нулю) с помощью обратного преобразования Парка рассчитывают значения напряжений να(t), νβ(t) в двухфазной стационарной системе координат αβ, значения которых далее подается на блок 4, где с помощью обратного преобразования Кларк определяют значения напряжений νa(t), νb(t), νc(t) в трехфазной системе координат. Полученные значения напряжений νa(t), νb(t), νc(t) подаются на блок широтно-импульсной модуляции 5, который генерирует шесть входных воздействий на инвертор на основе биполярных транзисторов с изолированным затвором. Затем инвертор 6 подает напряжения на фазы синхронного двигателя с постоянными магнитами 8. Потом снова происходит определение значения текущего углового положения ротора
поступает на блок с расширенным наблюдателем 1 для расчета стабилизирующего напряжения νq1(t), который далее принимается блоком с внутренней моделью 2 для определения компенсирующего напряжения νq2(t). Оба полученных напряжения νq1(t) и νq2(t) складываются с помощью сумматора С2 и формируют поперечную компоненту напряжения νq(t) во вращающейся системе координат dq, подаваемое на блок 3, в котором (с учетом того, что продольная компонента напряжения νd(t) равна нулю) с помощью обратного преобразования Парка рассчитывают значения напряжений να(t), νβ(t) в двухфазной стационарной системе координат αβ, значения которых далее подается на блок 4, где с помощью обратного преобразования Кларк определяют значения напряжений νa(t), νb(t), νc(t) в трехфазной системе координат. Полученные значения напряжений νa(t), νb(t), νc(t) подаются на блок широтно-импульсной модуляции 5, который генерирует шесть входных воздействий на инвертор на основе биполярных транзисторов с изолированным затвором. Затем инвертор 6 подает напряжения на фазы синхронного двигателя с постоянными магнитами 8. Потом снова происходит определение значения текущего углового положения ротора 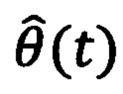 синхронного электродвигателя с постоянными магнитами 8, после чего последовательность действий повторяется.
синхронного электродвигателя с постоянными магнитами 8, после чего последовательность действий повторяется.
Эффективность предложенного способа при наличии внешних и параметрических возмущений подтверждена результатами экспериментов по управлению угловым положение ротора, представленными на фиг.2-фиг.4. Моделирование происходило с параметрами двигателя BMP0701F: сопротивление обмоток статора R=8,87 Ом, индуктивность обмоток статора L=40 мГн, количество пар полюсов k=5, момент инерции ротора j=5,9⋅105 кг⋅м2, коэффициента λm=0,2086 Вб, максимально допустимого фазного напряжения Umax=200 В, коэффициент вязкого трения f=0,006 Н⋅м⋅с/рад. Параметры блока определения положения: a=550, b=50, γ1=γ2=10. Параметры регулятора для предлагаемого способа: g1=64, g2=48, g3=12, ψ=100, с0=2,3297, с1=2,9122, с2=3084, с3=2935, и κ=1000. Параметры для ближайшего аналога: 1) коэффициенты регулятора тока: пропорциональный - 0,5, интегральный - 0,1; 2) коэффициенты регулятора скорости: пропорциональный - 1,2, интегральный - 0,1; 3) коэффициенты регулятора по положению: пропорциональный - 200, интегральный - 1. Желаемое угловое положение во всех случаях равно θ*(t)=5 рад. Параметрического возмущение моделировалось в виде увеличенного коэффициента трения со значением 0,6 Н⋅м⋅с/рад и момента инерции ротора равного 5,9⋅104 кг⋅м2. Внешнее возмущение моделировалось, как момент, приложенный к валу двигателя и изменяющийся по закону τL(t)=1,5+2sin (t) Н⋅м.
При наличии параметрического возмущения (фиг.3) или внешнего возмущения (фиг.4) при использовании предложенного способа (линия 1) регулятор обеспечивают нулевую установившуюся ошибку и сравнимую со случаем номинальных параметров длительность переходного процесса, а при использовании ближайшего аналога появляется статическая ошибка и заметно изменяется длительность переходного процесса.
Таким образом, заявленный способ позволяет улучшить качество управления по положению синхронным двигателем с постоянными магнитами при наличии параметрических и внешних возмущений.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ определения угла поворота ротора синхронного электродвигателя с постоянными магнитами | 2020 |
|
RU2750334C1 |
| СПОСОБ БЕЗДАТЧИКОВОГО ОПРЕДЕЛЕНИЯ НАЧАЛЬНОГО ПОЛОЖЕНИЯ РОТОРА СИНХРОННОГО ЭЛЕКТРОДВИГАТЕЛЯ С ПОСТОЯННЫМИ МАГНИТАМИ | 2015 |
|
RU2594358C1 |
| СПОСОБ БЕЗДАТЧИКОВОЙ ОЦЕНКИ УГЛОВОГО ПОЛОЖЕНИЯ РОТОРА МНОГОФАЗНОГО ЭЛЕКТРОДВИГАТЕЛЯ | 2010 |
|
RU2428784C1 |
| СПОСОБ ВЕКТОРНОГО УПРАВЛЕНИЯ СИНХРОННЫМ ЭЛЕКТРОДВИГАТЕЛЕМ С ПОСТОЯННЫМИ МАГНИТАМИ НА РОТОРЕ И ЭЛЕКТРОПРИВОД ДЛЯ ОСУЩЕСТВЛЕНИЯ ЭТОГО СПОСОБА | 1998 |
|
RU2141719C1 |
| УСТРОЙСТВО УПРАВЛЕНИЯ СИНХРОННОЙ МАШИНОЙ С ПОСТОЯННЫМИ МАГНИТАМИ | 2010 |
|
RU2561879C2 |
| Способ управления синхронным электродвигателем на постоянных магнитах | 2018 |
|
RU2683586C1 |
| УСТРОЙСТВО УПРАВЛЕНИЯ ЭЛЕКТРОДВИГАТЕЛЕМ С ПОСТОЯННЫМИ МАГНИТАМИ БЕЗ ИСПОЛЬЗОВАНИЯ ДАТЧИКОВ ПОЛОЖЕНИЯ | 2012 |
|
RU2560090C1 |
| Устройство для управления двигателем двойного питания | 2016 |
|
RU2625720C1 |
| СПОСОБ ВЕКТОРНОГО УПРАВЛЕНИЯ СКОРОСТЬЮ ВРАЩЕНИЯ ТРЕХФАЗНОЙ МАШИНЫ | 2013 |
|
RU2557071C2 |
| Система и способ векторного управления электродвигателем с постоянными магнитами | 2020 |
|
RU2760227C1 |
Изобретение относится к области электротехники и может быть использовано в системах бездатчикового управления синхронным электродвигателем с постоянными магнитами. Технический результат заключается в повышения качества управления по положению при наличии внешних и параметрических возмущений. Способ прямого бездатчикового управления угловым положением ротора синхронного электродвигателя заключается в измерении мгновенных значений сил токов и напряжений на фазах статора. Далее происходит трансформация их в стационарную систему координат αβ, определение положения ротора на основе оценок компонент потокосцепления. Расчет сигналов управления угловым положением ротора осуществляется с использованием робастного закона управления с расширенным наблюдателем, что позволяет компенсировать внешние и параметрические возмущения. 5 ил.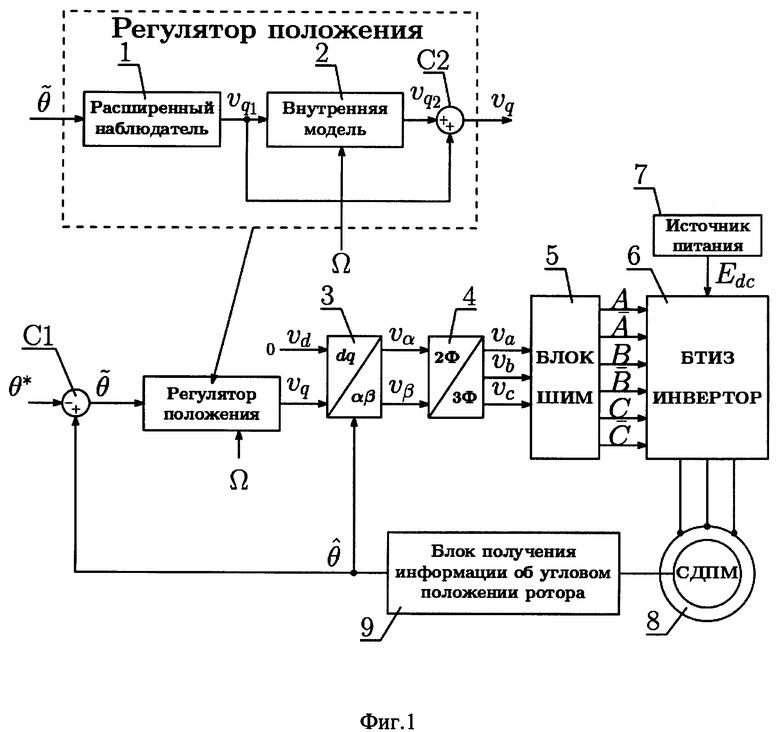
Способ прямого бездатчикового управления угловым положением ротора синхронного электродвигателя с постоянными магнитами, с учетом номинальных или измеренных значений сопротивления R и индуктивности L обмоток статора, количества пар полюсов k, момента инерции ротора j, коэффициента λm, связанного с потокосцеплением от постоянных магнитов, максимально допустимого фазного напряжения umax, выбранных значений настраиваемых параметров и заданного желаемого положения ротора θ*(t), заключающийся в формировании управляющих напряжений на фазы статора электродвигателя таким образом, что измеряют мгновенные значения силы тока в обмотках фаз статора и мгновенные значения напряжений на обмотках фаз статора, передают измерения в блок получения информации об угловом положении ротора, где полученные измерения преобразуют в мгновенные значения силы тока i(t) и напряжения u(t) в двухфазной стационарной системе координат αβ с помощью прямого преобразования Кларк и на их основе определяют оценку углового положения ротора 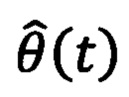 с помощью выражения:
с помощью выражения:
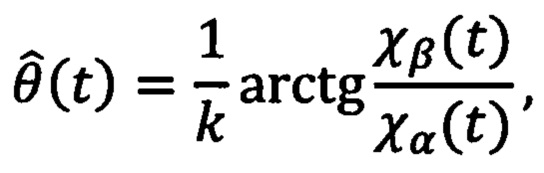
где χα(t) и χβ(t) - компоненты оценки потокосцепления 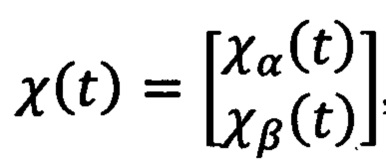 , создаваемого постоянными магнитами ротора в двухфазной системе координат αβ, которую определяют с помощью выражения:
, создаваемого постоянными магнитами ротора в двухфазной системе координат αβ, которую определяют с помощью выражения:
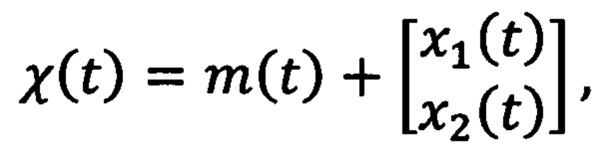
где
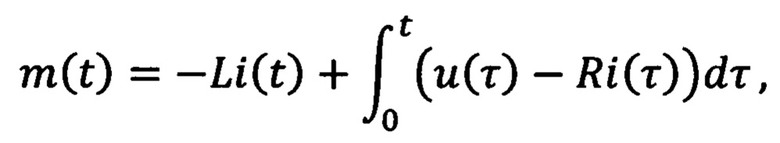
а x1(t) и x2(t) определяют с помощью выражения:
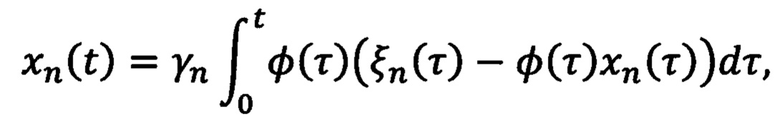
где n принимает значения 1 и 2, γn>0 - настраиваемые коэффициенты усиления, ξ1(t)=ρ2(t)y(t)-q2(t)z(t), ξ2(t)=q1(t)z(t)-ρ1(t)y(t), φ(t)=ρ2(t)q1(t)-q2(t)ρ1(t), a 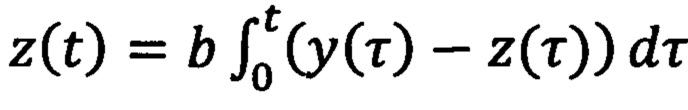 ,
,
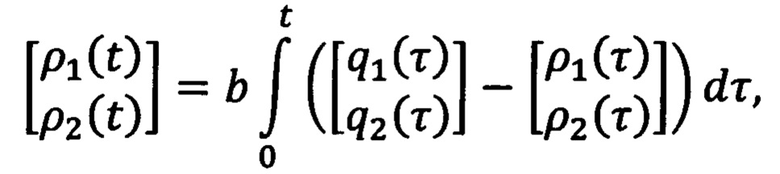
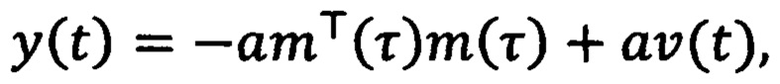

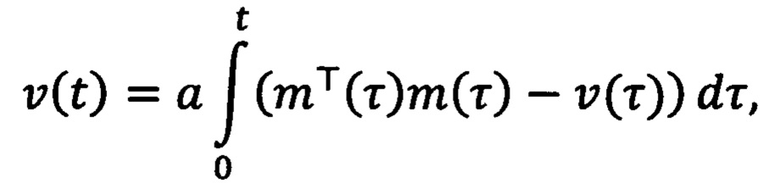
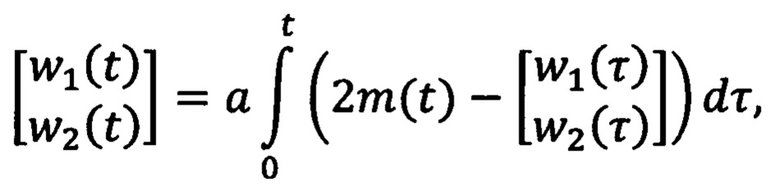
a>0 и b>0 - настраиваемые коэффициенты фильтрации, передают полученную оценку углового положения ротора на сумматор, где ее сравнивают с заданным угловым положением ротора и формируют ошибку регулирования 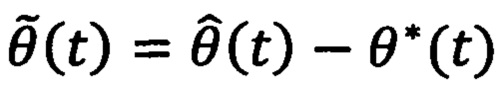 , которую передают на регулятор положения, где формируют напряжения νd(t), νq(t) во вращающейся системе координат dq, причем компоненту νd(t) принимают равной нулю, полученные напряжения передают на блок обратного преобразования Парка, где их преобразуют в напряжения να(t), νβ(t) в двухфазной стационарной системе координат αβ, которые передают в блок обратного преобразования Кларк, где их преобразуют в напряжения νa(t), νb(t), νc(t) в трехфазной системе координат, которые передают на блок широтно-импульсной модуляции, где формируют входные воздействия на инвертор на основе биполярных транзисторов с изолированным затвором, отличающийся тем, что в регуляторе положения формируют поперечную компоненту напряжения νq(t) во вращающейся системе координат dq путем суммирования двух напряжений νq1(t) и νq2(t), где νq1(t) меняют в зависимости от ошибки регулирования углового положения ротора
, которую передают на регулятор положения, где формируют напряжения νd(t), νq(t) во вращающейся системе координат dq, причем компоненту νd(t) принимают равной нулю, полученные напряжения передают на блок обратного преобразования Парка, где их преобразуют в напряжения να(t), νβ(t) в двухфазной стационарной системе координат αβ, которые передают в блок обратного преобразования Кларк, где их преобразуют в напряжения νa(t), νb(t), νc(t) в трехфазной системе координат, которые передают на блок широтно-импульсной модуляции, где формируют входные воздействия на инвертор на основе биполярных транзисторов с изолированным затвором, отличающийся тем, что в регуляторе положения формируют поперечную компоненту напряжения νq(t) во вращающейся системе координат dq путем суммирования двух напряжений νq1(t) и νq2(t), где νq1(t) меняют в зависимости от ошибки регулирования углового положения ротора 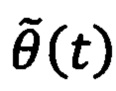 , a νq2(t) меняют в зависимости от известных параметров момента нагрузки, по следующим выражениям:
, a νq2(t) меняют в зависимости от известных параметров момента нагрузки, по следующим выражениям:
νq(t)=νq1(t)+νq2(t),
для формирования стабилизирующего напряжения νq1(t) в регулятор положения передают ошибку регулирования углового положения ротора 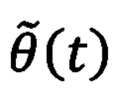 где в блоке с расширенным наблюдателем фильтруют ошибку углового положения ротора
где в блоке с расширенным наблюдателем фильтруют ошибку углового положения ротора 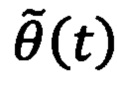 вместе с стабилизирующим напряжением νq1(t) и формируют фильтрованные сигналы
вместе с стабилизирующим напряжением νq1(t) и формируют фильтрованные сигналы 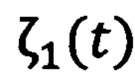 ,
, 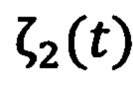 ,
,  и σ(t), фильтры реализуют по формулам:
и σ(t), фильтры реализуют по формулам:
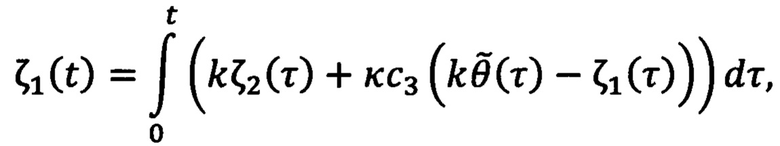
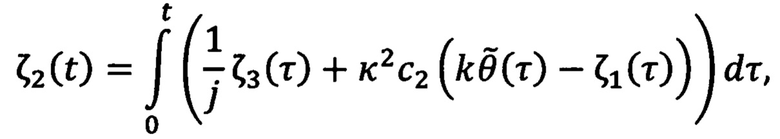
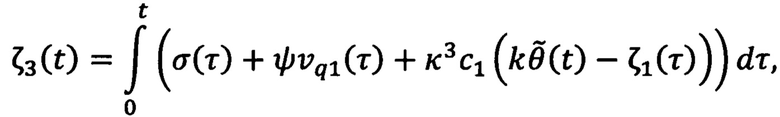
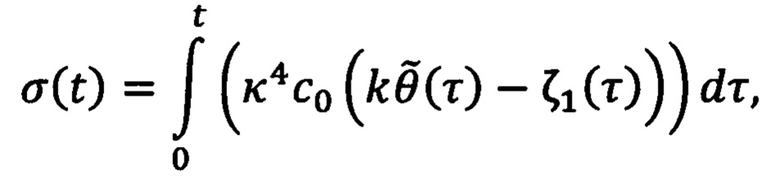
где j - момент инерции ротора двигателя, с0, c, с2, с3 и κ - настраиваемые параметры, ψ - ненулевая постоянная переменная, удовлетворяющая неравенству:
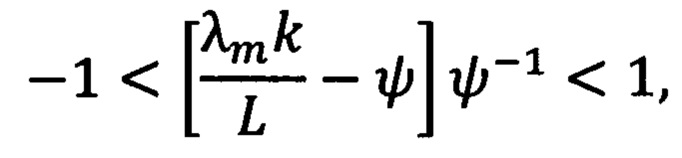
затем в этом блоке фильтрованные сигналы 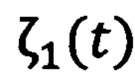 ,
, 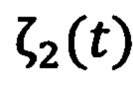 ,
,  объединяют в вектор состояния расширенного наблюдателя:
объединяют в вектор состояния расширенного наблюдателя:
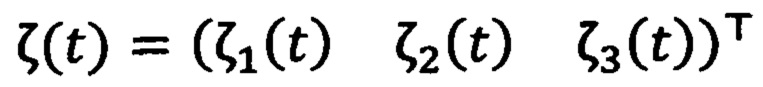
и формируют стабилизирующее напряжение νq1(t) в соответствии с выражением:
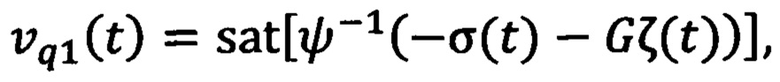
где G=(g1 g2 g3) - настраиваемые параметры регулятора, sat(⋅) - функция насыщения с выходным значениям в диапазоне [-umax, umax], далее стабилизирующее напряжение νq1(t) предают обратно в фильтр для формирования сигналов 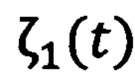 ,
, 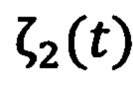 ,
,  и σ(t), а также в блок с внутренней моделью, здесь с помощью другого фильтра формируют компенсирующее напряжение νq2(t), фильтр реализуют по формуле:
и σ(t), а также в блок с внутренней моделью, здесь с помощью другого фильтра формируют компенсирующее напряжение νq2(t), фильтр реализуют по формуле:
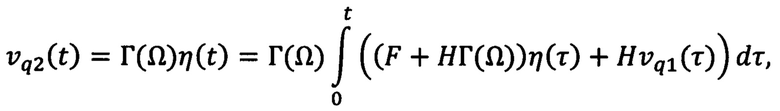
где η(t) - вектор состояния внутренней модели, F, Η - матрица состояния и вектор входа устойчивой системы в каноническом управляемом базисе соответственно, Γ(Ω) - вектор параметров, зависящих от номинальных значений частот гармоник момента нагрузки Ω.
| US 10291160 B1, 14.05.2019 | |||
| CN 109450328 A, 08.03.2019 | |||
| CN 109039204 A, 18.12.2018 | |||
| CN 107104620 A, 29.08.2017 | |||
| СПОСОБ ОПРЕДЕЛЕНИЯ ЧАСТОТЫ РОТОРА И/ИЛИ УГЛА РОТОРА РЕАКТИВНОЙ ЭЛЕКТРИЧЕСКОЙ МАШИНЫ, УПРАВЛЯЮЩЕЕ УСТРОЙСТВО, А ТАКЖЕ ПРИВОДНАЯ СИСТЕМА | 2015 |
|
RU2689117C2 |
Авторы
Даты
2021-06-11—Публикация
2020-10-07—Подача