ОБЛАСТЬ ТЕХНИКИ
[0001] Настоящее техническое решение относится к области квантовых технологий, в частности к методам реализации квантовых алгоритмов на цифровых квантовых компьютерах.
УРОВЕНЬ ТЕХНИКИ
[0002] Традиционные модели работы квантовых процессоров основаны на использовании двоичной квантовой логики, предполагающей манипулирование набором двухуровневых физических систем - кубитов (q-бит, кьюбит, кубит; от англ. quantum bit). В отличие от классических битов, которые могут принимать два возможных значения («логический 0», и «логическая 1»), кубиты могут находиться в произвольной квантовой суперпозиции этих двух состояний. Возможность создания состояний квантовой суперпозиции кубитов, а также их запутанных состояний является основой преимущества квантовых компьютеров над классическими.
[0003] Функционирование квантовых процессоров состоит из трех основных этапов: инициализации кубитов в некотором фиксированном состоянии, реализации последовательности преобразований над кубитами - квантового алгоритма, и измерения финального состояния кубитов. Представленное изобретение относится ко второму этапу -оптимизации реализации квантовых алгоритмов.
[0004] В общем случае квантовый алгоритм представляет собой последовательность квантовых логических операций, также именуемых квантовыми вентилями или гейтами. В зависимости от количества кубитов, на которые действует данная операция, различают следующие типы гейтов: однокубитные, двухкубитные, многокубитные (количество задействованных кубитов N > 2).
[0005] С точки зрения существующих аппаратных решений для квантовых процессоров, реализация квантового алгоритма сводится к последовательности применения однокубитных и двухкубитных операций. Все многокубитные операции осуществляются с помощью их декомпозиции на однокубитные и двухкубитные операции. При этом каждому кубиту обычно соответствует отдельный физический объект. Таким образом, однокубитные операции представляют собой воздействие на одиночный двухуровневый физический носитель квантовой информации, в то время как двухкубитным операциям соответствует организация управляемого взаимодействия между двумя двухуровневыми носителями квантовой информации.
[0006] На текущий момент достигнутый уровень техники в области квантовых вычислений заключается в создании управляемых квантовых устройств промежуточного масштаба, подверженных шумам (от англ. Noisy Intermediate-Scale Quantum Devices) [1-5], содержащих до около полусотни кубитов и позволяющих выполнять квантовые операции с уровнем ошибок в лучшем случае порядка долей процентов. Современные разработки дают возможность изучения свойств различных квантовых систем [6-9] и реализации базовых квантовых алгоритмов [10-14].
[0007] Одним из аппаратных решений, т.е. одной из доступных физических систем, на которых возможна реализация квантовых вычислений, являются ионы в ловушках. Квантовые компьютеры на основе ионов являются одним из наиболее перспективных направлений. Фундаментальные вопросы квантовых вычислений на основе ионов изучаются уже порядка 30 лет. В 2012 году Нобелевская премия по физике была присуждена Д. Уайнленду - известному во всем мире эксперту в области охлаждения ионов и управления ими (премия была присуждена совместно с С. Арошем). Именно с использованием ионных кубитов были впервые показаны двухкубитные операции (1995 год, группа Д. Уайнленда [15]), а в 2003 продемонстрирована реализация базовых квантовых алгоритмов (например, реализован алгоритм Дойча; 2003 год, группа Р. Блатта [16]). В данный момент рядом научных групп ведутся активные исследования в этой области. Следует в первую очередь подчеркнуть исследования группы Р. Блатта (Инсбрук, Австрия). В данный момент ими созданы полностью контролируемые системы из 20 кубитов [5], которые используются для квантово-химического моделирования [13] и изучения моделей физики высоких энергий [9]. Одним из лидеров данного направления является группа К. Монро (Мэриленд, США).
[0008] Важным фактором, влияющим на масштабируемость современных платформ квантовых вычислений, необходимую для решения серьезных прикладных задач, является несовершенство выполнения двухкубитных операций. В отличие от однокубитных операций, осуществляемых с помощью целевого воздействия на одиночный носитель квантовой информации, двухкубитные операции требуют организации сложного управляемого взаимодействия между двумя носителями квантовой информации. Именно двухкубитные операции являются основным источником ошибок и потери точности при реализации квантовых алгоритмов.
[0009] Ситуация становится еще более сложной в случае многокубитных гейтов, таких как N-кубитный гейт Тоффоли, который является ключевым элементом для квантовых алгоритмов, таких как алгоритмы Гровера [17] и Шора [18], а также для схем квантовой коррекции ошибок [19-21]. Распространенным подходом для решения данной задачи является использование так называемых кубитов-анцилл - вспомогательных кубитов, инициализированных в фиксированном состоянии и не участвующих в общей схеме алгоритма [22]. Необходимость использования части доступных физических кубитов в качестве кубитов-анцилл уменьшает количество свободных кубитов непосредственно используемых в квантовом алгоритме.
[0010] Одним из перспективных способов повышения эффективности квантовых процессоров является переход от двухуровневых квантовых систем (кубитов) к многоуровневым системам - кудитам (от англ. qudit, quantum digit), с количеством уровней d > 2. В частности, кудиты могут быть использованы для упрощения декомпозиции многокубитных гейтов и сокращения требуемого числа взаимодействий между носителями квантовой информации [23-28]. В ряде работ были рассмотрены схемы реализации квантовых алгоритмов на одиночных кудитах [29-31]. Также были предложены схемы использования кудитов для квантовых симуляторов [32, 33].
[0011] Однако все ранее предложенные подходы содержат ряд ограничений, не позволяющих во всей полноте реализовать доступный потенциал использования кудитов в универсальных квантовых вычислениях. Так, в работах [23-28] вводятся ограничения на размерности кудитов и их топологию связей друг с другом, в то время как в работах [29-31] не решается проблема обобщения на многокудитные системы.
[0012] Другие существующие предложения, связанные с использованием кудитов, сфокусированы либо на особенностях физической реализации [34-36], либо рассматривают общие вопросы создания унитарных операций на кудитах без привязки к конкретным алгоритмам [37].
[0013] В предлагаемом решении, для устранения недостатков, присущих подходам, известным из уровня техники, рассматривается объединение подхода по использованию дополнительных уровней кудитов в качестве кубитов-анцилл и использования пространства кудитов для размещения нескольких кубитов. Также впервые рассматривается задача оптимизации размещения кубитов в пространствах кудитов в зависимости от реализуемой цепочки операций. Использование такого решения позволяет добиться сокращения числа двухчастичных взаимодействий и уменьшения требуемого количества носителей квантовой информации.
[0014] Предлагаемый способ выполнения цепочки квантовых логических операций, реализуемый в качестве квантового процессора, может быть использован для оценки ресурсов, которые необходимы для выполнения квантового алгоритма, а также для выявления наиболее предпочтительного способа использования дополнительных уровней кудитов.
СУЩНОСТЬ ИЗОБРЕТЕНИЯ
[0015] Настоящее решение позволяет решить проблему, присущую известным подходам из уровня техники и предложить новый эффективный подход осуществления квантовых вычислений.
[0016] В предлагаемом решении, для устранения недостатков, присущих подходам, известным из уровня техники, предлагается переход от кубитов, двухуровневых систем, к кудитам (от англ. qudit, quantum digit), многоуровневым квантовым системам. Данный подход обусловлен тем фактом, что реальные физические объекты, используемые в качестве носителей квантовой информации (например, атомы, ионы, фотоны, и т.д.) также являются многоуровневыми.
[0017] Актуальной задачей, решаемой с помощью представленного изобретения, является сокращение общего количества задействованных физических носителей квантовой информации, а также уменьшение числа операций, требующих организации взаимодействия между двумя носителями квантовой информации при реализации квантовых алгоритмов. Это приводит к увеличению точности реализации квантового алгоритма.
[0018] В частности, в качестве кубитов-анцилл предлагается использовать дополнительные уровни кудитов, что позволяет добиться сокращения числа двухчастичных взаимодействий и увеличения доступного количества носителей квантовой информации. Кроме того, при реализации требуемой цепочки квантовых логических операций предлагается использование пространства состояний кудита для хранения нескольких кубитов, что позволяет перейти от двухкубитных операций, задействующих два носителя квантовой информации к однокудитным, реализуемым без необходимости организации такого взаимодействия.
[0019] Предлагаемый способ реализации квантовых вычислений с использованием кудитов включает в себя оценку ресурсов, необходимых для выполнения квантового алгоритма, а также выявляет наиболее предпочтительный способ использования ресурса доступных уровней кудитов.
[0020] Техническим результатом является повышение точности выполнения заданной цепочки квантовых логических операций за счет задействования дополнительных уровней кудитов.
[0021] Заявленное решение осуществляется за счет компьютерно-реализуемого способа представления цепочки квантовых логических операций (вентилей) над регистром кубитов (двухуровневых систем) в виде цепочки однокудитных и двухкудитных операций над регистром кудитов (d-уровневых систем) с заданным значением параметра d, определяемым физическими носителями квантовой информации - доступной физической системой, при этом способ содержит этапы, на которых:
a) получают входную цепочку квантовых логических операций, а также точности выполнения однокудитных, двухкудитных вентилей и считывающих измерений на доступной физической системе;
b) формируют возможные отображения уровней кубитов, входящих в исходную цепочку, на уровни кудитов доступной физической системы;
c) для каждого отображения, полученного на этапе b), производится декомпозиция квантовых вентилей исходной цепочки на однокудитные и двухкудитные квантовые вентили и вычисляется результирующая точность выполнения всей цепочки на основе числа входящих в декомпозицию однокудитных и двухкудитных вентилей и соответствующих им величин точности выполнения, полученных на этапе а);
d) определяют отображение, обеспечивающее максимально реализуемую точность выполнения исходной цепочки;
e) используют отображение, выявленное на этапе d), с соответствующей ему декомпозицией на однокудитные и двухкудитные операции, для оптимального выполнения входной цепочки логических квантовых операций на доступной физической системе.
[0023] В одном из частных примеров реализации способа, на этапе с) учитывается возможность использования уровней кудитов при декомпозиции многокубитных квантовых вентилей входной цепочки вместо вспомогательных кубитов-анцилл.
[0024] В другом частном примере реализации способа, при декомпозиции учитывается возможность сокращения количества двухкудитных операций, за счет замены N-кубитных операций однокудитными, в случае если задействованные N кубитов находятся в пространстве одного кудита в рамках рассматриваемого отображения, где N - натуральное число, больше 1.
[0025] Перечень физических носителей квантовой информации, с которыми может быть совместимо представляемое изобретение, включает в себя следующие физические системы, но не ограничивается ими: сверхпроводящие цепочки, твердотельные кубиты, ультрахолодные атомы и ионы, фотоны.
КРАТКОЕ ОПИСАНИЕ ЧЕРТЕЖЕЙ
[0026] Фиг. 1 иллюстрирует блок-схему заявленного способа.
[0027] Фиг. 2 иллюстрирует принцип декомпозиции многокудитных гейтов.
[0028] Фиг. 3 иллюстрирует дополнительные разложения многокудитных гейтов.
[0029] Фиг. 4 иллюстрирует пример входной цепочки квантовых логических операций,
подаваемой на вход кудитному квантовому процессору.
[0030] Фиг. 5 иллюстрирует разложение обобщенного гейта Тоффили с помощью CnZ гейтов и гейтов Адамара.
[0031] Фиг. 6 иллюстрирует входную цепочку квантовых логических операций, подаваемую на вход процессору, приведенную к операциям вида Cn-1Z и однокубитным операциям.
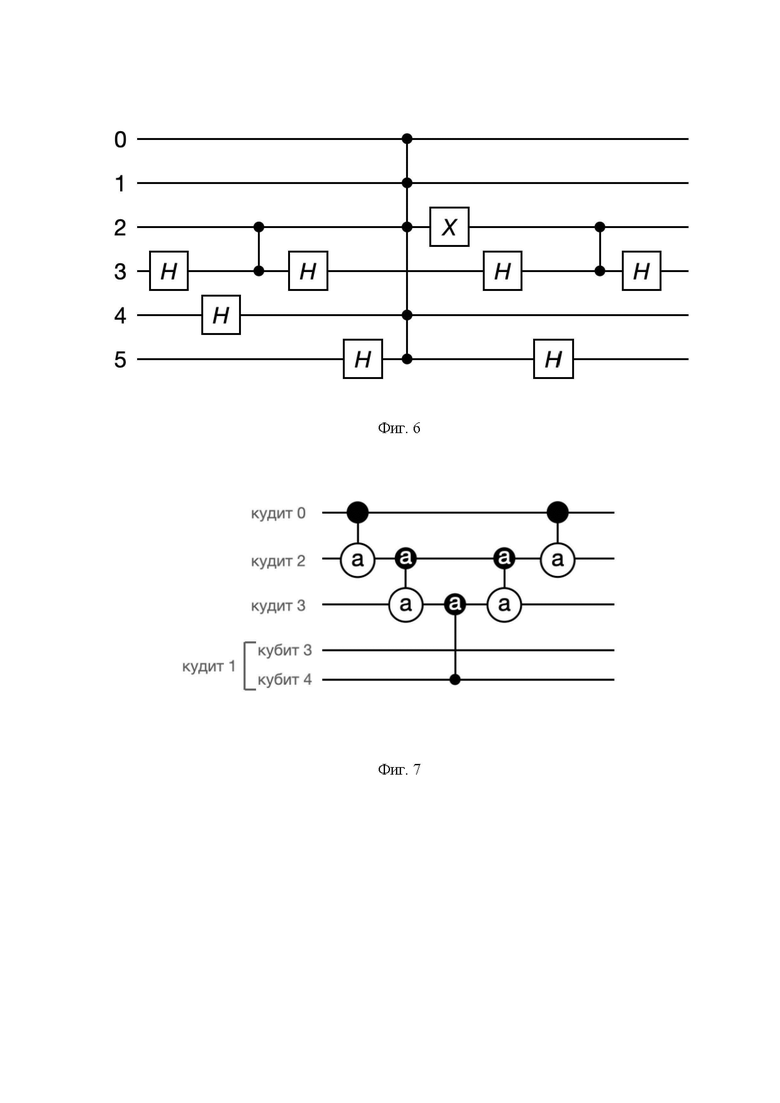
[0032] Фиг. 7 иллюстрирует промежуточную цепочку гейтов, соответствующую гейту C4Z на кудитах, построенную в соответствии с отображением кубитных уровней на уровни кудита {[0, 1], [2, 3], [4], [5]}.
[0033] Фиг. 8 иллюстрирует цепочку гейтов, соответствующую гейту типа (120) в промежуточном разложении гейта C4Z на кудитах, построенную в соответствии с отображением кубитных уровне на уровни кудита {[0, 1], [2, 3], [4], [5]}.
[0034] Фиг. 9 иллюстрирует финальную последовательность кудитных гейтов.
[0035] Фиг. 10 иллюстрирует пример вычислительного устройства.
ОСУЩЕСТВЛЕНИЕ ИЗОБРЕТЕНИЯ
[0036] Квантовый процессор предназначен для реализации квантовых алгоритмов, которые представляют собой последовательность выполнений квантовых логических операций над квантовым регистром (в котором содержатся носители квантовой информации). Предполагается, что в начальный момент времени реализации алгоритма квантовый регистр инициализирован так, что начальные состояния всех носителей информации соответствуют логическому «0». Считается заданным допустимый набор элементарных логических операций над квантовым регистром. Заданным по умолчанию является также тип измерений финального состояния квантового процессора после реализации всех операций над ним.
[0037] На Фиг. 1 представлена блок-схема выполнения заявленного способа (100) представления цепочки квантовых логических операций над регистром кубитов, которая будет детально описана далее в настоящих материалах заявки.
[0038] На первом этапе (101) выполнения заявленного способа (100) осуществляется получение входной цепочки квантовых логических операций и информации о доступном кудитном процессоре. Входная цепочка квантовых логических операций (квантовых вентилей, или гейтов) представляется в виде файла в произвольном формате.
[0039] Цепочка представляет последовательности одно-, двух-, и многокубитных гейтов, действующих на регистр кубитов, а также финальных считывающих измерений. В дальнейшем описании кубиты будут обозначаться индексами от 0 до Nqubits - 1, где Nqubits - суммарное количество кубитов во входной цепочке. В случае, если несколько гейтов исходной цепочки выполняются параллельно, вводится искусственное упорядочивание, например, на основе наименьшего индекса кубита, на который действует данный гейт. Далее производится преобразование всех двух- и многокубитных гейтов исходной кубитной цепочки к однокубитным операциям и операциям вида Cn-1Z, имеющих 2n×2n унитарную матрицу diag(1,1, …, 1, - 1). Для этой цели используются стандартный подход, изложенный в работе [22].
[0040] Информация о доступном кудитном процессоре, содержащаяся в файле произвольного формата, включает в себя количество доступных кудитов и их размерности, информацию о топологии связи кудитов друг с другом, где под связью понимается возможность осуществления элементарных двухкудитных операций, вид допустимых элементарных однокудитных и двухкудитных операций, а также информацию о точности выполнения различных однокудитных и двухкудитных операций и считывающих измерений. Под информацией о точности в настоящем решении следует понимать среднюю величину совпадения между идеальным входным состоянием и реальным выходным состоянием, посчитанную для всех чистых входных состояний физической системы для выполнения обработки входной цепочки. Отметим, что допустимые однокудитные операции должны давать возможность реализовывать произвольную однокудитную операцию, а топология связей должна обеспечивать возможность построения пути между произвольной парой кудитов.
[0041] На этапе (102) выполняется формирование возможных отображений уровней кубитов, входящих в исходную цепочку, на уровни кудитов доступной физической системы. Под физической системой при реализации заявленного решения понимаются следующие физические системы, но не ограничиваются ими: сверхпроводящие цепочки, ультрахолодные атомы и ионы, фотоны.
[0042] Доступные кудиты будут обозначаться индексами от 0 до Nqudits - 1, при этом индексация кудитов проводится в соответствии с уменьшением их размерности: di≤dj для i > j, где di и dj обозначают размерности кудитов с индексами i и j соответственно. Для каждого индекса i ∈ {0,1, …, Nqudits - 1} используется величина ni=[log2di], равная максимальному количеству кубитов, которые могут быть размещены в кудите с индексом i ([⋅] обозначает целую часть). Каждый кудит с индексом q содержит величину  определяющую максимальный уровень кудита, задействованный находящимися в его пространстве кубитами.
определяющую максимальный уровень кудита, задействованный находящимися в его пространстве кубитами.
[0043] Далее выполняется генерирование всех возможных последовательностей натуральных чисел вида

таким образом, чтобы выполнялись следующие соотношения: 0≤mi≤ni, mi≤mj для i > j, j, . Для каждой такой последовательности в свою очередь генерируются все возможные перестановки множества индексов {0,1, …, Nqubits - 1}, разбитые на Nqubits подгрупп, каждая из которых содержит mi элементов. При этом две перестановки, отличающиеся только порядком элементов внутри подгрупп, считаются эквивалентными. Все неэквивалентные перестановки, соответствующие сгенерированным последовательностям, заносятся в общий список. Каждая такая перестановка будет определять отображение кубитов исходной цепочки на уровни доступных кудитов в соответствии со следующим правилом: если кубиты с индексами
. Для каждой такой последовательности в свою очередь генерируются все возможные перестановки множества индексов {0,1, …, Nqubits - 1}, разбитые на Nqubits подгрупп, каждая из которых содержит mi элементов. При этом две перестановки, отличающиеся только порядком элементов внутри подгрупп, считаются эквивалентными. Все неэквивалентные перестановки, соответствующие сгенерированным последовательностям, заносятся в общий список. Каждая такая перестановка будет определять отображение кубитов исходной цепочки на уровни доступных кудитов в соответствии со следующим правилом: если кубиты с индексами 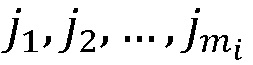 в рамках данной перестановки находятся в i-й группе, то состоянию кудита
в рамках данной перестановки находятся в i-й группе, то состоянию кудита 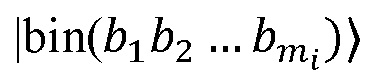 будет соответствовать состояние
будет соответствовать состояние  кубитов
кубитов 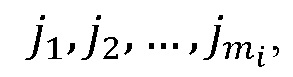 где
где  представляет собой натуральное число, бинарная запись которого имеет вид
представляет собой натуральное число, бинарная запись которого имеет вид  .
.
[0044] В настоящем описании также будут использованы следующие дополнительные обозначения. Натуральная величина qd[i] будет обозначать индекс кудита, в котором находится кубит с индексом i в соответствии с рассматриваемым отображением. Натуральная величина qb[i] будет обозначать порядковый номер кубита с индексом i внутри кудита qd[i]. Множество X[i, b] будет обозначать набор всех возможных  битовых строк длины ni, у которых на b-й позиции находится 1. Для каждой строки х из X[i, b] используется строка х' как строка, получающаяся из х заменой 1 на 0 в b-й позиции. Iα будет обозначать единичную матрицу размера α × α.
битовых строк длины ni, у которых на b-й позиции находится 1. Для каждой строки х из X[i, b] используется строка х' как строка, получающаяся из х заменой 1 на 0 в b-й позиции. Iα будет обозначать единичную матрицу размера α × α.
[0045] На этапе (103) выполняется декомпозиция входной цепочки на однокудитные и двухкудитные квантовые гейты для каждого отображения.
[0046] Для каждого отображения, полученного на этапе (102), производится преобразование полученной цепочки одно-, двух- и многокубитных квантовых логических операций на однокудитные и двухкудитные операции. Для этого для каждого отображения инициализируется пустая кудитная цепочка, и запускается цикл по всем гейтам и исходной цепочки. Каждому такому кубитному гейту и сопоставляется один или множество кудитных гейтов, которые добавляются к кудитной цепочке.
[0047] Далее будут рассмотрены отдельно два случая: когда гейт и является однокубитным или многокубитным.
[0048] Случай однокубитного гейта u. Пусть и действует на кубит с индексом i. Выполняется следующая последовательность действий.
• Вычисляется значение ν = qb[i] - 1
• Формируется унитарная матрица 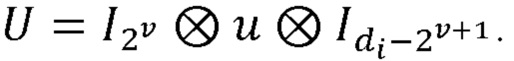
• Однокудитная операция U добавляется к кудитной цепочке к кудиту qd[i], при этом в зависимости от доступных однокудитных гейтов производится дополнительное разложение U на эти гейты.
[0049] Случай многокубитного гейта u. Выполняется следующая последовательность действий.
• Формируется список всех кудитов, содержащих в соответствии с анализируемым отображением кубиты, задействованные гейтом u.
• В случае, если данный список содержит только один кудит с индексом i, то к кудитной цепочке добавляется операция, действующая на данный кудит i и осуществляющая накрутку дополнительной фазы равной - 1 на базисные состояния, в которых кубиты, задействованные исходным гейтом u, находятся в состоянии 1. В зависимости от допустимых однокудитных операций производится дополнительное разложение этой операции на доступные однокудитные гейты. На этом процедура завершается и производится переход к следующему гейту и исходной цепочки или завершение цикла.
• В случае, если список содержит несколько кудитов, то для каждого кудита определяется его тип, в соответствии со следующей классификацией:
- кудит относится к типу А, если все содержащиеся в его пространстве кубиты, задействованы гейтом u, и дополнительные свободные уровни в данном кудите отсутствуют;
- кудит относится к типу В, если все содержащиеся в его пространстве кубиты, задействованы гейтом u, и присутствуют дополнительные свободные уровни, которые можно использовать в качестве промежуточного буфера для хранения квантовой информации;
- кудит относится к типу С, если в его пространстве помимо кубитов, задействованных гейтом u, имеются кубиты, не задействованные гейтом u.
• Далее формируется промежуточная цепочка гейтов (см. Фиг. 2), содержащая последовательность из многокудитного гейта, действующего на все кудиты типа А и одиночный кудит типа В, цепочку двухкудитных гейтов между кудитами типа В, многокудитный гейт между одиночным кудитом типа В и кубитами, задействованными гейтом u и входящими в состав кудитов типа С, цепочку двухкудитных гейтов между кудитами типа В и многокудитный гейт, действующий на кудиты типа А, и одиночный кудит типа В.
• Производится замена гейтов схемы, представленной на Фиг. 2, в соответствии с равенствами, представленными на Фиг. 3.
[0048] Многокудитный гейт (110), действующий на кудиты с индексами q1, …, qw, задается матрицей
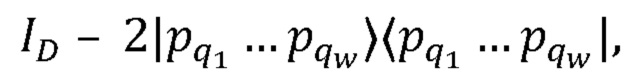
где  . Гейт Хα, действующий на кудит с индексом q, задается матрицей
. Гейт Хα, действующий на кудит с индексом q, задается матрицей

[0049] Гейт Нα, действующий на кудит с индексом q, задается матрицей
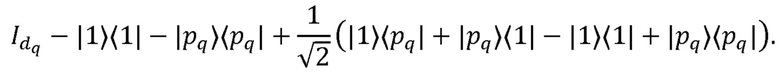
[0050] Каждый w-кудитный гейт (10) преобразуется по следующему правилу. Рассматривается стандартное разложение гейта Cw-1Z (в соответствии с [20]) на двухкубитные операции CZ и однокубитные операции. Далее каждому гейту кубитного разложения ставятся в соответствие кудитные гейты в исходной цепочке.
Однокубитному гейту ν сопоставляется гейт

действующий на кудит q, где q - индекс кудита, соответствующий кубиту, задействованному гейтом ν.
Двухкубитному гейту CZ сопоставляется гейт

где D = dqdr, q и r - индексы кудитов, соответствующие кубитам, задействованным гейтом CZ.
[0051] Каждый (w+1) кубитный гейт (120), действующий на кудит типа В с индексом q0 и набор из w кубитов внутри кудитов типа С преобразуется по следующему правилу. Рассматривается стандартное разложение гейта CwZ (в соответствии с [22]) на двухкубитные операции CZ и однокубитные операции. Каждому однокубитному гейту кубитного разложения, действующему на первый кубит, сопоставляется однокудитный гейт
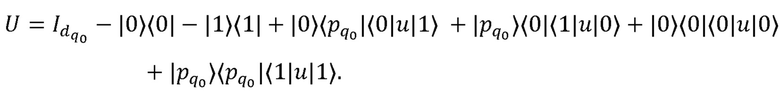
Всем однокубитным гейтам и, действующим на остальные кубиты, ставится в соответствие последовательность гейтов
 ,
,
где х пробегает значения из X[q, b], где индекс кудита q и индекс кубита b внутри кудита q соответствует кубиту, задействованному гейтом и в разложении гейта CwZ. Всем гейтам CZ, действующим на первый кубит и i-й кубит (i > 1) ставится в соответствие гейт
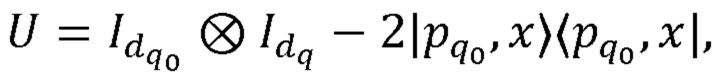
действующий на кудит типа В с индексом q0 и кудит с индексом q, в пространстве которого находится кубит с индексом i разложения гейта CwZ, а х пробегает значения из X[q, b], где b - индекс кубита внутри кудита q.
[0052] Всем гейтам CZ, действующим на i-й и j-й кубиты (i, j > 1), ставится в соответствие последовательность гейтов

действующих на кудиты и индексами qi и qj, в пространстве которых находятся кубиты с индексами i и j разложения гейта CwZ, ах и у пробегают значения из X[qi, bi] и X[qj, bj], где bi и bj - индексы кубитов внутри кудитов qi и qj.
[0053] После получения цепочки одно- и двухкудитных операций, проверяется, что все двухкудитные операции осуществляются между кудитами, связанными друг с другом в рамках имеющейся топологии связи. Если это не так, то добавляются двухкудитные гейты обмена, которые сначала перемещают кудиты друг к другу, а после совершения требуемой двухкудитной операции перемещают их обратно на исходные позиции. Также при необходимости производится дополнительное разложение однокудитных и двухкудитных гейтов на доступные однокудитные и двухкудитные операции.
[0054] Затем все однокубитные измерения в вычислительном базисе заменяются измерением соответствующих кудитов в вычислительном базисе.
[0055] Далее на этапе (104) выполняется определение оптимального отображения, обеспечивающего максимальную точность выполнения входной цепочки.
[0056] Для каждой полученной последовательности однокудитных и двухкудитных операций, реализующих исходную кубитную цепочку в соответствии с заданным отображением, вычисляется точность выполнения, исходя из доступной информации о точности выполнения однокудитных операций, двухкудитных операций и считывающих измерений.
Так, например, в случае идеальности считывающих измерений точность выполнения может быть вычислена по формуле
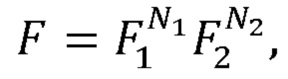
где F1 и F2 - точности выполнения однокудитных и двухкудитных операций, a N1 и N2 - количество однокудитных и двухкудитных гейтов соответственно. В зависимости от доступной информации о квантовом процессоре формула для вычисления точности выполнения может быть скорректирована (например, в случае, когда известно, что точность операций на одних уровнях кудитов отличается от точности выполнения на других уровнях, или точности выполнения операций на различных кудитах отличаются).
[0057] В результате каждому отображению ставится в соответствие результирующая точность выполнения операций. Далее выбирается отображение, обеспечивающее наивысшую точность выполнения из всех возможных. Выходные данные, представляющие собой оптимальное отображение и последовательность двухкудитных и однокудитных операций, реализующих входную цепочку, могут быть впоследствии переданы на этапе (105) на выполнение на реальном кудитном процессоре.
[0058] Пример реализации алгоритма
Пусть на вход подана цепочка квантовых логических операций с суммарным количеством кубитов Nqubits = 6, представленная на Фиг. 4. X и H обозначают стандартные гейты Адамара и инверсии соответственно:
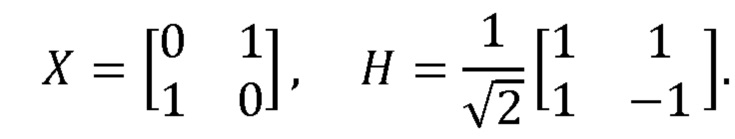
Пусть кудитный процессор состоит из Nqudits = 4 кудитов, каждый из которых имеет размерность d0 = d1 = d2 = d3 = 4. Пусть все кудиты связаны друг с другом в соответствии с полносвязной топологией, т.е. существует возможность произвести двухкудитную операцию между произвольной парой кудитов.
[0059] На первом шаге происходит упорядочивание выполняемых параллельно гейтов на основе наименьшего индекса кубита для дальнейшего преобразования всех двух- и многокубитных гейтов к однокубитным операциям и операциям вида Cn-1Z. В соответствии со стандартным разложением, представленным на Фиг. 5, после замены двух-и многокубитных операций на операции вида Cn-1Z и однокубитные операции, поданная на вход цепочка квантовых логических операций пример вид, представленный на Фиг. 6.
[0060] На следующем шаге происходит генерация возможных отображений уровней кубитов исходной квантовой логической цепочки на уровни 4-х доступных куквартов (кудитов с 4 уровнями). Для каждого из кудитов максимальное число кубитов, которые могут быть размещены к кудите, равняется ni = 2. Таким образом, структура заполнения пространства кудитов кубитами может иметь вид (2,2,2,0) и (2,2,1,1) (каждое число соответствует количеству кубитов, которые можно разместить в соответствующем кудите).
Список возможных отображений будет содержать элементы вида
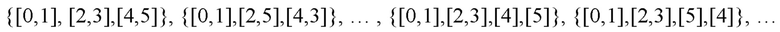
где в квадратных скобках записаны индексы кубитов, входящих в каждый кудит.
[0061] Рассмотрим декомпозицию входной цепочки на однокудитные и двухкудитные квантовые гейты для отображения {[0,1], [2,3], [4], [5]}. В таком отображении для первых двух кудитов величина, определяющая максимальный уровень, задействованный находящимися в его пространстве кубитами, р0 = р1 = 22 - 1 = 3. Для двух последних кудитов эта величина оказывается равной р2 = р3 = 21 - 1 = 1. Декомпозиция кубитной цепочки, состоящей из однокубитных операций и операций вида Cn-1Z, на однокудитные и двухкудитные гейты состоит из прохождения по каждому гейту исходной цепочки и сопоставлению каждому из них гейта или последовательности гейтов на кудите или кудитах. Первый гейт входной кубитной цепочки, преобразованной к виду из однокубитных операций и операций вида Cn-1Z (см. Фиг. 6) - это однокубитный гейт Адамара Н, действующий на 3-й кубит. В соответствии с заданным отображением уровней кубитов исходной квантовой логической цепочки на уровни 4-х доступных куквартов, 3-й кубит исходной цепочки является 2-м кубитом 1-го кудита, следовательно, гейту Адамара Н, действующему на 3-й кубит, ставится в соотвествие гейт

действующий на 2-й кудит в кудитной цепочке.
[0062] Следующим гейтом преобразованной кубитной цепочки является гейт Адамара Н, действующий на 4-й кубит. В соответствии с заданным отображением уровней кубитов на уровни кудитов, 4-й кубит расположен в отдельном 1-м кудите, в котором в последствии будет использован один дополнительный уровень, следовательно, ко 2-му кудиту применяется исходный кудитный гейт Адамара следующего вида:

где Н - кубитный гейт Адамара.
[0063] Затем в преобразованной кубитной цепочке выполняется двухкубитный гейт CZ на 2-м и 3-м кубитах. В соответствии с заданным отображением уровней кубитов на уровни кудитов, 2-й и 3-й кубит вместе представляют собой 1-й кудит, следовательно двухкубитному гейту CZ ставится в соответствие однокудитный гейт, накручивающий фазу -1 на 1-й кудит тогда и только тогда, когда он находился в состоянии |3〉:

[0064] Далее в преобразованной кубитной цепочке выполняются гейты Адамара Н на 3-м и 5-м кубитах, которым в кудитной цепочке ставятся в соответствие гейты, аналогичные, первым двум описанным выше кудитным гейтам U1 и U2.
[0065] Центральным элементом преобразованной кубитной цепочки является многокубитный гейт C4Z, действующий на все кубиты, за исключением 3-го. В соответствии с заданным отображением уровней кубитов на уровни кудитов, все кудиты содержат в себе кубиты, задействованные в кубитном гейте C4Z. Кудит 0 относится к типу A, т.к. все кубиты, содержащиеся в его пространстве, задействованы гейтом C4Z; дополнительные свободные уровни в данном кудите отсутствуют. Кудит 2 относится к типу B, т.к. содержащийся в нем кубит задействован гейтом C4Z и присутствуют свободные уровни, которые могут быть использованы в качестве промежуточного буфера для хранения квантовой информации. Кудит 3 также относится к типу В, т.к. содержащийся в нем кубит задействован гейтом C4Z и присутствуют свободные уровни, которые могут быть использованы в качестве промежуточного буфера для хранения квантовой информации. Кудит 1 относится к типу С, т.к. помимо задействованного гейтом C4Z 2-го кубита, он также содержит не задействованный гейтом C4Z 3-й кубит.
[0066] На основании описанной классификации кудитов формируется промежуточная цепочка гейтов, представленная на Фиг. 7. Она состоит из двухкудитного гейта, действующего на нулевой кудит типа А и 2-й кудит типа В, двухкудитного гейта между двумя кудитами типа В (между 2-м и 3-м), двухкудитного гейта между 3-м кудитом типа В и 1-м кудитом типа С, в который входит 2-й кубит, задействованный в гейте C4Z, двухкудитного гейта между двумя кудитами типа В (между 2-м и 3-м), двухкудитного гейта, действующего на нулевой кудит типа А и 2-й кудит типа В. Центральным элементом данной схемы является гейт типа (120) между 3-м кудитом типа В и 1-м кудитом типа С, в который входит 2-й кубит, задействованный в гейте C4Z. За счет того, что помимо задействованного кубита, 1-й кудит содержит также не задействованный в в гейте C4Z кубит, гейту типа (120) в итоговой кудитной цепочке будет поставлена в соответствие последовательность гейтов, представленная на Фиг. 8. В ней гейты Х12 и Х13 заданы следующим образом:

а гейтам CZ ставятся в соответствие гейты:

[0067] Замена остальных гейтов схемы декомпозиции гейта C4Z на кудитах, представленной на Фиг. 6, производится в соответствии с равенствами, представленными на Фиг. 3.
[0068] Далее к кудитной цепочке добавляется гейт, соответствующий гейту X на 2-ом кубите. Данный гейт будет иметь вид

[0069] Всем последующим гейтам преобразованной кубитной цепочки кудитные гейты ставятся в соответствие аналогично описанной ранее схеме. Полная кудитная цепочка, соответствующая исходной входной кубитной цепочке, представленной на Фиг. 4, приведена на Фиг. 9.
[0070] После построения кудитных цепочек, соответствующих входной кубитной цепочке, в соответствии с каждым из возможных отображений уровней кубитов на уровни кудитов, происходит определение оптимального отображения, обеспечивающего максимальную точность выполнения входной цепочки. Для этого для каждой из кудитных цепочек, реализующих исходную кубитную цепочку в соответствии с заданным отображением, вычисляется точность выполнения. Для рассмотренной выше кудитной цепочки, построенной в соответствии с отображением кубитных уровней на уровни кудита {[0,1], [2,3], [4], [5]} и при точности выполнения однокудитной операции F1=0.998 и точности выполнения двухкудитной операции F2=0.980, точность выполнения будет равной

[0071] Таким образом, в рассматриваемом примере отображение {[0,1], [2,3], [4], [5]} оказывается оптимальным, т.е. обеспечивает наивысшую точность выполнения из всех возможных для входной кубитной цепочки при заданной информации о кудитном процессоре.
[0072] Представленный способ (100) может быть реализован с помощью любого пригодного типа вычислительного устройства (200), представленного на Фиг. 10 в виде общей его схемы реализации. Таким устройством (200) может выступать, например, компьютер, сервер, ноутбук, смартфон и т.п.
[0073] В общем случае устройство (200) содержит такие компоненты, как: один или более процессоров (201), по меньшей мере одну оперативную память (202), средство постоянного хранения данных (203), интерфейсы ввода/вывода (204), средство В/В (205), средства сетевого взаимодействия (206).
[0074] Процессор (201) устройства выполняет основные вычислительные операции, необходимые для функционирования устройства (200) или функционала одного или более его компонентов. Процессор (201) исполняет необходимые машиночитаемые команды, содержащиеся в оперативной памяти (202).
[0075] Память (202), как правило, выполнена в виде ОЗУ и содержит необходимую программную логику, обеспечивающую требуемый функционал. Средство хранения данных (203) может выполняться в виде HDD, SSD дисков, рейд массива, сетевого хранилища, флэш-памяти, оптических накопителей информации (CD, DVD, MD, Blue-Ray дисков) и т.п. Средство (203) позволяет выполнять долгосрочное хранение различного вида информации, например, истории обработки запросов (логов), идентификаторов пользователей, данные камер, изображения и т.п.
[0076] Интерфейсы (204) представляют собой стандартные средства для подключения и работы с вычислительными устройствами. Интерфейсы (204) могут представлять, например, USB, RS232, RJ45, LPT, COM, HDMI, PS/2, Lightning, FireWire и т.п. Выбор интерфейсов (204) зависит от конкретного исполнения устройства (200), которое может представлять собой персональный компьютер, мейнфрейм, серверный кластер, тонкий клиент, смартфон, ноутбук и т.п., а также подключаемых сторонних устройств.
[0077] В качестве средств В/В данных (205) может использоваться: клавиатура, джойстик, дисплей (сенсорный дисплей), проектор, тачпад, манипулятор мышь, трекбол, световое перо, динамики, микрофон и т.п.
[0078] Средства сетевого взаимодействия (206) выбираются из устройства, обеспечивающий сетевой прием и передачу данных, например, Ethernet карту, WLAN/Wi-Fi модуль, Bluetooth модуль, BLE модуль, NFC модуль, IrDa, RFID модуль, GSM модем и т.п.С помощью средства (206) обеспечивается организация обмена данными по проводному или беспроводному каналу передачи данных, например, WAN, PAN, ЛВС (LAN), Интранет, Интернет, WLAN, WMAN или GSM, квантовый канал передачи данных, спутниковая связь и т.п.
[0079] Компоненты устройства (200), как правило, сопряжены посредством общей шины передачи данных.
[0080] В настоящих материалах заявки было представлено предпочтительное раскрытие осуществления заявленного технического решения, которое не должно использоваться как ограничивающее иные, частные воплощения его реализации, которые не выходят за рамки испрашиваемого объема правовой охраны и являются очевидными для специалистов в соответствующей области техники.
[0081] Настоящее изобретение было разработано в рамках реализации мероприятия №4 «Работа по защите интеллектуальной собственности» детализированного плана-графика за 2020 год программы деятельности Лидирующего исследовательского центра "Квантовые вычисления" (соглашение №014/20 от 18.05.2020), в соответствии с дорожной картой «сквозной» цифровой технологии - «Квантовые технологии» при поддержке Фонда НТИ и АО «РВК».
Источники информации
[1] Н. Bernien et al. Probing many-body dynamics on a 51-atom quantum simulator // Nature. - 2017. - T. 551. - № 7682. - C. 579-584.
[2] J. Zhang et al. Observation of a many-body dynamical phase transition with a 53-qubit quantum simulator // Nature. - 2017. - T. 551. - № 7682. - C. 601-604.
[3] D. Barredo et al. Synthetic three-dimensional atomic structures assembled atom by atom // Nature. - 2018. - T. 561. - № 7721. - C. 79-82.
[4] C. Neill et al. A blueprint for demonstrating quantum supremacy with superconducting qubits // Science. - 2018. - T. 360. - № 6385. - C. 195-199.
[5] N. Friis et al. Observation of entangled states of a fully controlled 20-qubit system // Physical Review X. - 2018. - T. 8. - № 2. - C. 021012.
[6] S. Trotzky et al. Probing the relaxation towards equilibrium in an isolated strongly correlated one-dimensional Bose gas // Nature physics. - 2012. - T. 8. - № 4. - C. 325-330.
[7] A. Mazurenko et al. A cold-atom Fermi-Hubbard antiferromagnet // Nature. - 2017. - T. 545. - № 7655. - C. 462-466.
[8] A. Keesling et al. Quantum Kibble-Zurek mechanism and critical dynamics on a programmable Rydberg simulator // Nature. - 2019. - T. 568 - № 7751. - C. 207-211.
[9] C. Kokail et al. Self-verifying variational quantum simulation of lattice models // Nature. -2019. - T. 569. - № 7756. - C. 355-360.
[10] A. Montanaro, Quantum algorithms: an overview // npj Quantum Information. - 2016. - T. 2. - № l. - C. 1-8.
[11] P.J.J. O'Malley et al. Scalable quantum simulation of molecular energies Physical Review X. - 2016. - T. 6. - № 3. - C. 031007.
[12] A. Kandala et al. Hardware-efficient variational quantum eigensolver for small molecules and quantum magnets // Nature. - 2017. - T. 549. - № 7671. - C. 242-246.
[13] C. Hempel et al. Quantum chemistry calculations on a trapped-ion quantum simulator // Physical Review X. - 2018. - T. 8. - № 3. - C. 031022.
[14] V. Havlicek et al. Supervised learning with quantum enhanced feature spaces // Nature. - 2019. - T. 567. - № 7747. - C. 209-212.
[15] Monroe C. et al. Demonstration of a fundamental quantum logic gate // Physical review letters. - 1995. - T. 75. - № 25. - C. 4714.
[16] Guide S. et al. Implementation of the Deutsch-Jozsa algorithm on an ion-trap quantum computer // Nature. - 2003. - T. 421. - № 6918. - C. 48-50.
[17] L.K. Grover. A fast quantum mechanical algorithm for database search // Proceedings of the twenty-eighth annual ACM symposium on Theory of computing. - 1996. - C. 212-219.
[18] P.W. Shor. Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer // SIAM review. - 1999. - T. 41. - № 2. - C. 303-332.
[19] D.G. Cory et al. Experimental quantum error correction // Physical Review Letters. - 1998. - T. 81. - № 10. - C. 2152.
[20] M.D. Reed et al. Realization of three-qubit quantum error correction with superconducting circuits // Nature. - 2012. - T. 482. - № 7385. - C. 382-385.
[21] P.W. Shor. Fault-tolerant quantum computation // Proceedings of 37th conference on foundations of computer science. - IEEE, 1996. - C. 56-65.
[22] A. Barenco et al. Elementary gates for quantum computation // Physical review A. - 1995. - Т. 52. - № 5. - C. 3457.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ И СИСТЕМА КОМПЕНСАЦИИ ШУМОВ НА КВАНТОВОМ ПРОЦЕССОРЕ С ПОМОЩЬЮ КВАНТОВОЙ ТОМОГРАФИИ ОПЕРАЦИЙ | 2022 |
|
RU2786349C1 |
| Архитектура квантовых вычислительных устройств для решения прикладных задач в области материаловедения | 2023 |
|
RU2821360C1 |
| Система и способ решения прикладных задач материаловедения с помощью сопряжения квантовых и классических устройств | 2023 |
|
RU2814969C1 |
| Квантовая вычислительная система на основе фотонных чипов | 2023 |
|
RU2806840C1 |
| ДВУХЭЛЕКТРОДНЫЙ БЫСТРОПЕРЕСТРАИВАЕМЫЙ ПО ПОТОКУ СВЕРХПРОВОДНИКОВЫЙ КУБИТ НА ОСНОВЕ КИНЕТИЧЕСКОЙ ИНДУКТИВНОСТИ | 2021 |
|
RU2780666C1 |
| СИСТЕМА И МЕТОД КОНТРОЛЯ ВЗАИМОДЕЙСТВИЯ МЕЖДУ СВЕРХПРОВОДНИКОВЫМИ КУБИТАМИ НА ОСНОВЕ ВЫСОКОЙ КИНЕТИЧЕСКОЙ ИНДУКТИВНОСТИ | 2022 |
|
RU2803401C1 |
| Устройство для реализации двухкубитного вентиля CZ между сверхпроводниковыми кубитами на основе высокой кинетической индуктивности | 2022 |
|
RU2795679C1 |
| Квантовая вычислительная система на основе нейтральных атомов | 2023 |
|
RU2814970C1 |
| СПОСОБ ПОЛУЧЕНИЯ УПРАВЛЯЮЩИХ ПАРАМЕТРОВ ДЛЯ КВАНТОВЫХ ВЫЧИСЛИТЕЛЬНЫХ СИСТЕМ НА ОСНОВЕ ИОНОВ В ЛОВУШКЕ, КОТОРЫЕ ЗАСТАВЛЯЮТ СИСТЕМУ МЕНЯТЬ СОСТОЯНИЯ, ЗАДАННЫЕ СОБСТВЕННЫМ ГАМИЛЬТОНИАНОМ, ТАК, ЧТО ЭВОЛЮЦИЯ В СИСТЕМЕ СООТВЕТСТВУЕТ ПРИМЕНЕНИЮ (ПОСЛЕДОВАТЕЛЬНОСТИ) ЛОГИЧЕСКИХ ОПЕРАЦИЙ | 2022 |
|
RU2830094C2 |
| КВАНТОВЫЙ РЕГИСТР НА ПРОСТРАНСТВЕННЫХ СОСТОЯНИЯХ ЭЛЕКТРОНОВ В ПОЛУПРОВОДНИКОВЫХ ДВОЙНЫХ КВАНТОВЫХ ТОЧКАХ | 2023 |
|
RU2817337C1 |




Изобретение относится к компьютерно-реализуемому способу представления цепочки квантовых логических операций над регистром кубитов в виде цепочки однокудитных и двухкудитных операций над регистром кудитов для их выполнения на квантовом процессоре. Технический результат заключается в формировании последовательности двухкудитных и однокудитных квантовых логических операций для исполнения квантовым процессором. В способе a) получают входную цепочку квантовых логических операций, а также информацию о точности выполнения однокудитных и двухкудитных логических операций и считывающих измерений на квантовом процессоре; b) формируют возможные отображения уровней кубитов, входящих в исходную цепочку, на уровни кудитов квантового процессора; c) для каждого отображения, полученного на этапе b), производится декомпозиция квантовых логических операций исходной цепочки на однокудитные и двухкудитные квантовые логические операции и вычисляется результирующая точность выполнения всей цепочки квантовых логических операций на основе числа входящих в декомпозицию однокудитных и двухкудитных квантовых логических операций и соответствующих им величин точности выполнения, полученных на этапе a); d) определяют отображение и соответствующую ему последовательность двухкудитных и однокудитных квантовых логических операций, обеспечивающее максимально реализуемую точность выполнения исходной цепочки квантовых логических операций на уровне кудитов для квантового процессора; e) передают полученную на этапе d) последовательность двухкудитных и однокудитных квантовых логических операций на квантовый процессор для ее выполнения. 2 з.п. ф-лы, 10 ил.
1. Компьютерно-реализуемый способ представления цепочки квантовых логических операций над регистром кубитов в виде цепочки однокудитных и двухкудитных операций над регистром кудитов для их выполнения на квантовом процессоре, при этом способ содержит этапы, на которых:
a) получают входную цепочку квантовых логических операций, а также информацию о точности выполнения однокудитных и двухкудитных логических операций и считывающих измерений на квантовом процессоре;
b) формируют возможные отображения уровней кубитов, входящих в исходную цепочку, на уровни кудитов квантового процессора;
c) для каждого отображения, полученного на этапе b), производится декомпозиция квантовых логических операций исходной цепочки на однокудитные и двухкудитные квантовые логические операции и вычисляется результирующая точность выполнения всей цепочки квантовых логических операций на основе числа входящих в декомпозицию однокудитных и двухкудитных квантовых логических операций и соответствующих им величин точности выполнения, полученных на этапе a);
d) определяют отображение и соответствующую ему последовательность двухкудитных и однокудитных квантовых логических операций, обеспечивающие максимально реализуемую точность выполнения исходной цепочки квантовых логических операций на уровне кудитов для квантового процессора;
e) передают полученную на этапе d) последовательность двухкудитных и однокудитных квантовых логических операций на квантовый процессор для ее выполнения.
2. Способ по п. 1, в котором на этапе c) учитывается возможность использования уровней кудитов при декомпозиции многокубитных квантовых вентилей входной цепочки вместо вспомогательных кубитов-анцилл.
3. Способ по п. 1, в котором при декомпозиции учитывается возможность сокращения количества двухкудитных операций за счет замены N-кубитных операций однокудитными, в случае если задействованные N кубитов находятся в пространстве одного кудита в рамках рассматриваемого отображения, где N – натуральное число, больше 1.
| E.O | |||
| KIKTENKO и др., "Multilevel superconducting circuits as two-qubit systems: Operations, state preparation, and entropic inequalities", 13.04.2015, доступно - https://arxiv.org/pdf/1411.0157 | |||
| A | |||
| BARENCO и др., "Elementary gates for quantum computation", 23.03.1995, доступно - https://arxiv.org/pdf/quant-ph/9503016 | |||
| Способ получения цианистых соединений | 1924 |
|
SU2018A1 |
Авторы
Даты
2021-12-13—Публикация
2020-12-28—Подача