Изобретение относится к вычислительной технике, в частности к области создания (программирования) параллельных программ. Результатом применения способа является сокращение временных затрат на выполнение сложных расчетов в циклических участках программ за счет автоматического выбора оптимального (с минимальным временем работы распараллеленного участка) средства распараллеливания под каждый цикл и текущего числа итераций (повторений) в цикле программы.
Реализация параллельных вычислений является сложной задачей. В большинстве случаев распараллеливание для выполнения задач осуществляется «вручную» разработчиком применительно к конкретному приложению и конкретной задаче. Такой подход является весьма трудоемким, и при этом может быть малоэффективным, по причине ошибок в обеспечении эффективности, которые может допустить разработчик при реализации. Особенно это характерно для инженерных и научно-технических расчетов, задач моделирования, задач реального времени. В этих направлениях наметилась устойчивая тенденция в сторону отказа от последовательных решений и классических однопроцессорных компьютеров. Такие расчеты обычно предполагают сложную обработку больших объемов данных, что, соответственно, требует использования значительных вычислительных ресурсов для обеспечения приемлемого времени выполнения расчетов особенно в условиях ограничения временного ресурса. При этом многие вычислительные задачи наиболее эффективно решаются с помощью многоядерных вычислительных систем с общей памятью (SMP Symmetric Multiprocessing) [1], а также созданных средств и методов параллельного программирования, ориентированных на эти системы, каждая из которых обладает своими особенностями.
Непосредственным объектом распараллеливания в целевой программе целесообразно рассматривать циклические участки программы, т.к. около 80% времени работы программы занимает выполнение именно циклов [2].
Полное оптимальное время исполнения распараллеленной программы определяется, как 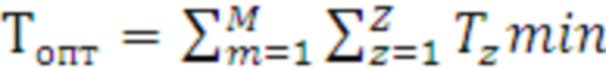 , где M - количество запусков распараллеленного участка кода программы; Z - количество распараллеленных участков кода программы (циклических участков);
, где M - количество запусков распараллеленного участка кода программы; Z - количество распараллеленных участков кода программы (циклических участков); 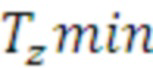 - минимальное время исполнения z-того циклического участка среди рассматриваемых средств параллельного программирования.
- минимальное время исполнения z-того циклического участка среди рассматриваемых средств параллельного программирования.
Таким образом сокращение временных затрат на выполнение целевой программы предполагает распараллеливание циклических участков целевой программы, при многопоточном параллельном выполнении программы в многоядерных ПЭВМ. Под целевой программой понимается разрабатываемая программа, требующая максимально эффективного использования предоставленных аппаратно-технических возможностей т.е. распараллеливания.
Известен способ [3], в котором описан подход к временной оптимизации программы путем трансформации структуры цикла и установки инструкций предварительной выборки данных для загрузки массивов в критические по времени выполнения цикла, при этом циклы определяются путем профилирования в вычислительной системе, для которой предназначено программное обеспечение. В данном способе существует обратная связь, в нем сначала создают программу без предложенного подхода оптимизации, далее измеряют рабочие характеристики на вычислительной системе, определяют критические циклы, устанавливают подходящие параметры оптимизации для данной вычислительной системы, модифицируют исходный код и перестраивают программу. В целом подход, описанный в данном способе полезен, но его эффективность для реальных сложных современных вычислительных систем мала, так как в предложенном подходе не учитывается, что в процессе работы программного обеспечения количество итераций одного и того же цикла меняется в процессе работы, тем самым меняются и данные о критических по времени циклах, что приводит к невозможности его применения при этих условиях.
Так же известен способ автоматического распараллеливания циклических областей в алгоритмической части программы [4], позволяющий максимизировать количество параллельных циклов путем применения меж процедурных и внутри процедурных оптимизаций, характеризующийся встраиванием в программу динамических проверок на эффективность распараллеливания, включающий множество шагов. Данный способ относится к области компьютерного программирования и, в частности, к области оптимизирующей компиляции. Оптимизирующий компилятор выполняет это преобразование так, чтобы достичь наилучшего показателя для получаемого кода по максимальной скорости исполнения программы на целевой архитектуре (платформе). Сложность использования данного способа заключается в том, что разработчик должен иметь заранее реализованные специализированные компиляторы и среды выполнения программ, при разработке которых использовался именно данный способ, а это не всегда реализуемо.
Однако возрастающую роль в рациональном использовании современных архитектур, поддерживающих параллелизм (многопроцессорных, многоядерных и т.д.) занимают универсальные средства программирования - стандарты и технологии, предназначенные для создания современных параллельных программ. Такие как языковые средства задания параллельности в программе (системы явного параллельного программирования - стандарт Open MP), так и автоматические средства поиска параллельных вычислений (компиляторы фирм Intel) и последующего представления их с использованием существующих библиотек поддержки параллельности (MPI). Сами средства распараллеливания для разработчика представляются «черным ящиком», они применяются с помощью внесения в программный код специальных дополнений (директив). Большое разнообразие средств параллельного программирования для многоядерных (многопроцессорных) вычислительных систем с общей памятью демонстрируют, что, хотя все они предоставляют разработчику (программисту) возможности работы с параллельными потоками, их интерфейсы и внутренняя структура сильно отличаются.
Наиболее близкими по технической сущности и совокупности существенных признаков аналогами (прототипами) к заявленному способу параллельного программирования для многоядерных (многопроцессорных) вычислительных систем с общей памятью является способ объединения средств распараллеливания и явного параллельного программирования предложенный в работе Wenmei Hwu и др., описанной в [5]. Идея состоит в создании системы неявного параллельного программирования. С одной стороны, программист на традиционных языках программирования (С, С++) создает программу с параллельными вычислениями. Средствами эти параллельные вычисления должны быть распознаны. В случае проблем с анализом, программист может добавить подсказки в программу, разрешив какой-либо конфликт, мешающий определению параллельности. Затем, найденные параллельные вычисления автоматически представляются в параллельных терминах конкретной архитектуры. По сути, это некоторая интерактивная среда разработки параллельных программ, в которой сбалансированы усилия человека и автоматических средств. В предложенном подходе основную роль по анализу, модернизации и инструментированию параллельного кода выполняет средство распараллеливания, а разработчик (программист) прагмами разрешает появляющиеся конфликты (если они конечно появляются), с которыми статический анализатор может не справляется. А так же близким решением является подход, описанный Андреевым А.Е. [6] о использовании нескольких средств распараллеливания в одной разрабатываемой программе.
Сопоставительный анализ показывает, что разработанные ранее способы применения средств параллельного программирования не учитывают:
- случайный характер изменений параметров в структуре одних и тех же циклов программы по количеству итераций цикла и времени выполнения, что приводит к изменению критических по времени выполнения циклов;
- зависимость эффективности использования различных средств параллельного программирования от числа итераций цикла и от внутренней структуры цикла.
В заявленном способе для устранения недостатков, отмеченных в прототипах учитывается и тот факт, что в зависимости от текущего контекста программы для одного того же участка программного кода временные затраты на выполнение могут отличаться у разных средства распараллеливания при решении прикладной задачи при одних и тех же требованиях к аппаратно-программному обеспечению. Выше указанные способы, относящиеся к области компьютерного программирования возможно модернизировать так, чтобы достичь минимального времени выполнения для получаемого кода программы на многоядерной (многопроцессорной) ЭВМ с общей памятью.
Разработанный способ реализует автоматический выбор оптимального средства распараллеливания из доступного набора средств под каждый циклический участок текущей программы по минимальному времени выполнения цикла. Для этого используются накопленные при тестировании статистические данные в виде массива время-итерационных профилей программы и составленной на их основе матрицы оптимальных средств распараллеливания. По входным номера цикла и количества итераций данного цикла. С использованием составленной матрицы оптимальных средств распараллеливания, в реальном масштабе времени определяется номер средства распараллеливания и автоматически подключается к процессу выполнения цикла с распараллеливанием выбранным средством.
Таким образом, заявленный способ, соответствует критерию изобретения «новизна» и проявляет новые свойства при применении средств параллельного программирования, что позволяет сократить время выполнения программы.
Заявленный способ предусматривает два этапа. Первый подготовительный, на этом этапе определяются и номеруются циклы в исходном коде программы. Расставляются метки начала и конца цикла, клонируются в тело программного кода равное количеству средств распараллеливания и добавляются прагмы каждого средства распараллеливания. Далее происходит компилирование программы и создание исполняемого файла. Второй этап выполняется в процессе тестового прогона разрабатываемой программы и заключается в сборе отсчетов времени выполнения каждого цикла каждым клоном (средством распараллеливания) и создания массива время-итерационных профилей первичной статистики. Первичная статистика сохраняется в виде строк таблицы следующих параметров: номера цикла, номера средства распараллеливания, время выполнения. Одна строка один время-итерационный профиль для конкретного цикла и средства распараллеливания. Далее по созданному массиву время-итерационных профилей первичной статистики программы и по разработанному алгоритму в способе строится прогноз автоматического выбора предпочтительного средства распараллеливания для конкретного цикла при текущем количестве итераций данного цикла. Главным критерием выбора оптимального средства является минимальное время исполнения текущего цикла при выполнении программы.
Достигаемый результат - сокращение времени выполнения каждого циклического участка, а в итоге временная оптимизация выполнения всей программы. Указанный результат достигается за счет того, что в известном способе параллельного программирования предназначенном для вычислительной системы с общей памятью, содержащей многоядерный (многопроцессорный) центральный процессор предлагается ввести следующие операции:
- проведение статического анализа программного кода с маркерным выделением циклических участков программного кода и их нумерация;
- копирование (клонирование) последовательного кода циклических участков в тело программного кода, количество копий равно количеству доступных средств распараллеливания;
- использование в каждом клоне прагм (дирректив) одного средства распараллеливания;
- выполнение многократного тестового прогона модифицированной, скомпилированной программы для сбора первичной статистики в виде вектора четырех параметров (номер цикла, количество итераций цикла, номер средства распараллеливания, минимального времени выполнения цикла при данном количестве итераций), который используется для отбора средств распараллеливания при следующих запусках.
- обработки массива первичной статистики для создания выборки (массива) отсчетов времен выполнения заданного цикла средства и количества итераций при многократных тестовых запусках программы
- построение эмпирической функции распределения времени выполнения каждого цикла по каждому средству распараллеливания и каждому имеющемуся числу итераций цикла. Ее аппроксимация и получение верхней границы доверительного интервала времени выполнения каждого цикла для определенного числа итераций;
- определение тренда изменения времени (по верхней границе доверительного интервала) выполнения цикла от количества итераций;
- формирование результирующей статистики имеющей вид массива с интервалами начального и конечного числа итераций цикла, номера оптимального средства распараллеливания для этого интервала итераций, что позволит осуществлять быстрый выбор оптимально средства.
- автоматический оптимальный выбор средства распараллеливания для каждого циклического участка программного кода по критерию минимального времени выполнения;
- пополнение первичной статистики по завершении работы штатной программы.
Для лучшего понимания заявленного изобретения далее приводится его описание в соответствии с чертежами.
На Фиг. 1 показана схема основных компонентов вычислительной системы, которая реализует предложенный способ. Представленная вычислительная система может также включать множество элементов, не показанных на Фиг. 1, таких как дисководы, сетевая связь и т.д. Вычислительная система содержит главную систему 200, выполненную с возможностью построения и оптимизации программы, а также получения массива (таблицы) соответствия предпочтительного средства распараллеливания для каждого цикла с определенным количеством итераций, которая соединена с устройством 201 назначения (устройством, предназначенным для выполнения построенной программы) посредством интерфейса 202. Процесс выполнения операций в главной системе 200 контролируют с помощью процессора 102, который управляет работой средств построения программы (компиляторы, компоновщики и др.), которые хранятся в памяти. Информацию о процессе построения программы демонстрируют на дисплее 101. Данные для создания и тестовых прогонов программы заносят в систему с помощью устройства ввода 103. Обмен информацией в главной системе осуществляют через шину данных 105. На выходе главной системы 200 в соответствии с предложенным способом получают рабочую распараллеленную программу с подключенными средствами распараллеливания и массив (таблицу) соответствия предпочтительного средства распараллеливания для каждого цикла с определенным числом итераций ее передают в память устройства назначения 201. В процессе функционирования устройство назначения управляется процессором, который выполняет результирующую программу. В памяти устройства назначения находится не только оптимизированная скомпилированная результирующая программа, но и дополнительный модуль мгновенного выбора средства распараллеливания по входным параметрам - номер цикла и числу его итераций.
Рассмотрим пошаговое выполнение заявленного способа в описанной выше системе (Фиг. 1, 5). Главное устройство 200 и устройство назначения 201 могут являться одним и тем же устройством при необходимости, либо иметь схожие характеристики и архитектуры. Исходный код программы строят (модифицируют, клонируют, добавляют прагмы средств распараллеливания и компонуют) в главной системе 200 при модификации программы 112 (поз.4,5). Модифицированный программный код компилируют по средствам компилятора (поз.5). Далее в результате тестовых прогонов в 113 (поз.6) получают 114 первичную статистику времен выполнения клонов циклов при примененных средствах распараллеливания, далее в 115 (поз.8-13) получают 116 обработанную статистику. Затем в 117 (поз.14-18) получают массив (таблицу) предпочтительных средств распараллеливания. В результате работы главного устройства 200 получают собранную и скомпилированную программу и массив предпочтительных средств распараллеливания.
В процессе функционирования устройство назначения управляется процессором, который выполняет программу, размещенную в памяти, а для выбора предпочтительного средства распараллеливания используется модуль мгновенного выбора средства распараллеливания (поз.22-30), который на основании входных параметров текущего цикла (номера цикла и числа итераций цикла) по таблице предпочтительных средств распараллеливания мгновенно находит номер оптимального средства и подключает клон с примененным средством распараллеливания. По завершению штатной работы программы в устройстве назначения 201 происходит пересчет время-итерационных профилей программы в 114 главной системы (поз.32, 7) для пополнения массива статистики.
На Фиг. 2 показан реальный пример массива (таблицы) время-итерационных профилей первичной статистики, который формируется в результате многократного тестового прогона цикла с возможностью распараллеливания пятью средствами распараллеливания, при дискретном числе итераций 20. Время-итерационный профиль программы первичной статистики представляет собой массив статистических данных состоящих из векторов четырех параметров: номер цикла (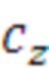 ), количество итераций цикла (
), количество итераций цикла (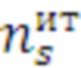 ), номер средства распараллеливания (
), номер средства распараллеливания (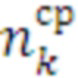 ), время работы (
), время работы (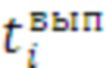 ).
).
На Фиг. 3 представлена таблица обработанных согласно способа время-итерационных профилей с расчетным временем (по верхней границе доверительного интервала) выполнения цикла. Представляет собой массив статистических данных состоящих из векторов четырех параметров: номер цикла (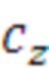 ), количество итераций цикла (
), количество итераций цикла (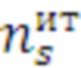 ), номер средства распараллеливания (
), номер средства распараллеливания (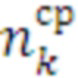 ), верхняя граница времени выполнения (
), верхняя граница времени выполнения (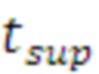 ).
).
На Фиг. 4 представлена конечная таблица оптимальных средств для указанного диапазона итераций цикла. Представляет собой матрицу статистических данных, состоящих из четырех параметров: номер цикла (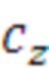 ), начальное количество итераций цикла (
), начальное количество итераций цикла (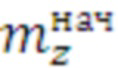 ), конечное количество итераций цикла (
), конечное количество итераций цикла (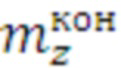 ), номер оптимального средства распараллеливания (
), номер оптимального средства распараллеливания (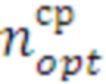 ).
).
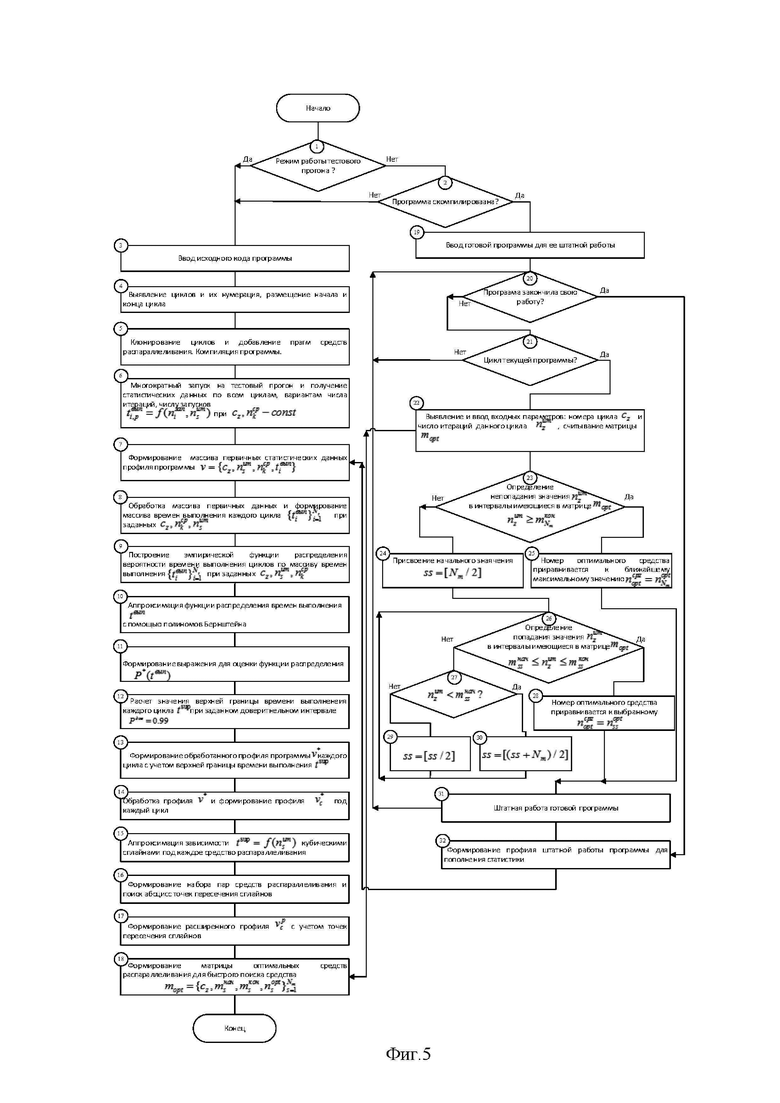
На Фиг. 5 показана алгоритмическая схема вычислительной системы объясняющая принцип работы способа согласно изобретению.
Рассмотрим алгоритм работы системы на подготовительном этапе по позициям алгоритма.
поз.1,2) на входной логический элемент системы поступает исходный (программный) код программы написанный на Си или подобном языке программирования. Логический элемент подтверждает выбранный режим работы системы - «тестовый», что характерно для первого входа в алгоритм.
поз.3) код программы транслируется и сохраняется на магнитном носителе (ЖД).
поз.4) разработчик (программист) модифицирует исходный программный код для этого определяет в коде наиболее время затратные циклы (циклические участки программы) номерует их, добавляет специальные дополнительные метки начала и конца цикла.
поз.5) затем повторно модифицируют размеченный исходный код программы, при этом клонируют циклические участки в код программы, создавая так называемые клоны. Далее добавляют в каждый клон средство распараллеливания в виде специальных директив из доступного набора средств распараллеливания. Таким образом, каждый цикл получает одинаковое количество клонов равное количеству доступных средств распараллеливания. Компилируют полученный код программы с учетом подключенных средств распараллеливания и формируют команду на запуск исполняемого файла;
поз.6) производится многократный запуск на тестовый (тренировочный) прогон для получения первых статистических данных по всем циклическим участкам, вариантам числа итераций и числу запусков всей программы.
В результате тестовых прогонов фиксируются параметры характеризующие время - итерационный профиль каждого из модифицированных циклических участков программы в виде: номера цикла 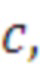 количества итераций
количества итераций 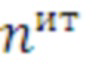 в данном цикле, номера средства распараллеливания
в данном цикле, номера средства распараллеливания 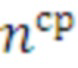 . и производится замер времени выполнения
. и производится замер времени выполнения 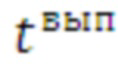 цикла с помощью счетчика времени заданным средством. Время - итерационный профиль каждого цикла представляет собой строку таблицы в виде:
цикла с помощью счетчика времени заданным средством. Время - итерационный профиль каждого цикла представляет собой строку таблицы в виде: 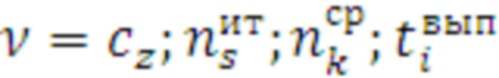
поз.7) формирование массива первичных статистических данных профиля программы.
На основании полученных параметров тестового прогона формируется довольно большой массив первичной статистики в виде табличных строк время - итерационного профиля: 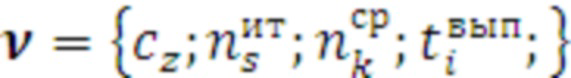 , которые сохраняются отдельно на электронном носителе информации (ЖД). Данный массив в процессе работы программы в штатном режиме будет постоянно обновляться.
, которые сохраняются отдельно на электронном носителе информации (ЖД). Данный массив в процессе работы программы в штатном режиме будет постоянно обновляться.
поз.8) обработка массива первичных статистических данных профиля программы и формирование массива времен выполнения каждого цикла.
Для этого считывается время-итерационный профиль программы первичных статистических данных 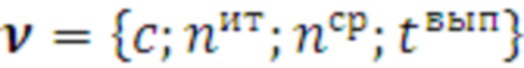 и из него формируется статистическая выборка для одного значения:
и из него формируется статистическая выборка для одного значения:
- номера цикла 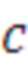 ;
;
- числа итераций 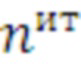 этого цикла;
этого цикла;
- номера средства распараллеливания 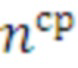 .
.
Соответственно, одна выборка при многократных тестовых запусках программы (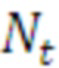 ) содержит массив отсчетов времен выполнения цикла
) содержит массив отсчетов времен выполнения цикла 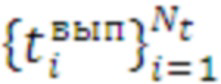 и представляет собой табличную строку в виде:
и представляет собой табличную строку в виде: 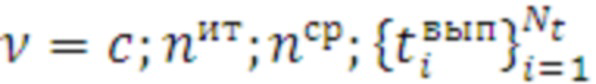 , при этом массив выборок по всем циклам, вариантам числа итераций и средствам распараллеливания выглядит так:
, при этом массив выборок по всем циклам, вариантам числа итераций и средствам распараллеливания выглядит так: 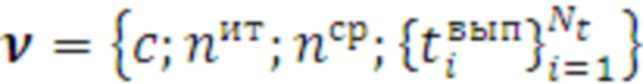
поз.9) по сформированному массиву 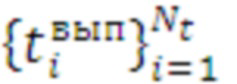 формируется эмпирическая функция распределения времени выполнения цикла следующим образом.
формируется эмпирическая функция распределения времени выполнения цикла следующим образом.
9.1. элементы массива времен выполнения цикла 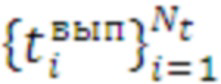 ранжируются по возрастанию значения времени.
ранжируются по возрастанию значения времени.
9.2. рассчитываются j-е значения функции распределения для ранжированного массива 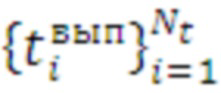 [7] по следующей формуле:
[7] по следующей формуле:
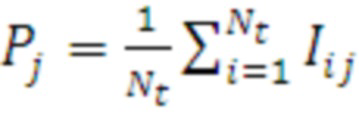 , (1)
, (1)
где 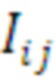 - индикаторная функция, принимающая значения:
- индикаторная функция, принимающая значения:
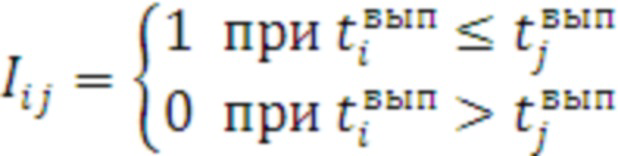 . (2)
. (2)
9.3. по имеющимся эмпирическим данным (набору времен выполнения цикла 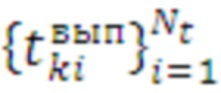 , где
, где 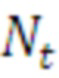 - число эмпирически полученных значений времени выполнения цикла) строится ступенчатая эмпирическая функция распределения
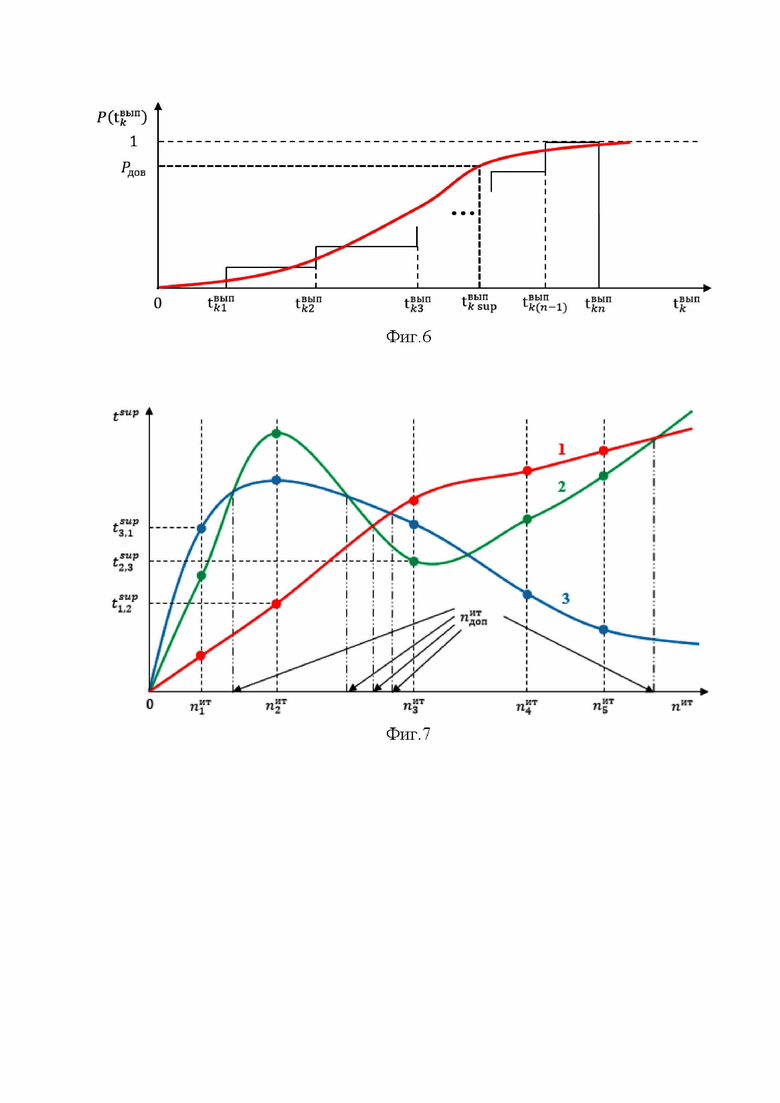
- число эмпирически полученных значений времени выполнения цикла) строится ступенчатая эмпирическая функция распределения 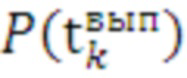 времени (Фиг. 6) выполнения цикла отдельно по каждому k-му средству распараллеливания и каждому имеющемуся числу итераций цикла.
времени (Фиг. 6) выполнения цикла отдельно по каждому k-му средству распараллеливания и каждому имеющемуся числу итераций цикла.
поз.10) затем ступенчатая эмпирическая функция распределения аппроксимируется гладкой кривой с помощью полиномов Бернштейна.
При выборе способа аппроксимации учитывается, что вид функции распределения времени выполнения цикла неизвестен. При этом плотность распределения может быть полимодальной, т.е. иметь несколько максимумов (при одном и том же числе итераций цикла, но при разных значениях исходных данных время выполнения цикла может быть различным).
Так как вид функции распределения неизвестен, то необходимо применять непараметрические методы аппроксимации. В [8] показано, что высокая точность аппроксимации непараметрическим методом как унимодальных, так и полимодальных распределений, заданных на конечных интервалах, обеспечивается применением полиномов Бернштейна. При этом оценка функции распределения описывается выражением:
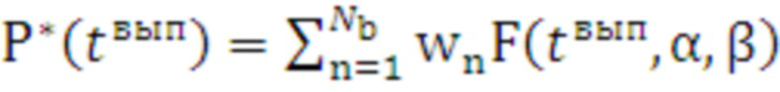 , (3)
, (3)
где 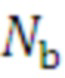 - степень полинома Бернштейна;
- степень полинома Бернштейна;
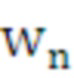 - весовые коэффициенты полинома Бернштейна;
- весовые коэффициенты полинома Бернштейна;
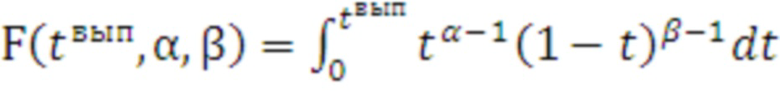 - функция распределения бэта-распределения.
- функция распределения бэта-распределения.
Расчет параметров 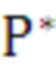 выполняется в два этапа:
выполняется в два этапа:
1) при заданной степени полинома 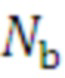 (начиная с минимального значения
(начиная с минимального значения 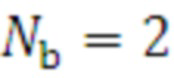 ) определяются значения весовых коэффициентов
) определяются значения весовых коэффициентов 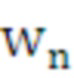 .
.
2) повторяется пункт 1 для набора значений 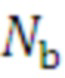 и выбирается величина
и выбирается величина 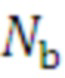 , при которой обеспечивается требуемая точность аппроксимации.
, при которой обеспечивается требуемая точность аппроксимации.
Реализуется следующий порядок расчета параметров аппроксимирующей функции.
10.1. Присваивается начальное значение степени полинома Бернштейна 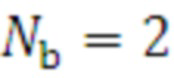 .
.
10.2. формируется матрица 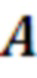 и вектор
и вектор 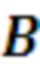 . Элементы матрицы и вектора определяются формулами:
. Элементы матрицы и вектора определяются формулами:
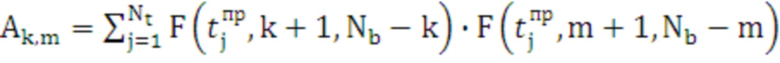 , (4)
, (4)
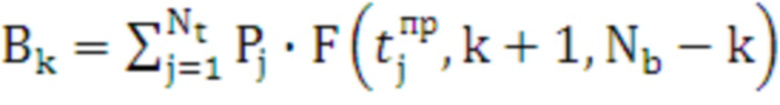 , (5)
, (5)
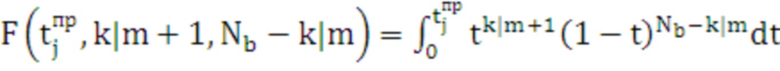 , (6)
, (6)
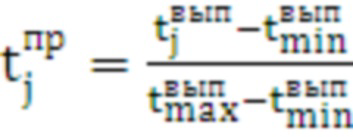 , (7)
, (7)
где 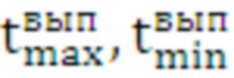 - соответственно максимальное и минимальное значение времени выполнения цикла в массиве
- соответственно максимальное и минимальное значение времени выполнения цикла в массиве 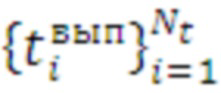 ;
;
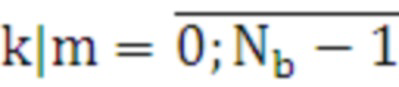 - номера элементов строки|столбца матрицы
- номера элементов строки|столбца матрицы 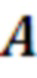 и вектора
и вектора 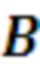 .
.
10.3. рассчитываются весовые коэффициенты полинома 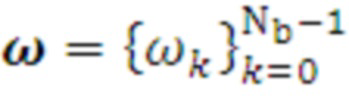 путем нахождения приближенного решения системы линейных уравнений, записываемых в матричном виде как:
путем нахождения приближенного решения системы линейных уравнений, записываемых в матричном виде как:
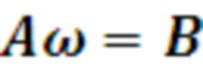 (8)
(8)
при ограничениях:
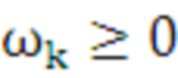 ,
, 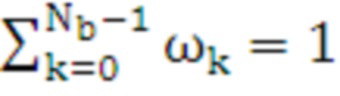 . (9)
. (9)
поз.11) определяется выражение для оценки функции распределения:
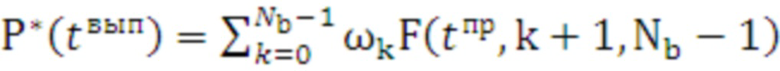 , (10)
, (10)
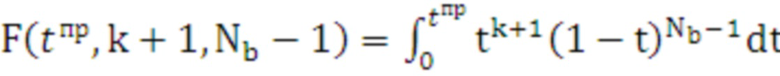 . (11)
. (11)
Для принятия решения о возможности использования аппроксимирующей функции рассчитывается доверительный интервал для каждого j-го значения эмпирической функции распределения:
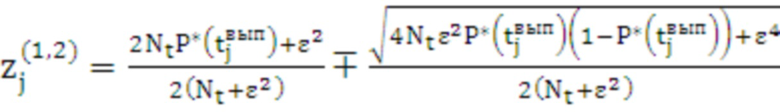 , (12)
, (12)
где  - квантиль нормального распределения для заданной доверительной вероятности (например, для
- квантиль нормального распределения для заданной доверительной вероятности (например, для 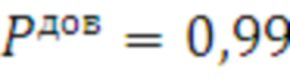 значение
значение 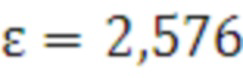 ).
).
Аппроксимирующая функция принимается при выполнении для всех j-ых значений эмпирической функции распределения условия:
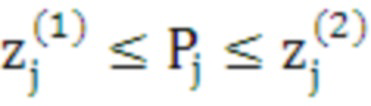 . (13)
. (13)
В противном случае степень полинома 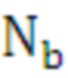 увеличивается на единицу
увеличивается на единицу
поз.12) для заданной доверительной вероятности по аппроксимированной функции распределения вероятности времени выполнения цикла рассчитывается значение верхней границы 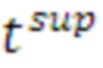 времени выполнения цикла путем решения уравнения:
времени выполнения цикла путем решения уравнения:
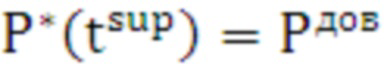 . (14)
. (14)
Ввиду того, что отсутствуют аналитические способы решения данного уравнения поиск 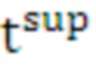 выполняется численным методом - методом половинного деления.
выполняется численным методом - методом половинного деления.
поз.13) с использованием рассчитанного значения 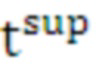 (верхней границы доверительного интервала времени выполнения цикла) формируется обработанный время-итерационный профиль программы:
(верхней границы доверительного интервала времени выполнения цикла) формируется обработанный время-итерационный профиль программы:
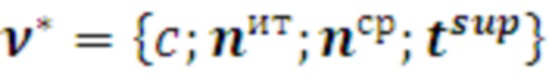
где 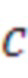 - порядковый номер цикла программы;
- порядковый номер цикла программы;
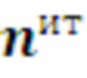 - вектор числа итераций цикла;
- вектор числа итераций цикла;
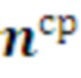 - вектор порядковых номеров средств распараллеливания;
- вектор порядковых номеров средств распараллеливания;
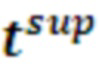 - вектор значений верхней границы времени выполнения цикла
- вектор значений верхней границы времени выполнения цикла
Данный профиль сохраняется отдельно на электронном носителе информации (ЖД).
поз.14) обработка профиля 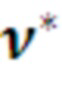 и формирование профиля
и формирование профиля 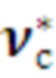 под каждый цикл выполняется следующим образом:
под каждый цикл выполняется следующим образом:
14.1 считывается обработанный время-итерационный профиль программы 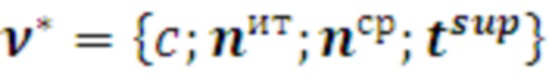 .
.
14.2 Для исследуемого порядкового номера цикла 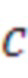 обработанный время-итерационный профиль представляется в виде массива:
обработанный время-итерационный профиль представляется в виде массива:
 , (15)
, (15)
где 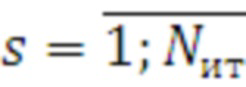 - порядковый номер числа итераций цикла;
- порядковый номер числа итераций цикла;
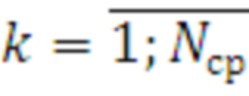 - порядковый номер средства распараллеливания.
- порядковый номер средства распараллеливания.
Массив ранжирован по возрастанию значений 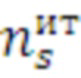 . Первый столбец матрицы состоит из нулевых элементов.
. Первый столбец матрицы состоит из нулевых элементов.
поз.15) выполняется интерполяция и экстраполяция зависимости верхней границы времени выполнения цикла 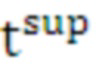 от числа итераций
от числа итераций 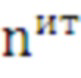 для всех рассматриваемых средств распараллеливания. (Фиг. 7).
для всех рассматриваемых средств распараллеливания. (Фиг. 7).
Интерполяция и экстраполяция обработанного время-итерационного профиля программы 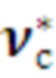 необходима для расчета величины
необходима для расчета величины 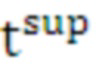 для любых значений
для любых значений 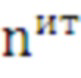 (не совпадающих со значениями
(не совпадающих со значениями 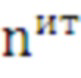 , содержащимися в профиле программы). При интерполяции и экстраполяции используется одинаковый подход, основанный на применении кубических сплайнов.
, содержащимися в профиле программы). При интерполяции и экстраполяции используется одинаковый подход, основанный на применении кубических сплайнов.
Хорошими вычислительными и аппроксимативными свойствами обладают сплайны, они обеспечивают простоту реализации вычислительных алгоритмов, полученных на их основе [9]. Преимущество интерполяции сплайнами по сравнению с обычными методами интерполяции заключается в сходимости и устойчивости вычислительного процесса. При этом достаточную точность обеспечивают сплайны третьей степени (кубические сплайны).
При использовании кубических сплайнов на каждом из отрезков 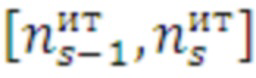 определяется аппроксимирующая функция для k-го средства распараллеливания:
определяется аппроксимирующая функция для k-го средства распараллеливания:
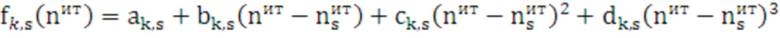 (16)
(16)
где 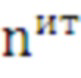 - текущее число итераций цикла;
- текущее число итераций цикла;
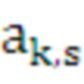 ,
, 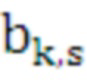 ,
, 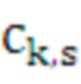 ,
, 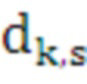 - коэффициенты сплайна для s-го числа итераций цикла
- коэффициенты сплайна для s-го числа итераций цикла 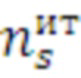 k-го средства распараллеливания;
k-го средства распараллеливания;
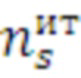 - s-е число итераций цикла.
- s-е число итераций цикла.
Используются следующие формулы для определения значений коэффициентов сплайна [10]:
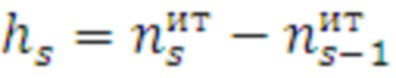 . (17)
. (17)
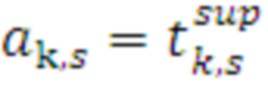 , (18)
, (18)
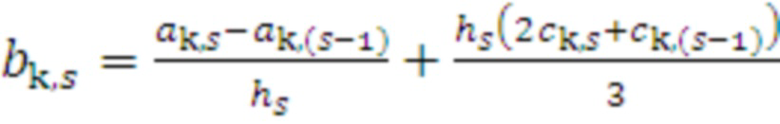 , (19)
, (19)
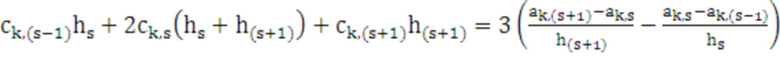 , (21)
, (21)
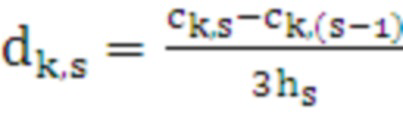 . (22)
. (22)
Коэффициенты рассчитываются методом прогонки для трехдиагональной матрицы [11, 12] Рассчитанные значения коэффициентов сохраняются в оперативной памяти для их дальнейшего использования на следующем шаге поз.16.
В результате нахождения аппроксимирующих функций 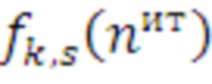 зависимости
зависимости 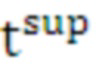 от
от 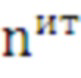 сглаживаются гладкими кривыми (Фиг. 7). На Фиг. 7 приведен пример для трех средств распараллеливания.
сглаживаются гладкими кривыми (Фиг. 7). На Фиг. 7 приведен пример для трех средств распараллеливания.
Как видно на Фиг. 7, могут возникать пересечения аппроксимирующих кривых разных средств распараллеливания. Поэтому в сформированный массив профиля программы 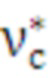 необходимо добавить столбцы по каждому такому дополнительному значению числа итераций
необходимо добавить столбцы по каждому такому дополнительному значению числа итераций 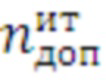 , возникающему в местах пересечения сплайнов. Данная операция выполняется путем формирования набора векторов-столбцов дополнительных значений числа итераций цикла.
, возникающему в местах пересечения сплайнов. Данная операция выполняется путем формирования набора векторов-столбцов дополнительных значений числа итераций цикла.
поз.16) формирование набора пар средств распараллеливания и поиск абсцисс точек пересечения сплайнов. (Фиг. 7).
Для формирования дополнительных элементов массива профиля программы необходимо найти абсциссы точек пересечения сплайнов для разных средств распараллеливания.
Так как оптимальное средство распараллеливания выбирается в процессе штатной работы программы, то необходимо минимизировать время выбора. Для этого обработанный время-итерационный профиль программы 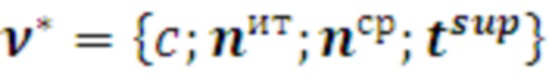 преобразуется в массив оптимальных средств распараллеливания
преобразуется в массив оптимальных средств распараллеливания 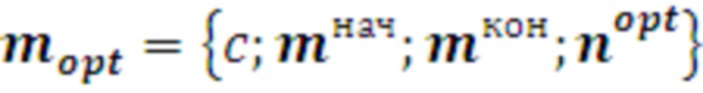 (
(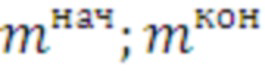 - соответственно начальное и конечное число итераций цикла,
- соответственно начальное и конечное число итераций цикла, 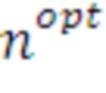 - номер оптимального средства распараллеливания для этого участка числа итераций). Выполнение такого преобразования требует нахождения участков
- номер оптимального средства распараллеливания для этого участка числа итераций). Выполнение такого преобразования требует нахождения участков 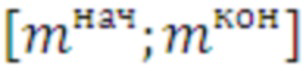 , на которых отсутствуют пересечения аппроксимирующих сплайнов разных средств распараллеливания.
, на которых отсутствуют пересечения аппроксимирующих сплайнов разных средств распараллеливания.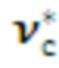
Для этого используя массив 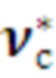 , организуется цикл по числу итераций
, организуется цикл по числу итераций 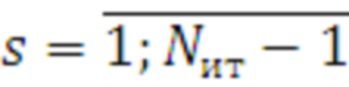 .
.
16.1. на каждом s-ом шаге цикла для значений числа итераций 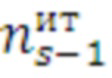 ,
, 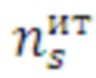 формируются наборы пар средств распараллеливания из k1-го и k2-го средств распараллеливания
формируются наборы пар средств распараллеливания из k1-го и k2-го средств распараллеливания 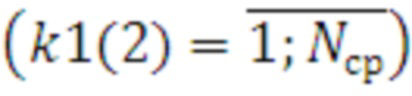 .
.
Для каждого средства этой пары из оперативной памяти считываются соответствующие значения коэффициентов сплайна 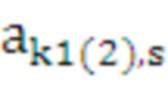 ,
, 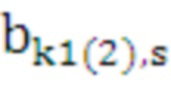 ,
, 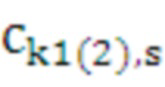 ,
, 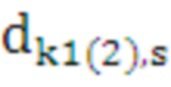 , рассчитанные на шаге 3.
, рассчитанные на шаге 3.
16.2 так как в точках пересечения сплайнов значения аппроксимирующих функций 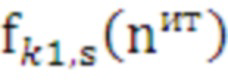 ,
, 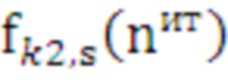 имеют одинаковую величину, то они приравниваются друг к другу. В результате этого выполняется поиск действительных корней кубического уравнения относительно переменной
имеют одинаковую величину, то они приравниваются друг к другу. В результате этого выполняется поиск действительных корней кубического уравнения относительно переменной 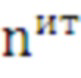 (абсцисс точек пересечения):
(абсцисс точек пересечения):
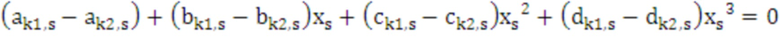 , (23)
, (23)
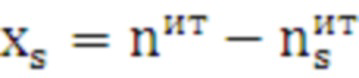 . (24)
. (24)
16.3 анализируется попадание найденных корней 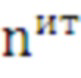 в рассматриваемый интервал
в рассматриваемый интервал 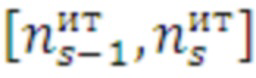 по выполнению условия:
по выполнению условия:
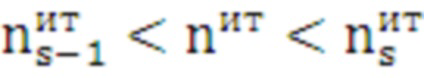 . (25)
. (25)
При этом для последнего значения 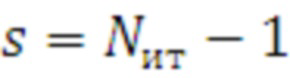 при проверке условия (25) принимается
при проверке условия (25) принимается 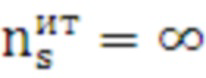 , так как последний отрезок используется для экстраполяции зависимости
, так как последний отрезок используется для экстраполяции зависимости 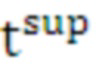 от
от 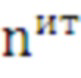 .
.
поз.17) формирование расширенного профиля программы 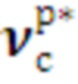 с учетом точек пересечения сплайнов.
с учетом точек пересечения сплайнов.
В случае выполнения условия (11) найденные действительные корни 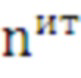 фиксируются как дополнительное значение числа итераций
фиксируются как дополнительное значение числа итераций 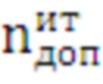 . Для каждого значения
. Для каждого значения 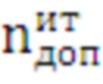 рассчитываются величины
рассчитываются величины 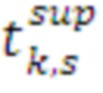 по каждому k-му средству распараллеливания. Таким образом, формируются дополнительные столбцы матрицы
по каждому k-му средству распараллеливания. Таким образом, формируются дополнительные столбцы матрицы 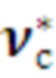 , которыми дополняется эта матрица. В результате дополнения формируется расширенная матрица время-итерационного профиля программы
, которыми дополняется эта матрица. В результате дополнения формируется расширенная матрица время-итерационного профиля программы 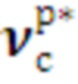 . Столбцы этой матрицы ранжируются в порядке возрастания значений
. Столбцы этой матрицы ранжируются в порядке возрастания значений 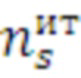 .
.
поз.18) формирование матрицы оптимальных средств распараллеливания цикла для быстрого поиска средства.
Для этого организуется цикл по расширенному числу итераций 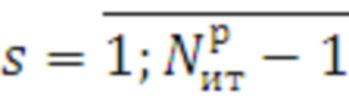 .
.
18.1 на каждом s-ом шаге цикла формируются значения числа итераций начала и конца диапазона:
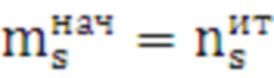 ,
, 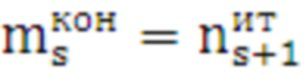 . (26)
. (26)
Для этого интервала 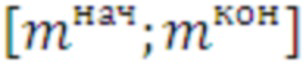 определяется номер средства распараллеливания, имеющего минимальное значение верхней границы времени выполнения цикла
определяется номер средства распараллеливания, имеющего минимальное значение верхней границы времени выполнения цикла 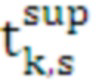 :
:
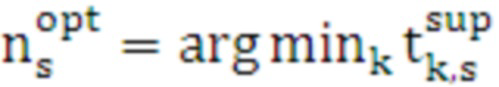 . (27)
. (27)
Формируется начальная матрица оптимальных средств распараллеливания:
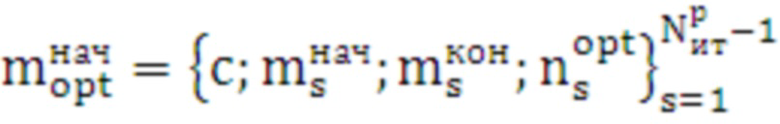 . (28)
. (28)
18.2 ввиду того, что некоторые смежные интервалы могут иметь одинаковые оптимальные средства распараллеливания, выполняется объединение таких смежных интервалов. В результате формируется конечная матрица оптимальных средств распараллеливания с числом элементов 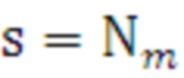 :
:
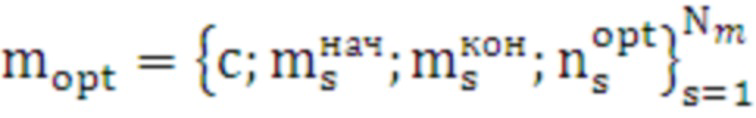 . (29)
. (29)
Полученная матрица 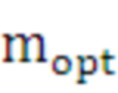 сохраняется в базе данных отдельно в память и является результатом работы главной системы. Которая используется в работе устройства назначения, как основной элемент в автоматическом выборе оптимального средства распараллеливания. Данная матрица представляет собой таблицу предпочтительного средства распараллеливания для каждого цикла с построенными верхней (начальной) и нижней (конечной) границами итерационного диапазона с целью мгновенного выбора оптимального средства распараллеливания при попадании в указанный диапазон входных данных количества итераций (
сохраняется в базе данных отдельно в память и является результатом работы главной системы. Которая используется в работе устройства назначения, как основной элемент в автоматическом выборе оптимального средства распараллеливания. Данная матрица представляет собой таблицу предпочтительного средства распараллеливания для каждого цикла с построенными верхней (начальной) и нижней (конечной) границами итерационного диапазона с целью мгновенного выбора оптимального средства распараллеливания при попадании в указанный диапазон входных данных количества итераций (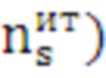 текущего цикла штатной программы.
текущего цикла штатной программы.
На этом главная система заканчивает свою работу.
Далее по общей алгоритмической схеме, представленной на Фиг. 5 рассмотрим работу устройства назначения.
При следующем запуске системы, программа, обеспечивающая работу системы, пройдя два логических элемента выходит на поз.19.
поз.19) ввод готовой программы для штатной работы.
поз.20;21) два логических элемента обеспечивают контроль за окончанием работы программы и выделения начала циклического участка, подлежащего распараллеливанию.
поз.22) выявление и ввод входных параметров цикла: номера цикла 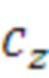 , и количества итераций цикла
, и количества итераций цикла 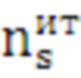 , а также из базы данных считывается матрица
, а также из базы данных считывается матрица 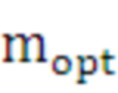 оптимальных средств распараллеливания цикла.
оптимальных средств распараллеливания цикла.
Далее методом половинного деления осуществляется поиск оптимального средства распараллеливания 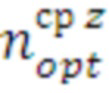 . Применение метода половинного деления позволяет ускорить поиск оптимального средства распараллеливания. Это особенно важно ввиду того, что поиск выполняется в ходе штатной работы программы в режиме реального времени. Такой подход позволяет найти оптимальное решение не более чем за
. Применение метода половинного деления позволяет ускорить поиск оптимального средства распараллеливания. Это особенно важно ввиду того, что поиск выполняется в ходе штатной работы программы в режиме реального времени. Такой подход позволяет найти оптимальное решение не более чем за 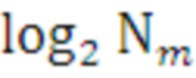 шагов.
шагов.
поз.23) логический элемент проверяющий выход значения 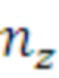 за пределы интервалов, имеющихся в матрице
за пределы интервалов, имеющихся в матрице 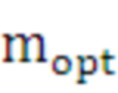 по выполнению условия:
по выполнению условия:
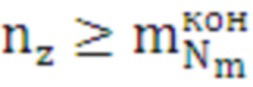 . (30)
. (30)
Если условие (30) выполняется, то происходит переход на поз.25.
поз.25) где присваивается 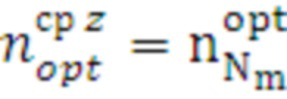 номер оптимального средства с максимальным числом итераций и поиск заканчивается. Номер присвоенного оптимального средства поступает на поз.31 штатной работы программы для автоматического управления включением оптимального средства распараллеливания (подключением ветки клона) данного цикла.
номер оптимального средства с максимальным числом итераций и поиск заканчивается. Номер присвоенного оптимального средства поступает на поз.31 штатной работы программы для автоматического управления включением оптимального средства распараллеливания (подключением ветки клона) данного цикла.
Если условие (30) не выполняется, то переход на поз.24.
поз.24) где присваивается начальное значение индекса матрицы 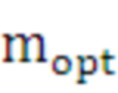 для выполнения поиска
для выполнения поиска 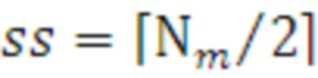 (операция нахождения большей целой части числа) и выход на логический элемент поз.26.
(операция нахождения большей целой части числа) и выход на логический элемент поз.26.
поз.26) логический элемент проверяющий попадание значения 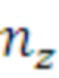 в интервалы, имеющиеся в матрице
в интервалы, имеющиеся в матрице 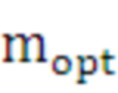 по выполнению условия:
по выполнению условия:
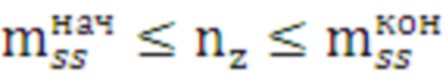 (31)
(31)
Если условие (31) выполняется, то происходит переход на поз.28
поз.28) где присваивается 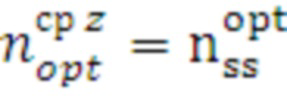 и поиск заканчивается. Номер присвоенного оптимального средства поступает на поз.31 штатной работы программы для автоматического управления включением оптимального средства распараллеливания (подключением ветки клона) данного цикла.
и поиск заканчивается. Номер присвоенного оптимального средства поступает на поз.31 штатной работы программы для автоматического управления включением оптимального средства распараллеливания (подключением ветки клона) данного цикла.
Если условие (31) не выполняется, то происходит переход на логический элемент поз.27
поз.27) логический элемент корректирует значение индекса поиска 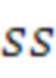 по выполнению условия:
по выполнению условия:
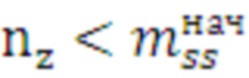 (32)
(32)
Если условие (32) выполняется, то происходит переход на поз.29.
поз.29) где присваивается 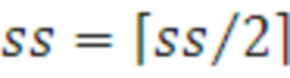 и выполняется переход к поз.26 и поиск продолжается.
и выполняется переход к поз.26 и поиск продолжается.
Если условие (32) не выполняется, то происходит переход на поз.30.
поз.30) где присваивается  и выполняется переход к поз.26 и поиск продолжается.
и выполняется переход к поз.26 и поиск продолжается.
поз.31) штатная работа программы.
В процессе работы модифицированной штатной программы после обнаружения циклического участка в реальном масштабе времени происходит автоматический выбор из сформированной матрицы оптимальных средств распараллеливания оптимального средства распараллеливания и его подключения (подключением ветки клона).
В процессе работы программы параметры время - итерационного профиля каждого выполненного цикла измеряются и сохраняются отдельно в памятипоз.32 По завершению работы программы по команде с поз.20 массив сохраненного время- итерационного профиля всей программы передается на вход формирователя массива первичных статистических данных поз.7, для их обновления.
Тело программного кода, увеличенное на количество клонов циклов, равное количеству средств распараллеливания, но при этом продолжительность исполнения программы не увеличивается, так как в процессе исполнения все клоны не выполняются, выполняется только один выбранный. Процесс автоматизации выбора клона (с оптимальным средством распараллеливания) позволяет снизить временные затраты выполнения циклических участков программы и в целом всей программы. Работа автоматизирована, по входным параметрам циклического участка целевой программы (номеру и числу итераций цикла) на основании выработанного критерия принятия решения о подключении одной из веток клонированного данного циклического участка программы с минимальным временем формируется команда на исполнение.
Для функционирования способа важно, чтобы тестовое построение первичных время-итерационных профилей циклических участков программы создавались на устройствах имеющих схожую архитектуру (архитектуру процессора) с архитектурой устройства назначения таких как Intel Core Duo, Sun UltraSPARC, AMD Opteron и др.
Задачей, которую решает данное изобретение является обеспечение возможности сокращения времени выполнения исходного кода программы в многоядерных (многопроцессорных) вычислительных системах с общей памятью за счет использования статического и динамического анализа исходного кода программы, а также автоматизации выбора и комплексного применения средств параллельного программирования для конкретной решаемой задачи.
В качестве доказательства возможности осуществления заявленного изобретения с достижением вышеуказанного технического результата рассматривается пятикратный тестовый прогон одного циклического участка (цикла), с возможностью распараллеливания пятью средствами при дискретной смене десяти вариантов числа итераций 0-20-50-100-210-345-560-700-810-930. По результатам тестовых прогонов умножения матриц на четырехядерном процессоре Core i5 3550 составлена таблица (Фиг. 2) сбора первичных статистических данных времени выполнения цикла, данная таблица представлена в сокращенном варианте, размер такой таблицы при заданных параметрах составляет 250 строк.
Математический аппарат изобретения представлен в виде программы в Mathcad 15.0. Результаты приведены в таблицах на Фиг. 3, Фиг. 4 Расчеты представлены на Фиг. 8, Фиг. 9. На Фиг. 3 представлена таблица обработанных время-итерационных профилей с расчетным временем верхней границы доверительного интервала. На Фиг. 4 представлена конечная матрица оптимальных средств для указанного диапазона итераций циклов. На Фиг. 8 представлена последовательность действий математического аппарата заявленного способа по построению эмпирической функции распределения случайной величины времени выполнения одного заданного цикла (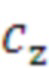 ); заданным средством распараллеливания (
); заданным средством распараллеливания (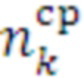 ), при заданном числе итераций цикла (
), при заданном числе итераций цикла (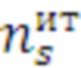 =20) и пятикратном (
=20) и пятикратном (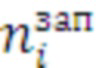 =5) запуске цикла. По функции распределения оценивается время выполнения цикла заданным средство распараллеливания (
=5) запуске цикла. По функции распределения оценивается время выполнения цикла заданным средство распараллеливания (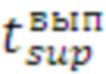 ) по верхней границе доверительного интервала, при заданной доверительной вероятности (
) по верхней границе доверительного интервала, при заданной доверительной вероятности (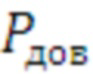 =0.99). В приведенном примере значение верхней границы времени выполнения цикла заданным средством составляет
=0.99). В приведенном примере значение верхней границы времени выполнения цикла заданным средством составляет 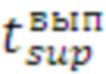 =2.096 с при этом появляется возможность сравнения разных средств распараллеливания цикла по этому параметру и выбрать с наименьшим временем. Поэтому для автоматизации выбора оптимального средства в данном примере необходимо аналогично строить эмпирические функции для всех средств распараллеливания с определением времени верхней границы. В примере данная операция опущена, так как действия аналогичны описанным выше, а результирующим является массив Фиг. 9 обработанного профиля программы в виде матрицы (v_c), где первая строка 10 дискретных значений количества итераций от 0 до 930, вторая строка - это время выполнения цикла одним средством в зависимости от числа итераций. Вертикальный столбец, это значения времен выполнения цикла по верхней границе (
=2.096 с при этом появляется возможность сравнения разных средств распараллеливания цикла по этому параметру и выбрать с наименьшим временем. Поэтому для автоматизации выбора оптимального средства в данном примере необходимо аналогично строить эмпирические функции для всех средств распараллеливания с определением времени верхней границы. В примере данная операция опущена, так как действия аналогичны описанным выше, а результирующим является массив Фиг. 9 обработанного профиля программы в виде матрицы (v_c), где первая строка 10 дискретных значений количества итераций от 0 до 930, вторая строка - это время выполнения цикла одним средством в зависимости от числа итераций. Вертикальный столбец, это значения времен выполнения цикла по верхней границе (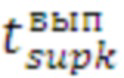 ) для разных средств распараллеливания. На основании данного массива строится графическое представление зависимости (
) для разных средств распараллеливания. На основании данного массива строится графическое представление зависимости (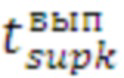 ) от дискретного значения количества итераций (
) от дискретного значения количества итераций (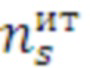 =0…930) для пяти средств распараллеливания. Для упрощения расчетов построение графиков производится без учета аппроксимации. По графикам видно, что кривые разных средств пересекаются, поэтому точки пересечения необходимо найти и включить в итоговую таблицу массива (v_c). Вектор дополнительного числа итераций составляет 1 элементов. Далее строится матрица (v_c_dop) дополнительных элементов. Затем необходимо включить дополнительные элементы и сформировать расширенный профиль программы (v_c_r). Далее расширенный профиль сортируется (v_c_r_sort) и создание начальной матрицы оптимальных средств распараллеливания (m_nach_opt), количество столбцов в матрице (v_c_r_sort), а количество строк в матрице (m_nach_opt) составляет 25 и 24 соответственно. Данные матрицы представлены в сокращенном варианте. В завершении подготовительной части способа формируется конечная матрица оптимальных средств (m_kon_opt). Далее демонстрируется поиск оптимального средства распараллеливания, заданным параметром для поиска является текущее число итераций цикла (для примера
=0…930) для пяти средств распараллеливания. Для упрощения расчетов построение графиков производится без учета аппроксимации. По графикам видно, что кривые разных средств пересекаются, поэтому точки пересечения необходимо найти и включить в итоговую таблицу массива (v_c). Вектор дополнительного числа итераций составляет 1 элементов. Далее строится матрица (v_c_dop) дополнительных элементов. Затем необходимо включить дополнительные элементы и сформировать расширенный профиль программы (v_c_r). Далее расширенный профиль сортируется (v_c_r_sort) и создание начальной матрицы оптимальных средств распараллеливания (m_nach_opt), количество столбцов в матрице (v_c_r_sort), а количество строк в матрице (m_nach_opt) составляет 25 и 24 соответственно. Данные матрицы представлены в сокращенном варианте. В завершении подготовительной части способа формируется конечная матрица оптимальных средств (m_kon_opt). Далее демонстрируется поиск оптимального средства распараллеливания, заданным параметром для поиска является текущее число итераций цикла (для примера 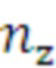 =65). В итоге программы поиска по таблице (m_kon_opt) при заданном количестве итераций 65 определило оптимальное средство (n_opt=4), что подтверждает физическую работоспособность способа.
=65). В итоге программы поиска по таблице (m_kon_opt) при заданном количестве итераций 65 определило оптимальное средство (n_opt=4), что подтверждает физическую работоспособность способа.
ИСТОЧНИКИ ИНФОРМАЦИИ
1. Automatic Paralleli/ation. Carnegie Mellon University, HPCA-4, February 1-4, 1998. Sutter H. The Free Lunch Is Over A Fundamental Turn Toward Concurrency in Software. Dr. Dobb's Journal, March 2005.
2. Воеводин В.В., Воеводин Вл.В. Параллельные вычисления. Спб.:Санкт-Петербург, 2002. 608 с.
3. Program conversion device and program conversion method. United States Patent Application Publication/ Teruo Kawabata, Hajime Ogawa, Taketo Heishi, Yasuhiro Yamamoto, Shohei Michimoto - №2006/0248520 2.11.2006.
4. Способ автоматического распараллеливания программ. Патент РФ/ А.Ю. Дроздов, С. В. Новиков - №2411569 от 10.02.2011 г.
5. Wenmei Hwu, Shane Ryoo, SainZee Ueng, John H. Kelm, Isaac Gelado, Sam S.Stone, Robert E. Kidd, Sara S. Baghsorkhi, Aqeel A. Mahesri, Stephanie C. Tsao, Nacho Navarro,Steve S. Lumetta, Matthew I. Frank, and Sanjay J. Patel, Implicit Parallel Programming Models for Thousand-Core Microprocessors, Proceedings of the 44th Annual Design Automation Conference, June 2007.
6. Андреев А.Е. Технологии программирования многопроцессорных систем: учеб. пособие / Андреев А.Е., Егунов В.А., Шаповалов О.В.; ВолгГТУ. Волгоград, 2015. 103 с.
7. Красовский Ю.М. Математические основы военной кибернетики: (Учеб. пособие) / Ю.М. Красовский, М. С.Любушкин; Отв. ред. М.С.Любушкин; Воен. командная акад. противовоздуш. обороны. Кафедра №12. - Калинин: [б. и.], 1971. - 446 с.
8. Голик Ф.В. Аппроксимация эмпирических распределений вероятностей полиномами Бернштейна. Журнал радиоэлектроники [электронный журнал]. 2018. №7.
9. Волков Е.А. Глава 1. Приближение функций многочленами. Сплайны// Численные методы. - Учеб. пособие для вузов. - 2-е изд., испр. - М.: Наука, 1987. - С.63-68. - 248 с.
10. https://ru.wikipedia.org/wiki/Кубический_сплайн
11. https://ru.wikipedia.org/wiki/Метод_прогонки
12. http://www.machinelearning.ru/wiki/index.php?title Интерполяция_кубическими_сплайнами
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ АВТОМАТИЧЕСКОГО РАСПАРАЛЛЕЛИВАНИЯ ПРОГРАММ | 2009 |
|
RU2411569C2 |
| СПОСОБ ОБРАБОТКИ ДЛЯ МНОГОЯДЕРНОГО ПРОЦЕССОРА И МНОГОЯДЕРНЫЙ ПРОЦЕССОР | 2012 |
|
RU2630753C2 |
| СИСТЕМА УПРАВЛЕНИЯ ТЕСТИРОВАНИЕМ ПРОГРАММНОГО ОБЕСПЕЧЕНИЯ | 2021 |
|
RU2774659C1 |
| Способ распараллеливания программ в среде логического программирования в вычислительной системе | 2018 |
|
RU2691860C1 |
| Способ автоматического создания параллельной программы с временной параметризацией многопроцессорных вычислительных систем с одинаковым доступом к памяти | 2022 |
|
RU2786347C1 |
| Способ распараллеливания программ в вычислительной системе | 2018 |
|
RU2685018C1 |
| УСТРОЙСТВО УПРАВЛЕНИЯ ВЫСОКОАДАПТИВНЫМ АВТОНОМНЫМ МОБИЛЬНЫМ РОБОТОМ | 2019 |
|
RU2705049C1 |
| ФОРМУЛЬНЫЙ ПРОЦЕССОР С КОМАНДОПОДОБНЫМИ ЛОГИЧЕСКИМИ УПРАВЛЯЮЩИМИ ЭЛЕМЕНТАМИ | 1997 |
|
RU2143726C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ КООРДИНАТ МОБИЛЬНОГО ПРИЕМНИКА СПУТНИКОВОЙ РАДИОНАВИГАЦИОННОЙ СИСТЕМЫ (СРНС) | 2010 |
|
RU2432584C2 |
| СПОСОБ ПОЛУЧЕНИЯ ОБЪЕКТНОГО КОДА | 2000 |
|
RU2206119C2 |


Изобретение относится к области вычислительной техники. Техническим результатом является ускорение выполнения программы в многоядерных вычислительных системах. Раскрыт способ параллельного программирования при котором происходит автоматический выбор средств распараллеливания во время исполнения программ в вычислительной системе, содержащей соединенные интерфейсом главную систему и устройство назначения, каждое из которых содержит многоядерный центральный процессор, память, кэш-инструкции, и выполняющей следующие операции: в главной системе формируют исходный код программы; формируют отчет времени выполнения циклических участков программы по тестовому прогону и сохраняют в памяти; проводят анализ программного кода на основании тестовых прогонов, определяют и номеруют наиболее время затратные циклические участки; модифицируют исходный программный код, при этом помещают в него дополнительные метки начала и конца время затратных циклических участков и применяемых средств распараллеливания на языке программирования; под каждый цикл формируют и сохраняют таблицу средств распараллеливания с обозначенными границами итерационного диапазона и номером средства распараллеливания с минимальным временем выполнения; распараллеленную программу с подключенными средствами распараллеливания и таблицу соответствия предпочтительных средств распараллеливания для каждого цикла с определенным числом итераций передают в память устройства назначения; в процессе функционирования управляют устройством назначения, которое обеспечивает выбор средства распараллеливания, используя модуль мгновенного выбора средства распараллеливания, находящийся в памяти устройства назначения, который для текущего цикла по номеру цикла и числу итераций цикла в таблице предпочтительных средств распараллеливания определяет номер оптимального средства распараллеливания и подключает клон с примененным средством распараллеливания. 7 з.п. ф-лы, 9 ил.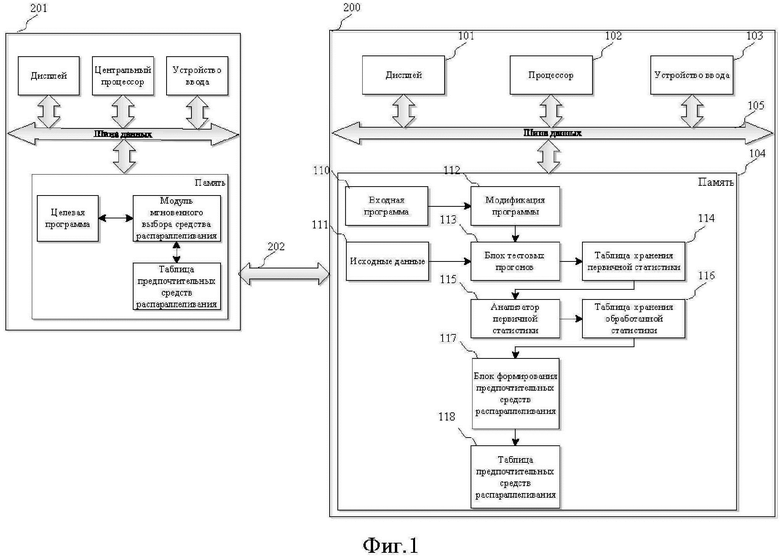
1. Способ параллельного программирования, при котором происходит автоматический выбор средств распараллеливания во время исполнения программ в вычислительной системе, содержащей соединенные интерфейсом главную систему и устройство назначения, каждое из которых содержит многоядерный центральный процессор, память, кэш-инструкции, и выполняющей следующие операции:
в главной системе формируют исходный код программы;
формируют отчет времени выполнения циклических участков программы по тестовому прогону и сохраняют в памяти;
проводят анализ программного кода на основании тестовых прогонов, определяют и номеруют наиболее время затратные циклические участки;
модифицируют исходный программный код, при этом помещают в него дополнительные метки начала и конца время затратных циклических участков и применяемых средств распараллеливания на языке программирования;
под каждый цикл формируют и сохраняют таблицу средств распараллеливания с обозначенными границами итерационного диапазона и номером средства распараллеливания с минимальным временем выполнения;
распараллеленную программу с подключенными средствами распараллеливания и таблицу соответствия предпочтительных средств распараллеливания для каждого цикла с определенным числом итераций передают в память устройства назначения;
в процессе функционирования управляют устройством назначения, которое обеспечивает выбор средства распараллеливания, используя модуль мгновенного выбора средства распараллеливания, находящийся в памяти устройства назначения, который для текущего цикла по номеру цикла и числу итераций цикла в таблице предпочтительных средств распараллеливания определяет номер оптимального средства распараллеливания и подключает клон с примененным средством распараллеливания.
2. Способ по п. 1, отличающийся тем, что после компиляции модифицированного кода выполняют многократный тестовый прогон скомпилированной модифицированной программы в главной системе, формируют и сохраняют массив первичной статистики времени выполнения циклических участков каждым клоном под управлением добавленного средства распараллеливания.
3. Способ по п. 1, отличающийся тем, что количество клонов одного цикла равно количеству применяемых средств распараллеливания для выбора оптимального.
4. Способ по п. 1, отличающийся тем, что массив первичной статистики хранится в виде таблицы, где строка характеризует один профиль с параметрами: номер цикла, количество итераций цикла, номер средства распараллеливания, время выполнения цикла.
5. Способ по п. 1, отличающийся тем, что границы итерационного диапазона содержат верхние и нижние границы.
6. Способ по п. 1, отличающийся тем, что модифицированная скомпилированная программа и таблица средств распараллеливания хранится в устройстве назначения.
7. Способ по п. 1, отличающийся тем, что выбор средства распараллеливания для каждого цикла определяется по минимальному времени выполнения из таблицы средств распараллеливания, а его подключение осуществляется при попадании входных данных о количестве итераций текущего цикла программы в границы итерационного интервала таблицы средств распараллеливания.
8. Способ по п. 2, отличающийся тем, что для пополнения массива первичной статистики по завершению работы штатной программы в устройстве назначения организована передача профиля вновь собранной статистики в массив первичной статистики.
| Устройство для закрепления лыж на раме мотоциклов и велосипедов взамен переднего колеса | 1924 |
|
SU2015A1 |
| Токарный резец | 1924 |
|
SU2016A1 |
| Способ защиты переносных электрических установок от опасностей, связанных с заземлением одной из фаз | 1924 |
|
SU2014A1 |
| СПОСОБ АВТОМАТИЧЕСКОГО РАСПАРАЛЛЕЛИВАНИЯ ПРОГРАММ | 2009 |
|
RU2411569C2 |
Авторы
Даты
2022-05-11—Публикация
2021-03-04—Подача