Область техники, к которой относится изобретение
Изобретение относится к вычислительной технике и может быть использовано для повышения эффективности средств электронной вычислительной техники (таких характеристик как производительность, надежность, объем памяти и др.).
Уровень техники
а) Описание аналогов
Известно, что для построения псевдослучайной последовательности длины n=2r-1 необходим примитивный многочлен V(z) степени r. Для примера рассмотрим многочлен

где r=4.
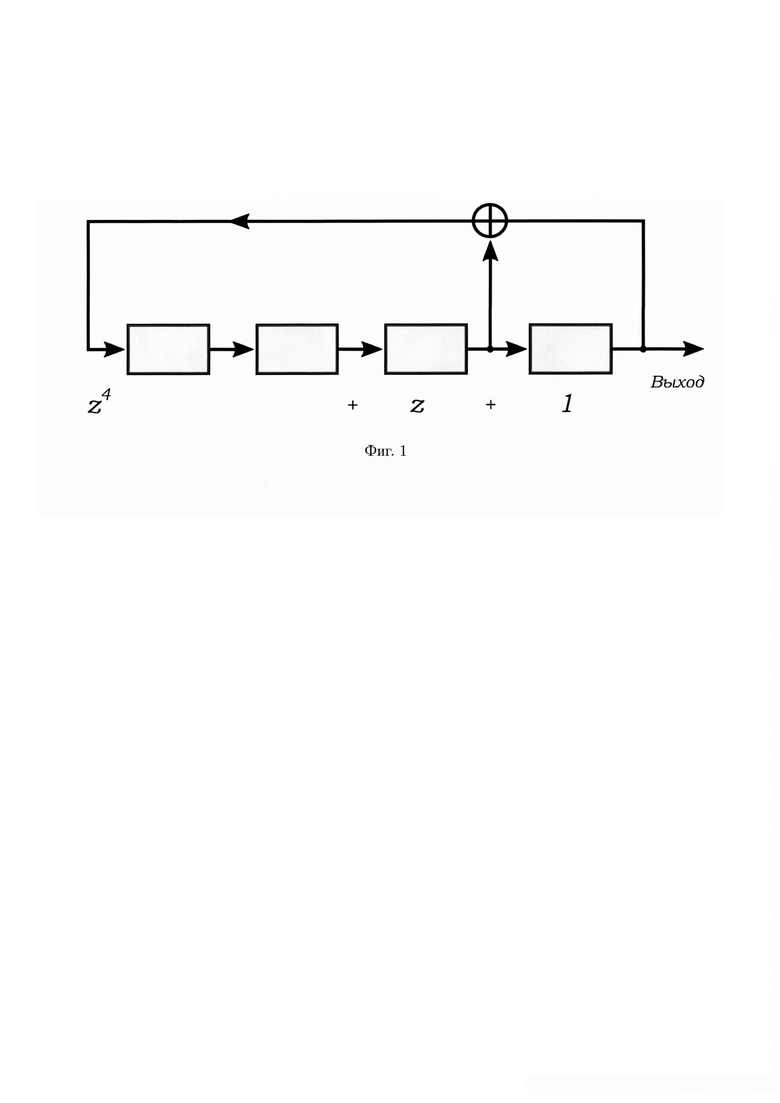
Многочлену (1) соответствует регистр сдвига с обратной связью [MacWilliams F., Sloane N. Pseudo-random sequences and arrays, Proc. IEEE, 64, pp. 1715-1729, 1976; Lidl R., Niederreiter H. Introduction to finite fields and their applications, Cambridge: Cambridge Univ. Press, 1987], представленный на фигуре 1.
Регистр сдвига состоит из r ячеек (запоминающих элементов, триггеров), каждая из которых в процессе работы устройства может содержать 0 или 1. В момент времени t (момент времени определяется некоторой тактовой частотой) содержимое всех ячеек сдвигается на одну ячейку (перемещается на один разряд) вправо. Здесь содержимое ячеек, соответствующих членам многочлена V(z), суммируется и поступает в крайнюю левую ячейку. Сумма вычисляется но модулю 2 и реализуется сумматором по модулю 2, (логическим элементом «ИСКЛЮЧАЮЩЕЕ ИЛИ»), выход которого определен условиями
0+0=1+1=0,
0+1=1+0=1.
В качестве примера рассмотрим регистр сдвига с обратной связью (фиг. 1), который в момент времени t содержит числа
at+3, at+2, at+1, at,
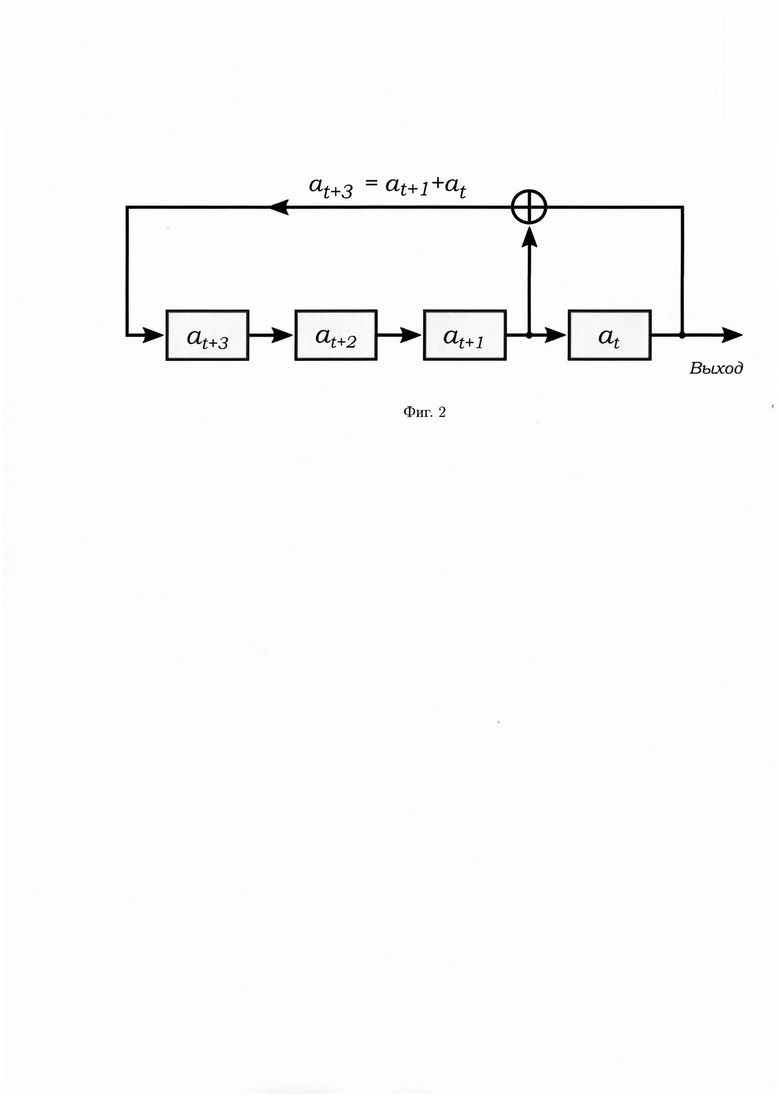
соответственно в момент времени t+1 в нем будут находиться числа (фиг. 2)
at+4=at+1+at, at+3, at+2, at+1.
Таким образом, регистр сдвига с обратной связью генерирует бесконечную последовательность а0, а1, а2, …, at, …, удовлетворяющую рекурсивному соотношению
at+4=at+1+at,
где t=0, 1, …; знак «+» - сложение по модулю 2. Для запуска процесса функционирования регистра сдвига с обратной связью необходимо задать начальное заполнение a0, a1, а2, …, ar-1.
б) Описание ближайшего аналога (прототипа)
Наиболее близким по своей технической сущности к заявленному техническому решению и принятым за прототип является устройство, описанное в [М.А. Ivanov, B.V. Kliuchnikova, Е.А. Salikov, A.V. Starikovskii. New class of non-binary pseudorandom number generators. - Proceedings of Intelligent Technologies in Robotics, Moscow, Russia, 2019, p. 255-262; Патент РФ №2740339, опубл. 13.01.2021].
Рассматриваемое устройство получения псевдослучайных последовательностей (генератор псевдослучайных чисел, функционирующий в конечном поле GF(q), где q - простое число), состоящий из r регистров разрядности 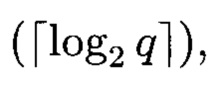 r-1 блоков сложения в GF(p), r блоков умножения в GF(p), причем величина, на которую происходит умножение в (i+1)-м блоке умножения, равна коэффициенту pi ∈ GF(q), характеристического многочлена
r-1 блоков сложения в GF(p), r блоков умножения в GF(p), причем величина, на которую происходит умножение в (i+1)-м блоке умножения, равна коэффициенту pi ∈ GF(q), характеристического многочлена
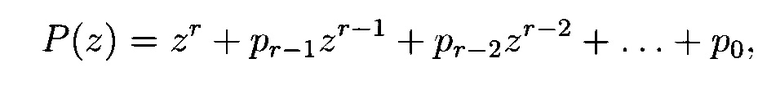
где i=0, 1, 2, …, r-1, P(z) - многочлен степени r, примитивный над GF(p), в котором выходы r-го регистра соединены со входами всех блоков умножения, выходы j-x блоков умножения соединены с первыми входами j-x блоков сложения, выходы которых соединены со входами j-x регистров, где j=1, 2, …, r, вторые входы всех блоков сложения образуют r групп управляющих входов генератора, выходы k-х регистров соединены с третьими входами (k+1)-х блоков сложения, выходы которых соединены со входами (j+1)-х регистров, где k=1, 2, …, r.
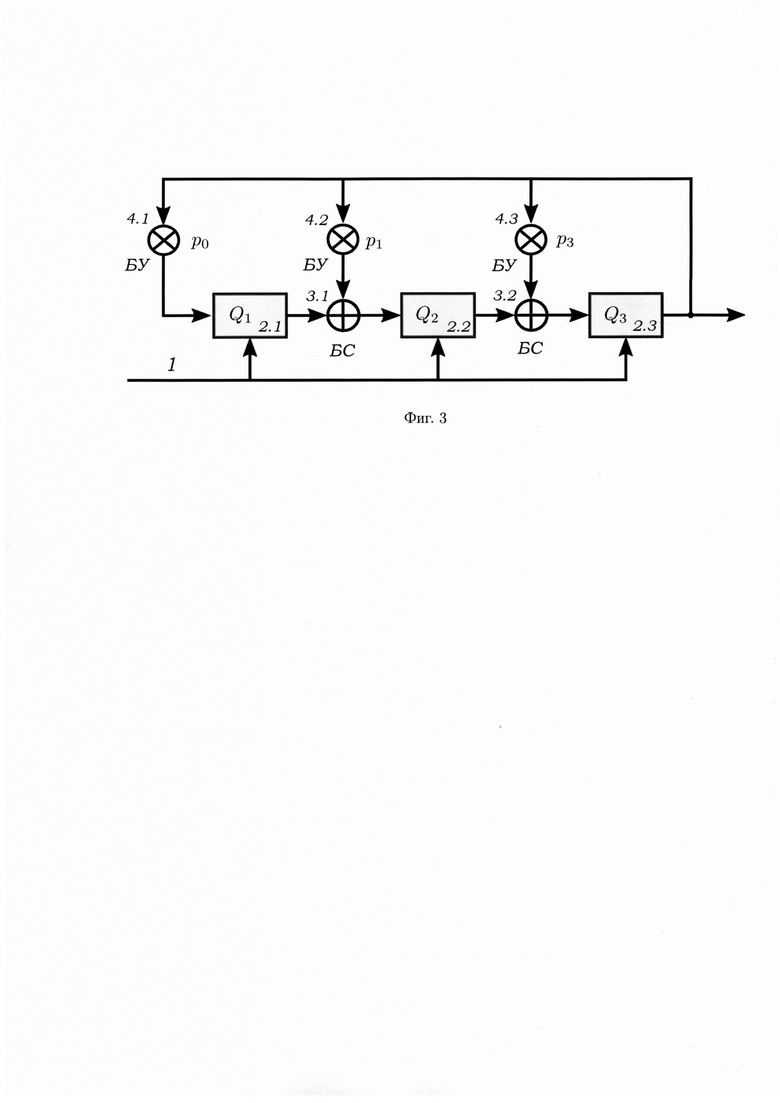
Структурная схема устройства-прототипа представлена на фиг. 3 для случая r=3,
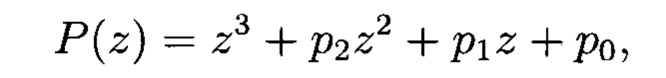
где pi ∈ GF(q), здесь 1 - тактовый вход генератора, 2.1, 2.2, 2.3 - 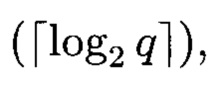 - разрядные регистры, 3.1 и 3.2 - блоки сложения в поле GF(q), 4.1, 4.2, и 4.3 - блоки умножения на р0, p1, и р2 в поле GF(q).
- разрядные регистры, 3.1 и 3.2 - блоки сложения в поле GF(q), 4.1, 4.2, и 4.3 - блоки умножения на р0, p1, и р2 в поле GF(q).
Недостаток известного устройства - отсутствие возможности реализации вычислений, при которых осуществляется формирование псевдослучайных комплексных чисел.
Раскрытие изобретения
а) Технический результат, на достижение которого направлено изобретение
Целью заявляемого технического решения является реализация процесса вычисления псевдослучайных комплексных чисел.
б) Совокупность существенных признаков
Технический результат изобретения достигается тем, что:
Поставленная цель достигается тем, что в устройство формирования псевдослучайных комплексных чисел, состоящее из r регистров разрядности 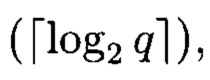 r-1 блоков сложения в GF(q), r блоков умножения в GF(q), причем величина, на которую происходит умножение в (i+1)-м блоке умножения, равна коэффициенту pi ∈ GF(q), характеристического многочлена
r-1 блоков сложения в GF(q), r блоков умножения в GF(q), причем величина, на которую происходит умножение в (i+1)-м блоке умножения, равна коэффициенту pi ∈ GF(q), характеристического многочлена
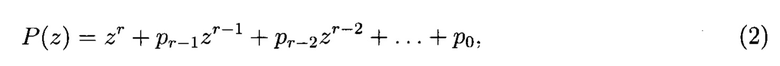
где r=0, 1, 2, …, r-1, P(z) - многочлен степени r, примитивный над GF(q), в котором выходы r-го регистра соединены со входами всех блоков умножения, выходы j-x блоков умножения соединены с первыми входами j-x блоков сложения, выходы которых соединены со входами j-x регистров, где j=1, 2, …, r, вторые входы всех блоков сложения образуют г групп управляющих входов генератора, выходы k-х регистров соединены с третьими входами (k+1)-х блоков сложения, выходы которых соединены со входами (j+1)-х регистров, где k=1, 2, … r, введены генератор псевдослучайных чисел, функционирующий в конечном поле GF(q), где q - простое число), состоящий из r регистров разрядности 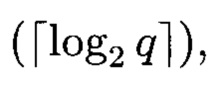 r-1 блоков сложения в GF(q), r блоков умножения в GF(q), причем величина, на которую происходит умножение в (i+1)-м блоке умножения, равна коэффициенту pi ∈ GF(q), характеристического многочлена
r-1 блоков сложения в GF(q), r блоков умножения в GF(q), причем величина, на которую происходит умножение в (i+1)-м блоке умножения, равна коэффициенту pi ∈ GF(q), характеристического многочлена
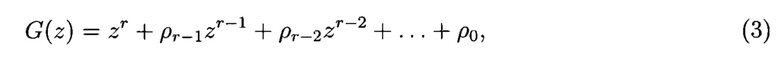
где i=0, 1, 2, …, r-1, G(z) - многочлен степени r, примитивный над GF(q), в котором выходы r-го регистра соединены со входами всех блоков умножения, выходы j-x блоков умножения соединены с первыми входами j-x блоков сложения, выходы которых соединены со входами j-x регистров, где j=1, 2, …, r, вторые входы всех блоков сложения образуют г групп управляющих входов генератора, выходы k-х регистров соединены с третьими входами (k+1)-х блоков сложения, выходы которых соединены со входами (j+1)-х регистров, где k=1, 2, …, r; блок формирования псевдослучайных комплексных чисел, содержащий блок умножения на мнимую единицу «i», блок сложения; выходы первого и второго генератора псевдослучайных чисел подключены соответственно к первому и второму входам блока формирования псевдослучайных комплексных чисел, первый вход которого является первым входом блока сложения, второй вход которого является выходом блока умножения на мнимую единицу «г», причем вход блока умножения на мнимую единицу «i» является вторым входом блока формирования псевдослучайных комплексных чисел; выход блока сложения является выходом блока формирования псевдослучайных комплексных чисел, выдающего значения 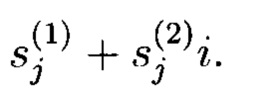
в) Причинно-следственная связь между признаками и техническим результатом
Благодаря введению в известный объект совокупности существенных отличительных признаков, в устройство формирования псевдослучайных комплексных чисел позволяет реализовать алгоритм формирования псевдослучайных комплекснозначных чисел для реализации перспективных высокопроизводительных вычислительных средств.
Доказательства соответствия заявленного изобретения условиям патентноспособности «новизна» и «изобретательский уровень»
Проведенный анализ уровня техники позволил установить, что аналоги, характеризующие совокупности признаков, тождественных всем признакам заявленного технического решения, отсутствуют, что указывает на соответствие заявленного способа условию патентноспособности «новизна».
Результаты поиска известных решений в данной и смежных областях техники с целью выявления признаков, совпадающих с отличительными от прототипа признаками заявленного объекта показали, что они не следуют явными из уровня техники. Из уровня техники также не выявлена известность отличительных существенных признаков, обуславливающих тот же технический результат, который достигнут в заявленном способе. Следовательно, заявленное изобретение соответствует уровню патентоспособности «изобретательский уровень».
Краткое описание чертежей
Заявленное устройство поясняется чертежами, на которых показано:
- на фиг. 1 - структурная схема регистра сдвига с обратной связью, соответствующего многочлену (1);
- на фиг. 2 - структурная схема регистра сдвига с обратной связью, определяющего рекурсивное соотношение;
- на фиг. 3 - структурная схема устройства прототипа;
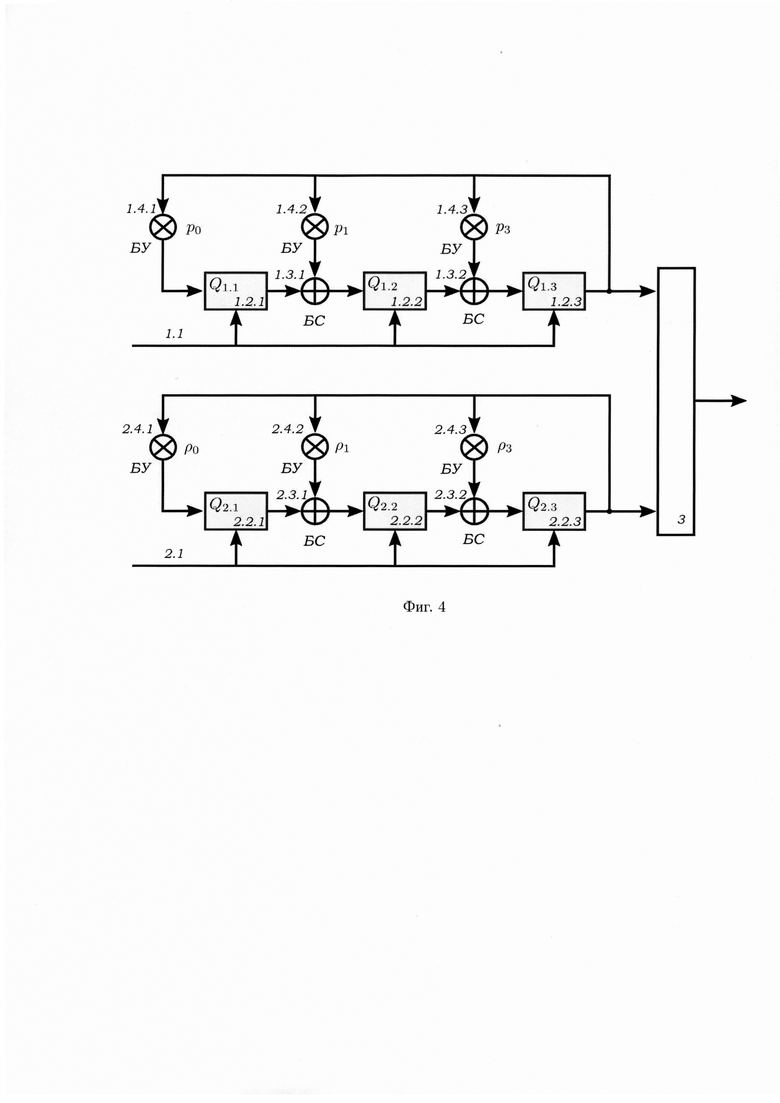
- на фиг. 4 - структурная схема предлагаемого устройства для случая r=3;
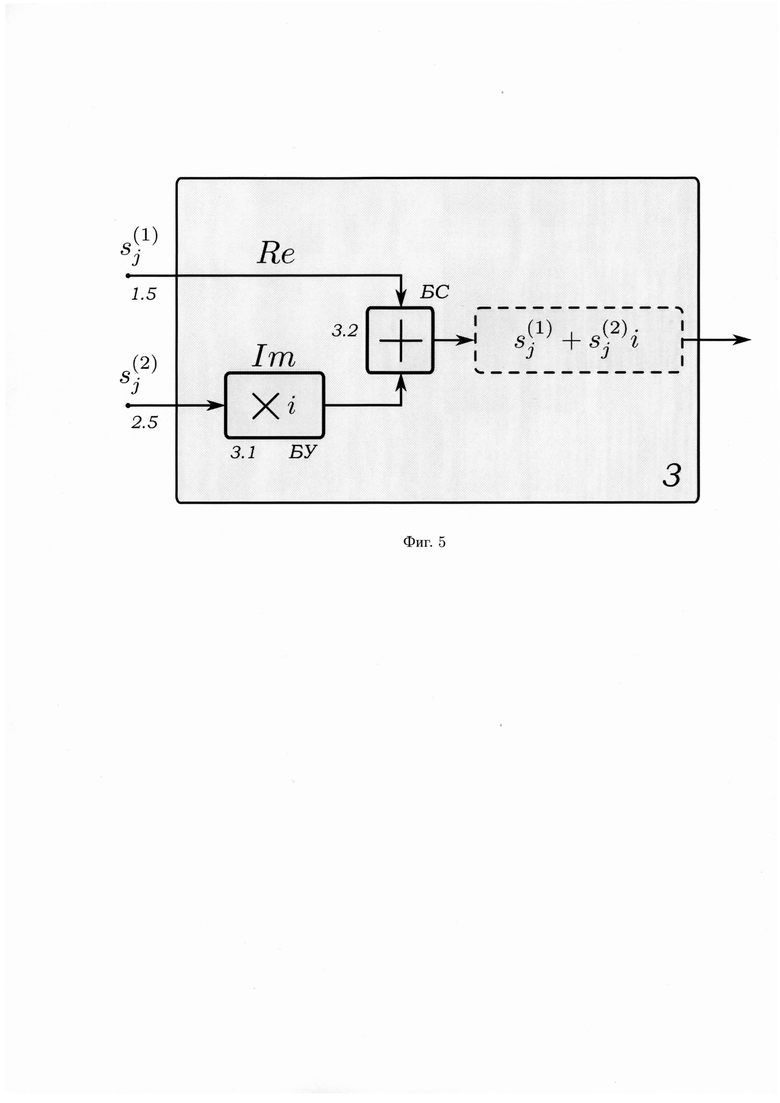
- на фиг. 5 - схема блока формирования псевдослучайных комплексного числа.
Осуществление изобретения
Предлагаемое устройство содержит первый генератор псевдослучайных чисел над GF(q) (регистра сдвига с обратной связью, g-РРС), второй генератор псевдослучайных чисел над GF(q), а также блок формирования псевдослучайных комплексных чисел.
Первый g-РРС построен на основе примитивного, неприводимого (характеристического) многочлена (2), где pi ∈ GF(q), и включает 1.1 - тактовый вход генератора, 1.2.1, 1.2.2, …, 1.2.r -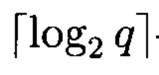 - разрядные регистры, 1.3.1, 1.3.2, …, 1.3.r-1 - блоки сложения в поле GF(q), 1.4.1, 1.4.2, …, 1.4.r - соответственно блоки умножения на р0, p1, …, pr-1 в поле GF(q); второй g-РРС построен на основе примитивного, неприводимого (характеристического) многочлена (3), где ρi ∈ GF(q), и включает 2.1 - тактовый вход генератора, 2.2.1, 2.2.2, …, 2.2.r-
- разрядные регистры, 1.3.1, 1.3.2, …, 1.3.r-1 - блоки сложения в поле GF(q), 1.4.1, 1.4.2, …, 1.4.r - соответственно блоки умножения на р0, p1, …, pr-1 в поле GF(q); второй g-РРС построен на основе примитивного, неприводимого (характеристического) многочлена (3), где ρi ∈ GF(q), и включает 2.1 - тактовый вход генератора, 2.2.1, 2.2.2, …, 2.2.r-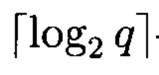 -разрядные регистры, 2.3.1, 2.3.2, …, 2.3.r-1 - блоки сложения в поле GF(q), 2.4.1, 2.4.2, …, 2.4.r - соответственно блоки умножения на ρ0, ρ1, …, ρr-1 в поле GF(q), 3 - блок формирования псевдослучайных комплексных чисел (фиг. 5), содержащий блок 3.1 умножения на мнимую единицу «i», блок 3.2 сложения, причем выходы первого и второго q-РРС подключены соответственно к первому и второму входам блока 3 формирования псевдослучайных комплексных чисел, первый вход которого является первым входом блока 3.2 сложения, второй вход которого является выходом блока 3.1 умножения на мнимую единицу «i», причем вход блока 3.1 умножения на мнимую единицу «i» является вторым входом блока 3 формирования псевдослучайных комплексных чисел; выход блока 3.2 сложения является выходом блока 3 формирования псевдослучайных комплексных чисел
-разрядные регистры, 2.3.1, 2.3.2, …, 2.3.r-1 - блоки сложения в поле GF(q), 2.4.1, 2.4.2, …, 2.4.r - соответственно блоки умножения на ρ0, ρ1, …, ρr-1 в поле GF(q), 3 - блок формирования псевдослучайных комплексных чисел (фиг. 5), содержащий блок 3.1 умножения на мнимую единицу «i», блок 3.2 сложения, причем выходы первого и второго q-РРС подключены соответственно к первому и второму входам блока 3 формирования псевдослучайных комплексных чисел, первый вход которого является первым входом блока 3.2 сложения, второй вход которого является выходом блока 3.1 умножения на мнимую единицу «i», причем вход блока 3.1 умножения на мнимую единицу «i» является вторым входом блока 3 формирования псевдослучайных комплексных чисел; выход блока 3.2 сложения является выходом блока 3 формирования псевдослучайных комплексных чисел
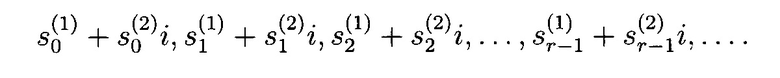
Рассмотрим алгоритм работы устройства.
Построение первого q-РРС осуществляется по заданному примитивному, неприводимому (характеристическому) многочлену (2), и построенному в соответствии с ним однородному рекуррентному уравнению:
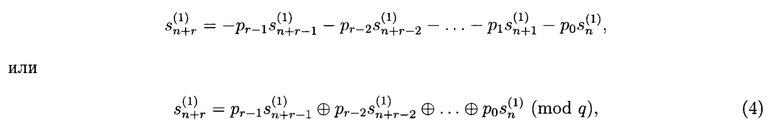
где n=0, 1, 2, …; pj ∈ GF(q), 0≤j≤r-1; ⊕ - символ сложения по mod q.
В общем случае после первого такта работы первый q-РРС содержит заполнение: 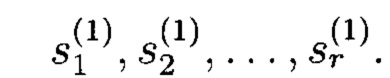 В целом первый q-РРС генерирует бесконечную выходную q-значную последовательность
В целом первый q-РРС генерирует бесконечную выходную q-значную последовательность 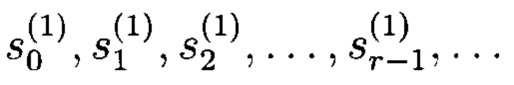 с периодом qr-1 (при ненулевом исходном состоянии), причем каждое ненулевое состояние появляется один раз за период. Сформированный сегмент выходной последовательности длины qr-1 является псевдослучайной последовательностью (ПСП) над GF(q).
с периодом qr-1 (при ненулевом исходном состоянии), причем каждое ненулевое состояние появляется один раз за период. Сформированный сегмент выходной последовательности длины qr-1 является псевдослучайной последовательностью (ПСП) над GF(q).
В терминах линейной алгебры очередной элемент ПСП 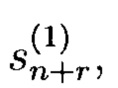 получаемый с помощью (4) вычисляется в соответствии с выражением:
получаемый с помощью (4) вычисляется в соответствии с выражением:
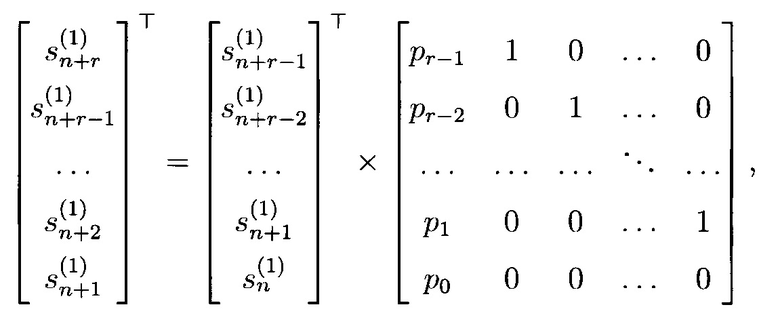
где Т - символ транспонирования.
Построение второго g-РРС осуществляется также по заданному примитивному, неприводимому (характеристическому) многочлену (3), и построенному в соответствии с ним однородному рекуррентному уравнению:
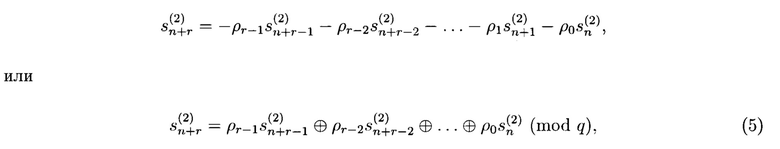
где n=0, 1, 2, …; ρj ∈ GF(q), 0≤j≤r-1; ⊕ - символ сложения по mod q.
После первого такта работы второй g-РРС содержит заполнение: 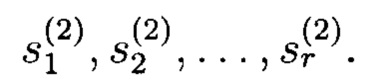 При этом второй q-РРС генерирует бесконечную выходную q-значную последовательность
При этом второй q-РРС генерирует бесконечную выходную q-значную последовательность 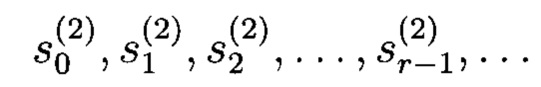 с периодом qr-1 (при ненулевом исходном состоянии), причем каждое ненулевое состояние появляется один раз за период. Сформированный сегмент выходной последовательности длины qr-1 является псевдослучайной последовательностью (ПСП) над GF(q).
с периодом qr-1 (при ненулевом исходном состоянии), причем каждое ненулевое состояние появляется один раз за период. Сформированный сегмент выходной последовательности длины qr-1 является псевдослучайной последовательностью (ПСП) над GF(q).
В терминах линейной алгебры очередной элемент ПСП 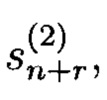 получаемый с помощью (5) также может быть получен в соответствии с выражением:
получаемый с помощью (5) также может быть получен в соответствии с выражением:
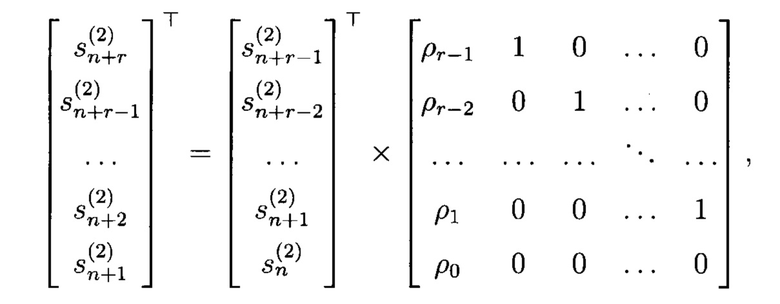
где Т - символ транспонирования.
Последовательность 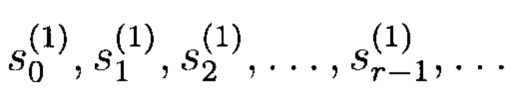 с выхода первого q-PPC поступают на первый вход блока 3 формирования псевдослучайных комплексных чисел (фиг. 5), в частности на первый вход блока 3.2 сложения. Первый вход блока 3.2 сложения соответствует действительной части (Re) комплексного числа. Последовательность
с выхода первого q-PPC поступают на первый вход блока 3 формирования псевдослучайных комплексных чисел (фиг. 5), в частности на первый вход блока 3.2 сложения. Первый вход блока 3.2 сложения соответствует действительной части (Re) комплексного числа. Последовательность 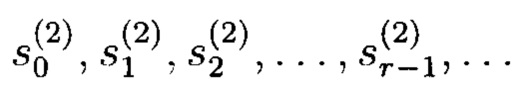 с выхода второго q-РРС поступает на второй вход блока 3 формирования псевдослучайных комплексных чисел, в частности на вход блока 3.1 умножения на мнимую единицу «г». С выхода блока 3.1 умножения на мнимую единицу «i» последовательность
с выхода второго q-РРС поступает на второй вход блока 3 формирования псевдослучайных комплексных чисел, в частности на вход блока 3.1 умножения на мнимую единицу «г». С выхода блока 3.1 умножения на мнимую единицу «i» последовательность 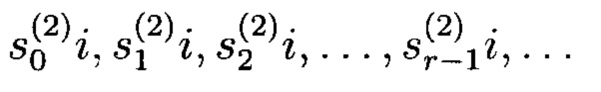 поступает на второй вход блока 3.2 сложения. Второй вход блока 3.2 сложения соответствует мнимой части (Im) комплексного числа. В блоке 3.2 сложения осуществляется окончательное формирование псевдослучайных комплексных чисел
поступает на второй вход блока 3.2 сложения. Второй вход блока 3.2 сложения соответствует мнимой части (Im) комплексного числа. В блоке 3.2 сложения осуществляется окончательное формирование псевдослучайных комплексных чисел
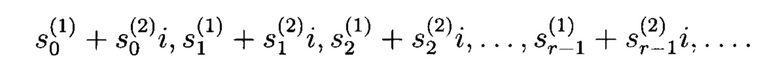
В процессе формирования комплексных чисел 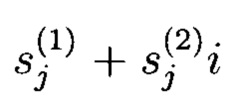 в блоке сложения 3.2 могут формироваться действительные числа, когда с выхода блока 3.1 умножения на мнимую единицу «i» в блок 3.2 сложения поступают действительные числа, то есть
в блоке сложения 3.2 могут формироваться действительные числа, когда с выхода блока 3.1 умножения на мнимую единицу «i» в блок 3.2 сложения поступают действительные числа, то есть 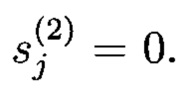 При этом числа вида
При этом числа вида 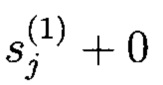 из вычислительного процесса удаляются.
из вычислительного процесса удаляются.
На фиг. 4 показана схема предлагаемого устройства для случая r=3, первый q-PPC построен на основе 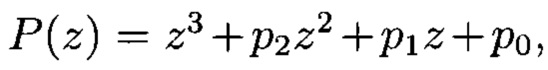 где pi ∈ GF(q), и включает 1.1 - тактовый вход генератора, 1.2.1, 1.2.2 и 1.2.3 -
где pi ∈ GF(q), и включает 1.1 - тактовый вход генератора, 1.2.1, 1.2.2 и 1.2.3 -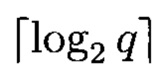 -разрядные регистры, 1.3.1 и 1.3.2 - блоки сложения в поле GF(q), 1.4.1, 1.4.2 и 1.4.3 - соответственно блоки умножения на р0, р1 и р2 в поле GF(q); второй g-РРС построен на основе
-разрядные регистры, 1.3.1 и 1.3.2 - блоки сложения в поле GF(q), 1.4.1, 1.4.2 и 1.4.3 - соответственно блоки умножения на р0, р1 и р2 в поле GF(q); второй g-РРС построен на основе 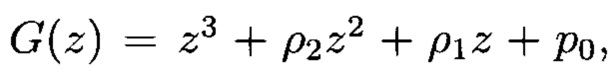 где ρi ∈ GF(q), и включает 2.1 - тактовый вход генератора, 2.2.1, 2.2.2 и 2.2.3 -
где ρi ∈ GF(q), и включает 2.1 - тактовый вход генератора, 2.2.1, 2.2.2 и 2.2.3 -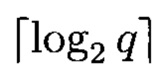 -разрядные регистры, 2.3.1 и 2.3.2 - блоки сложения в поле GF(q), 2.4.1, 2.4.2 и 2.4.3 - соответственно блоки умножения на ρ0, ρ1, и ρ2 в поле GF(q), 3 - блок формирования псевдослучайных комплексных чисел, содержащий блок 3.1 умножения на мнимую единицу «i», блок 3.2 сложения, причем выходы первого и второго q-РРС подключены соответственно к первому и второму входам блока 3 формирования псевдослучайных комплексных чисел, первый вход которого является первым входом блока 3.2 сложения, второй вход которого является выходом блока 3.1 умножения на мнимую единицу «i», причем вход блока 3.1 умножения на мнимую единицу «i» является вторым входом блока 3 формирования псевдослучайных комплексных чисел; выход блока 3.2 сложения является выходом блока 3 формирования псевдослучайных комплексных чисел
-разрядные регистры, 2.3.1 и 2.3.2 - блоки сложения в поле GF(q), 2.4.1, 2.4.2 и 2.4.3 - соответственно блоки умножения на ρ0, ρ1, и ρ2 в поле GF(q), 3 - блок формирования псевдослучайных комплексных чисел, содержащий блок 3.1 умножения на мнимую единицу «i», блок 3.2 сложения, причем выходы первого и второго q-РРС подключены соответственно к первому и второму входам блока 3 формирования псевдослучайных комплексных чисел, первый вход которого является первым входом блока 3.2 сложения, второй вход которого является выходом блока 3.1 умножения на мнимую единицу «i», причем вход блока 3.1 умножения на мнимую единицу «i» является вторым входом блока 3 формирования псевдослучайных комплексных чисел; выход блока 3.2 сложения является выходом блока 3 формирования псевдослучайных комплексных чисел
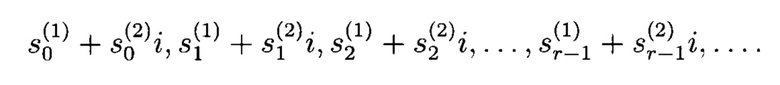
Заявленное изобретение может быть осуществлено с помощью средств и методов, описанных в доступных источниках информации. Это позволяет сделать вывод о соответствии заявленного изобретения признакам «промышленной применимости».
Пример. Рассмотрим генератор псевдослучайных комплексных чисел. Пусть задан первый q=3 РРС, генерирующий 3-значную ПСП максимальной длины над полем GF(33). Генератор построен по примитивному многочлену
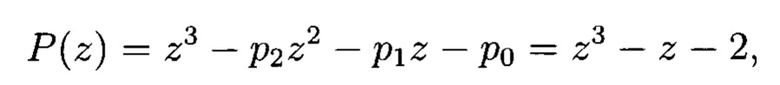
которому соответствует реккурентное уравнение следующего вида:
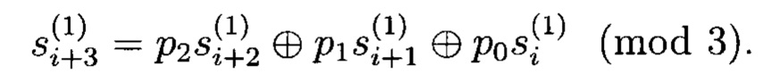
Учитывая, что р2=0, р1=1, р0=2 получим
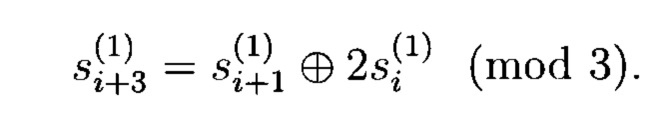
Если в качестве исходных данных регистра (начального заполнения) записать: 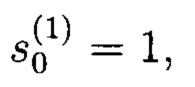
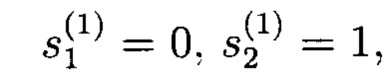 то на выходе генератора будет иметь место следующая ПСП:
то на выходе генератора будет иметь место следующая ПСП:
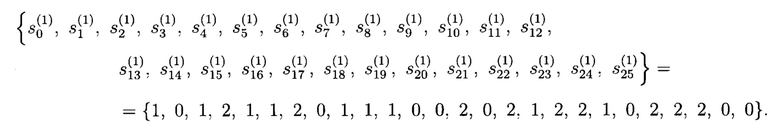
Получаемые элементы ПСП 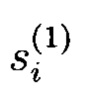 поступают на первый вход блока 3 формирования псевдослучайных комплексных чисел, в частности на первый вход блока 3.2 сложения.
поступают на первый вход блока 3 формирования псевдослучайных комплексных чисел, в частности на первый вход блока 3.2 сложения.
Пусть задан второй q=5 РРС, генерирующий 5-значную ПСП макисмальной длины над полем GF(52). Генератор построен по примитивному многочлену
G(z)=z2-ρ1z-ρ0=z2-4z-3,
которому соответствует реккурентное уравнение следующего вида:
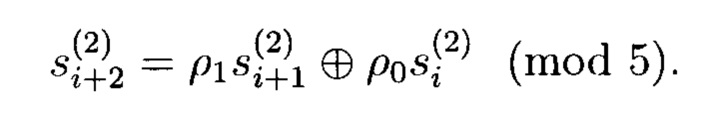
Учитывая, что ρ1=4, ρ0=3 получим
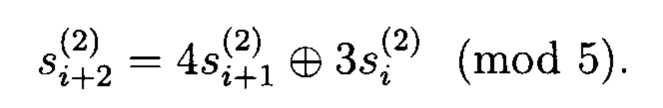
Если в качестве исходных данных регистра (начального заполнения) записать: 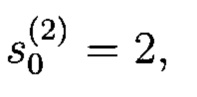
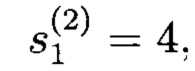 то на выходе генератора будет иметь место следующая ПСП:
то на выходе генератора будет иметь место следующая ПСП: 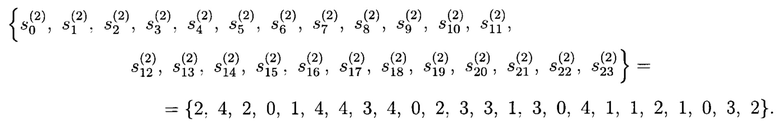
Далее, вычисленные элементы ПСП 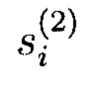 поступают на второй вход блока 3 формирования псевдослучайных комплексных чисел, в частности на вход блока 3.1 умножения на мнимую единицу «ш», в котором формируются следующие элементы псевдослучайных комплексного числа
поступают на второй вход блока 3 формирования псевдослучайных комплексных чисел, в частности на вход блока 3.1 умножения на мнимую единицу «ш», в котором формируются следующие элементы псевдослучайных комплексного числа
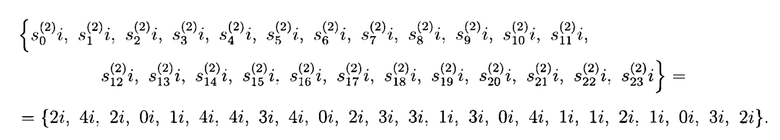
Затем с выхода блока 3.1 умножения на мнимую единицу «ш» элементы поступают на второй вход блока 3.2 сложения, в котором осуществляется окончательное формирование последовательности псевдослучайных комплексных чисел (указанная последовательность):
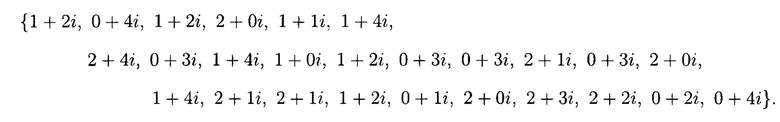
При этом в процессе формирования комплексных чисел, получаемые действительные числа удаляются

Приведенный пример показал, что заявляемое устройство формирования псевдослучайных комплексных чисел функционирует корректно, технически реализуемо и позволяет решить поставленную задачу.
| название | год | авторы | номер документа |
|---|---|---|---|
| УСТРОЙСТВО ФОРМИРОВАНИЯ ТРИПЛЕКСНЫХ ЧИСЕЛ | 2023 |
|
RU2812412C1 |
| ГЕНЕРАТОР ПСЕВДОСЛУЧАЙНЫХ ЧИСЕЛ | 2021 |
|
RU2776346C1 |
| ГЕНЕРАТОР ПСЕВДОСЛУЧАЙНЫХ ЧИСЕЛ | 2023 |
|
RU2815485C1 |
| ГЕНЕРАТОР ПСЕВДОСЛУЧАЙНЫХ ЧИСЕЛ | 2020 |
|
RU2740339C1 |
| УСТРОЙСТВО ДЛЯ ГЕНЕРАЦИИ ПСЕВДОСЛУЧАЙНЫХ ЧИСЕЛ | 2020 |
|
RU2761766C1 |
| ГЕНЕРАТОР ПСЕВДОСЛУЧАЙНЫХ ЧИСЕЛ | 2020 |
|
RU2756833C1 |
| УСТРОЙСТВО ПАРАЛЛЕЛЬНОГО ФОРМИРОВАНИЯ q-ЗНАЧНЫХ ПСЕВДОСЛУЧАЙНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ НА АРИФМЕТИЧЕСКИХ ПОЛИНОМАХ | 2021 |
|
RU2762209C1 |
| Генератор псевдослучайных последовательностей | 1986 |
|
SU1406738A1 |
| Счетчик | 1986 |
|
SU1422403A1 |
| УСТРОЙСТВО ДЛЯ ГЕНЕРАЦИИ ПСЕВДОСЛУЧАЙНОЙ ПОСЛЕДОВАТЕЛЬНОСТИ ДВОИЧНЫХ ЧИСЕЛ С ИСПОЛЬЗОВАНИЕМ ЭЛЛИПТИЧЕСКИХ КРИВЫХ | 2005 |
|
RU2294559C1 |
Настоящее техническое решение относится к области вычислительной техники. Технический результат заключается в повышении производительности вычислительного процесса за счёт реализации вычислений для формирования псевдослучайных комплексных чисел. Технический результат достигается за счёт того, что для формирования псевдослучайных комплексных чисел дополнительно введены генератор псевдослучайных чисел, функционирующий в конечном поле GF(q), состоящий из r регистров разрядности 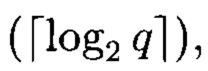 r-1 блоков сложения в GF(q), r блоков умножения в GF(q); блок формирования псевдослучайных комплексного числа, содержащий блок умножения на мнимую единицу «i», блок сложения; выходы первого и второго генератора псевдослучайных чисел подключены соответственно к первому и второму входам блока формирования псевдослучайных комплексных чисел, первый вход которого является первым входом блока сложения, второй вход которого является выходом блока умножения на мнимую единицу «i», причем вход блока умножения на мнимую единицу «i» является вторым входом блока формирования псевдослучайных комплексного числа; выход блока сложения является выходом блока формирования псевдослучайных комплексных чисел. 5 ил.
r-1 блоков сложения в GF(q), r блоков умножения в GF(q); блок формирования псевдослучайных комплексного числа, содержащий блок умножения на мнимую единицу «i», блок сложения; выходы первого и второго генератора псевдослучайных чисел подключены соответственно к первому и второму входам блока формирования псевдослучайных комплексных чисел, первый вход которого является первым входом блока сложения, второй вход которого является выходом блока умножения на мнимую единицу «i», причем вход блока умножения на мнимую единицу «i» является вторым входом блока формирования псевдослучайных комплексного числа; выход блока сложения является выходом блока формирования псевдослучайных комплексных чисел. 5 ил.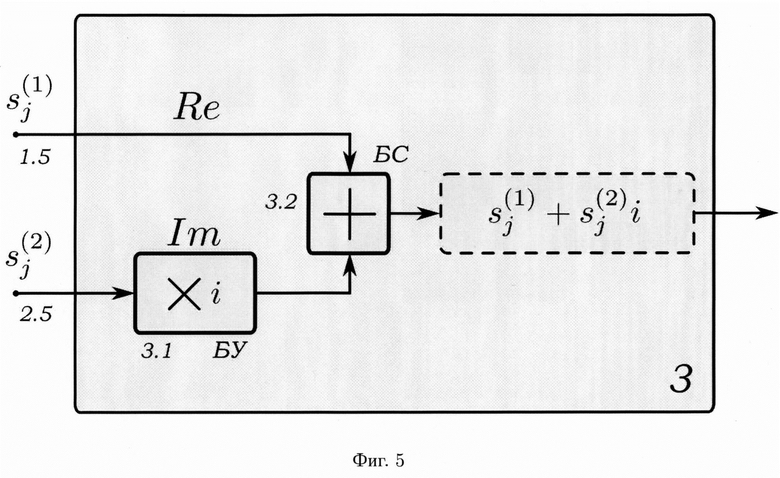
Устройство формирования псевдослучайных комплексных чисел, состоящее из r регистров разрядности 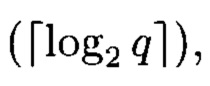 r-1 блоков сложения в GF(q), r блоков умножения в GF(q), причем величина, на которую происходит умножение в (i+1)-м блоке умножения, равна коэффициенту pi ∈ GF(q), характеристического многочлена
r-1 блоков сложения в GF(q), r блоков умножения в GF(q), причем величина, на которую происходит умножение в (i+1)-м блоке умножения, равна коэффициенту pi ∈ GF(q), характеристического многочлена
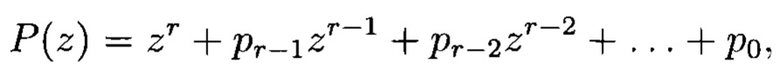
где i=0, 1, 2, …, r-1, P(z) - многочлен степени r, примитивный над GF(q), в котором выходы r-го регистра соединены со входами всех блоков умножения, выходы j-x блоков умножения соединены с первыми входами j-x блоков сложения, выходы которых соединены со входами j-x регистров, где j=1, 2, …, r, вторые входы всех блоков сложения образуют r группы управляющих входов генератора, выходы k-х регистров соединены с третьими входами (k+1)-х блоков сложения, выходы которых соединены со входами (j+1)-х регистров, где k=1, 2, …, r, отличающееся тем, что введены генератор псевдослучайных чисел, функционирующий в конечном поле GF(q), где q - простое число, состоящий из r регистров разрядности 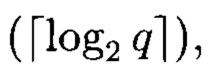 r-1 блоков сложения в GF(q), r блоков умножения в GF(q), причем величина, на которую происходит умножение в (i+1)-м блоке умножения, равна коэффициенту pi ∈ GF(q), характеристического многочлена
r-1 блоков сложения в GF(q), r блоков умножения в GF(q), причем величина, на которую происходит умножение в (i+1)-м блоке умножения, равна коэффициенту pi ∈ GF(q), характеристического многочлена
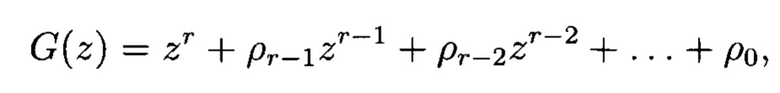
где i=0, 1, 2, …, r-1, G(z) - многочлен степени r, примитивный над GF(q), в котором выходы r-го регистра соединены со входами всех блоков умножения, выходы j-x блоков умножения соединены с первыми входами j-x блоков сложения, выходы которых соединены со входами j-x регистров, где j=1, 2, …, r, вторые входы всех блоков сложения образуют r группы управляющих входов генератора, выходы k-х регистров соединены с третьими входами (k+1)-х блоков сложения, выходы которых соединены со входами (j+1)-х регистров, где k=1, 2, …, r; блок формирования псевдослучайных комплексных чисел, содержащий блок умножения на мнимую единицу «i», блок сложения; выходы первого и второго генератора псевдослучайных чисел подключены соответственно к первому и второму входам блока формирования псевдослучайных комплексных чисел, первый вход которого является первым входом блока сложения, второй вход которого является выходом блока умножения на мнимую единицу «i», причем вход блока умножения на мнимую единицу «i» является вторым входом блока формирования псевдослучайных комплексных чисел; выход блока сложения является выходом блока формирования псевдослучайных комплексных чисел, выдающего значение 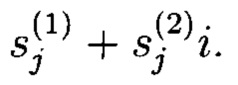
| ГЕНЕРАТОР ПСЕВДОСЛУЧАЙНЫХ ЧИСЕЛ | 2020 |
|
RU2740339C1 |
| УСТРОЙСТВО ДЛЯ ГЕНЕРАЦИИ ПСЕВДОСЛУЧАЙНЫХ ЧИСЕЛ | 2021 |
|
RU2774812C1 |
| US 7170997 B2, 30.01.2007 | |||
| СПОСОБ ИЗГОТОВЛЕНИЯ КЕРАМИЧЕСКОГО КИРПИЧА | 1995 |
|
RU2101257C1 |
| CN 111078191 A, 28.04.2020 | |||
| US 6275586 B1, 14.08.2001. | |||
Авторы
Даты
2023-07-19—Публикация
2022-10-10—Подача