Изобретение относится к области картографии и может быть использовано для повышения точности и детальности построения цифровой модели поверхности по данным космической стереосъемки.
Построение цифровой модели поверхности (ЦМП) по данным космической стереосъемки является одной из актуальнейших задач анализа данных дистанционного зондирования Земли, поскольку позволяет извлекать из снимков высотную информацию, представляющую собой ценный источник информации для различных прикладных задач. Однако стереобработка космических изображений сопряжена с рядом фундаментальных трудностей, таких как: высокая изменчивость поля яркости, вызванная атмосферными и иными явлениями; малый размер объектов интереса, сопоставимый с геометрическими искажениями, вызванными разницей углов съемки; сложная траектория движения космического аппарата и специфический способ получения снимков; существенный объем данных для обработки.
Точность ЦМП определяется точностью определения высот объектов местности (высот рельефа и относительных высот зданий и сооружений) и точностью положения объектов в плане. Детальность ЦМП определяется наличием относительно небольших по площади (порядка десятков кв. метров) и по высоте (порядка единиц метров) объектов, выступающих на фоне рельефа или на фоне плоскостей более крупных объектов. Точность и детальность ЦМП может быть измерена путем сравнения с эталонной моделью поверхности, построенной по результатам воздушного лазерного сканирования и имеющей более высокую (сантиметровую) точность в плане и по высоте.
Важнейшим вопросом при создании способа построения ЦМП является выбор алгоритма стереосопоставления. В подавляющем большинстве современных способов и пакетов программ авторы используют алгоритм [1] Semi-Global Matching (SGM). Данный алгоритм совмещает в себе высокую вычислительную эффективность с не менее высоким качеством построенной карты глубины. Однако, эта эффективность достигается на стереопарах сантиметровой точности, получаемых при аэросъемке, которые обладают более детализированной и предсказуемой структурой по сравнению с космическими стереопарами. В то же время точность и детальность работы данного алгоритма на космических стереопарах, получаемых, например, системой Pleiades [2], имеющих пространственное разрешение порядка 0.5 м, недостаточны. Альтернативой данному методу является метод разрезов графа GraphCut (GC) [3], который благодаря своей глобальной структуре лучше подходит для космических снимков. Однако, он не обладает той же чувствительностью к малым изменениям глубины, то есть к микрорельефу, что и алгоритм SGM.
Описание алгоритмов GC и SGM нахождения сдвигов между соответственными точками эпиполярно выравненных изображений приведено в Приложениях 1 и 2 соответственно.
Прототипом предлагаемого способа построения ЦМП является работа [4], в которой предлагается способ построения ЦМП, а также приводятся результаты сравнения качества полученной ЦМП для различных алгоритмов стереосопоставления.
Представленная в прототипе последовательность операций состоит из следующих шагов.
1. Загрузка входных данных, состоящих из панхроматического снимка с разрешением не менее 1 м и 4-х канального мультиспектрального изображения, включающего красный, зеленый, синий и инфракрасный каналы яркости, с разрешением не менее 2 м, а также RPC коэффициентов математического преобразования координат точек (пикселей) космического изображения на точки местности и обратно.
2. Предварительная обработка исходных данных, включающая выбор соответственных точек для коррекции RPC-коэффициентов и повышение пространственного разрешения мультиспектральных изображений до разрешения панхроматического.
3. Эпиполярное выравнивание изображений стереопары, обеспечивающее размещение соответственных точек в одноименных строках выравненных изображений.
4. Нахождение матрицы D сдвигов пар соответственных точек на стереоснимках через сопоставление стереоизображений поверхности (решение задачи стереосопоставления). Матрица сдвигов D соответственных точек состоит из элементов D(p), каждый из которых представляет собой расстояние в пикселях между точкой р первого изображения, и точкой р+D(p) второго изображения стереопары, причем, поскольку предварительно выполняется эпиполярное выравнивание, то смещение возможно только вдоль строки.
5. Построение цифровой модели рельефа и нормализованной ЦМП.
6. Создание ортотрансформированного изображения.
7. Классификация областей растительности, а также строений и сооружений
8. Извлечение и моделирование отдельных объектов (зданий и сооружений).
Недостатком данного способа при формировании ЦМП по космическим снимкам является недостаточно высокая точность и детальность, достигаемая используемыми алгоритмами.
Целью изобретения является создание способа построения более точной и высоко детальной ЦМП по данным космической стереосъемки.
Для достижения поставленной цели повышения точности и детальности ЦМП, в отличие от прототипа, предлагается:
- учитывать априорно известную цифровую модель рельефа (ЦМР) с разрешением не ниже 150 метров на пиксель;
- выполнять построение ЦМП по стереоснимкам, в которых априорно исключены из рассмотрения области, маскируемые облаками, а также водные поверхности;
- выполнять сегментацию панхроматических изображений и учитывать ее при стереосопоставлении снимков таким образом, чтобы избежать значительных скачков высоты внутри сегментов;
- находить матрицу 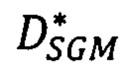 сдвигов пар соответственных точек на стереоснимках (задача стереосопоставления) за счет модификации алгоритмов GC и SGM и их комбинирования.
сдвигов пар соответственных точек на стереоснимках (задача стереосопоставления) за счет модификации алгоритмов GC и SGM и их комбинирования.
Модификация алгоритма GC состоит в определении для каждой точки первого и второго изображения вектор-признака DAISY(p) (дескриптора DAISY [5]) и замене в выражении для энергетической функций EGC(DCC), приведенной в приложении 1, меры близости EGC_data(DGC) на
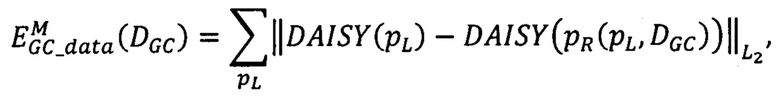
где DGC - матрица сдвигов соответственных точек на стереоснимках, формируемая алгоритмом GC,
||а||L2 - норма вектора а в пространстве L2;
pL - точки первого снимка стереопары,
pR(pL,DGC) - точки второго снимка стереопары, соответствующие точкам pL и находящиеся с ними в одной строке.
Модификация алгоритма SGM состоит в замене обоих слагаемых в приведенной в приложении 2 энергетической функции 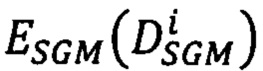 : первого - меры близости
: первого - меры близости 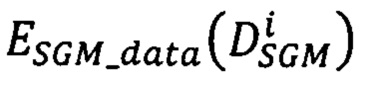 точек pR второго изображения к точкам pL первого изображения на
точек pR второго изображения к точкам pL первого изображения на 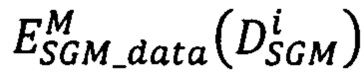 , и второго слагаемого
, и второго слагаемого 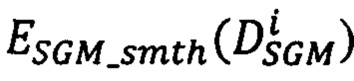 , представляющего собой штраф за несовпадение сдвига
, представляющего собой штраф за несовпадение сдвига 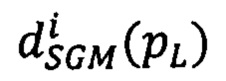 в точке pL и сдвигов в соседних точках q, находящихся в окрестности точки pL фиксированного радиуса, на модификацию
в точке pL и сдвигов в соседних точках q, находящихся в окрестности точки pL фиксированного радиуса, на модификацию 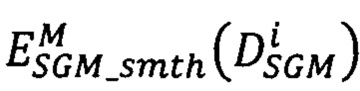 . Модифицированная энергетическая функция имеет вид
. Модифицированная энергетическая функция имеет вид
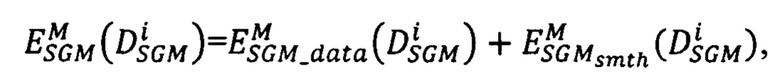
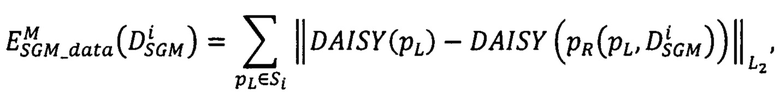
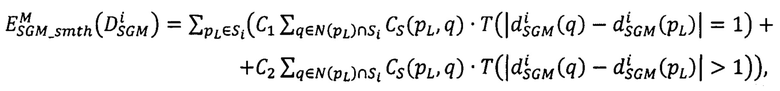
где 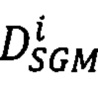 - вектор сдвигов
- вектор сдвигов 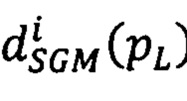 точек второго изображения pR относительно точек pL первого, находящихся на луче Si, направленном в точку р первого изображения, для которой ищется сдвиг,
точек второго изображения pR относительно точек pL первого, находящихся на луче Si, направленном в точку р первого изображения, для которой ищется сдвиг,
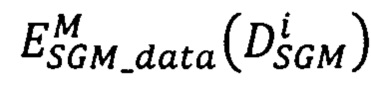 - модифицированная мера близости точек pR второго изображения относительно точек pL первого изображения, находящихся на луче Si, направленном в точку р первого изображения,
- модифицированная мера близости точек pR второго изображения относительно точек pL первого изображения, находящихся на луче Si, направленном в точку р первого изображения,
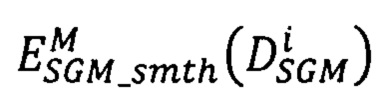 - суммарный штраф, модифицированный за счет введения штрафных коэффициентов CS(pL,q) за несовпадение сдвигов в точках pL, расположенных на луче Si, и сдвигов в соседних с pL точках q из окрестности фиксированного радиуса,
- суммарный штраф, модифицированный за счет введения штрафных коэффициентов CS(pL,q) за несовпадение сдвигов в точках pL, расположенных на луче Si, и сдвигов в соседних с pL точках q из окрестности фиксированного радиуса,
CS(pL, q) - коэффициент сегментации, который равен 1, если яркости точек pL и q в сегментированном изображении не равны, и 3 - в противном случае,
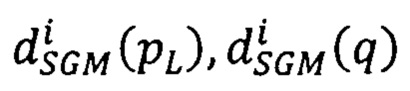 - сдвиги точек второго изображения, соответствующих точкам pL и q из первого изображения, находящихся на луче Si,
- сдвиги точек второго изображения, соответствующих точкам pL и q из первого изображения, находящихся на луче Si,
pL ∈ Si - точки первого изображения, расположенные на луче Si,
С1 и С2 - штрафы за несовпадение сдвигов в соседних точках,
q ∈ N(pL)∈Si - множество точек, расположенных на луче Si, из окрестности фиксированного радиуса с центром в точке pL,
Т(⋅) - функция, которая возвращает 1, если условие в скобках верно, и ноль в противном случае.
Комбинирование модифицированных алгоритмов заключается в том, что по матрице 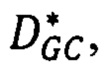 которая доставляет минимум функции
которая доставляет минимум функции 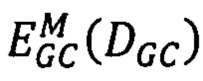 , находят грубые оценки сдвигов соответственных точек второго изображения относительно точек первого. Далее локально в точке р и входящих в нее лучей Si в интервалах сдвигов, которые определяются сдвигами
, находят грубые оценки сдвигов соответственных точек второго изображения относительно точек первого. Далее локально в точке р и входящих в нее лучей Si в интервалах сдвигов, которые определяются сдвигами 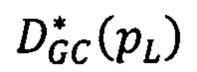 (где pL ∈ Si, записанными в матрице
(где pL ∈ Si, записанными в матрице 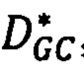 , по минимумам энергетических функций
, по минимумам энергетических функций 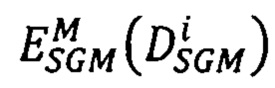 для всех лучей Si находят в точке р первого изображения точную оценку сдвига
для всех лучей Si находят в точке р первого изображения точную оценку сдвига 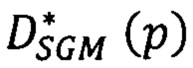 соответственной ей точки второго изображения.
соответственной ей точки второго изображения.
Более подробно сущность предлагаемого способа поясняется дальнейшим описанием и чертежами:
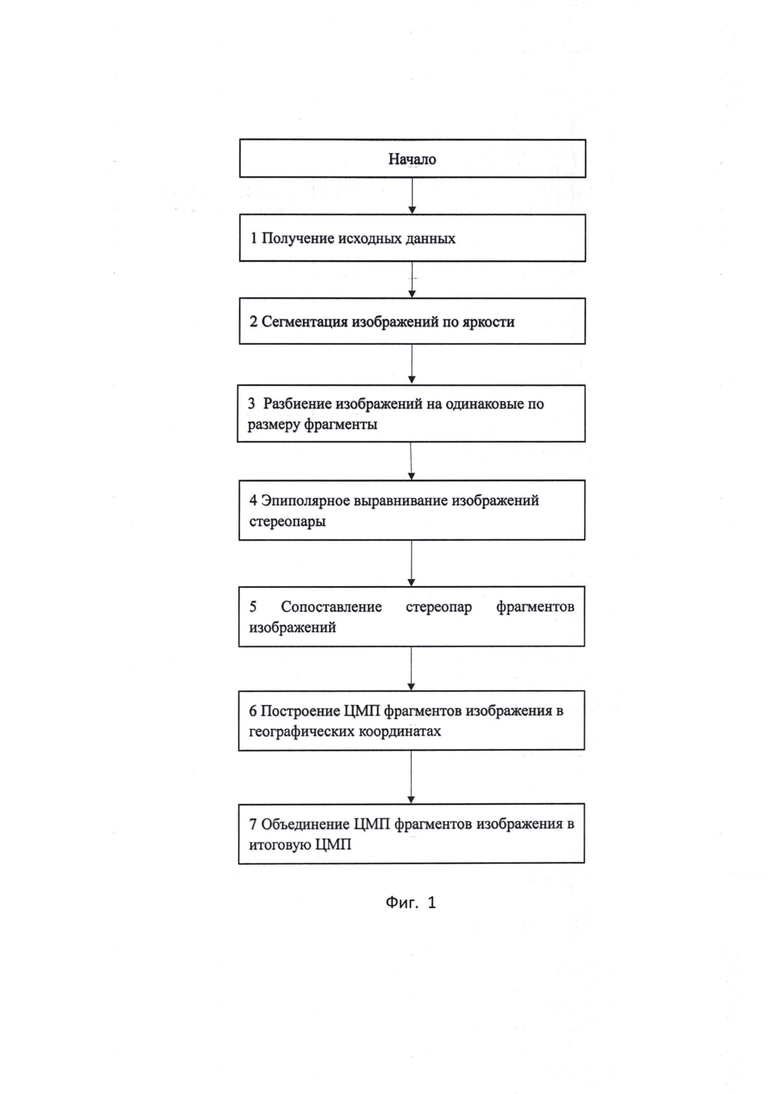
на фиг. 1 представлен предлагаемый алгоритм построения ЦМП по данным космической стереосъемки;
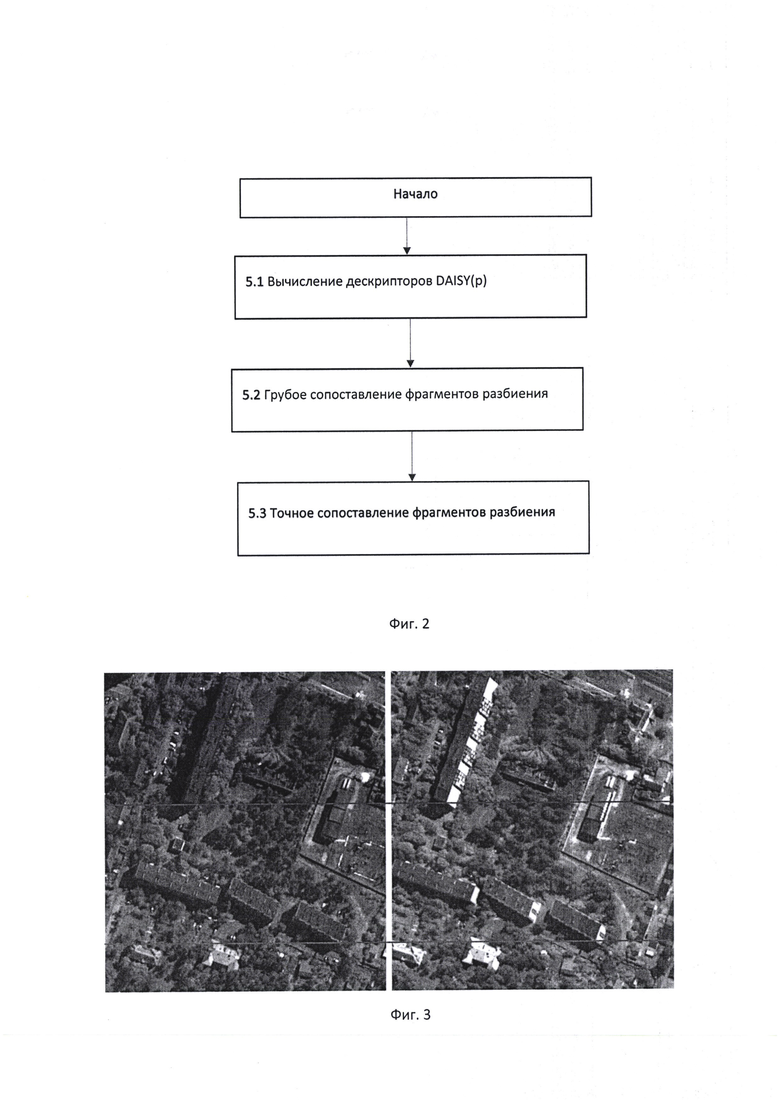
на фиг. 2 представлен предлагаемый алгоритм стереосопоставления фрагментов изображений стереопары;
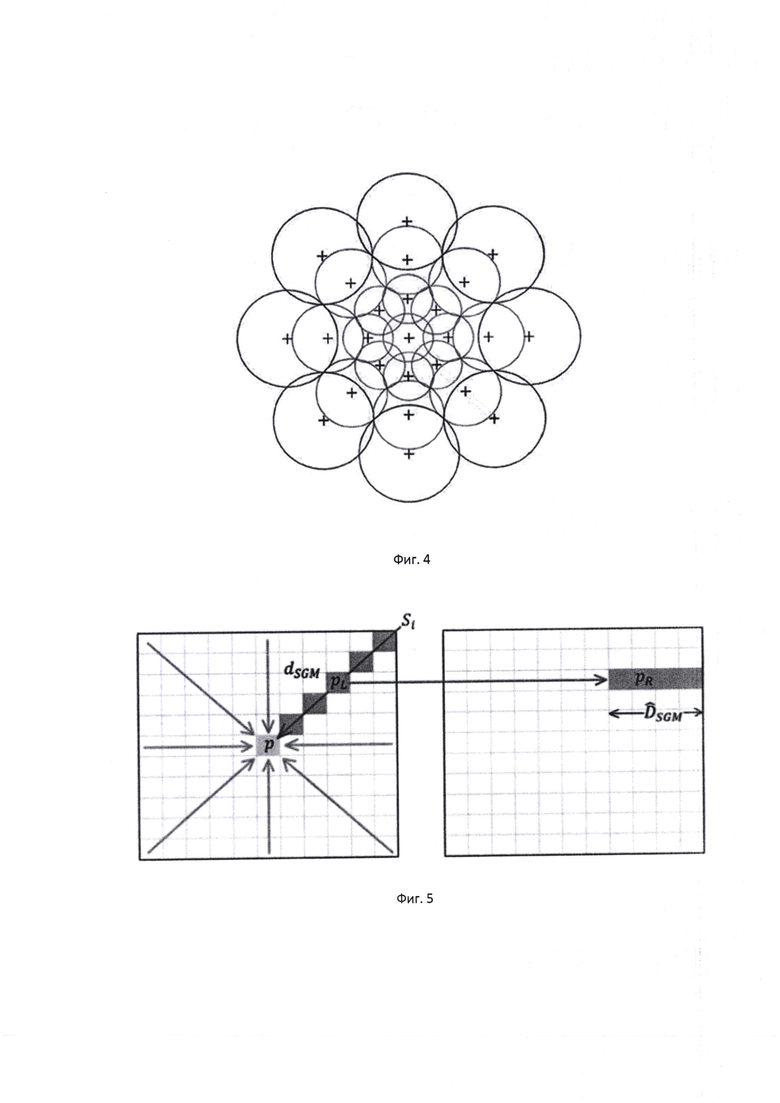
на фиг. 3 представлен пример эпиполярно выравненных фрагментов стереоснимков;
на фиг. 4 представлена схема расположения ключевых точек для вычисления дескриптора DAISY;
на фиг. 5 представлена геометрическая связь точки pL на луче Si с точками pR в зоне поиска сдвига точки соответствия 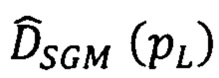 ;
;
на фиг. 6 представлены для сравнения два ЦМП: первое изображение, полученное предлагаемым способом по данным космической стереосъемки, второе изображение (эталонное ЦМП) по данным лазерной аэросъемки.
Предлагаемый способ построения ЦМП по данным космической стереосъемки в соответствии со схемой фиг. 1 и фиг. 2 производится в последовательности:
1. Получение входных данных (поз. 1 фиг. 1), включающих:
- пары стереоснимков местности в панхроматическом диапазоне с исключенными пикселями, соответствующими местоположению облаков и водной поверхности;
- априорно известную ЦМР с разрешением не ниже 150 метров на пиксель;
- RPC-коэффициенты математического преобразования координат точек (пикселей) космического изображения на точки местности и обратно;
2. Сегментацию изображений стереопары (поз. 2 фиг. 1) по яркости методом анизотропной медианной фильтрации для удаления шума и мелких выбросов яркости, включающую:
- выпуск из каждой точки изображения 16 лучей длиною 7 пикселей,
- вычисление дисперсии яркости вдоль каждого луча,
- вычисление медианы яркости точек вдоль луча с наименьшей дисперсией,
- присвоение точке панхроматического изображения найденное значение медианы,
3. Разбиение стереоснимков на одинаковые по размеру меньшие фрагменты (поз. 3 фиг. 1);
4. Эпиполярное выравнивание фрагментов изображений стереопары в панхроматическом диапазоне через повороты изображений относительно центров снимков так, чтобы смещения, вызванные сменой ракурса при получении стереопары, лежали вдоль одной строки (поз. 4 фиг 1). Пример эпиполярного выравнивания приведен на фиг. 3, горизонтальные линии вдоль снимков соответствуют строкам выровненных изображений;
5. Выполнение процедуры стереосопоставления (поз. 5 фиг. 1), в результате которой получают матрицу сдвигов соответственных точек. Процедура стереосопоставления включает в себя следующие этапы.
5.1 Вычисление дескриптора DAISY (р) для каждой точки р изображений стереопары (поз. 5.1 фиг. 2) по алгоритму:
- вокруг точки р панхроматического изображения строят набор из трех концентрических окружностей радиусами 3, 6 и 9 пикселей;
- на каждой из этих окружностей выбирают по 8 точек, равномерно распределенных вдоль окружности, геометрия размещения точек приведена на фиг. 4;
- в исходной точке р, а также в 8 точках окружности радиусом 3 пикселя выполняют свертку с гауссовым ядром модулей градиентов яркости по 8 направлениям, радиус гауссового ядра 2 пикселя;
- в каждой из 8 точек окружности радиусом 6 пикселей выполняют свертку с гауссовым ядром модулей градиентов яркости по 8 направлениям, радиус гауссового ядра 3 пикселя;
- в каждой из 8 точек окружности радиусом 9 пикселей выполняют свертку с гауссовым ядром модулей градиентов яркости по 8 направлениям, радиус гауссового ядра 4 пикселя;
- объединяют полученные значения в вектор размерности 200 (25 точек по 8 направлений градиента в каждой);
- нормализуют полученный вектор, который считают вектором-признаком (дескриптором) DAISY (р) точки р изображения.
5.2 Выполнение первого этапа стереосопоставления с помощью модифицированного алгоритма GC (поз. 5.2 фиг. 2) в последовательности:
- определяют диапазон поиска 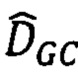 сдвигов точек соответствия по цифровой матрице рельефа (ЦМР) как интервал
сдвигов точек соответствия по цифровой матрице рельефа (ЦМР) как интервал
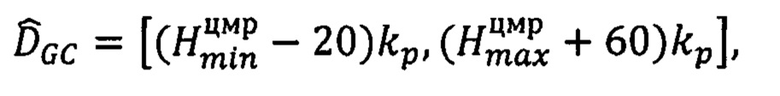
где kp - коэффициент перевода 1 м высоты местности в пиксели смещения на стереопаре, вычисляемый индивидуально для каждого фрагмента по RPC-коэффициентам снимков,
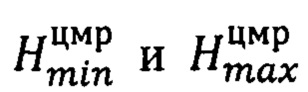 - минимальная и максимальная высота рассматриваемой местности по ЦМР в пределах фрагмента;
- минимальная и максимальная высота рассматриваемой местности по ЦМР в пределах фрагмента;
- находят методом оптимальную матрицу сдвигов 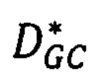 такую, что значение
такую, что значение 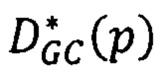 каждого элемента матрицы принадлежит интервалу
каждого элемента матрицы принадлежит интервалу 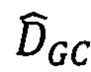 , то есть
, то есть 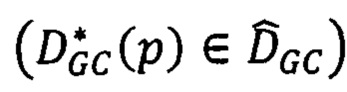 , и для которой достигается минимум модифицированной энергетической функции
, и для которой достигается минимум модифицированной энергетической функции 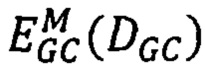 :
:
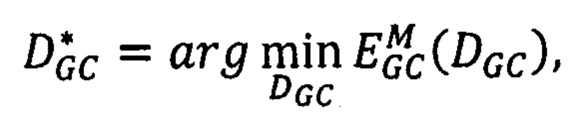
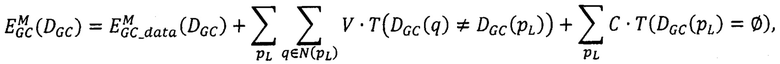
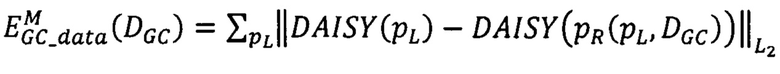
где 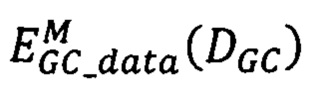 - мера близости точек pL первого изображения точкам pR второго изображения,
- мера близости точек pL первого изображения точкам pR второго изображения,
pL=(xL,yL) - точки первого снимка стереопары,
pR(pL,DGC)=(xR,yR)=(xL+DGC(pL),yL) - точка второго снимка стереопары, сдвиг которой относительно точки pL первого снимка равен DGC(pL) и находится в пределах интервала 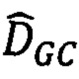 ,
,
DGC(pL) - сдвиг точки второго изображения относительно точки pL первого изображения, находящихся в одноименных строках изображений и в пределах интервала 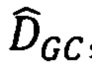 ,
,
N(pL)- множество точек в окрестности точки pL фиксированного радиуса,
V - весовой коэффициент штрафной функции,
Т(⋅) - функция, которая возвращает 1, если условие в скобках верно, и ноль в противном случае,
С - весовой коэффициент штрафной функции для условия DGC(pL)=∅ (∅ - пустое множество) означающего, что сдвиг точки pR относительно точки pL не определен.
5.3 Выполнение второго этапа стереосопоставления (точного сопоставления фрагментов разбиения) с помощью модифицированного алгоритма SGM (поз. 5.3 фиг. 2) в последовательности:
определяют диапазон поиска 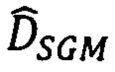 сдвигов для каждой точки снимка pL как интервал
сдвигов для каждой точки снимка pL как интервал
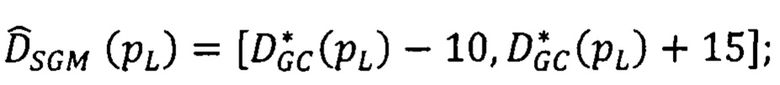
в точку р первого изображения от края изображения проводят 16 равномерно разнесенных по углу лучей (i=1…16). В дальнейшем тексте точки первого изображения, находящиеся на Si луче, обозначены pL. Расположение точек р и pL на луче Si показано на фиг. 5;
для i-того луча находят вектор 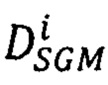 сдвигов
сдвигов 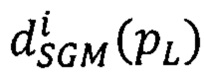 соответственных точек второго изображения, находящихся в одноименных с pL строках, (связь точек pL с зоной поиска
соответственных точек второго изображения, находящихся в одноименных с pL строках, (связь точек pL с зоной поиска 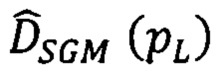 соответственной точки pR иллюстрирует фиг. 5) следующим образом:
соответственной точки pR иллюстрирует фиг. 5) следующим образом:
- рассматривают множество вариантов 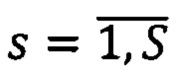 вектора сдвигов
вектора сдвигов 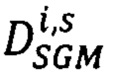 точек pRs второго изображения относительно точек pL ∈ Si первого изображения, координаты которого - последовательные значения
точек pRs второго изображения относительно точек pL ∈ Si первого изображения, координаты которого - последовательные значения 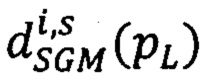 (из заранее заданного диапазона)
(из заранее заданного диапазона)
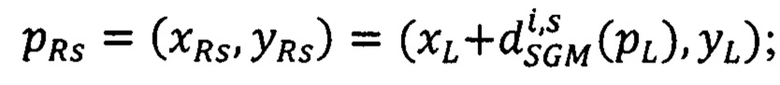
- для s-того варианта вектора сдвигов 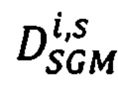 определяют значение энергетической функции
определяют значение энергетической функции 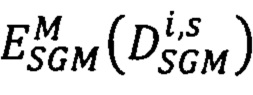 :
:
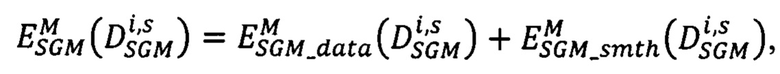
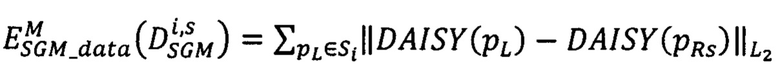
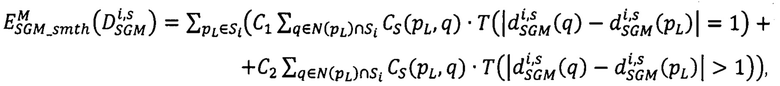
где 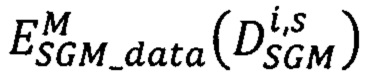 - мера близости всех точек pL первого изображения, расположенных на луче Si, к точкам pRs второго изображения, имеющих сдвиги
- мера близости всех точек pL первого изображения, расположенных на луче Si, к точкам pRs второго изображения, имеющих сдвиги 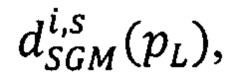
CS(pL,q) - коэффициент сегментации, который равен 1, если яркости точек pL и q в сегментированном изображении не равны, и 3 - в противном случае,
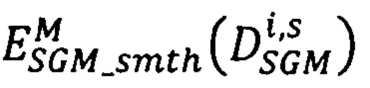 - модифицированный за счет введения коэффициентов CS(pL,q) суммарный штраф за несовпадение сдвигов в точках pL, расположенных на луче Si, и сдвигов в соседних с pL точках q ∈ Si из окрестности фиксированного радиуса,
- модифицированный за счет введения коэффициентов CS(pL,q) суммарный штраф за несовпадение сдвигов в точках pL, расположенных на луче Si, и сдвигов в соседних с pL точках q ∈ Si из окрестности фиксированного радиуса,
pL ∈ Si - точки первого изображения, расположенные на луче Si,
С1 и С2 - штрафы за несовпадение сдвигов в соседних точках,
q ∈ N(pL) - множество точек в окрестности фиксированного радиуса с центром в точке pL луча Si,
Т(⋅) - функция, которая возвращает 1, если условие в скобках верно, и ноль в противном случае;
- находят методом динамического программирования среди множества векторов 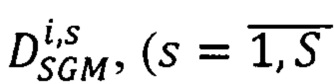 ) оптимальный вектор
) оптимальный вектор 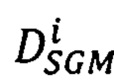 сдвигов соответственных точек второго изображения, для которого достигается минимум энергетической функции
сдвигов соответственных точек второго изображения, для которого достигается минимум энергетической функции 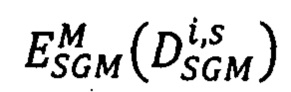
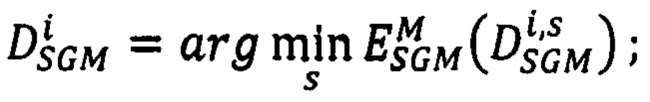
повторяют шаги определения вектора 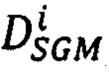 для каждого луча Si;
для каждого луча Si;
выбирают среди полученных 16-ти векторов-сдвигов 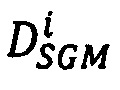 тот, для которого достигается наименьшее значение
тот, для которого достигается наименьшее значение 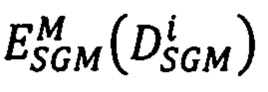
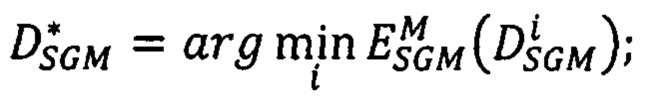
выбирают в векторе 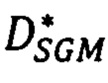 первую координату, отвечающую точке р первого изображения, значение сдвига, записанное в этой точке, является искомым точным значением сдвига
первую координату, отвечающую точке р первого изображения, значение сдвига, записанное в этой точке, является искомым точным значением сдвига 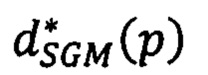 соответственной точки второго изображения;
соответственной точки второго изображения;
повторяют вычисление сдвига 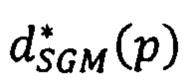 для всех точек р первого изображения и формируют для этого изображения результирующую матрицу сдвигов
для всех точек р первого изображения и формируют для этого изображения результирующую матрицу сдвигов 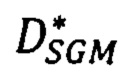 , в которой на месте яркости h(р) исходного изображения стоит значение
, в которой на месте яркости h(р) исходного изображения стоит значение 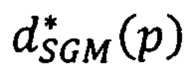
6. Построение ЦМП фрагментов изображения в географических координатах (поз. 6 фиг. 1) в последовательности:
вычисляют высоту местности в пикселе р по найденным сдвигам 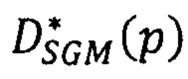 , базовой высоте
, базовой высоте 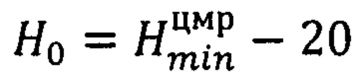 фрагмента и коэффициенту kp перевода метров высоты в пиксели изображения:
фрагмента и коэффициенту kp перевода метров высоты в пиксели изображения:
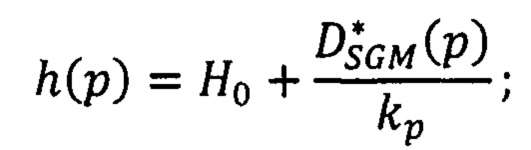
по матрице h(p) вычисляют географические координаты точек поверхности Н(Х, Y) с помощью RPC-коэффициентов для того, чтобы получить ЦМП, привязанную к местности.
7. Объединение ЦМП всех фрагментов разбиения Н(Х, Y) в итоговую ЦМП (поз. 7 фиг. 1) и выполнение медианной фильтрации полученной матрицы высот.
Для проверки работоспособности способа был проведен вычислительный эксперимент по построению цифровой модели местности по данным космической стереосъемки. Было выполнено сравнение качества ЦМП, построенной предлагаемым способом, с ЦМП прототипа, использующего сопоставление стереоснимков по алгоритму GC. Сравнение проводилось по значениям среднеквадратического отклонения оценок высоты ЦМП от эталонной ЦМП, построенной по данным воздушной лазерной съемки. Сравнение производилось по областям, не отмеченным в ходе предварительной классификации как водная поверхность и облачный или растительный покров. Полученное в прототипе среднеквадратичное значение ошибки (СКО) 3,74 м было улучшено до 2,93 м., что составляет уменьшение СКО ошибки на 21,6%. При этом для полученной ЦМП также были оценены точность по высоте (среднее абсолютное отклонение высот объектов ЦМП от высот объектов на эталоне), которая составила 1,81 м и точность в плане (отклонение границ объектов ЦМП - строений от границ этих же объектов на эталоне), которая составила 1,87 м.
На фиг. 6 показаны фрагменты матрицы высот рельефа, вычисленных предложенным методом, и соответствующие им результаты лидарной съемки. Визуальное сравнение показывает, что вычисленные матрицы высот рельефа качественно близки к результатам лидарной съемки.
Представленный способ построения ЦМП может найти свое применение для решения широкого круга задач, которые удобно разбить на три направления.
Первым важным направлением является формирование эталонных ЦМП по космическим стереоснимкам, необходимых для навигации беспилотных летательных аппаратов. Вне зависимости от типа задачи, данный способ обладает рядом важных преимуществ в сравнении с построением ЦМП по аэросъемке: более широкое покрытие; возможность получения данных на территории, где использование беспилотных летательных аппаратов невозможно; меньшая стоимость; высокая оперативность получения требуемой информации.
Второе направление связано с управлением территориями, картографией, контролем темпов строительства и обнаружения объектов незаконного строительства, корректировкой кадастровой и градостроительной документации, оценкой геоморфологических изменений.
Третье направление - природный и экологический мониторинг, инвентаризация сельскохозяйственных угодий, оценка динамики изменения площади лесных массивов, создание тематических природных карт.
Приложение 1
Алгоритм GC поиска матрицы сдвигов между соответственными точками эпиполярно выравненных стереоизображений
Задачу поиска матрицы сдвигов D между точками первого pL и второго pR эпиполярно выровненных стереоизображений решают через нахождение минимума «энергетической» функции EGC(⋅). Значения элементов матриц D для алгоритмов GC и SGM определяются по-разному, поэтому в дальнейшем тексте обозначаются DGC для алгоритма GC и DSGM для алгоритма SGM.
Энергетическая функция EGC(DGC) имеет вид:
EGC(DGC)=EGC_data(DGC)+EGC_smth(DGC),
где 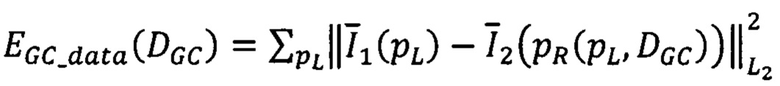 - мера близости точек pL первого изображения точкам pR второго изображения,
- мера близости точек pL первого изображения точкам pR второго изображения,
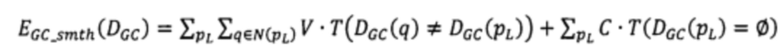 - суммарный штраф за несовпадение сдвигов в точках pL и сдвигов в соседних с pL точках q из окрестности фиксированного радиуса,
- суммарный штраф за несовпадение сдвигов в точках pL и сдвигов в соседних с pL точках q из окрестности фиксированного радиуса,
pL=(.xL,yL) - каждая точка первого снимка стереопары,
pR(pL,DGC)=(xR,yR)=(xL+DGC(pL),yL) - точка второго снимка стереопары, сдвиг которой относительно точки pL первого снимка равен DGC(pL),
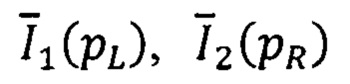 - средние яркости первого и второго изображений стереопары в окрестностях точек pL и pR соответственно,
- средние яркости первого и второго изображений стереопары в окрестностях точек pL и pR соответственно,
N(pL) - множество точек в окрестности точки pL фиксированного радиуса,
V - весовой коэффициент штрафной функции,
Т(⋅) - функция, которая возвращает 1, если условие в скобках верно, и ноль в противном случае,
С - весовой коэффициент штрафной функции для условия DGC(pL)=∅ (∅ - пустое множество) означающего, что сдвиг точки pR относительно точки pL не определен.
Минимум функции EGC(DGC) в алгоритме GC ищут для всех точек изображения одновременно специальным численным методом, который относится к классу глобальных алгоритмов.
Приложение 2
Алгоритм SGM поиска матрицы сдвигов между точками эпиполярно выравненных изображений
В алгоритме SGM поиск минимума функции ESGM(⋅), в отличие от алгоритма GC, осуществляется не глобально для всех точек сразу, а для каждой точки р первого изображения отдельно и независимо от других, поэтому алгоритм относится к классу полу-глобальных. Для этого
- в точку р первого изображения от края изображения проводят 16 равномерно разнесенных по углу лучей Si, в дальнейшем тексте точки первого изображения, находящиеся на луче Si, обозначаем pL=(xL,yL),
- для i-того луча находят вектор 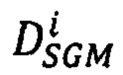 сдвигов
сдвигов 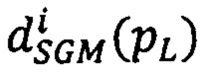 соответственных точек второго изображения, находящихся в одноименных с pL строках, следующим образом:
соответственных точек второго изображения, находящихся в одноименных с pL строках, следующим образом:
рассматривают множество вариантов 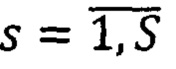 вектора сдвигов
вектора сдвигов 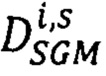 точек pRs второго изображения относительно точек pL ∈ Si первого изображения, координаты которого - последовательные значения
точек pRs второго изображения относительно точек pL ∈ Si первого изображения, координаты которого - последовательные значения 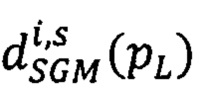 (из заранее заданного диапазона)
(из заранее заданного диапазона)
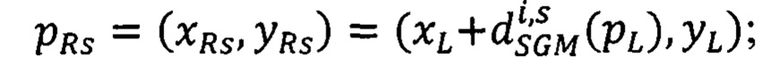
для s-того варианта вектора сдвигов 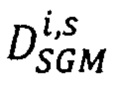 определяют значение энергетической функции
определяют значение энергетической функции 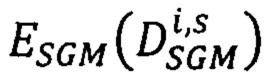
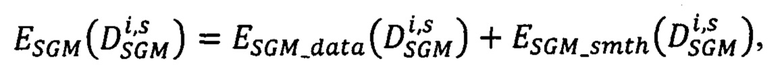
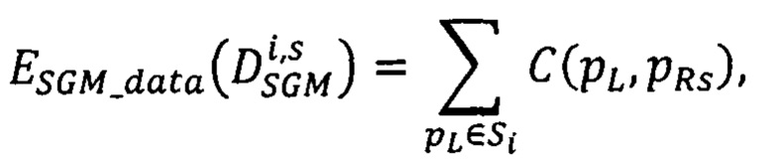
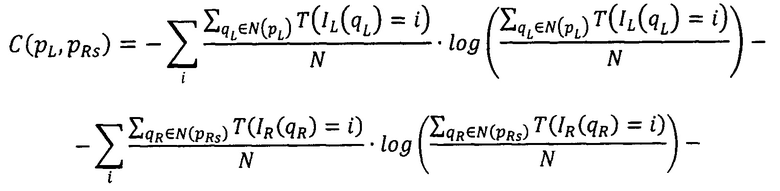
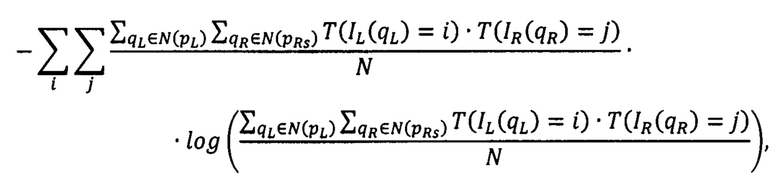
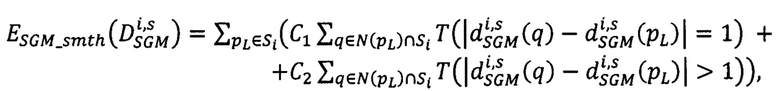
где 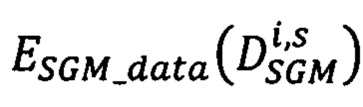 - мера близости всех точек pL первого изображения, расположенных на луче Si, к точкам pRs второго изображения, имеющих сдвиги
- мера близости всех точек pL первого изображения, расположенных на луче Si, к точкам pRs второго изображения, имеющих сдвиги 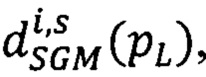
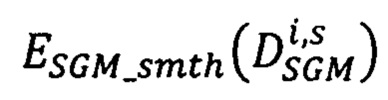 - суммарный штраф за несовпадение сдвигов
- суммарный штраф за несовпадение сдвигов 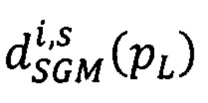 в точках pL, расположенных на луче Si, и сдвигов
в точках pL, расположенных на луче Si, и сдвигов 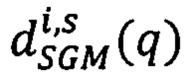 в соседних с pL точках q ∈ Si из окрестности фиксированного радиуса,
в соседних с pL точках q ∈ Si из окрестности фиксированного радиуса,
pL ∈ Si - точки первого изображения, расположенные на луче Si,
С1 и С2 - штрафы за несовпадение сдвигов в соседних точках,
qL ∈ N(pL) - множество точек первого изображения в окрестности точки pL фиксированного радиуса,
qR ∈ N(pRs) - множество точек второго изображения в окрестности точки pRs фиксированного радиуса,
Т(⋅) - функция, которая возвращает 1, если условие в скобках верно, и ноль в противном случае,
IL(qL) - яркость первого изображения в точке pL,
IR(qR) - яркость второго изображения в точке qR,
N - количество точек в заданной окрестности;
находят методом динамического программирования среди множества векторов 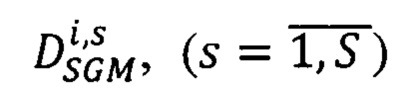 оптимальный вектор
оптимальный вектор 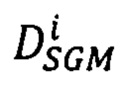 сдвигов соответственных точек второго изображения, для которого достигается минимум энергетической функции
сдвигов соответственных точек второго изображения, для которого достигается минимум энергетической функции 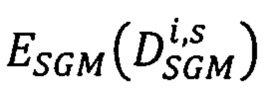
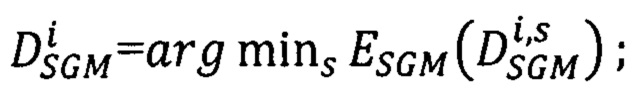
- повторяют шаги определения вектора 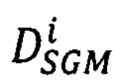 для каждого луча Si,
для каждого луча Si,
- выбирают среди полученных 16-ти векторов-сдвигов 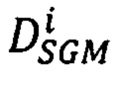 тот, для которого достигается наименьшее значение
тот, для которого достигается наименьшее значение 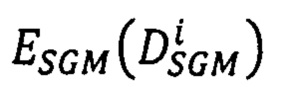
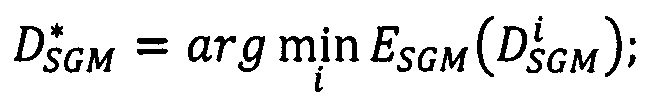
- выбирают в векторе 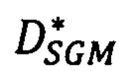 первую координату, отвечающую точке р первого изображения. Значение сдвига, записанное в этой точке, является искомым точным значением сдвига
первую координату, отвечающую точке р первого изображения. Значение сдвига, записанное в этой точке, является искомым точным значением сдвига 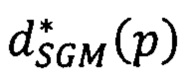 соответственной точки второго изображения;
соответственной точки второго изображения;
- повторяют вычисление сдвига 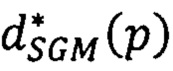 для всех точек р первого изображения и формируют для этого изображения результирующую матрицу сдвигов
для всех точек р первого изображения и формируют для этого изображения результирующую матрицу сдвигов 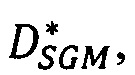 в которой на месте яркости IL(р) исходного изображения стоит значение
в которой на месте яркости IL(р) исходного изображения стоит значение 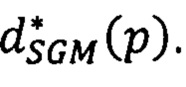
Литература
[1] H. Hirschmuller. Stereo Processing by Semi-Global Matching and Mutual Information // IEEE Transactions on Pattern Analysis and Machine Intelligence, Volume: 30, Issue: 2, Feb. 2008. P. 328-341.
[2] https://racurs.ru/ers-data/optical-images/pleiades/
[3] V. Kolmogorov, R. Zabih, Computing visual correspondence with occlusions using graph cuts. In: Proc. Int'l. Conf. Computer Vision, pp. 5 08-515 (2001) DOI: 10.1109/ICCV.2001.937668
[4] T. Kraub, M. Lehner, P. Reinartz. Generation of coarse 3D models of urban areas from high resolution stereo satellite images // The International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences. Vol. XXXVII. Part Bl. Beijing 2008. P. 1091-1098.
[5] Tola E. A DAISY: An Efficient Dense Descriptor Applied to Wide-Baseline Stereo / Tola E., Lepetit V., Fua P. // IEEE Transactions on Pattern Analysis and Machine Intelligence. - 2010 - Vol. 32. Is. 5. P. 815-830.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ СОВЕРШЕНСТВОВАНИЯ ФОТОТРИАНГУЛЯЦИИ ПРИ СОЗДАНИИ ЦИФРОВЫХ МОДЕЛЕЙ МЕСТНОСТИ | 2023 |
|
RU2835990C2 |
| Способ получения набора объектов трехмерной сцены | 2019 |
|
RU2803287C1 |
| СПОСОБ УЛУЧШЕНИЯ ПЛОТНОЙ И РАЗРЕЖЕННОЙ КАРТ ДИСПАРАНТНОСТИ, ТОЧНОСТИ РЕКОНСТРУИРУЕМОЙ ТРЕХМЕРНОЙ МОДЕЛИ И УСТРОЙСТВО ДЛЯ РЕАЛИЗАЦИИ СПОСОБА | 2012 |
|
RU2479039C1 |
| МЕТОД ОПРЕДЕЛЕНИЯ ЗОНЫ ДВИЖЕНИЯ И САМОСТОЯТЕЛЬНОГО ОБЪЕЗДА ПРЕПЯТСТВИЙ ДЛЯ БЕСПИЛОТНОГО ТРАНСПОРТНОГО ОБОРУДОВАНИЯ В ПОДЗЕМНЫХ ЗАМКНУТЫХ ПРОСТРАНСТВАХ | 2022 |
|
RU2803671C1 |
| СИСТЕМА И СПОСОБ ФОРМИРОВАНИЯ И ВОСПРОИЗВЕДЕНИЯ ТРЕХМЕРНОГО ВИДЕОИЗОБРАЖЕНИЯ | 2009 |
|
RU2421933C2 |
| Способ взаимной калибровки видеокамеры и устройства многолучевого лазерного подсвета | 2024 |
|
RU2840117C1 |
| СПОСОБ ВЗАИМНОЙ КАЛИБРОВКИ ВИДЕОКАМЕРЫ И УСТРОЙСТВА ВЕЕРНОГО ЛАЗЕРНОГО ПОДСВЕТА | 2021 |
|
RU2788666C1 |
| Способ автоматического создания цифровой модели местности по стереоснимкам | 1991 |
|
SU1793226A1 |
| УСТРОЙСТВО ДЛЯ ОПРЕДЕЛЕНИЯ РАССТОЯНИЯ И СКОРОСТЕЙ ОБЪЕКТОВ НА ОСНОВЕ СТЕРЕОПОДХОДА | 2012 |
|
RU2582853C2 |
| СПОСОБ БЕСКОНТАКТНОГО ИЗМЕРЕНИЯ КООРДИНАТ ТОЧЕК ОБЪЕКТОВ, НАХОДЯЩИХСЯ В ЖИДКОСТИ | 2003 |
|
RU2248523C1 |

Изобретение относится к области вычислительной техники для анализа стереоизображений при построении цифровой модели поверхности (ЦМП) по данным космической стереосъемки. Технический результат заключается в повышении точности и детальности построения цифровой модели поверхности по данным космической стереосъемки. Технический результат достигается за счет сопоставления стереоизображений с нахождением матрицы сдвигов точек второго изображения относительно точек первого изображения в два этапа. На первом этапе построение матрицы сдвигов 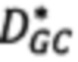 выполняется через нахождение минимума модифицированной энергетической функции
выполняется через нахождение минимума модифицированной энергетической функции 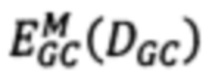 алгоритмом GraphCut (GC), а на втором нахождение методом Semi-global matching (SGM) точной матрицы сдвигов
алгоритмом GraphCut (GC), а на втором нахождение методом Semi-global matching (SGM) точной матрицы сдвигов 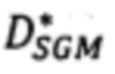 в каждой точке р первого изображения по минимуму модифицированной энергетической функции
в каждой точке р первого изображения по минимуму модифицированной энергетической функции 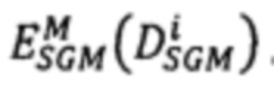 для каждого i-го луча, исходящего из точки р. Для каждой точки р изображения стереопары формируется вектор-признак, называемый дескриптором DAISY(р). Координаты дескриптора DAISY(p) являются двумерными свертками модулей градиентов яркости по 8 направлениям с гауссовыми ядрами различных радиусов, вычисленных в точке р и еще в 24-х точках, равномерно распределенных по трем концентрическим окружностям с центром в точке р. 6 ил.
для каждого i-го луча, исходящего из точки р. Для каждой точки р изображения стереопары формируется вектор-признак, называемый дескриптором DAISY(р). Координаты дескриптора DAISY(p) являются двумерными свертками модулей градиентов яркости по 8 направлениям с гауссовыми ядрами различных радиусов, вычисленных в точке р и еще в 24-х точках, равномерно распределенных по трем концентрическим окружностям с центром в точке р. 6 ил.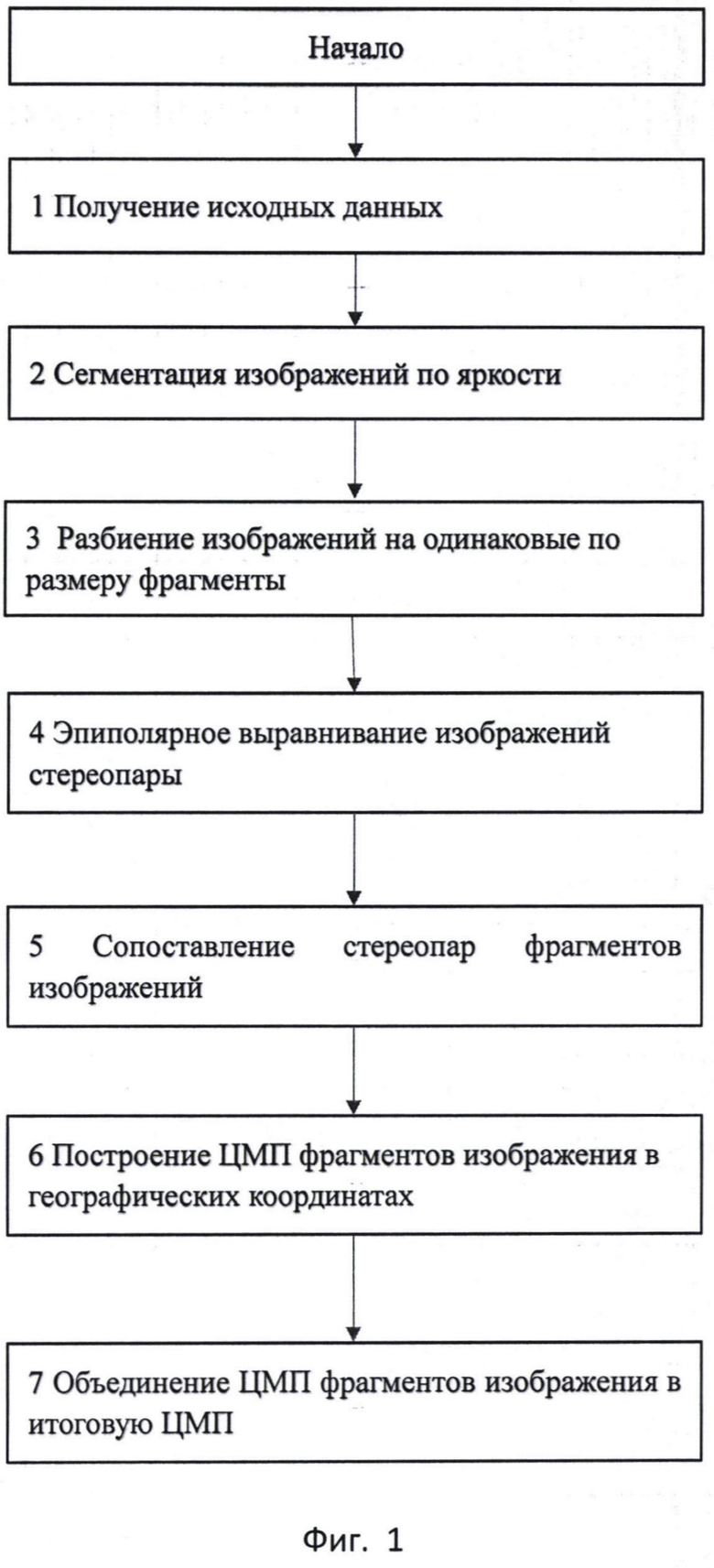
Способ построения цифровой модели поверхности (ЦМП) по данным космической стереосъемки включает получение пары стереоснимков местности в панхроматическом диапазоне и RPC-коэффициентов математического преобразования координат точек (пикселей) космического изображения на точки местности и обратно; разбиение стереоснимков на одинаковые по размеру меньшие фрагменты; эпиполярное выравнивание фрагментов изображений стереопары в панхроматическом диапазоне через повороты изображений относительно центров фрагментов снимков так, чтобы смещения, вызванные сменой ракурса при получении стереопары, лежали вдоль одной строки; выполнение процедуры стереосопоставления, в результате которой получают матрицу сдвигов соответственных точек; процедура стереосопоставления включает в себя: нахождение оптимальной матрицы сдвигов 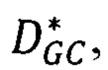 для которой достигается минимум энергетической функции EGC(DGC)
для которой достигается минимум энергетической функции EGC(DGC)
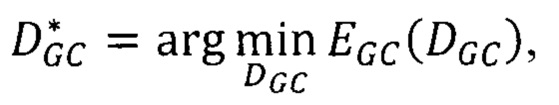
EGC(DGC)=EGC_data(DGC)+EGC_smth(DGC),
где EGC_data(DGC) - мера близости точек pL первого изображения к точкам pR второго изображения,
EGC_smth(DGC) - суммарный штраф за несовпадение сдвигов в точках pL и сдвигов в соседних с pL точках q из окрестности фиксированного радиуса;
значение EGC_smth (DGC) определяется выражением
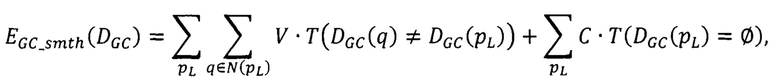
где pL=(xL, yL) - каждая точка первого снимка стереопары,
pR(pL,DDC)=(xR, yR)=(xL+DGC(pL),yL) - соответственная точка второго снимка стереопары, сдвиг которой относительно точки pL первого снимка равен DGC(pL),
DGC(pL) - сдвиг соответственной точки второго изображения относительно точки pL первого изображения, находящихся в одноименных строках изображений,
N(pL) - множество точек в окрестности точки pL фиксированного радиуса,
V - весовой коэффициент штрафной функции,
Т(⋅) - функция, которая возвращает 1, если условие в скобках верно, и ноль - в противном случае,
С - весовой коэффициент штрафной функции для условия DGC(pL)=∅ (∅ - пустое множество), означающего, что сдвиг точки pR относительно точки pL не определен;
строят ЦМП фрагментов изображения в географических координатах в последовательности:
вычисляют высоту местности h(p) в пикселе р по найденным сдвигам и параметрам съемки; вычисляют по матрице h(p) географические координаты точек поверхности H(X,Y) с помощью RPC-коэффициентов для того, чтобы получить ЦМП, привязанную к местности; объединяют ЦМП всех фрагментов разбиения H(X,Y) в итоговую ЦМП и выполняют медианную фильтрацию полученной матрицы высот; отличающийся тем, что из панхроматических стереоснимков, принимаемых для построения ЦМП, в результате предварительной обработки исключены пиксели, соответствующие местоположению облаков и водной поверхности; в состав исходной информации для построения ЦМП включена априорно известная цифровая модель рельефа (ЦМР) с разрешением не ниже 150 метров на пиксель; перед разбиением стереоснимков выполняют сегментацию изображений стереопары методом анизотропной медианной фильтрации для удаления шума и мелких выбросов яркости, сегментация изображений включает: выпуск из каждой точки р изображения 16 лучей длиною 7 пикселей, вычисление дисперсии яркости изображения вдоль каждого луча, вычисление медианы яркости точек вдоль луча с наименьшей дисперсией, присвоение точке р панхроматического изображения найденного значения медианы; в операции стереосопоставления перед нахождением оптимальной матрицы сдвигов 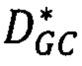 для каждой точки р изображений стереопары вычисляют вектор-признак точки, называемый дескриптором DAISY(p), и диапазон поиска
для каждой точки р изображений стереопары вычисляют вектор-признак точки, называемый дескриптором DAISY(p), и диапазон поиска 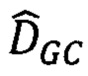 сдвигов соответственных точек по ЦМР; дескриптор DAISY (р) вычисляют по алгоритму: вокруг точки р панхроматического изображения строят набор из трех концентрических окружностей радиусами 3, 6 и 9 пикселей; на каждой из этих окружностей выбирают по 8 точек, равномерно распределенных вдоль окружности; в исходной точке р, а также в 8 точках, выбранных на окружности с радиусом 3 пикселя, выполняют двумерную свертку с гауссовым ядром модулей градиентов яркости по 8 направлениям, радиус гауссова ядра 2 пикселя; в каждой из 8 точек, выбранных на окружности с радиусом 6 пикселей, выполняют свертку с гауссовым ядром модулей градиентов яркости по 8 направлениям, радиус гауссова ядра 3 пикселя; в каждой из 8 точек, выбранных на окружности с радиусом 9 пикселей, выполняют свертку с гауссовым ядром модулей градиентов яркости по 8 направлениям, радиус гауссова ядра 4 пикселя; объединяют полученные значения в вектор размерности 200; нормализуют полученный вектор, который считают дескриптором DAISY(р) точки р изображения; диапазон поиска
сдвигов соответственных точек по ЦМР; дескриптор DAISY (р) вычисляют по алгоритму: вокруг точки р панхроматического изображения строят набор из трех концентрических окружностей радиусами 3, 6 и 9 пикселей; на каждой из этих окружностей выбирают по 8 точек, равномерно распределенных вдоль окружности; в исходной точке р, а также в 8 точках, выбранных на окружности с радиусом 3 пикселя, выполняют двумерную свертку с гауссовым ядром модулей градиентов яркости по 8 направлениям, радиус гауссова ядра 2 пикселя; в каждой из 8 точек, выбранных на окружности с радиусом 6 пикселей, выполняют свертку с гауссовым ядром модулей градиентов яркости по 8 направлениям, радиус гауссова ядра 3 пикселя; в каждой из 8 точек, выбранных на окружности с радиусом 9 пикселей, выполняют свертку с гауссовым ядром модулей градиентов яркости по 8 направлениям, радиус гауссова ядра 4 пикселя; объединяют полученные значения в вектор размерности 200; нормализуют полученный вектор, который считают дескриптором DAISY(р) точки р изображения; диапазон поиска 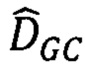 сдвигов соответственных точек по ЦМР вычисляется как интервал
сдвигов соответственных точек по ЦМР вычисляется как интервал
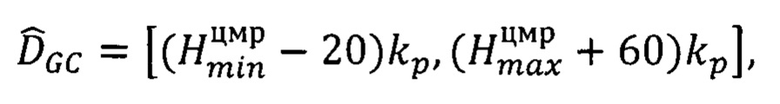
где kp - коэффициент перевода 1 м высоты местности в пиксели смещения на стереопаре, вычисляемый для каждого фрагмента по RPC-коэффициентам снимков,
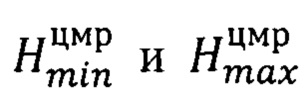 - минимальная и максимальная высота рассматриваемой местности по ЦМР в пределах фрагмента;
- минимальная и максимальная высота рассматриваемой местности по ЦМР в пределах фрагмента;
вычисления энергетической функции EGC(DGC) выполняют для пар точек первого pL и второго рR изображения, сдвиг между которыми DGC(pL) находится в пределах интервала 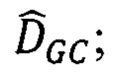 после нахождения оптимальной матрицы сдвигов
после нахождения оптимальной матрицы сдвигов 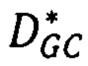 ищется матрица точных значений
ищется матрица точных значений 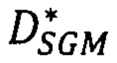 в локальных областях каждой точки р первого снимка модифицированным алгоритмом SGM в последовательности: определяют диапазон поиска
в локальных областях каждой точки р первого снимка модифицированным алгоритмом SGM в последовательности: определяют диапазон поиска 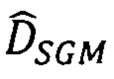 сдвигов для каждой точки снимка pL как интервал
сдвигов для каждой точки снимка pL как интервал
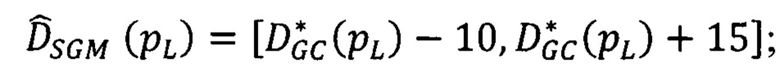
в точку р первого изображения от края изображения проводят 16 равномерно разнесенных по углу лучей Si (i=1…16); в дальнейшем тексте по алгоритму SGM точки первого изображения, находящиеся на луче Si, обозначены pL; для i-того луча находят вектор 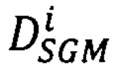 сдвигов
сдвигов 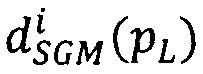 соответственных точек второго изображения, находящихся в одноименных с pL строках, для этого рассматривают множество вариантов
соответственных точек второго изображения, находящихся в одноименных с pL строках, для этого рассматривают множество вариантов 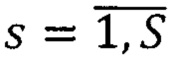 вектора сдвигов
вектора сдвигов 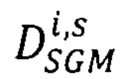 точек pRs второго изображения относительно точек pL ∈ Si первого изображения, координаты которого - последовательные значения
точек pRs второго изображения относительно точек pL ∈ Si первого изображения, координаты которого - последовательные значения 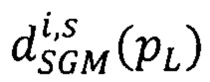
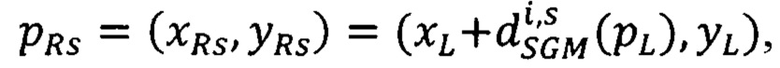
для s-того варианта вектора сдвигов 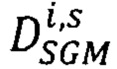 определяют значение энергетической функции
определяют значение энергетической функции 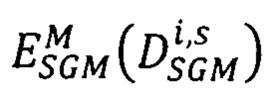 по формуле:
по формуле:
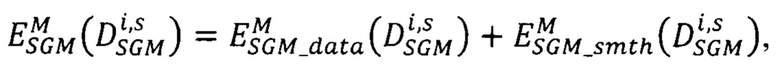
где
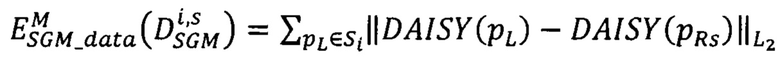 - модифицированная мера близости всех точек pL первого изображения, расположенных на луче Si, к точкам pRs второго изображения, имеющим сдвиги
- модифицированная мера близости всех точек pL первого изображения, расположенных на луче Si, к точкам pRs второго изображения, имеющим сдвиги 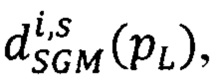
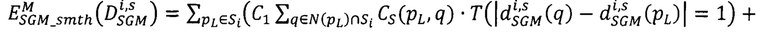
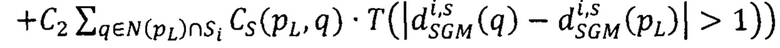 - модифицированный за счет введения коэффициентов CS(pL, q) суммарный штраф за несовпадение сдвигов в точках pL, расположенных на луче Si, и сдвигов в соседних с pL точках q ∈ Si из окрестности фиксированного радиуса,
- модифицированный за счет введения коэффициентов CS(pL, q) суммарный штраф за несовпадение сдвигов в точках pL, расположенных на луче Si, и сдвигов в соседних с pL точках q ∈ Si из окрестности фиксированного радиуса,
CS(pL,q) - коэффициент сегментации, который равен 1, если яркости точек pL и q в сегментированном изображении не равны, и 3 - в противном случае,
pL ∈ Si - точки первого изображения, расположенные на луче Si,
С1 и С2 - штрафы за несовпадение сдвигов в соседних точках,
q ∈ N(pL) ∩ Si - множество точек луча Si в окрестности фиксированного радиуса с центром в точке pL,
находят методом динамического программирования среди множества векторов 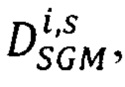
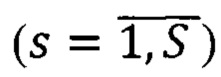 оптимальный вектор
оптимальный вектор 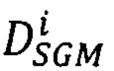 сдвигов соответственных точек второго изображения, для которого достигается минимум энергетической функции
сдвигов соответственных точек второго изображения, для которого достигается минимум энергетической функции 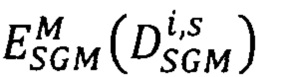
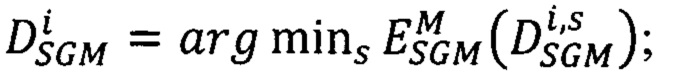
повторяют шаги определения вектора 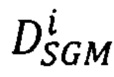 для каждого луча Si;
для каждого луча Si;
выбирают среди полученных 16-ти векторов-сдвигов 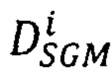 тот, для которого достигается наименьшее значение
тот, для которого достигается наименьшее значение 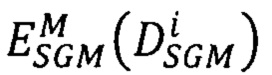
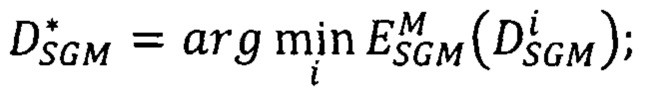
выбирают в векторе 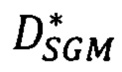 первую координату, отвечающую точке р первого изображения, значение сдвига, записанное в этой точке, является искомым точным значением сдвига
первую координату, отвечающую точке р первого изображения, значение сдвига, записанное в этой точке, является искомым точным значением сдвига 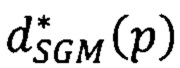 соответственной точки второго изображения; повторяют вычисление сдвига
соответственной точки второго изображения; повторяют вычисление сдвига 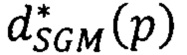 для всех точек р первого изображения и формируют для этого изображения результирующую матрицу сдвигов
для всех точек р первого изображения и формируют для этого изображения результирующую матрицу сдвигов 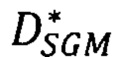 , в которой на месте яркости IL(р) исходного изображения стоит значение
, в которой на месте яркости IL(р) исходного изображения стоит значение 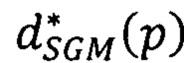 ; в операциях построения ЦМП фрагментов изображения в географических координатах значение h(р) - высоты местности в пикселе р определяют по найденным сдвигам
; в операциях построения ЦМП фрагментов изображения в географических координатах значение h(р) - высоты местности в пикселе р определяют по найденным сдвигам 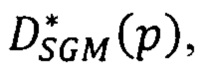 базовой высоте
базовой высоте 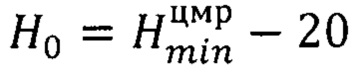 фрагмента и коэффициенту kp перевода метров высоты в пиксели изображения:
фрагмента и коэффициенту kp перевода метров высоты в пиксели изображения:
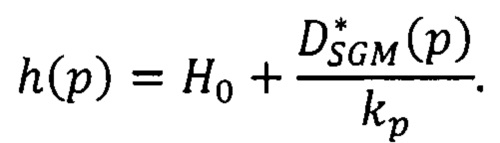
| Пресс для выдавливания из деревянных дисков заготовок для ниточных катушек | 1923 |
|
SU2007A1 |
| Способ приготовления лака | 1924 |
|
SU2011A1 |
| Автомобиль-сани, движущиеся на полозьях посредством устанавливающихся по высоте колес с шинами | 1924 |
|
SU2017A1 |
| Приспособление для суммирования отрезков прямых линий | 1923 |
|
SU2010A1 |
| ОБЪЕДИНЕНИЕ ДАННЫХ 3D ИЗОБРАЖЕНИЯ И ГРАФИЧЕСКИХ ДАННЫХ | 2010 |
|
RU2538335C2 |
Авторы
Даты
2022-08-15—Публикация
2021-07-02—Подача