Заявленное техническое решение относится к области обработки изображений, а именно к технике построения 3D-модели объекта из изображений, получаемых в условиях ограниченной доступности объекта для наблюдения и измерения его параметров.
Заявленное изобретение может быть использовано для повышения точности построения 3D-модели объекта в условиях ограниченной доступности объекта для наблюдения и измерения его параметров.
Известным способом реконструкции 3D-модели объекта является процесс вычисления математического представления трехмерной поверхности объекта из двумерных проекций объекта, получаемых с разных точек просмотра, как описано в книге [1]. Реконструированная 3D-модель объекта затем может быть в цифровом виде сохранена, обработана и отображена и физически воссоздана, например, с использованием устройств 3D-печати.
Реконструкция 3D-модели объекта широко используется в различных сферах деятельности, таких как развлечения (кинофильмы, анимация, компьютерные игры и т.д.), анализ и обработка изображений, медицина, дизайн интерьеров, архитектура, промышленный дизайн, технологии прототипирования различных разрабатываемых технических устройств и строительных объектов.
Типовыми условиями реконструкции 3D-модели объекта является возможность наблюдения объекта в трехмерном пространстве с множества выбранных точек наблюдения, а также возможность непосредственного измерения его параметров, таких как форма, геометрические размеры, цветовые структуры и отражающая способность поверхности объекта.
Однако 3D-реконструкция является затрудненной в условиях ограниченной доступности объекта для наблюдения, характерных для ряда физических объектов космического, воздушного, наземного и подводного базирования. Например, для многих космических тел природного и искусственного происхождения сложно и чрезмерно дорого получение снимков всех частей поверхности этих тел, необходимых для построения его 3D-модели. В условиях ограниченной доступности подобных объектов также сложно с высокой точностью определить их форму, геометрические размеры и другие параметры. Например, большие сложности вызывает оценка формы и геометрических размеров затонувших кораблей, ушедших под воду старинных сооружений и т.п. В ряде случаев требуется оценить параметры поврежденных и деформированных в результате катастроф, взрывов и пожаров различных наземных объектов, доступ к которым может быть затруднен последствиями произошедших событий в виде химического, биологического, радиоактивного и других видов заражения. Также 3D-реконструкция является затрудненной в системах мониторинга и разведки местности и объектов при противодействии этому третьей стороны.
Известны подходы к 3D-реконструкции, которые основаны на различных оптических системах, используемых для захвата изображений. Обычно оптическая система может быть выполнена либо в виде специализированной камеры глубины (например, активного датчика глубины или стереокамеры), либо в виде традиционной монокулярной камеры. Специализированная камера глубины может захватывать карты глубины (либо непосредственно в случае активного датчика глубины, либо после обработки пары скорректированных стереоизображений в случае стереокамеры) объекта или среды в реальном времени. Каждый пиксель в картах глубины соответствует дискретному измерению расстояния, получаемому посредством камеры из 3D-точки в среде. Например, способ 3D-реконструкции объекта по патенту US 8587583 [2] описывает подход, в котором местоположение камеры оценивают с использованием захваченной карты глубины, причем все карты глубины непрерывно объединяют во внутренней памяти обрабатывающего устройства с использованием оцененного местоположения камеры. Этот подход имеет два недостатка: во-первых, он требует дорогостоящего аппаратного обеспечения для реализации датчика глубины, используемого для захвата карт глубины, и, во-вторых, алгоритм обработки является вычислительно сложным и требует мощного графического процессора для обработки данных.
В подходах на основе монокулярной камеры может быть использован способ 3D-реконструкции на основе силуэта. В этом способе изображения, захваченные посредством камеры, используются для извлечения силуэтов, которые затем при построении 3D-модели образуют вместе с их пересечениями объемную структуру. Такой способ описан в патенте US 8270704 [3] и выдает построенную 3D-модель в виде полигональной сетки с цветовой текстурой. Недостатком этого способа является его вычислительная сложность построения объемной структуры и извлечения силуэтов, что затрудняет его реализацию. Другой недостаток состоит в том, что этот способ не может восстанавливать вогнутости поверхности объектов, которые не выявляются на изображениях силуэтов.
Другим классом способов, использующих аппаратное обеспечение на основе монокулярной камеры, являются способы реконструкции 3D-модели на основе определения структуры по движению объекта, в которых изображения характерных точек объекта извлекают и сопровождают для последовательных захваченных изображений. Вычисленную траекторию совокупности характерных точек используют затем для реконструкции 3D-местоположения объекта и перемещения снимающей камеры. Такой подход описан в патенте US 8532367 [4]. Недостатком этого подхода является то, что он реконструирует объект в виде облака 3D-точек или полигональной сетки без текстур, что снижает естественность реконструированной 3D-модели объекта. Также, для большей точности этот подход требует вычисления очень большого количества характерных точек объекта, что увеличивает вычислительные затраты.
Общим недостатком указанных аналогов является необходимость получения изображений объекта с множества точек наблюдения в трехмерном пространстве вокруг объекта, что недостижимо в условиях ограниченной доступности объекта для наблюдения и измерения его параметров.
Наиболее близким по своей технической сущности к заявленному способу реконструкции 3D-модели объекта является способ реконструкции 3D-модели объекта по патенту РФ №2642167, описанный в [5]. Способ - прототип реконструкции 3D-модели объекта включает сканирование посредством модуля сканирования объекта вдоль траектории вокруг объекта и захвата изображений объекта из разных точек на этой траектории, сохранение захваченных натурных изображений в блоке электронной памяти, используя по меньшей мере один процессор, оценку во время сканирования объекта местоположения модуля сканирования, соответствующего каждому из захваченных изображений, сохранение оцененных местоположений модуля сканирования в блоке электронной памяти, уточнение, после завершения сканирования объекта, оцененных местоположений модуля сканирования, сохраненных в блоке электронной памяти, с использованием информации о начальной и конечной точках траектории, и сохранение уточненных местоположений модуля сканирования в блоке памяти, конструирование карты глубины, соответствующей каждому из уточненных местоположений модуля сканирования и каждому из захваченных изображений, объединение всех карт глубины для генерации 3D-представления объекта, создание поверхностной сетки объекта на основе 3D-представления, наложение цветных текстур на поверхностной сетке объекта для реконструкции 3D-модели объекта, сохранение реконструированной 3D-модели объекта в блоке электронной памяти, и отображение 3D-модели объекта на модуле отображения.
В данном способе-прототипе реконструкции 3D-модели объекта выполняют реконструкцию модели объекта из изображений, генерируемых посредством сканирования объекта в пространстве на все 360 градусов, причем изображения объекта получают при его наблюдении со всех ракурсов. Однако если некоторая часть поверхности объекта не наблюдаема, то этот способ не обеспечивает построение невидимых частей 3D-модели объекта. А при невозможности непосредственного измерения параметров поверхности объекта, точность оценки отражательной способности поверхности объекта и его цветовых структур в недоступной для наблюдения и измерения части его построенной 3D-модели оказывается невысокой.
Таким образом, недостатком ближайшего аналога (прототипа) способа реконструкции 3D-модели объекта является относительно низкая точность построения модели, обусловленная недостаточным количеством изображений объекта и его измеренных параметров, в условиях ограниченной доступности объекта для наблюдения и измерения его параметров.
Техническим результатом заявляемого решения является разработка способа реконструкции 3D-модели объекта, обеспечивающего повышение точности построения модели в условиях ограниченной доступности объекта для наблюдения и измерения его параметров.
Указанный технический результат в заявляемом способе реконструкции 3D-модели объекта достигается тем, что в известном способе реконструкции 3D-модели объекта, включающем получение набора натурных изображений объекта, сохранение реконструированной 3D-модели объекта в электронной памяти и ее отображение на модуле отображения, дополнительно на полученном наборе натурных изображений объекта выполняют обучение сверточной нейронной сети, первоначально создают множество текущих версий 3D-модели объекта на основе полученного набора натурных изображений объекта и результатов измерений объекта. Формируют из каждой текущей версии 3D-модели объекта текущие наборы фотореалистичных изображений, причем каждое фотореалистичное изображение из каждой текущей версии 3D-модели объекта является результатом рендеринга этой модели.
Обнаруживают объект на перемешанных текущем наборе фотореалистичных изображений объекта и наборе натурных изображений других объектов с использованием обученной сверточной нейронной сети, вычисляют текущие значения вероятности обнаружения объекта на каждом текущем наборе фотореалистичных изображений, выбирают среди вычисленных текущих значений вероятности обнаружения объекта М>2 наибольших значений вероятности обнаружения объекта и М соответствующих им текущих версий 3D-модели объекта.
Из каждой выбранной версии 3D-модели объекта создают множество текущих версий 3D-модели объекта путем изменения не менее одного параметра ее формы, геометрических размеров, цветовых текстур и отражающей способности поверхности.
Повторно формируют из каждой текущей версии 3D-модели объекта текущие наборы фотореалистичных изображений и выполняют последующие действия до тех пор, пока возрастает значение хотя бы одного из наибольших значений вероятности обнаружения объекта, иначе принимают в качестве реконструированной 3D-модели объекта текущую версию 3D-модели объекта с наибольшим значением вероятности обнаружения объекта.
В предлагаемой совокупности действий при априорном неполном знании всех характеристик объекта создают множество текущих версий 3D-модели объекта, различающихся между собой по неизвестным характеристикам объекта, точность созданных версий оценивают с использованием обученной на доступных натурных изображениях объекта сверточной нейронной сети (СНС), отбирают текущие версии 3D-модели с наибольшей точностью, которые итеративно изменяют для достижения более высокой точности. Данный эволюционный алгоритм последовательного уточнения модели объекта с проверкой на каждом шаге корректности внесенных изменений с учетом известной информации об объекте позволяет реконструировать 3D-модель объекта с максимально достижимой точностью.
Поэтому указанная новая совокупность действий позволяет обеспечить повышение точности построения 3D-модели объекта в условиях ограниченной доступности объекта для наблюдения и измерения его параметров.
Заявленный способ поясняется чертежами, на которых показаны:
- на фиг. 1 - система реконструкции 3D-модели объекта;
- на фиг. 2 - алгоритм реконструкции 3D-модели объекта;
- на фиг. 3 - примеры натурных изображений объекта;
- на фиг. 4 - визуализация точной трехмерной модели объекта;
- на фиг. 5 - примеры визуализации некоторых построенных трехмерных моделей из первоначального множества текущих версий 3D-модели объекта;
- на фиг. 6 - иллюстрация метода бросания лучей при рендеринге;
- на фиг. 7 - пример графа создания и выбора текущих версий 3D-модели объекта;
- на фиг. 8 - примеры визуализации некоторых построенных трехмерных моделей, созданных из ранее выбранной версии 3D-модели, показанной на фиг. 5б);
- на фиг. 9 - визуализация реконструированной 3D-модели объекта.
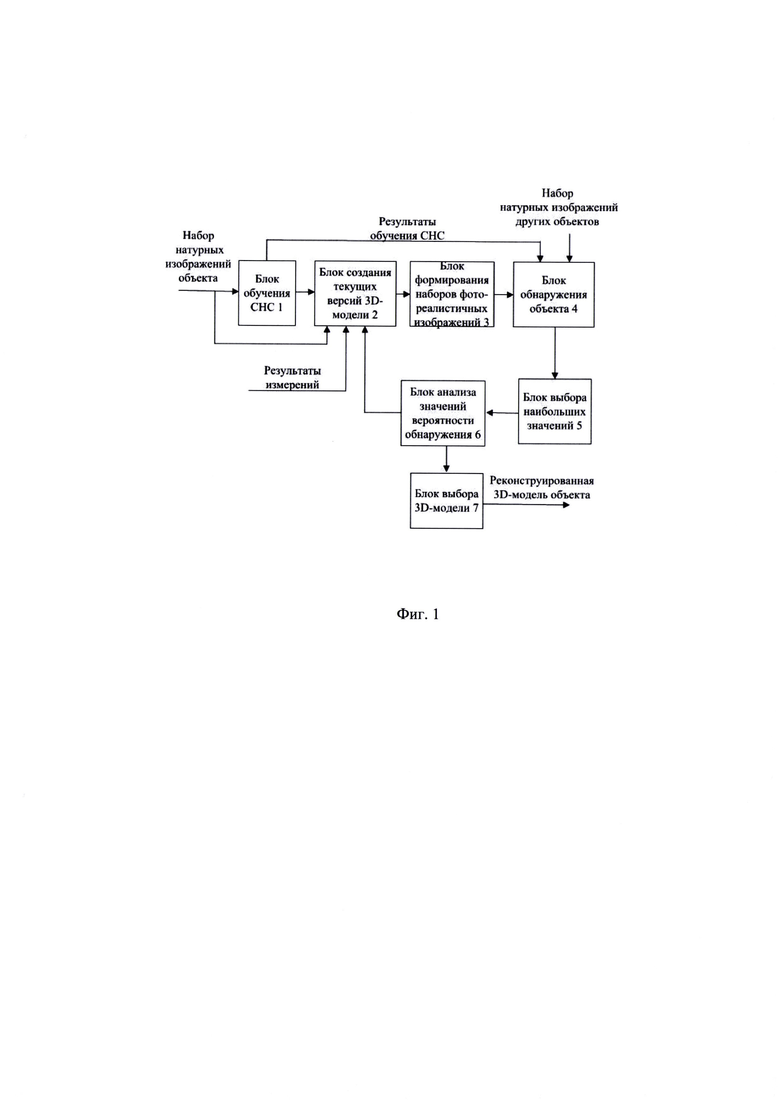
Реализация заявленного способа представлена на примере системы реконструкции 3D-модели объекта, показанной на фиг. 1. На вход блока обучения СНС 1 поступает набор имеющихся натурных изображений объекта, на основе которого выполняют обучение сверточной нейронной сети с выделением собственно изображений объекта без фона. Этот набор имеющихся натурных изображений объекта также поступает на вход блока создания текущих версий 3D-модели 2, на второй вход которого при их наличии поступают результаты измерений объекта. На основе имеющейся информации в данном блоке создают множество текущих версий 3D-модели объекта. Из каждой созданной текущей версии 3D-модели объекта в блоке формирования наборов фотореалистичных изображений 3 формируют соответствующий набор фотореалистичных изображений. На каждом перемешанном текущем наборе фотореалистичных изображений объекта и наборе натурных изображений других объектов в блоке обнаружения объекта 4, созданном на основе обученной сверточной нейронной сети, выполняют обнаружение объекта и подсчитывают текущие значения вероятности обнаружения объекта на каждом текущем наборе изображений. В блоке выбора наибольших значений 5 среди текущих значений вероятности обнаружения объекта выбирают М>2 наибольших значений вероятности обнаружения объекта и М соответствующих им текущих версий 3D-модели объекта. Далее в блоке анализа значений вероятности обнаружения 6 проверяют, есть ли увеличение значения хотя бы одного из выбранных наибольших значений вероятности обнаружения объекта относительно ранее полученных значений. Если прогресс имеется, то для каждой из М выбранных текущих версий 3D-модели объекта в блоке создания текущих версий 3D-модели 2 изменяют не менее одного параметра ее формы, геометрических размеров, цветовых текстур и отражающей способности поверхности, и повторно формируют из каждой текущей версии 3D-модели объекта наборы фотореалистичных изображений и выполняют последующие действия. Если в блоке анализа значений вероятности обнаружения 6 определяют, что значение вероятности обнаружения объекта больше не увеличивается, то в блоке выбора 3D-модели 7 принимают в качестве реконструированной 3D-модели объекта текущую версию 3D-модели объекта с наибольшим значением вероятности обнаружения объекта.
В способе реализуют следующую последовательность действий.
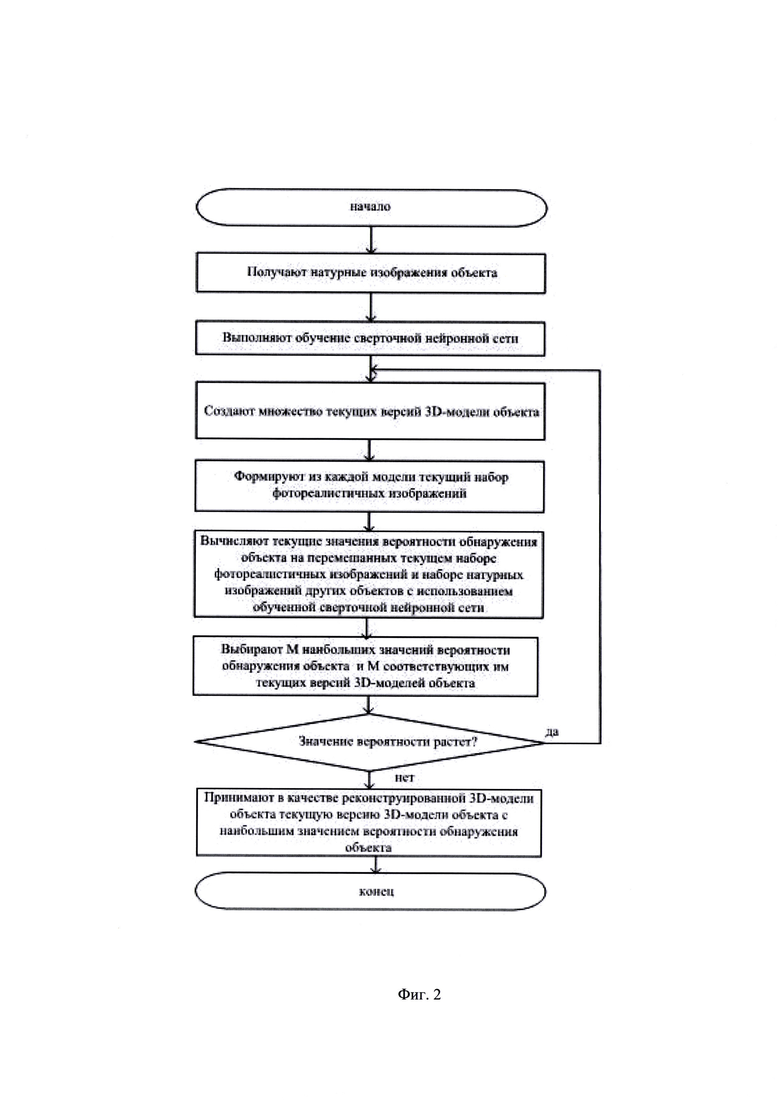
Алгоритм реконструкции 3D-модели объекта представлен на фигуре 2.
Способы предварительного получения набора натурных изображений объекта известны, натурные изображения объекта получают, например, с использованием электронных фотоаппаратов для изображений видимого диапазона, с использованием радиолокационных станций для изображений СВЧ-диапазона, с использованием инфракрасных датчиков для изображений ИК-диапазона и т.п. В условиях ограниченной доступности объекта для наблюдения натурные изображения могут быть получены только с некоторых ракурсов наблюдения объекта и не отображать вид всех частей данного объекта. Например, на фиг. 3 показаны примеры ограниченного числа полученных натурных изображений видимого диапазона объекта вида боевая машина M109. Имеются наблюдения объекта с передней части, сверху, с левой и правой сторон, но отсутствуют изображения этого объекта с задней стороны.
На полученном наборе натурных изображений объекта выполняют обучение сверточной нейронной сети для последующего обнаружения этого объекта на других изображениях. В сверточной нейронной сети для выполнения базовой операции свертки используют только ограниченная матрица весов небольшого размера, которую смещают по всему обрабатываемому слою, формируя после каждого сдвига сигнал активации для нейрона следующего слоя с аналогичной позицией [6]. То есть для различных нейронов выходного слоя используются одна и та же матрица весов, которую называют ядром свертки. Ее интерпретируют как графическое кодирование какого-либо признака, например, наличие наклонной линии под определенным углом. Тогда следующий слой, получившийся в результате операции свертки такой матрицей весов, показывает наличие данного признака в обрабатываемом слое и ее координаты, формируя так называемую карту признаков. Соответственно, в сверточной нейронной сети используют ряд наборов весов, кодирующих элементы изображения (например, линии и дуги под разными углами). При этом такие ядра свертки не закладываются исследователем заранее, а формируются на этапе обучения сети различными способами, описанными, например, в книге [6].
Обучение сверточной нейронной сети на полученном наборе натурных изображений объекта выполняют, например, следующим образом, описанным в патенте РФ на изобретение [7], где для каждого изображения из набора с помощью сверточной нейронной сети вычисляют вектор признаков в пространстве признаков изображений, для набора натурных изображений вычисляют значение функции потерь, отображающей множество вероятностей, где каждая вероятность из множества вероятностей характеризует гипотезу, ассоциирующую изображение из набора натурных изображений классом, ассоциируемым с этим изображением. При этом функция потерь дополнительно отображает множество значений расстояния, где каждое значение расстояния вычисляют в пространстве признаков изображений между вектором признаков, представляющим изображение из набора натурных изображений, и центром класса, ассоциируемого с этим изображением. На основе вычисленного значения функции потерь выполняют настройку одного или более параметров сверточной нейронной сети. Данную последовательность действий итеративно выполняют множество раз, добиваясь минимизации значения функции потерь. Если на очередных итерациях дальнейшего уменьшения значения функции потерь не происходит, то для набора натурных изображений обучение сверточной нейронной сети для обнаружения объекта считают завершенным.
Способ первоначального создания множества текущих версий 3D-модели объекта на основе полученного набора натурных изображений объекта и результатов измерений объекта заключается в следующем. Для построения трехмерных моделей объектов разработан ряд программных средств, таких как 3ds Max, Maya, Cinema 4D, Blender, в которых трехмерные модели различных объектов создают в результате их 3D-моделирования. Для построения 3D-модели объекта используют его натурные изображения с разных ракурсов, измеренные геометрические размеры, оценки его формы, параметры цветовых текстур и отражающей способности поверхности. Полученные 3D-модели объектов должны удовлетворять следующим требованиям: высокая степень реалистичности их наблюдения, визуального подобия геометрических форм создаваемых моделей самим объектам, соответствие габаритных размеров моделей размерам объектов, достаточный уровень детализации моделей, высокая точность форм, положения и размеров отдельных конструктивных элементов. Например, трехмерное моделирование объектов, представляемых изображениями в видимом диапазоне, описано в [8].
При создании трехмерных моделей наиболее распространенным способом является построение объемных фигур из сетки полигонов, описываемых вершинами, ребрами и гранями. Трехмерная модель объекта, состоящая из множества полигонов, представляет собой полигональную сетку. Для обеспечения фотореалистичности изображения поверхностям трехмерной модели объекта придают вид реальных материалов, таких как металл, дерево, пластик и т.п. Поверхность при необходимости становится прозрачной или зеркальной. Для этого, например, используется функция редактора материалов Material Editor в программном средстве моделирования 3ds Мах.
Например, с использованием всех натурных изображений и результатов измерений без ограничения доступности к моделируемому объекту на фиг. 4 показана визуализация трехмерной модели боевой машины M109. Для данной модели известны все необходимые для построения модели входные данные, поэтому такая 3D-модель, соответствующая реальному объекту, является точной. Для удобства последующего сравнения с создаваемыми текущими версиями 3D-модели этого объекта на фиг. 4 показана визуализация точной трехмерной модели объекта с ненаблюдаемой стороны в полученном наборе натурных изображений объекта (вид с задней стороны объекта).
При наличии изображений объекта во всех требуемых ракурсах и достаточно полных результатов измерений этого объекта известные способы моделирования способны создавать точные трехмерные модели объекта. Но в условиях ограниченной доступности объекта для наблюдения и измерения его параметров для построения точной трехмерной модели объекта входных данных недостаточно, поэтому с использованием известных средств 3D-моделирования предлагается создавать множество текущих версий 3D-модели объекта, в каждой из которых недостающие данные заменяют некоторыми значениями параметров, выбранными из предполагаемого множества возможных значений. Например, при неизвестности геометрических размеров и формы ненаблюдаемых поверхностей объекта из множества возможных значений размера, определяемого размерами наблюдаемых поверхностей объекта, и множества возможных форм поверхности, для каждой текущей версии 3D-модели объекта поочередно выбирают величины размера и тип формы поверхностей объекта. Выбор может осуществляться, например, последовательным перебором значений размера и типов формы с выбираемой величиной шага изменения. Предполагаемое множество возможных значений неизвестного параметра объекта, например, геометрического размера ненаблюдаемой его части, определяют как дискретное множество значений, например, от минимального значения, равного минимальному размеру детализации объекта на трехмерной модели, до максимального значения, определяемого как наибольший размер любой из наблюдаемых и измеряемых частей объекта. Полученный диапазон значений может или равномерно разделен на множество значений с шагом, не менее минимального размера детализации объекта на трехмерной модели, или по методу дихотомии диапазон значений делят пополам и далее при уточнении модели объекта выбранный половинный поддиапазон значений снова делят пополам и т.д. Отметим, что в каждой текущей версии 3D-модели объекта известные из полученного набора натурных изображений объекта и результатов измерений объекта при их наличии параметры модели остаются неизменными, модификации подвергаются только неизвестные параметры модели.
В условиях неизвестности многих параметров моделируемого объекта создаваемое множество текущих версий 3D-модели объекта может составлять десятки, сотни и более версий 3D-модели объекта, в каждой из которых один или несколько неизвестных параметров объекта различаются. Например, на фиг. 5 показаны примеры визуализации некоторых построенных трехмерных моделей из первоначального множества текущих версий 3D-модели объекта. Очевидно, что из-за неизвестности ряда исходных данных ни одна из построенных трехмерных моделей из первоначального множества текущих версий не является достаточно близкой к точной 3D-модели объекта, совпадающей с его 3D-моделью, представленной на фиг. 4. Таким образом, создаваемое множество текущих версий 3D-модели объекта представляет из себя множество вариантов моделирования исследуемого объекта, у которых точно отображены наблюдаемые и измеренные параметры объекта, а неизвестные параметры объекта описываются правдоподобными значениями, которые могут как совпадать или быть достаточно близкими с реальными значениями параметров этого объекта, так и существенно от них отличаться.
Затем из каждой текущей версии 3D-модели объекта формируют соответствующий текущий набор фотореалистичных изображений, причем каждое изображение из каждой текущей версии 3D-модели объекта является результатом рендеринга этой модели. Для этого каждое фотореалистичное изображение из текущего набора фотореалистичных изображений получают изменением ракурса наблюдения текущей версии трехмерной модели этого объекта по азимуту и углу места, масштаба изображения, освещенности и параметров датчика получения изображения, например, фокусного расстояния и диафрагменного числа объектива, размера и числа элементов регистрирующей матрицы. При этом текущий набор фотореалистичных изображений получают путем наблюдения текущей версии 3D-модели объекта со многих виртуальных точек трехмерного пространства вокруг модели. При этом часть точек наблюдения текущей версии 3D-модели объекта совпадает или близка с точками наблюдения реального объекта при получении натурных изображений, а часть точек наблюдения текущей версии 3D-модели объекта соответствует недоступным для наблюдения сторонам реального объекта.
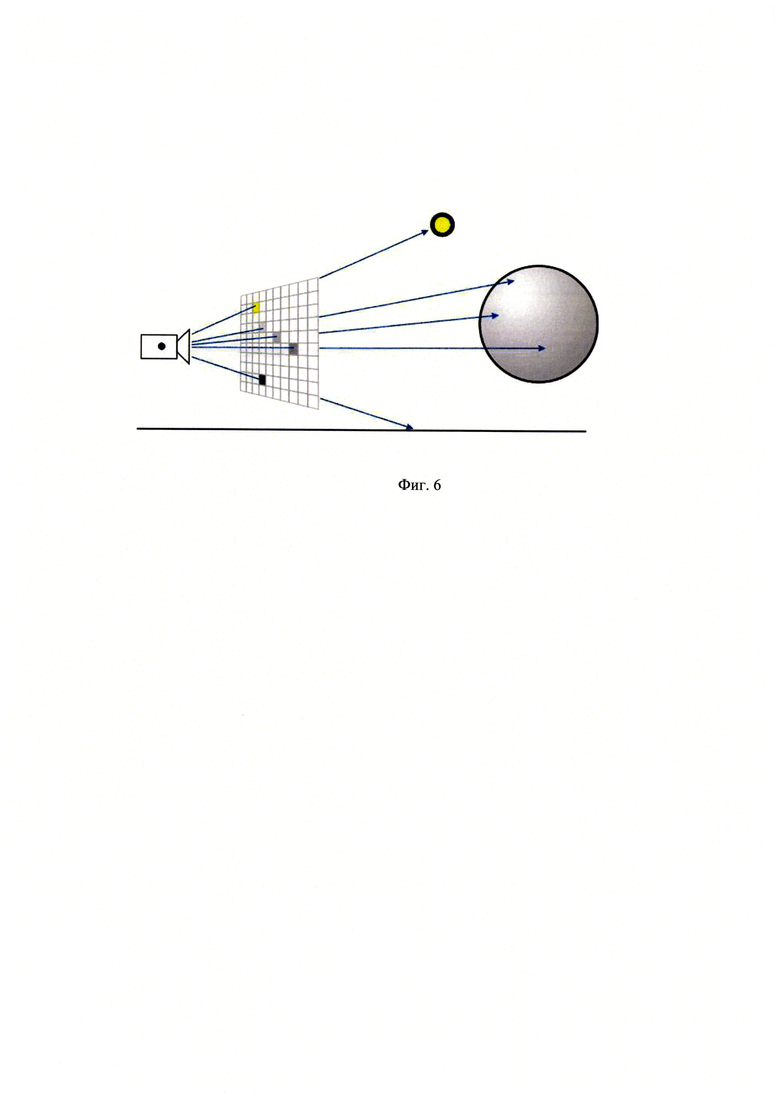
При рендеринге из виртуально наблюдаемой стороны текущей версии трехмерной модели объекта с помощью вычислительной системы создают двумерное фотореалистичное изображение объекта. Например, одним из способов рендеринга является метод трассировки лучей [9]. При этом методе формируемое изображение рассматривается как наблюдаемое из определенной точки. Из точки наблюдения на текущую версию трехмерной модели объекта направляются лучи, с помощью которых в каждой точке поверхности модели объекта определяется интенсивность и цвет отображаемого пикселя на двумерном изображении. Лучи прекращают свое распространение, когда достигают поверхности текущей версии трехмерной модели или используемой фоновой поверхности. Иллюстрация метода трассировки лучей при рендеринге показана на фиг. 6.
Для формирования текущего набора фотореалистичных изображений существующую в виде электронного образа в вычислительной системе текущую версию трехмерной модели объекта виртуально поворачивают на заданные угол азимута и угол места и формируют наблюдаемый ракурс изображения объекта. Значения углов азимута и углов места наблюдения текущей версии трехмерной модели объекта выбирают, исходя из возможных ракурсов физического наблюдения этого объекта, таких как вид спереди, сзади, с боков, горизонтально земной поверхности или под углом, включая вид сверху. Шаг изменения угла азимута и угла места выбирают не более нескольких градусов для увеличения числа изображений в текущем наборе фотореалистичных изображений, что повышает детальность представления текущих версий трехмерной модели объекта.
Далее каждый созданный текущий набор фотореалистичных изображений перемешивают случайным образом с набором натурных изображений других объектов и на перемешанных наборах выполняют операцию обнаружения объекта с использованием обученной сверточной нейронной сети, для которой априори неизвестно, какое изображение соответствует какому объекту. Вычисляют текущие значения вероятности обнаружения объекта на каждом текущем наборе фотореалистичных изображений. Вероятность обнаружения объекта на текущем наборе фотореалистичных изображений определяют как отношение числа изображений из текущего набора фотореалистичных изображений, на которых обученная сверточная нейронная сеть обнаруживает объект, к общему числу изображений в текущем наборе фотореалистичных изображений. Способы обнаружения объекта на изображении с использованием обученной сверточной нейронной сети описаны в работе [6].
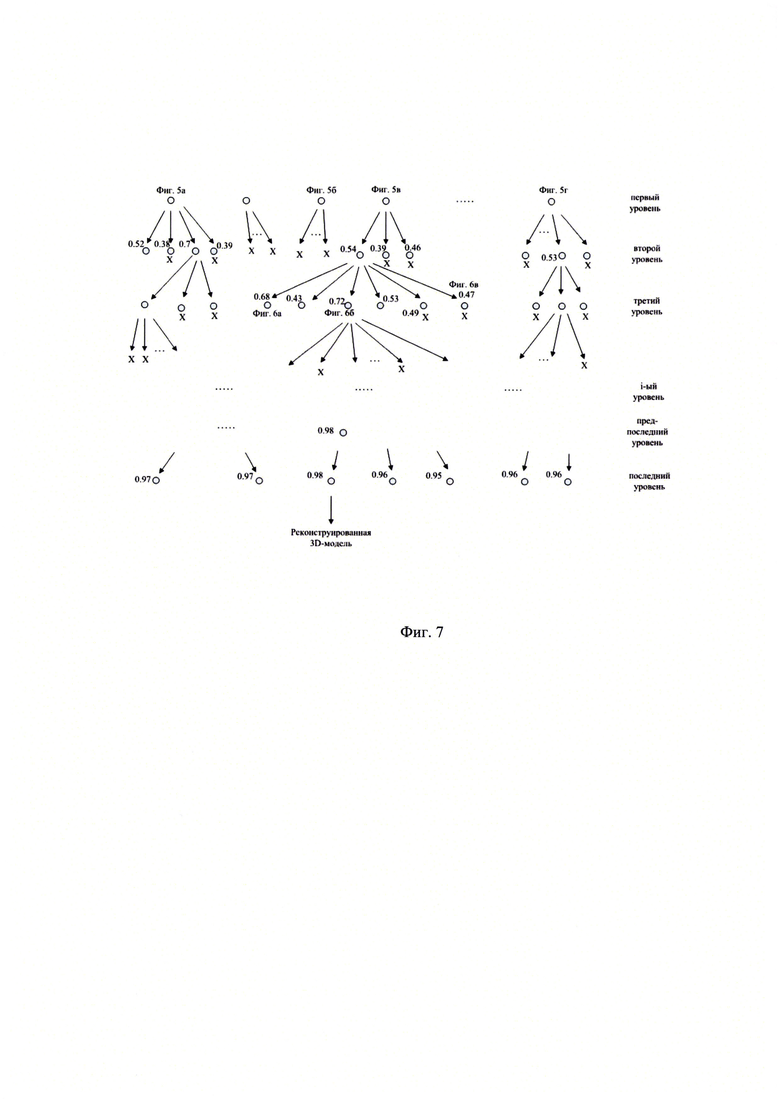
Чем ближе созданная текущая версия трехмерной модели объекта к точной модели этого объекта, тем выше полученное текущее значение вероятности обнаружения объекта на соответствующем ей наборе фотореалистичных изображений. Например, первоначально на текущих наборах фотореалистичных изображений определены значения вероятности обнаружения объекта 0.52, 0.38, 0,7, 0,39, …, 0.54, 0.39, 0.46 и т.д., как показано на фиг. 7 на первом уровне.
Затем среди вычисленных текущих значений вероятности обнаружения объекта выбирают М>2 наибольших значений вероятности обнаружения объекта и М соответствующих им текущих версий 3D-модели объекта. Способы выбора нескольких наибольших значений среди группы значений описаны в книге [10], и заключаются в поочередном сравнении между собой двух очередных значений вероятности, выбор в каждой паре большего значения, сортировке выбранных значений по мере возрастания значений вероятности и выборе среди отсортированных значений вероятности первых М значений с наибольшими значениями вероятности обнаружения объекта. Число М целесообразно выбирать не менее десятков, чтобы на очередной итерации не отбросить текущую версию трехмерной модели объекта, которая на данный момент не является явным лидером по обеспечиваемой вероятности обнаружения объекта, но которая при последующих изменениях совокупности своих параметров способна максимизировать данную вероятность, как рекомендуется при построении генетических алгоритмов, моделирующих процесс естественного отбора среди конкурирующих образцов [11].
В результате худшие текущие версии 3D-модели объекта отбрасываются, а лучшие сохраняются. Выбранные текущие версии 3D-модели объекта на текущей итерации реконструкции трехмерной модели являются среди сравниваемых наиболее близкими к точной модели этого объекта. Далее в соответствии с принципами эволюции лучшие на текущей итерации текущие версии 3D-модели объекта подвергают мутациям для получения на последующих итерациях более точных версии 3D-модели объекта. Например, первоначально на текущих наборах фотореалистичных изображений выбраны М текущих версий 3D-модели объекта со значениями вероятности обнаружения объекта 0.7, 0.59, 0.54, 0.53, как показано на фиг. 7 на первом уровне.
Способы создания из каждой выбранной версии 3D-модели объекта множества текущих версий 3D-модели объекта путем изменения не менее одного параметра ее формы, геометрических размеров, цветовых структур и отражающей способности поверхности заключаются в следующем. В каждой выбранной версии 3D-модели объекта изменяют описанным ранее образом недоступные для наблюдения и измерения параметры модели. При неизвестности геометрических размеров и формы ненаблюдаемых поверхностей объекта из множества возможных значений размера, определяемого размерами наблюдаемых поверхностей объекта, и множества возможных типов формы поверхностей, для каждой текущей версии 3D-модели объекта поочередно выбирают величины размера и тип формы. Например, на предыдущем этапе, в данном случае на первом уровне, при формировании множества текущих версий 3D-модели были определены возможные диапазоны геометрических размеров и типы форм ненаблюдаемых поверхностей объекта, далее для выбранных версий 3D-модели объекта значения этих параметров итеративно уточняются: для каждой текущей версии 3D-модели возможный диапазон геометрических размеров и перечень типов форм ненаблюдаемых поверхностей объекта сужаются за счет не оправдавших себя значений параметров отброшенных при выборе текущих версий 3D-модели объекта.
Также при неизвестности цветовых текстур и отражающей способности поверхности для каждой текущей версии 3D-модели объекта поочередно выбирают тип цветовой текстуры из предполагаемого множества возможных типов и значение отражающей способности поверхности из предполагаемого множества возможных значений. Например, предполагаемое множество возможных типов цветовых текстур состоит из вариантов камуфляжной окраски объекта, а предполагаемое множество возможных значений отражающей способности поверхности включает варианты освещения поверхности в различное время суток.
Для каждой текущей версии 3D-модели объекта возможно одновременно менять значение только одного параметра, формируя множество текущих версий 3D-модели объекта с последовательно изменяемыми значениями или типами по каждому параметру, или случайным образом выбирать два и более изменяемых параметра.
Например, на фиг. 8 показаны примеры визуализации текущих версий 3D-модели, созданных из ранее выбранной версии 3D-модели, показанной на фиг. 5в). Видно, что текущая версия 3D-модели на фиг. 8б) более точно отражает объект по сравнению с предшествующей ей ранее выбранной версией 3D-модели на фиг. 5в). Отметим, что на одно изменение какого-либо параметра модели объекта в сторону приближения к ее точной модели может приходиться десятки и сотни изменений, удаляющих текущую модель от ее точной модели. Но текущие модели с полезными изменениями параметров имеют больше шансов быть выбранными и сохраненными для дальнейшей эволюции по сравнению с текущими моделями с изменениями, уводящими в сторону от ее точной модели. Например, из первоначальной текущей версии 3D-модели, визуализация которой показана на фиг. 5в), которая имеет значение вероятности обнаружения объекта 0.54, созданы текущие версии 3D-модели второго уровня, для которых получены значения вероятности обнаружения объекта 0.68, 0.43, 0.72, …, 0.53, 0.49, 0.47, как показано на фиг. 7.
Повторно формируют из каждой текущей версии 3D-модели объекта текущие наборы фотореалистичных изображений и выполняют последующие действия до тех пор, пока возрастает значение хотя бы одного из наибольших значений вероятности обнаружения объекта. Например, на фиг. 7 показан граф создания и выбора текущих версий 3D-модели объекта. На первом (верхнем на рисунке) уровне представлено первоначально созданное множество текущих версий 3D-модели объекта, часть из которых изображена на фиг. 5а), фиг. 5б) и фиг. 5в). Из каждой первоначальной текущей версии 3D-модели созданы несколько текущих версий 3D-модели второго уровня, для каждой из которых вычислено текущее значение вероятности обнаружения объекта на соответствующем наборе изображений. Например, из первоначальной текущей версии 3D-модели, показанной на фиг. 5в) и имеющей значение вероятности обнаружения объекта 0.54, созданы текущие версии 3D-модели второго уровня, для которых получены значения вероятности обнаружения объекта от 0.47 до 0.72. Из всех созданных текущих версий 3D-модели второго уровня выбраны М текущих версий с максимальными значениями вероятности обнаружения объекта. Например, выбранные максимальные значения вероятности обнаружения объекта оказались в диапазоне от 0.52 до 0.72. Данные М текущих версий с максимальными для этого уровня значениями вероятности обнаружения объекта будут участвовать в дальнейшей эволюции текущих версий, и из них будут созданы текущие версии модели следующего уровня, а показавшие худшие результаты вероятности обнаружения объекта текущие версии далее не используются, что показано крестом на фиг. 7. Из М выбранных текущих версий 3D-модели второго уровня создают текущие версии 3D-модели третьего уровня и т.д. Например, из текущей версии 3D-модели второго уровня с максимальным значением вероятности обнаружения объекта 0.72, создают текущие версии 3D-модели третьего уровня с рядом значений вероятности обнаружения объекта от 0.47 до 0.75, то есть возрастает значение хотя бы одного из наибольших значений вероятности обнаружения объекта по сравнению с достигнутым значением на предыдущем уровне. Это свидетельствует о росте точности реконструируемой модели объекта.
Эволюционный процесс реконструкции 3D-модели объекта может состоять из десятков и сотен последовательных уровней, может заходить в тупик на лучшей по предыдущему значению вероятности обнаружения объекта текущей версии 3D-модели и продолжаться на других сохраняемых версиях модели и т.д. По своей физической сути данный эволюционный процесс реконструкции 3D-модели объекта выполняет направленный перебор возможных значений неизвестных параметров объекта с сохранением лучших версий и отбрасыванием худших версий.
В итоге процесса на последующих уровнях текущих версий 3D-модели прекращается рост вероятности обнаружения объекта по сравнению с предыдущими уровнями. Это означает исчерпание возможности дальнейшего уточнения модели. Например, на фиг. 7 на последнем уровне для текущих версий 3D-модели объекта максимальное значение вероятности обнаружения объекта 0.98 не превышает максимального значения вероятности обнаружения объекта на предыдущем уровне, равное 0.98.
В качестве реконструированной 3D-модели объекта из последнего достигнутого уровня текущих версий принимают текущую версию 3D-модели объекта с наибольшим значением вероятности обнаружения объекта и записывают ее в электронную память. Например, для реконструированной 3D-модели объекта типа боевая машина получено значение вероятности обнаружения объекта 0.98. Полученная реконструированная 3D-модель объекта показана на фиг. 9, она достаточно близка к точной 3D-модели объекта, изображенной на фиг. 4.
Проверка теоретических предпосылок заявленного способа реконструкции 3D-модели объекта выполнялась путем разработки и тестирования имитационной программы, реализующей предлагаемый способ.
Для различных объектов, являющимися самолетами различных типов и наземными транспортными средствами, в условиях полной доступности для наблюдения и измерения были созданы их точные 3D-модели. Затем для этих же объектов была существенно ограничена их доступность для наблюдения и измерения, и на основе неполных данных в соответствии с предлагаемым способом были реконструированы их 3D-модели. Попарное сравнение точных 3D-моделей и реконструированных 3D-моделей объектов показало практическую возможность существенного повышения точности построения 3D-модели различных объектов в условиях ограниченной доступности объекта для наблюдения и измерения его параметров.
Проведенные исследования подтверждают, что при использовании предлагаемого способа обеспечивается повышение повышения точности построения 3D-модели объекта в условиях ограниченной доступности объекта для наблюдения и измерения его параметров.
Источники информации
[1] Гайсина С. В. "Робототехника. 3D-моделирование, прототипирование". - СПб., Каро, 2017, -208 с.
[2] Patent US №8587583 В2. Three-dimensional environment reconstruction. 31.01.2011.
[3] Patent US №8270704 B2. Method and apparatus for reconstructing 3D shape model of object by using multi-view image information. 15.12.2008.
[4] Patent US №8532367 System and method for 3D wireframe from video. 17.08.2010.
[5] Способ реконструкции 3D-модели объекта. Патент РФ №2642167 от 14.08.2015, МПК G01V 3/18 (2006.01).
[6] Хайкин, Саймон. Нейронные сети: полный курс, 2-е издание.: Пер. с англ. - М.: Издательский дом "Вильяме", 2006. - 1104 с.
[7] Способ обучения нейронной сети. Патент РФ №2707147 от 31.10.2018, МПК G06N 3/08 (2006.01).
[8] Гарбуль А.А., Жданов Д.Д., Потемкин И.С., Соколов В.Г. Компьютерное моделирование изображений сложных трехмерных сцен, сформированных моделями реальных оптических систем: // Журнал Научная визуализация. МИФИ. 2013, том 5, номер 4. - С. 88-117.
[9] Ульянов А.Ю., Котюжанский Л.А., Рыжкова Н.Г. Метод трассировки лучей как основная технология фотореалистичного рендеринга: // Журнал Фундаментальные исследования. УФУ. 2015, №11. - С. 1124-1128.
[10] М. Сибуя, Т. Ямамото "Алгоритмы обработки данных". - М., Мир, 1986, стр. 122-134.
[11] Вороновский Г.К., Махотило К.В., Петрашев С.Н., Сергеев С.А., Генетические алгоритмы, искусственные нейронные сети и проблемы виртуальной реальности, Харьков, ОСНОВА, 1997. - 112 с.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ОБРАБОТКИ ИЗОБРАЖЕНИЙ ОБУЧЕННЫМИ НЕЙРОННЫМИ СЕТЯМИ | 2021 |
|
RU2779281C1 |
| Способ получения информации о форме и размерах трехмерного объекта по его двухмерному изображению | 2022 |
|
RU2816504C1 |
| СПОСОБ ОБРАБОТКИ ИЗОБРАЖЕНИЙ СВЕРТОЧНЫМИ НЕЙРОННЫМИ СЕТЯМИ | 2020 |
|
RU2771442C1 |
| СИСТЕМА ДЛЯ ГЕНЕРАЦИИ ВИДЕО С РЕКОНСТРУИРОВАННОЙ ФОТОРЕАЛИСТИЧНОЙ 3D-МОДЕЛЬЮ ЧЕЛОВЕКА, СПОСОБЫ НАСТРОЙКИ И РАБОТЫ ДАННОЙ СИСТЕМЫ | 2024 |
|
RU2834188C1 |
| НЕЙРОННАЯ ТОЧЕЧНАЯ ГРАФИКА | 2019 |
|
RU2729166C1 |
| ВИЗУАЛИЗАЦИЯ РЕКОНСТРУКЦИИ 3D-СЦЕНЫ С ИСПОЛЬЗОВАНИЕМ СЕМАНТИЧЕСКОЙ РЕГУЛЯРИЗАЦИИ НОРМАЛЕЙ TSDF ПРИ ОБУЧЕНИИ НЕЙРОННОЙ СЕТИ | 2023 |
|
RU2825722C1 |
| Способ распознавания речевых эмоций при помощи 3D сверточной нейронной сети | 2023 |
|
RU2816680C1 |
| СПОСОБ ОБРАБОТКИ ИЗОБРАЖЕНИЙ, УСТРОЙСТВО ОБРАБОТКИ ИЗОБРАЖЕНИЙ И НОСИТЕЛЬ ДАННЫХ | 2018 |
|
RU2709437C1 |
| НЕЙРОСЕТЕВОЙ ПЕРЕНОС ВЫРАЖЕНИЯ ЛИЦА И ПОЗЫ ГОЛОВЫ С ИСПОЛЬЗОВАНИЕМ СКРЫТЫХ ДЕСКРИПТОРОВ ПОЗЫ | 2020 |
|
RU2755396C1 |
| Способ обеспечения компьютерного зрения | 2022 |
|
RU2791587C1 |





Изобретение относится к области обработки изображений, и, в частности, оно ориентировано на построение 3D-модели объекта из изображений, получаемых в условиях ограниченной доступности объекта для наблюдения и измерения его параметров. Заявлен способ реконструкции 3D-модели объекта, согласно которому получают доступный набор натурных изображений объекта, на котором выполняют обучение сверточной нейронной сети. Первоначально создают множество текущих версий 3D-модели объекта на основе полученного набора натурных изображений объекта, формируют из каждой текущей версии 3D-модели объекта наборы изображений, обнаруживают объект на наборах изображений с использованием обученной сверточной нейронной сети. Вычисляют текущие значения вероятности обнаружения объекта на наборах изображений, выбирают среди вычисленных текущих значений вероятности обнаружения объекта М>2 наибольших значений вероятности обнаружения объекта и М соответствующих им текущих версий 3D-модели объекта. Из каждой выбранной версии 3D-модели объекта создают множество текущих версий 3D-модели объекта путем изменения не менее одного параметра ее формы, геометрических размеров, цветовых текстур и отражающей способности поверхности. Повторно формируют из каждой текущей версии 3D-модели объекта наборы изображений и выполняют последующие действия до тех пор, пока возрастает значение хотя бы одного из наибольших значений вероятности обнаружения объекта, иначе принимают в качестве реконструированной 3D-модели объекта текущую версию 3D-модели объекта с наибольшим значением вероятности обнаружения объекта. Технический результат - повышение точности построения модели в условиях ограниченной доступности объекта для наблюдения и измерения его параметров. 3 з.п. ф-лы, 9 ил.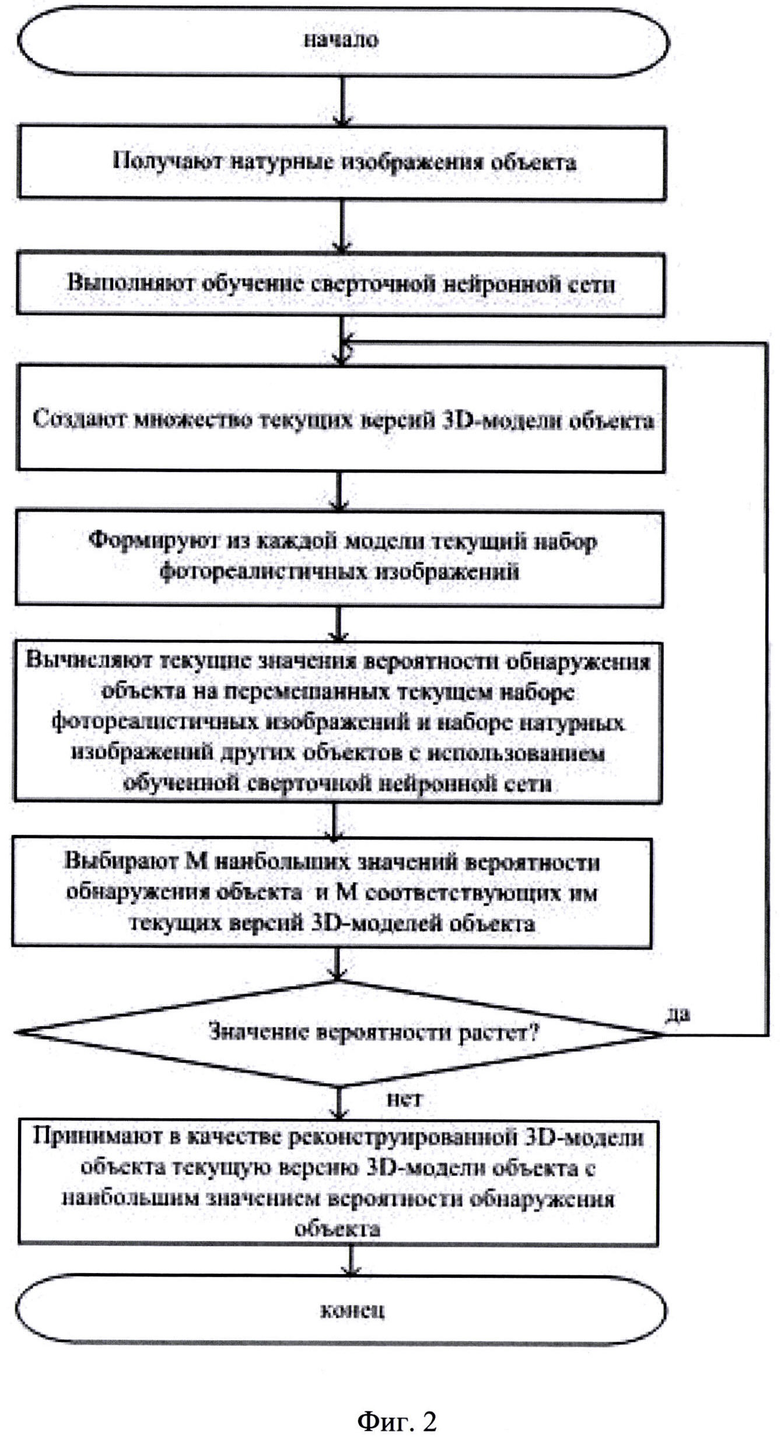
1. Способ реконструкции 3D-модели объекта, включающий получение набора натурных изображений объекта, сохранение реконструированной 3D-модели объекта в электронной памяти и ее отображение на модуле отображения, отличающийся тем, что на полученном наборе натурных изображений объекта выполняют обучение сверточной нейронной сети, первоначально создают множество текущих версий 3D-модели объекта, формируют из каждой текущей версии 3D-модели объекта текущие наборы фотореалистичных изображений, обнаруживают объект на перемешанных изображениях текущего набора фотореалистичных изображений объекта и набора натурных изображений других объектов с использованием обученной сверточной нейронной сети, вычисляют текущие значения вероятности обнаружения объекта на каждом текущем наборе фотореалистичных изображений, выбирают среди вычисленных текущих значений вероятности обнаружения объекта М>2 наибольших значений вероятности обнаружения объекта и М соответствующих им текущих версий 3D-модели объекта, из каждой выбранной версии 3D-модели объекта создают множество текущих версий 3D-модели объекта путем изменения не менее одного ее параметра, повторно формируют из каждой текущей версии 3D-модели объекта текущие наборы фотореалистичных изображений и выполняют последующие действия до тех пор, пока возрастает значение хотя бы одного из наибольших значений вероятности обнаружения объекта, иначе принимают в качестве реконструированной 3D-модели объекта текущую версию 3D-модели объекта с наибольшим значением вероятности обнаружения объекта.
2. Способ по п. 1, отличающийся тем, что создание множества текущих версий 3D-модели объекта первоначально выполняют на основе полученного набора натурных изображений объекта и результатов измерений объекта.
3. Способ по п. 1, отличающийся тем, что каждое фотореалистичное изображение из каждой текущей версии 3D-модели объекта является результатом рендеринга этой модели.
4. Способ по п. 1, отличающийся тем, что из каждой выбранной версии 3D-модели объекта создание множества текущих версий 3D-модели объекта выполняют путем изменения не менее одного параметра ее формы, геометрических размеров, цветовых текстур и отражающей способности поверхности.
| CN 111652966 A, 11.09.2020 | |||
| US 20190147642 A1, 16.05.2019 | |||
| EP 3690756 A1, 05.08.2020 | |||
| KR 2020080970 A, 07.07.2020 | |||
| ОБУЧЕНИЕ НЕЙРОННОЙ СЕТИ ПОСРЕДСТВОМ СПЕЦИАЛИЗИРОВАННЫХ ФУНКЦИЙ ПОТЕРЬ | 2018 |
|
RU2707147C1 |
| CN 110288697 A, 27.09.2019. | |||
Авторы
Даты
2022-09-05—Публикация
2020-11-12—Подача