Область техники
Изобретение относится к способам оптимизации условий кристаллизации белков для последующего выращивания белкового кристалла в оптимизированных условиях и расшифровки структуры белка с высоким разрешением с помощью рентгеноструктурного анализа и может быть применено в области белковой кристаллографии.
Уровень техники
Основным методом определения трехмерных структур белков на сегодняшний день является рентгеноструктурный анализ. Однако, для применения метода рентгеноструктурного анализа, особенно при определении структуры с высоким разрешением, необходимо вырастить высокосовершенный кристалл белка. Несмотря на успехи последних лет, получение высокосовершенного кристалла белка сложная и дорогостоящая задача, требующая хорошо оснащенной лаборатории.
Известен метод получения кристаллов белка из растворов с добавлением специальных добавок - осадителей. Подбор составов растворов в настоящее время производится методом проб и ошибок, когда вручную или автоматизировано осуществляется так называемый скрининг - проверка на наличие кристаллов белка большого числа растворов с широкой вариацией состава и концентраций осадителя, белка и буферных компонент.
К недостаткам данного метода относятся:
а) большое время, в течение которого происходит образование кристалла - в ряде случае на это уходят месяцы;
б) необходимость сравнительно больших количеств испытуемого белка, приводящего ввиду высокой стоимости и трудоемкости выделения чистых белков к дороговизне метода;
в) кристаллы необходимо тестировать с использованием источника синхротронного излучения на каждой итерации оптимизации условий кристаллизации.
Таким образом, стоимость кристаллизации белка определяется стоимостью реактивов и стоимостью доступа к оборудованию, в том числе, к источникам синхротронного излучения и может составлять от десятков тысяч до миллионов долларов за определение структуры белка при высоком разрешении.
В настоящее время существует множество подходов для улучшения качества белковых кристаллов. В качестве примера можно привести ряд методов, основанных на уменьшении конвекционного транспорта вещества к растущему кристаллу [K.M. Boyko, V.O. Popov, M.V. Kovalchuk 854 Russ. Chem. Rev. 84 (8) 853-859 (2015)]. Один из наиболее эффективным из таких подходов является выращивание кристаллов в условиях истинной микрогравитации. Существует множество примеров, где показано, что кристаллы, выращенные в условиях истинной микрогравитации имеют больший объем и лучшее дифракционное качество [V.A. Erdmann, C. Lippmann, C. Betzel, Z. Dauter, K. Wilson, R. Hilgenfeld, J. Hoven, A. Liesum, W. Saenger, A. Mullerfahrnow, W. Hinrichs, M. Duvel, G.E. Schulz, C.W. Muller, H.G. Wittmann, A. Yonath, G. Weber, K. Stegen, A. Plaaslink. FEBS Lett., 259, 194 (1989)]. Однако, очевидным недостатком такого подхода является его техническая сложность и дороговизна.
Наиболее близкой по технической сущности к заявляемому изобретению является измерение концентрации олигомеров кристаллизуемого белка методом малоуглового рассеяния рентгеновских лучей при проведении оптимизационного скрининга условий белковой кристаллизации [Investigation of the Initial Crystallization Stage in Lysozyme Solutions by Small-Angle X-ray Scattering Mikhail V. Kovalchuk, Alexander E. Blagov, Yulia A. Dyakova, Andrey Yu. Gruzinov, Margarita A. Marchenkova, Georgy S. Peters, Yury V. Pisarevsky, Vladimir I. Timofeev, and Vladimir V. Volkov Crystal Growth & Design 2016 16 (4), 1792-1797 DOI: 10.1021/acs.cgd.5b01662]. Была обнаружена связь между определенными физико-химическими условиями и формированием ассоциатов молекул белков, определенных размера и формы. Предложенный в данной работе метод ускоряет поиск условий кристаллизации белков и заключается в том, что с помощью малоуглового рассеяния рентгеновских лучей разнообразные растворы белка проверяются на наличие в них предкристаллизационной фазы, состоящей из олигомеров исследуемого белка. Если при определенных условиях в растворе обнаруживаются олигомеры белка, то такие условия считаются оптимальными для роста кристалла испытуемого белка и используются для дальнейшего выращивания белкового кристалла.
Недостатком данного метода является большое время образования олигомеров некоторых белков, высокая стоимость реактивов, необходимых в больших количествах, и необходимость в доступе к оборудованию для проведения экспериментов по малоугловому рассеянию рентгеновских лучей.
В последнее время развивается направление в вычислительной биологии, относящееся к исследованию белков в кристаллическом состоянии. Можно привести работы, в которых вычислительная биология используется для исследования процессов кристаллизации, например [PHYSICAL REVIEW Е 91, 033311 (2015) Simulation of protein association: Kinetic pathways towards crystal contacts Aaron Taudt, Axel Arnold and Jurgen Pleiss], где была предпринята попытка оценить изменение свободной энергии при формировании кристаллических контактов, но не исследовался состав кристаллизационных растворов, или [Biophysical Journal Volume 106 February 2014 677-686 Dependence of Protein Crystal Stability on Residue Charge States and Ion Content of Crystal Solvent Antonija Kuzmanic and Bojan Zagrovic], где изучалась зависимость стабильности кристалла белка от концентрации ионов, а также зарядов на поверхностных аминокислотных остатках, но при этом исследовалась сама кристаллическая структура белка, а не олигомеры, выделенные из неё.
В связи с тем, что вычислительный эксперимент позволяет не тратить дорогостоящий белок на стадии скрининга условий кристаллизации авторами заявляемого изобретения предлагается вместо метода малоуглового рассеяния рентгеновских лучей, использовать метод молекулярной динамики (МД). Это позволит ускорить процесс поиска наилучших условий кристаллизации, т.к. при МД расчётах не требуется ждать образования олигомеров.
Технической проблемой, на решение которой направлено заявляемое изобретение является уменьшение времени и стоимости процесса получения кристаллов белков.
Раскрытие сущности изобретения
Техническим результатом заявленного изобретения является удешевление и ускорение этапа оптимизационного скрининга условий кристаллизации белков.
Для достижения технического результата предложен способ оптимизации условий кристаллизации белков с применением метода молекулярной динамики, заключается в том, что выделяют олигомеры, содержащиеся в предкристаллизационном растворе, к полученным олигомерам применяют вычисление молекулярной динамики и изменения свободной энергии при формировании олигомера в различных условиях pH, типа осадителя, концентрации осадителя, температуры согласно следующему протоколу, заключающемуся в том, что для каждых моделируемых условий кристаллизации сначала задают pH системы путём определения состояний протонирования аминокислотных остатков в составе олигомеров с помощью программы PROPKA, после чего все расчёты и подготовку структур к ним выполняют в программном пакете GROMACS, подготовленные структуры помещают в центр ячейки моделирования, при этом, минимальное расстояние между её краем и молекулой белка составляет 1 нм, при этом, остальное пространство ячейки заполняют водой, в систему добавляют компоненты осадителя в необходимой концентрации, осуществляют минимизацию энергии и NVT- и NPT-уравновешивание систем, проводят вычисление продуктивной МД в NPT-ансамбле, при этом, интегрирование производят по стандартному алгоритму leap-frog с временным шагом интегрирования 2 фс и длительностью рассчитанных траекторий 100 нс, при этом, перед анализом полученных траекторий устраняют артефакты, возникающие из-за квазибесконечных периодических граничных условий, по данным полученных траекторий строят графики среднеквадратичных флуктуаций атомов Сц (RMSF) и вычисляют изменения энергий при образовании олигомеров белка, при этом, для расчётов изменения свободной энергии при образовании олигомеров используют метод MM/GBSA, проводят вычисление свободной энергии для каждой траектории по результатам МД-моделирования, с помощью программы GROMACS, на 1000 фреймах с применением модуля gmx MMPBSA версии 1.4.0 в сочетании со скриптом MMPBSA.py и пакетом AmberTools20, устанавливают оптимальные для кристаллизации исследуемого белка параметры, при которых наблюдаются наименьшие среднеквадратичные флуктуации атомов олигомеров и наибольшее уменьшение свободной энергии.
Краткое описание чертежей
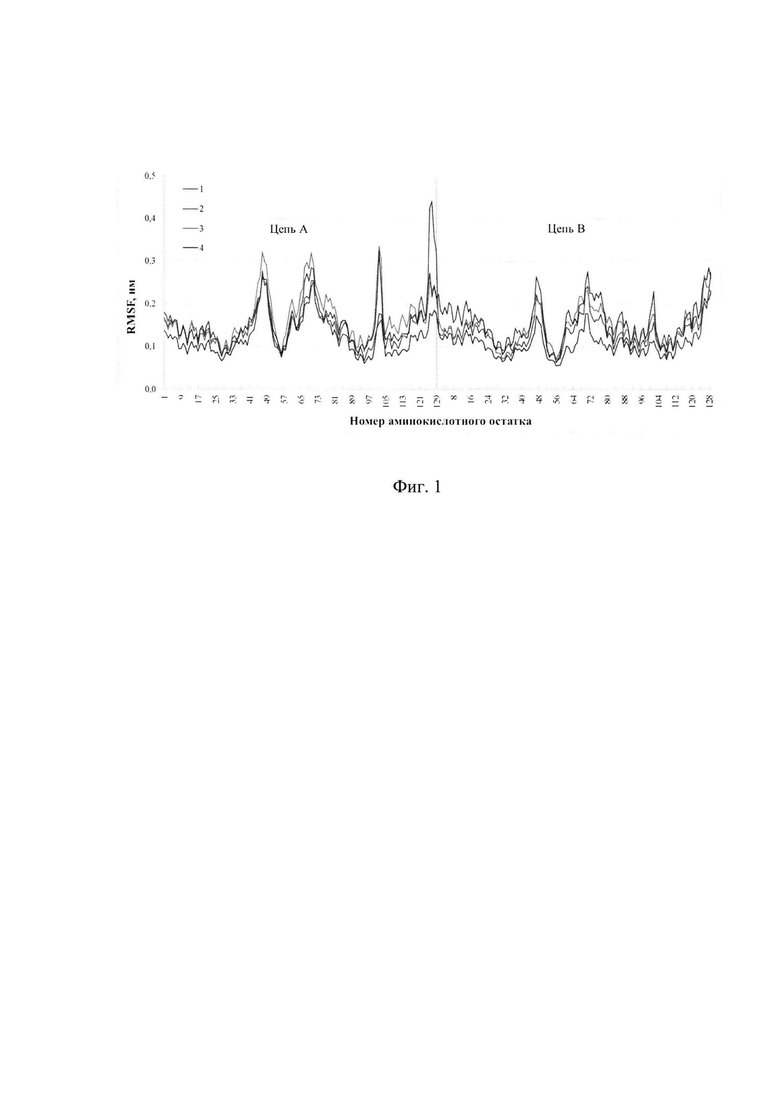
На фиг. 1 показаны графики RMSF атомов Сα разных моделей димеров, смоделированных в растворе с осадителем: с ионами Na и Cl, связанными с белком (1), только с ионами Na в структуре димера (2) и без ионов осадителя, встроенных в молекулу лизоцима (3), а также без ионов Na и Cl как в растворе, так и в структуре белка (4).
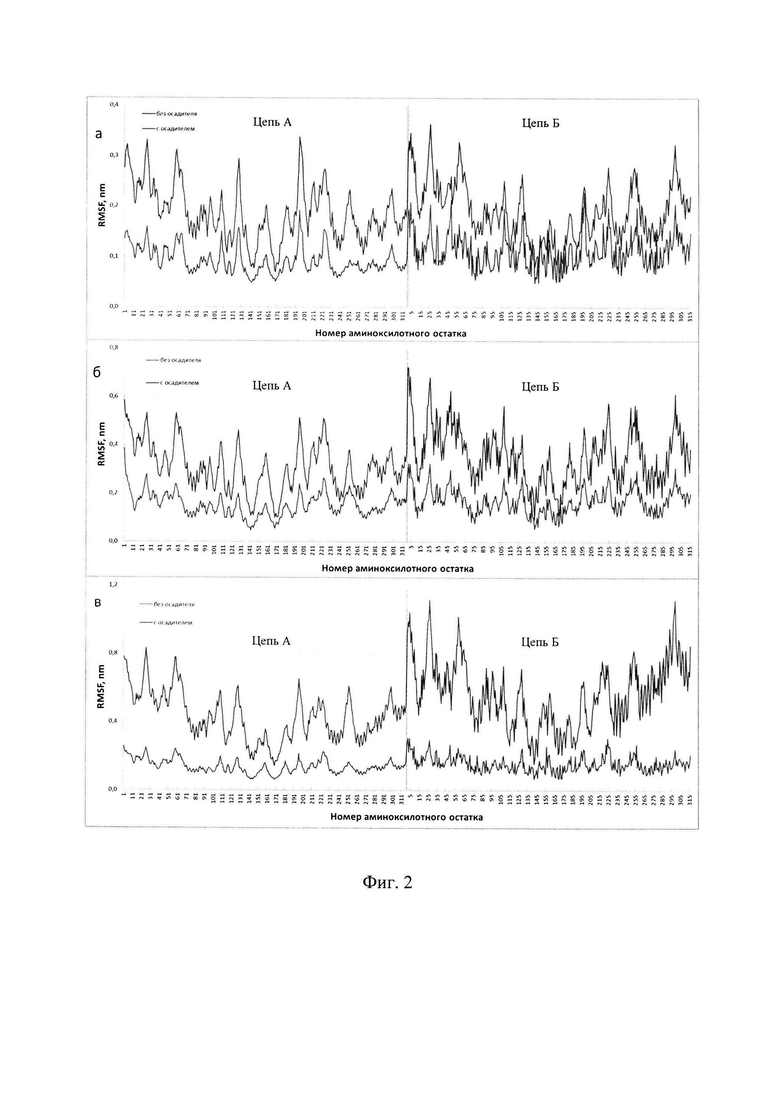
На фиг. 2 показаны графики RMSF атомов Сα димеров термолизина, смоделированных в растворе с осадителем (синяя кривая) и без него (красная) при 10 (а), 15 (б) и 20°С (в).
Осуществление изобретения
Способ оптимизации условий кристаллизации белков с применением метода молекулярной динамики заключается в моделировании МД выделенных из кристаллической структуры олигомеров белка в различных условиях (состав раствора, температура и т.д.), последующей оценки их стабильности в моделируемых условиях на основе анализа среднеквадратичных флуктуаций атомов белка и изменения свободной энергии при образовании ассоциатов молекул белка методом MM-GBSA и в конечном итоге выборе наиболее оптимальных для кристаллизации условий, при которых наблюдались наибольшая стабильность и уменьшение свободной энергии связывания.
Заявляемое решение состоит из следующих этапов:
1. Выделяют олигомеры, содержащиеся в предкристаллизационном растворе.
2. К полученным олигомерам применяют вычисление молекулярной динамики и изменения свободной энергии при формировании олигомера в различных условиях согласно следующему протоколу.
Для каждых моделируемых условий кристаллизации сначала задают рН системы путем определения состояний протонирования аминокислотных остатков в составе олигомеров с помощью программы PROPKA.
После этого все расчеты и подготовку структур к ним выполняют в программном пакете GROMACS. Подготовленные структуры помещают в центр ячейки моделирования, при этом минимальное расстояние между ее краем и молекулой белка составляет 1 нм. Остальное пространство ячейки заполняют водой. Далее в систему добавляют компоненты осадителя в необходимой концентрации.
Затем осуществляют минимизацию энергии и NVT- и NPT-уравновешивание систем. Вычисления продуктивной МД производят в NPT-ансамбле. Интегрирование происходит по стандартному алгоритму leap-frog, с временным шагом интегрирования 2 фс. Длительность рассчитанных траекторий составляет 100 нс.
Перед анализом полученных траекторий устраняют артефакты, возникающие из-за квазибесконечных периодических граничных условий. После чего по данным полученных траекторий строят графики среднеквадратичных флуктуаций атомов Сα (RMSF) и вычисляют изменения энергий при образовании олигомеров белка.
Для расчетов изменения свободной энергии при образовании олигомеров используют метод MM/GBSA. Цель данного подхода состоит в определении разницы между значениями свободной энергии сольватированной молекулы в связанном и свободном состояниях.
Вычисление свободной энергии для каждой траектории проводят по результатам МД-моделирования, проведенного с помощью программы GROMACS, на 1000 фреймах с применением модуля gmx_MMPBSA версии 1.4.0 в сочетании со скриптом MMPBSA.py, после чего выбирают параметры с наименьшими среднеквадратичными флуктуациями атомов и наибольшим уменьшением свободной энергии.
3. Выбранные концентрации осадителя, тип осадителя, рН, температура, соответствующие наибольшему уменьшению свободной энергии и наименьшим RMSF применяют для выращивания кристалла белка.
4. Выращенный кристалл белка исследуют с использованием источника синхротронного излучения.
5. На основе полученного рентгенодифракционного набора устанавливают трехмерную структуру белка при высоком разрешении. В качестве результата возникает набор координат атомов исследуемого белка, связанных с белком функциональных лигандов, а также связанных с белком молекул воды и ионов.
Примеры реализации.
Первые испытания проводились с использованием модельного белка лизоцима.
1. Молекулярные модели возможных единиц роста кристаллов лизоцима выделялись из кристаллических структур лизоцима тетрагональной сингонии из Protein Data Bank (PDB ID: 4WLD и 6QWY). Данные структуры отличаются тем, что в молекуле 4WLD присутствует только ион натрия, связанный с подвижной петлей 37-72, тогда как в 6QWY удалость выявить ряд дополнительных позиций ионов натрия и хлора: на один мономер белка приходится 3 иона натрия и 4 иона хлора. В PDB файлах 4WLD и 6QWY присутствуют остатки (4WLD: AS 77, 6QWY: ASN 19, ASN 59 и SER 85), существующие в кристалле в двух конформациях с одинаковыми коэффициентами заполнения (0.5), из которых была оставлена конформация А. С помощью программы PyMOL, применяя соответствующие операторы (-X,-Y,l/2+Z; 1/2-Y,l/2+X,3/4+Z; l/2+Y,l/2-X,l/4+Z; l/2-X,l/2+Y,3/4-Z; l/2+X,l/2-Y,l/4-Z; Y,X,-Z; -Y,-X,l/2-Z), были восстановлены фрагменты кристаллической решетки лизоцима тетрагональной сингонии и получены координаты димера.
Все расчеты и подготовка структур к были выполнены с помощью программного пакета GROMACS версии 5.0.4 [Van Der Spoel D. et al. GROMACS: Fast, flexible, and free // Journal of Computational Chemistry. 2005.]. В качестве силового поля использовалось Amber ff99SB-ILD [Lindorff-Larsen K. et al. Improved side-chain torsion potentials for the Amber ff99SB protein force field // Proteins Struct. Funct. Bioinforma. 2010. Vol. 78, №8. P. 1950-1958.], поскольку в него добавлены новые параметры потенциалов для некоторых торсионных углов.
2. Расчет ионизационных состояний аминокислотных остатков при рН 4.5 (в соответствии с экспериментальными условиями) проводили с помощью сервера PROPKA [Dolinsky T.J. et al. PDB2PQR: An automated pipeline for the setup of Poisson-Boltzmann electrostatics calculations // Nucleic Acids Res. 2004.].
Димеры помещались в центр кубической ячейки моделирования, размеры которой задавались таким образом, чтобы расстояние между любым атомом белка и краем ячейки составляло не менее 1 нм. При уравновешивании системы и продуктивной симуляции МД применялись периодические граничные условия по трем координатам, а дальнодействующие электростатические взаимодействия учитывались методом ускоренного суммирования по Эвальду РМЕ [Essmann U. et al. A smooth particle mesh Ewald method // J. Chem. Phys. 1995. Vol. 103. P. 8577-8592.] с кубической интерполяцией и шагом сетки в Фурье-пространстве 0.16 нм. Нековалентные взаимодействия учитывались только для атомов, находящихся на расстоянии не более 1 нм друг от друга. Для накладывания ограничений на все связи применялся алгоритм LINCS [Hess В. et al. LINCS: A Linear Constraint Solver for molecular simulations //J. Comput. Chem. 1997. Vol. 18. P. 1463-1472.].
Для заполнения ячейки моделирования растворителем была выбрана 4-сайтовая модель воды типа TIP4P-Ew [Horn H.W. et al. Development of an improved four-site water model for biomolecular simulations: TIP4P-Ew // J. Chem. Phys. 2004. Vol. 120, №20. P. 9665-9678.] для выполнения МД расчетов с применением метода суммирования зарядов по Эвальду. В случаях расчетов с добавлением осадителя в растворы молекулы воды заменялись ионами Na и Cl таким образом, чтобы концентрация осадителя в ячейке составляла 0.4 М. Для нейтрализации суммарного заряда каждой системы добавлялось незначительное количество ионов хлора.
Перед каждым запуском расчетов продуктивной МД проводилась минимизация энергии системы методом наискорейшего спуска (50000 шагов) до тех пор, пока сила, действующая на любой атом, не оказывалась меньше 1000 кДж⋅M-1нм-1. Затем производились 100-пикосекундное термостатирование системы улучшенным методом Берендсена [Berendsen H.J.С. et al. Molecular dynamics with coupling to an external bath // J. Chem. Phys. 1984. Vol. 81, №8. P. 3684-3690.] и баростатирование методом Паринелло-Рамана [Parrinello М., Rahman A. Strain fluctuations and elastic constants // J. Chem. Phys. 1982. Vol. 76, №5. p.2662-2666.] (100 пс), при этом на все неводородные атомы белка накладывались ограничивающие силы (kpr=1000 кДж/(М⋅нм2)).
Моделирование МД проводилось в изотермическо-изобарическом ансамбле с использованием термостата Берендсена и баростата Паринелло-Рамана (при Р=1 атм для всех систем) при 10°С. Интегрирование производилось с помощью стандартного интегратора leap-frog [Van Gunsteren W.F., Berendsen H.J.C. A Leap-Frog Algorithm for Stochastic Dynamics // Mol. Simul. 1988. Vol.1, №3. P. 173-185.], временной шаг интегрирования равнялся 2 фс. Длительность каждой рассчитанной траектории димеров белка составила 100 нс. Работа была выполнена с использованием суперкомпьютера «Комплекс моделирования и обработки данных исследовательских установок мега-класса» НИЦ «Курчатовский институт».
Перед анализом полученных траекторий артефакты, возникшие из-за квазибесконечных периодических граничных условий, устранялись с помощью команды gmx trjconv с флагом -pbc nojump, возвращая димер обратно в ячейку моделирования. После чего были посчитаны значения и построены графики среднеквадратичных флуктуаций атомов Сα (RMSF).
Из сравнения полученных графиков RMSF (фиг. 1) заметно, что кривая, соответствующая модели димера с учетом всех ионов осадителя, лежит ниже остальных. Это свидетельствует об относительной устойчивости данной модели. Из фиг. 1 видно, что наибольшая разница в значениях RMSF (в диапазоне от 0.1 до 0.27 нм) между разными моделями наблюдается в области аминокислотных остатков ARG125, GLY126, CYS127, ARG128, LEU129 цепи А и LYS1 цепи В. Максимальное значение RMSF на фиг. 1 составляет 0.44 нм (для LYS1 цепи В димера со встроенными ионами Na) и говорит о том, что исследуемые траектории димеров достаточно стабильны для применения к ним метода MM/GBSA.
В таблице 1 приведены результаты усреднения значений RMSF по всем атомам для каждой кривой, представленной на фиг. 1.

Как видно из табл. 1 наименее стабильным является димер, моделируемый без учета каких-либо ионов осадителя, т.к. усредненное значение RMSF его атомов в этом случае является наибольшим (0.1566 нм).
Изменение свободной энергии при связывании мономеров с образованием димера вычислялось методом MM/GBSA с помощью модуля gmx_MMPBSA [Mario S. Valdes Tresanco, Mario E. Valdes-Tresanco, Pedro A. Valiente & E.M.F. gmx_MMPBSA (Version vl.4.1). Zenodo. http://doi.org/10.5281/zenodo.4569307.] версии 1.4.0 в сочетании со скриптом MMPBSA.py [Miller B.R. et al. MMPBSA.py: An efficient program for end-state free energy calculations // J. Chem. Theory Comput. 2012. Vol. 8, №9. P. 3314- 3321.] и пакетом AmberTools20 [D.A. Case, K. Belfon, I.Y. Ben-Shalom, S.R. Brozell, D.S. Cerutti, Т.Е. Cheatham, III, V.W.D. Cruzeiro, T.A. Darden, R.E. Duke, G. Giambasu, M.K. Gilson, H. Gohlke, A.W. Goetz, R. Harris, S. Izadi, S.A. Izmailov, K. Kasavajhala, A. Kovalenko, R. Krasny, T D.M.Y. and P.A.K. AMBER 2020, University of California, San Francisco. 2020.]. Вычисление свободной энергии для каждой траектории проводилось на 1000 фреймах. Результаты расчетов изменения свободной энергии образования димеров представлены в таблице 2.
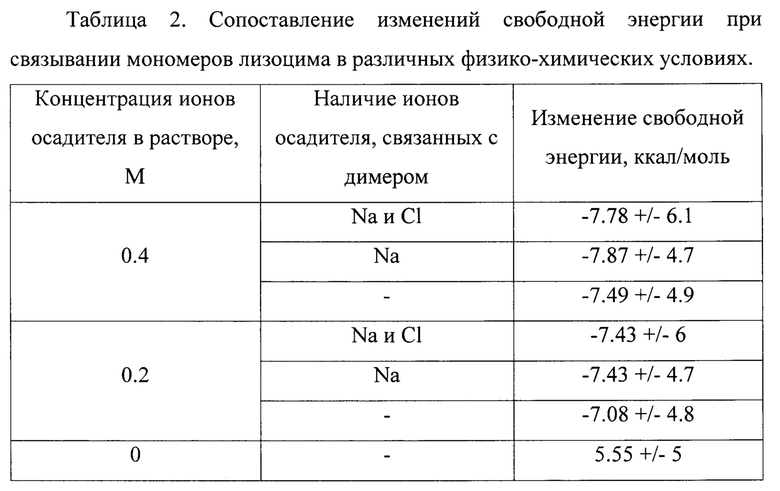
Из таблицы 2 следует, что наиболее энергетически выгодной является система с учетом ионов осадителя, причем с увеличением концентрации NaCl от 0.2 до 0.4 М, а также при моделировании димеров с ионами осадителя, встроенных в белок (всех или только анионов - не имеет существенного значения), энергия мономеров при их связывании понижается. Следует отметить, что в случае отсутствия ионов осадителя в растворе, для молекул лизоцима более энергетически выгодным является мономерное состояние.
Таким образом, по результатам оценки стабильности димеров по графикам RMSF и расчетов изменения свободной энергии при связывании мономеров показано, что наличие осадителя NaCl в растворе, а также учет ионов осадителя, встроенных в белок, приводит к тому, что формирование димеров из молекул лизоцима становится энергетически выгодным.
В следующих испытаниях исследовалась стабильность димера белка термолизина при температуре 10, 15 и 20°С.
1. Молекулярные модели возможных единиц роста кристаллов термолизина были выделены из кристаллической структуры термолизина гексагональной сингонии из Protein Data Bank (PDB ID: 3DNZ), определенной с разрешением 1.2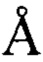 . В PDB файле 3DNZ присутствуют остатки (THR 49, SER 53, ASN 89, МЕТ 120, TYR 157 и SER 161), существующие в кристалле в двух конформациях с одинаковыми коэффициентами заполнения (0.5), из которых была оставлена конформация А. С помощью программы PyMOL, применяя соответствующие операторы симметрии (-Y,X-Y,Z+1/3; -X+Y,-X,Z+2/3; -X,-Y,Z+1/2; Y,-X+Y,Z+5/6; X-Y,X,Z+l/6; Y,X,-Z+1/3; X-Y,-Y,-Z; -X,-X+Y,-Z+2/3; -Y,-X,-Z+5/6; -X+Y,Y,-Z+1/2; X,X-Y,-Z+1/6), был восстановлен фрагмент кристаллической решетки термолизина гексагональной сингонии и получены координаты димера. В структуре олигомеров были оставлены лиганды (ионы кальция и цинка), связанные с термолизином (на одну молекулу белка приходится 4 иона кальция и 1 ион цинка), и удалена кристаллическая вода.
. В PDB файле 3DNZ присутствуют остатки (THR 49, SER 53, ASN 89, МЕТ 120, TYR 157 и SER 161), существующие в кристалле в двух конформациях с одинаковыми коэффициентами заполнения (0.5), из которых была оставлена конформация А. С помощью программы PyMOL, применяя соответствующие операторы симметрии (-Y,X-Y,Z+1/3; -X+Y,-X,Z+2/3; -X,-Y,Z+1/2; Y,-X+Y,Z+5/6; X-Y,X,Z+l/6; Y,X,-Z+1/3; X-Y,-Y,-Z; -X,-X+Y,-Z+2/3; -Y,-X,-Z+5/6; -X+Y,Y,-Z+1/2; X,X-Y,-Z+1/6), был восстановлен фрагмент кристаллической решетки термолизина гексагональной сингонии и получены координаты димера. В структуре олигомеров были оставлены лиганды (ионы кальция и цинка), связанные с термолизином (на одну молекулу белка приходится 4 иона кальция и 1 ион цинка), и удалена кристаллическая вода.
2. Все расчеты и подготовка структур к были выполнены с помощью программного пакета GROMACS версии 5.0.4 [Van Der Spoel D. et al. GROMACS: Fast, flexible, and free // Journal of Computational Chemistry. 2005.]. Молекулярная динамика моделировалась в поле Amber ff99SB-ILDN [Lindorff-Larsen К. et al. Improved side-chain torsion potentials for the Amber ff99SB protein force field // Proteins Struct. Funct. Bioinforma. 2010. Vol. 78, №8. P. 1950-1958.]. Состояния протонирования аминокислотных остатков в составе димеров термолизина при рН 8.5 (в соответствии с экспериментальными условиями) были определены с помощью сервера PROPKA. [Dolinsky Т.J. et al. PDB2PQR: An automated pipeline for the setup of Poisson-Boltzmann electrostatics calculations // Nucleic Acids Res. 2004.].
Моделирование проводилось с применением периодических граничных условий по трем координатам. Была создана кубическая ячейка моделирования, в центр которой помещался димер белка. Размеры ячейки моделирования задавались таким образом, чтобы расстояние между любым атомом термолизина и краем ячейки составляло не менее 1 нм. При уравновешивании системы и продуктивной симуляции МД дальнодействующие электростатические взаимодействия учитывались методом ускоренного суммирования по Эвальду РМЕ [Essmann U. et al. А smooth particle mesh Ewald method // J. Chem. Phys. 1995. Vol. 103. P. 8577-8592.] с кубической интерполяцией и шагом сетки в Фурье-пространстве 0.16 нм. Нековалентные взаимодействия учитывались только для атомов, находящихся на расстоянии не более 1 нм друг от друга. Для накладывания ограничений на все связи применялся алгоритм LINCS [Hess В. et al. LINCS: A Linear Constraint Solver for molecular simulations // J. Comput. Chem. 1997. Vol. 18. P. 1463-1472.].
Для заполнения ячейки моделирования растворителем была выбрана 4-сайтовая модель воды TIP4P-Ew [Horn H.W. et al. Development of an improved four-site water model for biomolecular simulations: TIP4P-Ew // J. Chem. Phys. 2004. Vol. 120, №20. P. 9665-9678.]. В случаях расчетов с добавлением осадителя в растворы молекулы воды заменялись ионами аммония и сульфата таким образом, чтобы концентрация осадителя в ячейке составляла 0.75 М. Трехмерная структура аммония была взята из PDB (code: NH4). 3D структура сульфата была получена из PLMD (Peptide Ligand Molecular Dynamics) модуля и конвертирована из формата mol2 в pdb с помощью алгоритма Antechamber. Общий заряд системы нейтрализовался добавлением незначительного количества ионов хлора (2 иона).
Перед каждым запуском расчетов продуктивной МД проводилась минимизация энергии системы методом наискорейшего спуска (50000 шагов) до тех пор, пока сила, действующая на любой атом, не оказывалась меньше 1000 нДж⋅М-1нм-1. Затем производились 100-пикосекундное термостатирование системы улучшенным методом Берендсена [Berendsen H.J.C. et al. Molecular dynamics with coupling to an external bath // J. Chem. Phys. 1984. Vol. 81, №8. P. 3684-3690.] и баростатирование методом Паринелло-Рамана [Parrinello М., Rahman A. Strain fluctuations and elastic constants // J. Chem. Phys. 1982. Vol. 76, №5. P. 2662-2666.] (100 пс), при этом на все неводородные атомы белка накладывались ограничивающие силы (kpr=1000 кДж/(М⋅нм2)).
Моделирование МД проводилось в изотермическо-изобарическом ансамбле с использованием термостата Берендсена и баростата Паринелло-Рамана (при Р=1 атм для всех систем) при 10°С. Интегрирование производилось с помощью стандартного интегратора leap-frog [Van Gunsteren W.F., Berendsen H.J.C. A Leap-Frog Algorithm for Stochastic Dynamics // Mol. Simul. 1988. Vol. 1, №3. P. 173-185.], временной шаг интегрирования равнялся 2 фс. Расчет МД димеров происходил по три раза при 283, 288 и 293 К. Для каждого значения температуры динамика моделировалась в водном растворе как в присутствии осадителя, так и в его отсутствие. Длительность каждой рассчитанной траектории димеров белка составила 100 нс. Работа была выполнена с использованием суперкомпьютера «Комплекс моделирования и обработки данных исследовательских установок мега-класса» НИЦ «Курчатовский институт».
Перед анализом полученных траекторий артефакты, возникшие из-за квазибесконечных периодических граничных условий, устранялись с помощью команды gmx trjconv с флагом -pbc nojump, возвращая димер обратно в ячейку моделирования. После чего были посчитаны значения и построены графики среднеквадратичных флуктуаций атомов Сα (RMSF).
Из полученных результатов (фиг. 2) видно, что при каждой рассматриваемой температуре красная кривая, соответствующая случаю димера в растворе без осадителя, лежит выше синей кривой, отвечающей за моделирование с добавлением осадителя в раствор, т.е. в присутствии осадителя в растворе димер стабильнее, чем без него. Это свидетельствует о том, что оценка относительной стабильности димера термолизина по графикам RMSF согласуется с результатами экспериментов по МУРР, указывающих на наличие димеров в предкристаллизационном растворе термолизина и их отсутствие в водном растворе без осадителя.
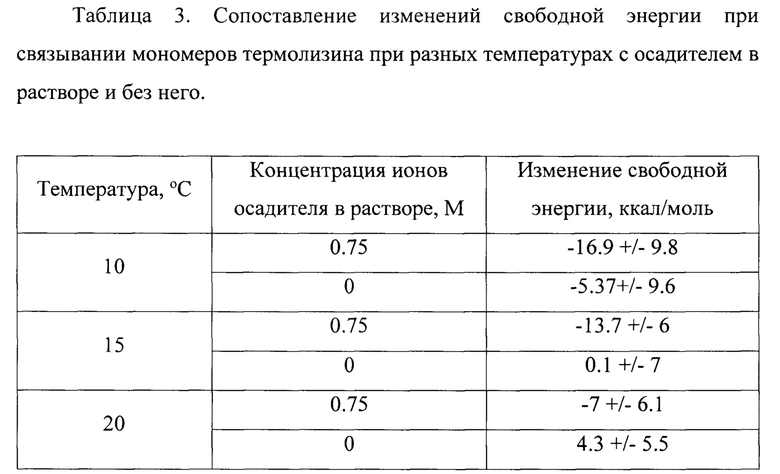
Из табл. 3 следует, что при всех рассматриваемых температурах наиболее энергетически выгодной является система с учетом ионов осадителя добавленных в раствор. Кроме того, с увеличением температуры связывание мономеров становится все менее энергетически выгодным, что согласуется с экспериментом по МУРР, в результате которого было обнаружено, что концентрация димеров термолизина в предкристаллизационном растворе падает с ростом температуры.
Таким образом, по результатам оценки стабильности димеров по графикам RMSF и расчетов изменения свободной энергии при связывании мономеров показано, что формирование димеров из молекул термолизина является более энергетически выгодным при добавлении осадителя сульфата аммония в раствор, а также уменьшении температуры до 10°С.
Из данных испытаний понятна потенциальная применимость данного метода для оптимизации условий кристаллизации белков. Показано, что параметры смоделированных систем, при которых наблюдаются наименьшие среднеквадратичные флуктуации атомов олигомеров и наибольшее уменьшение свободной энергии при их образовании, совпадают с параметрами, известными как наиболее оптимальные для кристаллизации лизоцима и термолизина.
Таким образом, предложен улучшенный способ проведения оптимизационного скрининга условий белковой кристаллизации, заменяющий измерение концентрации олигомеров кристаллизуемого белка методом малоуглового рассеяния рентгеновских лучей моделированием поведения белковых олигомеров в различных физико-химических условиях и оценки их стабильности в моделируемых условиях на основе анализа среднеквадратичных флуктуаций атомов белка и изменения свободной энергии при образовании ассоциатов молекул белка методом MM-GBSA.
Совокупность приведенных выше признаков приводит к тому, что существенно сокращаются:
1. время проведения оптимизационного скрининга;
2. требуемое количество испытуемого белка, а, следовательно, и стоимость кристаллизационного эксперимента.
| название | год | авторы | номер документа |
|---|---|---|---|
| УСТРОЙСТВО И СПОСОБЫ ДЛЯ ОТБОРА АНТИТЕЛ | 2014 |
|
RU2742070C2 |
| СПОСОБ ИДЕНТИФИКАЦИИ УЧАСТКОВ СВЯЗЫВАНИЯ БЕЛКОВЫХ КОМПЛЕКСОВ | 2020 |
|
RU2743316C1 |
| Способ определения условий кристаллизации белков | 2016 |
|
RU2626576C1 |
| Способ получения упорядоченных пленок лизоцима на твердых подложках в ленгмюровской ванне | 2017 |
|
RU2672410C1 |
| КРИСТАЛЛ БЕЛКА, СШИТОГО МНОГОФУНКЦИОНАЛЬНЫМ СШИВАЮЩИМ АГЕНТОМ (ВАРИАНТЫ), УСТРОЙСТВО, СОДЕРЖАЩЕЕ ЭТОТ КРИСТАЛЛ, И СПОСОБ ПОЛУЧЕНИЯ АСПАРТАМА | 1991 |
|
RU2124052C1 |
| МОДИФИЦИРОВАННАЯ АЦИЛ-АСР ДЕСАТУРАЗА | 1997 |
|
RU2228356C2 |
| СПОСОБЫ МОДЕЛИРОВАНИЯ МЕЖМОЛЕКУЛЯРНОГО ВЗАИМОДЕЙСТВИЯ И ОСНОВАННЫЙ НА НИХ СПОСОБ ПРОГНОЗИРОВАНИЯ СВЯЗЫВАНИЯ МОЛЕКУЛЫ-ЛИГАНДА С МОЛЕКУЛОЙ-МИШЕНЬЮ | 2003 |
|
RU2265243C2 |
| СБОР ТЕПЛОВОЙ ЭНЕРГИИ НАНОМАШИНАМИ | 2022 |
|
RU2829764C2 |
| ДНК-АПТАМЕРЫ, ИНГИБИРУЮЩИЕ ТРОМБИН, И СПОСОБ СТАБИЛИЗАЦИИ ИХ СТРУКТУРЫ | 2009 |
|
RU2429293C1 |
| СПОСОБ ПОЛУЧЕНИЯ ОЛИГОМЕРОВ ВЫСШИХ ЛИНЕЙНЫХ АЛЬФА-ОЛЕФИНОВ | 2011 |
|
RU2483052C2 |
Изобретение относится к способам оптимизации условий кристаллизации белков для последующего выращивания белкового кристалла в оптимизированных условиях и расшифровки структуры белка с высоким разрешением с помощью рентгеноструктурного анализа и может быть применено в области белковой кристаллографии. Техническим результатом является удешевление и ускорение этапа оптимизационного скрининга условий кристаллизации белков. Для его достижения предложен способ оптимизации условий кристаллизации белков с применением метода молекулярной динамики, заключающийся в том, что выделяют олигомеры, содержащиеся в предкристаллизационном растворе, к полученным олигомерам применяют вычисление молекулярной динамики и изменения свободной энергии при формировании олигомера в различных условиях рН, типа осадителя, концентрации осадителя, температуры согласно следующему протоколу, заключающемуся в том, что для каждых моделируемых условий кристаллизации сначала задают рН системы путем определения состояний протонирования аминокислотных остатков в составе олигомеров с помощью программы PROPKA, после чего все расчеты и подготовку структур к ним выполняют в программном пакете GROMACS, подготовленные структуры помещают в центр ячейки моделирования, при этом минимальное расстояние между ее краем и молекулой белка составляет 1 нм, при этом остальное пространство ячейки заполняют водой, в систему добавляют компоненты осадителя в необходимой концентрации, осуществляют минимизацию энергии и NVT- и NPT-уравновешивание систем, проводят вычисление продуктивной МД в NPT-ансамбле, при этом интегрирование производят по стандартному алгоритму leap-frog с временным шагом интегрирования 2 фс и длительностью рассчитанных траекторий 100 нс, при этом перед анализом полученных траекторий устраняют артефакты, возникающие из-за квазибесконечных периодических граничных условий, по данным полученных траекторий строят графики среднеквадратичных флуктуаций атомов Сα (RMSF) и вычисляют изменения энергий при образовании олигомеров белка, при этом для расчетов изменения свободной энергии при образовании олигомеров используют метод MM/GBSA, проводят вычисление свободной энергии для каждой траектории по результатам МД-моделирования, с помощью программы GROMACS, на 1000 фреймах с применением модуля gmx_MMPBSA версии 1.4.0 в сочетании со скриптом MMPBSA.py и пакетом AmberTools20, устанавливают оптимальные для кристаллизации исследуемого белка параметры, при которых наблюдаются наименьшие среднеквадратичные флуктуации атомов олигомеров и наибольшее уменьшение свободной энергии. 2 ил., 3 табл., 1 пр.
Способ оптимизации условий кристаллизации белков с применением метода молекулярной динамики, заключающийся в том, что выделяют олигомеры, содержащиеся в предкристаллизационном растворе, к полученным олигомерам применяют вычисление молекулярной динамики и изменения свободной энергии при формировании олигомера в различных условиях рН, типа осадителя, концентрации осадителя, температуры согласно следующему протоколу, заключающемуся в том, что для каждых моделируемых условий кристаллизации сначала задают рН системы путем определения состояний протонирования аминокислотных остатков в составе олигомеров с помощью программы PROPKA, после чего все расчеты и подготовку структур к ним выполняют в программном пакете GROMACS, подготовленные структуры помещают в центр ячейки моделирования, при этом минимальное расстояние между ее краем и молекулой белка составляет 1 нм, при этом остальное пространство ячейки заполняют водой, в систему добавляют компоненты осадителя в необходимой концентрации, осуществляют минимизацию энергии и NVT- и NPT-уравновешивание систем, проводят вычисление продуктивной МД в NPT-ансамбле, при этом интегрирование производят по стандартному алгоритму leap-frog с временным шагом интегрирования 2 фс и длительностью рассчитанных траекторий 100 нс, при этом перед анализом полученных траекторий устраняют артефакты, возникающие из-за квазибесконечных периодических граничных условий, по данным полученных траекторий строят графики среднеквадратичных флуктуаций атомов Сα (RMSF) и вычисляют изменения энергий при образовании олигомеров белка, при этом для расчетов изменения свободной энергии при образовании олигомеров используют метод MM/GBSA, проводят вычисление свободной энергии для каждой траектории по результатам МД-моделирования, с помощью программы GROMACS, на 1000 фреймах с применением модуля gmx_MMPBSA версии 1.4.0 в сочетании со скриптом MMPBSA.py и пакетом AmberTools20, устанавливают оптимальные для кристаллизации исследуемого белка параметры, при которых наблюдаются наименьшие среднеквадратичные флуктуации атомов олигомеров и наибольшее уменьшение свободной энергии.
| Способ определения условий кристаллизации белков | 2016 |
|
RU2626576C1 |
| ЛОПАСТНОЙ ВЫСОКОМОМЕНТНЫЙ ГИДРОМОТОР | 0 |
|
SU182997A1 |
| Kordonskaya Y.V., Marchenkova M.A., Timofeev V.I., Dyakova Y.A., Pisarevsky Y.V., Kovalchuk M.V | |||
| Precipitant ions influence on lysozyme oligomers stability investigated by molecular dynamics simulation at different temperatures | |||
| J | |||
| Biomol | |||
| Struct | |||
| Dyn., 08.08.2020, р.1-8 | |||
| Kordonskaya Y.V., | |||
Авторы
Даты
2022-10-04—Публикация
2021-09-29—Подача