Изобретение относится к разработке новых соединений для медицины, биотехнологии, физики конденсированных сред и различных областей материаловедения, в которых существенны межмолекулярные взаимодействия.
Изобретение может быть использовано при разработке новых лекарственных препаратов методами in silico, то есть путем численного моделирования комплекса лекарственного вещества с рецептором или целевым белком методами молекулярной динамики или молекулярной механики. В ходе такого моделирования могут быть получены численные значения параметров, характеризующие взаимодействие белка и лекарственного вещества и позволяющие сделать вывод об устойчивости комплекса лекарственного вещества с рецептором или целевым белком и, следовательно, об эффективности лекарственного соединения.
В настоящее время для решения вышеуказанных задач широко используются модели силового поля как эмпирические, так и ab-initio. Наиболее популярные из них - эмпирические модели семейства MMn, различные модификации моделей AMBER, последняя из которых - AMBER2002, OPLS-AA, CHARMM, ab-initio силовое поле MMFF, а также множество других моделей для параметризации взаимодействия конкретных молекул - например ab-initio параметризованная модель SAPT-5s для молекулы воды.
В аспекте настоящего изобретения интерес представляет возможность параметризации силового поля при помощи ab-initio методов квантовой химии, т.е. методов, основанных на базовых положениях квантовой теории. Эти методы часто называют неэмпирическими в отличие от полуэмпирических и других, в которых в теоретические расчеты вводится большое количество эмпирических параметров, измеренных экспериментально.
Так, в цикле работ Халгрена [1] разработана модель MMFF (Merck Molecular Force Field), предназначенная в основном для изучения взаимодействия протеин-лиганд, где в качестве лиганда могут выступать соединения, принадлежащие к различным группам органических соединений. Это является отличительной чертой силового поля MMFF, так как большинство других силовых полей, применяемых в биологии и медицинской химии, были оптимизированы для узкого класса соединений (вода, пептиды, молекулы ДНК и РНК). Таким образом, силовое поле MMFF принадлежит к новому поколению моделей (силовое поле класса II).
Силовое поле MMFF создано для возможно более точного воспроизведения энергии конформеров молекул и межмолекулярного взаимодействия, так как эти параметры важны для определения характеристик, описывающих образования комплексов белок-лиганд. В то же время воспроизведение частот колебаний молекул, а также теплоты образования молекул не являлось целью построения этого силового поля. Так как точные экспериментальные данные об энергии межмолекулярного взаимодействия и энергии конформеров для широкого класса молекул отсутствуют, то естественным является использование для параметризации данных, полученных из квантово-химических расчетов.
Электростатическое взаимодействие в силовом поле MMFF представлено смещенным кулоновским потенциалом точечных зарядов. Величины точечных зарядов определяются правилами расстановки, которые основаны на величинах относительной электроотрицательности соседних атомов. Эти параметры подбираются таким образом, чтобы результирующее распределение зарядов наилучшим образом описывало электростатический потенциал, рассчитанный по методу Хартри-Фока в базисе 6-31G*. Детали правил расстановки опубликованы в работах Халгрена [1].
Ван-дер-Ваальсово взаимодействие атомов представлено в MMFF смещенным потенциалом 14-7.
Часть силового поля MMFF, описывающая растяжение ковалентных связей, определена до слагаемых, содержащих межатомное расстояние в четвертой степени, для изгиба связей соответствующий вклад определен до члена, кубичного по углу. Кроме того, силовое поле MMFF содержит выражения для смешанной энергии растяжения-изгиба и внеплоскостного изгиба (out-of-plane bending). Энергия поляризации явным образом не описывается силовым полем MMFF, однако заряды, определяющие электростатическое взаимодействие, определены с учетом поляризации средой с диэлектрической проницаемостью, близкой к 80 (неявный учет поляризации). Эти заряды отражают увеличение дипольных моментов молекул, находящихся в водном окружении, по сравнению с величинами в вакууме. Аналогичный подход используется и в других современных моделях силового поля (AMBER, CHARMM, OPLS-AA).
Известна также модель силового поля для молекулы воды [2], параметризация которой опирается на разложение энергии взаимодействия димера воды по методу Симметризованной Теории Возмущения (SAPT - Symmetry Adapted Perturbation Theory [3]). Модель силового поля имеет спектроскопическое качество (т.е. способна воспроизвести детали колебательно-вращательного спектра димера воды). Последняя модификация модели представляет собой сумму парных потенциалов взаимодействия между силовыми центрами. В качестве силовых центров выступают атомы в составе молекулы воды, а также дополнительные центры. Общее количество центров для молекулы воды составляет 8. В результате параметризации с использованием достаточно сложной функциональной формы удалось достичь точности до 0.1 ккал/моль в широком диапазоне энергий взаимодействия молекул в димере воды. Для моделирования олигомеров воды, а также для моделирования свойств жидкой воды парные взаимодействия дополнялись неаддитивной трехчастичной компонентой. Описанный подход хорошо соответствует задачам моделирования олигомеров воды, однако отдельные энергетические компоненты в модели поля не имеют определенного физического смысла, так как достигается согласование только с полной энергией взаимодействия. Следствием этого является то, что параметры силового поля, определенные, в частности, для воды, с трудом могут применяться для других классов соединений.
В патенте США 6,460,014 описан способ моделирования взаимодействий путем создания электростатической части силового поля, описывающей взаимодействие молекул как взаимодействие локальных атомных мультипольных моментов - как постоянных, так и наведенных электростатическим полем. Наведенные мультипольные моменты определяются при помощи анизотропного тензора дипольной поляризуемости. Электростатическое поле может иметь как внешнюю природу, так и создаваться соседними атомами и молекулами в рассматриваемой системе. Таким образом, индивидуальными атомными параметрами в схеме параметризации, представленной в патенте США 6,460,014, являются атомные мультипольные моменты и атомные тензоры дипольной поляризуемости. Эти параметры присваиваются атомам на основании подгонки с целью получить значения мультипольных моментов всей молекулы близкими к результатам неэмпирических расчетов методами квантовой химии. Такой подход позволяет авторам вычислять энергию электростатического взаимодействия точнее, чем при использовании только атомных монополей (атомных зарядов). Кроме того, учитывается поляризация молекулы как внешним электростатическим полем, так и полем, наводимым другими атомами в составе молекулы.
Однако известно, что реальное электростатическое взаимодействие между молекулами не может быть описано как взаимодействие точечных мультиполей, так как имеет место пространственное распределение электронного заряда в молекуле, что ведет к эффектам перекрывания электронных плотностей. В результате этого точечные параметры не описывают адекватно взаимодействие молекул, особенно на коротких расстояниях. К тому же вычисление электростатической энергии взаимодействия произвольно расположенных мультиполей требует большого компьютерного времени, что нежелательно для применения модели силовых полей в молекулярно-динамических расчетах. Кроме того, при вычислении поляризационной энергии с помощью параметров тензора дипольной поляризуемости, присваиваемых отдельным атомам, возникает так называемая поляризационная катастрофа, которая состоит в том, что при определенных расстояниях между двумя точечными поляризационными центрами, описываемыми тензорами дипольной поляризуемости, и определенной величине электростатического поля результирующий наведенный дипольный момент всей системы обращается в бесконечность. Причина появления поляризационной катастрофы также заключается в пренебрежении пространственным распределением электронной плотности в реальных молекулах. Использование мультипольных разложений требует много компьютерного времени и существенно ограничивает применение предложенной методики для молекулярно-динамического моделирования.
К недостаткам данного известного способа, раскрытого в патенте США 6,460,014, можно отнести то, что в нем обеспечивается моделирование только одного типа взаимодействий, а именно только электростатических взаимодействий, которые составляют только часть междуатомных и межмолекулярных взаимодействий. При этом для неэлектростатических взаимодействий предлагается использовать какие-либо известные выражения, полученные в других работах на основе разных методик. Это приводит к несбалансированности вкладов различных типов взаимодействий и сравнительно невысокой точности вычислений. Вследствие того что в известном способе электростатические взаимодействия описываются как взаимодействие локальных атомных мультипольных моментов, это приводит не только к значительным ошибкам при моделировании взаимодействия на малых межмолекулярных расстояниях, но может при определенных конфигурациях молекул приводить также к сингулярностям (так называемая поляризационная катастрофа), делающим невозможным вычисление энергии взаимодействия. Последний недостаток особенно существен при применении силового поля в молекулярно-динамических расчетах, когда рассматривается большое количество различных конфигураций. Кроме того, предлагаемое в известном способе мультипольное разложение требует сравнительно большого компьютерного времени, что существенно ограничивает использование предложенного в этом патенте силового поля в молекулярно-динамическом моделировании.
Таким образом, задачей настоящего изобретения является создание способа моделирования межмолекулярного взаимодействия, обеспечивающего создание силового поля, в котором с помощью единой методологии учитываются все типы межмолекулярных взаимодействий, а его электростатическая составляющая формируется с учетом того, что реальные заряды в молекулах распределены в пространстве непрерывным образом. Техническим результатом является достижение точности создаваемых потенциалов взаимодействия, определяемой уровнем точности данных, по которым проводится определение потенциалов взаимодействия, а также упрощение обработки с использованием полученных аналитических выражений для потенциалов взаимодействия, обеспечивающих возможность осуществления сравнительно быстрой численной обработки при молекулярно-динамическом моделировании.
Рассматриваемое изобретение включает в себя способы моделирования межмолекулярного взаимодействия и основанный на них способ прогнозирования молекул-лигандов, связывающихся с заданной молекулой-мишенью. Способы моделирования основываются на вводе данных о трехмерной структуре молекул и потенциалов межмолекулярного взаимодействия в компьютер. Трехмерные структуры и состав молекулы-мишени и молекулы-лиганда получают с помощью измерений, например, методами рентгеноструктурного анализа, или рассеяния нейтронов, или ядерного магнитного резонанса, или считыванием предварительно сохраненных данных с соответствующих носителей информации.
Предложены два способа моделирования процесса связывания молекулы-лиганда с молекулой-мишенью: молекулярно-динамический и молекулярно-механический. В обоих способах моделирования используются параметры моделирования, которые подбираются так, чтобы полученные при моделировании числовые данные, характеризующие интенсивность связывания молекулы-лиганда с молекулой-мишенью, совпадали с заданной точностью с экспериментально измеренными величинами, характеризующими интенсивность связывания упомянутых молекул друг с другом. К рассчитываемым и измеряемым величинам, характеризующим интенсивность связывания молекулы-лиганда и молекулы-мишени, относится свободная энергия связывания или другие величины, такие как константа связывания, константа диссоциации, константа ассоциации, константа ингибирования, концентрация половинного ингибирования, энтальпия связывания, энтропия связывания и их комбинации. После того, как параметры моделирования будут подобраны для воспроизведения экспериментально измеренных числовых данных, характеризующих интенсивность связывания для определенного множества молекул-мишеней и молекул-лигандов, эти параметры и соответствующую методику моделирования предлагается использовать для прогнозирования молекул-лигандов, наиболее сильно связываемых с заданной молекулой-мишенью.
При молекулярно-динамическом и молекулярно-механическом моделировании координаты молекулы-мишени и координаты молекулы-лиганда считываются в компьютер и над ними производятся вычисления так, что расстояния от атомов молекулы-лиганда до заданных атомов молекулы-мишени попадают в заданный диапазон, т.е. молекула-лиганда оказывается расположенной достаточно близко к заданному месту в молекуле-мишени. После этого в обоих способах моделирования производятся вычислительные операции, включающие в модель растворитель, в котором происходит процесс связывания молекулы-лиганда с молекулой-мишенью.
После этого в молекулярно-динамическом моделировании определяются траектории движения всех взаимодействующих друг с другом атомов молекулы-мишени и молекулы-лиганда с учетом наличия растворителя путем решения уравнений Ньютона или Лагранжа при учете теплового движения атомов и с помощью этих траекторий вычисляются величины, характеризующие интенсивность связывания молекулы-лиганда с молекулой-мишенью, и эти величины записываются на носитель информации.
При молекулярно-механическом моделировании после считывания в компьютер координат атомов молекулы-мишени и молекулы-лиганда, их преобразования так, чтобы расстояния от атомов молекулы-лиганда до заданных атомов молекулы-мишени попали в заданный диапазон значений, и проведения вычислительных операций, включающих растворитель, вычисляют полную энергию системы взаимодействующих молекулы-мишени, лиганда и растворителя как функцию координат атомов молекулы-мишени, атомов лиганда и параметров, характеризующих растворитель, определяют минимальное значение этой полной энергии системы при варьировании положений атомов молекулы-мишени, молекулы-лиганда и параметров растворителя и записывают на носитель информации координаты атомов и параметры, характеризующие растворитель, при которых достигается минимум полной энергии системы взаимодействующих молекулы-мишени, лиганда и растворителя. Для полученных так координат атомов и параметров, характеризующих растворитель, вычисляют внутреннюю энергию молекулы-лиганда и энергию взаимодействия молекулы-лиганда с молекулой-мишенью и растворителем как сумму вкладов от парных потенциалов взаимодействия, где в каждой паре атомов один принадлежит молекуле-лиганду, а второй - молекуле-мишени, либо растворителю, причем в соответствии с различными типами потенциалов взаимодействия энергию взаимодействия вычисляют как сумму по меньшей мере двух отдельных компонент - электростатической и Ван-дер-Ваальсовой.
Затем с помощью координат атомов молекулы-лиганда, параметров, характеризующих растворитель, и потенциалов их взаимодействия вычисляют полную энергию системы взаимодействующих лиганда и растворителя без молекулы-мишени и находят ее минимальное значение при варьировании положений атомов молекулы-лиганда и параметров, характеризующих растворитель. Для найденных так координат атомов молекулы-лиганда и параметров, характеризующих растворитель, вычисляют внутреннюю энергию молекулы-лиганда и энергию взаимодействия молекулы-лиганда с растворителем как сумму по меньшей мере трех отдельных компонент - электростатической, Ван-дер-Ваальсовой и кавитационной.
Наконец, вычисляют разности между значениями соответствующих компонент энергии взаимодействия молекулы-лиганда с молекулой-мишенью и растворителем, а также значениями внутренней энергии лиганда в случае, когда молекула-лиганд связана с молекулой-мишенью, и в случае, когда молекула-лиганд находится в растворителе без молекулы-мишени. Полученные разности энергий используются для составления из этих величин оценочного значения свободной энергии связывания молекулы-мишени и лиганда в виде линейной или нелинейной комбинации этих величин с весовыми коэффициентами и записывают полученное оценочное значение свободной энергии связывания молекулы-мишени и лиганда на носитель информации.
При молекулярно-динамическом и при молекулярно-механическом моделировании используются два типа модели растворителя. Один из них с явным учетом растворителя, когда молекулы растворителя с их координатами и соответствующими потенциалами взаимодействия добавляются в компьютере к массиву координат и потенциалов взаимодействия молекулы-мишени и молекулы-лиганда. Во втором типе модели растворителя с использованием координат атомов молекулы-мишени и молекулы-лиганда вычисляются координаты точек, находящихся на поверхности, доступной растворителю, которая охватывает молекулу-мишень, молекулу-лиганд и их комплекс, и с помощью этих точек строится математическая модель неявного учета растворителя. Используется одна из трех разновидностей математической модели неявного учета растворителя. В первой из них используется совокупность программных средств, реализующих решение уравнения Пуассона и описывающих взаимодействие молекулы-мишени и молекулы-лиганда с непрерывной средой, заполняющей все пространство вне поверхности, доступной растворителю и имеющей диэлектрическую проницаемость, равную диэлектрической проницаемости растворителя; во второй разновидности математической модели неявного учета растворителя используют совокупность программных средств, реализующих решение уравнений, описывающих взаимодействие молекулы-мишени и молекулы-лиганда с непрерывным проводником, заполняющим все пространство вне поверхности доступной растворителю; в третьей разновидности математической модели неявного учета растворителя используется совокупность программных средств, реализующих решение уравнения Пуассона-Больцмана и описывающих взаимодействие молекулы-мишени и молекулы-лиганда с непрерывной средой, имеющей отличную от нуля диэлектрическую проницаемость и отличную от нуля проводимость и заполняющей все пространство вне поверхности, доступной растворителю.
В случае модели неявного учета растворителя вычисляют также значения свободной энергии сольватации молекулы-лиганда, молекулы-мишени и их комплекса как сумму по меньшей мере трех компонент: электростатической, Ван-дер-Ваальсовой и кавитационной, и при определении оценочного значения свободной энергии связывания молекулы-лиганда с молекулой-мишенью используют также разности между соответствующими компонентами свободной энергии сольватации комплекса молекулы-мишени и молекулы-лиганда с одной стороны, и суммой соответствующих компонент свободной энергии сольватации молекулы-мишени и компонент свободной энергии сольватации молекулы-лиганда, с другой стороны.
Рассматриваемое изобретение включает в себя также реализуемый компьютером способ определения потенциалов межмолекулярного взаимодействия. Этот способ основан на вычислении энергии межмолекулярного взаимодействия с помощью высокоточных неэмпирических квантовых расчетов. Определение потенциалов взаимодействия происходит следующим образом. Выбираются пары молекул таким образом, чтобы их атомы соответствовали типам атомов, встречающихся в молекулах-мишенях и молекулах-лигандах, причем тип атома определяется положением в таблице Менделеева соответствующего элемента, характеризующегося атомным номером и атомным весом, и соседними атомами в молекуле-мишени или молекуле-лиганде. Для выбранной пары молекул считывают геометрические параметры каждой молекулы в память компьютера в соответствующем формате и с помощью соответствующей компьютерной программы вычисляют набор координат атомов этих молекул, соответствующих различным взаимным расположениям этих молекул, и записывают полученные данные на носитель информации в виде множества точек в пространстве межмолекулярного комплекса. Далее из множества всех точек в пространстве межмолекулярного комплекса формируют два его подмножества: обучающее подмножество для подгонки параметров взаимодействия и тестовое подмножество для проверки качества полученных потенциалов. Для каждой точки этих множеств вычисляют полную энергию взаимодействия рассматриваемых молекул друг с другом и ее различных компонент с помощью квантовых расчетов, основанных на решении уравнения Шредингера, описывающих поведение электронов в заданном поле атомных ядер молекул. Компоненты взаимодействия группируют в четыре основных типа энергии взаимодействия, включающих энергию электростатического взаимодействия, обменную, индукционную и дисперсионную энергию, и записывают полученные числовые данные, сгруппированные по указанным четырем компонентам, на носитель информации. Эту процедуру проделывают для всех точек обучающего и тестового множеств из пространства межмолекулярного комплекса. Таким образом, на носителе информации оказываются записанными для каждой точки обучающего и тестового множеств по четыре компоненты энергии межмолекулярного взаимодействия, рассчитанные с помощью точных неэмпирических квантовых расчетов.
После этого для каждой точки обучающего и тестового множеств из пространства межмолекулярного комплекса вычисляют энергию взаимодействия рассматриваемых молекул друг с другом как сумму взаимодействий между входящими в состав молекул парами атомов с помощью содержащих параметры взаимодействия классических потенциалов, представляющих собой энергию взаимодействия двух частиц, характеризуемых массой и положением в пространстве, причем энергия взаимодействия заданной пары атомов вычисляется как сумма классических потенциалов, соответствующих различным компонентам взаимодействия.
Функциональная зависимость классического потенциала, соответствующего заданной компоненте энергии взаимодействия, содержит параметры взаимодействия, и эти параметры определяются следующим образом. Целевая функция для заданной компоненты межмолекулярного взаимодействия вычисляется как сумма квадратов разностей соответствующих величин для всех точек обучающего подмножества, полученных с помощью квантовых расчетов, с одной стороны, и полученных с помощью классических потенциалов, с другой стороны. Эта целевая функция минимизируется при варьировании параметров взаимодействия, входящих в упомянутую функциональную зависимость, выбранную для заданной компоненты энергии межмолекулярного взаимодействия, и записывают на носитель информации значения параметров, при которых целевая функция достигает своего минимума. Для этих значений параметров взаимодействия вычисляют такую же целевую функцию для точек из тестового множества пространства межмолекулярного комплекса, и если она не превышает заданную величину, соответствующую точности квантовых расчетов, то определение параметров взаимодействия для заданной компоненты межмолекулярного взаимодействия считается законченным, и использованные параметры взаимодействия присваиваются соответствующим атомам, входящим в рассматриваемую пару молекул. Если же целевая функция, вычисленная на точках из тестового множества, превышает заданную точность, соответствующую точности квантовых расчетов, то обучающее множество пространства межмолекулярного комплекса расширяют или изменяют функциональную зависимость потенциала рассматриваемого взаимодействия, и повторяют подгонку параметров взаимодействия до тех пор, пока целевая функция не уменьшится до требуемой величины.
Функциональная зависимость классического потенциала, соответствующего заданной компоненте энергии взаимодействия, выбирается таким образом, что весь набор параметров взаимодействия для заданной пары молекул разбивается однозначным образом на подмножества параметров взаимодействия, соотнесенных с каждым отдельным типом атомов или пар атомов, и обеспечивается возможность формирования потенциалов взаимодействия между любой заданной парой молекул как суммы соответствующих классических потенциалов для всех пар атомов, один из которых принадлежит первой молекуле, а второй атом - второй молекуле.
Приведенная выше процедура определения параметров взаимодействия повторяется для всех четырех компонент энергии межмолекулярного взаимодействия, и окончательные значения параметров взаимодействия записываются на носитель информации для их последующего использования при молекулярно-динамическом или молекулярно-механическом моделировании.
Изобретение поясняется на примерах осуществления, иллюстрируемых чертежами, на которых представлено следующее:
Фиг.1 - блок-схема алгоритма способа прогнозирования связывания молекулы-лиганда с молекулой-мишенью, соответствующего изобретению.
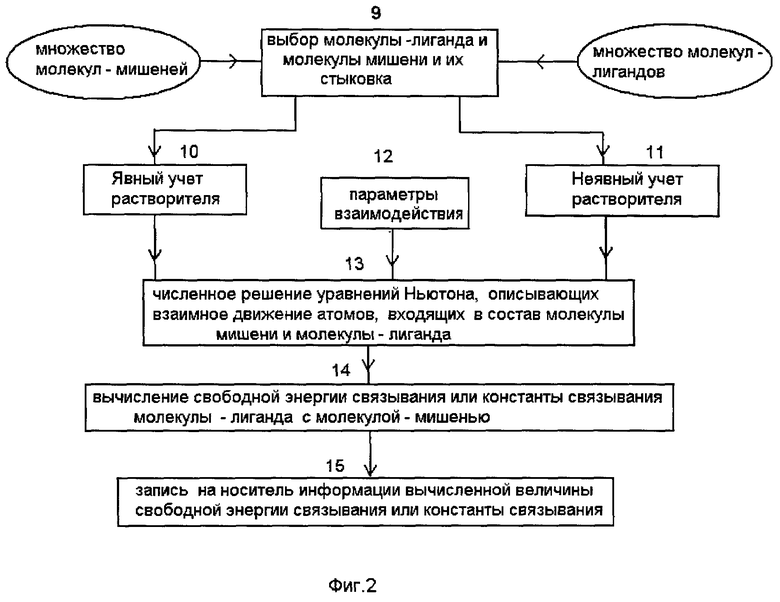
Фиг.2 - блок-схема алгоритма способа молекулярно-динамического моделирования, который может быть использован на этапе 3 в способе по фиг.1.
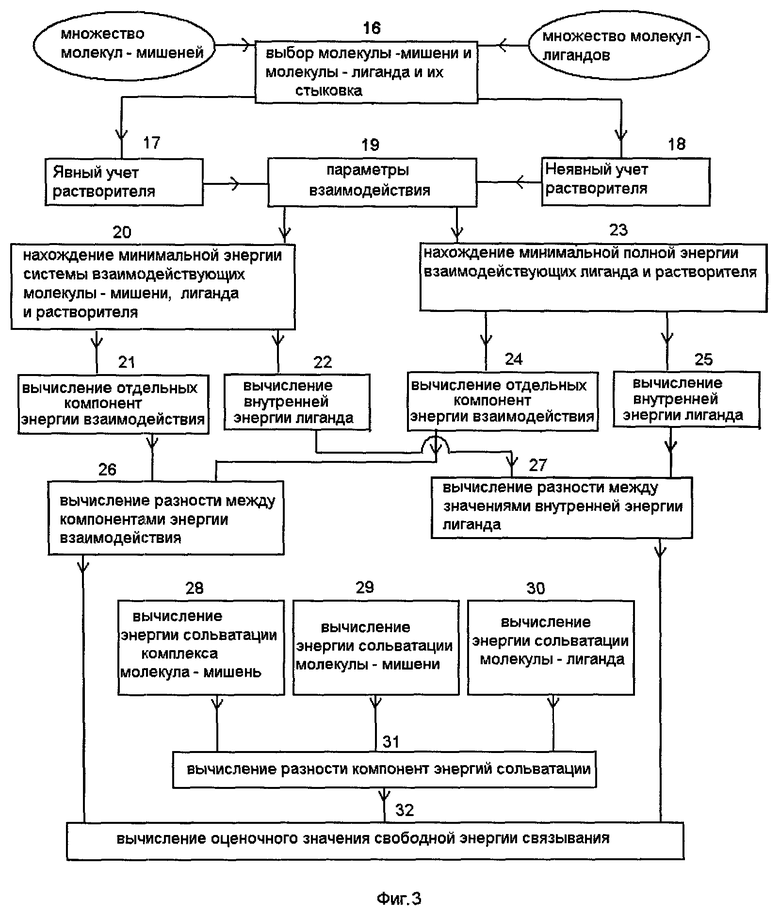
Фиг.3 - блок-схема алгоритма способа молекулярно-механического моделирования, который может быть использован на этапе 3 в способе по фиг.1.
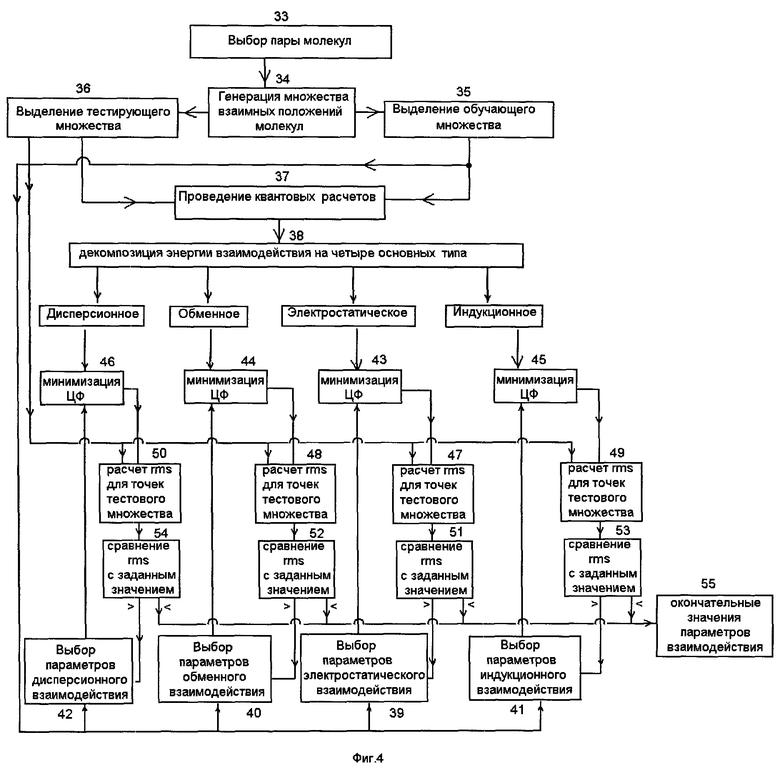
Фиг.4 - блок-схема алгоритма определения параметров, описывающих потенциалы межмолекулярного взаимодействия, который может быть использован в способе по фиг.1.
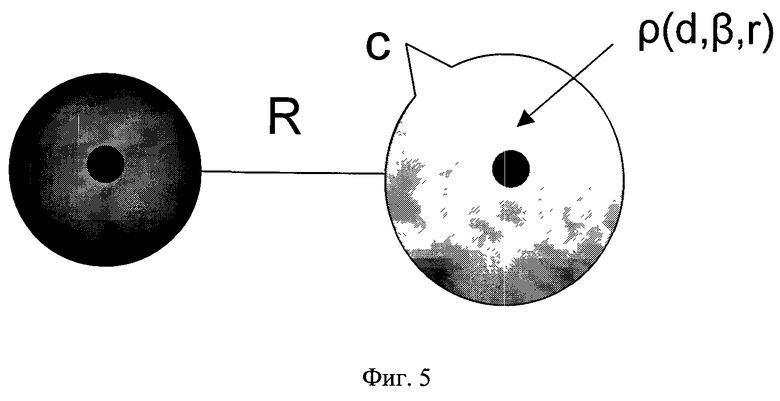
Фиг.5 - Распределения заряда в атомах, где c - общий заряд на центре, d - диффузный заряд на центре.
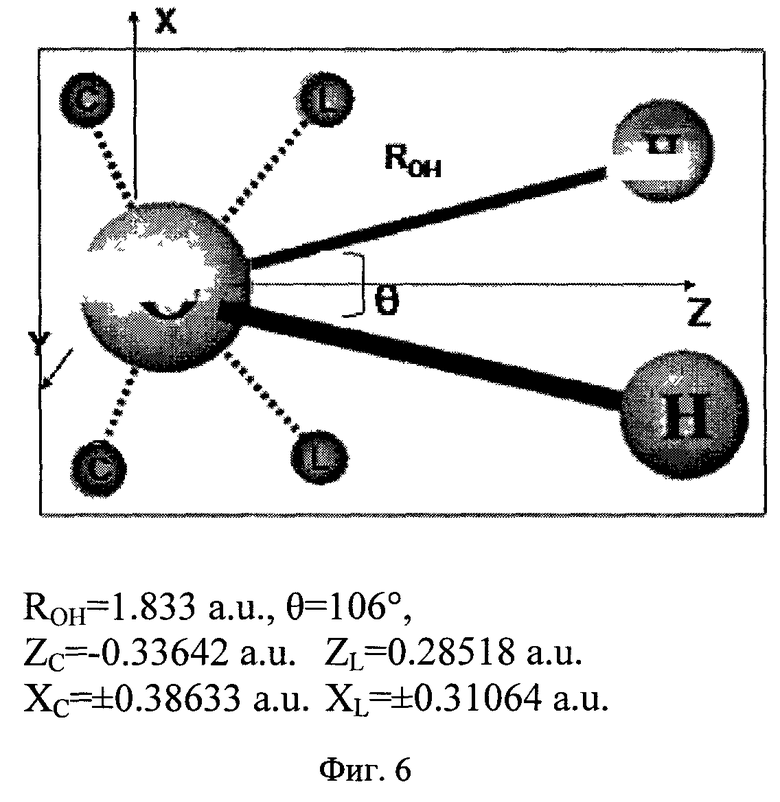
Фиг.6 - Геометрия и параметры модели силового поля для молекулы воды.
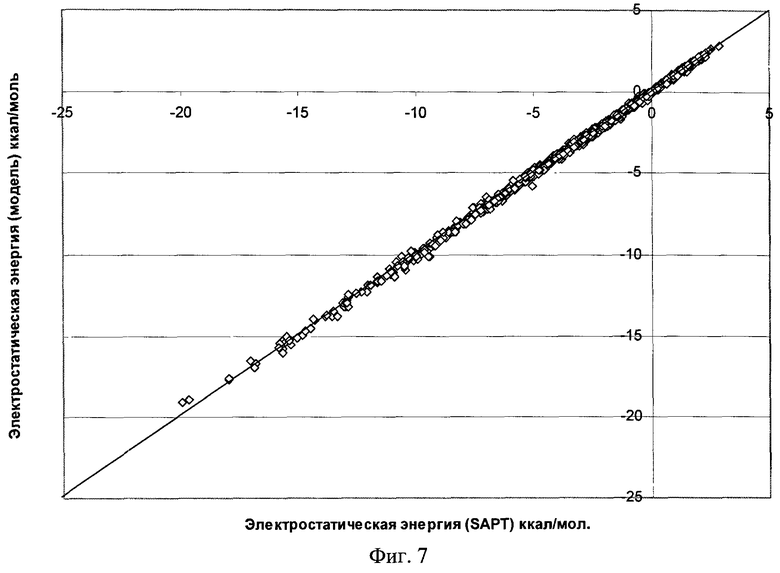
Фиг.7 - Результаты параметризации модели электростатического взаимодействия для димера воды (RMS=0,115 ккал/моль).
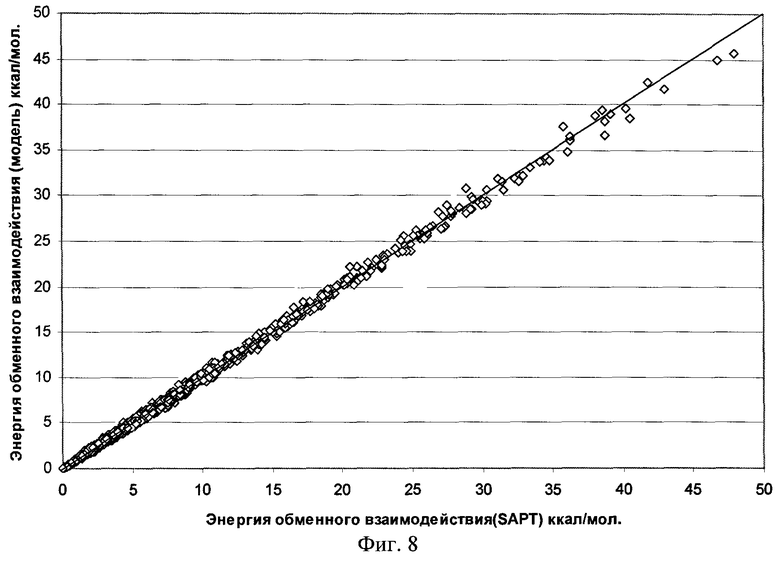
Фиг.8 - Результаты параметризации модели обменного взаимодействия для димера воды (RMS=0,306 ккал/моль).
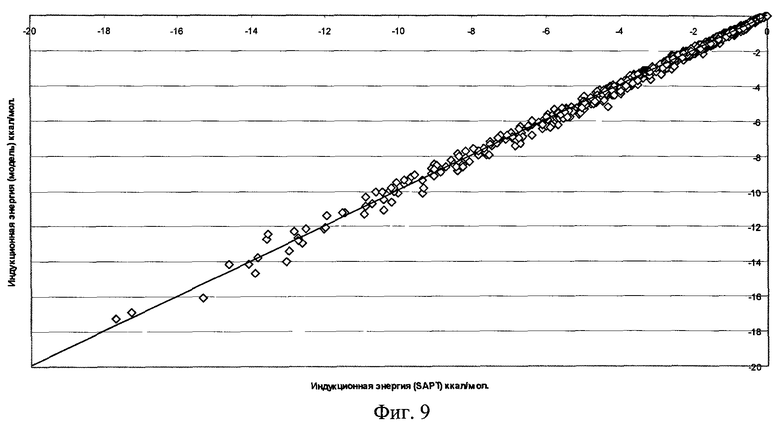
Фиг.9 - Результаты параметризации модели индукционного взаимодействия для димера воды (RMS=0,144 ккал/моль).
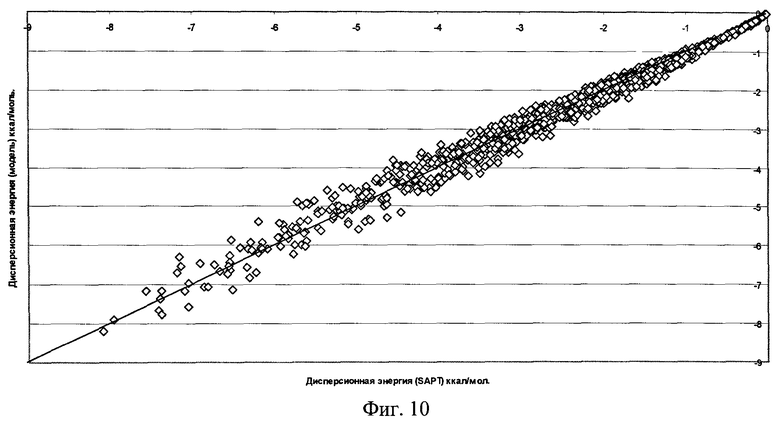
Фиг.10 - Результаты параметризации модели дисперсионного взаимодействия для димера воды (RMS=0,188 ккал/моль).
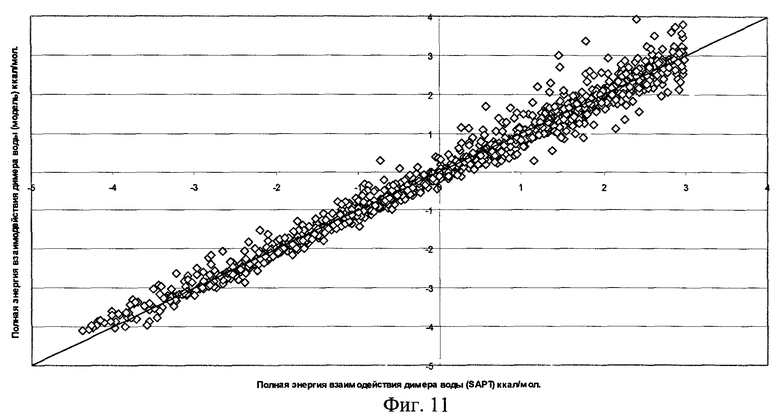
Фиг.11 - Результаты параметризации полной энергии взаимодействия для димера воды (RMS=0,229 ккал/моль).
Заявленные способы моделирования межмолекулярного взаимодействия и основанный на них способ прогнозирования связывания молекулы-лиганда с молекулой-мишенью описаны ниже на фиг.1-4. На фиг.1 изображен способ прогнозирования связывания молекулы-лиганда с молекулой-мишенью. Из множества молекул-мишеней и множества молекул-лигандов на этапе 1 выбирается заданная пара молекулы-мишени и молекулы-лиганда, и информация об их структуре и составе, а также координаты атомов этих молекул записываются на носитель информации в соответствующем формате. Структуру и состав молекулы-мишени и молекулы-лиганда получают с помощью измерений, например, методами рентгено-структурного анализа или рассеяния нейтронов или ядерного магнитного резонанса, или считыванием предварительно сохраненных данных с соответствующих носителей информации. Например, данные о структуре белков, которые могут быть использованы в качестве молекулы-мишени, обычно получаются из соответствующей базы данных (Protein Data Bank) [4], доступ к которой может быть получен через Интернет.
Далее на этапе 2 выбирают параметры моделирования, к которым могут относиться как параметры, описывающие потенциалы взаимодействия между атомами, входящими в состав молекулы-мишени и молекулы-лиганда, так и другие параметры, необходимые для построения модели, описывающей связывание молекулы-лиганда с молекулой-мишенью, например параметры, описывающие модель термостата при молекулярно-динамическом моделировании, или параметры, определяющие влияние растворителя. После этого на этапе 3 проводят моделирование процесса связывания заданной молекулы-лиганда с заданной молекулой-мишенью с использованием информации о структуре молекулы-мишени и молекулы-лиганда и других параметрах моделирования. В результате проведения моделирования получают числовые данные, характеризующие интенсивность связывания молекулы-лиганда с молекулой-мишенью, и записывают полученные числовые данные на носитель информации. В качестве величин, характеризующих интенсивность связывания молекулы-лиганда и молекулы-мишени между собой, вычисляются величины, выбранные из группы, включающей свободную энергию связывания, константу связывания, константу диссоциации, константу ассоциации, константу ингибирования, концентрацию половинного ингибирования, энтальпию связывания, энтропию связывания и их комбинации.
На этапе 4 проводятся эксперименты, в результате которых измеряются величины, характеризующие интенсивность связывания заданной молекулы-лиганда с заданной молекулой-мишенью. На следующем этапе 5 осуществляют сравнение рассчитанных при моделировании на этапе 3 величин, характеризующих интенсивность связывания заданной молекулы-лиганда с заданной молекулой-мишенью, и аналогичных величин, полученных в результате измерений на этапе 4. В случае расхождения между рассчитанными и измеренными величинами, характеризующими интенсивность связывания между молекулой-мишенью и молекулой-лигандом, превышающего заданную величину, на этапе 6 корректируют параметры моделирования, используемые программой, моделирующей взаимодействие между молекулой-мишенью и молекулой-лигандом (возврат на этап 2 выбора параметров), повторно проводят моделирование на этапе 3 и рассчитывают величины, характеризующими интенсивность связывания между молекулой-мишенью и молекулой-лигандом. Этот процесс подгонки параметров моделирования продолжается до тех пор, пока расхождение между рассчитанными и измеренными величинами, характеризующими связывание молекул между собой, не станет меньше заданной величины. После этого процесс подгонки параметров моделирования для заданной пары молекулы-мишени и молекулы-лиганда считается законченным.
Далее выбирается другая пара молекулы-лиганда и молекулы-мишени, и для нее описанные выше этапы моделирования 3, измерения 4, сравнения 5 результатов моделирования и измерений и корректировка 6 параметров моделирования повторяются, причем в качестве начальных используются значения параметров моделирования, полученные для предыдущей пары молекулы-мишени и молекулы-лиганда. Затем выбирается следующая пара молекулы-мишени и молекулы-лиганда и т.д.
В результате такой процедуры определяются значения параметров моделирования, которые в результате моделирования позволяют получать значения величин, характеризующих интенсивность связывания молекулы-лиганда с молекулой-мишенью, например, свободную энергию связывания, с заданной точностью для определенного множества пар молекул-мишеней и молекул-лигандов. Этот процесс расширения множества пар молекул-мишеней и молекул-лигандов и самосогласованной подгонки параметров моделирования продолжается до тех пор, пока для очередной взятой вновь пары молекулы-мишени и молекулы-лиганда характеризующие интенсивность связывания величины, вычисленные с использованием параметров моделирования, полученных для других пар молекул, не будут совпадать с заданной точностью с измеренными для данной пары молекул величинами, характеризующими интенсивность связывания. После этого окончательные значения параметров моделирования записываются на этапе 7 (фиг.1) на носитель информации, и в дальнейшем они используются для прогнозирования.
Прогнозирование на этапе 8 молекул-лигандов, которые достаточно сильно связываются с заданной молекулой-мишенью, заключается в следующем. Для заданной молекулы-мишени выбирается молекула-лиганд из определенного набора молекул, и для нее проводится моделирование процесса связывания с использованием окончательных значений параметров моделирования, полученных и записанных на носитель информации на этапе 7. В результате такого моделирования получаются величины, характеризующие интенсивность связывания этой молекулы-лиганда с заданной молекулой-мишенью, например величина свободной энергии связывания. Далее берется другая молекула-лиганд и для нее тоже в результате моделирования вычисляется свободная энергия связывания при использовании тех же самых параметров моделирования. Так перебираются все молекулы из определенного множества молекул-лигандов и из них выбираются лучшие, имеющие наибольшее значение свободной энергии связывания или других величин, характеризующих интенсивность связывания. Например, считается, что молекула-лиганд связывается достаточно интенсивно в водном растворе с заданным протеином, если ее свободная энергия связывания с заданным протеином находится в диапазоне (5-15) ккал/моль. Множество молекул-лигандов, из которого выбираются кандидаты для прогнозирования, может быть получено разными путями. Это могут быть базы данных, содержащие информацию о структуре молекул, полученную в различных экспериментах, или базы данных, содержащих координаты атомов молекул, построенных с помощью различных компьютерных программ. Количество молекул в таких базах данных может быть огромным (миллионы и даже миллиарды соединений), и каждая из этих молекул существует в реальности или может быть синтезирована. Важно, чтобы для молекул этого множества имелась информация об их трехмерной структуре, составе и координатах всех атомов. Те молекулы-лиганды, для которых прогнозируется хорошее связывание, могут быть использованы в реальных химических экспериментах по связыванию с заданной молекулой-мишенью. Таким образом, предлагаемое в настоящем изобретении прогнозирование молекул-лигандов, которые связываются наилучшим образом с заданной молекулой-мишенью, позволяет избежать огромных материальных и временных затрат на синтез новых веществ и проведение экспериментов по измерению величин, характеризующих интенсивность связывания молекул друг с другом.
В соответствии с настоящим изобретением на фиг.2 и 3 представлены блок-схемы, иллюстрирующие два варианта этапа 3 на фиг.1 способа моделирования величин, характеризующих интенсивность связывания молекулы-лиганда с молекулой-мишенью.
На фиг.2 приведен молекулярно-динамический способ моделирования, который заключается в следующем. На этапе 9 считывают данные о структуре молекулы-мишени и молекулы-лиганда с носителя информации в память компьютера и выполняют преобразование координат атомов этих молекул таким образом, чтобы наименьшее расстояние между каждым из атомов лиганда и заданными атомами молекулы-мишени находилось в заданном диапазоне, например в диапазоне 1-5 ангстрем, и записывают новые координаты атомов молекулы-мишени и молекулы-лиганда в память компьютера. Такая процедура стыковки или, как чаще принято называть, докинга необходима для совмещения в пространстве двух молекул, так как обычно координаты их атомов получаются из различных источников информации.
Процесс связывания молекулы-лиганда с молекулой-мишенью часто происходит в растворителе, например в воде. Поэтому при моделировании процесса связывания надо учесть наличие растворителя и его взаимодействие с другими молекулами. В изобретении предусматриваются две модели учета растворителя: явного учета (этап 10) и неявного учета (этап 11).
При использовании модели явного учета растворителя на этапе 10 к координатам атомов молекулы-мишени и молекулы-лиганда добавляются координаты атомов молекул растворителя (например, воды) так, чтобы средняя плотность расположения в пространстве молекул растворителя соответствовала экспериментально наблюдаемой плотности растворителя, и молекулы растворителя заполняли собой без взаимопересечений и пересечений с атомами молекулы-мишени и молекулы-лиганда пространство как между молекулой-мишенью и молекулой-лигандом, так и вокруг них.
При использовании модели неявного учета растворителя на этапе 11 с использованием координат атомов молекулы-мишени и лиганда формируют координаты точек, находящихся на поверхности, доступной растворителю, которая охватывает молекулу-мишень и лиганд, и с помощью этих точек строят математическую модель неявного учета растворителя. Заявленный способ предусматривает использование трех типов модели неявного учета растворителя. В первом из них в качестве математической модели неявного учета растворителя используют совокупность программных средств, реализующих решение уравнения Пуассона и описывающих взаимодействие молекулы-мишени и молекулы-лиганда с непрерывной средой, заполняющей все пространство вне поверхности, доступной растворителю и имеющей диэлектрическую проницаемость, равную диэлектрической проницаемости растворителя. Во втором типе модели неявного учета растворителя при использовании растворителя с большим значением диэлектрической проницаемости растворителя (например, вода имеет диэлектрическую проницаемость около 80 при комнатной температуре) в качестве математической модели неявного учета растворителя используют совокупность программных средств, реализующих решение уравнений, описывающих взаимодействие молекулы-мишени и молекулы-лиганда с непрерывным проводником, заполняющим все пространство вне поверхности, доступной растворителю. В третьем типе модели неявного учета растворителя при использовании растворителя, характеризуемого отличными от нуля диэлектрической проницаемостью и проводимостью, в качестве математической модели неявного учета растворителя используют совокупность программных средств, реализующих решение уравнения Пуассона-Больцмана и описывающих взаимодействие молекулы-мишени и молекулы-лиганда с непрерывной средой, имеющей отличную от нуля диэлектрическую проницаемость и отличную от нуля проводимость и заполняющей все пространство вне поверхности, доступной растворителю.
После того, как координаты атомов молекулы-мишени и молекулы-лиганда объединены с моделью растворителя в памяти компьютера, туда же вводятся конкретные численные значения всех остальных необходимых параметров моделирования (этап 12), например параметры, определяющие потенциалы межатомного взаимодействия, характеристики термостата, и т.д., и на этапе 13 определяются траектории движения всех взаимодействующих друг с другом атомов молекулы-мишени и молекулы-лиганда с учетом наличия растворителя путем решения уравнений Ньютона или Лагранжа при учете их теплового движения. Время, в течение которого определяют эти траектории, должно быть достаточно большим, чтобы в системе молекула-мишень, молекула-лиганд и растворитель установилось тепловое равновесие. Например, для системы протеин-лиганд в водном растворе это десятки или даже сотни пикосекунд при разумных значениях временного шага меньше или порядка одной фемтосекунды. После этого, зная траектории равновесного движения, на этапе 14 вычисляются свободная энергия связывания, константа связывания или другая величина, характеризующая интенсивность связывания молекулы-лиганда с молекулой-мишенью. Эта вычисленная величина на этапе 15 записывается на носитель информации для дальнейшего использования в процессе прогнозирования. Существует несколько различных методов вычисления свободной энергии связывания по молекулярно-динамическим траекториям движения, среди которых можно выделить как самые популярные метод термодинамического интегрирования, метод термодинамической теории возмущений, а также более быстрый, но менее точный метод LIE.
В настоящем изобретении предлагается и другой способ моделирования - молекулярно-механический. Этот способ обычно требует значительно меньше времени, чем молекулярно-динамический, однако в нем, как правило, используется значительно большее число параметров моделирования.
На фиг.3 приведена последовательность действий молекулярно-механического способа моделирования, который заключается в следующем. На этапе 16 считывают данные о структуре молекулы-мишени и молекулы-лиганда с носителя информации в память компьютера и выполняют преобразование координат атомов этих молекул таким образом, чтобы наименьшее расстояние между каждым из атомов лиганда и заданными атомами молекулы-мишени находилось в заданном диапазоне, например в диапазоне 1-5 ангстрем, и записывают новые координаты атомов молекулы-мишени и молекулы-лиганда в память компьютера. Такая процедура стыковки (докинга) необходима для совмещения в пространстве двух молекул, так как обычно координаты их атомов получаются из различных источников информации.
Координаты атомов молекулы-мишени и молекулы-лиганда объединяются на этапах 17, 18 учета растворителя соответственно с моделью явного или неявного учета растворителя в памяти компьютера и туда же вводятся на этапе 19 конкретные численные значения всех остальных необходимых параметров моделирования, например такие, как параметры, определяющие потенциалы межатомного взаимодействия.
Далее вычисления проводятся для двух разных систем. Одна из них - это система взаимодействующих молекулы-лиганда и молекулы-мишени при наличии растворителя, а вторая - молекула-лиганда при наличии растворителя. Разность энергетических характеристик этих двух систем и определяет выигрыш по энергии при переходе молекулы-лиганда из растворителя в связанное состояние с молекулой-мишенью. Более детально осуществляются следующие операции.
На этапе 20 вычисляют полную энергию системы взаимодействующих молекулы-мишени, лиганда и растворителя как функцию координат атомов молекулы-мишени, атомов лиганда, параметров, характеризующих растворитель, и потенциалов их взаимодействия, определяют ее минимальное значение при варьировании положений атомов молекулы-мишени, молекулы-лиганда и параметров растворителя, и записывают на носитель информации координаты атомов и параметры, характеризующие растворитель, при которых достигается минимум энергии системы взаимодействующих молекулы-мишени, лиганда и растворителя. Для этих координат атомов на этапе 21 вычисляют энергию взаимодействия молекулы-лиганда с молекулой-мишенью и растворителем как суммы вкладов от парных потенциалов взаимодействия, где в каждой паре атомов один принадлежит молекуле-лиганду, а второй - молекуле-мишени либо растворителю, причем в соответствии с различными типами потенциалов энергию взаимодействия вычисляют как сумму по меньшей мере трех отдельных компонент - электростатической, Ван-дер-Ваальсовой и кавитационной. Для этих же координат атомов на этапе 22 вычисляют внутреннюю энергию лиганда и записывают на носитель информации отдельные компоненты энергии взаимодействия и внутренней энергии лиганда.
На этапе 23 с помощью координат атомов молекулы-лиганда, параметров, характеризующих растворитель, и потенциалов их взаимодействия вычисляют полную энергию системы взаимодействующих лиганда и растворителя в отсутствие молекулы-мишени и находят минимальную этой энергии при варьировании положений атомов молекулы-лиганда и параметров, характеризующих растворитель, и записывают на носитель информации координаты атомов молекулы-лиганда и параметры, характеризующие растворитель, при которых достигается этот минимум. Для этих координат атомов на этапе 24 вычисляют энергию взаимодействия молекулы-лиганда с растворителем как сумму по меньшей мере трех отдельных компонент - электростатической, Ван-дер-Ваальсовой и кавитационной, а также вычисляют внутреннюю энергию молекулы-лиганда 25 и записывают на носитель информации отдельные компоненты энергии взаимодействия молекулы-лиганда с растворителем и внутреннюю энергию молекулы-лиганда.
На этапе 26 вычисляют разности между соответствующими компонентами энергии взаимодействия молекулы-лиганда с молекулой-мишенью и растворителем в состоянии, когда молекула-лиганд связана с молекулой-мишенью, и компонентами энергии взаимодействия молекулы-лиганда с растворителем, когда молекула-лиганд находится в свободном состоянии в растворителе без молекулы-мишени. На этапе 27 вычисляют разность между внутренними энергиями молекулы-лиганда в связанном и свободном состоянии.
Для координат атомов, полученных на этапе 20 при оптимизации полной энергии связанных молекулы-лиганда с молекулой-мишенью в растворителе, на этапе 28 вычисляют свободную энергию сольватации комплекса молекулы-мишени и молекулы-лиганда, причем свободную энергию сольватации комплекса вычисляют как сумму по меньшей мере трех компонент: электростатической, Ван-дер-Ваальсовой и кавитационной. Для этих же координат атомов на этапе 29 вычисляют свободную энергию сольватации молекулы-мишени без молекулы-лиганда, причем свободную энергию сольватации молекулы-мишени вычисляют как сумму по меньшей мере трех компонент: электростатической, Ван-дер-Ваальсовой и кавитационной.
Для координат атомов, полученных на этапе 23 при оптимизации полной энергии свободной молекулы-лиганда в растворителе, на этапе 30 вычисляют свободную энергию сольватации молекулы-лиганда без молекулы-мишени, причем свободную энергию сольватации молекулы-лиганда вычисляют как сумму по меньшей мере трех компонент: электростатической, Ван-дер-Ваальсовой и кавитационной.
На этапе 31 (фиг.3) вычисляют разности между соответствующими компонентами свободной энергии сольватации молекулярного комплекса, состоящего из молекулы-мишени и молекулы-лиганда, с одной стороны, и суммой соответствующих компонент свободной энергии сольватации молекулы-мишени и компонент свободной энергии сольватации молекулы-лиганда, с другой стороны.
На этапе 32 (фиг.3) используют разности энергий, полученные на этапах 26, 27 и 31 (фиг.3) для составления из этих величин оценочного значения свободной энергии связывания молекулы-мишени и лиганда в виде линейной или нелинейной комбинации этих величин с весовыми коэффициентами и записывают полученное оценочное значение свободной энергии связывания молекулы-мишени и лиганда на носитель информации. Эта величина и есть результат молекулярно-механического моделирования связывания молекулы-лиганда с молекулой мишенью. Весовые коэффициенты, входящие в оценочное значение свободной энергии связывания, являются параметрами моделирования и подбираются в соответствие со схемой, представленной на фиг.1.
В данном изобретении предлагается также реализуемый компьютером способ определения параметров взаимодействия, описывающих потенциалы межмолекулярного взаимодействия, предназначенный для использования в способе по фиг.1. Этот способ определения параметров взаимодействия схематически изображен на фиг.4.
На этапе 33 для заданной пары молекул считывают геометрические параметры каждой молекулы в память компьютера в соответствующем формате и на этапе 34 с помощью соответствующей компьютерной программы вычисляют набор координат атомов этих молекул, соответствующих различным взаимным расположениям этих молекул, и записывают полученные данные на носитель информации в виде множества точек в пространстве межмолекулярного комплекса.
Из множества всех точек в пространстве межмолекулярного комплекса на этапах 35 и 36 формируют два его подмножества: обучающее подмножество для подгонки параметров взаимодействия и тестовое подмножество для проверки качества полученных потенциалов, соответственно. Для каждой точки пространства межмолекулярного комплекса на этапе 37 вычисляют энергию взаимодействия рассматриваемых молекул друг с другом с помощью неэмпирических квантовых расчетов, описывающих поведение электронов в заданном поле атомных ядер молекул. При этом существенно, чтобы вычислялась не только полная энергия взаимодействия этих двух молекул друг с другом, но и значения различных компонент энергии взаимодействия. Неэмпирические квантовые расчеты проводятся с помощью компьютерных программ, решающих систему уравнений движения на основе законов квантовой механики, например, уравнение Шредингера, или уравнение Хартри-Фока-Рутана с учетом корреляции электронов. Наиболее подходящей для целей настоящего изобретения является Симметризованная Теория Возмущений (в англоязычной литературе именуемая как SAPT). В соответствующем методе можно выделить большое количество различных компонент взаимодействия. Различные компоненты энергии взаимодействия на этапе 38 группируются в четыре основных типа энергии взаимодействия, включающих энергию электростатического взаимодействия, обменную, индукционную и дисперсионную энергию, и записывают полученные числовые данные, сгруппированные по указанным четырем компонентам, на носитель информации. Таким образом, на носителе информации для каждой точки пространства межмолекулярного комплекса записываются четыре числа, соответствующих упомянутым четырем компонентам энергии межмолекулярного взаимодействия.
Для всех точек обучающего множества пространства межмолекулярного комплекса вычисляют энергию взаимодействия рассматриваемых молекул друг с другом с помощью содержащих параметры взаимодействия классических потенциалов, представляющих собой энергию взаимодействия двух частиц, характеризуемых массой и положением в пространстве. При этом энергию взаимодействия двух молекул друг с другом вычисляют как сумму взаимодействий между входящими в состав молекул парами атомов. Энергию взаимодействия каждой пары атомов вычисляют как сумму классических потенциалов, соответствующих различным компонентам взаимодействия.
На этапах 39, 40, 41 и 42 выбирают функциональную зависимость классических потенциалов и значения входящих в них параметров для электростатической, обменной, индукционной и дисперсионной компонент взаимодействия, соответственно.
На этапах 43, 44, 45 и 46 определяют соответственно параметры электростатического, обменного, индукционного и дисперсионного взаимодействия путем минимизации целевой функции, соответствующей заданной компоненте межмолекулярного взаимодействия, для всех точек обучающего подмножества. При этом целевую функцию для заданной компоненты межмолекулярного взаимодействия вычисляют как корень квадратный из суммы квадратов разностей соответствующих величин для всех точек обучающего подмножества, полученных с помощью квантовых расчетов, с одной стороны, и полученных с помощью классических потенциалов, с другой стороны.
Минимизация целевых функций на этапах 43, 44, 45 и 46 происходит при варьировании параметров взаимодействия, входящих в упомянутую функциональную зависимость классического потенциала, выбранную для заданной компоненты энергии межмолекулярного взаимодействия, и значения этих параметров, при которых соответствующая целевая функция достигает минимума, записываются на носитель информации.
На этапах 47, 48, 49 и 50 вычисляют среднеквадратичное отклонение соответственно для электростатической, обменной, индукционной и дисперсионной компоненты межмолекулярного взаимодействия для точек пространства межмолекулярного комплекса из тестового подмножества при использовании значений параметров взаимодействия, полученных при минимизации целевых функций на этапах 43, 44, 45 и 46. При этом среднеквадратичное отклонение вычисляют как корень квадратный из суммы квадратов разностей соответствующих величин для всех точек тестового подмножества, полученных с помощью квантовых расчетов, с одной стороны, и полученных с помощью классических потенциалов, с другой стороны.
На этапах 51, 52, 53 и 54 проводится сравнение среднеквадратичного отклонения соответственно для электростатической, обменной, индукционной и дисперсионной компонент взаимодействия, полученного на этапах 47, 48, 49 и 50, точностью квантовых расчетов, которая составляет обычно 0,1-0,3 ккал/моль.
Если среднеквадратичное отклонение для заданной компоненты взаимодействия не превышает заданную величину, соответствующую точности квантовых расчетов, то этап определения параметров взаимодействия для заданной компоненты энергии межмолекулярного взаимодействия завершают и присваивают использованные значения параметров взаимодействия соответствующим атомам, входящим в рассматриваемую пару молекул.
Если среднеквадратичное отклонение для заданной компоненты взаимодействия превышает заданную величину, соответствующую точности квантовых расчетов, то расширяют обучающее подмножество пространства межмолекулярного комплекса или изменяют функциональную зависимость потенциала соответствующего взаимодействия до тех пор, пока соответствующая целевая функция не уменьшится до требуемой величины. Эту процедуру повторяют для всех четырех компонент энергии межмолекулярного взаимодействия и на этапе 55 записывают полученные окончательные значения параметров взаимодействия на носитель информации в качестве набора параметров взаимодействия заданных двух молекул.
Приведенное выше силовое поле в виде совокупности потенциалов взаимодействия по следующим параметрам превосходит описанные аналоги:
- использование высокоточных квантово-химических методов для получения поверхности потенциальной энергии молекулярных комплексов. Использованная заявителем Симметризованная Теория Возмущений дает точность воспроизведения энергии, значительно превышающую расчеты, использованные для параметризации поля MMFF;
- использование раздельной параметризации основных составляющих энергии межмолекулярного взаимодействия (электростатика, обменное взаимодействие, индукционное взаимодействие, дисперсия) существенно упрощает процесс параметризации. Кроме того, использование физически обоснованных компонент потенциала позволяет получить переносимость параметров между различными классами соединений;
- использование более точных аналитических выражений для конкретных составляющих межмолекулярного взаимодействия, в частности: электростатический потенциал, учитывающий диффузное распределение заряда, модифицированный потенциал Борна-Майера для обменного взаимодействия, индукционное взаимодействие, учитывающее как эффекты поляризации, так и эффекты переноса заряда. Наконец, дисперсионное взаимодействие описывается функциональной формой Танга-Тонниса.
Результатом предлагаемого изобретения является повышение точности описания межмолекулярного взаимодействия в результате:
- высокого уровня неэмпирического расчета с помощью Симметризованной теории возмущения или иного метода, учитывающего корреляцию движения электронов,
- раздельной параметризации физически обоснованных компонент энергии межмолекулярного взаимодействия,
- применения теоретически строгих выражений для компонент энергии,
- лучшей переносимости параметров силового поля.
Приведенный выше способ определения параметров взаимодействия, описывающих потенциалы межмолекулярного взаимодействия, был осуществлен авторами настоящего изобретения для молекул воды. Эта параметризация силового поля основывается на серии расчетов димеров воды при помощи неэмпирического метода квантовой химии высокого уровня. Необходимым условием возможности применения такого метода является корректное описание явления корреляции электронного движения, что необходимо для воспроизведения дисперсионного взаимодействия. В частности, использовалась Симметризованная теория возмущений (SAPT) [3], в которой электронная корреляция учитывается по теории возмущений до четвертого порядка включительно. Использовалась раздельная параметризация основных составляющих энергии межмолекулярного взаимодействия таких, как электростатика, обменное взаимодействие, индукционное взаимодействие и дисперсия, что существенно упрощает и улучшает процесс параметризации. Для получения достаточно высокой точности таких расчетов (0,2-0,3 ккал/моль) помимо учета электронной корреляции необходимо также применение одноэлектронного базиса достаточной полноты. Возможно использование базисов aug-cc-pVTZ, aug-cc-pVQZ, других полных электронных базисов, а также базисов SAPTbs, специально предназначенных для SAPT расчетов. Авторами использовались базисы SAPTbs.
Относительные положения молекул воды в димере воды определялись методами Монте-Карло. Каждое относительное положение двух молекул воды определяет точку на многомерной поверхности потенциальной энергии (ППЭ) комплекса. Количество точек N на ППЭ, которые необходимо использовать для параметризации, определяется качеством параметризации силового поля, которое, например, может определяться величиной среднеквадратичного отклонения энергии, получаемой по модели силового поля от энергии, вычисленной неэмпирическим методом
rms=sqrt((∑(Ei(ab-initio)-Ei(fit))2)/N),
где Ei(ab-initio) - значение полной энергии взаимодействия для i-й точки пространства межмолекулярного комплекса, полученное в квантово-химическом расчете с помощью программы SAPT [3], Ei(fit) - подгоночное значение энергии взаимодействия для той же точки пространства межмолекулярного комплекса, полученное с помощью классических потенциалов.
С увеличением числа точек величина rms падает. Необходимо обеспечить значения rms не хуже, чем точность неэмпирического метода, используемого для построения ППЭ, что в случае димера воды в наших расчетах составляло обычно 0,2-0,3 ккал/моль. Соответствующее число точек N составляет при этом несколько тысяч для небольших молекул таких, как молекула воды.
Оказалось целесообразным генерировать несколько наборов точек на поверхности потенциальной энергии молекулярного комплекса:
- группу точек, представляющих конфигурацию комплекса, в котором мономеры тесно сближены (такие точки важны для параметризации короткодействующих взаимодействий),
- группу точек, представляющих далеко разнесенные мономеры (такие точки важны для получения некоторых электростатических параметров и асимптотики дисперсионного взаимодействия).
В процессе генерации точек на ППЭ молекулярного комплекса могут получаться геометрии комплекса, обладающие большой энергией межмолекулярного взаимодействия. Так как для параметризации силового поля нас интересуют энергии, лишь на несколько ккал/моль превышающие энергию дна потенциальной ямы, то точки с большой энергией межмолекулярного взаимодействия не должны участвовать в процессе параметризации.
Для этого предлагается:
- в процессе параметризации (уменьшения целевой функции ошибок) использовать весовую функцию, уменьшающую вклад в целевую функцию точек с высокой энергией;
- в процессе генерации точек производить сравнительно простым и быстрым квантово-химическим методом первоначальную оценку энергии взаимодействия мономеров в данной геометрии и на основании этих предварительных расчетов исключать точки с высокой энергией.
Разложение энергии межмолекулярного взаимодействия в рамках Симметризованной Теории Возмущений и реализующей ее программы SAPT дает детальную картину физического явления. Однако большое количество составляющих энергии затрудняет параметризацию каждого компонента. Кроме того, поведение многих составляющих с изменением межатомных расстояний сходно. По этой причине, возможно, провести процедуру группировки отдельных составляющих, сходных по своему физическому смыслу, и в результате получить традиционные для силового поля компоненты энергии: электростатическую, обменную, индукционную и дисперсионную. При этом группировка компонент энергии производится следующим образом (в обозначениях, принятых в программе SAPT):
а) Электростатическая энергия получается как сумма электростатических энергий в первом (EES (10)) и высших (EES (H)) порядках теории возмущения
UES=EES (10)+EES (H).
б) Обменная энергия есть сумма обменной энергии в первом (EEX (10)) и высших (EEX (H)) порядках теории возмущения. Кроме того, в обменную энергию включается смешанная обменно-индукционная энергия во втором (EEX-IND (20)) и высших (EEX-IND (H)) порядках теории возмущения наряду с обменно-дисперсионной энергией в высших порядках (EEX-DISP (H)). Также сюда включается разность (δ(HF)) между энергией взаимодействия молекул, которая получена Хартри-Фоковским супермолекулярным расчетом и суммой соответствующих компонент энергии по теории SAPT: электростатической энергии первого порядка, обменной энергии первого порядка, индукционной энергии второго порядка и обменно-индукционной энергии второго порядка
UEX =EEX (10)+EEX-IND (20)+δ(HF)+EEX (H)+EEX-IND (H)+EEX-DISP (H).
в) Индукционная энергия есть сумма индукционной энергии во втором (EIND (20)) и высших (EIND (H)) порядках теории возмущения
UIND=EIND (20) + EIND (H).
г) Дисперсионная энергия есть сумма всех дисперсионных компонент по теории SAPT (EDISP (H))
UDISP=EDISP (H).
Пример разложения межмолекулярной энергии взаимодействия для димера воды, когда конфигурация димера близка к точке абсолютного минимума энергии, приведен в таблице 1.
Пример разложения межмолекулярной энергии взаимодействия по методу SAPT для димера воды.
После выделения нескольких главных составляющих энергии каждая из них используется для построения модели соответствующего взаимодействия.
Предлагаемый метод в корне отличается от процедуры параметризации только полной энергии взаимодействия, что обычно производится при построении моделей силового поля. В этом последнем случае нельзя ожидать, что отдельные компоненты энергии могут правильно передаваться такими моделями, так как даже в случае неправильных отдельных компонент можно получать хорошие значения полной энергии в результате компенсации ошибок. Иногда такая компенсация подразумевается изначально в процессе создания силового поля. Так, простое кулоновское взаимодействие не способно описать реальную картину взаимодействия диффузных зарядов. Поэтому соответствующую разность между истинной энергией и модельной электростатической энергией (энергию проникновения) включают в другое - обменное - взаимодействие.
Также при подгонке модели только под одно значение полной энергии можно получить нефизичные значения параметров из-за переопределенности задачи оптимизации (слишком большое количество одновременно оптимизируемых параметров).
В случае предложенной авторами раздельной оптимизации компонент энергии количество параметров оптимизации существенно уменьшается, что устраняет переопределенность задачи. Кроме того, компенсация ошибок невозможна, и каждый компонент силового поля несет конкретный физический смысл.
Таким образом, в результате группировки электростатическая часть потенциала содержит компоненты кулоновского взаимодействия зарядовых распределений молекул с учетом внутримолекулярной корреляции, но без учета индукции. Обменная часть потенциала аккумулирует обменное взаимодействие первого и высших порядков в рамках SAPT, а также включает смешанные обменно-индукционный и обменно-дисперсионый термы. Кроме того, возможно включение в обменную часть разницы между супермолекулярной хартри-фоковской энергией и суммарной энергией по первому порядку теории возмущения.
Индукционная часть включает индукционную энергию второго и высших порядков.
Дисперсионная часть включает дисперсионную энергию второго и высших порядков.
Выбор функциональной формы для описания каждого взаимодействия должен основываться на адекватных физических моделях.
Так, наиболее простая функциональная форма электростатического взаимодействия как взаимодействия точечных зарядов не отражает реального диффузного распределения электронной плотности в молекуле и не может воспроизвести эффекты, связанные с перекрыванием электронной плотности молекул (эффект проникновения). Применение распределенного мультипольного (DMA) анализа не решает проблему в корне, хотя и улучшает среднеквадратичное отклонение модельных значений от квантово-химического расчета в два-три раза. Нами был использован последовательный метод построения модели электростатического взаимодействия, в котором электронная плотность молекулы рассматривается как суперпозиции точечных и диффузных зарядов. Под диффузными зарядами мы понимаем некое непрерывное распределение заряда с плотностью ρ, так что интеграл от плотности по всему объему является конечным диффузным зарядом. Распределение заряда на каждом центре может быть как анизотропным, так и сферически симметричным с различной зависимостью электронной плотности от радиуса - экспоненциальной, гауссовской и др. В частности, мы использовали сферически симметричную экспоненциальную форму распределения диффузного заряда d
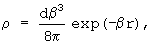
где β - параметр экспоненциального затухания электронной плотности.
Диффузные и точечные заряды центрованы на силовых центрах, которые совпадают или не совпадают с положениями атомов в молекуле (фиг.5). Так, на фиг.6 показаны соответствующее распределение и силовые центры для модели молекулы воды. Количество силовых центров - 7. Три из них совпадают с положениями атомов, а четыре находятся в плоскости, проходящей через ось симметрии молекулы и перпендикулярной плоскости молекулы. Учитывая симметрию молекулы, общее количество геометрических параметров, подлежащих оптимизации наряду с параметрами диффузных и точечных зарядов, равно 4. Количество дополнительных центров, необходимых для построения модели, диктуется зарядовым распределением молекулы и необходимой точностью подгонки энергии взаимодействия. Выражение для потенциала электростатического взаимодействия имеет вид
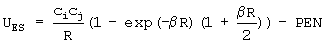
где слагаемое, описывающее эффект проникновения, описывается формулой
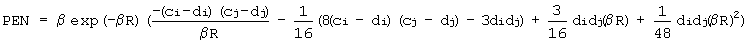
где индексы (i) и (j) характеризуют два силовых центра, параметры взаимодействия - это параметры β, ci, сj, di, dj (ci - полный заряд i-ого центра, di - его диффузный заряд, β - параметр экспоненциального затухания электронной плотности), а R представляет собой расстояние между этими центрами.
Это выражение для электростатической энергии представляет собой парный межцентровый потенциал, где взаимодействие между каждой парой центров включает два слагаемых: первое слагаемое соответствует кулоновскому взаимодействию неперекрывающихся полных зарядов на силовых центрах, а второе учитывает эффект проникновения. В таблице 2 приведены параметры электростатического взаимодействия молекул воды друг с другом.
Параметры, описывающие электростатическое взаимодействие молекул воды:
β=2,3989 a.u-1
Энергия обменного отталкивания может описываться стандартными потенциалами (Борна-Майера, Букингема и т.д.). Авторы применили усовершенствованную форму потенциала Борна-Майера, основывающуюся на теории поверхностного интеграла для взаимодействия атомов инертных газов [5]
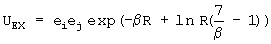
где индексы (i) и (j) характеризуют два силовых центра, параметры взаимодействия - это параметры β, ei, ej, а R представляет собой расстояние между этими центрами, причем параметр экспоненциального затухания электронной плотности β в этом случае оказывается одинаковым для электростатической модели и модели обменного взаимодействия. Использование такой формы улучшает качество оптимизации обменного взаимодействия в среднем на 20%. Кроме того, параметр экспоненциального затухания электронной плотности β в этом случае оказывается одинаковым для электростатической модели и модели обменного взаимодействия. Полученные нами параметры для обменного взаимодействия молекул воды приведены в таблице 3.
Параметры, описывающие обменное взаимодействие молекул воды:
Индукционная составляющая энергии описывается выражением, содержащим парный, аддитивный, экспоненциально-затухающий, межцентровой потенциал, описывающий эффекты переноса заряда (см. ниже, формула (а)). Функциональная форма этого потенциала может быть близкой к потенциалу, определенному для обменного взаимодействия. Оставшаяся часть взаимодействия отвечает неаддитивному поляризационному взаимодействию, природа которого состоит в изменении электронного распределения молекулы под влиянием электрического поля, наводимого окружением (см. ниже, формула (b)). Для этих обоих взаимодействий использовались следующие потенциалы:
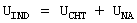
где UIND - полная индукционная энергия, UCHT - парная межцентровая составляющая часть индукционной энергии, описывающая процессы переноса заряда, UNA - неаддитивная поляризационная составляющая индукционной энергии;
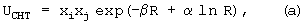
где xi - параметры переноса заряда на силовых центрах молекулы;
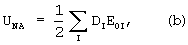 ,
,
где DI удовлетворяет условию самосогласования:
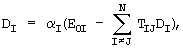 ,
,
αI - атомные поляризуемости, E0I - электрическое поле, наводимое постоянными зарядами,
TIJ - тензор диполь-дипольного взаимодействия.
Силовые центры взаимодействия, определяемого переносом заряда, могут находиться как на атомах молекулы, так и на дополнительных центрах, положение которых было определено в ходе параметризации электростатического и обменного взаимодействий. Силовые центры для поляризационного взаимодействия находятся на атомах. Для описания поляризационного взаимодействия могут применяться различные модели, в частности модель поляризуемых диполей [6], либо модель флуктуирующих зарядов. В случае модели поляризуемых диполей соответствующие атомные поляризуемости могут быть взяты из литературы, либо получены с помощью дополнительной оптимизационной процедуры. Эти параметры могут быть присвоены каждому атому химического элемента, что уменьшает количество параметров, подлежащих оптимизации в ходе построения модели силового поля для конкретного класса химических соединений. Таким образом, оптимизация необходима только для параметров переноса заряда на атомах и дополнительных центрах.
Например, для параметризации модели силового поля молекулы воды использована модель поляризуемых диполей. Электрическое поле, действующее на каждом силовом центре и индуцирующее электрический диполь, состоит из двух частей:
- электрического поля, создаваемого комбинацией точечных и диффузных зарядов других молекул, если рассматриваемые молекулы невелики. В случае больших молекул может применяться концепция зарядовых групп. При этом рассматривается также влияние зарядов от самой молекулы, если эти заряды расположены на других зарядовых группах. Возможно также применение различных "смягчающих" функций, при помощи которых эффективно уменьшается вклад в электростатическое поле на силовом центре от близко расположенных зарядов;
- электрического поля всех иных индуцированных диполей.
Взаимодействие диполя с иными индуцированными диполями описывается тензором диполь-дипольного взаимодействия Т (см. формулу (b)). Компоненты тензора Т могут подвергаться процедуре "смягчения" [6], чтобы принять во внимание диффузную природу реального электронного распределения и избежать "поляризационной катастрофы".
Для описания дисперсионного взаимодействия может применяться функциональная форма, предложенная Тангом и Тоннисом [7], либо в исходном виде, либо в упрощенном виде. Так, для рассматриваемой модели воды нами применялась упрощенная форма Танга-Тонниса, где слагаемые более высокого порядка, чем r-6 были исключены
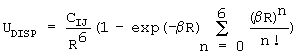
где Сij - парные параметры дисперсионного взаимодействия центров (i) и (j), а параметр взаимодействия β отличается от соответствующих параметров β, фигурирующих в формулах для электростатического, и обменного, и индукционного взаимодействия, R - расстояние между центрами (i) и (j); центры дисперсионного взаимодействия располагаются на атомах (3 центра - O, H, H): COO=54,25806, COH=9,42289, CHH=0,97517, β=2,064.
В случае применения развернутой функциональной формы могут возникать сложности с оптимизацией, так как большое количество параметров, подлежащих определению, делают оптимизационную задачу переопределенной. Это приводит к тому, что получающаяся модель содержит нефизичные параметры, хотя и дает прекрасные результаты по воспроизведению квантово-химических значений дисперсионной энергии.
Качество полученной функциональной формы для модели силового поля молекулы воды продемонстрировано на фиг.7-11, где отложены точки на кривой потенциальной энергии димера воды в координатах, соответствующих энергии димера, рассчитанной методом SAPT, и энергии, получаемой по модели силового поля, метод параметризации которого является предлагаемым здесь изобретением.
Для получения этой модели силового поля использовалась описанная выше процедура параметризации отдельных составляющих энергии межмолекулярного взаимодействия по 1569 точкам на ППЭ димера воды. Соответствующие среднеквадратичные отклонения значения энергии по этому набору точек указаны на рисунках. Для проверки качества параметризации модели силового поля было выполнено сравнение энергии ППЭ воды для дополнительных 1418 точек, которые не использовались в процессе параметризации. Были найдены следующие среднеквадратичные отклонения модельных энергий от расчетных:
Среднеквадратичное отклонение полной энергии для полученной модели силового поля не хуже точности метода SAPT в его современном воплощении.
Модель силового поля для молекулы воды, таким образом, наряду с экспериментальными геометрическими параметрами длины связи OH и угла HOH содержит 4 параметра для координат дополнительных силовых центров «c» и «l» (см. фиг.6). Для каждого из 4 различных силовых центров модель содержит величины точечного заряда, диффузного заряда, обменного параметра и параметра, описывающего перенос заряда. Кроме того, оптимизируется показатель экспоненты β.
Дисперсионное взаимодействие описывается 4 параметрами.
Параметры, описывающие поляризационное взаимодействие в рамках модели Тола, были взяты из литературы [6] и не оптимизировались. Таким образом, общее количество параметров, подлежащих оптимизации для модели силового поля молекулы воды, составляет 24 (учитывая ограничение на полный заряд молекулы).
Использованная литература
1. T.A.Halgren, J.Comp.Chem. 17 (1996) 490-641; ibid, 20 (1999) 720-748.
2. E.M.Mas, R.Bukowski, K.Szalewicz, J.Chem. Phys.113 (2000) 6687.
3. R.Moszynski, B.Jeziorski, K.Szalewicz J.Chem. Phys.100 (1994) 1312.
4. H.M.Berman, J.Westbrook, Z.Feng, G.Gilliland, T.N.Bhat, H.Weissig, I.N.Shindyalov, P.E.Bourne, Nucleic Acids Research 28 (2000) 235-242, http://www.rcsb.org/pdb.
5. U.Kleinekathoefer, K.T.Tang, J.P.Toennies, C.L.Yiu, J.Chem. Phys. 103 (1995) 6617-6630.
6. Piet Th. Van Duijnen, M.Swart, J.Chem. Phys. A. 102 (1998) 2399-2407.
7. K.T.Tang, J.P.Toennies, J.Chem. Phys. 80 (1984) 3726-3741.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ МОДЕЛИРОВАНИЯ И ПРОГНОЗИРОВАНИЯ СВЯЗЫВАНИЯ МОЛЕКУЛ-ЛИГАНДОВ С МОЛЕКУЛАМИ-МИШЕНЯМИ МЕТОДАМИ КВАНТОВОЙ МЕХАНИКИ С УЧЕТОМ ВЛИЯНИЯ РАСТВОРИТЕЛЯ | 2003 |
|
RU2265244C2 |
| СПОСОБЫ И ПРИБОРЫ ДЛЯ ОБНАРУЖЕНИЯ И ИДЕНТИФИКАЦИИ ЗАКОДИРОВАННЫХ ГРАНУЛ И БИОЛОГИЧЕСКИХ МОЛЕКУЛ | 2007 |
|
RU2487169C2 |
| СПОСОБ ОПТИМИЗАЦИИ УСЛОВИЙ КРИСТАЛЛИЗАЦИИ БЕЛКОВ С ПРИМЕНЕНИЕМ МЕТОДА МОЛЕКУЛЯРНОЙ ДИНАМИКИ | 2021 |
|
RU2781051C1 |
| СПОСОБ ИДЕНТИФИКАЦИИ ЭПИТОПОВ Т-КЛЕТОК И ЕГО ПРИМЕНЕНИЕ ДЛЯ ПОЛУЧЕНИЯ МОЛЕКУЛ СО СНИЖЕННОЙ ИММУНОГЕННОСТЬЮ | 2002 |
|
RU2303264C2 |
| СПОСОБ ИДЕНТИФИКАЦИИ ПРОМЕЖУТОЧНЫХ ПРОДУКТОВ | 2019 |
|
RU2814953C2 |
| СПОСОБ ИДЕНТИФИКАЦИИ УЧАСТКОВ СВЯЗЫВАНИЯ БЕЛКОВЫХ КОМПЛЕКСОВ | 2020 |
|
RU2743316C1 |
| ДОМЕН СВЯЗЫВАНИЯ БАКТЕРИАЛЬНОЙ АТР-СИНТАЗЫ | 2005 |
|
RU2418001C2 |
| ОСНОВАННОЕ НА СТРУКТУРЕ ПРОГНОЗНОЕ МОДЕЛИРОВАНИЕ | 2014 |
|
RU2694321C2 |
| УСТРОЙСТВО И СПОСОБ ИЗМЕРЕНИЯ КОНЦЕНТРАЦИЙ МОЛЕКУЛ ЧЕРЕЗ БАРЬЕР | 2005 |
|
RU2424320C2 |
| Способ разметки лиганд-белковых сайтов связывания | 2024 |
|
RU2838984C1 |
Изобретение относится к разработке новых соединений для медицины, биотехнологии, физики конденсированных сред и различных областей материаловедения, в которых существенны межмолекулярные взаимодействия. Техническим результатом является обеспечение требуемой точности создаваемых потенциалов взаимодействия и упрощение обработки с использованием аналитических выражений для потенциалов взаимодействия, обеспечивающих возможность быстрой численной обработки при молекулярно-динамическом моделировании. Предложенные способы моделирования процесса связывания молекулы-лиганда с молекулой-мишенью опираются на подгонку некоторого числа параметров под результаты экспериментального измерения величин, характеризующих процесс связывания. Молекулярно-динамический способ моделирования основан на подгонке меньшего числа параметров под эксперимент, но требует значительных затрат компьютерного времени, так как необходимо найти траектории движения всех входящих в молекулу-мишень и молекулу-лиганд атомов при учете их теплового движения. Молекулярно-механический способ включает в себя большее число параметров, определяемых из эксперимента, но требует провести лишь оптимизацию полной энергии системы взаимодействующих друг с другом молекулы-мишени и молекулы-лиганда. Оба способа моделирования учитывают влияние растворителя, в котором может происходить процесс связывания, причем растворитель моделируется либо явным образом путем введения в систему молекул растворителя, либо неявным образом, когда растворитель заменяется на непрерывную среду с заданными характеристиками, такими как диэлектрическая проницаемость и проводимость. Оба способа моделирования основаны на определении классических потенциалов взаимодействия между атомами молекулы-мишени и молекулы-лиганда с помощью высокоточных неэмпирических квантово-механических расчетов. 4 н. и 24 з.п. ф-лы, 11 ил., 3 табл.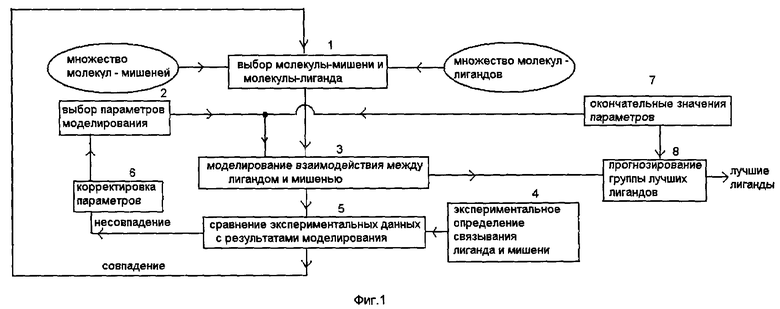
а) получают структуру и состав молекулы-мишени;
б) получают структуру и состав молекулы-лиганда;
в) сохраняют данные о структуре и составе молекулы-мишени и молекулы-лиганда на носителе информации в соответствующем формате;
г) выбирают параметры моделирования для использования в программе моделирования взаимодействия между молекулой-мишенью и молекулой-лигандом в растворе в соответствии с молекулярно-динамическим или молекулярно-механическим моделированием упомянутого воздействия;
д) считывают упомянутые сохраненные данные и осуществляют их обработку, по меньшей мере, одним процессором с помощью упомянутой программы моделирования взаимодействия между молекулой-мишенью и молекулой-лигандом с использованием заданных параметров моделирования,
е) получают результаты моделирования в виде числовых данных, характеризующих интенсивность связывания молекулы-лиганда с молекулой-мишенью, и сохраняют полученные числовые данные на носителе информации;
ж) осуществляют реальные химические измерения величин, характеризующих интенсивность связывания упомянутых молекул между собой;
з) сравнивают данные, полученные в измерениях на этапе (ж), с результатами моделирования, полученными на этапе (е);
и) в случае расхождения между рассчитанными и измеренными величинами, характеризующими взаимодействие между молекулой-мишенью и молекулой-лигандом, превышающего заданную величину, корректируют параметры моделирования, используемые программой, моделирующей взаимодействие между молекулой-мишенью и молекулой-лигандом;
к) повторяют этапы (г)-(и) до тех пор, пока расхождение между рассчитанными на этапе (е) и измеренными на этапе (ж) величинами, характеризующими связывание молекул между собой, не станет меньше заданной величины;
л) повторяют этапы (а)-(к) для другой пары молекулы-мишени и молекулы-лиганда;
м) повторяют этапы (а)-(л) до тех пор, пока для каждой новой пары молекул расхождение между измеренными и рассчитанными величинами, характеризующими связывание молекул между собой, не будет меньше заданной заранее величины при параметрах моделирования, полученных на этапах (а)-(л) для других пар молекул, и сохраняют окончательные значения параметров моделирования на носителе информации;
н) используют созданные на этапах (а)-(м) параметры моделирования связывания молекулы-лиганда с молекулой-мишенью для прогнозирования с помощью компьютерного моделирования молекул-лигандов, которые связываются наилучшим образом с молекулой-мишенью.
а) считывают данные о структуре молекулы-мишени и молекулы-лиганда с носителя информации в память компьютера и выполняют преобразование координат атомов этих молекул таким образом, чтобы наименьшее расстояние между каждым из атомов молекулы-лиганда и заданными атомами молекулы-мишени находилось в заданном диапазоне, и сохраняют новые координаты атомов молекулы-мишени и молекулы-лиганда в памяти компьютера;
б) осуществляют запись в память компьютера параметров, характеризующих растворитель, для последующей совместной обработки с координатами атомов молекулы-мишени и молекулы-лиганда;
в) определяют траектории движения всех взаимодействующих друг с другом атомов молекулы-мишени и молекулы-лиганда с учетом наличия растворителя, используя потенциалы межмолекулярного взаимодействия с параметрами взаимодействия, определенными компьютерным способом, путем решения уравнений Ньютона или Лагранжа при учете их теплового движения;
г) вычисляют величины, характеризующие интенсивность связывания молекулы-лиганда с молекулой-мишенью в растворителе;
д) сохраняют на носителе информации вычисленные на этапе (г) величины, характеризующие интенсивность связывания молекулы-лиганда с молекулой-мишенью в растворителе.
а) считывают данные о структуре молекулы-мишени и молекулы-лиганда с носителя информации в память компьютера и выполняют преобразования координат над этими данными таким образом, чтобы наименьшее расстояние между каждым из атомов молекулы-лиганда и заданными атомами молекулы-мишени находилось в заданном диапазоне, и записывают новые координаты атомов молекулы-мишени и молекулы-лиганда в память компьютера;
б) добавляют к множеству координат атомов молекулы-мишени и молекулы-лиганда, сформированному на этапе (а), параметры, характеризующие растворитель;
в) вычисляют полную энергию системы взаимодействующих молекулы-мишени, молекулы-лиганда и растворителя как функцию координат атомов молекулы-мишени, атомов молекулы-лиганда, параметров, характеризующих растворитель, и потенциалов их взаимодействия с параметрами взаимодействия, определенными компьютерным способом;
г) определяют минимальное значение полной энергии системы взаимодействующих молекулы-мишени, молекулы-лиганда и растворителя при варьировании положений атомов молекулы-мишени, молекулы-лиганда и параметров растворителя, и сохраняют на носителе информации координаты атомов и параметры, характеризующие растворитель, при которых достигается минимум энергии системы взаимодействующих молекулы-мишени, молекулы-лиганда и растворителя,
д) для координат атомов, полученных на этапе (г), вычисляют энергию взаимодействия молекулы-лиганда с молекулой-мишенью и растворителем как суммы вкладов от парных потенциалов взаимодействия, где в каждой паре атомов один принадлежит молекуле-лиганду, а второй - молекуле-мишени, либо растворителю, причем в соответствии с различными типами потенциалов энергию взаимодействия вычисляют как сумму, по меньшей мере, двух отдельных компонент - электростатической и Ван-дер-Ваальсовой;
е) для координат атомов, полученных на этапе (г), вычисляют внутреннюю энергию молекулы-лиганда;
ж) сохраняют на носителе информации отдельные компоненты энергии взаимодействия и внутренней энергии молекулы-лиганда;
з) с помощью координат атомов молекулы-лиганда, параметров, характеризующих растворитель, и потенциалов их взаимодействия вычисляют полную энергию системы взаимодействующих молекулы-лиганда и растворителя;
и) находят минимальную полную энергию системы взаимодействующих молекулы-лиганда и растворителя без молекулы-мишени при варьировании положений атомов молекулы-лиганда и параметров, характеризующих растворитель, и сохраняют на носителе информации координаты атомов молекулы-лиганда и параметры, характеризующие растворитель, при которых достигается минимум энергии системы взаимодействующих молекулы-лиганда и растворителя;
к) для координат атомов, полученных на этапе (и), вычисляют энергию взаимодействия молекулы-лиганда с растворителем как сумму, по меньшей мере, трех отдельных компонент - электростатической, Ван-дер-Ваальсовой и кавитационной, а также вычисляют внутреннюю энергию молекулы-лиганда и сохраняют на носителе информации отдельные компоненты энергии взаимодействия молекулы-лиганда с растворителем и внутреннюю энергию молекулы-лиганда;
л) вычисляют разность между соответствующими компонентами энергии взаимодействия молекулы-лиганда с молекулой-мишенью и растворителем, сохраненными на носителе информации на этапе (ж), и компонентами энергии взаимодействия молекулы-лиганда с растворителем, сохраненными на носителе информации на этапе (к);
м) вычисляют разность между внутренней энергией молекулы-лиганда, сохраненной на носителе информации на этапе (з), и внутренней энергией молекулы-лиганда, сохраненной на носителе информации на этапе (к);
н) используют разности энергий, полученных на этапах (л) и (м), для составления из этих величин оценочного значения свободной энергии связывания молекулы-мишени и молекулы-лиганда в виде линейной или нелинейной комбинации этих величин с весовыми коэффициентами и сохраняют полученное оценочное значение свободной энергии связывания молекулы-мишени и молекулы-лиганда на носителе информации.
а) для заданной пары молекул считывают геометрические параметры каждой молекулы в память компьютера в соответствующем формате;
б) используя геометрические параметры этих молекул, с помощью соответствующей компьютерной программы вычисляют набор координат атомов этих молекул, соответствующих различным взаимным расположениям этих молекул, и сохраняют полученные данные на носителе информации в виде множества точек в пространстве межмолекулярного комплекса;
в) из множества всех точек в пространстве межмолекулярного комплекса формируют два его подмножества: обучающее подмножество для подгонки параметров взаимодействия и тестовое подмножество для проверки качества полученных потенциалов;
г) вычисляют энергию взаимодействия рассматриваемых молекул друг с другом с помощью квантовых расчетов, описывающих поведение электронов в заданном поле атомных ядер молекул, при этом
г.1) считывают с носителя информации в память компьютера данные, соответствующие одной точке из пространства межмолекулярного комплекса, представляющие собой координаты атомов, соответствующие одному определенному положению двух молекул относительно друг друга;
г.2) вычисляют полную энергию взаимодействия двух рассматриваемых молекул друг с другом и значения различных компонент энергии взаимодействия с помощью предварительно записанной на носитель информации и считанной в память компьютера программы, решающей систему уравнений движения на основе законов квантовой механики, и сохраняют полученные значения на носителе информации;
г.3) группируют различные компоненты энергии взаимодействия в четыре основных типа энергии взаимодействия, включающих энергию электростатического взаимодействия, обменную, индукционную и дисперсионную энергию и записывают полученные числовые данные, сгруппированные по указанным четырем компонентам, на носитель информации;
г.4) повторяют подэтапы (г.1)-(г.3) для всех точек пространства межмолекулярного комплекса, относящихся к обучающему подмножеству и к тестовому подмножеству, для формирования на носителе информации данных для каждой точки пространства межмолекулярного комплекса четырех чисел, соответствующих упомянутым четырем компонентам энергии межмолекулярного взаимодействия;
д) вычисляют энергию взаимодействия рассматриваемых молекул друг с другом с помощью содержащих параметры взаимодействия классических потенциалов, представляющих собой энергию взаимодействия двух частиц, характеризуемых массой и положением в пространстве, при этом
д.1) считывают с носителя информации в память компьютера данные, соответствующие одной точке из пространства межмолекулярного комплекса, представляющие собой координаты атомов, соответствующих одному определенному положению двух молекул относительно друг друга;
д.2) вычисляют энергию взаимодействия двух молекул друг с другом для точки пространства межмолекулярного комплекса, соответствующей данным, считанным на подэтапе (д.1), как сумму взаимодействий между входящими в состав молекул парами атомов;
д.3) вычисляют энергию взаимодействия каждой пары атомов как сумму классических потенциалов соответствующих различным компонентам взаимодействия;
д.4) выбирают функциональную зависимость классического потенциала, содержащего параметры взаимодействия и соответствующего заданной компоненте энергии взаимодействия;
е) определяют параметры взаимодействия путем выполнения подэтапов, на которых
е.1) формируют целевую функцию по значениям заданной компоненты межмолекулярного взаимодействия для всех точек обучающего подмножества, при этом целевую функция для заданной компоненты межмолекулярного взаимодействия вычисляют как сумму квадратов разностей соответствующих величин для всех точек обучающего подмножества, полученных с помощью квантовых расчетов на этапе (г), с одной стороны, и полученных с помощью классических потенциалов на этапе (д), с другой стороны;
е.2) минимизируют целевую функцию при варьировании параметров взаимодействия, входящих в упомянутую функциональную зависимость, выбранную для заданной компоненты энергии межмолекулярного взаимодействия, и сохраняют на носителе информации значения параметров, при которых целевая функция достигает своего минимума;
е.3) вычисляют целевую функцию для заданной компоненты межмолекулярного взаимодействия для точек пространства межмолекулярного комплекса из тестового подмножества при использовании значений параметров взаимодействия, полученных на подэтапе (е.2), при этом целевую функцию для точек пространства межмолекулярного комплекса из тестового подмножества вычисляют как сумму квадратов разностей соответствующих величин для всех точек текстового подмножества, полученных с помощью квантовых расчетов на этапе (г), с одной стороны, и полученных с помощью классических потенциалов на этапе (д), с другой стороны;
е.4) если целевая функция, вычисленная на подэтапе (е.3), не превышает заданную величину, соответствующую точности квантовых расчетов, то этап определения параметров взаимодействия для заданной компоненты энергии межмолекулярного взаимодействия завершают и присваивают использованные значения параметров взаимодействия соответствующим атомам, входящим в рассматриваемую пару молекул;
е.5) если целевая функция, вычисленная на подэтапе (е.3), превышает заданную величину, соответствующую точности квантовых расчетов, то расширяют обучающее подмножество пространства межмолекулярного комплекса или изменяют функциональную зависимость потенциала соответствующего взаимодействия на подэтапе (д.4) и повторяют подэтапы (е.1)-(е.5) до тех пор, пока целевая функция не уменьшится до требуемой величины;
е.6) повторяют подэтапы (е.1)-(е.5) для всех четырех компонент энергии межмолекулярного взаимодействия и сохраняют полученные окончательные значения параметров взаимодействия на носителе информации в качестве набора параметров взаимодействия заданных двух молекул.
групп точек, представляющих конфигурацию комплекса из двух тесно сближенных молекул, причем такие точки используют для нахождения параметров взаимодействий на малых расстояниях,
групп точек, представляющих конфигурацию комплекса из двух далеко разнесенных молекул, причем такие точки используют для получения электростатических параметров и параметров дисперсионного взаимодействия.
а) при нахождении параметров взаимодействия используют весовую функцию, уменьшающую вклад в целевую функцию точек с высокой энергией;
б) в процессе вычисления точек осуществляют первоначальную оценку энергии взаимодействия молекул в данной конфигурации комплекса из двух молекул и на основании этой первоначальной оценки исключают точки с высокой энергией.
| US 6230102 B1, 08.05.2001.WO 01/18627 A2, 15.03.2001.US 5495423 A, 27.02.1996.RU 2132853 C1, 10.07.1999. |
Авторы
Даты
2005-11-27—Публикация
2003-08-29—Подача