Изобретение относится к области радиоэлектроники и гидроакустики, а именно к способам обнаружения и определения соответствия сигнала известной формы при наличии помех высокой интенсивности в канале передачи.
Способ ориентирован на применение в устройствах, работающих в каналах передачи данных, радиолокационных и сонарных применений с соотношением сигнал/шум достигающих значений масштаба SNR=0.01 и использующих сигналы известной формы.
Предлагаемый способ представляет собой усовершенствование классической схемы использования корреляторов для фиксации наличия сигнала заданной формы в системах цифровой обработки реального времени.
В таких системах поступающая информация после предварительной обработки представляет собой набор дискретных значений, которые обрабатываются детекторами.
Для радарных и сонарных применений для определения дальности передающий тракт посылает зондирующий сигнал известной формы. Приемный тракт проводит прослушивание среды и детектирует в нем наличие эхо-сигнала. По факту обнаружения эхо-сигнала рассчитывается задержка между отправкой тестового сигнала и обнаружением эхо-сигнала. Знание скорости распространения сигнала обеспечивает возможность расчета дальности до объекта, отразившего зондирующий сигнал.
Для коммуникационных применений результатом обработки является принятие решения о наличии сигнала известной формы. В системах с бинарным кодированием необходимо использование двух типов сигналов, один из которых используется для кодирования логической 1, второй для логического 0. В системах с тональным кодированием количество сигналов зависит от набора используемых команд.
В такого рода системах использование корреляционной обработки является сложившейся практикой [Варакин Л.Е. Системы связи с шумоподобными сигналами. М. Радио и Связь, 1985, с. 25-26]
При обработке очередного отсчета производится расчет корреляционной функции путем расчета дискретной свертки с набором дискретных значений для зондирующего или коммуникационных сигналов. Максимум этой корреляционной функции сравнивается с максимумом эталонной корреляционной функции. В случае превышения порога детектирующее устройство фиксирует наличие сигнала. Эталонная корреляционная функция и, соответственно, ее максимум рассчитываются в предположении отсутствия помех в канале распространения используемого сигнала.
Изобретение базируется на феномене подобия формы корреляционных функций, который был обнаружен в результате проведения имитационных расчетов с использованием разных типов сигналов, разных значений SNR и параметров реализации корреляционных детекторов. Способ заключается в использовании векторно-косинусной меры подобия при сравнении эталонной корреляционной функции и корреляционной функции, формируемой из принимаемой информации из канала.
Для количественной оценки меры подобия корреляционных функций используется векторное описание корреляционных функций и косинус угла между этими векторами. Мера подобия, рассчитанная таким способом, используется в пороговом детекторе для разделения случаев наличия сигнала заданной формы или его отсутствия путем сравнения с назначаемым порогом.
Техническим результатом предлагаемого метода является увеличение вероятности правильного обнаружения и одновременное уменьшение вероятности ложного обнаружения сигнала при малых значениях соотношения сигнал-шум в канале передачи.
Эта возможность обеспечивается существенно возросшими возможностями современной элементной базы. Современные микроконтроллеры обеспечивают возможность реализации алгоритмов цифровой обработки сигналов (ЦОС), требующих использования многоразрядных аналогово-цифровых преобразователей (АЦП), большого объема вычислений с плавающей точкой и памяти. В работе [Астапкович A.M., Матвеев Д.П. Микроконтроллерные платформы «Миландр» и «Мультикор». Компоненты и технологии, №4, 2020, с. 10-17] зафиксирована тенденция перехода на микроконтроллеры второго поколения. Такие микроконтроллеры используют многоядерную архитектуру, включающую DSP ядра и многоразрядные АЦП. Это обеспечивает возможность эффективной с точки зрения практики реализации предлагаемого метода.
B патенте US 5469403 A [Digitalsonarsystem. Youngetal.21.11.1995] описан принцип работы сонарной системы, использующей композитный многочастотный сигнал заданной формы.
В соответствии с патентом в системе имеется канал формирования и посылки зондирующего сигнала и канал обработки эхо-сигнала. Для обработки эхо-сигнала предлагается использовать цифровую обработку данных. В частности, используется эталонная дискретная корреляционная функция и дискретная корреляционная функция для эхо-сигнала. Т.к. форма зондирующего сигнала известна, она используется для построения эталонной корреляционной функции. Ее максимальное значение Rmax используется при обработке эхо-сигнала.
В канале обработки эхо-сигнала используется аналого-цифровое преобразование аналогового сигнала из гидрофона. По этим данным в режиме реального времени рассчитывается текущее значение R для корреляционной функции с использованием массива значений для зондирующего импульса. Для ее расчета используется свертка дискретных значений зондирующего сигнала с динамически формируемым набором значений эхо-сигнала, полученного из оцифрованного входного сигнала.
Текущее значение корреляционной функции R сравнивается с максимальным значением для эталонной корреляционной функции. Рекомендованное условие фиксации эхо сигнала R>0.7Rmax.
Заявлено, что это позволяет увеличить точность измерения временного интервала между посылкой зондирующего импульса и фиксации наличия эхо-сигнала, по сравнению с аналоговыми решениями более чем в 100 раз. Этот способ выбран в качестве прототипа.
В данном патенте не приводятся данные по уровню шумов, вероятностям фиксации сигнала р(Н1) при его наличии и вероятности ложной фиксации р(Н0) сигнала при его отсутствии.
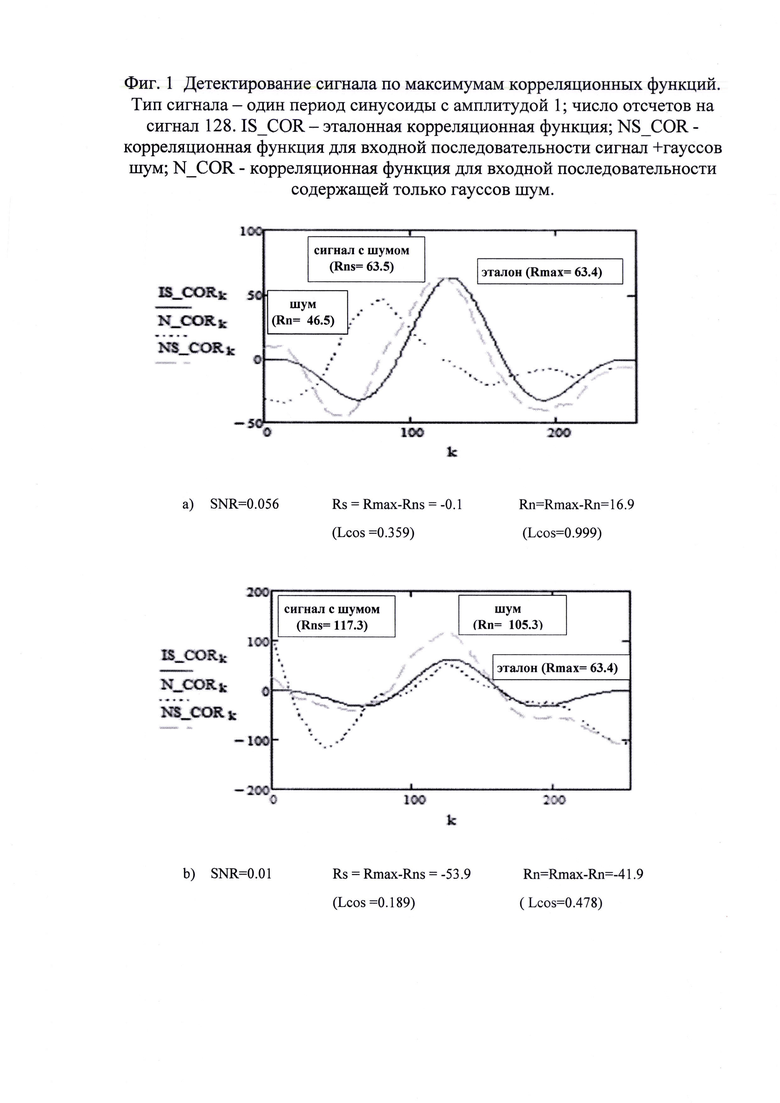
Применение такого способа детектирования в среде с большим уровнем шумов (SNR масштаба 0.01) вызывает ряд проблем. Для иллюстрации характера возникающих сложностей на фиг. 1 представлены результаты корреляционной обработки сигнала в виде одного периода синусоиды для двух вариантов реализации аддитивного гауссового шума (SNR=0.056 и SNR=0.01).
На каждом из графиков представлены корреляционные функции для случая наличия сигнала в потоке и при его отсутствии. Кроме этого, на графиках имеется эталонная корреляционная функция. При относительно малом уровне шума SNR=0.056 максимумы эталонной корреляционной функции и корреляционной функции при наличии сигнала в обрабатываемом фрагменте практически совпадают. Тем не менее, максимум для корреляционной функции при наличии сигнала превышает максимум эталона. Соответственно, разница максимумов становится отрицательной.
Эта ситуация становится более выраженной для большего уровня шума SNR=0.01. В этом случае максимум корреляционной функции почти в два раза превышает максимум для эталонной корреляционной функции. В принципе, ситуацию со знаком можно исправить, используя абсолютное значение разницы максимумов в детекторе наличия сигнала. Но проблема существенной разницы показывает, что рекомендуемый порог 0.7Rmax не будет работать.
Кроме этого, максим корреляционной функции при отсутствии сигнала в потоке смещен относительно максимума эталона. Эти значения для обоих рассмотренных случаев достаточно велики.
Эти эффекты более выражены при использовании полигармонических сигналов.
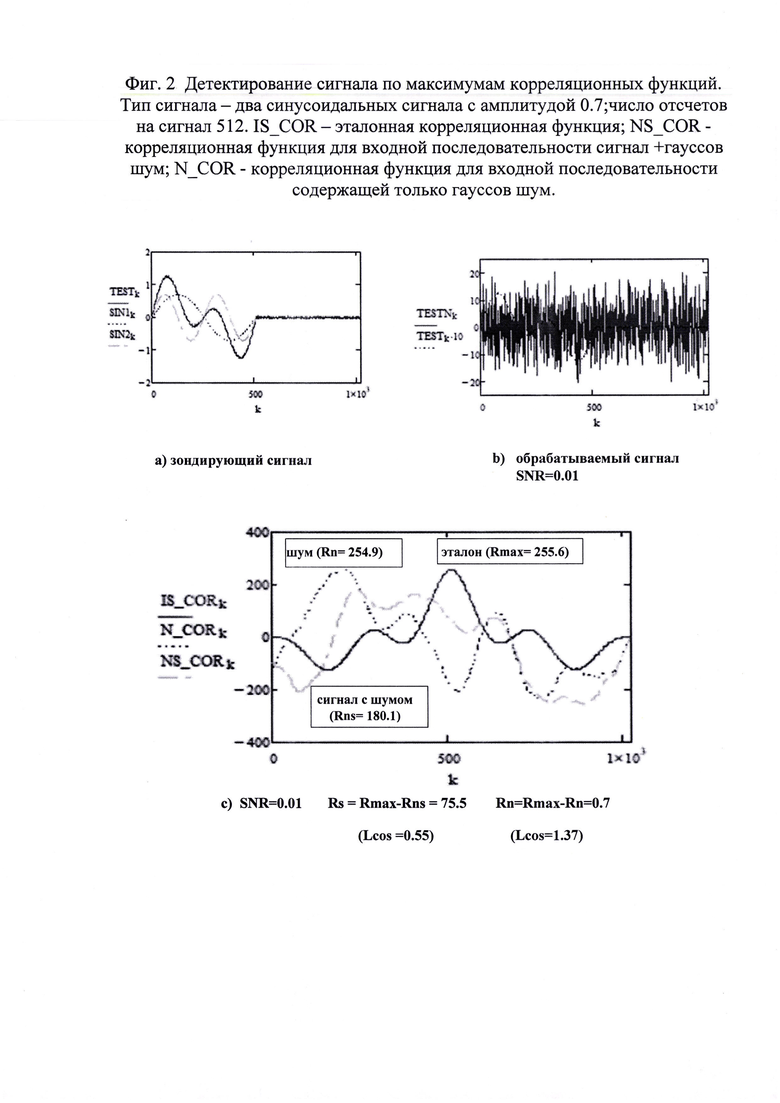
На фиг. 2а) приведен иллюстрирующий пример корреляционной обработки сигнала, сформированного из двух типов синусоид с амплитудой 0.7. Частоты сигналов отличаются в два раза. На фиг. 2b) приведен сигнал с аддитивным гауссовым шумом с параметрами, обеспечивающими отношение сигнал/шум SNR=0.01. На этом графике для наглядности приведен масштабированный (увеличенный в 10 раз) зондирующий сигнал.
Как следует из графика фиг. 2с) максимум корреляционной функции для случая отсутствия зондирующего сигнала практически равен максимуму эталонной корреляционной функции. Соответственно, при обработке сигнала будет зафиксировано наличие зондирующего сигнала при его отсутствии. В терминах теории обработки сигналов [Бутырский Е.Ю. Методы моделирования и оценивания случайных величин и процессов - СПб,: Стратегия будущего, 2020 - с. 555] это означает вероятность ложного обнаружения сигналов р(Н0).
Известен также способ определения соответствия кода сигнала, принимаемого от передатчика, коду сигнала, хранящемуся в памяти приемника, использующий встроенный генератор образцовых помех [Патент РФ 2716027 С1. Коррелятор полезного сигнала с обнаружением и классификацией помех Малыгин И.В. 05.03.2020].
Описанный способ реализуем для систем с постоянной передачей сигналов известной формы. Получаемая информация обрабатывается с помощью коррелятора, путем сравнения с моделями, хранящимися в памяти приемника. При этом при классификации сигналов используется ряд характерных особенностей корреляционных функций. Однако в описании не указывается, какие конкретно особенности предлагается использовать.
Способ базируется на принципиальной возможности классификации и построения модели помехи. Отсутствие сигнала интерпретируется, как наличие нового типа помехи, для которой строится соответствующая модель. Предполагается, что с помощью этой модели на следующем этапе обработки данных окажется возможным повысить помехозащищенность системы цифровой обработки данных. Способ, в принципе, позволяет повысить помехоустойчивость, но имеет существенный недостаток, т.к. процедура построения модели помехи, в общем случае, требует затрат времени.
Соответственно, способ имеет ряд существенных ограничений применительно к системам с асинхронной передачей пакетов цифровых данных, а именно, к системам цифровой связи или локационным системам освещения обстановки (радиолокация, гидролокация и т.п.). В такого рода системах требуется обработка данных в режиме реального времени.
Хотя способ и ориентирован на повышение помехозащищенности в его описании не приводится оценок для уровня шумов, параметров сигналов и устройства. Соответственно, это не позволяет на количественном уровне оценить степень эффективности предлагаемого подхода.
Тем не менее, данный способ имеет общие черты с предлагаемым способом, так как ориентирован на выработку универсального подхода с точки зрения описания типа обнаруживаемого сигнала и базируется на использовании корреляционных функций для классификации сигналов.
Ближайшим аналогом по принципам обработки корреляционной функции является способ, описанный в патенте РФ 2570430 С1 [Способ классификации шумящих объектов. Тимошенков В.Г. 13.10.2014].
Этот способ использует форму корреляционной функции для фиксации наличия и классификации сигналов.
Под термином «шумящий объект» подразумевается источник сигнала с известным спектральным портретом. При этом предполагается, что сигнал по этому признаку является стационарным. Кроме этого источников сигнала может быть несколько.
Для классификации шумящего объекта используется автокорреляционная функция последовательных взаимных спектров. Количество источников шумоизлучения определяют по числу перегибов автокорреляционной функции. При наличии одного источника классификация объекта производится по набору заранее определенных классификационных признаков. В частности, указывается, что в качестве классификационных признаков может использоваться ширина, число перегибов автокорреляционной функции. Таким образом, задача фиксации наличия в обрабатываемом потоке данных сигнала с известным набором признаков решается путем формирования описания корреляционной функции и анализом ее формы.
Применительно к области обнаружения и определения сигналов известной формы при наличии помех высокой интенсивности в канале передачи, такой способ обладает рядом недостатков.
Как следует из описания способа, он является узкоспециализированным из-за специфичности набора классификационных признаков. Наиболее существенным недостатком является потенциально недостаточная помехозащищенность этого способа. По крайней мере данных по помехозащищенности в данном патенте не приводится.
Кроме этого, судя по приведенному описанию структуры устройства, для реализации этого способа предусматривается наличие оператора. В соответствии с описанием определение числа источников шумоизлучения может происходить либо на основе разработанных алгоритмов, либо оператором на основе визуальной оценки вида автокорреляционной функции и имеющегося опыта работы. Это означает, что скорость обнаружения сигнала будет малой, а габариты системы большими.
Таким образом, этот способ имеет ряд существенных ограничений, что затрудняет или делает невозможным его применение во встраиваемых системах реального времени, предназначенных для обработки высокоскоростных сигналов, принимаемых из среды с большим уровнем шумом.
Тем не менее, рациональным зерном в этом способе по сравнению с прототипом [US 5469403А. Digitalsonarsystem. Youngetal. 21.11.1995] является использование алгоритмов анализа формы корреляционных функций. При этом способ ее построения не принципиален.
Предлагаемый способ существенным образом отличается в части использования метода фиксации наличия сигнала известной формы от известных решений.
Этот способ использует универсальный подход к анализу формы корреляционной функции. Существенным отличием предлагаемого метода от прототипа и аналогов является использование феномена подобия эталонной корреляционных функции и динамически формируемой функции по потоку поступающих дискретных данных.
Феномен подобия корреляционных функций обнаружен в ходе большого количества имитационных экспериментов, выполненных при исследовании алгоритмов ЦОС. Для использования этого феномена предлагается новый способ количественного измерения меры подобия дискретных функций, базирующийся на векторном описании сравниваемых корреляционных функций. Такой способ количественной степени оценки подобия двух функций далее будем называть векторно-косинусной мерой подобия. Для ее обозначения далее будем использовать символьное обозначение Lcos.
Так как предлагаемый подход является новым даже в теоретическом плане, детально рассмотрим его особенности.
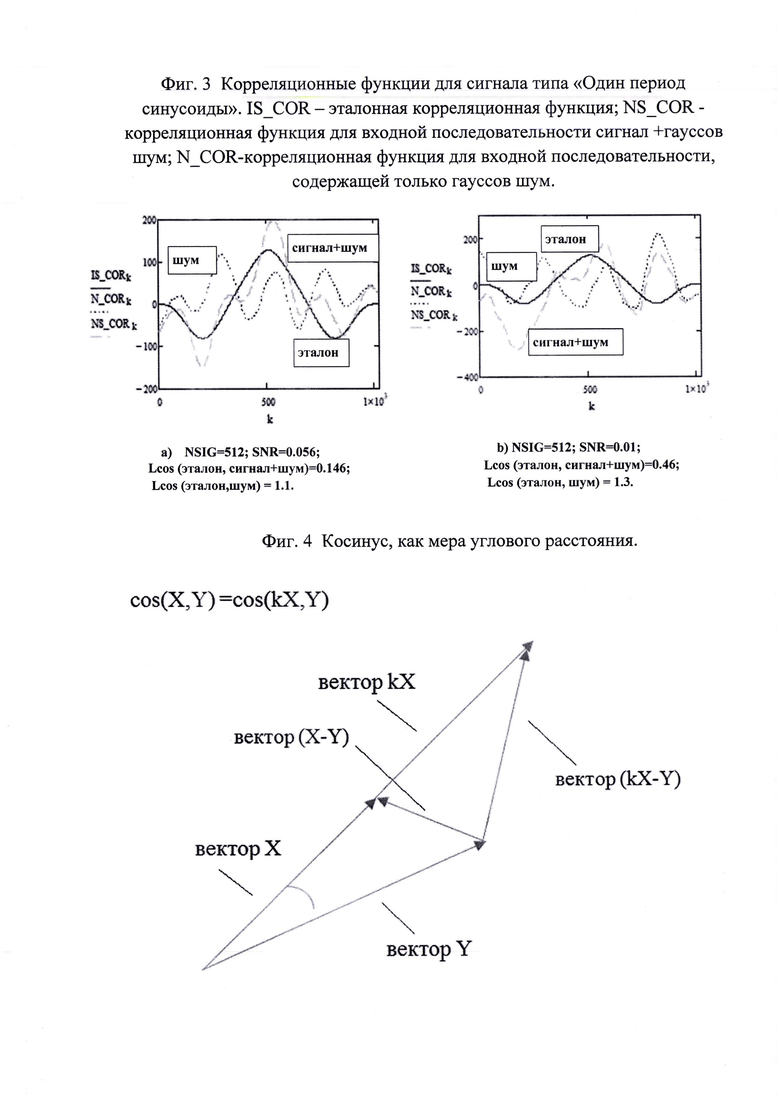
На фиг. 1 представлена эталонная корреляционная функции для сигнала типа «Один период синусоиды». При расчете эталона к сигналу не добавляется гауссов шум, т.е. сигнал передается по идеальному каналу.
Визуально видно, что формы эталонной корреляционной функций и корреляционной функции для сигнала с добавленным гауссовым шумом подобны. При этом форма корреляционной функции для чистого гауссового шума больше отличается от эталона.
При введении меры подобия и обоснования его следует учитывать, что речь идет об обработке случайного процесса. На фиг. 3 a, b представлены корреляционные функции для одной реализации гауссового шума. При этом для каждого из графиков реализации отличались. Этот вопрос будет рассмотрен после описания количественного способа измерения подобия двух дискретных функций.
Зондирующий сигнал, гауссов шум и корреляционные функции описываются конечным набором значений. Это позволяет интерпретировать каждый из таких наборов как вектор. Описание алгоритмов обработки с использованием такой интерпретации универсально, так как в явном виде не привязано к виду конкретной функции.
Суть предлагаемого подхода заключается в использовании векторного представления для сравниваемых функций и использования в качестве меры подобия косинуса угла между этими векторами.
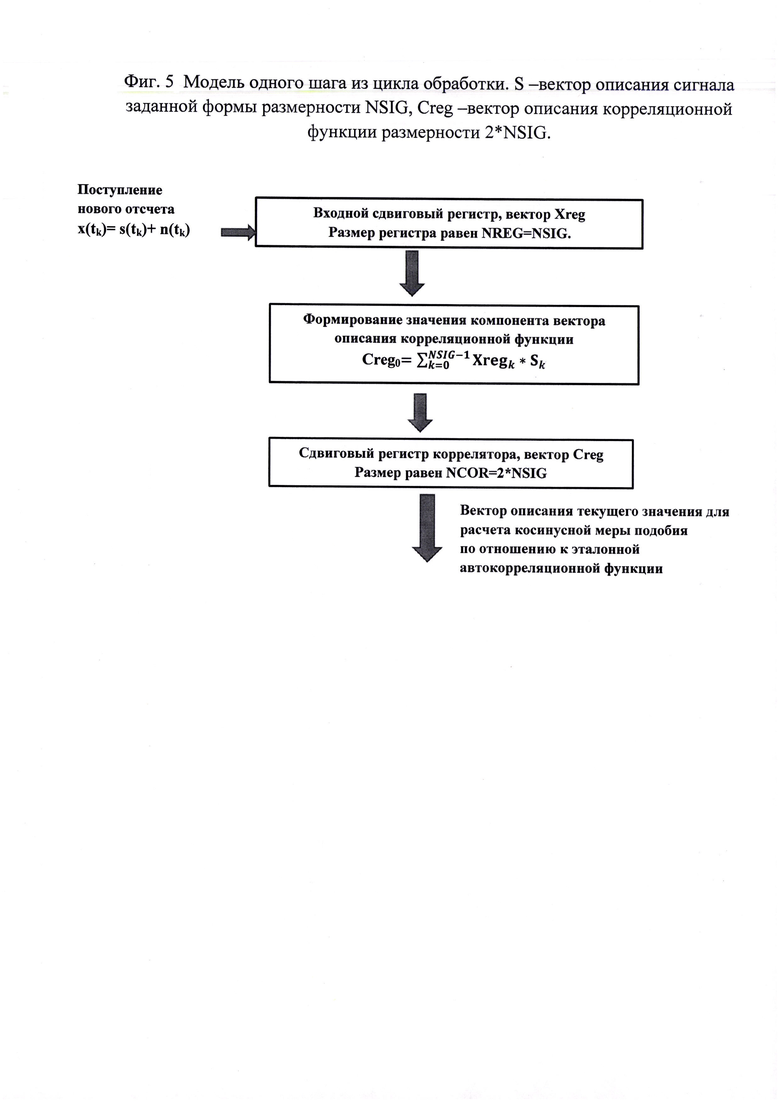
Косинус угла между двумя векторами [Беллман Р. Введение в теорию матриц. М. Наука - 1969, с. 37] представляет собой скалярное произведение нормированных векторов. Косинус имеет качественное отличие от классического понятия нормы. Это отличие иллюстрируется фиг. 4.
При использовании классической нормы расстояние между парой векторов X и Y и парой kX и Y разные. При использовании же косинуса в качестве меры эти пары векторов не различаются, так как его значение не чувствительно к масштабированию вектора.
В линейной алгебре для двух N-мерных векторов X и Y скалярное произведение стандартно определяется [Беллман Р. Введение в теорию матриц. М. Наука - 1969, с. 36] в виде:

Косинус угла между векторами в N-мерном пространстве определяется через скалярное векторов, нормированных к 1
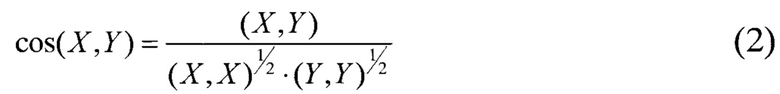
Возможность такого подхода вытекает из неравенства Коши-Буняковского, так как значение (2) находится в диапазоне [-1, +1]. Косинус угла между двумя нормированными векторами X и Y равен 1, когда Х=mY для любого m>0.
Для введения меры подобия двух дискретных функций, представленных наборами дискретных значений размерностями N, представим их в виде двух N мерных векторов Х и Y. При этом предполагаем, что компоненты векторов X(tk) и Y(tk) соответствуют одним и тем же номерам временных отсчетов k. Как правило, временной интервал между двумя отсчетами постоянен и равен шагу дискретизации.
В этом случае (2) является удобной количественно оценкой меры подобия функций. В простейшем случае умножение на множитель m всех компонент вектора Y не влияет на значение косинуса угла между ними:
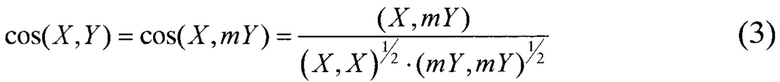
Полное подобие функций соответствует значению косинуса равному 1, и это значение представляется целесообразным взять в качестве точки отсчета. В этом случае количественная оценка меры подобия принимает выражение

где cos(X, Y) определен в соответствии с (1).
Соответственно, чем ближе к нулю значение Lcos, тем больше подобие функций. Кроме этого, мера подобия Lcos естественным способом нормирована, так как ее значения лежат в диапазоне [0, 2] и не зависят от размерности векторов N. Применительно к цифровой обработке сигналов размерность векторов N равна количеству используемых отсчетов NSIG на представление сигнала. Это позволяет количественным образом сравнивать варианты реализации устройств по этому параметру.
За счет введения порога EPS случаи наличия и отсутствия сигнала заданной формы в обрабатываемом входном потоке разделяются по правилу:
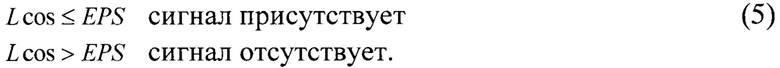
Формулы (1)-(5) описывают алгоритм функционирования векторно-косинусного детектора.
Универсальность и практичность использования векторно-косинусной меры подобия в системах ЦОС, обеспечивается использованием табличного способа представления набора детектируемых сигналов и эталонных корреляционных функции для них. В этом случае описание представляется в виде набора численных значений, которые хранятся в энергонезависимой памяти устройства ЦОС.
Возможны разные варианты реализации детектора такого типа. Приводимые далее иллюстрации работоспособности предлагаемого способа используют традиционный подход.
С целью облегчения интерпретации иллюстрирующих примеров на фиг. 5 приведена блок-схема алгоритма формирования вектора текущего описания корреляционной функции.
Алгоритм описан в стандартных терминах цифровой схемотехники. Для расчета вектора описания корреляционной функции используется два сдвиговых регистра:
Xreg - регистр для хранения дискретных значений входного потока;
Creg - регистр для хранения значений корреляционной функции
Предполагается, что форма сигнала известна, и он описывается конечным числом отсчетов NSIG. Устройство обработки принимает и сохраняет каждый новый отсчет во входном сдвиговом регистре. Регистр имеет размер, равный количеству отсчетов, используемых для описания детектируемого сигнала известной формы NREG=NSIG. При записи нового значения, ранее полученные отсчеты, сдвигаются.
Текущее содержание входного сдвигового регистра описывается вектором Xreg. Этот вектор, используется для обновления содержания сдвигового регистра коррелятора. Размер сдвигового регистра коррелятора равен удвоенному значению количества отсчетов, используемых для описания детектируемого сигнала NCOR=2NSIG.
При обработке очередного отсчета используется вектор Xreg. Для этого осуществляется свертка (скалярное произведение) вектора Xreg c вектором описания детектируемого сигнала:

где S - вектор описания детектируемого в потоке сигнала;
Xreg - вектор описания обрабатываемого фрагмента входного потока.
Это значение поступает на вход сдвигового регистра коррелятора Creg. Имеющиеся значения сдвигаются на одну позицию. На освободившееся место записывается значения Creg0. Сформированный таким образом вектор описания текущего состояния корреляционной функции далее используется для расчета меры подобия Lcos по формуле (3).
Использование удвоенной размерности сдвигового регистра коррелятора по отношению к размерности детектируемого сигнала позволяет описывать полный цикл прохождения сигнала от поступления первого отсчета на устройство обработки до ухода последнего.
Возможность реализации векторно-косинусного порогового детектора с алгоритмом (5), реализованного с использованием определений (1)-(4) иллюстрируется значениями Lcos с фиг. 1-3. Существенная разница значений Lcos при сравнении с эталоном векторов описания корреляционных функций при наличии или отсутствии сигнала позволяет уверенно разделить случаи наличия и отсутствия сигнала.
Как уже отмечалось выше, приведенные результаты относятся к однократной реализации гауссового шума. Для обоснования работоспособности алгоритмов обработки сигналов, передаваемых по каналу с шумами, особенно с большим уровнем шума, следует использовать ансамбли реализаций.
В идеале требуется получить функциональные зависимости для вероятности р(Н1) обнаружения сигнала при его наличии в потоке и вероятности р(Н0) ложного обнаружения сигнала при его отсутствии при разных параметрах реализации.
С учетом ориентации на универсальность способа требуется использовать предположение о форме сигнала и иметь в качестве параметра количество используемых отсчетов на сигнал NSIG и значение отношения сигнал/шум SNR. При этом важным обстоятельством, существенно усложняющим задачу, является, тот факт, что мера подобия является случайной величиной. В такой постановке получить решение в аналитическом виде на нынешнем уровне развития математики не представляется реалистичным [Рудько И.М. Применение порядковых статистик в задачах обнаружения, УБС, 2012, выпуск 37, с. 63-83].
Представленные далее результаты расчетов в обоснование предлагаемого способа получены с помощью метода имитационного моделирования.
Такой подход имеет определенные ограничения с точки зрения общности получаемых результатов. Эти ограничения, тем не менее, обходятся, при выполнении параметрических исследований по набору варьируемых параметров. В принципе, это требует большого объема вычислений. Однако уровень развития современной вычислительной техники обеспечивает возможность проведения такого рода расчетов за разумное время.
Методика имитационного моделирования включает в себя следующие ключевые этапы. Ее ядром является разработка модели обработки. Эта модель используется для проведения имитационных экспериментов со статистически значимым набором реализаций обрабатываемого входного потока. При этом фиксируются значения параметров модели, например, количество отсчетов NSIG, отношения сигнал/шум SNR, величина порога EPS.
На этапе первичной обработки статистическими методами оцениваются анализируемые значения, например, вероятность р(Н1) или вероятность р(Н0). Требуемые функциональные зависимости получаются в табличном виде, путем параметрического исследования по каждому из интересующих параметров. Полученные таблицы позволяют анализировать интересующие функциональные зависимости.
Модель формирования дискретного входного потока, которая использована для имитационного моделирования, базируется на предположениях:
- детектирующее устройство производит непрерывное прослушивание канала;
- осуществляется аналого-цифровое преобразование с фиксированным шагом дискретизации;
- обеспечивается точность аналого-цифрового преобразования, позволяющая пренебречь ошибками дискретизации;
- входной сигнал имеет конечную протяженность и для его описания достаточно конечного числа отсчетов.
Общая схема реализации одного цикла обработки входного потока при наличии в нем сигнала заданной формы заключается в использовании вектора описания зондирующего сигнала и суммировании его с вектором реализации гауссового шума. Для каждого цикла используется новая реализация гауссового шума.
Параметры шума фиксированы и определяют соотношение сигнал/шум (SNR). С теоретической точки зрения оценка SNR зависит от назначения системы ЦОС [Сергиенко А.Б. Цифровая связь. СПб. СПбГЭТУ «ЛЭТИ», 2012. с. 8].
Для оценки SNR в приведенных ниже результатах имитационного моделирования использовалось относительное значение:

где РСИГ - мощность сигнала;
РШУМ - мощность шума;
А - амплитуда синусоидального сигнала;
sigma - дисперсия гауссового шума.
Для сигнала в виде двух синусоид (см фиг. 2) соотношение (7) было модифицировано в части учета вклада каждой гармоники в мощность сигнала. В этом случае использовались равные по амплитуде сигналы А=0.7 и вклад каждой гармоники в РСИГ имел вес 0.5.
Формируемый на каждом шаге вектор описания корреляционной функции в соответствии с алгоритмом с фиг. 5 используется для расчета меры подобия Lcos c эталонной корреляционной функцией.
Полученное значение сохраняется, как элемент формируемого массива промежуточных результатов. Количество элементов такого массива представляет собой назначаемый параметр, определяющий количество реализаций. В зависимости от целей конкретного имитационного эксперимента эта схема может дополняться. Например, при расчете вероятностей р(Н1) и р(Н0) в нее добавляется модель векторно-косинусного детектора, а входной поток формируется с наличием или без наличия в нем сигнала заданной формы.
Полученные таким образом массивы промежуточных данных статистически обрабатываются в соответствии с целями эксперимента.
Приведенные ниже иллюстрирующие примеры используют количество реализаций NTRY=2000. Это связано с необходимостью обеспечить должный уровень точности при оценке вероятности реализации гипотезы р(Н0).
На этапе разработки предлагаемого способа был выполнен большой объем параметрических исследований для разных типов сигналов и параметров реализации корреляционной обработки. Эффект подобия корреляционных функций, лежащий в основе предлагаемого метода, и был выявлен на предварительном этапе.
Метод исследовался на широком спектре сигналов и параметрах реализации и продемонстрировал свою работоспособность применительно к обработке сигналов, передаваемых по каналам с большим уровнем шума.
Для иллюстрации работоспособности предлагаемого метода использовалось два типа сигналов, которые часто используются на практике. Например, возможность использования предлагаемого метода, требует демонстрации его работоспособности при наличии доплеровского эффекта. Соответственно, для иллюстрации использовались сигналы типа «Пакет синусоид» и «Пакет синусоид с линейной модуляцией частоты». Конкретные реализации этих сигналов и эталонные корреляционные для них представлены на фиг. 6.
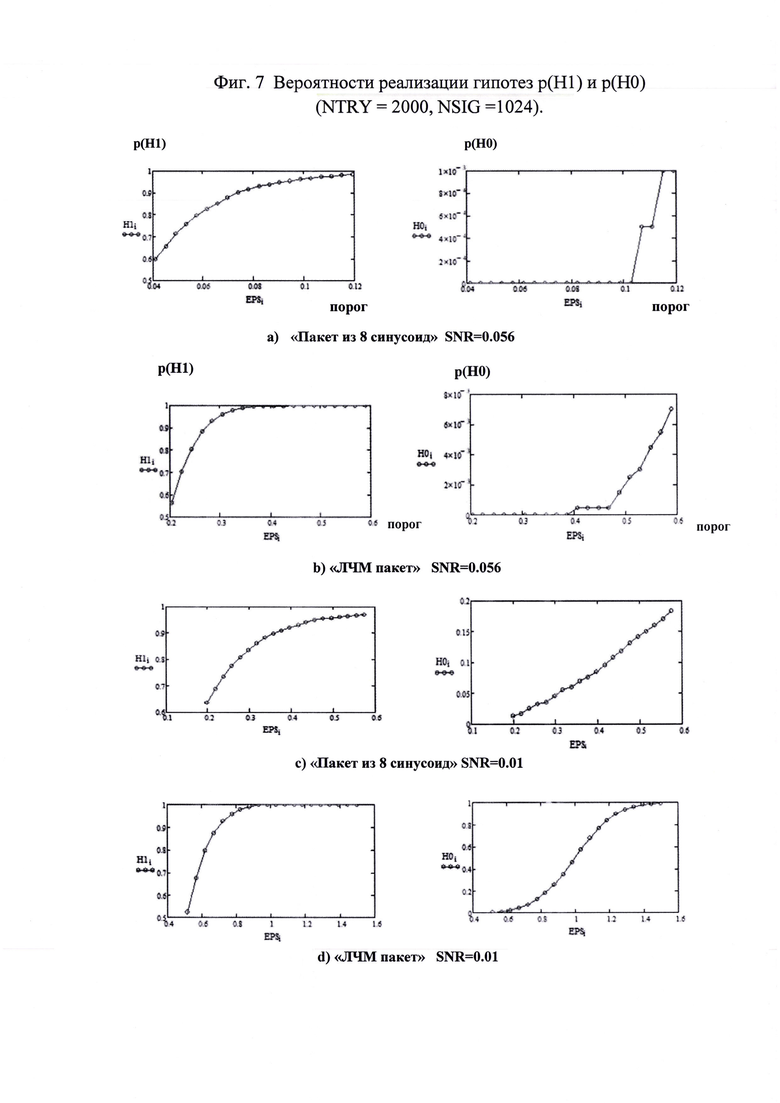
С практической точки зрения основными характеристиками приемных трактов, обрабатывающих зашумленные сигналы являются вероятности реализации гипотез р(Н1) и р(Н0). Метод имитационного моделирования позволяет получить количественные оценки влияния порога EPS в зависимости от количества отсчетов на сигнал и уровня шума.
Для получения количественных оценок для вероятностей р(Н1) и р(Н0) на первом этапе получены оценки параметров векторно-косинусной меры подобия, трактуемой как случайная величина. Для каждого типа сигнала и параметров шума проводился имитационный эксперимент, и формировались массивы данных для значений Lcos при наличии и отсутствии сигнала в NTRY реализаций входного потока.
Эти массивы использовались для статистической оценки параметров Lcos, трактуемой как случайная величина. Полученные результаты приведены в табл. 1.
При интерпретации этих данных следует иметь ввиду, что в табл. 1 в колонках muS и muNS приведены данные для математического ожидания для Lcos при наличии сигнала в потоке и его отсутствии. Существенная разница в этих значениях и позволяет использовать векторно-косинусную меру подобия для реализации детекторов сигналов заданной формы. Кроме этого, следует обратить внимание на разницу значений для среднеквадратичных отклонений для разных типов сигналов.
Следует также учитывать особенности определения меры подобия с использованием (4).
Значение Lcos=l при сравнении эталонной корреляционной функции и корреляционной функцией для чистого гауссового шума с mu=0 означает, что косинус угла между соответствующими векторами равен 0. В теории обработки сигналов [Сергиенко А.Б. Цифровая связь. СПб. СПбГЭТУ «ЛЭТИ», 2012. с. 22] вклад в корреляционную функцию шумовой составляющей в виде гауссового шума с mu=0 должен быть равен 0.
Таким образом, приведенные в табл. 1 данные для muNS косвенным образом дают оценку точности для приведенных ниже результатов моделирования.
На фиг. 7 приведен пример сравнительной количественной оценки влияния величины порога на вероятности обнаружения и пропуска сигнала при разных уровнях шума. Эти данные иллюстрируют возможность, как выбора типа сигнала, так и оптимизации параметров устройств ЦОС на основе векторно-косинусного порогового детектора.
Для получения функциональных зависимостей, использовалась модель мульти порогового детектора. В качестве минимального значения порога принималось величина EPS=muS из табл. 1, своя для каждого типа сигнала и значения SNR. Массив значений порогов имел размерность 20, а шаг формирования массива порогов принимался равным 0.1
Оценка эффективности предлагаемого метода осуществлялась методом имитационного моделирования для двух типов пороговых детекторов: стандартной модели амплитудного детектора и модели векторно-косинусного детектора.
Модифицированная модель амплитудного детектора использует в качестве меры абсолютное значение разницы максимума эталонной корреляционной функции и максимума корреляционной функции для детектируемого сигнала с добавленным гауссовым шумом. Далее эта мера будет обозначаться как Rabs. Соответственно, для обозначения меры для векторно-косинусного детектора используется обозначение Lcos.
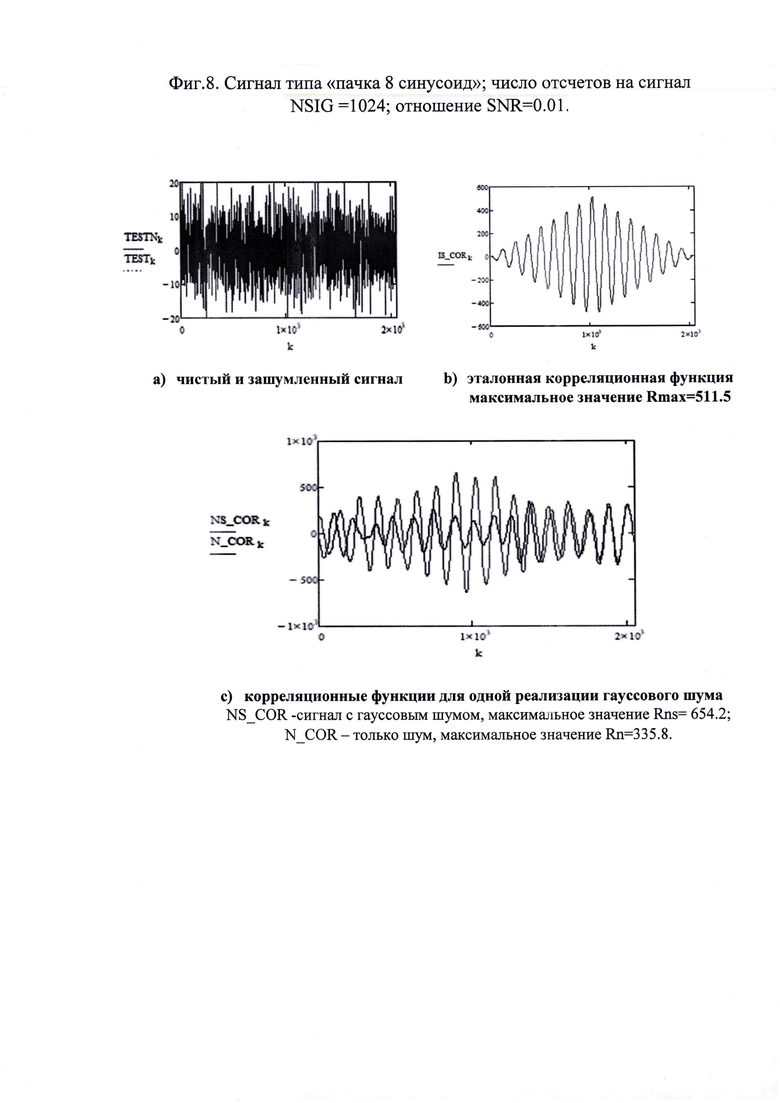
Сравнение проводилось для часто используемого на практике типа сигнала «пачка из 8 синусоид» для канала с гауссовым шумом, дающего соотношение SNR=0.01.
Виды сигналов и эталонные корреляционные функции для числа отсчетов на сигнал NSIG=1024 приведены на фиг. 8. Эти зависимости демонстрируют целесообразность модификации модели амплитудного детектора по сравнению с патентом [US 5469403 A Digitalsonarsystem. Youngetal. 21.11.1995].
В частности, как следует из фиг. 11 значение максимума для эталонной корреляционной функции 511.5 существенно меньше максимума для корреляционной функции для сигнала с шумом 654. При этом максимальное значение для корреляционной функции для чистого гауссового шума в этом случае равен 335.8. Важно подчеркнуть, что эти значения соответствуют одной реализации гауссового шума. Приведенные далее численные значения соответствуют модифицированной модели амплитудного детектора, использующего абсолютное значение для разницы максимумов корреляционных функций.
Оценки для математического ожидания и среднеквадратичного отклонения производились по результатам, полученным в результате имитационного моделирования для двух типов детекторов и разного количества отсчетов на сигнал.
В каждом из экспериментов использовалось по 1000 реализаций. Параметры гауссового шума назначались таким образом, чтобы соотношение SNR=0.01. Статические оценки приведены в таблице 2.
Для содержательной интерпретации данных, приведенные в этой таблице, требуются пояснения.
Для амплитудного детектора максимальное значение Rmax для эталонной корреляционной функции практически линейно зависит от количества отсчетов. Для амплитудного детектора желательно, чтобы оценка математического ожидания для abs(Rns - Rmax) была как можно ближе к нулю.
В таблице 2 приведены оценки как в абсолютных значениях, так и в относительных с нормированием к Rmax. Относительные значения приведены в скобках. С увеличением числа отсчетов относительные оценки для математических ожиданий для случаев наличия сигнала во входном потоке и его отсутствии степень выполнения этих критериев улучшается.
Отметим, что векторно-косинусная мера подобия по определению масштабирована.
Приведенные данные позволяют в первом приближении оценить функциональные свойства этих двух типов детекторов. Пороговый детектор должен обеспечить разделение случаев наличия и отсутствия сигнала в обрабатываемом входном потоке. Как следует из приведенных данных для амплитудного детектора разница относительных значений для оценок математических ожиданий по сравнению с векторно-косинусным детектором существенно меньше.
Детальный анализ требует учета оценок для среднеквадратичных значений. Выполнить его аналитическими методами затруднительно, если это вообще возможно. Для сравнения использовалась методика имитационного моделирования. Для получения вероятностей фиксации сигнала р(Н1) и его пропуска р(Н0) были реализованы две модели пороговых детекторов. Одна для амплитудного детектора, а вторая для детектора на основе векторно-косинусной меры подобия.
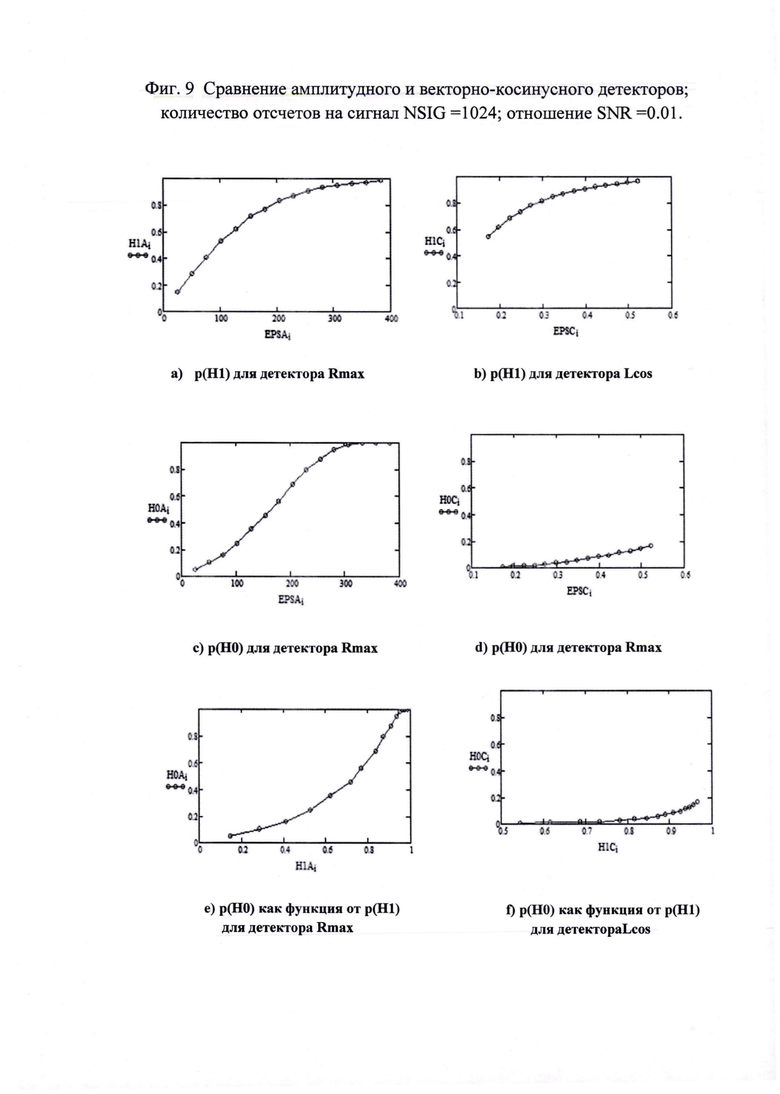
Значения оценок математических ожиданий использовались для получения зависимостей р(Н1) и р(Н0), как функций от значения порога. Эти зависимости получены путем имитационного моделирования для NSIG=1024 и приведены на фиг. 9.
При этом вектора значений порогов формируется на основе оценок математических ожиданий из таблицы 2. Важно понимать, что по логике работы значения порогов существенно отличаются друг от друга. Левый столбец графиков с фиг. 9 соответствует детектору Rmax, а правый - Lcos.
Преимущество использования детектора следует из сравнения графиков фиг. 9е) и f). Это графики зависимости вероятности ложного обнаружения сигнала р(Н0), как функции от вероятности p(H1) правильного обнаружения сигнала при его наличии.
Как следует из сравнения этих графиков, для векторно-косинусного детектора вероятность ложного обнаружения сигнала существенно ниже, чем для амплитудного детектора при одних и тех же значениях для вероятности р(Н1).
Это демонстрирует существенные преимущества его применения, по крайней мере, для обработки сигналов типа «пакет синусоид» с большим уровнем аддитивного гауссового шума.
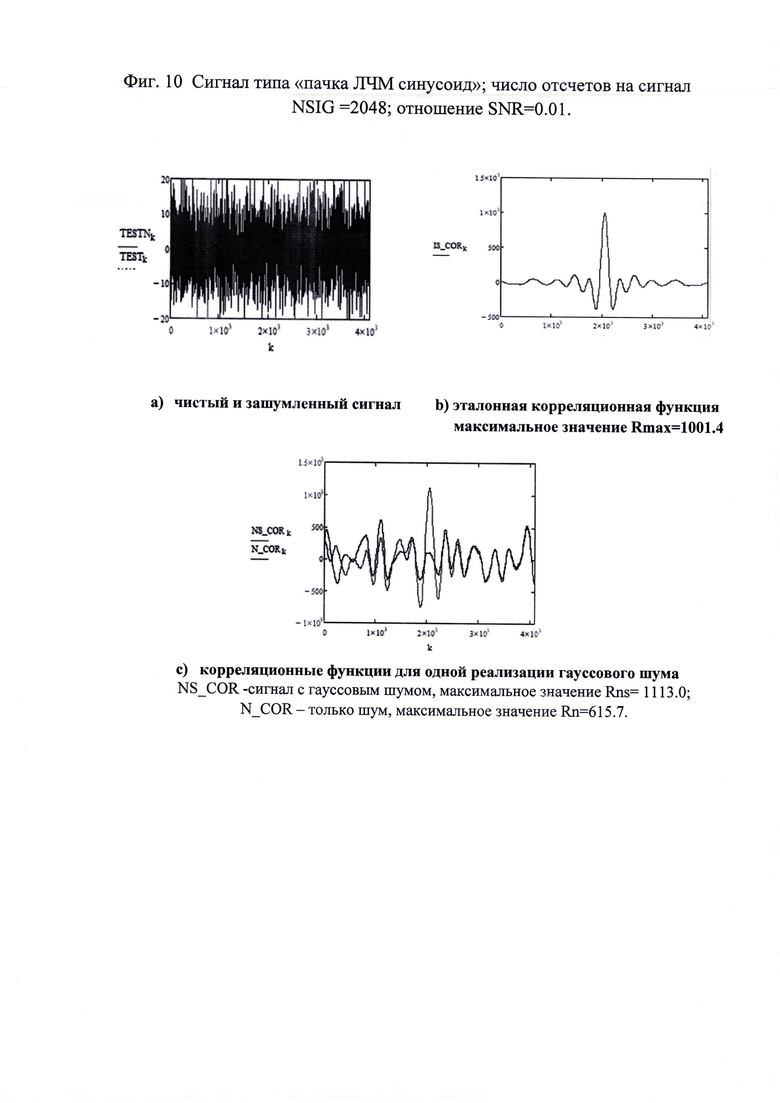
Пользуясь аналогичной методикой, выполним сравнение для другого, часто используемого типа сигнала, а именно, пакет синусоид с линейно модулированной частотой (пачка ЛЧМ синусоид).
На фиг. 10 представлены графики корреляционных функций для этого типа сигналов для числа отсчетов 2048. Следует иметь в виду, что эти графики соответствуют одной реализации гауссового шума. Эталонная корреляционная функция имеет своеобразную форму, которая существенно отличается от эталонной корреляционной функции для сигнала типа «пачка 8 синусоид» (см. фиг. 8b).
В таблице 3 содержатся статистические оценки для математических ожиданий и среднеквадратичных отклонений при использовании амплитудного и векторно-косинусного способов измерения. Для амплитудного способа в соответствующих столбцах в скобках приведены относительные значения разницы максимумов. В качестве нормирующего множителя использовалось максимальное значение эталонной корреляционной функции.
Как следует из данных для числа отсчетов на сигнал NSIG=512 амплитудный детектор будет неработоспособен, так как оценка математического ожидания для случаев наличия и отсутствия сигнала ведут себя с точностью до наоборот. Для работоспособного детектора требуется, чтобы эти значения для случая наличия сигнала были, по крайней мере меньше, чем для случая его отсутствия в потоке.
Для этого же числа отсчетов векторно-косинусный способ измерения дает приблизительно двух кратную разницу правильного знака. Это первый весомый аргумент в пользу использования детекторов на основе векторно-косинусной меры подобия. С практической точки зрения это означает возможность при прочих равных использования меньшего числа отсчетов на сигнал. А это существенным образом уменьшает требования к объемам памяти для бортового вычислителя.
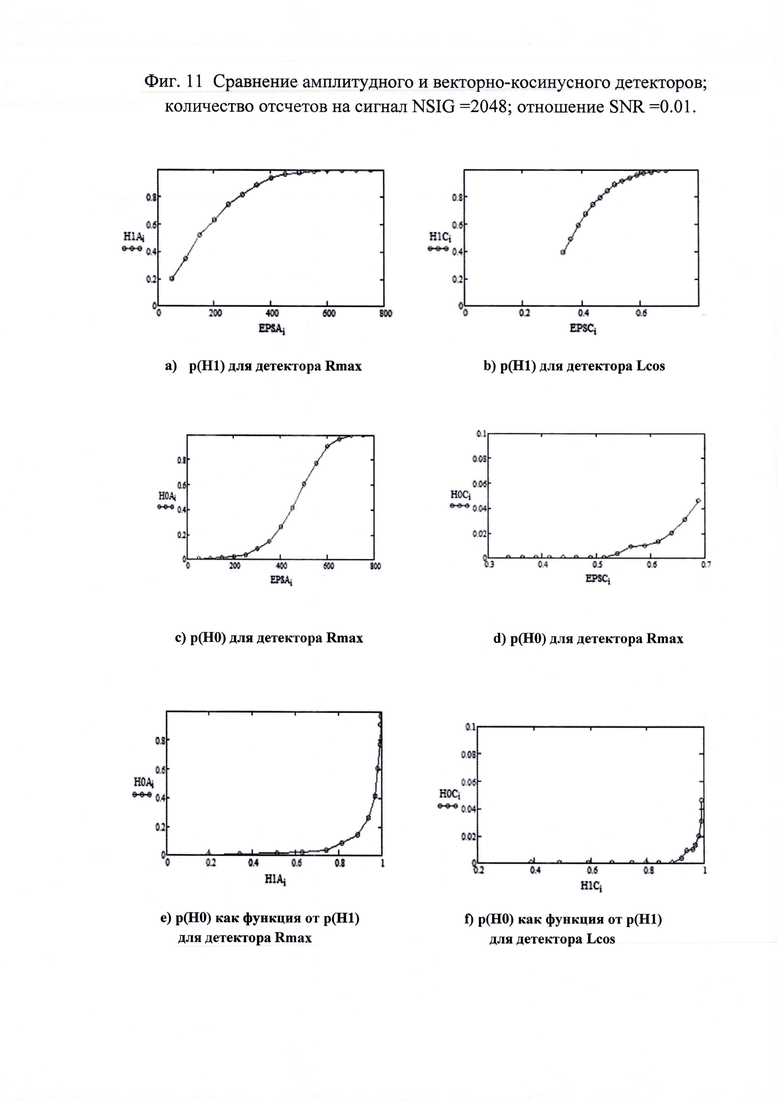
В силу этого обстоятельства для оценки вероятностей р(Н1) и р(Н0), которые требуются для получения более весомых аргументов при сравнении двух способов использовалось число отсчетов на сигнал NSIG=2048.
На фиг. 11 приведены оценки вероятностей р(Н1) и р(Н0), как функции от значения используемого порога (см. фиг. 11a)-d)). Следует заметить, что на фиг. 11d) и f) использованы разные масштабы, отличающиеся в 10 раз. Как следует из представленных данных, векторно-косинусный детектор, в принципе, обеспечивает большую вероятность для р(Н1) и меньшую для р(Н0).
Однако при этом возникает проблема сравнения по значению порогов, так как используются разные меры. Решающим аргументом в преимущества использования векторно-косинусного детектора является сравнение графиков с фиг. 11 е) и f). Как следует из сравнения этих графиков, вероятность ложного обнаружения р(Н0) при заданной вероятности детектирования сигнала р(Н1) для векторно-косинусного детектора существенно ниже.
Анализ этих данных показывает перспективность использования представленного способа для реализации детекторов наличия сигналов заданной формы для каналов с большим уровнем шумов. В частности, для уровня шума SNR=0.056 для ЛЧМ сигнала и порога уровня 0.4 вероятность реализации гипотезы р(Н0) имеет значение масштаба 0.001, в то время, как р(Н1) приближается к 1. Уточнение этих данных, естественно, возможно и требует увеличение числа реализаций приблизительно на порядок.
Это не является критической проблемой, так как такого рода расчеты выполняются на этапе разработки системы ЦОС, когда могут быть применяться высокопроизводительные вычислительные средства.
На фиг. 12 представлена структурно-функциональная схема устройства, реализующая предлагаемый способ для обнаружения одного вида сигнала.
Устройство содержит
1. блок формирования входного потока цифровых данных;
2. блок расчета текущего вектора описания корреляционной функции;
3. блок выдачи векторов описания эталонной корреляционной функции;
4. блок пороговых детекторов на базе векторно-косинусной меры подобия;
5. блок фиксации и обработки по целевому назначению;
6. блок управления и синхронизации.
Это устройство реализует предлагаемый способ следующим образом.
Входной сигнал поступает из приемного тракта на блок 1 формирования входного потока цифровых данных. Этот блок включает АЦП и формирует поток цифровых данных с назначенным периодом дискретизации. Эти данные по мере формирования поступают на блок 2 формирования вектора описания корреляционной функции.
Блок 2 формирования текущего вектора описания корреляционной функции обеспечивает реализацию структурно-функциональной схемы с рис. 5. С блока 2 вектор описания текущего значения корреляционной функции передается на блок 4 пороговых детекторов.
Блок 4 представляет собой набор пороговых детекторов на основе векторно-косинусной меры подобия. Каждый из детекторов этого блока обеспечивает обработку входного потока с использованием собственного вектора описания идеальной корреляционной функции и порога для разделения случаев наличия и отсутствия сигнала для каждого из сигналов из используемого набора. Вектора описаний и пороги для каждого из типов детектируемых сигналов передаются в блок 2 либо на этапе инициализации устройства, либо в режиме реального времени по командам с блока 6 управления и синхронизации.
Результат обработки в виде двоичного числа (сигнал обнаружен/сигнал не обнаружен) для каждого типа сигнала передается на блок 5 фиксации и обработки по целевому назначению.
Блок 6 управления и синхронизации осуществляет управление и выработку сигналов для временной синхронизации работы блоков устройства. В частности, блок управления 6 осуществляет передачу вектора описания эталонной корреляционной функции либо на этапе инициализации устройства, либо в режиме реального времени.
Устройство, представленное на фиг. 12, может быть реализовано с использованием современных микроконтроллеров, программируемой логики или на основе комбинированных решений.
Как показал выполненный в [Астапкович A.M., Матвеев Д.П. Микроконтроллерные платформы «Миландр» и «Мультикор». Компоненты и технологии, №4, 2020, с. 10-17] анализ современные микроконтроллеры второго поколения фактически перешли на использование многоядерных 32 битных архитектур с большими объемами оперативной памяти.
При этом сами ядра имеют смешанную структуру, включающую микропроцессорное ядро и несколько DSP модулей с возможностью быстрого выполнения операций умножения с данными, представляемыми в формате с плавающей запятой. Кроме этого существенно возросли возможности периферийных модулей АЦП по разрядности.
Устройство обеспечивает возможность детектирования наличия во входном потоке набора сигналов заданной формы. При этом важно, что предлагаемый способ базируется на использовании универсального способа описания набора сигналов, что обеспечивает возможность использования унифицированных аппаратных решений.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ И УСТРОЙСТВО ОБНАРУЖЕНИЯ СЛОЖНЫХ ШИРОКОПОЛОСНЫХ ЧАСТОТНО-МОДУЛИРОВАННЫХ СИГНАЛОВ С ФИЛЬТРАЦИЕЙ В МАСШТАБНО-ВРЕМЕННОЙ ОБЛАСТИ | 2004 |
|
RU2282209C1 |
| СПОСОБ ОБРАБОТКИ СИГНАЛОВ С ИСПОЛЬЗОВАНИЕМ АЛГОРИТМА СИГМА-ТОЧЕЧНОГО ФИЛЬТРА КАЛМАНА | 2024 |
|
RU2840100C1 |
| СПОСОБ И УСТРОЙСТВО ПЕРЕДАЧИ ДИСКРЕТНОЙ ИНФОРМАЦИИ ДЛЯ БЫСТРОДВИЖУЩИХСЯ ОБЪЕКТОВ | 2017 |
|
RU2658649C1 |
| СПОСОБ ОБРАБОТКИ СИГНАЛОВ | 2022 |
|
RU2801897C1 |
| Способ вибродиагностики технического состояния газотурбинных двигателей на ресурсосберегающих режимах с применением теории инвариантов | 2020 |
|
RU2754479C1 |
| Способ спектрально-корреляционного обнаружения летательных аппаратов по квазинепрерывным импульсным сигналам бортовых радиоэлектронных систем | 2021 |
|
RU2768370C1 |
| Способ вибродиагностики технического состояния газотурбинных двигателей на ресурсосберегающих режимах с применением теории инвариантов | 2020 |
|
RU2754476C1 |
| СПОСОБ ОЦЕНКИ ОТНОШЕНИЯ СИГНАЛ/ШУМ В УСТРОЙСТВАХ БЕСПРОВОДНОЙ СВЯЗИ | 2023 |
|
RU2809969C1 |
| СПОСОБ ОБРАБОТКИ ГИДРОАКУСТИЧЕСКИХ ШУМОПОДОБНЫХ ФАЗОМАНИПУЛИРОВАННЫХ СИГНАЛОВ | 2014 |
|
RU2552534C1 |
| Способ обработки сигналов с гиперболической частотной модуляцией | 2018 |
|
RU2711420C1 |


Изобретение относится к области радиоэлектроники и гидроакустики, а именно к способам обнаружения и определения соответствия сигнала известной формы при наличии помех высокой интенсивности в канале передачи. Техническим результатом изобретения является увеличение вероятности правильного обнаружения и одновременное уменьшение вероятности ложного обнаружения сигнала при малых значениях соотношения сигнал-шум в канале передачи. Способ обнаружения сигналов известной формы на основе векторно-косинусной меры подобия заключается в приеме смеси сигнала известной формы с шумом, ее аналогово-цифровом преобразовании, в расчете текущего значения корреляционной функции, в сравнении ее с эталонной корреляционной функцией, в формировании меры подобия текущего вектора описания корреляционной функции и эталонной корреляционной функции и принятии решения о наличии или отсутствии полезного сигнала путем сравнения меры подобия с заданным порогом, формировании из принятой смеси известного сигнала и шума векторного представления текущего состояния корреляционной функции. Мера подобия формируется с использованием косинуса угла между вектором текущего состояния корреляционной функции и вектором описания эталонной корреляционной функции. 12 ил.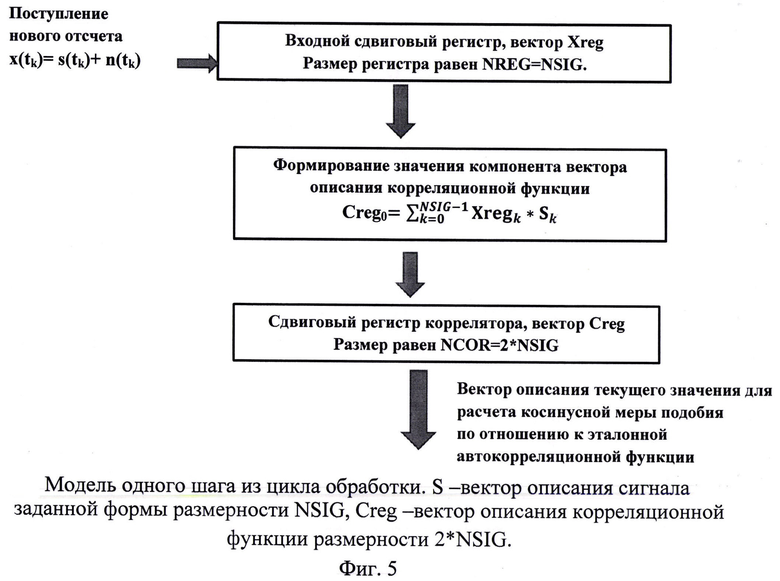
Способ обнаружения сигналов известной формы на основе векторно-косинусной меры подобия, заключающийся в приеме смеси сигнала известной формы с шумом, ее аналогово-цифровом преобразовании, в расчете текущего значения корреляционной функции, в сравнении ее с эталонной корреляционной функцией, в формировании меры подобия текущего вектора описания корреляционной функции и эталонной корреляционной функции и принятии решения о наличии или отсутствии полезного сигнала путем сравнения меры подобия с заданным порогом, отличающийся тем, что из принятой смеси известного сигнала и шума формируют векторное представление текущего состояния корреляционной функции, а мера подобия формируется с использованием косинуса угла между вектором текущего состояния корреляционной функции и вектором описания эталонной корреляционной функции.
| US 5469403 A1, 21.11.1995 | |||
| Коррелятор полезного сигнала с обнаружением и классификацией помех | 2019 |
|
RU2716027C1 |
| СПОСОБ КЛАССИФИКАЦИИ ШУМЯЩИХ ОБЪЕКТОВ | 2014 |
|
RU2570430C1 |
| СПОСОБ И УСТРОЙСТВО ДЛЯ ОПРЕДЕЛЕНИЯ НАЛИЧИЯ ЭТАЛОННОГО ОБРАЗЦА В ПРИНИМАЕМОМ СИГНАЛЕ, КОТОРЫЙ ВОЗМОЖНО МАРКИРОВАН ВОДЯНЫМ ЗНАКОМ | 2009 |
|
RU2482553C2 |
| Гидролокационный способ обнаружения объекта и измерения его параметров | 2017 |
|
RU2674552C1 |
| Cosine Similarity Definition URL: https://deepai.org/machine-learning-glossary-and-terms/cosine-similarity, Дата публик | |||
| Устройство для электрической сигнализации | 1918 |
|
SU16A1 |
| БУРДИНСКИЙ И.Н | |||
| Цифровая | |||
Авторы
Даты
2022-11-21—Публикация
2021-08-06—Подача